Cosmic Ray Anisotropy and Spectra as Probes for Nearby Sources
Abstract
:1. Introduction
2. Model and Methods
2.1. Spatially Dependent Diffusion
2.2. Background Sources
2.3. Nearby Source
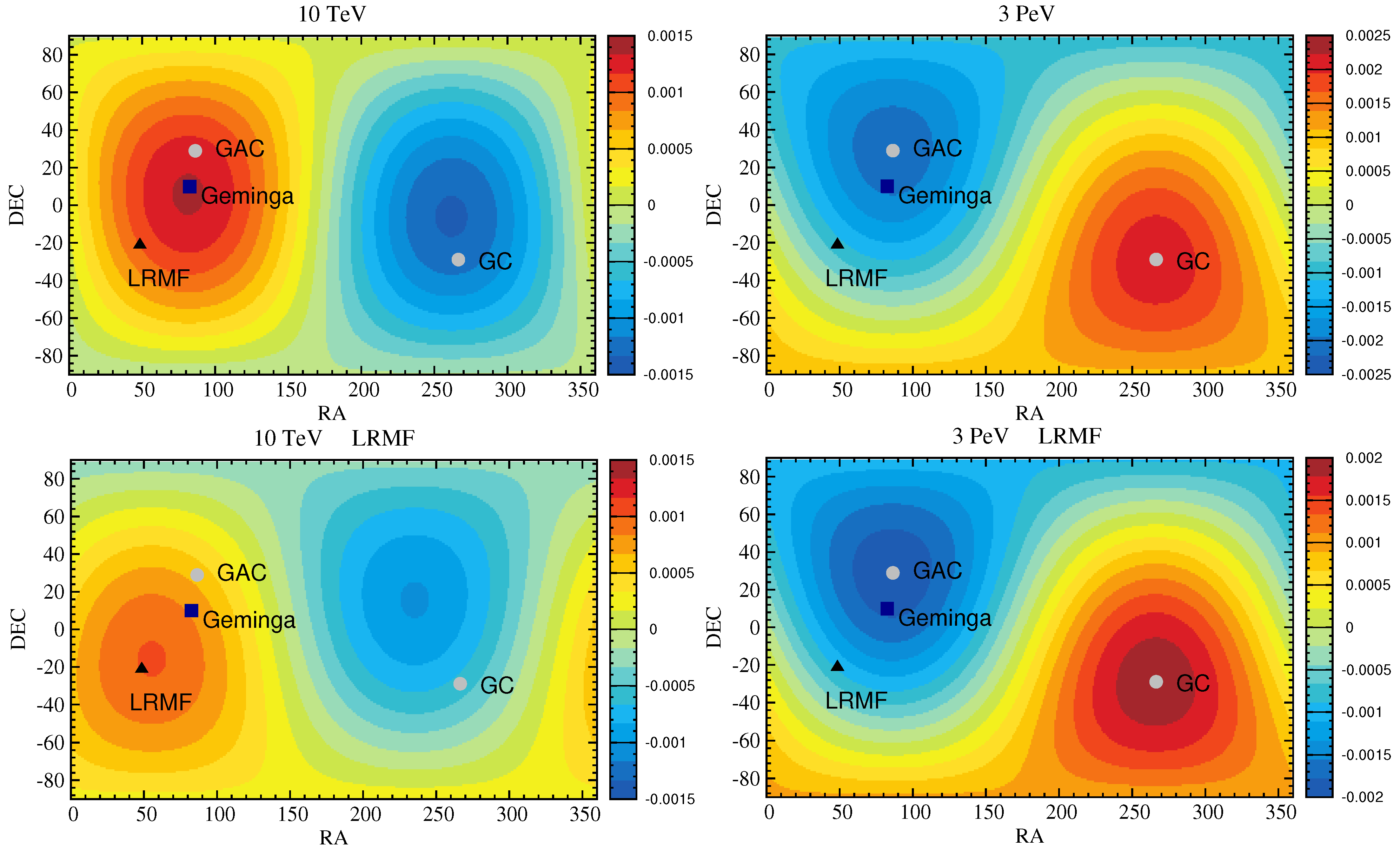
2.4. Anisotropic Diffusion and Large-Scale Anisotropy
3. Results and Discussion
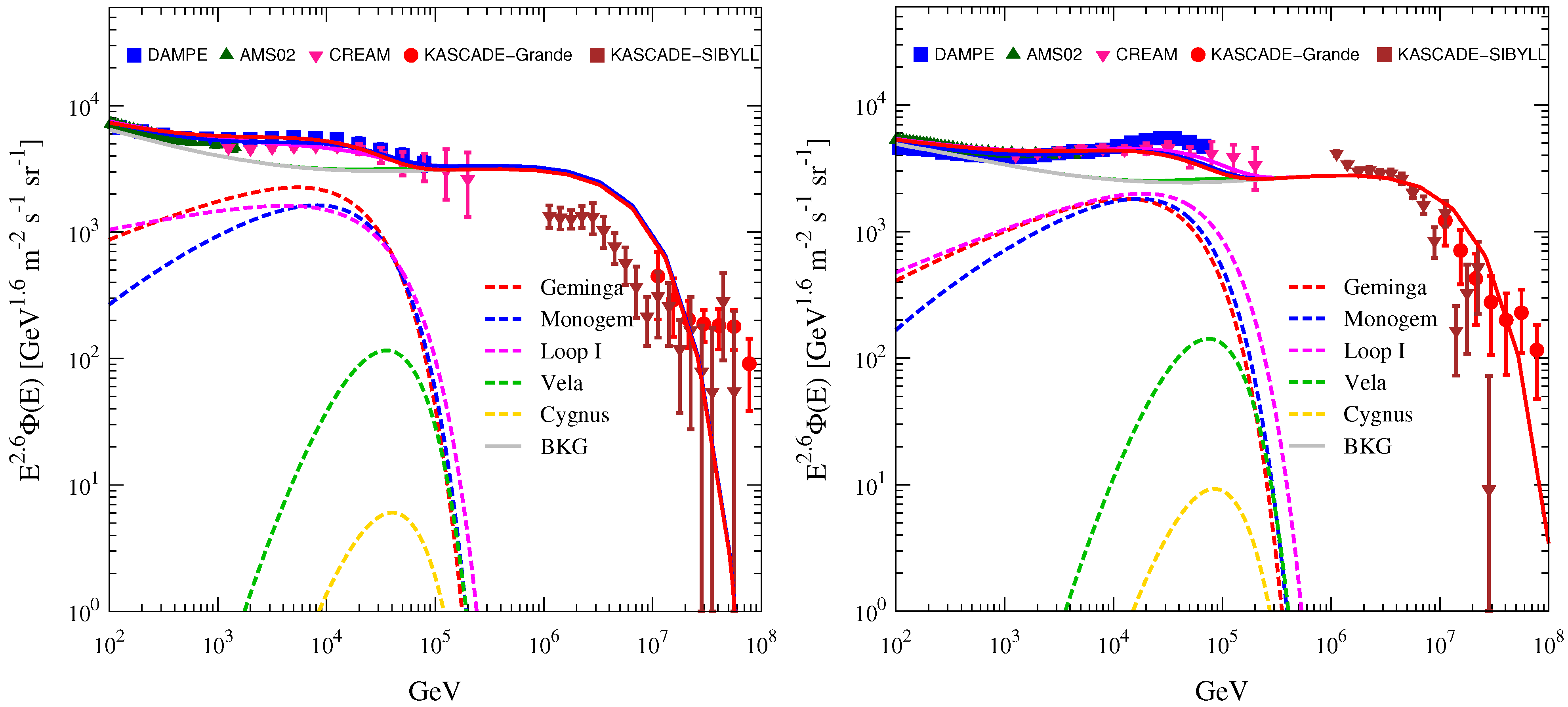
3.1. Proton and Helium Spectra of Five Nearby Sources
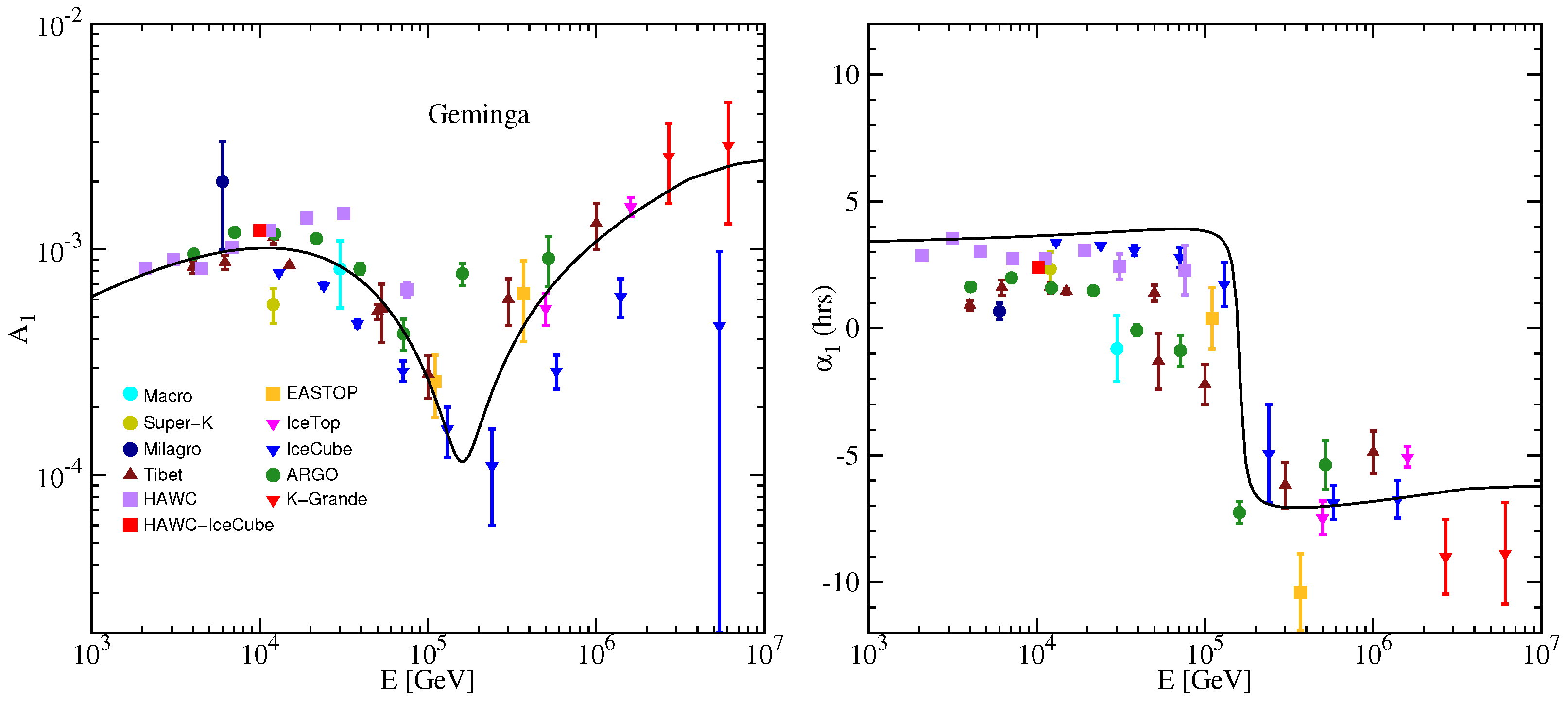
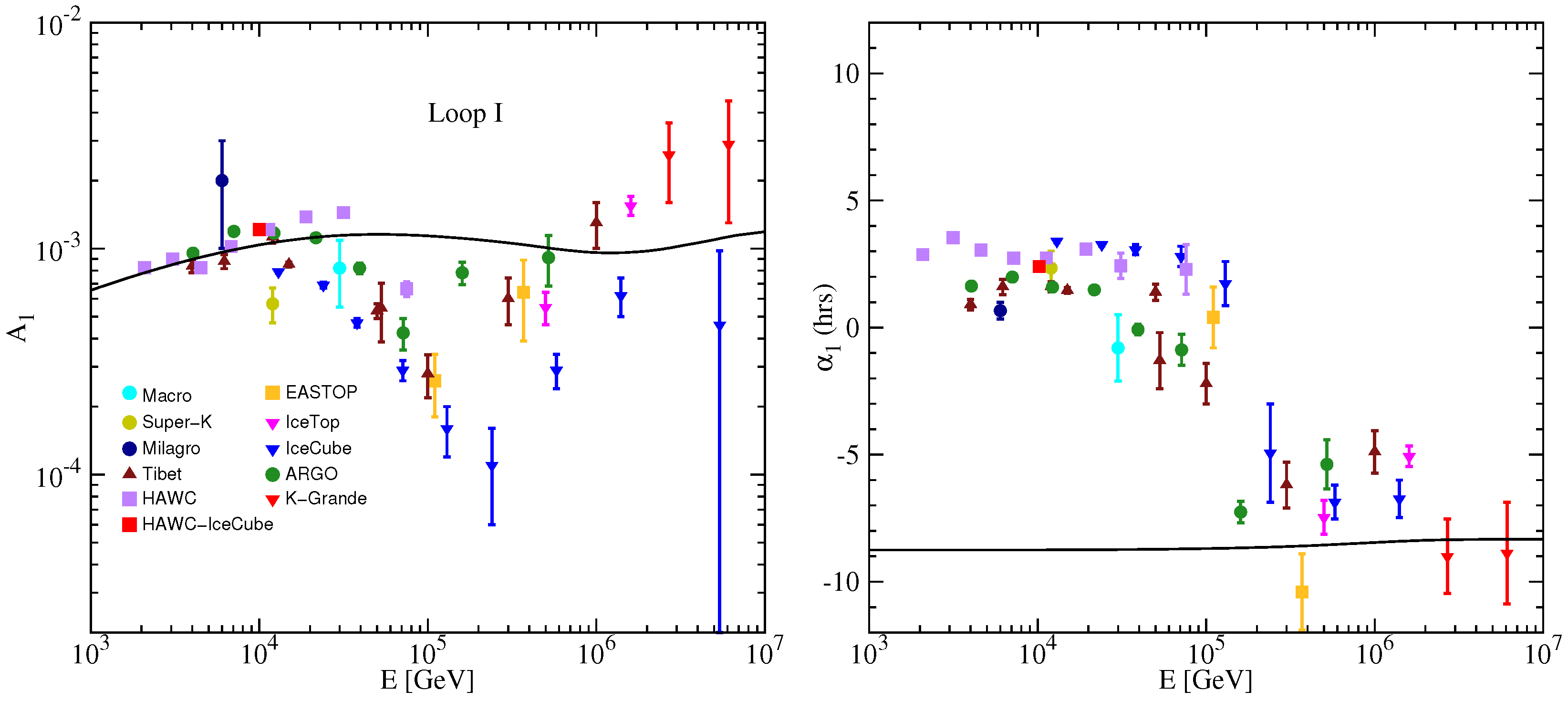
3.2. Anisotropy of Geminga, Monogem, and Loop I
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Detection of the Characteristic Pion-Decay Signature in Supernova Remnants. Science 2013, 339, 807–811. [Google Scholar] [CrossRef]
- Blasi, P. The origin of galactic cosmic rays. A&A Rev. 2013, 21, 70. [Google Scholar]
- Panov, A.D.; Adams, J.H.; Ahn, H.S.; Batkov, K.E.; Bashindzhagyan, G.L.; Watts, J.W.; Panov, A.D.; Adams, J.H.; Ahn, H.S.; Batkov, K.E.; et al. Elemental energy spectra of cosmic rays from the data of the ATIC-2 experiment. Bull. Russ. Acad. Sci. Phys. 2007, 71, 494–497. [Google Scholar] [CrossRef]
- Ahn, H.S.; Allison, P.; Bagliesi, M.G.; Beatty, J.J.; Bigongiari, G.; Childers, J.T.; Conklin, N.B.; Coutu, S.; DuVernois, M.A.; Ganel, O.; et al. Discrepant Hardening Observed in Cosmic-ray Elemental Spectra. Astrophys. J. Lett 2010, 714, L89–L93. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Ahn, H.S.; Allison, P.S.; Bagliesi, M.G.; Beatty, J.J.; Bigongiari, G.; Boyle, P.J.; Childers, J.T.; Conklin1, N.B.; Coutu, S.; et al. Cosmic-ray Proton and Helium Spectra from the First CREAM Flight. Astrophys. J. 2011, 728, 122. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Borisov, S.; et al. PAMELA Measurements of Cosmic-Ray Proton and Helium Spectra. Science 2011, 332, 69. [Google Scholar] [CrossRef]
- Aguilar, M.; Aisa, D.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. Precision Measurement of the Proton Flux in Primary Cosmic Rays from Rigidity 1 GV to 1.8 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2015, 114, 171103. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, M.; Aisa, D.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. Precision Measurement of the Helium Flux in Primary Cosmic Rays of Rigidities 1.9 GV to 3 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2015, 115, 211101. [Google Scholar] [CrossRef] [PubMed]
- Adriani, O.; Akaike, Y.; Asano, K.; Asaoka, Y.; Bagliesi, M.G.; Berti, E.; Bigongiari, G.; Binns, W.R.; Bonechi, S.; Bongi, M.; et al. Direct Measurement of the Cosmic-Ray Proton Spectrum from 50 GeV to 10 TeV with the Calorimetric Electron Telescope on the International Space Station. Phys. Rev. Lett. 2019, 112, 181102. [Google Scholar] [CrossRef] [PubMed]
- DAMPE Collaboration; An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Chang, J.; Chen, D.Y.; Chen, H.F.; et al. Measurement of the cosmic ray proton spectrum from 40 GeV to 100 TeV with the DAMPE satellite. Science 2019, 5, eaax3793. [Google Scholar]
- Alemanno, F.; An, Q.; Azzarello, P.; Barbato, F.C.T.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Catanzani, E.; Chang, J.; Chen, D.Y.; et al. Measurement of the Cosmic Ray Helium Energy Spectrum from 70 GeV to 80 TeV with the DAMPE Space Mission. Phys. Rev. Lett. 2021, 126, 201102. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Anderson, T.; Barrau, A.; Conklin, N.B.; Coutu, S.; Derome, L.; Han, J.H.; Jeon, J.A.; Kim, K.C.; Kim, M.H.; et al. Proton and Helium Spectra from the CREAM-III Flight. Astrophys. J. 2017, 839, 5. [Google Scholar] [CrossRef]
- Atkin, E.; Bulatov, V.; Dorokhov, V.; Gorbunov, N.; Filippov, S.; Grebenyuk, V.; Karmanov, D.; Kovalev, I.; Kudryashov, I.; Kurganov, A.; et al. New Universal Cosmic-Ray Knee near a Magnetic Rigidity of 10 TV with the NUCLEON Space Observatory. J. Exp. Theor. Phys. Lett. 2018, 108, 5–12. [Google Scholar] [CrossRef]
- Thoudam, S.; Hörandel, J.R. Nearby supernova remnants and the cosmic ray spectral hardening at high energies. MNRAS 2012, 421, 1209–1214. [Google Scholar] [CrossRef]
- Liu, W.; Guo, Y.Q.; Yuan, Q. Indication of nearby source signatures of cosmic rays from energy spectra and anisotropies. J. Cosmol. Astropart. Phys. 2019, 2019, 010. [Google Scholar] [CrossRef]
- Biermann, P.L.; Becker, J.K.; Dreyer, J.; Meli, A.; Seo, E.S.; Stanev, T. The Origin of Cosmic Rays: Explosions of Massive Stars with Magnetic Winds and Their Supernova Mechanism. Astrophys. J. 2010, 725, 184–187. [Google Scholar] [CrossRef]
- Thoudam, S.; Rachen, J.P.; Van Vliet, A.; Achterberg, A.; Buitink, S.; Falcke, H.; Hörandel, J.R. Cosmic-ray energy spectrum and composition up to the ankle: The case for a second Galactic component. Astron. Astrophys. 2016, 595, A33. [Google Scholar] [CrossRef]
- Tomassetti, N. Origin of the Cosmic-Ray Spectral Hardening. Astrophys. J. Lett. 2012, 752, L13. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, B.; Bi, X.J. Cosmic ray spectral hardening due to dispersion in the source injection spectra. Phys. Rev. D. 2011, 84, 043002. [Google Scholar] [CrossRef]
- Zatsepin, V.I.; Sokolskaya, N.V. Three component model of cosmic ray spectra from 10 GeV to 100 PeV. Astron. Astrophys. 2006, 458, 1–5. [Google Scholar] [CrossRef]
- Amenomori, M.; Ayabe, S.; Bi, X.J.; Chen, D.; Cui, S.W.; Danzengluobu; Ding, L.K.; Ding, X.H.; Feng, C.F.; Feng, Z.; et al. Anisotropy and Corotation of Galactic Cosmic Rays. Science 2006, 314, 439–443. [Google Scholar] [CrossRef]
- Amenomori, M.; Bi, X.J.; Chen, D.; Cui, S.W.; Ding, L.K.; Ding, X.H.; Fan, C.; Feng, C.F.; Feng, Z.; Feng, Z.Y.; et al. On Temporal Variations of the Multi-TeV Cosmic Ray Anisotropy using the Tibet III Air Shower Array. Astrophys. J. 2010, 711, 119–124. [Google Scholar]
- Amenomori, M.; Bi, X.J.; Chen, D.; Chen, T.L.; Chen, W.Y.; Cui, S.W.; Danzengluobu; Ding, L.K.; Feng, C.F.; Feng, Z.; et al. Northern Sky Galactic Cosmic Ray Anisotropy between 10 and 1000 TeV with the Tibet Air Shower Array. Astrophys. J. 2017, 836, 153. [Google Scholar] [CrossRef]
- Guillian, G.; Hosaka, J.; Ishihara, K.; Kameda, J.; Koshio, Y.; Minamino, A.; Mitsuda, C.; Miura, M.; Moriyama, S.; Nakahata, M.; et al. Observation of the anisotropy of 10TeV primary cosmic ray nuclei flux with the Super-Kamiokande-I detector. Phys. Rev. D 2007, 75, 062003. [Google Scholar] [CrossRef]
- Abdo, A.A.; Allen, B.; Aune, T.; Berley, D.; Blaufuss, E.; Casanova, S.; Chen, C.; Dingus, B.L.; Ellsworth, R.W.; Fleysher, L.; et al. Discovery of Localized Regions of Excess 10-TeV Cosmic Rays. Phys. Rev. Lett. 2008, 101, 221101. [Google Scholar] [CrossRef] [PubMed]
- Abdo, A.A.; Allen, B.T.; Aune, T.; Berley, D.; Casanova, S.; Chen, C.; Dingus, L.; Ellsworth, R.W.; Fleysher, L.; Fleysher, R.; et al. The Large-Scale Cosmic-Ray Anisotropy as Observed with Milagro. Astrophys. J. 2009, 698, 2121–2130. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Andeen, K.; Auffenberg, J.; Bai, X.; Baker, M.; et al. Measurement of the Anisotropy of Cosmic-ray Arrival Directions with IceCube. Astrophys. J. Lett. 2010, 718, L194–L198. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Andeen, K.; Auffenberg, J.; Bai, X.; et al. Observation of Anisotropy in the Arrival Directions of Galactic Cosmic Rays at Multiple Angular Scales with IceCube. Astrophys. J. 2011, 740, 16. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Allen, M.M.; Altmann, D.; Andeen, K.; et al. Observation of Anisotropy in the Galactic Cosmic-Ray Arrival Directions at 400 TeV with IceCube. Astrophys. J. 2011, 746, 33. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abbasi, R.; Abdou, Y.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Andeen, K.; Auffenberg, J.; et al. Observation of Cosmic-Ray Anisotropy with the IceTop Air Shower Array. Astrophys. J. 2013, 765, 55. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Anderson, T.; Ansseau, I.; et al. Anisotropy in Cosmic-Ray Arrival Directions in the Southern Hemisphere Based on Six Years of Data from the IceCube Detector. Astrophys. J. 2016, 826, 220. [Google Scholar] [CrossRef]
- Bartoli, B.; Bernardini, P.; Bi, X.J.; Bolognino, I.; Branchini, P.; Budano, A.; Calabrese Melcarne, A.K.; Camarri, P.; Cao, Z.; Cardarelli, R.; et al. Medium scale anisotropy in the TeV cosmic ray flux observed by ARGO-YBJ. Phys. Rev. D 2013, 88, 082001. [Google Scholar] [CrossRef]
- Bartoli, B.; Bernardini, P.; Bi, X.J.; Cao, Z.; Catalanotti, S.; Chen, S.Z.; Chen, T.L.; Cui, S.W.; Dai, B.Z.; D’Amone, A.; et al. ARGO-YBJ Observation of the Large-scale Cosmic Ray Anisotropy During the Solar Minimum between Cycles 23 and 24. Astrophys. J. 2015, 809, 90. [Google Scholar] [CrossRef]
- Aglietta, M.; Alekseenko, V.V.; Alessandro, B.; Antonioli, P.; Arneodo, F.; Bergamasco, L.; Bertaina, M.; Bonino, R.; Castellina, A.; Chiavassa, A.; et al. Evolution of the Cosmic-Ray Anisotropy Above 1014 eV. Astrophys. J. 2009, 692, L130–L133. [Google Scholar] [CrossRef]
- Chiavassa, A.; Apel, W.; Arteaga-Velazquez, J.; Bekk, K.; Bertaina, M.; Blümer, J.; Bozdog, H.; Brancus, I.M.; Cantoni, E.; Cossavella, F.; et al. A study of the first harmonic of the large scale anisotropies with the KASCADE-Grande experiment. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), Den Haag, The Netherlands, 30 July–6 August 2015; Volume 34, p. 281. [Google Scholar]
- Apel, W.D.; Arteaga-Velázquez, J.C.; Bekk, K.; Bertaina, M.; Blümer, J.; Bonino, R.; Bozdog, H.; Brancus, I.M.; Cantoni1, E.; Chiavassa, A.; et al. Search for Large-scale Anisotropy in the Arrival Direction of Cosmic Rays with KASCADE-Grande. Astrophys. J. 2019, 870, 91. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Solares, H.A.A.; Barber, A.S.; Baughman, B.M.; Bautista-Elivar, N.; et al. Observation of Small-scale Anisotropy in the Arrival Direction Distribution of TeV Cosmic Rays with HAWC. Astrophys. J. 2014, 796, 108. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Rojas, D.A.; Solares, H.A.A.; Becerril, A.; Belmont-Moreno, E.; et al. Observation of Anisotropy of TeV Cosmic Rays with Two Years of HAWC. Astrophys. J. 2018, 865, 57. [Google Scholar] [CrossRef]
- Funsten, H.O.; DeMajistre, R.; Frisch, P.C.; Heerikhuisen, J.; Higdon, D.M.; Janzen, P.; Larsen, B.A.; Livadiotis, G.; McComas, D.J.; Möbius, E.; et al. Circularity of the Interstellar Boundary Explorer Ribbon of Enhanced Energetic Neutral Atom (ENA) Flux. Astrophys. J. 2013, 776, 30. [Google Scholar] [CrossRef]
- Li, A.; Yin, S.; Liu, M.; Wang, H.; Li, X.; Li, Y. Interpretation of the Spectra and Anisotropy of Galactic Cosmic Rays. Universe 2022, 8, 307. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Arceo, R.; Arteaga-Velázquez, J.C.; Rojas, D.A.; Belmont-Moreno, E.; BenZvi, S.Y.; Brisbois, C.; Capistrán, T.; et al. All-sky Measurement of the Anisotropy of Cosmic Rays at 10 TeV and Mapping of the Local Interstellar Magnetic Field. Astrophys. J. 2019, 871, 96. [Google Scholar] [CrossRef]
- Ahlers, M. Deciphering the Dipole Anisotropy of Galactic Cosmic Rays. Phys. Rev. 2016, 117, 151103. [Google Scholar] [CrossRef] [PubMed]
- Compton, A.H.; Getting, I.A. An Apparent Effect of Galactic Rotation on the Intensity of Cosmic Rays. Phys. Rev. 1935, 47, 817–821. [Google Scholar] [CrossRef]
- Luo, Q.; Qiao, B.Q.; Liu, W.; Cui, S.W.; Guo, Y.Q. Statistical Study of the Optimal Local Sources for Cosmic Ray Nuclei and Electrons. Astrophys. J. 2022, 930, 82. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, W.; Yuan, Q.; Hu, H.B.; Bi, X.J.; Wu, H.R.; Zhou, X.-X.; Guo, Y.-Q. Geminga SNR: Possible Candidate of the Local Cosmic-Ray Factory. Astrophys. J. 2022, 926, 41. [Google Scholar] [CrossRef]
- Tang, T.P.; Xia, Z.Q.; Shen, Z.Q.; Zu, L.; Feng, L.; Yuan, Q.; Fan, Y.-Z.; Wu, J. Explanation of nearby SNRs for primary electron excess and proton spectral bump. Phys. Lett. B. 2022, 825, 13684. [Google Scholar] [CrossRef]
- Schwadron, N.A.; Adams, F.C.; Christian, E.R.; Desiati, P.; Frisch, P.; Funsten, H.O.; Jokipii, J.R.; McComas, D.J.; Moebius, E.; Zank, G.P.; et al. Global Anisotropies in TeV Cosmic Rays Related to the Sun’s Local Galactic Environment from IBEX. Science 2014, 343, 988–990. [Google Scholar] [CrossRef]
- Liu, W.; Lin, S.J.; Hu, H.; Guo, Y.Q.; Li, A.F. Two Numerical Methods for the 3D Anisotropic Propagation of Galactic Cosmic Rays. ApJ 2020, 892, 6. [Google Scholar] [CrossRef]
- Caraveo, P.A.; Bignami, G.F.; Mignani, R.; Taff, L.G. Parallax Observations with the Hubble Space Telescope Yield the Distance to Geminga Astrophys. J. Lett. 1996, 461, L91. [Google Scholar] [CrossRef]
- Plucinsky, P.P.; Snowden, S.L.; Aschenbach, B.; Egger, R.; Edgar, R.J.; McCammon, D. ROSAT Survey Observations of the Monogem Ring. Astrophys. J. 1996, 463, 224. [Google Scholar] [CrossRef]
- Cha, A.N.; Sembach, K.R.; Danks, A.C. The Distance to the Vela Supernova Remnant. Astrophys. J. 1999, 515, L25–L28. [Google Scholar] [CrossRef]
- Egger, R.J.; Aschenbach, B. Interaction of the Loop I supershell with the Local Hot. Astron. Astrophys. 1995, 294, L25–L28. [Google Scholar]
- Sun, X.H.; Reich, W.; Han, J.L.; Reich, P.; Wielebinski, R. New λ6 cm observations of the Cygnus Loop. Astron. Astrophys. 2006, 447, 937–947. [Google Scholar] [CrossRef]
- Andrew, W.S.; Igor, V.M.; Vladimir, S.P. Cosmic-Ray Propagation and Interactions in the Galaxy. Annu. Rev. Nucl. Part. Sci. 2007, 27, 285–327. [Google Scholar]
- Tomassetti, N. Cosmic-ray protons, nuclei, electrons, and antiparticles under a two-halo scenario of diffusive propagation. Phys. Rev. D 2015, 92, 8. [Google Scholar] [CrossRef]
- Feng, J. Tomassetti Nicola and Oliva Alberto. Bayesian analysis of spatial-dependent cosmic-ray propagation: Astrophysical background of antiprotons and positrons. Phys. Rev. D 2016, 94, 12. [Google Scholar] [CrossRef]
- Guo, Y.-Q.; Tian, Z.; Jin, C. Spatial-dependent Propagation of Cosmic Rays Results in the Spectrum of Proton, Ratios of P/P, and B/C, and Anisotropy of Nuclei. Astrophys. J. 2016, 819, 54. [Google Scholar] [CrossRef]
- Liu, W.; Yao, Y.-h.; Guo, Y.-Q. Revisiting the Spatially Dependent Propagation Model with the Latest Observations of Cosmic-Ray Nuclei. Astrophys. J. 2018, 869, 176. [Google Scholar] [CrossRef]
- Guo, Y.-Q.; Yuan, Q. Understanding the spectral hardenings and radial distribution of Galactic cosmic rays and Fermi diffuse γ rays with spatially-dependent propagation. Phys. Rev. D 2018, 97, 063008. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Rojas, D.A.; Solares, H.A.A.; Barber, A.S.; et al. Extended gamma-ray sources around pulsars constrain the origin of the positron flux at Earth. Science 2017, 358, 6365. [Google Scholar] [CrossRef]
- Aharonian, F.; An, Q.; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; Cai, H.; et al. Extended Very-High-Energy Gamma-Ray Emission Surrounding PSR J 0622 +3749 Observed by LHAASO-KM2A. Phys. Rev. Lett. 2021, 126, 24. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Grasso, D.; Maccione, L. Cosmic Ray propagation in the Galaxy and diffuse gamma-ray emission. Am. Inst. Phys. Conf. Series. 2008, 1085, 380–383. [Google Scholar]
- Case, G.; Bhattacharya, D. Revisiting the galactic supernova remnant distribution. Astron. Astrophys. Suppl. 1996, 120, 437–440. [Google Scholar]
- Blasi, P.; Amato, E. Diffusive propagation of cosmic rays from supernova remnants in the Galaxy. II: Anisotropy. J. Cosmol. Astropart. Phys. 2012, 1, 11. [Google Scholar] [CrossRef]
- Sveshnikova, L.G.; Strelnikova, O.N.; Ptuskin, V.S. Spectrum and anisotropy of cosmic rays at TeV-PeV-energies and contribution of nearby sources. Astropart. Phys. 2013, 50, 33–46. [Google Scholar] [CrossRef]
- Giacalone, J.; Jokipii, J.R. The Transport of Cosmic Rays across a Turbulent Magnetic Field. ApJ 1999, 520, 204–214. [Google Scholar] [CrossRef]
- Cerri, S.S.; Gaggero, D.; Vittino, A.; Evoli, C.; Grasso, D. A signature of anisotropic cosmic-ray transport in the gamma-ray sky. J. Cosmol. Astropart. Phys. 2017, 10, 019. [Google Scholar] [CrossRef]
- Snodin, A.P.; Shukurov, A.; Sarson, G.R.; Bushby, P.J.; Rodrigues, L.F.S. Global diffusion of cosmic rays in random magnetic fields. Mon. Not. R. Astron. Soc. 2016, 457, 3975–3987. [Google Scholar] [CrossRef]
- De Marco, D.; Blasi, P.; Stanev, T. Numerical propagation of high energy cosmic rays in the Galaxy: I. Technical issues. J. Cosmol. Astropart. Phys. 2007, 6, 027. [Google Scholar] [CrossRef]
- Aguilar, M.; Cavasonza, L.A.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; Barrau, A.; et al. Precision Measurement of the Boron to Carbon Flux Ratio in Cosmic Rays from 1.9 GV to 2.6 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2016, 117, 231102. [Google Scholar] [CrossRef]
- Aguilar, M.; Cavasonza, L.A.; Alpat, B.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; et al. Observation of the Identical Rigidity Dependence of He, C, and O Cosmic Rays at High Rigidities by the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2017, 119, 251101. [Google Scholar] [CrossRef]
- Atkin, E.; Bulatov, V.; Dorokhov, V.; Gorbunov, N.; Filippov, S.; Grebenyuk, V.; Karmanov, D.; Kovalev, I.; Kudryashov, I.; Kurganov, A.; et al. First results of the cosmic ray NUCLEON experiment. J. Cosmol. Astropart. Phys. 2017, 2017, 020. [Google Scholar] [CrossRef]
- Antoni, T.; Apel, W.D.; Badea, A.F.; Bekk, K.; Bercuci, A.; Blümer, J.; Bozdog, H.; Brancus, I.M.; Chilingarian, A.; Daumiller, K.; et al. KASCADE measurements of energy spectra for elemental groups of cosmic rays: Results and open problems. Astropart. Physics. 2005, 24, 1–25. [Google Scholar] [CrossRef]
- Apel, W.D.; Arteaga-Velázquez, J.C.; Bekk, K.; Bertaina, M.; Blümer, J.; Bozdog, H.; Brancus, I.M.; Cantoni, E.; Chiavassa, A.; Cossavella, F.; et al. KASCADE-Grande measurements of energy spectra for elemental groups of cosmic rays. Astropart. Phys. 2013, 47, 54–66. [Google Scholar] [CrossRef]
- Ambrosio, M.; Antolini, R.; Baldini, A.; Barbarino, G.C.; Barish, B.C.; Battistoni, G.; Becherini, Y.; Bellotti, R.; Bemporad, C.; Bernardini, P.; et al. Search for the sidereal and solar diurnal modulations in the total MACRO muon data set. Phys. Rev. D 2003, 67, 042002. [Google Scholar] [CrossRef]
- Aglietta, M.; Alessandro, B.; Antonioli, P.; Arneodo, F.; Bergamasco, L.; Bertaina, M. Study of the Cosmic Ray Anisotropy at Eo ∼100 TeV from EAS-TOP: 1992–1994. Int. Cosmic Ray Conf. 1995, 2, 800. [Google Scholar]
- Amenomori, M.; Ayabe, S.; Cui, S.W.; Danzengluobu; Ding, L.K.; Ding, X.H.; Feng, C.F.; Feng, Z.Y.; Gao, X.Y.; Geng, X.Q.; et al. Large-Scale Sidereal Anisotropy of Galactic Cosmic-Ray Intensity Observed by the Tibet Air Shower Array. Astrophys. J. 2005, 626, L29–L32. [Google Scholar] [CrossRef]


| SNR | l | b | d | ||
|---|---|---|---|---|---|
| Geminga | 330 | 345 | 1 | ||
| Monogem | 288 | 86 | 2 | ||
| Vela | 295 | 11 | 3 | ||
| Loop I | 170 | 200 | 4 | ||
| Cygnus Loop | 540 | 10 | 5 |
| Background | Geminga Source | Monogem Source | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Element | Normalization † | ||||||||
| PV | GeV −1 | TV | GeV −1 | TV | |||||
| p | 2.34 | 7 | 2.16 | 25 | 2.20 | 22 | |||
| He | 2.27 | 7 | 2.08 | 25 | 2.18 | 22 | |||
| C | 2.31 | 7 | 2.13 | 25 | 2.13 | 22 | |||
| N | 2.34 | 7 | 2.13 | 25 | 2.13 | 22 | |||
| O | 2.36 | 7 | 2.13 | 25 | 2.13 | 22 | |||
| Ne | 2.28 | 7 | 2.13 | 25 | 2.13 | 22 | |||
| Mg | 2.39 | 7 | 2.13 | 25 | 2.13 | 22 | |||
| Si | 2.37 | 7 | 2.13 | 25 | 2.13 | 22 | |||
| Fe | 2.29 | 7 | 2.13 | 25 | 2.13 | 22 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, A.; Liu, W.; Guo, Y. Cosmic Ray Anisotropy and Spectra as Probes for Nearby Sources. Symmetry 2024, 16, 236. https://doi.org/10.3390/sym16020236
Li A, Liu W, Guo Y. Cosmic Ray Anisotropy and Spectra as Probes for Nearby Sources. Symmetry. 2024; 16(2):236. https://doi.org/10.3390/sym16020236
Chicago/Turabian StyleLi, Aifeng, Wei Liu, and Yiqing Guo. 2024. "Cosmic Ray Anisotropy and Spectra as Probes for Nearby Sources" Symmetry 16, no. 2: 236. https://doi.org/10.3390/sym16020236
APA StyleLi, A., Liu, W., & Guo, Y. (2024). Cosmic Ray Anisotropy and Spectra as Probes for Nearby Sources. Symmetry, 16(2), 236. https://doi.org/10.3390/sym16020236






