Thermally Driven Convection Generated by Reaction Fronts in Viscous Fluids
Abstract
:1. Introduction
2. Equations of Motion
2.1. Linear Stability Analysis
2.2. Nonlinear Equations
3. Numerical Methods
4. Results
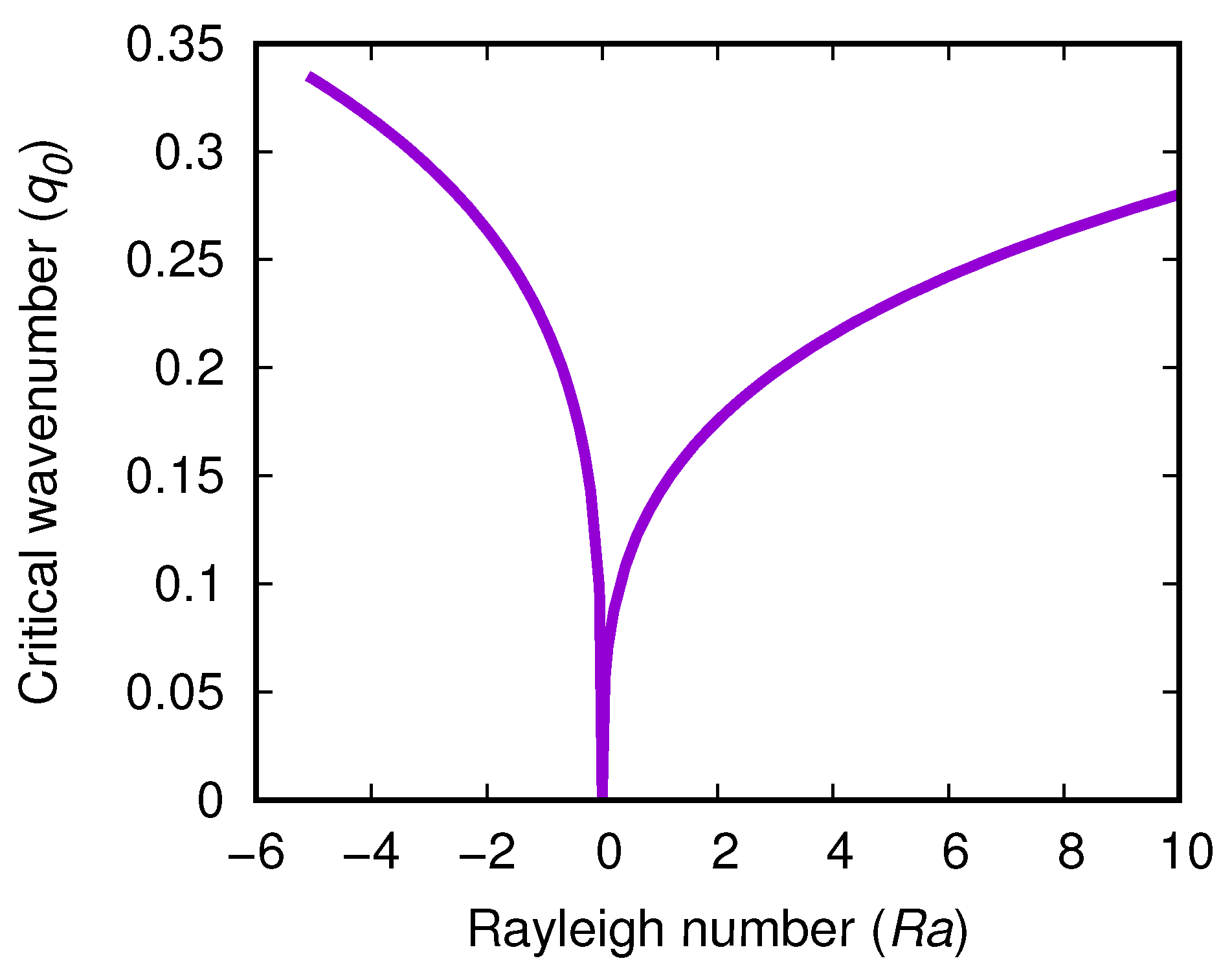
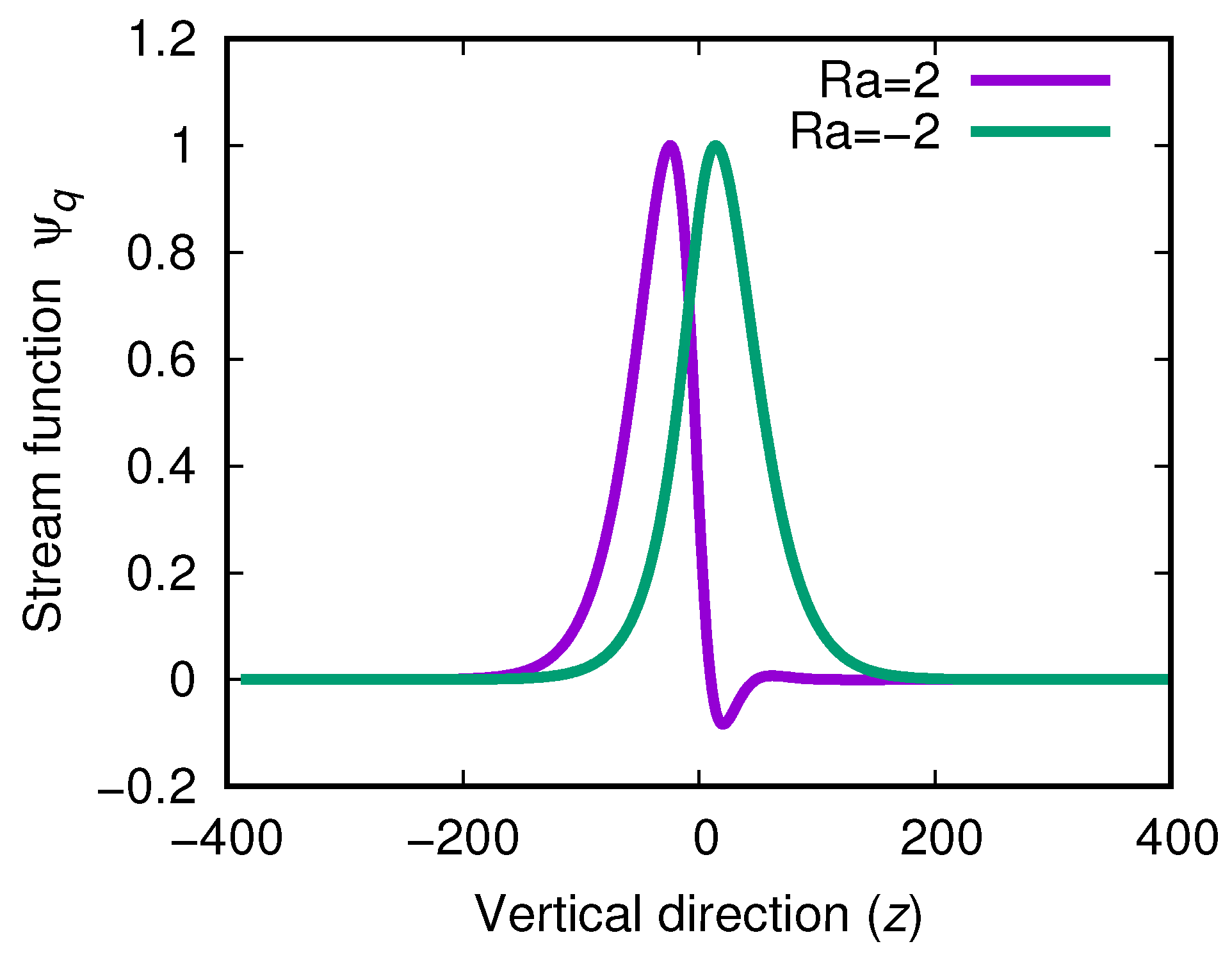
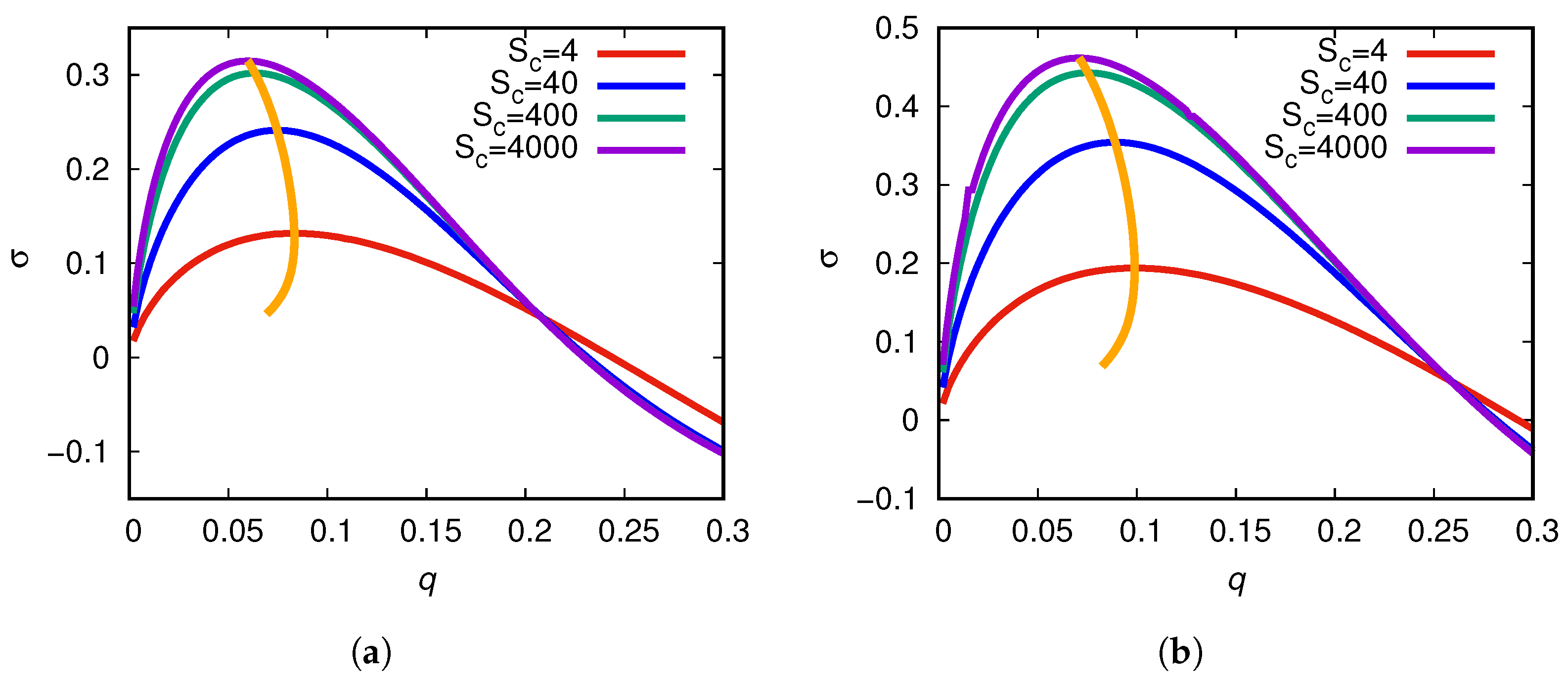
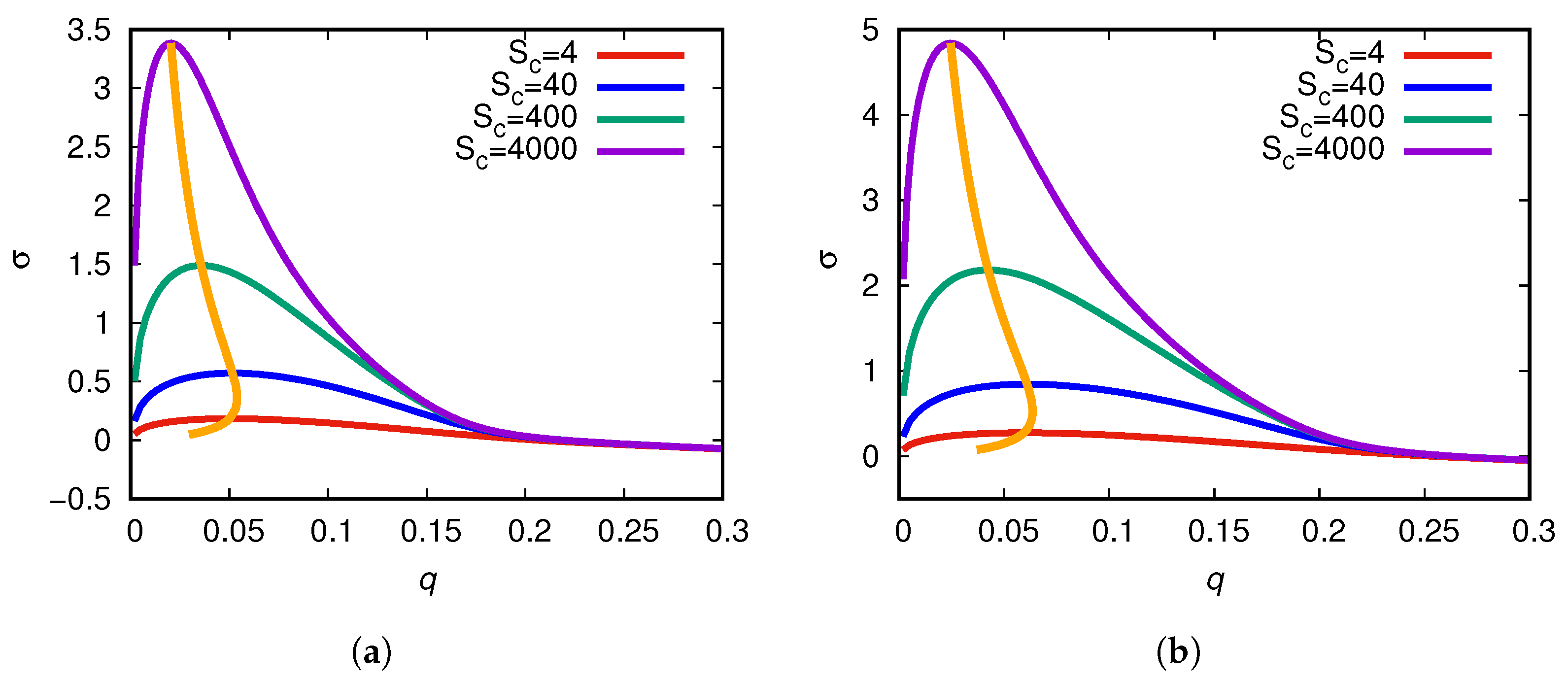
4.1. Linear Stability Analysis
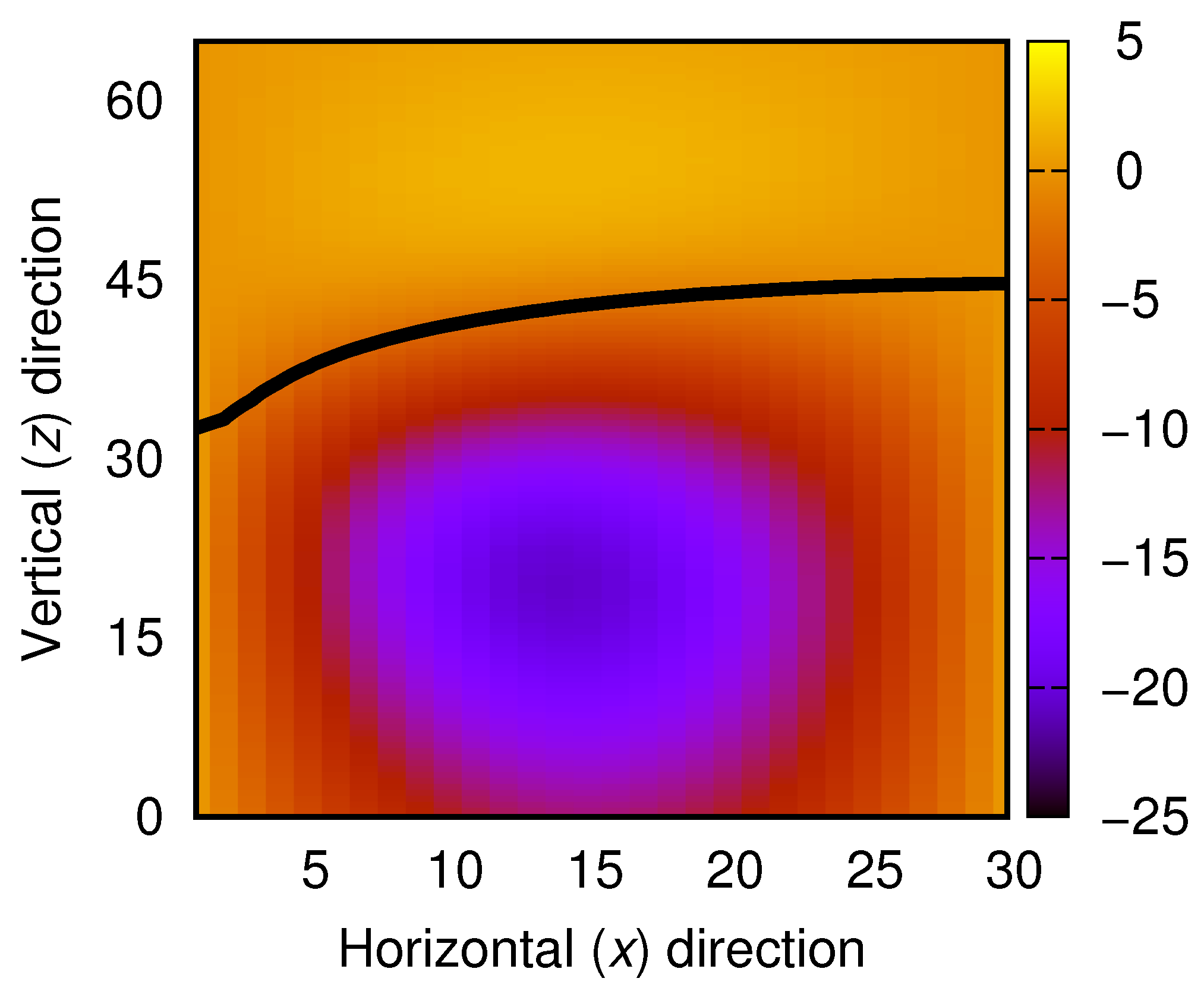
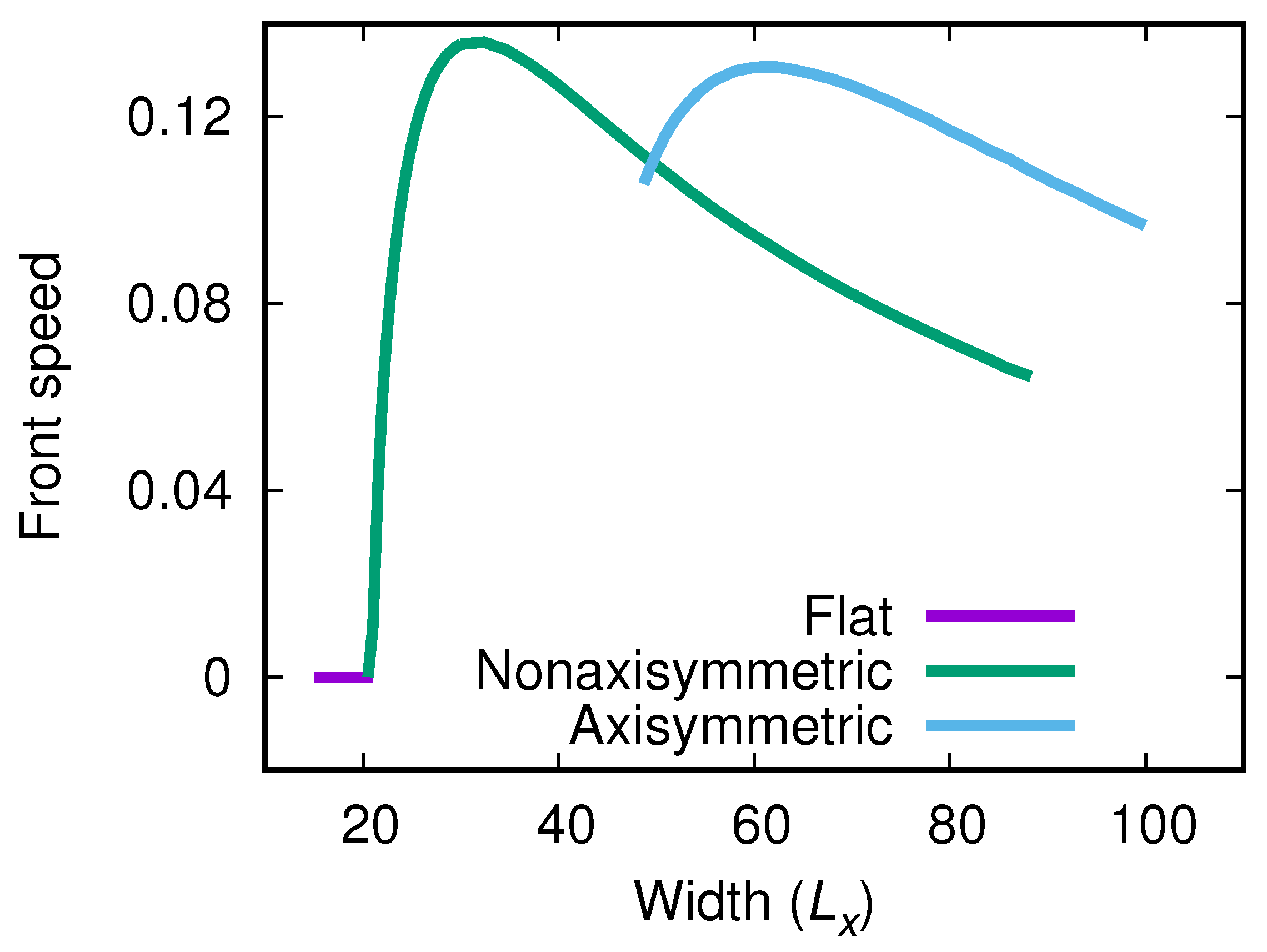
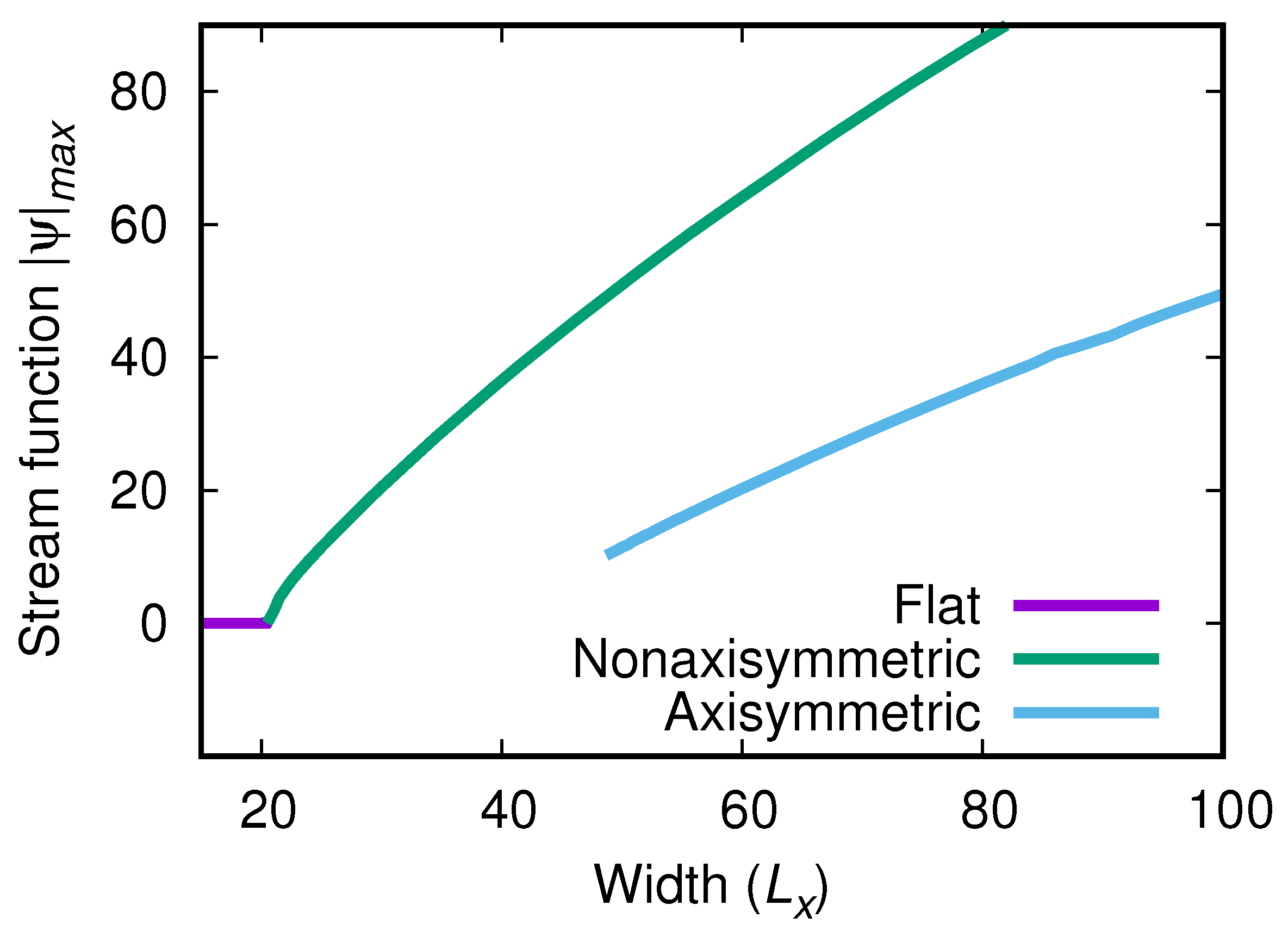
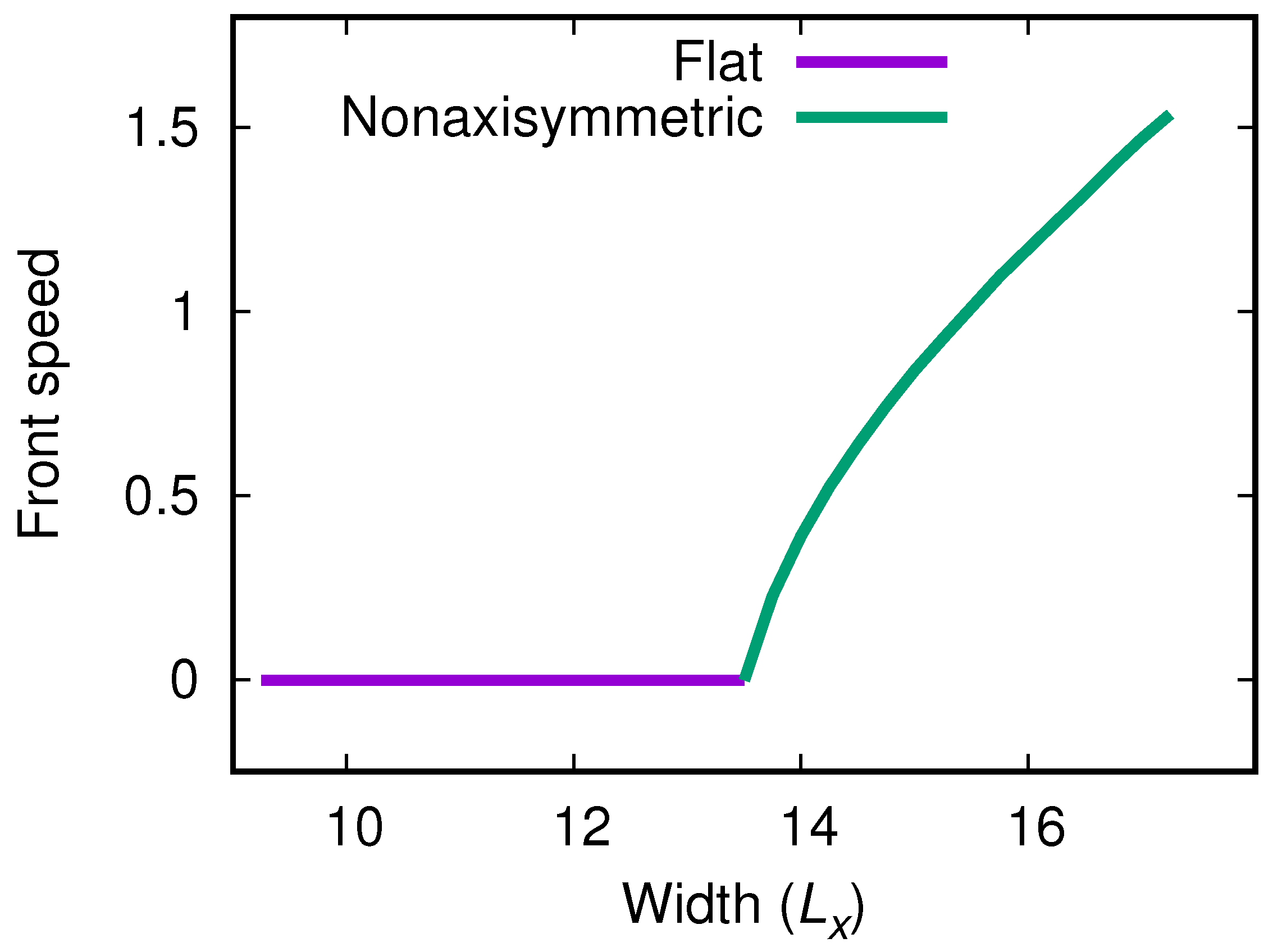
4.2. Nonlinear Front Propagation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sivashinsky, G.I. Nonlinear analysis of hydrodynamic instability in laminar flames—I. Derivation of basic equations. Acta Astronaut. 1977, 4, 1177–1206. [Google Scholar] [CrossRef]
- Altantzis, C.; Frouzakis, C.E.; Tomboulides, A.G.; Matalon, M.; Boulouchos, K. Hydrodynamic and thermodiffusive instability effects on the evolution of laminar planar lean premixed hydrogen flames. J. Fluid Mech. 2012, 700, 329–361. [Google Scholar] [CrossRef]
- Matalon, M.; Metzener, P. The effect of thermal expansion on diffusion flame instabilities. J. Fluid Mech. 2010, 647, 453–472. [Google Scholar] [CrossRef]
- Fetecau, C.; Shah, N.A.; Vieru, D. General Solutions for Hydromagnetic Free Convection Flow over an Infinite Plate with Newtonian Heating, Mass Diffusion and Chemical Reaction. Commun. Theor. Phys. 2017, 68, 768–782. [Google Scholar] [CrossRef]
- Qayyum, S.; Hayat, T.; Alsaedi, A.; Ahmad, B. MHD nonlinear convective flow of thixotropic nanofluid with chemical reaction and Newtonian heat and mass conditions. Results Phys. 2017, 7, 2124–2133. [Google Scholar] [CrossRef]
- Ahmed, S.; Zueco, J.; López-González, L.M. Effects of chemical reaction, heat and mass transfer and viscous dissipation over a MHD flow in a vertical porous wall using perturbation method. Int. J. Heat Mass Transf. 2017, 104, 409–418. [Google Scholar] [CrossRef]
- De Wit, A. Chemo-Hydrodynamic Patterns and Instabilities. Annu. Rev. Fluid Mech. 2020, 52, 531–555. [Google Scholar] [CrossRef]
- De Wit, A.; Eckert, K.; Kalliadasis, S. Introduction to the Focus Issue: Chemo-Hydrodynamic Patterns and Instabilities. Chaos 2012, 22, 037101. [Google Scholar] [CrossRef] [PubMed]
- Edwards, B.F.; Wilder, J.W.; Showalter, K. Onset of convection for autocatalytic reaction fronts: Laterally unbounded system. Phys. Rev. A 1991, 43, 749–760. [Google Scholar] [CrossRef] [PubMed]
- Pojman, J.A.; Epstein, I.R.; McManus, T.J.; Showalter, K. Convective effects on chemical waves. 2. Simple convection in the iodate-arsenous acid system. J. Phys. Chem. 1991, 95, 1299–1306. [Google Scholar] [CrossRef]
- Masere, J.; Vasquez, D.A.; Edwards, B.F.; Wilder, J.W.; Showalter, K. Nonaxisymmetric and axisymmetric convection in propagating reaction-diffusion fronts. J. Phys. Chem. 1994, 98, 6505–6508. [Google Scholar] [CrossRef]
- Wilder, J.W.; Vasquez, D.A.; Edwards, B.F. Nonlinear front evolution of hydrodynamic chemical waves in vertical cylinders. Phys. Rev. E 1997, 56, 3016–3019. [Google Scholar] [CrossRef]
- Sebestíková, L.; D’Hernoncourt, J.; Hauser, M.J.B.; Müller, S.C.; De Wit, A. Flow-field development during finger splitting at an exothermic chemical reaction front. Phys. Rev. E 2007, 75, 026309. [Google Scholar] [CrossRef]
- Bánsági, T., Jr.; Horváth, D.; Tóth, A. Multicomponent convection in the chlorite–tetrathionate reaction. Chem. Phys. Lett. 2004, 384, 153–156. [Google Scholar] [CrossRef]
- Bánsági, T., Jr.; Horváth, D.; Tóth, A.; Yang, J.; Kalliadasis, S.; De Wit, A. Density fingering of an exothermic autocatalytic reaction. Phys. Rev. E 2003, 68, 055301. [Google Scholar] [CrossRef] [PubMed]
- Horváth, D.; Bánsági, T., Jr.; Tóth, A. Orientation-dependent density fingering in an acidity front. J. Chem. Phys. 2002, 117, 4399–4402. [Google Scholar] [CrossRef]
- Tóth, T.; Horváth, D.; Tóth, A. Thermal effects in the density fingering of the chlorite–tetrathionate reaction. Chem. Phys. Lett. 2007, 442, 289–292. [Google Scholar] [CrossRef]
- Rongy, L.; Schuszter, G.; Sinkó, Z.; Tóth, T.; Horváth, D.; Tóth, A.; De Wit, A. Influence of thermal effects on buoyancy-driven convection around autocatalytic chemical fronts propagating horizontally. Chaos 2009, 19, 023110. [Google Scholar] [CrossRef] [PubMed]
- Schuszter, G.; Pótári, G.; Horváth, D.; Tóth, A. Three-dimensional convection-driven fronts of the exothermic chlorite-tetrathionate reaction. Chaos 2015, 25, 064501. [Google Scholar] [CrossRef]
- Pojman, J.A.; Nagy, I.P.; Epstein, I.R. Convective effects on chemical waves. 3. Multicomponent convection in the iron (II)-nitric acid system. J. Phys. Chem. 1991, 95, 1306–1311. [Google Scholar] [CrossRef]
- Vasquez, D.A.; Edwards, B.F.; Wilder, J.W. Finite thermal diffusivity at onset of convection in autocatalytic systems: Discontinuous fluid density. Phys. Fluids 1995, 7, 2513–2515. [Google Scholar] [CrossRef]
- Guzman, R.; Vasquez, D.A. Front instabilities in the presence of convection due to thermal and compositional gradients. Chaos 2024, 34, 013123. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Paul, M.R. Velocity and geometry of propagating fronts in complex convective flow fields. Phys. Rev. E 2019, 99, 012213. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Paul, M.R. Propagating fronts in fluids with solutal feedback. Phys. Rev. E 2020, 101, 032214. [Google Scholar] [CrossRef] [PubMed]
- D’Hernoncourt, J.; De Wit, A.; Zebib, A. Double-diffusive instabilities of autocatalytic chemical fronts. J. Fluid Mech. 2007, 576, 445–456. [Google Scholar] [CrossRef]
- D’Hernoncourt, J.; Zebib, A.; De Wit, A. Reaction Driven Convection around a Stably Stratified Chemical Front. Phys. Rev. Lett. 2006, 96, 154501. [Google Scholar] [CrossRef]
- Leconte, M.; Martin, J.; Rakotomalala, N.; Salin, D.; Yortsos, Y.C. Mixing and reaction fronts in laminar flows. J. Chem. Phys. 2004, 120, 7314–7321. [Google Scholar] [CrossRef]
- Hanna, A.; Saul, A.; Showalter, K. Detailed studies of propagating fronts in the iodate oxidation of arsenous acid. J. Am. Chem. Soc. 1982, 104, 3838–3844. [Google Scholar] [CrossRef]
- Kestin, J.; Sokolov, M.; Wakeham, W.A. Viscosity of liquid water in the range -8 °C to 150 °C. J. Phys. Chem. Ref. Data 1978, 7, 941–948. [Google Scholar] [CrossRef]
- Holz, M.; Heil, S.R.; Saccob, A. Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate H NMR PFG measurements. Phys. Chem. Chem. Phys. 2000, 2, 4740–4742. [Google Scholar] [CrossRef]
- Kalliadasis, S.; Yang, J.; De Wit, A. Fingering instabilities of exothermic reaction-diffusion fronts in porous media. Phys. Fluids 2004, 16, 1395–1409. [Google Scholar] [CrossRef]
- Gérard, T.; De Wit, A. Stability of exothermic autocatalytic fronts with regard to buoyancy-driven instabilities in presence of heat losses. Wave Motion 2011, 48, 814–823. [Google Scholar] [CrossRef]
- Wilder, J.W.; Edwards, B.F.; Vasquez, D.A. Finite Thermal Diffusivity at Onset of Convection in Autocatalytic Systems: Continuous Fluid Density. Phys. Rev. A 1992, 45, 2320–2327. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilela, P.M.; Guzman, R.; Vasquez, D.A. Thermally Driven Convection Generated by Reaction Fronts in Viscous Fluids. Symmetry 2024, 16, 269. https://doi.org/10.3390/sym16030269
Vilela PM, Guzman R, Vasquez DA. Thermally Driven Convection Generated by Reaction Fronts in Viscous Fluids. Symmetry. 2024; 16(3):269. https://doi.org/10.3390/sym16030269
Chicago/Turabian StyleVilela, Pablo M., Roberto Guzman, and Desiderio A. Vasquez. 2024. "Thermally Driven Convection Generated by Reaction Fronts in Viscous Fluids" Symmetry 16, no. 3: 269. https://doi.org/10.3390/sym16030269




