Dynamic Spatiotemporal Correlation Graph Convolutional Network for Traffic Speed Prediction
Abstract
:1. Introduction
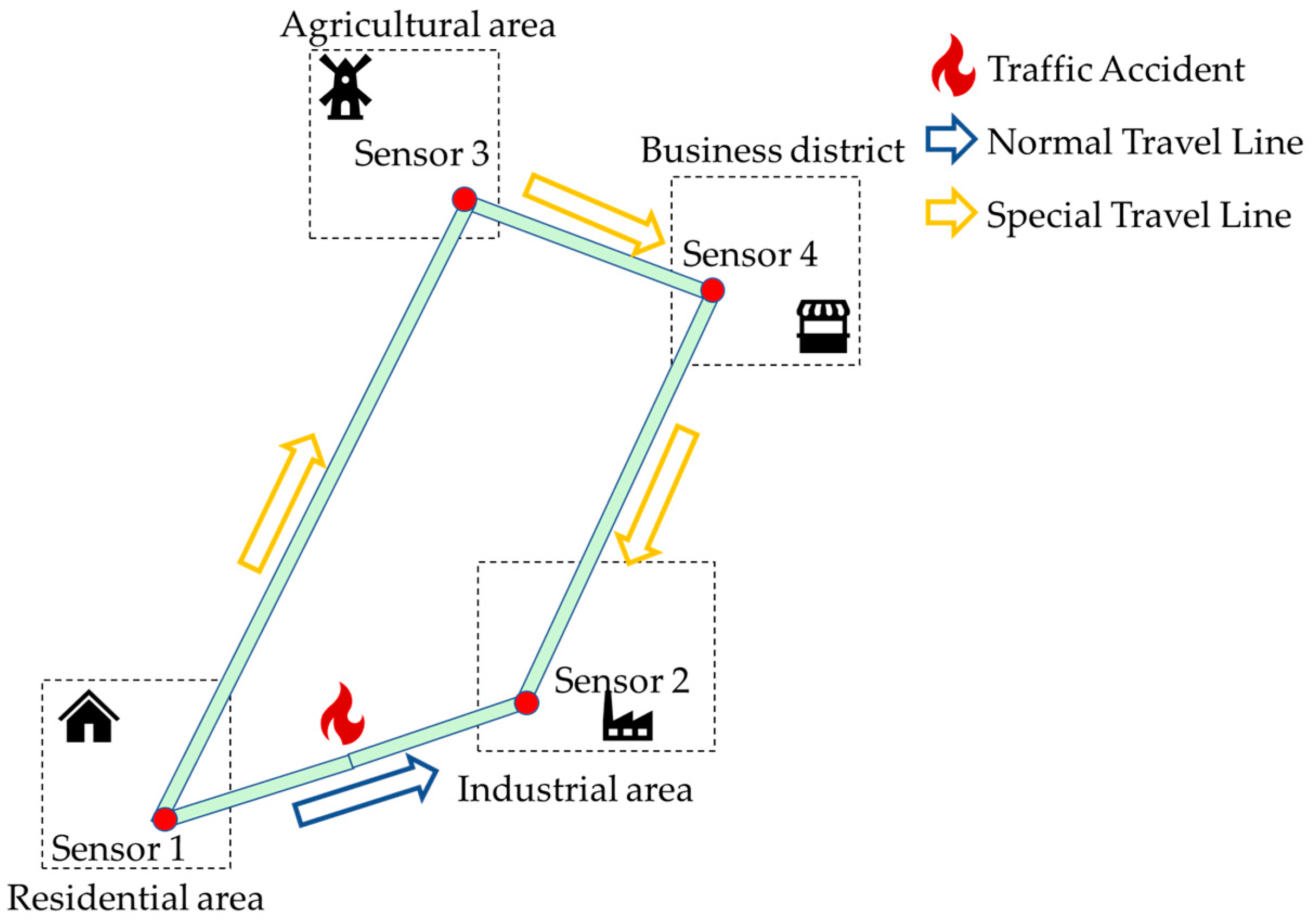
- Dynamic correlation between nodes. In previous studies, the correlation between nodes was often described using a static adjacency matrix, but in reality, the relationship among intersections within the traffic grid fluctuates over time. As shown in Figure 1, residents departing from a residential area to work in an industrial area often choose the route marked with a blue arrow due to its shorter distance. However, if a traffic accident occurs on this section, rendering it impassable, residents would be forced to choose the route marked with a yellow arrow to reach the industrial area. During this process, the originally strong correlation between nodes 1 and 2 would weaken or even become irrelevant. Therefore, learning the dynamic spatiotemporal correlations between nodes is very necessary.
- Oversmoothing problem of graphs. Although existing models have achieved relatively good results in traffic prediction using deep graph neural networks, deep graph neural networks gradually lose the graph structure and node feature information, leading to a decline in network performance. Therefore, it is necessary to forget irrelevant information layer by layer progressively.
- Long-term temporal feature extraction. Traffic data are not only influenced by short-term traffic conditions but also by long-term time dependence, such as people using a certain road to commute to work and returning home at the end of the day. On workdays, traffic congestion on the road significantly increases during morning and evening rush hours. However, on weekends or holidays, as most people do not go to work, the traffic flow on this road will be reduced and congestion will be significantly reduced. Therefore, observing the traffic data of this road over a long period will reveal clear cyclical changes in traffic flow and congestion.
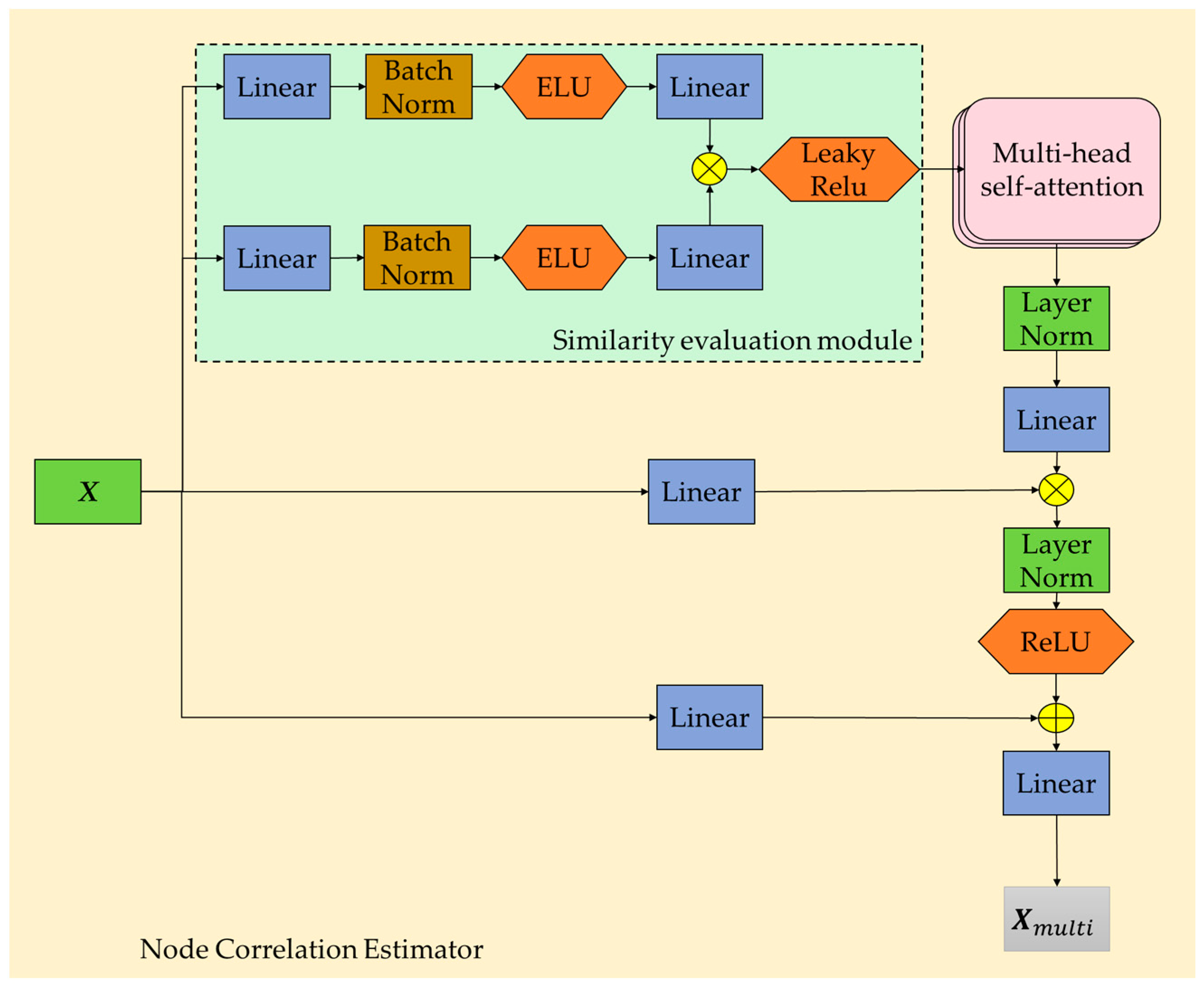
- The NCE module is constructed in this paper to learn the dynamic spatiotemporal correlation between nodes using the matrix dot product after linear transformation and the multi-head self-attention mechanism.
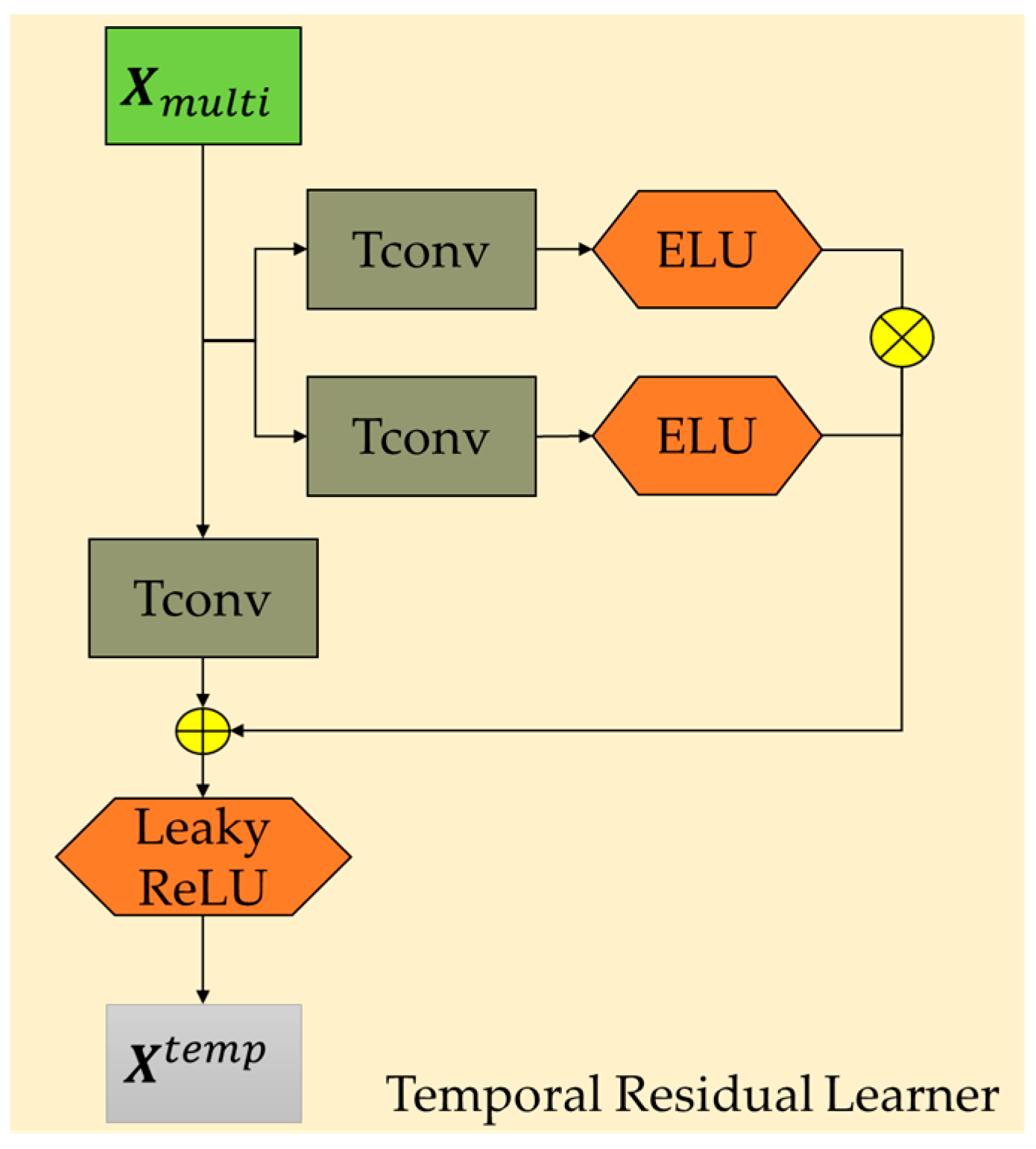
- The time residual learner module is designed to learn long-term sequence information in traffic data, while the gated graph convolutional fusion module is used to effectively learn spatial information in traffic data and filter out useless information during the iterative process.
- This study leverages two authentic traffic datasets, METR–LA and PEMS–BAY, to validate the predictive performance of the novel MSGSGCN model presented. The empirical findings indicate that the model outshines eight reference models in various forecasting challenges.
2. Related Work
2.1. Traffic Speed Prediction with Classical Statistical Models
2.2. Traffic Speed Prediction with Traditional Machine Learning
2.3. Traffic Speed Prediction with Deep Learning
3. Methodology
3.1. Problem Definition
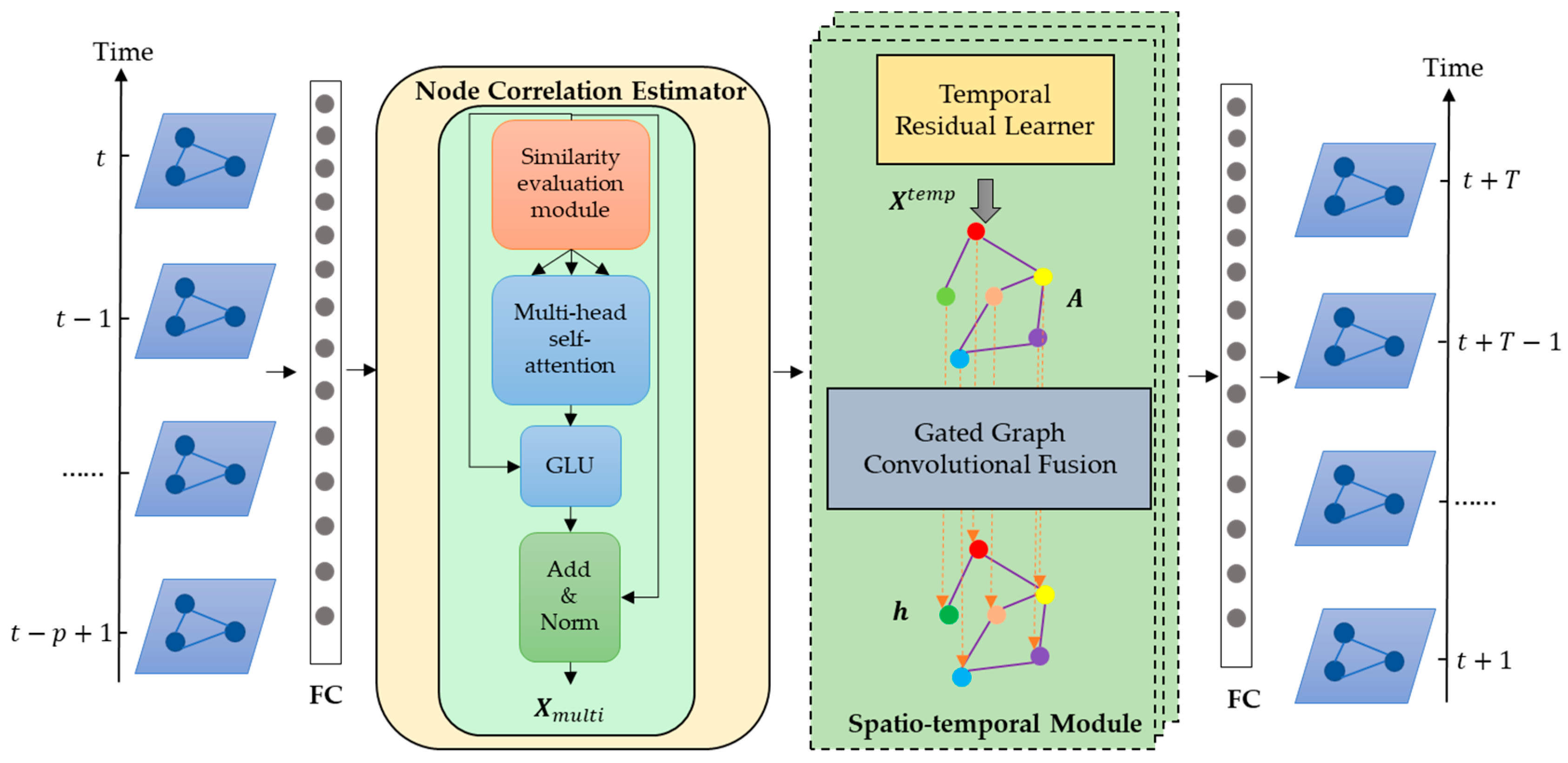
3.2. Overview
3.3. Node Correlation Estimator
3.4. Spatiotemporal Module
3.4.1. Temporal Residual Learner
3.4.2. Adaptive Diffusion Graph Convolution Network
3.4.3. Gated Graph Convolutional Fusion
3.4.4. Loss Function
3.5. Training Process
| Algorithm 1: Training process of MSGSGCN. |
| Input:. . . Output: Trained MSGSGCN model.
|
4. Experiments
4.1. Datasets
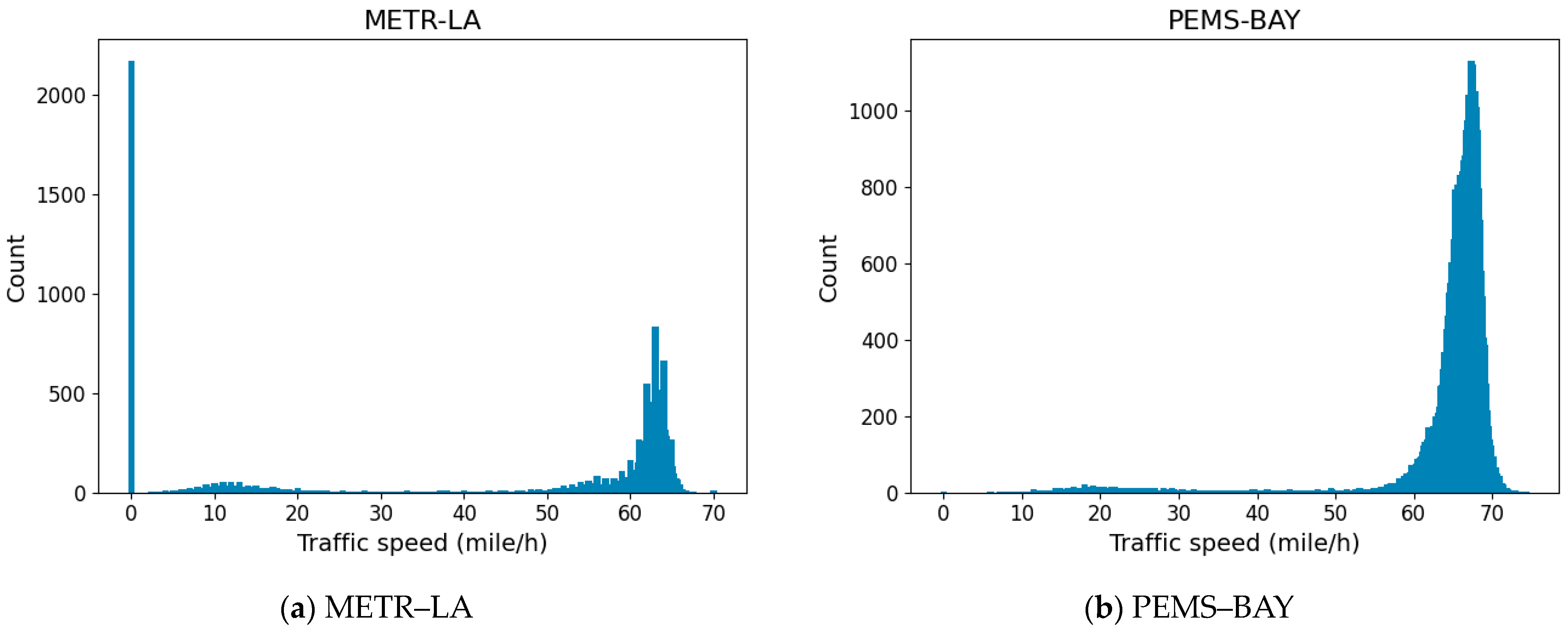
- METR–LA. The METR–LA dataset is an open dataset for traffic speed prediction. The dataset collects data from 207 sensors on the freeways of Los Angeles from March to June. Figure 6a presents the dataset through a visual graph.
- PEMS–BAY. The PEMS–BAY dataset contains data collected from 325 nodes from January 2017 to June 2017. Figure 6b presents the dataset through a visual graph.
4.2. Experimental Setup
4.2.1. Data Splitting
4.2.2. Hyperparameter Settings
4.3. Baseline Models and Evaluation Metrics
4.3.1. Evaluation Metrics
4.3.2. Baseline Models
- ARIMA [9]. Integrating moving-average autoregressive models and using the difference to deal with time series problems.
- SVR [40]. Support vector regression, a commonly used time series analysis model.
- DCRNN [35]. Diffusion convolutional recurrent neural networks that learn spatiotemporal features using diffusion convolutions.
- STGCN [35]. Spatiotemporal convolutional models, combining graph convolutional layers and convolutional sequences to learn spatiotemporal features.
- ASTGCN [34]. Time is divided into three parts: adjacent, daily, and weekly.
- STSGCN [37]. Three consecutive adjacent time slices are constructed into a local spatial graph.
- CCRNN [41]. A hierarchical coupling mechanism is proposed to fuse the adjacency matrices of different layers.
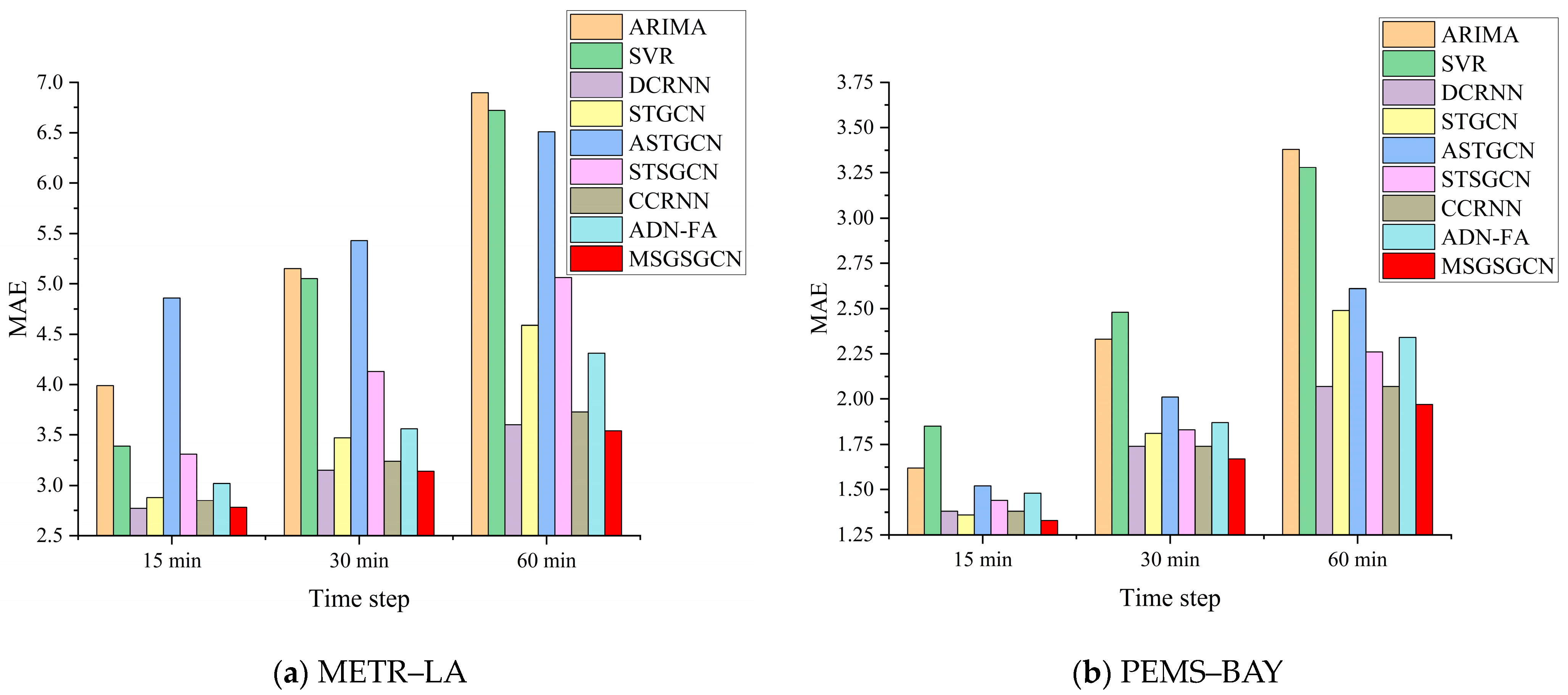
4.4. Results
4.4.1. Comparative Experiment
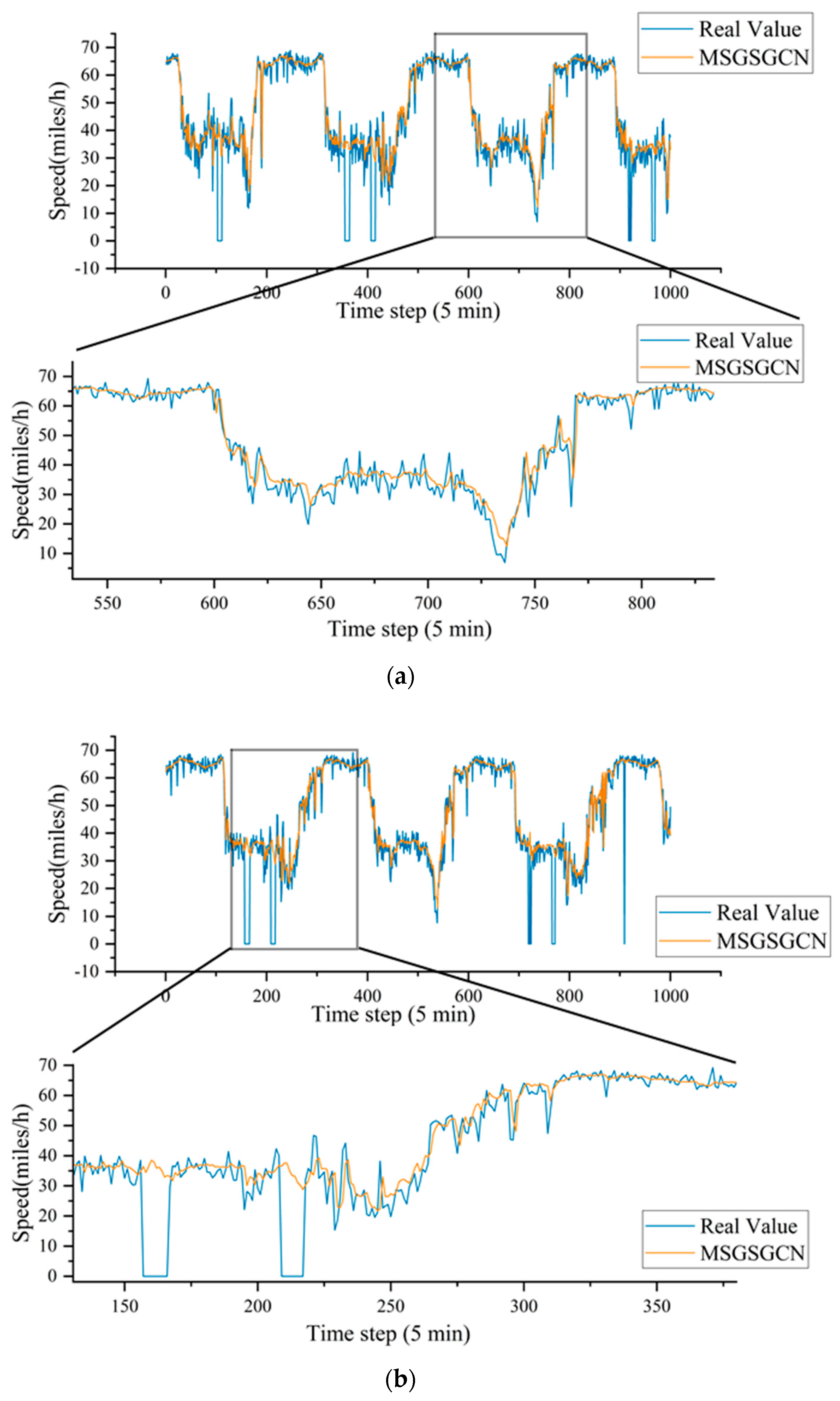
4.4.2. Visualization
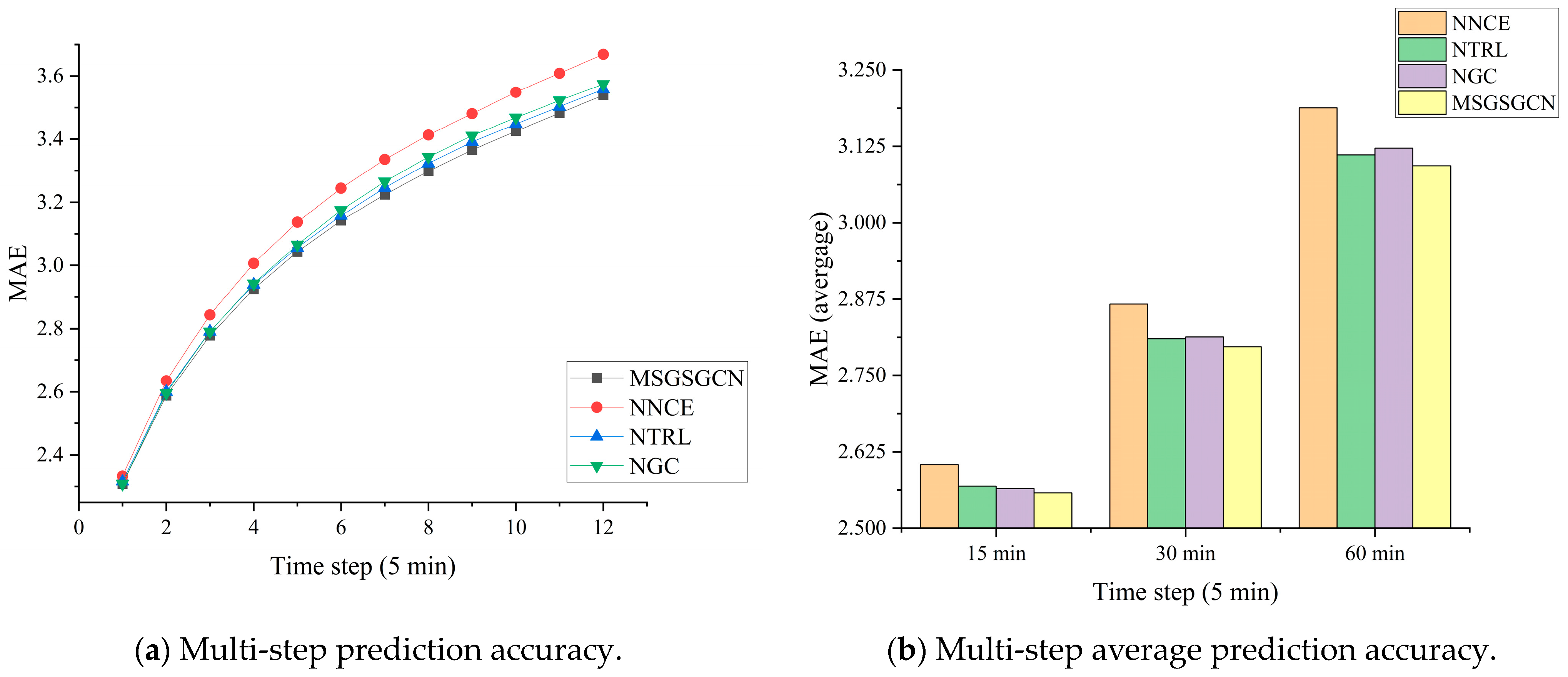
4.4.3. Ablation Study
- NNCE. The node correlation estimator module is removed, and the feedforward network is used instead.
- NTRL. The TRL module is removed, using only a single TCN with ELU activation.
- NGC. The Gated Graph Convolutional Fusion module is removed, and only Adaptive Diffusion Graph Convolution is used.
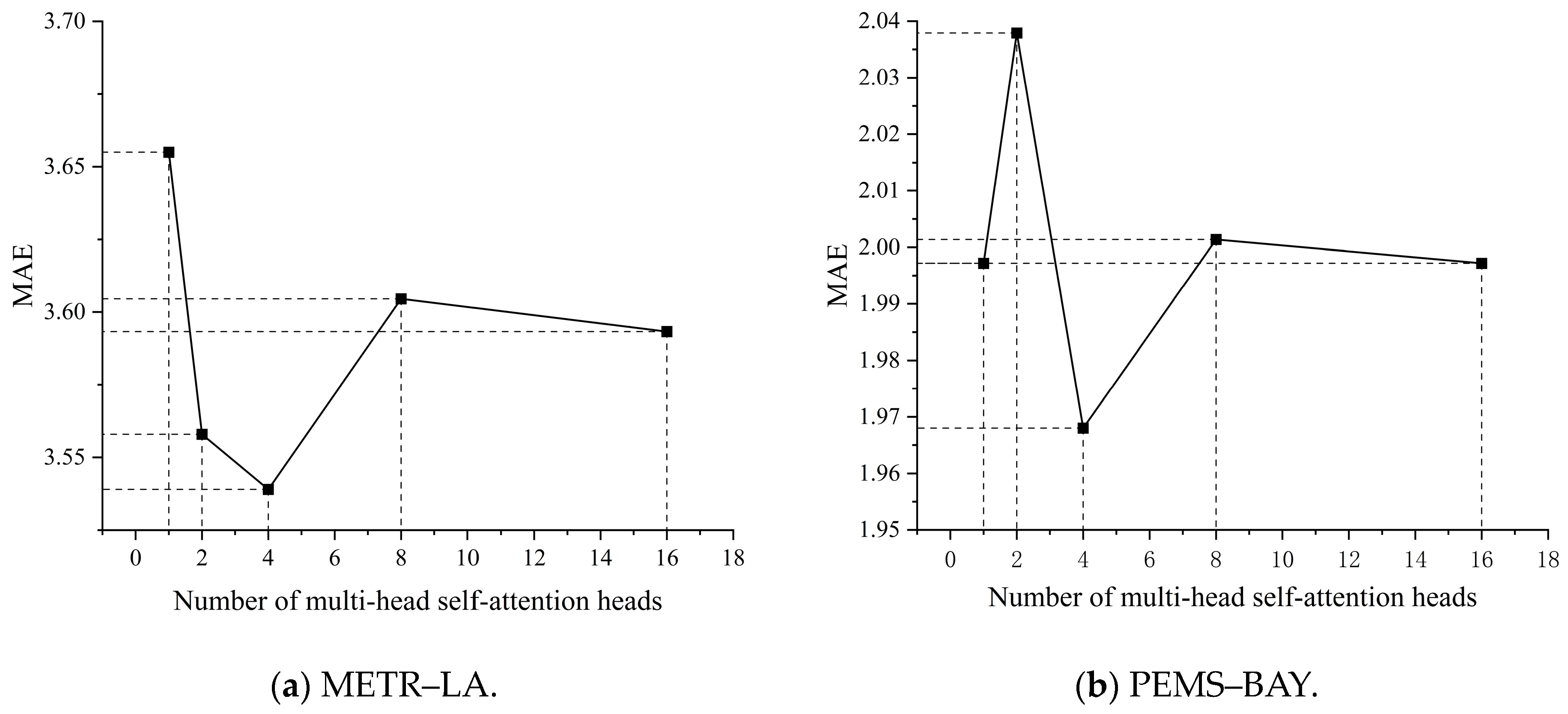
4.4.4. Parameter Sensitivity
4.5. Discussion
5. Conclusions
- In terms of computational efficiency, the GGCF module requires a longer training time compared to the NCE module, and the accuracy improvement is not significant. This is mainly because each gating unit needs to train many learnable parameters, whereas the parameters for each spatiotemporal module layer are not shared.
- In terms of model generalizability, an adjacency matrix that describes the network structure still needs to be constructed before training, which limits the model’s versatility across different road networks.
- In terms of considering external factors, the model’s architecture does not sufficiently take into account other external influences that affect network data, such as weather and holidays, which leads to the model’s inability to simulate real-world traffic patterns accurately.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, H.M.; Wang, G. Partial differential grey model based on control matrix and its application in short-term traffic flow prediction. Appl. Math. Model. 2023, 116, 763–785. [Google Scholar] [CrossRef]
- Feng, A.; Tassiulas, L. Adaptive graph spatial-temporal transformer network for traffic forecasting. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 3933–3937. [Google Scholar]
- Liu, H.T.; Wang, H.F. Real-time anomaly detection of network traffic based on CNN. Symmetry 2023, 15, 1205. [Google Scholar] [CrossRef]
- Han, X.; Zhu, G.; Zhao, L.; Du, R.H.; Wang, Y.H.; Chen, Z.; Liu, Y.; He, S.L. Ollivier–Ricci curvature based spatio-temporal graph neural networks for traffic flow forecasting. Symmetry 2023, 15, 995. [Google Scholar] [CrossRef]
- Xiao, J.; Zhou, Z. Research progress of RNN language model. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 27–29 June 2020; pp. 1285–1288. [Google Scholar]
- Wang, Y.H.; Fang, S.; Zhang, C.X.; Xiang, S.M.; Pan, C.H. TVGCN: Time-variant graph convolutional network for traffic forecasting. Neurocomputing 2022, 471, 118–129. [Google Scholar] [CrossRef]
- Jiang, W.W.; Luo, J.Y.; He, M.; Gu, W.X. Graph neural network for traffic forecasting: The research progress. ISPRS Int. J. Geo-Inf. 2023, 12, 100. [Google Scholar] [CrossRef]
- Bui, K.H.N.; Cho, J.; Yi, H. Spatial-temporal graph neural network for traffic forecasting: An overview and open research issues. Appl. Intell. 2022, 52, 2763–2774. [Google Scholar] [CrossRef]
- Ding, C.; Duan, J.X.; Zhang, Y.R.; Wu, X.K.; Yu, G.Z. Using an ARIMA-GARCH modeling approach to improve subway short-term ridership forecasting accounting for dynamic volatility. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1054–1064. [Google Scholar] [CrossRef]
- Mehdi, H.; Pooranian, Z.; Vinueza Naranjo, P.G.V. Cloud traffic prediction based on fuzzy ARIMA model with low dependence on historical data. Trans. Emerg. Telecommun. Technol. 2022, 33, e3731. [Google Scholar] [CrossRef]
- Luo, X.; Peng, J.; Liang, J. Directed hypergraph attention network for traffic forecasting. IET Intell. Transp. Syst. 2022, 16, 85–98. [Google Scholar] [CrossRef]
- Hou, Z.W.; Du, Z.X.; Yang, G.; Yang, Z. Short-term passenger flow prediction of urban rail transit based on a combined deep learning model. Appl. Sci. 2022, 12, 7597. [Google Scholar] [CrossRef]
- Williams, B.M.; Hoel, L.A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: Theoretical basis and empirical results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef]
- Kumar, B.P.; Hariharan, K. Time series traffic flow prediction with hyper-parameter optimized ARIMA models for intelligent transportation system. J. Sci. Ind. Res. 2022, 81, 408–415. [Google Scholar]
- Yao, E.Z.; Zhang, L.J.; Li, X.H.; Yun, X. Traffic forecasting of back servers based on ARIMA-LSTM-CF hybrid model. Int. J. Comput. Intell. Syst. 2023, 16, 65. [Google Scholar] [CrossRef]
- Lohrasbinasab, I.; Shahraki, A.; Taherkordi, A.; Jurcut, A.D. From statistical-to machine learning-based network traffic prediction. Trans. Emerg. Telecommun. Technol. 2022, 33, e4394. [Google Scholar] [CrossRef]
- Cai, P.L.; Wang, Y.P.; Lu, G.Q.; Chen, P.; Ding, C.; Sun, J.P. A spatiotemporal correlative k-nearest neighbor model for short-term traffic multistep forecasting. Transp. Res. Part C Emerg. Technol. 2016, 62, 21–34. [Google Scholar] [CrossRef]
- Feng, X.X.; Ling, X.Y.; Zheng, H.F.; Chen, Z.H.; Xu, Y.W. Adaptive multi-kernel SVM with spatial–temporal correlation for short-term traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2001–2013. [Google Scholar] [CrossRef]
- Xie, P.; Li, T.R.; Liu, J.; Du, S.D.; Yang, X.; Zhang, J.B. Urban flow prediction from spatiotemporal data using machine learning: A survey. Inf. Fusion 2020, 59, 1–12. [Google Scholar] [CrossRef]
- Razali, N.A.M.; Shamsaimon, N.; Ishak, K.K.; Ramli, S.; Amran, M.F.M.; Sukardi, S. Gap, techniques and evaluation: Traffic flow prediction using machine learning and deep learning. J. Big Data. 2021, 8, 152. [Google Scholar] [CrossRef]
- Ai, D.H.; Jiang, G.Y.J.; Lam, S.K.; He, P.L.; Li, C.W. Computer vision framework for crack detection of civil infrastructure—A review. Eng. Appl. Artif. Intell. 2023, 117, 105478. [Google Scholar] [CrossRef]
- Goyal, S.; Doddapaneni, S.; Khapra, M.M.; Ravindran, B. A survey of adversarial defenses and robustness in NLP. ACM Comput. Surv. 2023, 55, 1–39. [Google Scholar] [CrossRef]
- Seshia, S.A.; Jha, S.; Dreossi, T. Semantic adversarial deep learning. IEEE Des. Test. 2020, 37, 8–18. [Google Scholar] [CrossRef]
- Zhang, Y.; Qian, F.; Xiao, F. GS-RNN: A novel RNN optimization method based on vanishing gradient mitigation for HRRP sequence estimation and recognition. In Proceedings of the 2020 IEEE 3rd International Conference on Electronics Technology (ICET), Chengdu, China, 8–12 May 2020; pp. 840–844. [Google Scholar]
- Tian, Y.; Zhang, K.L.; Li, J.Y.; Lin, X.X.; Yang, B.L. LSTM-based traffic flow prediction with missing data. Neurocomputing 2018, 318, 297–305. [Google Scholar] [CrossRef]
- Kang, D.; Lv, Y.; Chen, Y. Short-term traffic flow prediction with LSTM recurrent neural network. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–6. [Google Scholar]
- Abdullah, S.M.; Periyasamy, M.; Kamaludeen, N.A.; Towfek, S.K.; Marappan, R.; Raju, S.K.; Alharbi, A.H.; Khafaga, D.S. Optimizing traffic flow in smart cities: Soft GRU-based recurrent neural networks for enhanced congestion prediction using deep learning. Sustainability 2023, 15, 5949. [Google Scholar] [CrossRef]
- Ma, C.X.; Zhao, Y.P.; Dai, G.W.; Xu, X.C.; Wong, S.C. A novel STFSA-CNN-GRU hybrid model for short-term traffic speed prediction. IEEE Trans. Intell. Transp. Syst. 2022, 24, 3728–3737. [Google Scholar] [CrossRef]
- Bao, Y.X.; Shi, Q.; Shen, Q.Q.; Cao, Y. Spatial-temporal 3D residual correlation network for urban traffic status prediction. Symmetry 2021, 14, 33. [Google Scholar] [CrossRef]
- Ni, Q.J.; Zhang, M. STGMN: A gated multi-graph convolutional network framework for traffic flow prediction. Appl. Intell. 2022, 52, 15026–15039. [Google Scholar] [CrossRef]
- Bao, Y.X.; Liu, J.L.; Shen, Q.Q.; Cao, Y.; Ding, W.P.; Shi, Q. PKET-GCN: Prior knowledge enhanced time-varying graph convolution network for traffic flow prediction. Inf. Sci. 2023, 634, 359–381. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.J.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H.F. T-GCN: A temporal graph convolutional network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3848–3858. [Google Scholar] [CrossRef]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv 2017, arXiv:1709.04875. [Google Scholar]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 922–929. [Google Scholar]
- Li, Y.G.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. arXiv 2017, arXiv:1707.01926. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph WaveNet for deep spatial-temporal graph modeling. arXiv 2019, arXiv:1906.00121. [Google Scholar]
- Song, C.; Lin, Y.; Guo, S.; Wan, H. Spatial-temporal synchronous graph convolutional networks: A new framework for spatial-temporal network data forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 914–921. [Google Scholar]
- Ye, Y.Q.; Xiao, Y.; Zhou, Y.X.; Li, S.W.; Zang, Y.F.; Zhang, Y.X. Dynamic multi-graph neural network for traffic flow prediction incorporating traffic accidents. Expert Syst. Appl. 2023, 234, 121101. [Google Scholar] [CrossRef]
- Hassanat, A.; Alkafaween, E.; Tarawneh, A.S.; Elmougy, S. Applications review of hassanat distance metric. In Proceedings of the International Conference on Emerging Trends in Computing and Engineering Applications (ETCEA), Karak, Jordan, 23–24 November 2022; pp. 1–6. [Google Scholar]
- Shao, Z.; Zhang, Z.; Wei, W.; Wang, F.; Xu, Y.; Cao, X. Decoupled dynamic spatial-temporal graph neural network for traffic forecasting. arXiv 2022, arXiv:2206.09112. [Google Scholar] [CrossRef]
- Ye, J.; Sun, L.; Du, B.; Fu, Y.; Xiong, H. Coupled layer-wise graph convolution for transportation demand prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 4617–4625. [Google Scholar]
- Rad, A.C.; Lemnaru, C.; Munteanu, A. A comparative analysis between efficient attention mechanisms for traffic forecasting without structural priors. Sensors 2022, 22, 7457. [Google Scholar] [CrossRef]
- Drakulic, D.; Andreoli, J.M. Structured time series prediction without structural prior. arXiv 2022, arXiv:2202.03539. [Google Scholar]


| Model Type | Model | Advantage | Disadvantage |
|---|---|---|---|
| Classical Statistical Model | ARIMA [9] | Earlier models for dealing with time series problems. | Struggles to handle complex nonlinear issues. |
| Traditional Machine Learning | KNN [17] | Easy to understand and implement. | Unable to handle high-dimensional data. |
| SVM [18] | Can handle medium- to small-sized datasets. | Computational performance is suboptimal when handling large datasets. | |
| Classic Deep Learning Method | T-GCN [32] | Spatiotemporal characteristics of traffic data are considered. | A pre-built adjacency matrix is required. |
| STGCN [33] | The receptive field of CNN is improved. | Difficult to capture long-term dependency features. | |
| ASTGCN [34] | Time series is divided into neighboring features, daily features, and weekly features. | It cannot simulate dynamic graph data. | |
| DCRNN [35] | Traffic movement is modeled as a process of dispersion. | Global graph structure information is ignored. | |
| Graph WaveNet [36] | The gating unit is used to control the information flow. | The spatiotemporal correlation between nodes is not considered | |
| STSGCN [37] | Combines adjacent time steps into a new adjacency matrix. | High complexity. | |
| The proposed model. | MSGSGCN | Learns the dynamic spatiotemporal correlations and long-term temporal patterns in the road network. | The impact of external factors in the real world, such as weather and holidays, is not considered. |
| Dataset | METR–LA | PEMS–BAY |
|---|---|---|
| Area | Los Angeles | Bay Area of California |
| Nodes | 207 | 325 |
| Time interval | 5 min | 5 min |
| Target | Speed | Speed |
| Start time | 1 March 2012 | 1 January 2017 |
| End time | 27 June 2012 | 30 June 2017 |
| Data | Models | 15 min | 30 min | 60 min | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | ||
| METR–LA | ARIMA | 3.99 | 8.21 | 9.60% | 5.15 | 10.45 | 12.70% | 6.90 | 13.23 | 17.40% |
| SVR | 3.39 | 8.45 | 9.30% | 5.05 | 10.87 | 12.10% | 6.72 | 13.76 | 16.70% | |
| DCRNN | 2.77 | 5.38 | 7.30% | 3.15 | 6.45 | 8.80% | 3.60 | 7.60 | 10.50% | |
| STGCN | 2.88 | 5.74 | 7.62% | 3.47 | 7.24 | 9.57% | 4.59 | 9.40 | 12.70% | |
| ASTGCN | 4.86 | 9.27 | 9.21% | 5.43 | 10.61 | 10.13% | 6.51 | 12.52 | 11.64% | |
| STSGCN | 3.31 | 7.62 | 8.06% | 4.13 | 9.77 | 10.29% | 5.06 | 11.66 | 12.91% | |
| CCRNN | 2.85 | 5.54 | 7.50% | 3.24 | 6.54 | 8.90% | 3.73 | 7.65 | 10.59% | |
| ADN-FA | 3.02 | 6.01 | 8.20% | 3.56 | 7.30 | 10.22% | 4.31 | 8.70 | 12.61% | |
| MSGSGCN | 2.78 | 5.36 | 7.26% | 3.14 | 6.32 | 8.67% | 3.54 | 7.25 | 10.16% | |
| Data | Models | 15 min | 30 min | 60 min | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | ||
| PEMS–BAY | ARIMA | 1.62 | 3.30 | 3.50% | 2.33 | 4.76 | 5.40% | 3.38 | 6.50 | 8.30% |
| SVR | 1.85 | 3.59 | 3.80% | 2.48 | 5.18 | 5.50% | 3.28 | 7.08 | 8.00% | |
| DCRNN | 1.38 | 2.95 | 2.90% | 1.74 | 3.97 | 3.90% | 2.07 | 4.74 | 4.90% | |
| STGCN | 1.36 | 2.96 | 2.90% | 1.81 | 4.27 | 4.17% | 2.49 | 5.69 | 5.79% | |
| ASTGCN | 1.52 | 3.13 | 3.22% | 2.01 | 4.27 | 4.48% | 2.61 | 5.42 | 6.00% | |
| STSGCN | 1.44 | 3.01 | 3.04% | 1.83 | 4.18 | 4.17% | 2.26 | 5.21 | 5.40% | |
| CCRNN | 1.38 | 2.90 | 2.90% | 1.74 | 3.87 | 3.90% | 2.07 | 4.65 | 4.87% | |
| ADN-FA | 1.48 | 3.04 | 3.05% | 1.87 | 4.12 | 4.16% | 2.34 | 5.22 | 5.72% | |
| MSGSGCN | 1.33 | 2.84 | 2.80% | 1.67 | 3.81 | 3.77% | 1.97 | 4.53 | 4.61% | |
| Ablation | 15 min | 30 min | 60 min | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MHD | MAE | RMSE | MHD | MAE | RMSE | MHD | |
| NNCE | 2.604 | 4.897 | 0.1662 | 2.867 | 5.625 | 0.1699 | 3.188 | 6.460 | 0.1743 |
| NTRL | 2.569 | 4.770 | 0.1657 | 2.810 | 5.423 | 0.1692 | 3.111 | 6.209 | 0.1735 |
| NGC | 2.565 | 4.771 | 0.1656 | 2.813 | 5.428 | 0.1692 | 3.122 | 6.212 | 0.1736 |
| MSGSGCN | 2.558 | 4.739 | 0.1655 | 2.797 | 5.392 | 0.1690 | 3.093 | 6.155 | 0.1732 |
| Ablation | Total Params (Units) | FLOPs (M) | Training Time (s/epoch) | Inference Time (s) |
|---|---|---|---|---|
| NNCE | 299,620 | 18,143.29 | 63.4374 | 2.3665 |
| NTRL | 279,024 | 15,338.2 | 58.5805 | 2.2593 |
| NGC | 305,968 | 13,927.34 | 40.2114 | 1.7264 |
| MSGSGCN | 312,304 | 18,159.91 | 64.8359 | 2.4975 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, C.; Bao, Y.; Shi, Q.; Shen, Q. Dynamic Spatiotemporal Correlation Graph Convolutional Network for Traffic Speed Prediction. Symmetry 2024, 16, 308. https://doi.org/10.3390/sym16030308
Cao C, Bao Y, Shi Q, Shen Q. Dynamic Spatiotemporal Correlation Graph Convolutional Network for Traffic Speed Prediction. Symmetry. 2024; 16(3):308. https://doi.org/10.3390/sym16030308
Chicago/Turabian StyleCao, Chenyang, Yinxin Bao, Quan Shi, and Qinqin Shen. 2024. "Dynamic Spatiotemporal Correlation Graph Convolutional Network for Traffic Speed Prediction" Symmetry 16, no. 3: 308. https://doi.org/10.3390/sym16030308
APA StyleCao, C., Bao, Y., Shi, Q., & Shen, Q. (2024). Dynamic Spatiotemporal Correlation Graph Convolutional Network for Traffic Speed Prediction. Symmetry, 16(3), 308. https://doi.org/10.3390/sym16030308





