Adaptive Feedback Control of Nonminimum Phase Boost Converter with Constant Power Load
Abstract
:1. Introduction
2. System Description and Modeling
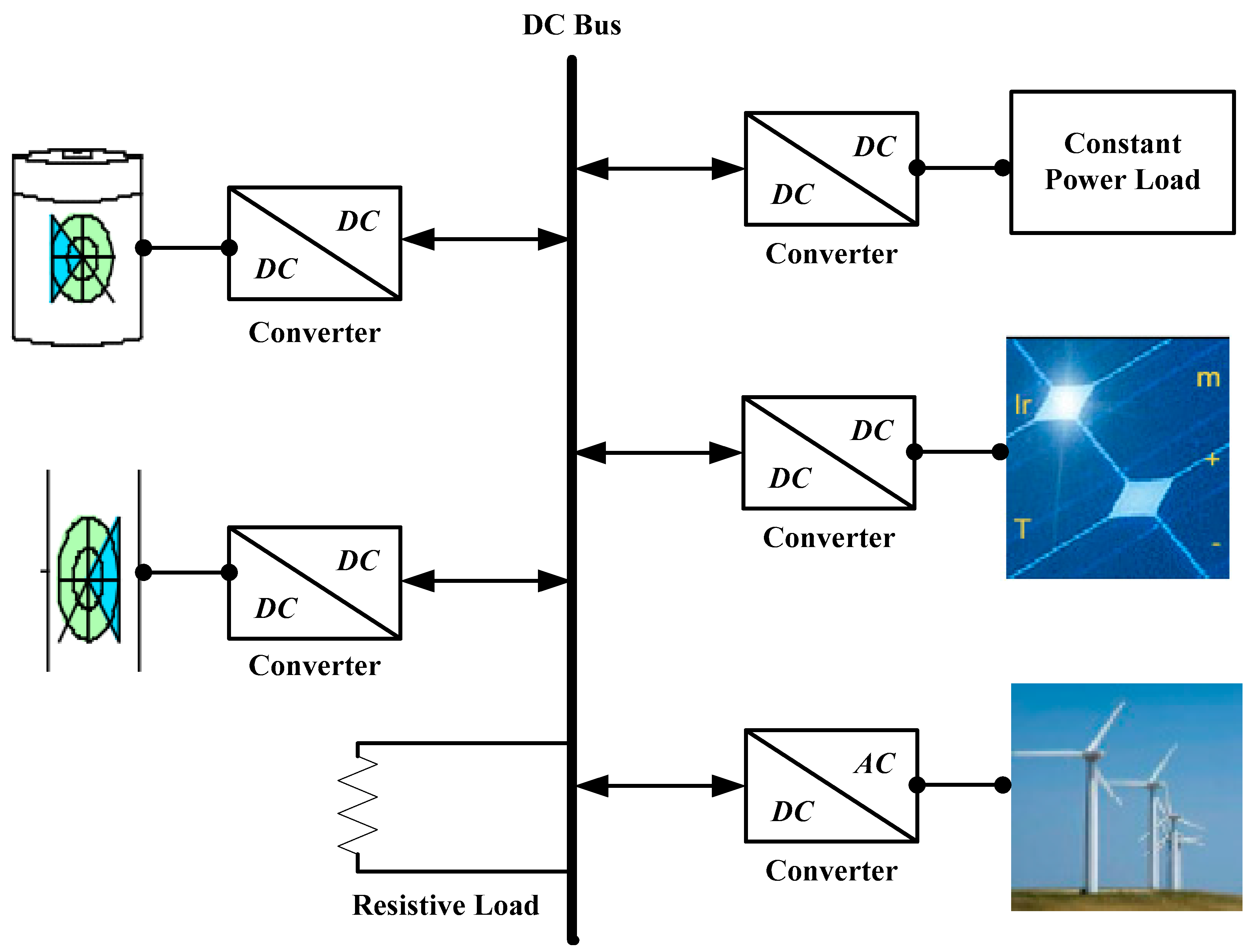
2.1. System Description
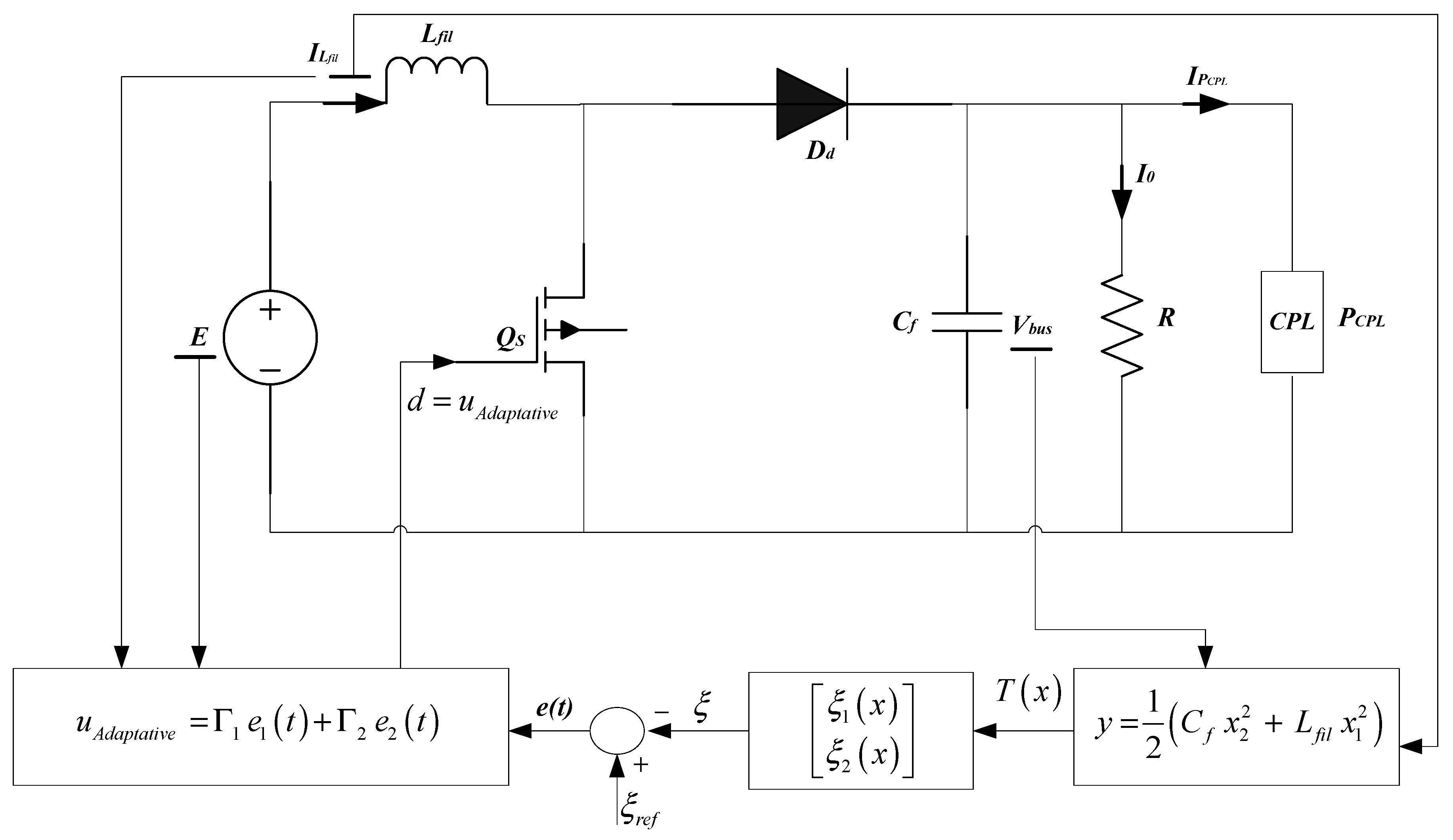
2.2. Modeling System
3. System Analysis and Problem Formulation
3.1. System Analysis
- (i).
- The rank of the matrix is constant and equal to n for any x near x0.
- (ii).
- The vector field set is involutory at x = x0.
3.2. Problem Formulation
4. Nonlinear Adaptative Feedback Controller
Remarks
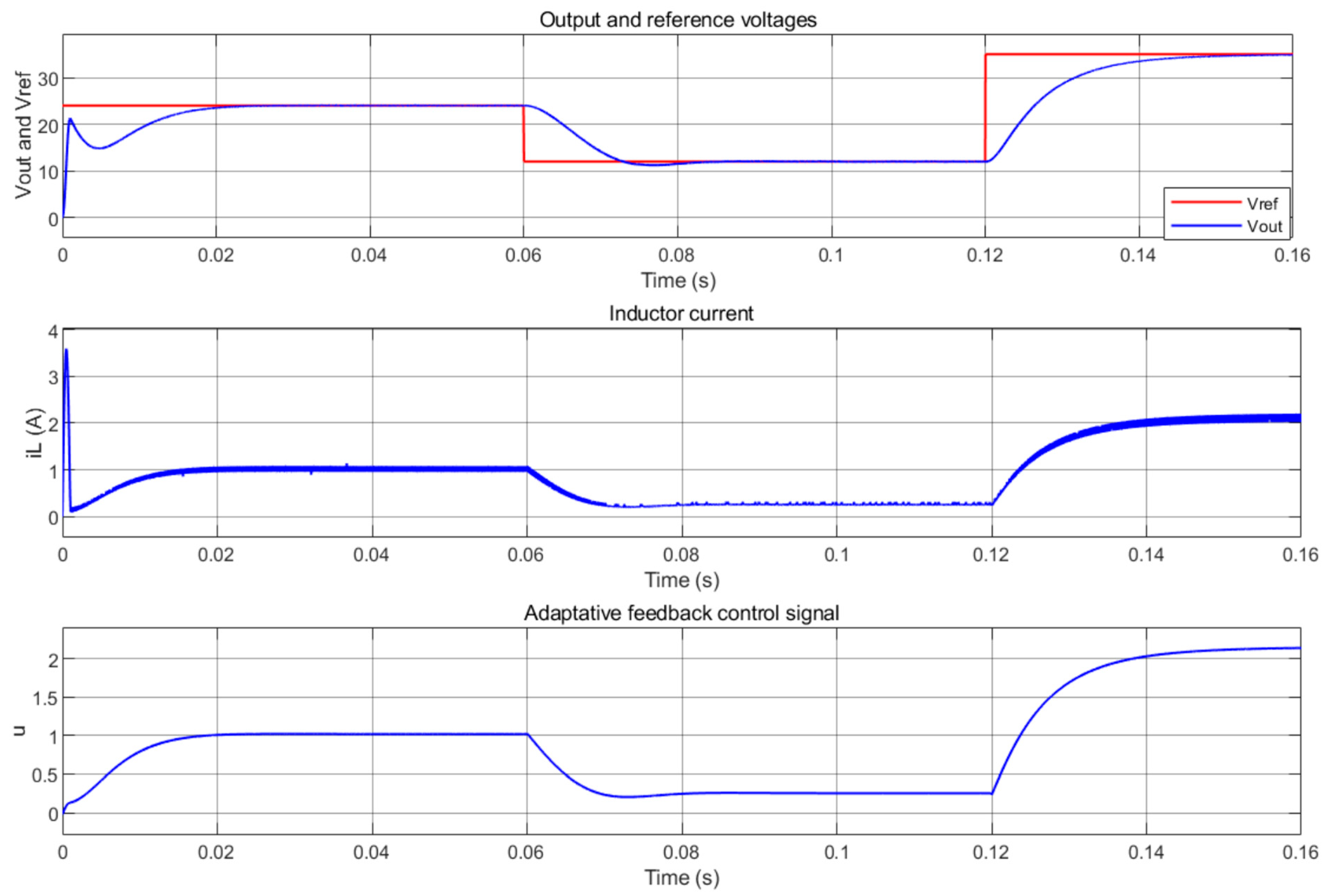
5. Simulation Results
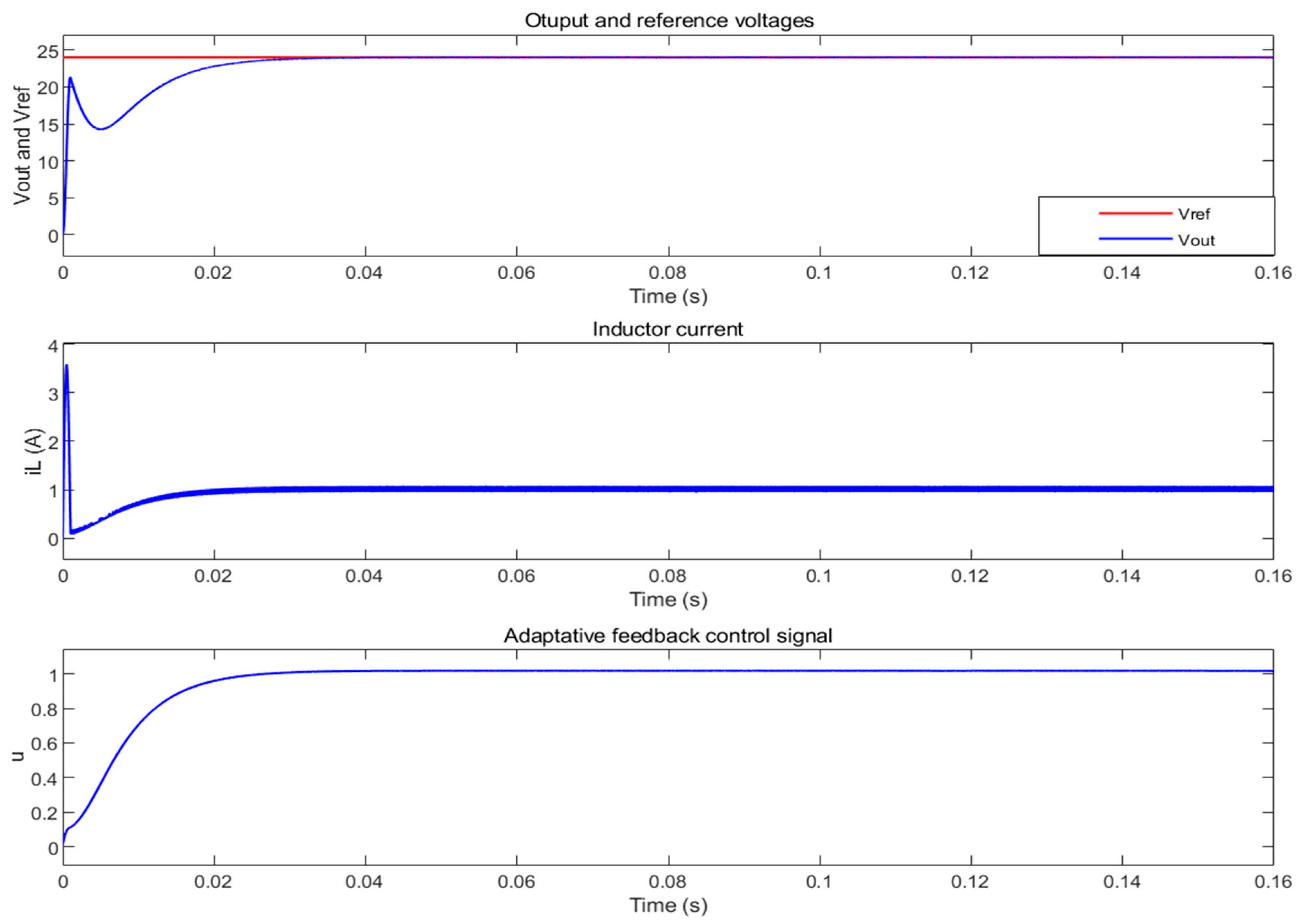
5.1. Case 1
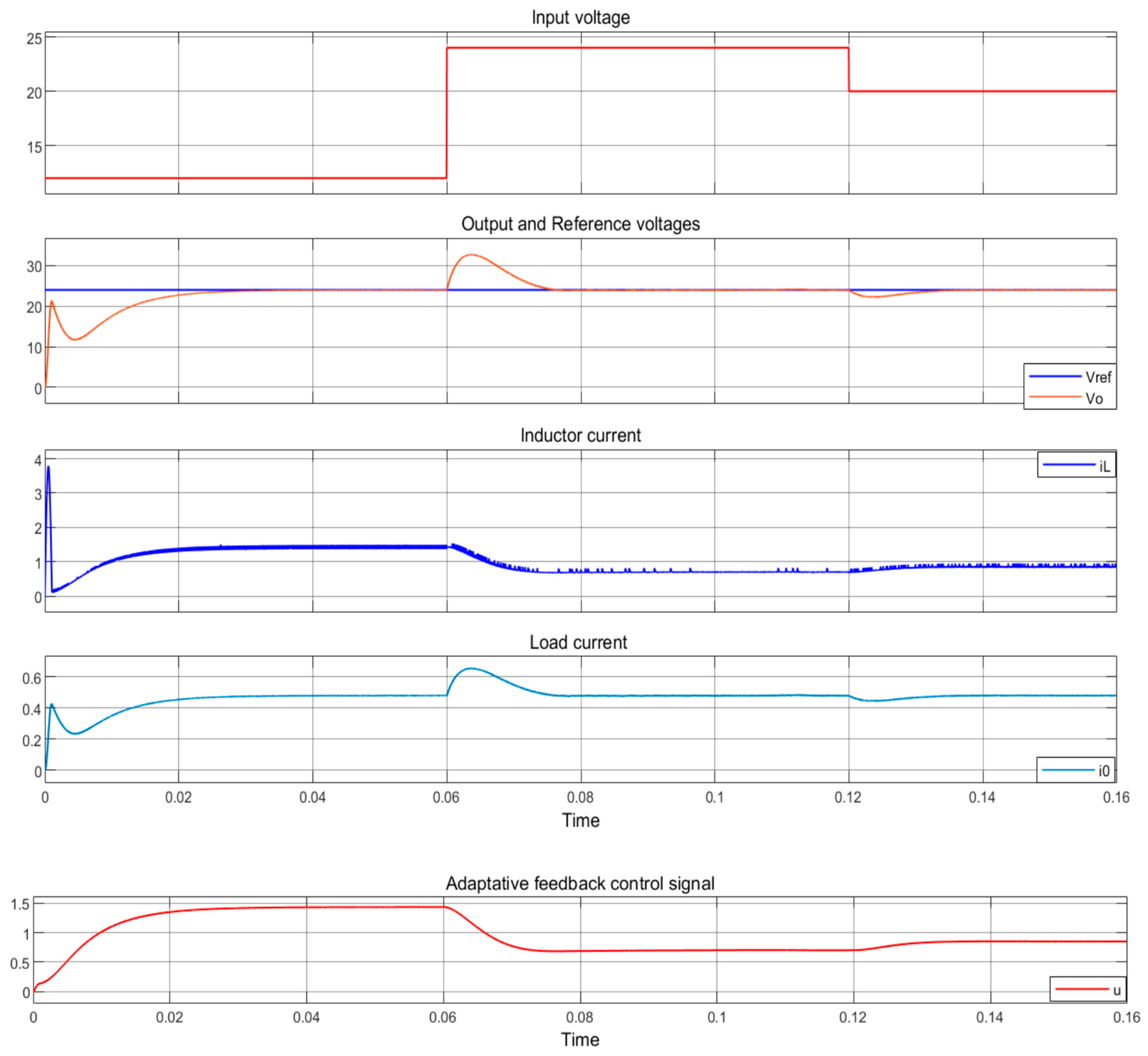
5.2. Case 2
5.3. Case 3
5.4. Case 4
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rahimi, A.M.; Emadi, A. An analytical investigation of DC/DC power electronic converters with constant power loads in vehicular power systems. Trans. Veh. Technol. 2009, 58, 2689–2702. [Google Scholar] [CrossRef]
- Lu, X.; Sun, K.; Guerrero, J.M.; Vasquez, J.C.; Huang, L.; Wang, J. Stability enhancement based on virtual impedance for dc microgrids with constant power loads. IEEE Trans. Smart Grid 2015, 6, 2770–2783. [Google Scholar] [CrossRef]
- Chang, X.; Li, Y.; Li, X.; Chen, X. An active damping method based on a supercapacitor energy storage system to overcome the destabilizing effect of instantaneous constant power loads in DC microgrids. IEEE Trans. Energy Convers. 2017, 32, 36–47. [Google Scholar] [CrossRef]
- Khaligh, A.; Rahimi, A.M.; Emadi, A. Negative Impedance Stabilizing Pulse Adjustment Control Technique for DC/DC Converters Operating in Discontinuous Conduction Mode and Driving Constant Power Loads. IEEE Trans. Veh. Technol. 2007, 56, 2005–2016. [Google Scholar] [CrossRef]
- Zhang, X.; He, W.; Zhang, Y. An Adaptive Output Feedback Controller for Boost Converter. Electronics 2022, 11, 905–914. [Google Scholar] [CrossRef]
- Cespedes, M.; Xing, L.; Sun, J. Constant power load system stabilization by passive damping. IEEE Trans. Power Electron. 2011, 26, 1832–1836. [Google Scholar] [CrossRef]
- Jouili, K.; Madani, A. Nonlinear Lyapunov control of a photovoltaic water pumping system. Energies 2023, 16, 2241. [Google Scholar] [CrossRef]
- Jouili, K.; Belhadj, W. Robust stabilization for uncertain non-minimum phase switched nonlinear System under arbitrary switchings. Symmetry 2023, 15, 596. [Google Scholar] [CrossRef]
- Rahimi, A.; Emadi, A. Discontinuous-Conduction Mode DC/DC Converters Feeding Constant-Power Loads. IEEE Trans. Ind. Electron. 2010, 57, 1318–1329. [Google Scholar] [CrossRef]
- Kwasinski, A.; Krein, P.T. Stabilization of constant power loads in dc-dc converters using passivity-based control. In Proceedings of the INTELEC 07–29th International Telecommunications Energy Conference, Rome, Italy, 30 September–4 October 2007; pp. 867–874. [Google Scholar]
- Zeng, J.; Zhang, Z.; Qiao, W. An interconnection and damping assignment passivity-based controller for a dc-dc boost converter with a constant power load. IEEE Trans. Ind. Appl. 2014, 50, 2314–2322. [Google Scholar] [CrossRef]
- Kwasinski, A. Dynamic behavior and stabilization of dc microgrids with instantaneous constant-power loads. IEEE Trans. Power Electron. 2011, 26, 822–834. [Google Scholar] [CrossRef]
- Villarroel, F.A.; Espinoza, J.R.; Pérez, M.A.; Ramírez, R.O.; Baier, C.R.; Sbárbaro, D.; Silva, J.J.; Reyes, M.A. Stable Shortest Horizon FCS-MPC Output Voltage Control in Non-Minimum Phase Boost-Type Converters Based on Input-State Linearization. IEEE Trans. Energy Convers. 2021, 36, 1378–1390. [Google Scholar] [CrossRef]
- Byrnes, C.; Isidori, A.; Willems, J. Passivity, feedback equivalence, and the global stabilization of minimum phase nonlinearsystems. IEEE Trans. Autom. Control 1991, 36, 1228–1240. [Google Scholar] [CrossRef]
- Singh, S.; Gautam, A.R.; Fulwani, D. Constant power loads and their effects in DC distributed power systems: A review. Renew. Sustain. Energy Rev. 2017, 72, 407–421. [Google Scholar] [CrossRef]
- Li, Y.; Vannorsdel, K.R.; Zirger, A.J.; Norris, M.; Maksimovic, D. Current mode control for boost converters with constant power loads. IEEE Trans. Circuits Syst. 2012, 59, 198–206. [Google Scholar] [CrossRef]
- Santi, E.; Li, D.; Monti, A.; Stankovic, A.M. A geometric approach to large-signal stability of switching converters under sliding mode control and synergetic control. In Proceedings of the Power Electronics Specialists Conference, Recife, Barazil, 16 June 2005; pp. 1389–1395. [Google Scholar]
- Jouili, K. Robuststabilization of non-minimum phase switched nonlinear systems with uncertainty. J. Syst. Sci. Complex. 2020, 33, 289–311. [Google Scholar]
- Zengshi, C.; Wenzhong, G.; Jiangang, H.; Xiao, Y. Closed-Loop Analysis and Cascade Control of a Nonminimum Phase Boost Converter. IEEE Trans. Power Electron. 2011, 26, 1237–1252. [Google Scholar]
- Mahmoudi, H.; Aleenejad, M.; Ahmadi, R. A new modulated model predictive control method for mitigation of effects of constant power loads. In Proceedings of the IEEE Power and Energy Conference at Illinois, Urbana, IL, USA, 19–20 February 2016; pp. 1–5. [Google Scholar]
- Emadi, A.; Khaligh, A.; Rivetta, C.; Williamson, G. Constant power loads and negative impedance instability in automotive systems:definition, modeling, stability, and control of power electronic converters and motor drives. IEEE Trans. Veh. Technol. 2006, 55, 1112–1125. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiao, W.; Ha, D. A sliding-mode duty-ratio controller for dc/dc buck converters with constant power loads. IEEE Trans. Ind. Appl. 2014, 50, 1448–1458. [Google Scholar] [CrossRef]
- Baev, S.; Sheessel, Y. Causal output tracking in nonminimum phase boost DC/DC converter using sliding mode techniques. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 77–82. [Google Scholar]
- Talebi, H.A.; Patel, R.V.; Khorasani, K. Control of Flexible-Link Manipulators Using Neural Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; p. 261. [Google Scholar]
- Sira-Ramirez, H.; Ortega, R. Passivity-basedcontrollers for the stabilization of dc-to-dc power converters, Decision and Control. In Proceedings of the 1995 34th IEEE Conference on Decision and Control, New Orleans, LA, USA, 13–15 December 1995; Volume 4, pp. 3471–3476. [Google Scholar]
- Escobar, G.; Ortega, R.; Sira-Ramirez, H.; Vilain, J.; Zein, I. An experimental comparison of several nonlinear controllers for power converters. IEEE Control. Syst. Mag. 1999, 19, 66–82. [Google Scholar]
- Ortega, R.; Perez, J.A.L.; Nicklasson, P.J.; Sira-Ramirez, H. Passivity-Based Control of Euler-Lagrange Systems: Mechanical, Electrical and Electromechanical Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Slotine, J.-J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Roshan, Y.M.; Moallem, M. Control of nonminimum phase loadcurrent in a boost converterusing output redefinition. IEEE Trans. Power Electron. 2014, 29, 5054–5062. [Google Scholar] [CrossRef]
- Jouili, K.; Braiek, N.B. Controllers design for stabilization of non-minimum phase of switched nonlinear systems. JCEAI Control. Eng. Appl. Inform. J. 2019, 21, 21–30. [Google Scholar]
- Alam, Z.; Ghosh, S.K.; Alkhateeb, A.F.; Roy, T.K.; Islam, M.S.; Saha, S.; Hussain, M.A. Robust hybrid nonlinear control approach for stability enhancement of a constant power load DC-DC boost converter. Alex. Eng. J. 2023, 74, 535–545. [Google Scholar] [CrossRef]
- Rahimi, A.; Khalilgh, A.; Emadi, A. Sub-Harmonic Problem in Multi-Converter Vehicular Power Systems. In Proceedings of the 2006 IEEE Vehicle Power and Propulsion Conference, Windsor, UK, 6–8 September 2006. [Google Scholar]
- Antonio, M.; Licea, R. Polytopic Robust Stability for a Dual-Capacitor Boost Converter in Symmetric and Non-Symmetric Configurations. Symmetry 2022, 14, 2331–2339. [Google Scholar]
- Emadi, A.; Ehsani, M. Negative impedance stabilizing controls for pwm dc-dc converters using feedback linearization techniques, Collection of Technical Papers. In Proceedings of the 35th Intersociety Energy Conversion Engineering Conference and Exhibit, Las Vegas, NV, USA, 24–28 July 2000; Volume 1, pp. 613–620. [Google Scholar]
- Trujillo, S.C.; Candelo-Becerra, J.E.; Hoyos, F.E. Numerical Validation of a Boost Converter Controlled by a Quasi-Sliding Mode Control Technique with Bifurcation Diagrams. Symmetry 2022, 14, 694–709. [Google Scholar] [CrossRef]
- Zhou, J.; Hassan, M.A.; Zhang, J.; Hou, M.; Wu, S.; Xing, G.; Chi, S. Stabilization of Constant Power Loads in DC Microgrid Systems Using an Adaptive Continuous Control Set Model Predictive Control. Symmetry 2021, 13, 1112–1140. [Google Scholar] [CrossRef]
- Bhavani, S.; Sivaprakasam, A. Dual Mode Symmetrical Proportional Resonant Controlled Quadratic Boost Converter for PMSM-Drive. Symmetry 2023, 15, 147–166. [Google Scholar] [CrossRef]
- Jiarong, W.; Yimin, L. Adaptive Backstepping Sliding Mode Control for Boost Converter with Constant Power Load. IEEE Access 2019, 7, 50797–50807. [Google Scholar]
- Villarroel, F.A.; Espinoza, J.R.; Pérez, M.A.; Ramírez, R.O.; Baier, C.R.; Sbárbaro, D.; Silva, J.J.; Reyes, M.A. A Predictive Shortest-Horizon Voltage Control Algorithm for Non-Minimum Phase Three-Phase Rectifiers. IEEE Access 2022, 10, 107598–107615. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jouili, K.; Charfeddine, M.; Alqarni, M. Adaptive Feedback Control of Nonminimum Phase Boost Converter with Constant Power Load. Symmetry 2024, 16, 352. https://doi.org/10.3390/sym16030352
Jouili K, Charfeddine M, Alqarni M. Adaptive Feedback Control of Nonminimum Phase Boost Converter with Constant Power Load. Symmetry. 2024; 16(3):352. https://doi.org/10.3390/sym16030352
Chicago/Turabian StyleJouili, Khalil, Monia Charfeddine, and Mohammed Alqarni. 2024. "Adaptive Feedback Control of Nonminimum Phase Boost Converter with Constant Power Load" Symmetry 16, no. 3: 352. https://doi.org/10.3390/sym16030352







