New Approach of Normal and Shear Stress Components for Multiple Curvilinear Holes Which Weakened a Flexible Plate

Abstract

In this article, a thin infinite flexible plate weakened by multiple curvilinear holes is considered. The strength shapes are mapped outside a unit circle with the assistance of particular conformal mapping under certain conditions. The mathematical model that governs the rounded forces of the current physical problem is the boundary value problem of elastic media. This study is applicable to many phenomena throughout nature, like tunnels, caves, and excavations in soil or rock. The Cauchy method for complex variables is used to get the closed forms of Gaursat functions and change the problem to a second-type integrodifferential equation with a Cauchy kernel, which is used for a large area of the contact problems. Then, the normal and shear stress components that act on the model are derived. Afterward, some of the physical applications are studied, and different stress components at specific values in each application are calculated and plotted using Maple 2023.

1. Introduction

There is often more stress concentrated in the vicinity of holes in plate structural components when external loads are applied. To assess the stability and strengthening of the structure, it is crucial to compute the stresses on the edges of the holes precisely. Odishelidze and Criado-Aldeanueva [1] studied axially symmetric problems of the plane theory of elasticity with partially unknown limits, where these problems were studied for a rhombus weakened by one or two holes. Manickam et al. [2] attempted to study the nonlinear thermo-elastic buckling characteristics of composite variable stiffness beams with layers using curvilinear fibers under a thermal environment. Hsieh and Hwu [3] derived a full-field solution for an infinite anisotropic plate containing a hole perturbed from an ellipse subjected to uniform loading at infinity with Stroh formalism. Kaloerov et al. [4] presented a general solution to the problems of elasticity theory for anisotropic half-planes and strips with arbitrary holes and cracks. Li et al. [5] presented a modified Laurent series to investigate the elastic field around holes and inclusions under plane deformation. Akinola [6] emphasized the alternate formulation of the Cauchy–Riemann criteria for the analyticity of a complex variable function. Using the complex variable method, Guo and Lu [7] proposed a new approach to solving the elastic–plastic fields close to the elliptical hole’s major-axis line. Ioakimidis and Theocaris [8] suggested a numerical approach for the solution of Cauchy-type singular integral equations along contours in the complex plane. Strack and Verruijt [9] derived an analytical solution for an energetic tunnel in a flexible half-plane. The half-plane’s surface is stress-free, and the tunnel experiences a defined displacement within its circumference. Li and Fan [10] developed the complex variable technique for the plane elasticity theory of icosahedral quasi-crystals. Yu et al. [11] investigated the linear piezoelastic behavior of one-dimensional (1D) hexagonal quasicrystals using the symmetry operations of point groups. Jiao et al. [12] investigated the Reddy-proposed dual mesh control domain method (DMCDM), which combines the benefits of the finite element approach (variable interpolation) and the finite volume method (a global form of the fulfillment of the governing equations).

Identifying ${\chi }_1\left(r\right)$ and ${\varpi }_1\left(r\right)$, two analytic functions of a single complex input $z=x+iy$, is known to be the equivalent (see [13]) of solving the first and second boundary value problems. These functions have to satisfy the following boundary conditions:

$$L{\chi }_1\left(r\right)-r\overline{{\chi }_1^{\prime }\left(r\right)}-\overline{r{\varpi }_1\left(r\right)}=g\left(r\right),$$

(1)

where $g\left(r\right)$ is a predefined function of stresses for the first boundary value problem with $L=-1$. For the second boundary value problem, $g\left(r\right)$ is a known function of displacement. If $\left|\tau \right|>1$, then the area outside of a closed contour that is infinite can be conformally mapped outside of the unit circle. This concerns the rational mapping function $z=c\xi \left(\tau \right)$, where $c>0$ and ${\varpi }^{\prime }\left(\tau \right)$ do not go away or become infinite. Both ${\chi }_1\left(r\right)$ and ${\varpi }_1\left(r\right)$ are complex potential functions of the following forms (see [14]):

$${Ø}_1\left(z\right)=-\frac{S_x+i{S}_y}{2\pi (1+k)}ln\tau +c\Gamma \tau +\chi \left(\tau \right),$$

(2)

and

$${\$}_1\left(z\right)=\frac{k\left(S_x-i{S}_y\right)}{2\pi (1+k)}ln\tau +c{\Gamma }^{+}\tau +\varpi \left(\tau \right).$$

(3)

Several authors, including [14,15,16], have discussed the boundary problems for holed infinite plates. A few of them described the solutions as power series using the Laurent theorem. Another technique for dealing with complex variables is the application of Gaursat functions. They take advantage of the characteristics of the circle or any mapped region of Cauchy integrals outside of a unit circle by using the general rational mapping function $z=c\xi \left(\tau \right)$. They obtain a solution in the form of two complex functions. Abdou et al. [15] applied the Gaursat functions in the complex variable approach to deduce the first and second types on a limitless plate with two holes that curve. Abdou and Monaquel [17] solved the fundamental problems of an infinite plate with a hole that is weakened by a strong pole in any form using the Cauchy singular technique. Mattei and Lim [18] defined a density basis function on the inclusion’s border using the coordinate system made available by the exterior conformal mapping of the inclusion. To create a closed form of Gaursat functions with variant time, Alhazmi et al. [19] used the complex variables approach and assumed an infinite elastic plate that had two holes weakening it. Leonhardt [20] created a generic formula for designing media that produces perfect invisibility while maintaining geometrical optic precision. Trefethen [21] developed new methods for numerical conformal mapping based on the least-squares fitting on the boundary and rational approximations for solving Dirichlet problems. Caprini [22] discussed a reformulation of QCD perturbation theory as an expansion in terms of a set of nonpower functions of the strong coupling. Kiosak et al. [23] have investigated the conformal mappings of particular quasi-Einstein spaces. Symm [24] presented an integral equation technique for determining the conformal mapping of a given simply connected domain onto the unit circle’s interior. O’Donnell and Rokhlin [25] presented a method for creating conformal mappings from any simply linked region in the complex plane onto the unit disk. Fu et al. [26] obtained the equivalent invariant under a class of conformal mappings between two semi-Riemannian manifolds. Moreover, Ghods et al. [27] applied conformal mapping to create the permeance network for complex-geometry air-gap regions. Mukherjee and Fok [28] presented a novel method for computing the fiber field in a generic artery cross-section by applying conformal maps. The technique relies on finding a rational approximation of the conformal map. Wu et al. [29] proposed a numerical method for the conformal mapping of closed-box girder bridges and applied it to flutter performance prediction, which is crucial for ensuring the safety and sustainability of bridge structures.

In this work, we consider a thin infinite flexible plate with a thickness h weakened by multiple curvilinear holes. The plate is subject to external stress that acts in all directions (see Figure 1). If we ignore any effects related to the physical media surrounding the plate, like temperature, dryness, viscosity, etc., we assume that the stress forces are distributed evenly over the area of the plate, except at the holes. These holes are the important regions of the current study and take different shapes; each one has a physical meaning and a different intensity of effect from the stress forces. The current approach in this work is to reduce the area of energy dissipation, the hole regions, to a finite uniform domain. To accomplish this, we use conformal mapping, which does not vanish or become infinite outside a unit circle. The technique’s idea is to transfer the complex plane, which has curvilinear holes. To achieve this, we use a specific conformal mapping. The conformal mapping technique is tailored to this problem in two dimensions. An algorithm is introduced to compute the conformal map for the chosen boundaries to simply study shapes from the conformal map. We apply the complex variables method with the Cauchy technique to solve the boundary value problem and obtain a closed form of the Gaursat functions. Then, the problem is reduced to the integrodifferential equation of the second type with a Cauchy kernel. Moreover, the normal and shear stress components are derived. After that, we explain different physical applications, and then the normal and shear stress components for each one at the chosen values are calculated and plotted using the Maple 2023 software. Finally, the main results of the work are discussed.

2. Basic Equations

In the given area, the boundary S is in the z-plane and is occupied by the plate’s center plane. This boundary is mapped onto the unit circle $\delta$ in the $\tau$-plane by the rational mapping $z=c\xi \left(\tau \right)$. Using the formula $\tau =\rho e^{i\theta }$, curvilinear coordinates $(\rho ,\theta )$ are introduced as maps of the polar conditions into the z-plane. The following result is obtained when we apply $z=c\xi \left(\tau \right)$ to (1):

$$L{\chi }_1\left(c\xi \left(\tau \right)\right)-\frac{\xi \left(\tau \right)}{{\xi }^{\prime }\left(\tau \right)}{\chi }_1\left(c\xi \left(\tau \right)\right)-{\varpi }_1\left(c\xi \left(\tau \right)\right)=g\left(c\xi \left(\tau \right)\right).$$

(4)

In the $\tau$-plane, the first and second boundary value problems are represented by Formula (4). The related formulas of (1) are as follows:

$${\chi }_1\left(r\right)+r\overline{{\chi }_1^{\prime }\left(r\right)}+\overline{{\varpi }_1\left(r\right)}=\frac{1}{2G}{\int }_0^s[iY\left(s\right)-Z\left(s\right)]\mathrm{d}s+c,$$

(5)

$$k{\chi }_1\left(r\right)-r\overline{{\chi }_1^{\prime }\left(r\right)}-\overline{{\varpi }_1\left(r\right)}=p+iq,$$

(6)

where the applied stresses, denoted as $Y\left(s\right)$ and $Z\left(s\right)$, are defined on the edge of the plane; the displacement variables are p and q, the length is s, and the modulus of shear is G. In addition, the following conditions must be fulfilled by the applied stresses $Y\left(s\right)$ and $Z\left(s\right)$:

$$Y\left(s\right)={\sigma }_{xx}\frac{\mathrm{d}y}{\mathrm{d}s}-{\sigma }_{xy}\frac{\mathrm{d}x}{\mathrm{d}s},$$

(7)

$$Z\left(s\right)={\sigma }_{yx}\frac{\mathrm{d}y}{\mathrm{d}s}-{\sigma }_{yy}\frac{\mathrm{d}x}{\mathrm{d}s}.$$

(8)

In elastic problems of the plate, the stress components are given by

$${\sigma }_{xx}-{\sigma }_{yy}+2i{\sigma }_{xy}=-4G\left[z\overline{{\chi }^{″}\left(z\right)}+\overline{{\varpi }^{\prime }\left(z\right)}\right],$$

$${\sigma }_{xx}+{\sigma }_{yy}=4G\left[{\chi }^{\prime }\left(z\right)+\overline{{\chi }^{\prime }\left(z\right)}\right].$$

(9)

3. Conformal Mapping and Special Cases

We consider an infinitely thin plate with a curvilinear hole S whose origin is outside the unit circle $\delta$ in the $\tau$-plane $\left(\tau =\rho e^{i\theta },0\le \theta \le 2\pi \right)$ with a rational mapping function

$$z=c\xi \left(\tau \right)=c\frac{\tau +{\sum }_{i=1}^3{m}_i{\tau }^{-il}}{{\prod }_{i=1}^3\left(1-n_i{\tau }^{-l}\right)},$$

(10)

where $z^{\prime }\left(\tau \right)$ does not become infinite or vanish, $m_i$ are complex numbers, and $n_i$ are real numbers.

The study focused on normal and shear stress components for flexible plates, which were weakened by curvilinear holes conformally mapped on the domain outside a unit circle by the rational function (10). The physical interest of mapping comes from the different shapes of holes it treats, as shown in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.

Special Cases:

i.

When $\left|n_i\right|<1$, the mapping represents a skew-symmetric simple closed curve. See Figure 2, Figure 3, Figure 4 and Figure 5.

ii.

When $\left|n_i\right|>1$, the mapping reduces to $(i+1)$ crossed curves. So, the curvilinear holes degenerate into multiple closed curves and have strong poles. See Figure 6, Figure 7, Figure 8 and Figure 9.

iii.

At the values of n in Figure 10, Figure 11, Figure 12 and Figure 13, the curvilinear holes generated two skew-symmetric poles around the x-axis.

4. The Method of Solution

The complex Gaursat functions, $\chi \left(\tau \right)$ and $\varpi \left(\tau \right)$, are derived using the complex variable technique (see [30,31]). Furthermore, after determining the Gaursat functions, the three stress components, ${\sigma }_{xx}$, ${\sigma }_{xy}$, and ${\sigma }_{yy}$, will be completely determined. With the boundary condition (1) and the conformal mapping (4), the expression $\xi \left(\tau \right)/{\xi }^{\prime }\left({\tau }^{-1}\right)$ yields

$$\frac{\xi \left(\tau \right)}{{\xi }^{\prime }\left({\tau }^{-1}\right)}=\alpha \left(\tau \right)+\beta \left({\tau }^{-1}\right),$$

(11)

where $\beta \left(\tau \right)$ is a regular function, and

$$\alpha \left(\tau \right)=\frac{h_1}{\tau -n_1}+\frac{h_2}{\tau -n_2}+\frac{h_3}{\tau -n_3},$$

(12)

with

$$h_j=:\frac{Q}{R},$$

where

$$Q=\left[n_j^{\nu +2}+m_1{n}_j^{\nu +1}+m_2{n}_j+m_3\right]\left(1-n_j^2\right){\left(1-n_1{n}_2\right)}^2{\left(1-n_1{n}_3\right)}^2{\left(1-n_2{n}_3\right)}^2,$$

$$\begin{array}{cc}\hfill R=& \left(n_j-n_{\pm 1}\right)\hfill \\ & \times \left[\left(1-n_j^2\right)\left(1-n_1{n}_2\right)\left(1-n_1{n}_3\right)\left(1-n_2{n}_3\right){\gamma }_j^{\left(1\right)}-ln{\gamma }_j^{\left(2\right)}\left(n_1+n_2+n_3-2n_j{n}_{j+1}\right)\right],\hfill \end{array}$$

$${\gamma }_j^{\left(2\right)}=1+m_1{n}_j^{\nu }+m_2{n}_j^{\nu +1}+m_3{n}_j^{\nu +2},$$

(13)

for $j=1,2,3,$ and $\left|\tau \right|>1$. By virtue of (2), (3), and (11), the condition at the boundary (4) is

$$k\chi \left(\sigma \right)-\alpha \left(\sigma \right)\overline{{\chi }^{\prime }\left(\sigma \right)}-\overline{{\varpi }_{*}\left(\sigma \right)}=g_{*}\left(\sigma \right),$$

(14)

where $\sigma =e^{i\theta }$ denotes the value on the edge of the unit circle,

$$\begin{array}{cc}\hfill {\varpi }_{*}\left(\tau \right)& =\varpi \left(\tau \right)+\beta \left(\tau \right){\chi }^{\prime }\left(\tau \right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill g_{*}\left(\tau \right)& =F\left(\tau \right)-ck{l}^{-1}\tau +c\overline{{\Gamma }^{*}}{\tau }^{-1}+N\left(\tau \right)[\alpha \left(\tau \right)+\overline{\beta \left(\tau \right)]},\hfill \end{array}$$

with

$$\begin{array}{cc}\hfill N\left(\tau \right)& =c\overline{\Gamma }-\frac{S_x-i{S}_y}{2\pi (1+k)}\tau ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill F\left(\tau \right)& =g\left(r\right)=g\left(c\xi \right(\tau \left)\right).\hfill \end{array}$$

The Hölder condition (see [32]) is thought to be satisfied by the function $g\left(\sigma \right)$ and its derivatives. Our aim is to use the mapping $z=c\frac{\tau +m{\tau }^{-1}}{1-n{\tau }^{-1}}$ to obtain the functions $\chi \left(\zeta \right)$ and $\varpi \left(\zeta \right)$ for various boundary value problems. To achieve this, we multiply both sides of this mapping by $\frac{d\sigma }{2\pi i(\sigma -\tau )}$. Then, we integrate the resulting integrals using residue theorems. Thus, we obtain

$$\begin{array}{c}L\chi \left(\tau \right)+\frac{1}{2\pi i}{\int }_{\gamma }\frac{\alpha \left(\sigma \right)\overline{{\chi }^{\prime }\left(\sigma \right)}}{\sigma -\tau }d\sigma =c\overline{{\Gamma }^{*}}{\tau }^{-1}+A\left(\tau \right)+\frac{h_1}{\tau -n_1^{\nu -1}}N\left(n_1^{\varpi -1}\right)\hfill \\ +\frac{h_2}{\tau -n_2^{\nu -1}}N\left(n_2^{\varpi -1}\right)+\frac{h_3}{\tau -n_3^{\nu -1}}N\left(n_3^{\varpi -1}\right),\hfill \end{array}$$

(15)

where

$$\nu =1+\frac{1}{l},$$

and

$$A\left(\tau \right)=\frac{1}{2\pi i}\sum _{\eta =0}^{\infty }{\tau }^{-\eta -1}{\int }_{\delta }{\sigma }^{\eta }F\left(\sigma \right)\mathrm{d}\sigma .$$

(16)

Using (11) in the integral term of (15), we assume

$$\frac{1}{2\pi i}{\int }_{\delta }\frac{\alpha \left(\sigma \right)\overline{{\chi }^{\prime }\left(\sigma \right)}}{\sigma -\tau }\mathrm{d}\sigma =\frac{c{h}_1{b}_1}{n_1^{\nu -1}-\tau }+\frac{c{h}_2{b}_2}{n_2^{\nu -1}-\tau }+\frac{c{h}_1{b}_1}{n_3^{\nu -1}-\tau },$$

(17)

where the complex constants $b_i$’s are yet to be found. Therefore, we have

$$-L\chi \left(\tau \right)=A\left(\tau \right)-c\overline{{\Gamma }^{*}}{\tau }^{-1}=\sum _{j=1}^3\frac{h_j\left(c{b}_j+N\left(n_j^{\nu -1}\right)\right.}{h_j^{\nu -1}-\tau }.$$

(18)

Differentiating (18) with respect to $\tau$ and using the ${\chi }^{\prime }\left(\sigma \right)$ result from (17), we obtain

$$cL{b}_j+c{n}_j^2{\Gamma }^{*}+d_j{h}_j\left[\overline{c{b}_j}+\overline{N\left(n_j^{\nu -1}\right)}\right]=-\overline{A^{\prime }\left(n_j\right)},forj=1,2,3.$$

(19)

The general solution of (19) is

$$b_j=\frac{K{E}_j-h_j{d}_j\overline{E_j}}{c\left(K^2-h_j^2{d}_j^2\right)},$$

where

$$E_j=-\overline{A^{\prime }\left(n_j\right)-c{\Gamma }^{*}}{n}_j^{2(\nu -1)}-h_j{d}_j\overline{N\left(n_j^{\nu -1}\right)},$$

and

$$d_j=n_j^{2(\nu -1)}{\left(1-n_1^{\nu -1}{n}_2^{\nu -1}{n}_3^{\nu -1}\right)}^{-2}\overline{N\left(n_j^{\nu -1}\right).}$$

(20)

From the boundary condition (14), $\varpi \left(\tau \right)$ can be determined in the form

$$\begin{array}{c}\varpi \left(\tau \right)=\frac{cL\overline{\Gamma }}{\tau }-\frac{\xi \left(\tau \right)}{{\xi }^{\prime }\left({\tau }^{-1}\right)}{\chi }_{*}\left(\tau \right)+\frac{h_1\tau }{1-n_1^{\nu -1}\tau }{\chi }_{*}\left(n_1^{\xi -1}\right)+\frac{h_2\tau }{1-n_2^{\nu -1}\tau }{\chi }_{*}\left(n_2^{\xi -1}\right)\hfill \\ \hfill +\frac{h_3\tau }{1-n_3^{\nu -1}\tau }{\chi }_{*}\left(n_3^{\xi -1}\right)+B\left(\tau \right)-B,\hfill \end{array}$$

(21)

where

$$\begin{array}{cc}\hfill {\chi }_{*}\left(\tau \right)& ={\chi }^{\prime }\left(\tau \right)+\overline{N\left(\tau \right)},\hfill \\ \hfill B\left(\tau \right)& =\frac{1}{2\pi i}{\int }_{\delta }\frac{F\left(\sigma \right)}{\sigma -\tau }\mathrm{d}\sigma ,\hfill \end{array}$$

and

$$B=\frac{1}{2\pi i}{\int }_{\delta }\frac{\overline{F\left(\sigma \right)}}{\sigma -\tau }\mathrm{d}\sigma .$$

(22)

Using (18) in (9), after some derivatives and algebraic relations, we have

$$\begin{array}{c}{\sigma }_{xx}=2G\left[-\delta \left(z^2+4z\overline{z}+{\overline{z}}^2\right)Imz+Re\left(2{\chi }^{\prime }\left(\tau \right)-M(\tau ,\overline{\tau })\right)\right],\\ {\sigma }_{yy}=2G\left[\delta \left(z^2+{\overline{z}}^2\right)Imz+Re\left(2{\chi }^{\prime }\left(\tau \right)+M(\tau ,\overline{\tau })\right)\right],\\ {\sigma }_{xy}=2G\left[\delta \left(z\overline{z}-2{(Imz)}^{2}Rez+ImM(\tau ,\overline{\tau })\right)\right],\end{array}$$

(23)

where

$$\begin{array}{cc}\hfill M(\tau ,\overline{\tau })=& \left[c\left(\tau \right)-\frac{\overline{\xi \left(\tau \right)}}{{\xi }^{\prime }\left(\tau \right)}\right]\overline{{\chi }^{″}\left(\tau \right)}+\frac{S_x-i{s}_y}{2\pi (1+k)}\frac{\overline{\xi \left(\tau \right)}}{{\xi }^{\prime }\left(\tau \right)}+ck\Gamma {\tau }^2\hfill \\ & -\frac{\overline{\xi \left(\tau \right)}}{{\xi }^{\prime }\left(\tau \right)}\left[\overline{{\chi }^{\prime }\left(\tau \right)}+N\left(\tau \right)\right]+\overline{B^{\prime }\left(\tau \right)}+\sum _{i=1}^3\frac{h_j\tau }{{\left(\tau -n_j^{\nu -1}\right)}^2}{\chi }_{*}\left(n_j^{\nu -1}\right),\hfill \end{array}$$

and

$$\delta =\frac{(1+\nu )r_0^2}{2{\left(z\overline{z}\right)}^2}.$$

(24)

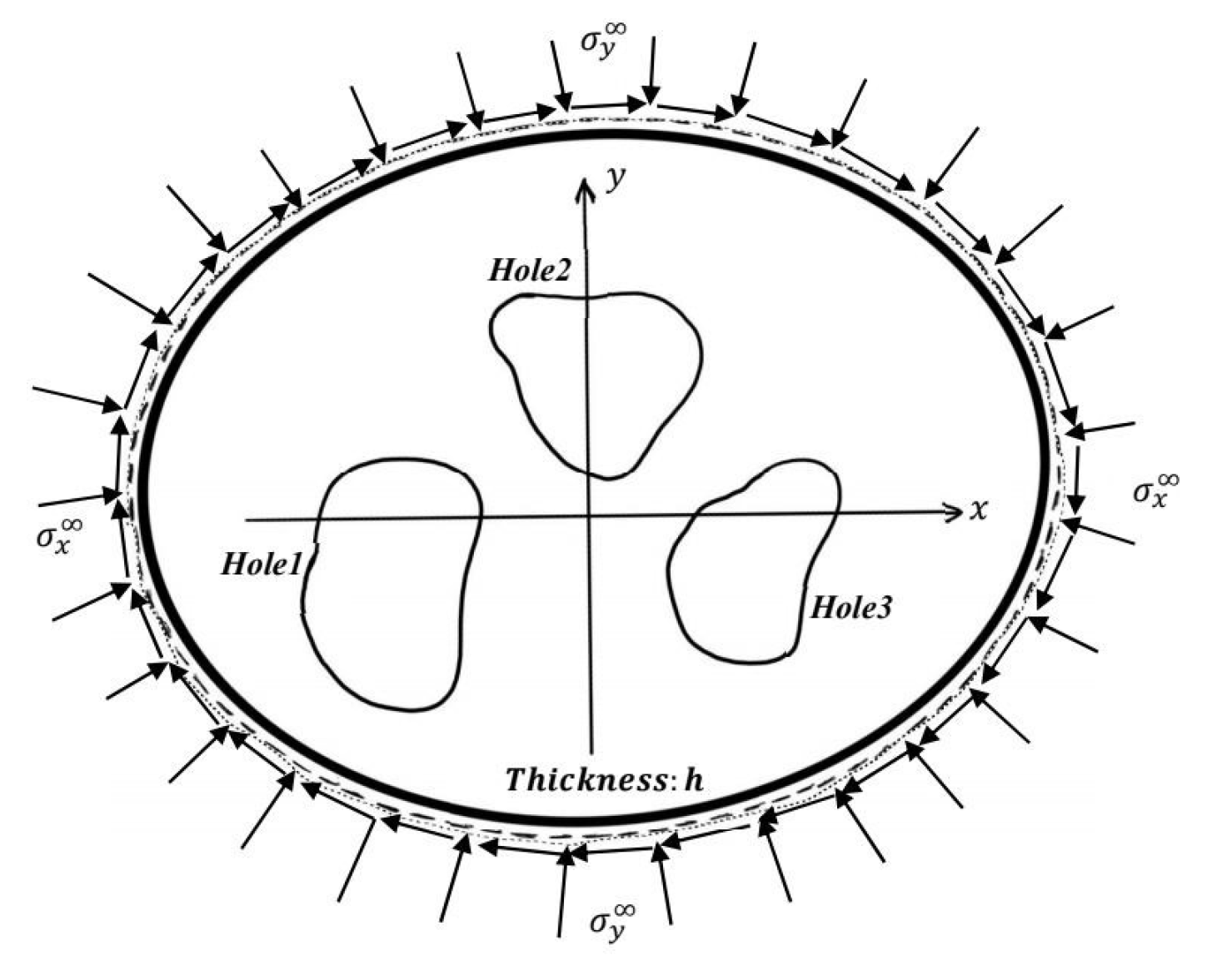
5. Applications

In this section, we resolve the first and second boundary value problems by assuming various values for the given functions. In this case, the Gaursat functions will then be obtained, allowing for the direct calculation of the stress components.

Application 1: A curvilinear hole with uniform tensile stress on an infinite plate: There is an applied uniform tensile tension of intensity P to an infinite plate, stretching it to infinity and forming an angle $\theta$ with the x-axis in the given conditions: $L=-1,{\Gamma }^{*}=\frac{p}{4},{\Gamma }^{*}=\frac{-p}{2}{e}^{-2i\theta },0\le \theta \le 2\pi$, and $S_x=S_y=g=0$. The two complex functions of (19) and (21) result in the plate becoming weaker due to a curvilinear hole S that is not under any stress:

$$\chi \left(\tau \right)=\frac{cp}{2}{e}^{2i\theta }{\tau }^{-1}+\sum _{j=1}^3\frac{L_j^{\left(1\right)}}{n_j^{\nu -1}-\tau },$$

(25)

$$\varpi \left(\tau \right)=\frac{-cp}{2}{\tau }^{-1}-\frac{\xi \left({\tau }^{-1}\right)}{{\xi }^{\prime }\left(\eta \right)}{\chi }_{*}\left(\tau \right)+\sum _{j=1}^3\frac{h_j\tau }{1-n_j^{\nu -1}\tau }{\chi }_{*}\left(n_j^{\xi -1}\right),$$

(26)

where

$$L_j^{\left(1\right)}=\frac{P{h}_i}{4}\left[\frac{1-2n_j^{2(\nu -1)}cos2\theta }{1-h_j{d}_j}+\frac{2n_j^{2(\nu -1)}sin2\theta }{1+h_j{d}_j}\right],$$

and

$${\chi }_{*}\left(\tau \right)={\chi }^{\prime }\left(\tau \right)+\frac{cp}{4}.$$

Using (25) and (26) in (23), it is possible to obtain the stress components ${\sigma }_{xx},{\sigma }_{yy},{\sigma }_{xy}$ directly. Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 show the equations that relate these stress components to the angle $\theta$.

Application 2: A two-pole curvilinear hole with a uniformly pressured edge: In the case of $L=-1,S_x=S_y=\Gamma ={\Gamma }^{*}=0$, and $g\left(f\right(r\left)\right)=Pr$, where P is a real constant, the Equations (19) and (21) become

$$\begin{array}{cc}\hfill \chi \left(\tau \right)=& \frac{cP\left(n_1^{1+\nu }+m_1{n}_1+m_2\right)}{\left(n_1^{\nu -1}-\tau \right)\left(1-h_1{d}_1\right)\left(n_1-n_2\right)}+\frac{cP\left(n_2^{1+\nu }+m_2{n}_2+m_1\right)}{\left(n_2^{\nu -1}-\tau \right)\left(1-h_2{d}_2\right)\left(n_2-n_1\right)}\hfill \\ & +\frac{cP\left(n_2^{1+\nu }+m_2{n}_2+m_3\right)}{\left(n_2^{\nu -1}-\tau \right)\left(1-h_2{d}_2\right)\left(n_2-n_3\right)}+\frac{cP\left(n_1^{1+\nu }+m_1{n}_1+m_3\right)}{\left(n_1^{\nu -1}-\tau \right)\left(1-h_1{d}_1\right)\left(n_1-n_3\right)}\hfill \\ & +\frac{cP\left(n_3^{1+\nu }+m_3{n}_3+m_1\right)}{\left(n_3^{\nu -1}-\tau \right)\left(1-h_3{d}_3\right)\left(n_3-n_1\right)}+\frac{cP\left(n_3^{1+\nu }+m_3{n}_3+m_2\right)}{\left(n_3^{\nu -1}-\tau \right)\left(1-h_3{d}_3\right)\left(n_3-n_2\right)},\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \varpi \left(\tau \right)=& -cP\left(n_1+n_2+n_3+{\tau }^{-1}\right)-\frac{\xi \left({\tau }^{-1}\right)}{{\xi }^{\prime }\left(\tau \right)}{\chi }^{\prime }\left(\tau \right)+\frac{h_1\tau }{1-n_1^{\nu -1}\tau }{\chi }^{*}\left(n_1^{\nu -1}\right)\hfill \\ & +\frac{h_2\tau }{1-n_2^{\nu -1}\tau }{\chi }^{*}\left(n_2^{\nu -1}\right)+\frac{h_3\tau }{1-n_3^{\nu -1}\tau }{\chi }^{*}\left(n_3^{\nu -1}\right).\hfill \end{array}$$

(28)

Hence, when a constant pressure of P is applied to the hole’s edge, Equations (27) and (28) provide the solution to the first boundary value problem. On the other hand, when the edge is under a uniform tangential stress of T, as stated in (27) and (28), we replace P with $iT$ in (27) and (28).

Figure 20, Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25 show the equations relating the stress components to the angle $\theta$.

Application 3: The curvilinear hole’s center is where the force acts. We assume that the strains, in this case, finish at infinity. The kernel’s lack of rotation is immediately apparent. The kernel usually stays in its original location. Consequently, the Gaursat functions are determined by assuming that $\Gamma ={\Gamma }^{*}=f\left(t\right)=0$ and $L=k$. Thus,

$$\begin{array}{cc}\hfill -k\chi \left(\tau \right)=\frac{c}{2\pi (1+k)}& \sum _{j=1}^3\frac{h_j{n}_j}{n_j^{\nu -1}-\tau }\left[\frac{k{h}_j{d}_j\left(S_x-i{S}_y\right)}{c\left(k^2-h_j^2{d}_j^2\right)}\right.\hfill \\ & \left.-\left(1+\frac{h_j{d}_j^2}{c\left(k^2-h_j^2{d}_j^2\right)}\right)\left(S_x-i{S}_y\right)\right],\hfill \end{array}$$

(29)

and

$$\begin{array}{c}{\chi }_{*}\left(\tau \right)=\frac{h_1\tau }{1-n_1^{\nu -1}\tau }{\chi }_{*}\left(n_1^{1-\nu }\right)+\frac{h_2\tau }{1-n_2^{\nu -1}\tau }{\chi }_{*}\left(n_2^{1-\nu }\right)+\frac{h_3\tau }{1-n_3^{\nu -1}\tau }{\chi }_{*}\left(n_3^{1-\nu }\right)\hfill \\ \hfill -\frac{\xi \left({\gamma }^{-1}\right)}{{\xi }^{\prime }\left(\tau \right)}{\chi }_{*}\left(\tau \right),\hfill \end{array}$$

(30)

where

$${\chi }_{*}\left(\tau \right)={\chi }^{\prime }\left(\tau \right)-\frac{S_x+i{S}_y}{2\pi (1+k)\tau }.$$

As a result, the second boundary value problem is resolved, where the curvilinear kernel’s center is subject to a force $(S_x,S_y)$.

The equations relating the stress components to the angle $\theta$ are shown in Figure 26, Figure 27, Figure 28, Figure 29, Figure 30 and Figure 31.

6. Conclusions

In this work, we examined a thin infinite flexible plate with a thickness h weakened by multiple curvilinear holes. There was external stress acting in all directions on the plate. The stress forces are distributed uniformly throughout the plate, except for the edges of the holes, and we disregarded any effects associated with the physical medium surrounding the plate. These holes, which were the focal point of the present investigation, came in various forms, and each had a distinct physical significance and a varying degree of stress force impact. The area of energy dissipation, or the hole area, was reduced to a limited uniform domain using the present methodology; we achieved this by using a certain conformal mapping $z=c\zeta \left(\tau \right)$, where c > 0 to provide the solution to the boundary value problem as a discontinuous kernel integrodifferential equation. This kind of integrodifferential equation plays a famous role in many important applications of contact problems in elastic media and material engineering sciences; see [33,34,35]. The Cauchy technique is a powerful tool that allows us to simplify the singular or super-strong singular problem, enabling us to handle it more efficiently. After obtaining the two Gaursat functions, $\chi \left(\tau \right)$, $\varpi \left(\tau \right)$, the components of normal and shear stress were determined. The theoretical knowledge is explained, applicably, by the chosen applications in Section 5, as follows:

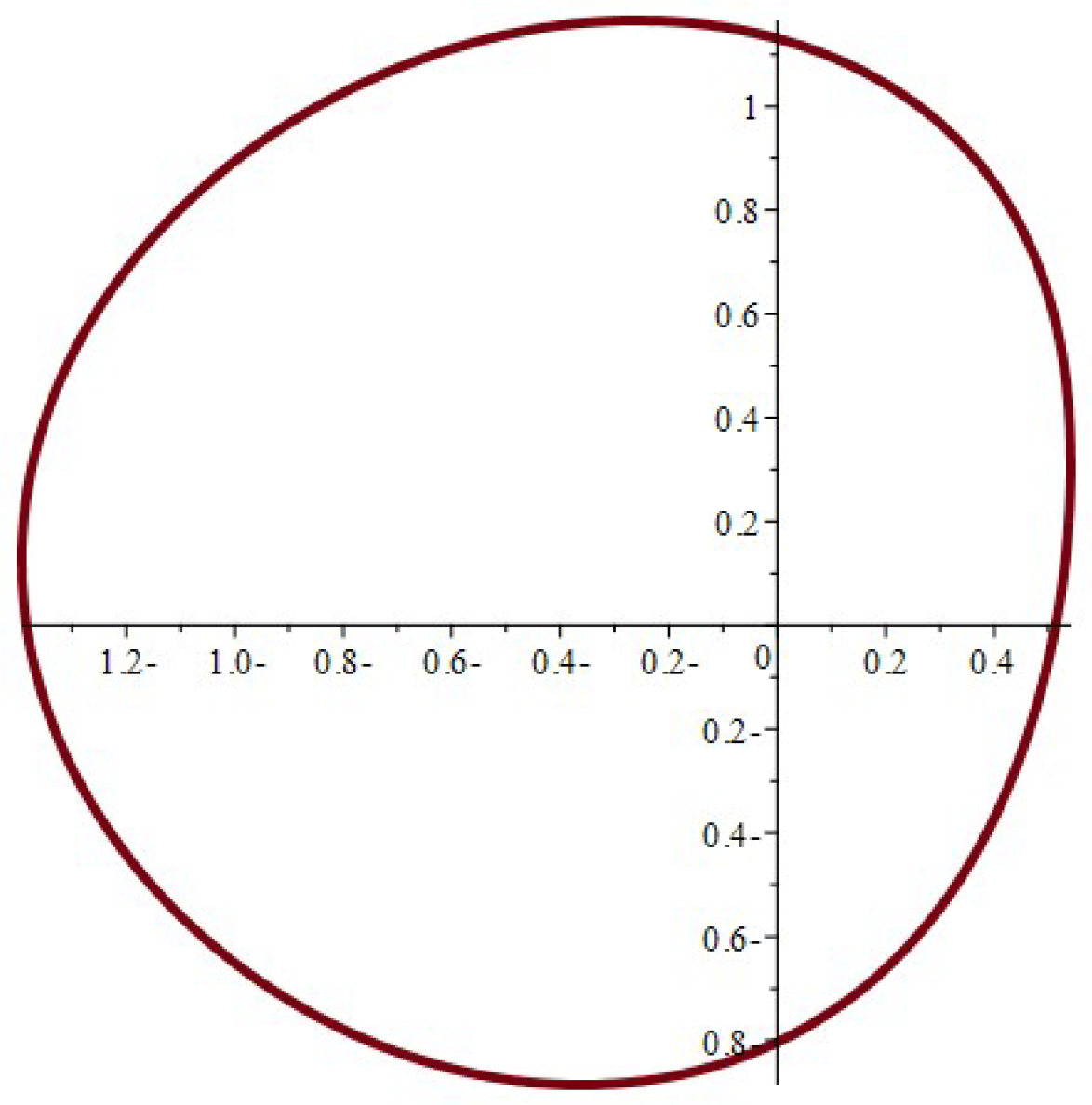
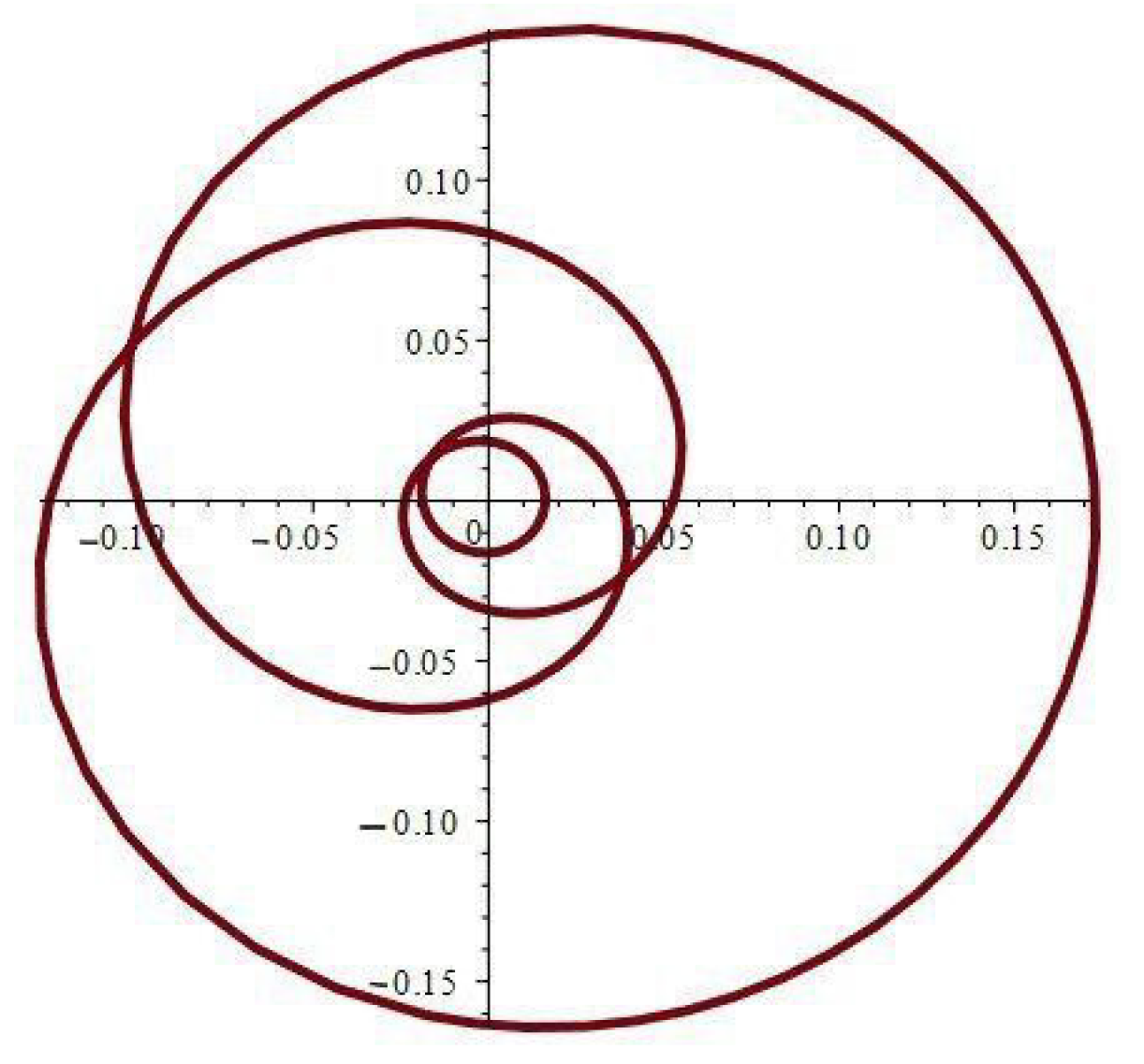
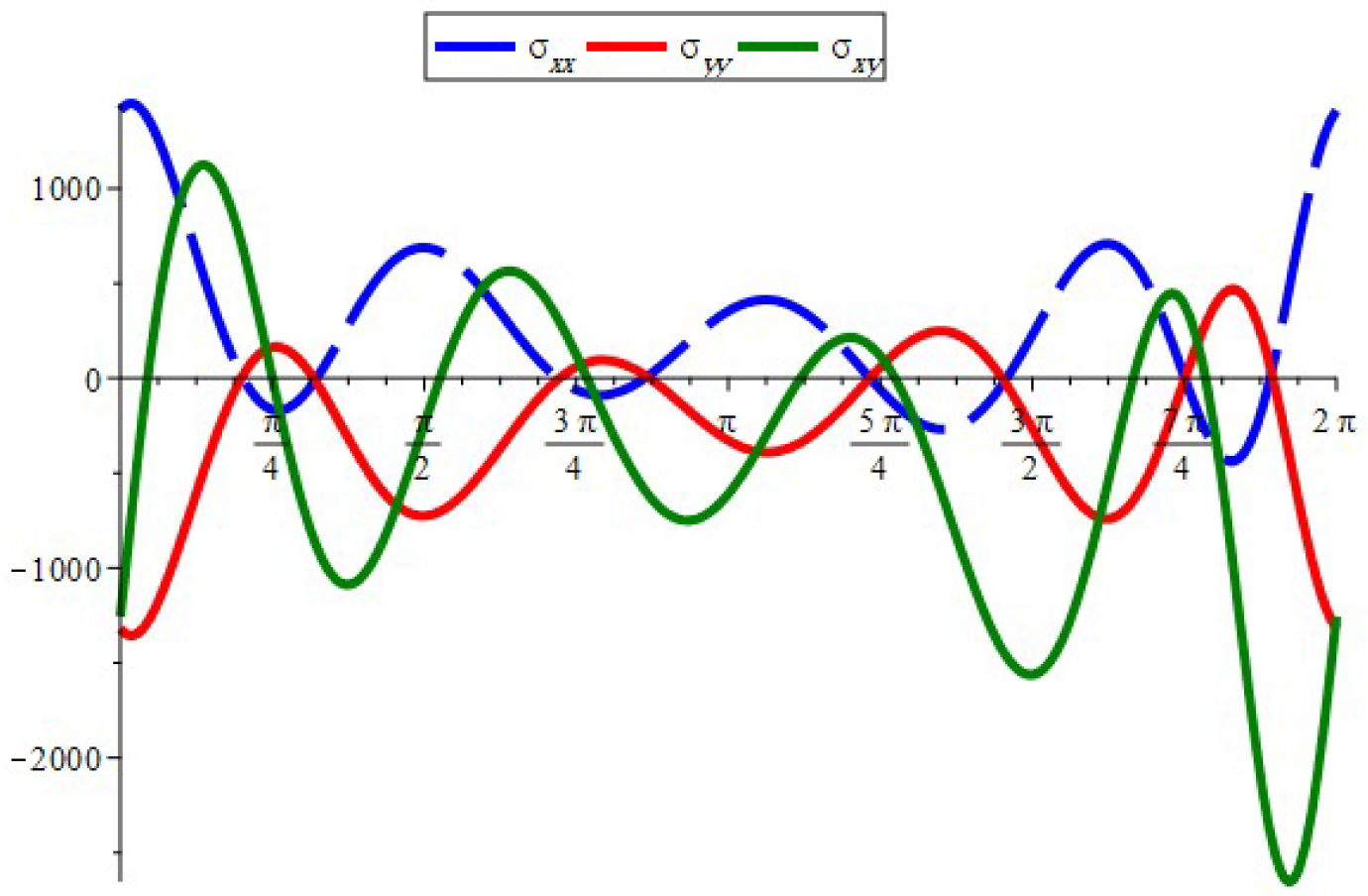
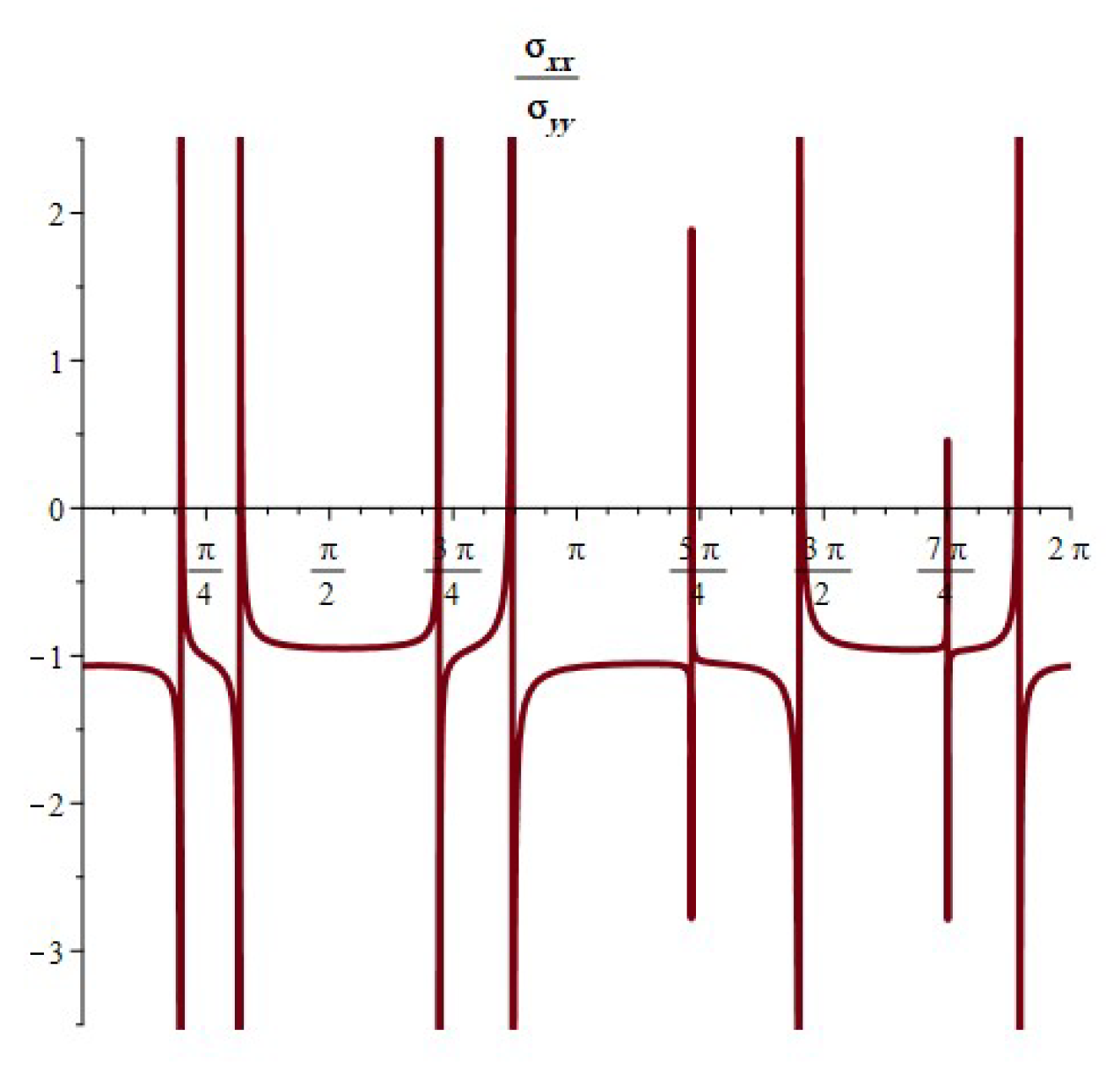
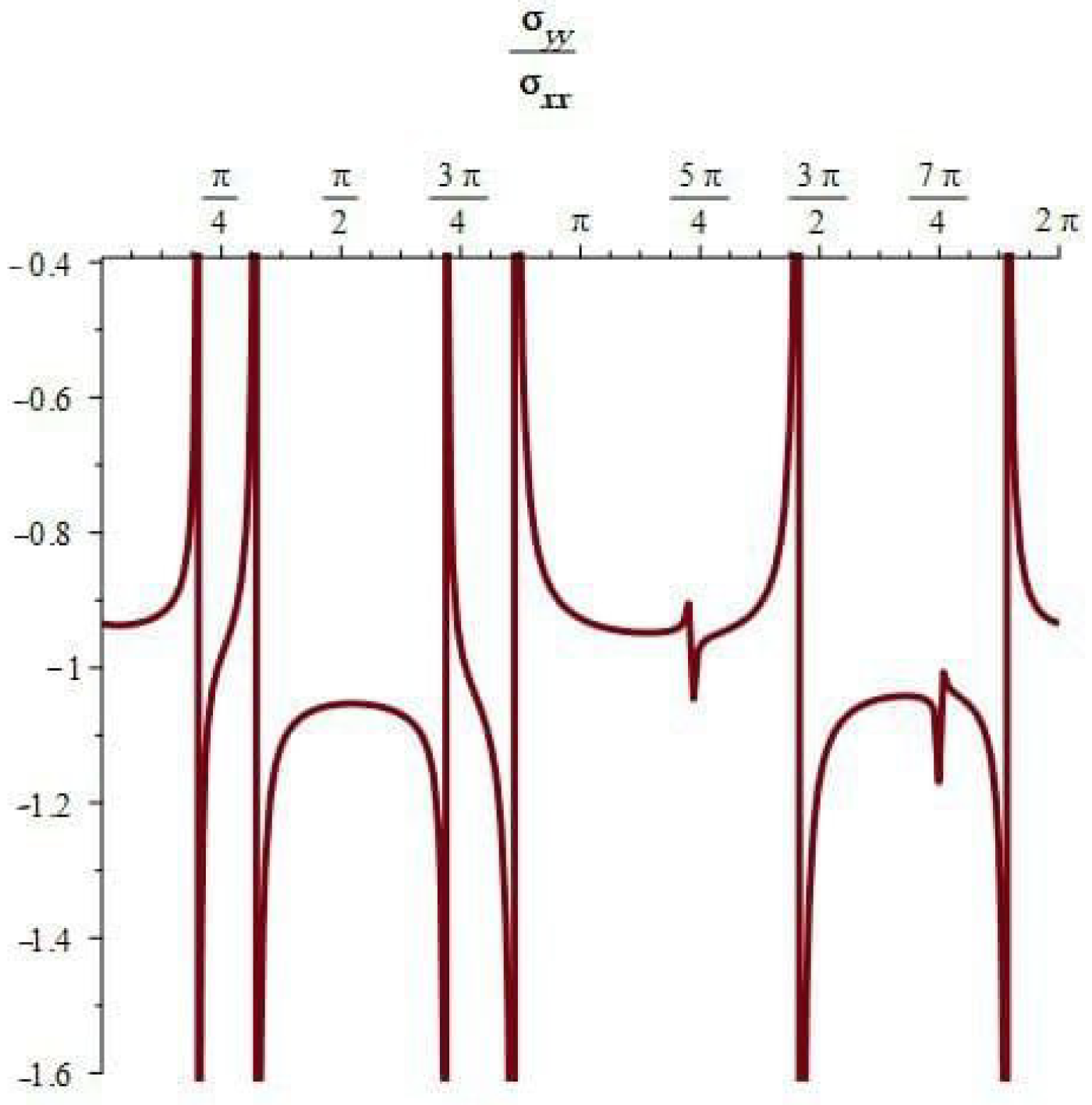
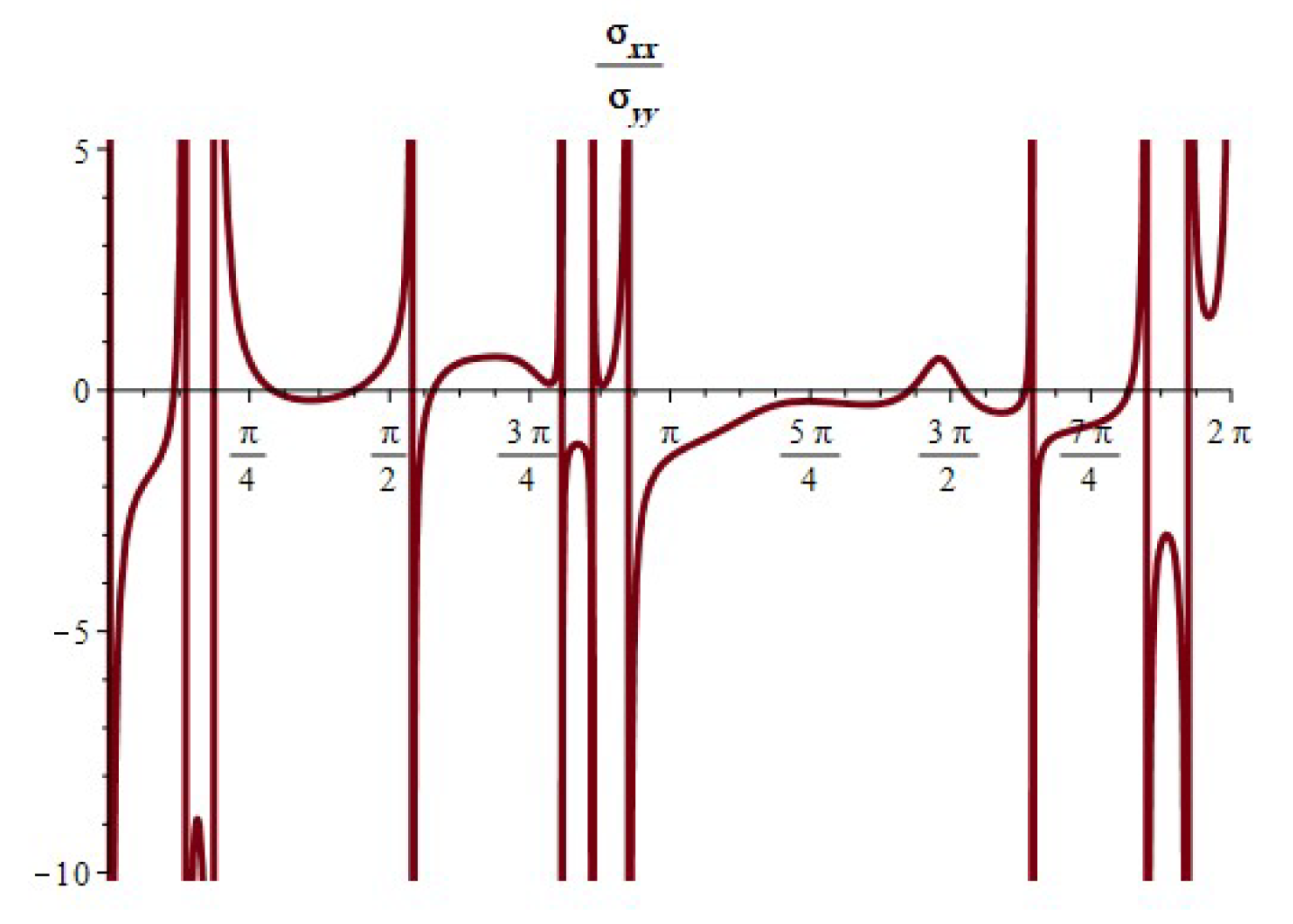
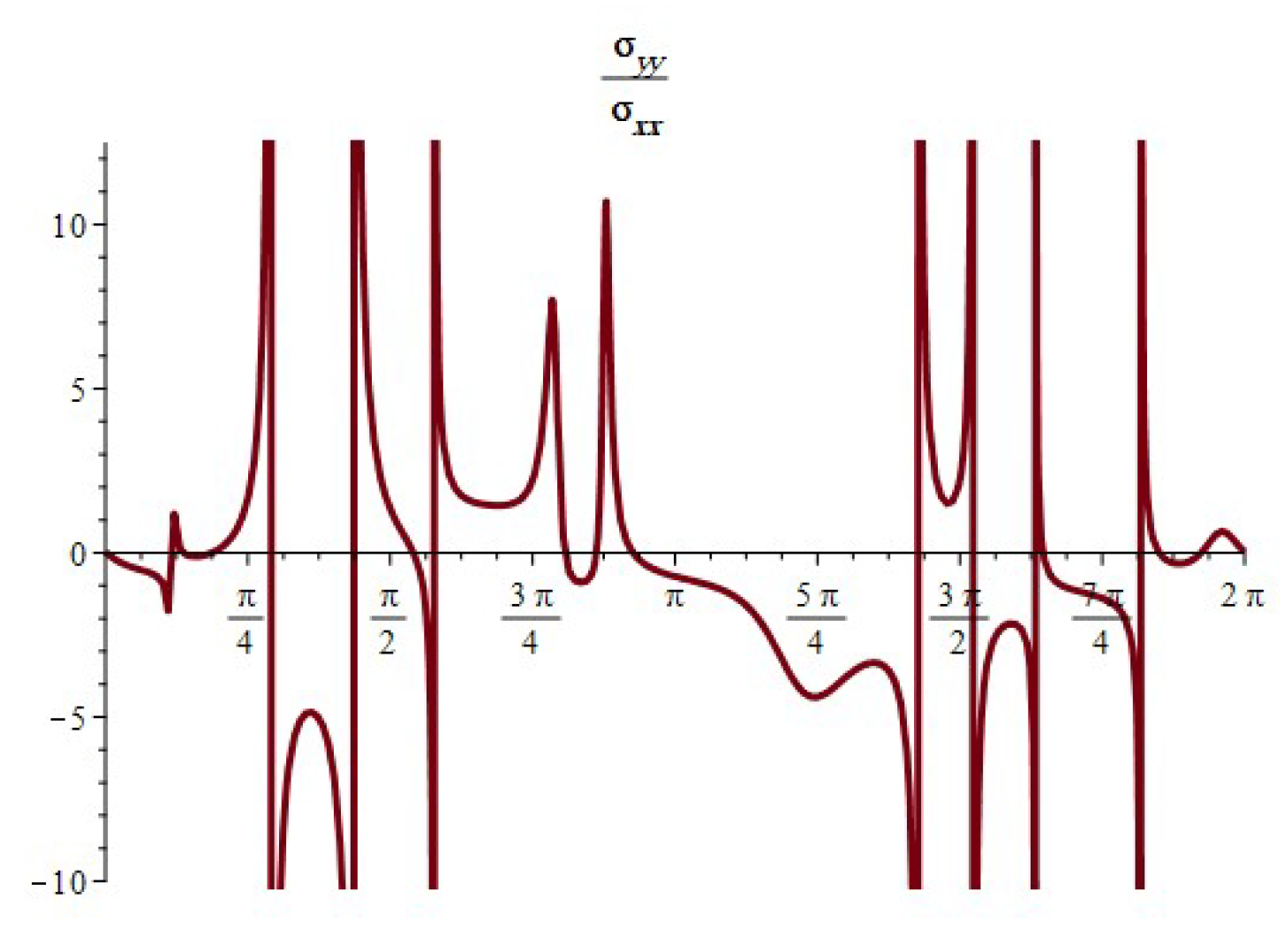
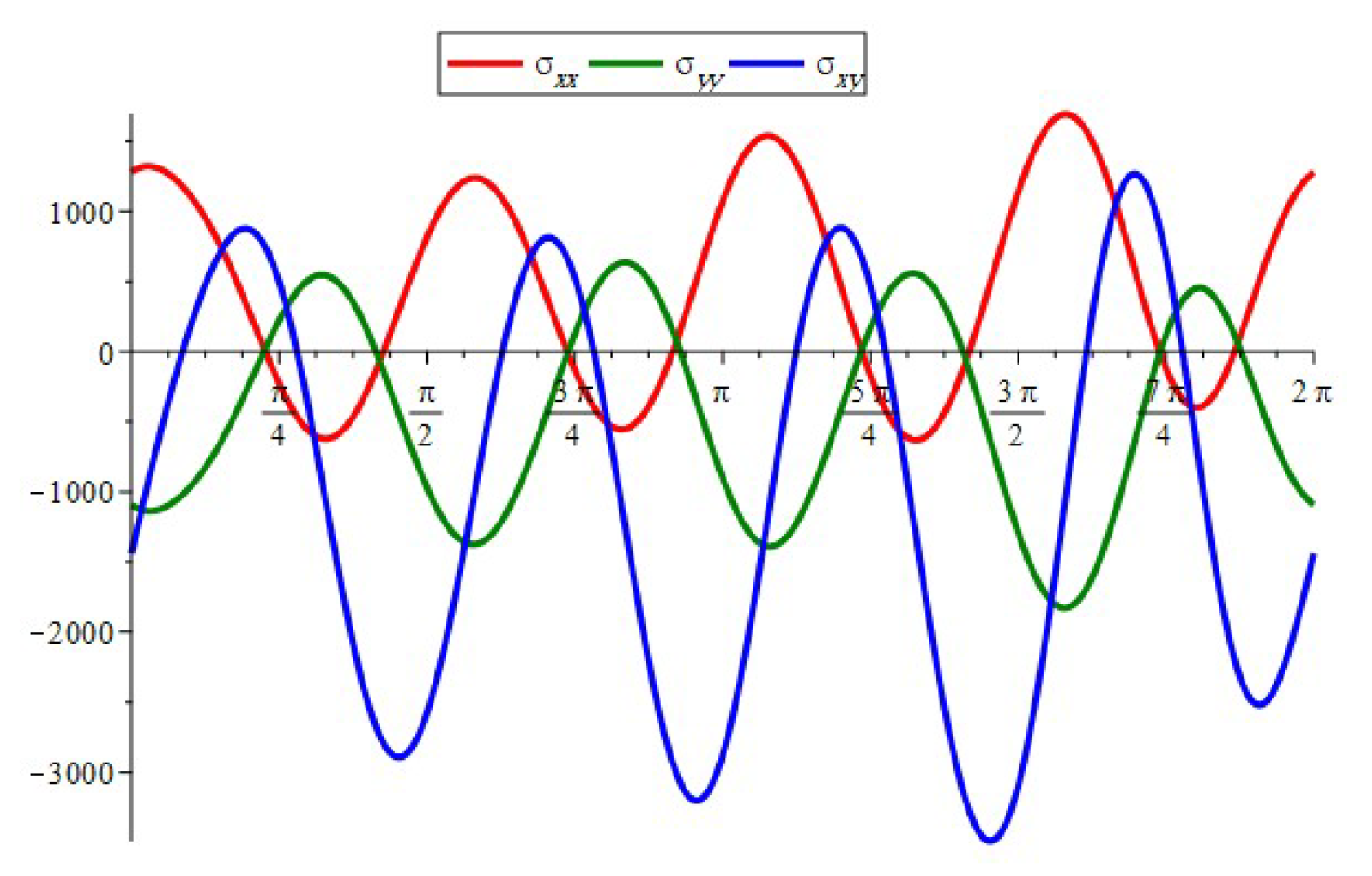
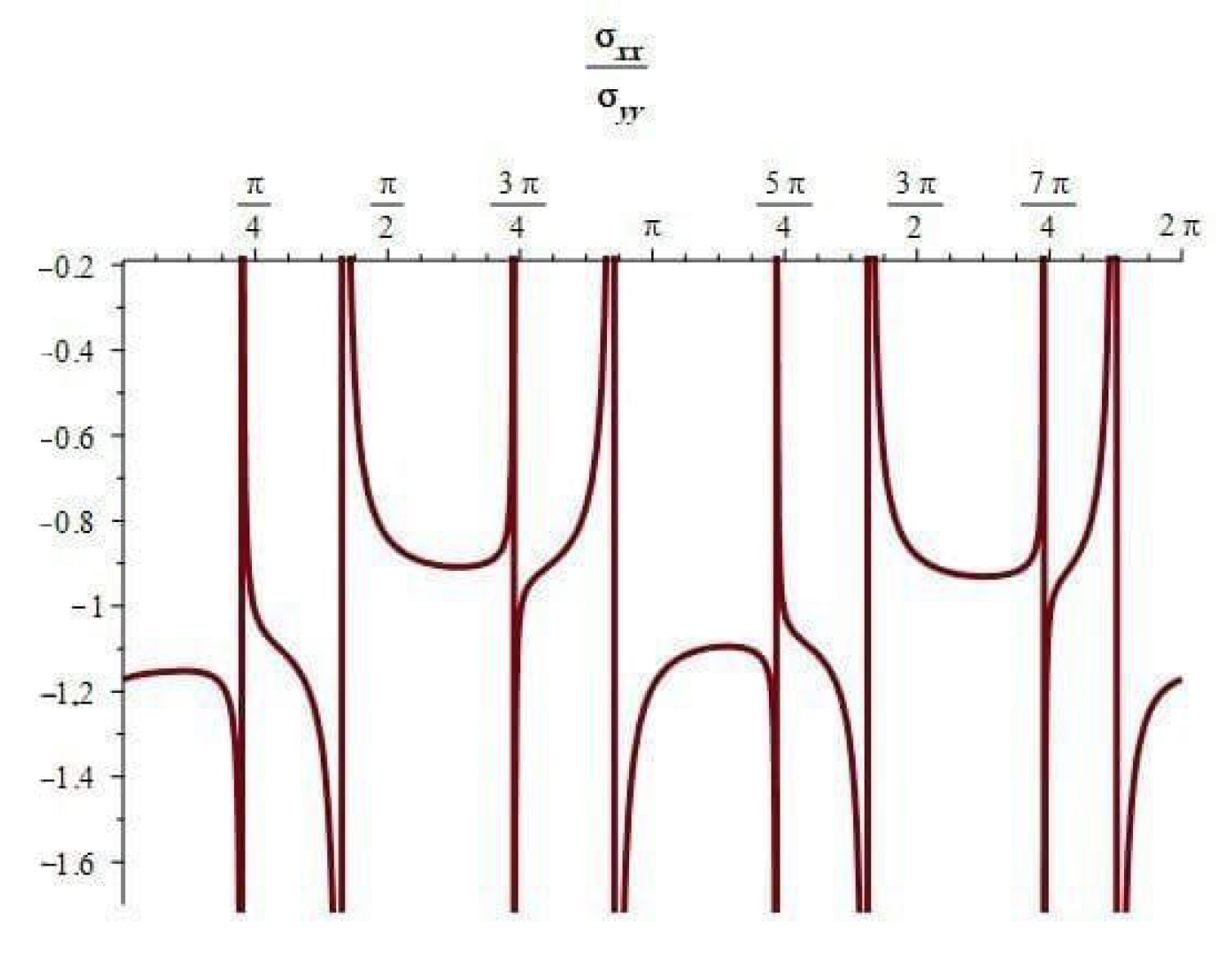
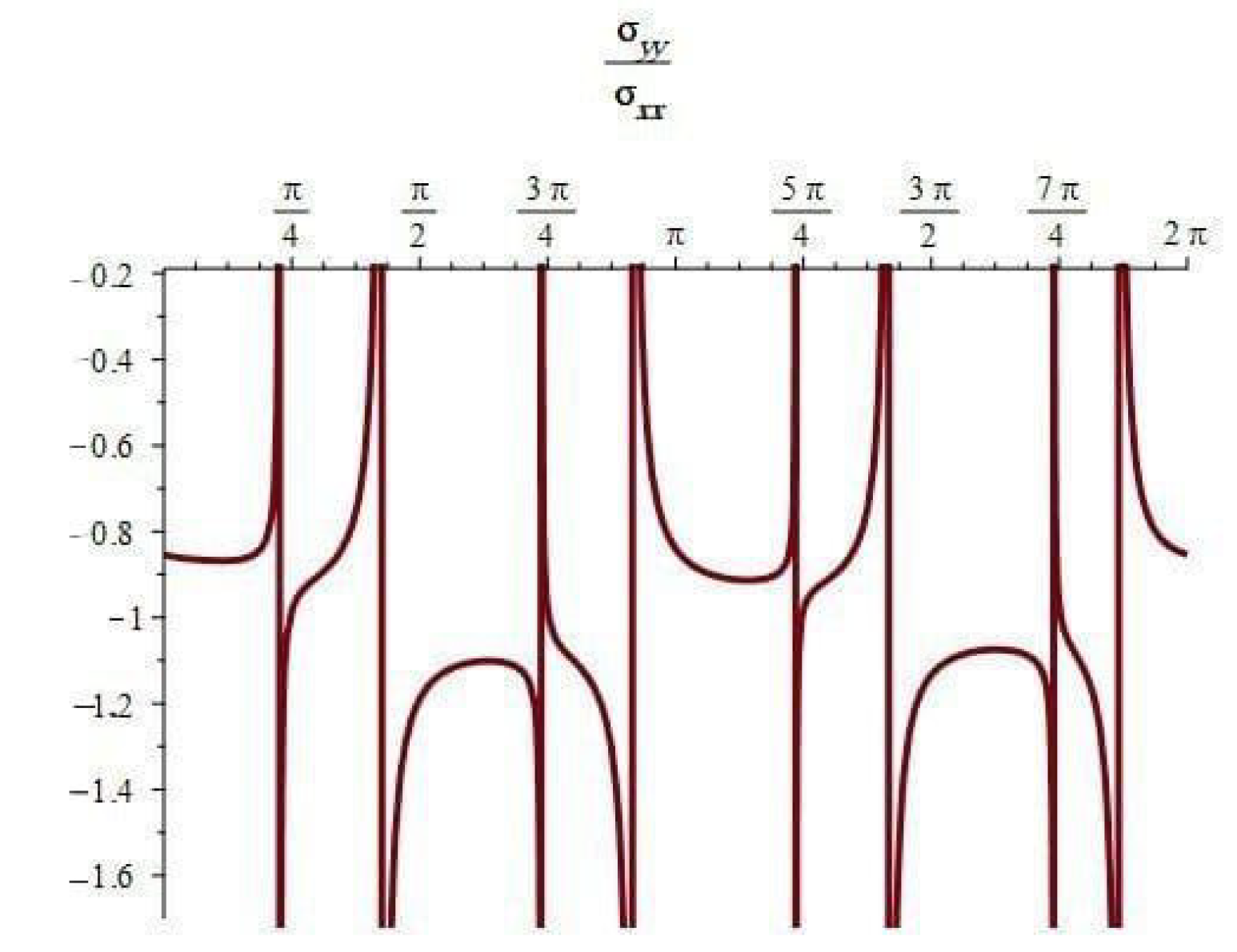
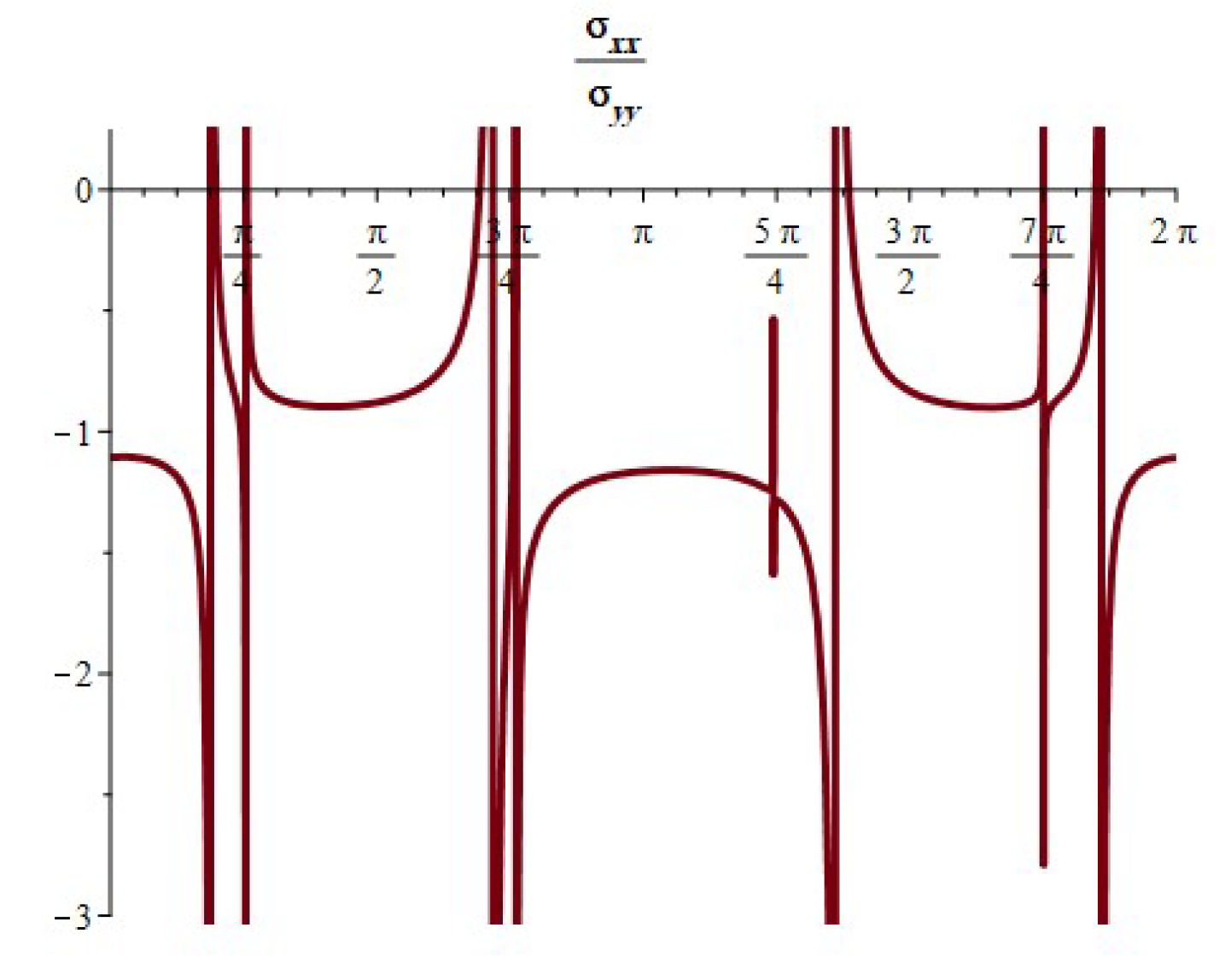
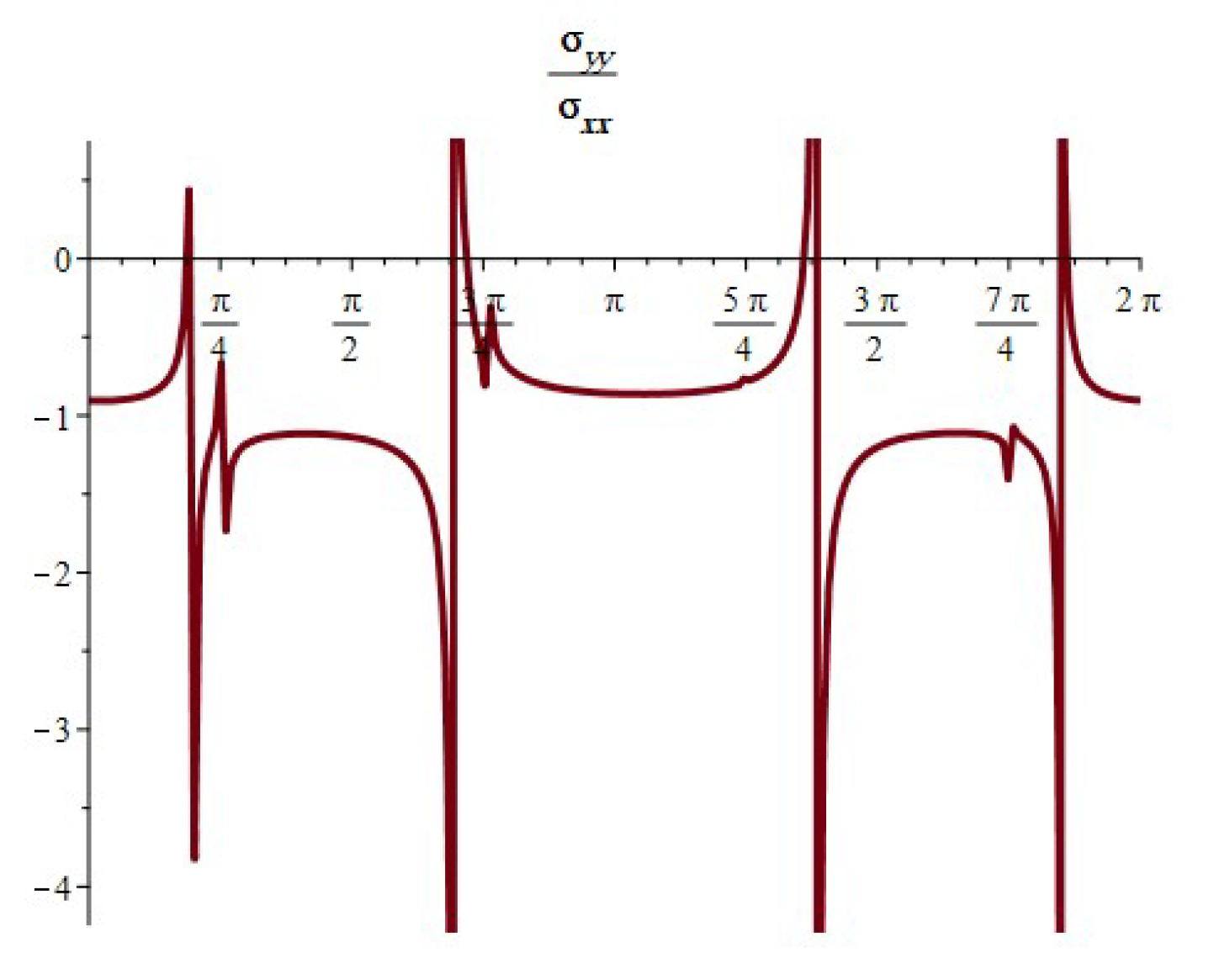
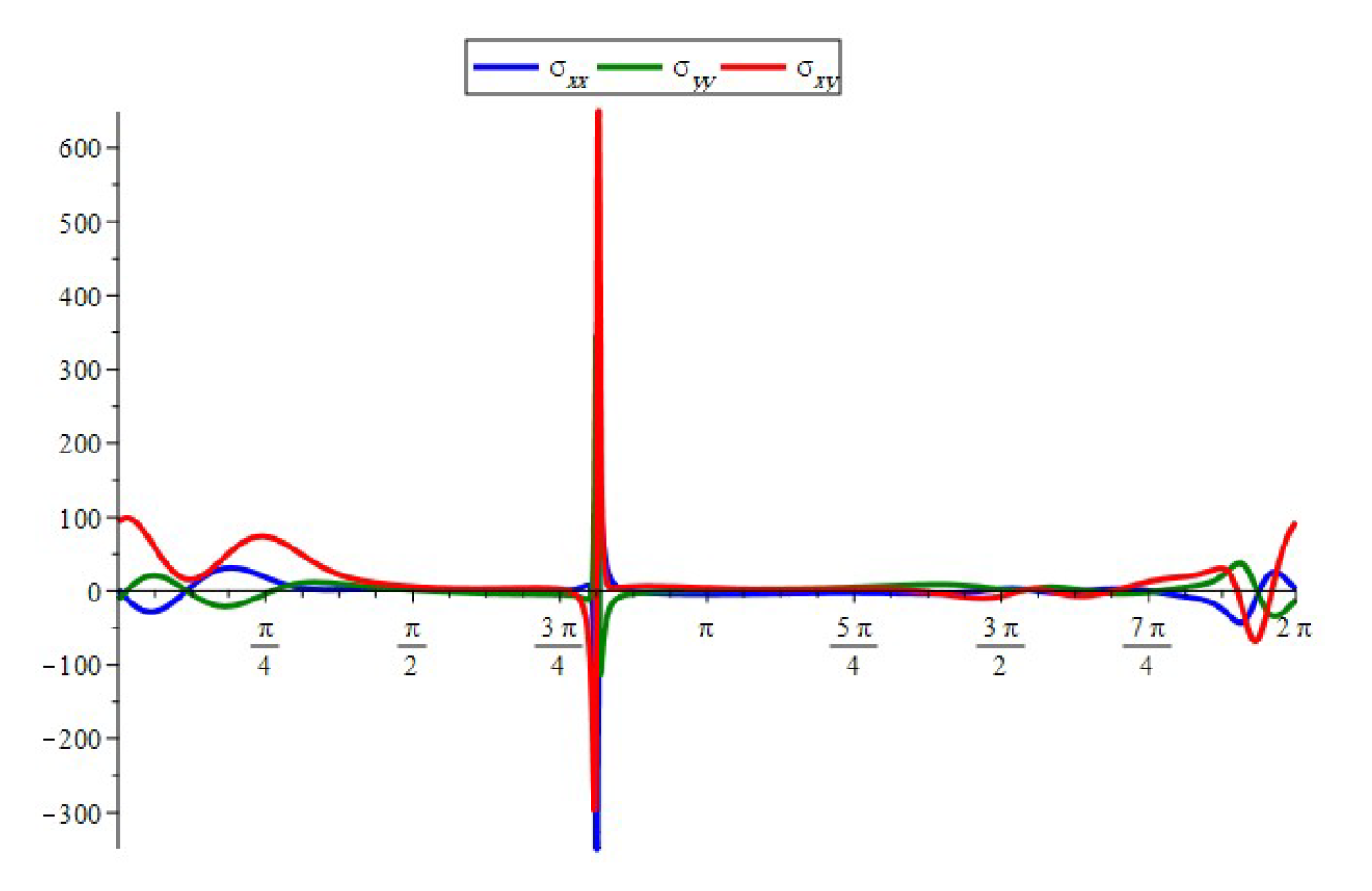
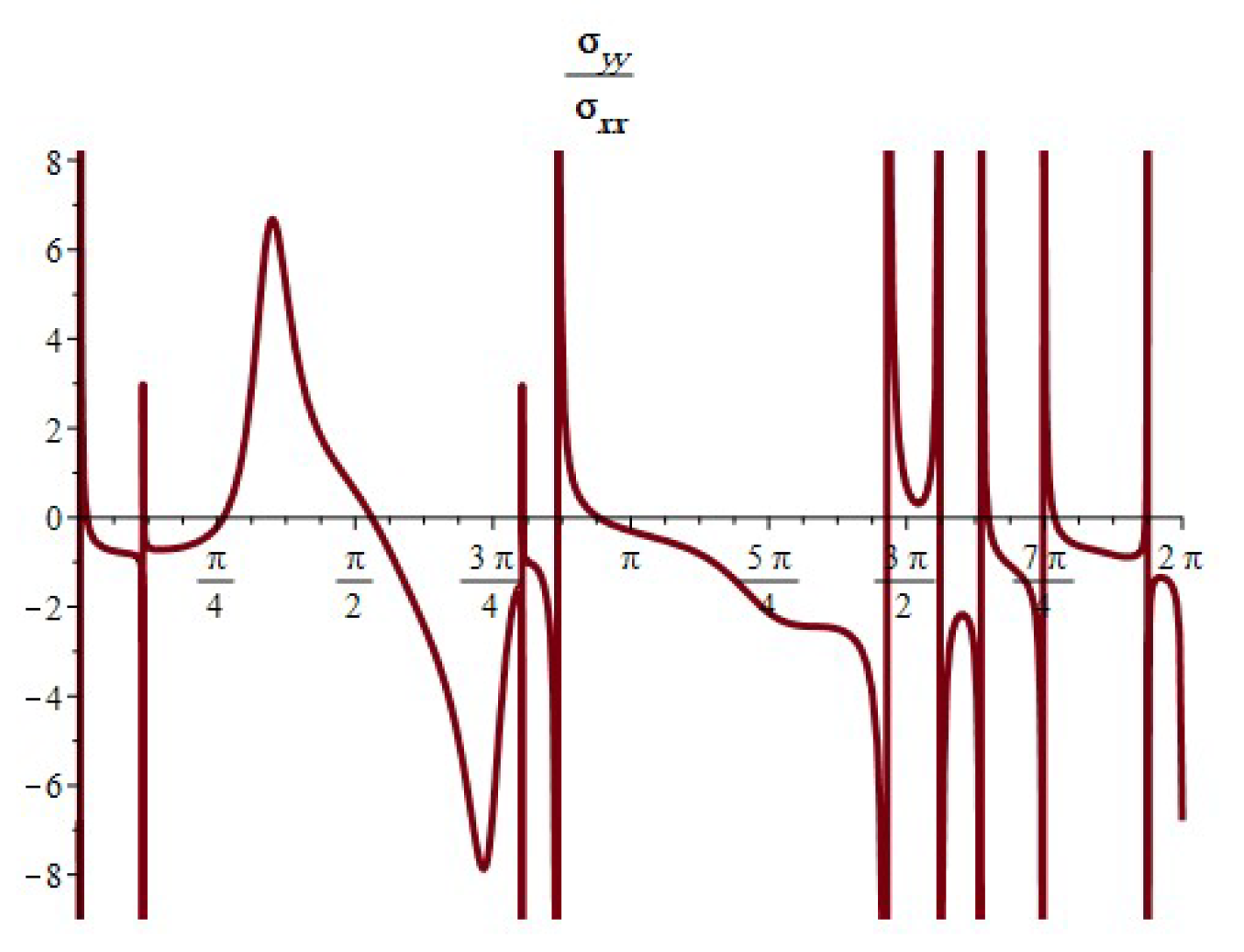
• When $\left|n_i\right|>1$, the component of the stress acts as a tensile force. The normal and shear stress component take the shapes of nonhomogeneous waves and form an angle with the x-axis; see Figure 14, Figure 23 and Figure 26. Furthermore, the stress ratio $\frac{{\sigma }_{xx}}{{\sigma }_{yy}}$ and ${\left(\frac{{\sigma }_{xx}}{{\sigma }_{yy}}\right)}^{-1}$ represents the uniform oscillation; see Figure 15, Figure 16, Figure 24, Figure 25, Figure 27 and Figure 28.
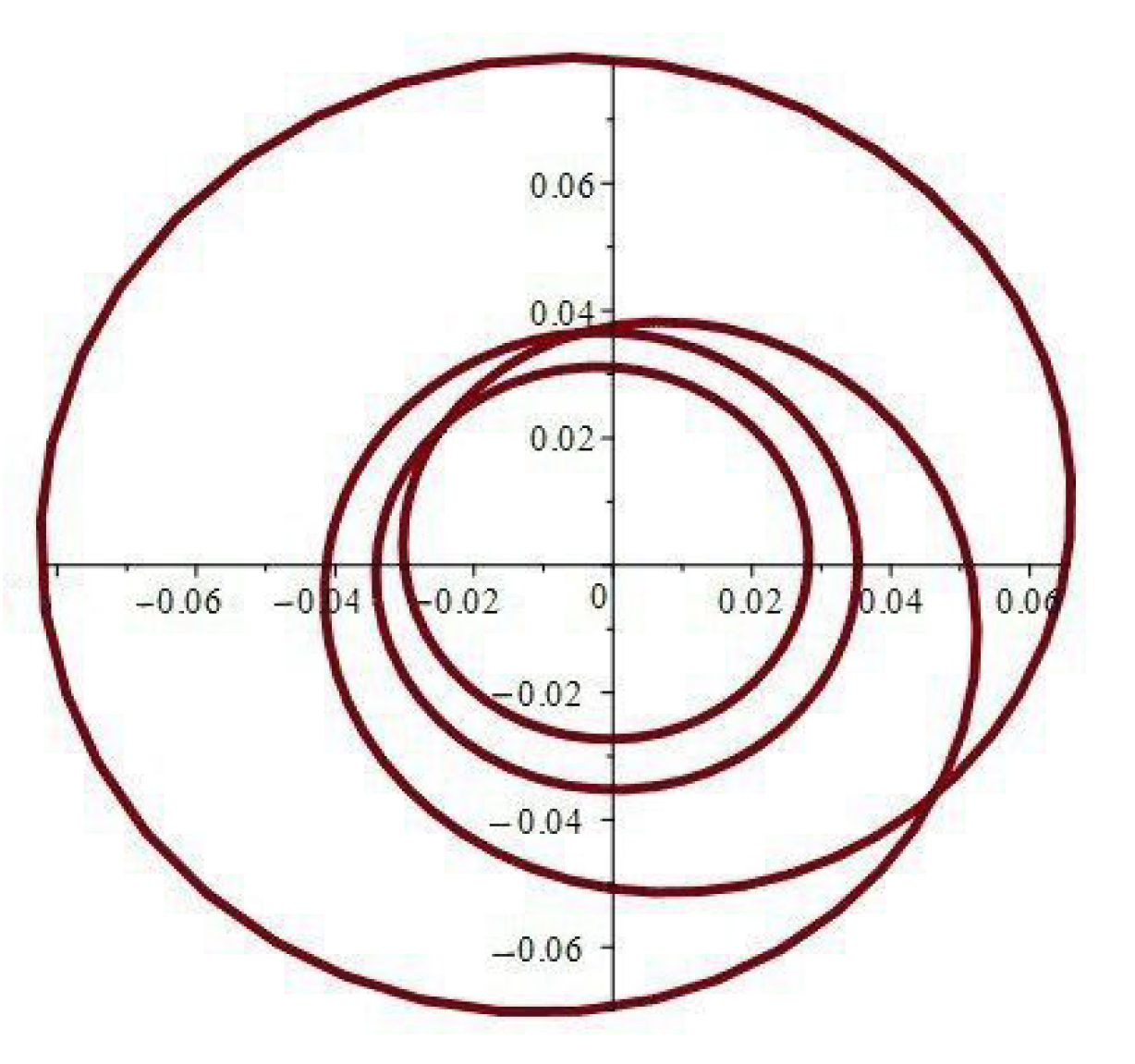
• When $\left|n_i\right|<1$, the component of the stress acts as a compression force. The normal and shear stress component take the shapes of compressed interfering waves and form an angle with the x-axis; see Figure 17, Figure 20 and Figure 29. Furthermore, the stress ratio $\frac{{\sigma }_{xx}}{{\sigma }_{yy}}$ and ${\left(\frac{{\sigma }_{xx}}{{\sigma }_{yy}}\right)}^{-1}$ represents a compressed oscillation; see Figure 18, Figure 19, Figure 21, Figure 22, Figure 30 and Figure 31.

Future Work:

• Study the physical model when the complex potential functions are functions of time. Also, study it in the presence of external forces like flowing heat or a normal magnetic field.
• Study the anomaly model as an application in the medical field. For example, osteoporosis is characterized by a reduction in bone tissue volume and thickness. This causes the bones to weaken and break more easily. Another example is sickle cell anemia, an inherited condition in which red blood cells have an irregular crescent shape, block small blood vessels, and live a shorter life than normal red blood cells.