Estimation of Multiresponse Multipredictor Nonparametric Regression Model Using Mixed Estimator
Abstract
:1. Introduction
2. Materials and Methods
2.1. The MMNR Model
2.2. Mixed Smoothing Spline and Fourier Series Estimator
2.3. Reproducing Kernel Hilbert Space (RKHS)
- (i)
- If is a vector, then , namely, is the subspace of a vector space over , which is notated by (X,);
- (ii)
- If is equipped with an inner product, , then it will be a Hilbert space;
- (iii)
- If is a linear evaluation functional that is defined by for every X, then the linear evaluation functional is bounded.
2.4. Penalized Weighted Least Square (PWLS) Optimization
3. Results and Discussions
- ; ; ;…; ; ;
- ;…; ;
- ; ;…;
- ; ;
- ; …; .
3.1. Determining Smoothing Spline Component of MMNR Model
- ;
- ;
- ;
- ;
- .
3.2. Determining Fourier Series Component of MMNR Model
- ;
- ;
- .
3.3. Determining Goodness of Fit and Penalty Components of PWLS Optimization
- ;
- ;
- .
3.4. Estimating the MMNR Model
3.5. Estimating Weight Matrix W
3.6. Selecting Optimal Smoothing and Oscillation Parameters in the MMNR Model
- ,
- , and
- .
3.7. Consistency of Regression Function Estimator of MMNR Model
3.8. Simulation Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eubank, R.L. Nonparametric Regression and Spline Smoothing, 2nd ed.; Marcel Dekker: New York, NY, USA, 1999. [Google Scholar]
- Cheruiyot, L.R. Local linear regression estimator on the boundary correction in nonparametric regression estimation. J. Stat. Theory Appl. 2020, 19, 460–471. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Huang, T.; Liu, P.; Peng, H. Bias reduction for nonparametric and semiparametric regression models. Stat. Sin. 2018, 28, 2749–2770. [Google Scholar] [CrossRef]
- Chamidah, N.; Zaman, B.; Muniroh, L.; Lestari, B. Designing local standard growth charts of children in East Java province using a local linear estimator. Int. J. Innov. Creat. Change 2020, 13, 45–67. [Google Scholar]
- Delaigle, A.; Fan, J.; Carroll, R.J. A design-adaptive local polynomial estimator for the errors-in-variables problem. J. Am. Stat. Assoc. 2009, 104, 348–359. [Google Scholar] [CrossRef]
- Francisco-Fernandez, M.; Vilar-Fernandez, J.M. Local polynomial regression estimation with correlated errors. Comm. Stat. Theory Methods 2001, 30, 1271–1293. [Google Scholar] [CrossRef]
- Benhenni, K.; Degras, D. Local polynomial estimation of the mean function and its derivatives based on functional data and regular designs. ESAIM Probab. Stat. 2014, 18, 881–899. [Google Scholar] [CrossRef]
- Kikechi, C.B. On local polynomial regression estimators in finite populations. Int. J. Stats. Appl. Math. 2020, 5, 58–63. [Google Scholar]
- Wand, M.P.; Jones, M.C. Kernel Smoothing, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 1995. [Google Scholar]
- Cui, W.; Wei, M. Strong consistency of kernel regression estimate. Open J. Stats. 2013, 3, 179–182. [Google Scholar] [CrossRef]
- De Brabanter, K.; De Brabanter, J.; Suykens, J.A.K.; De Moor, B. Kernel regression in the presence of correlated errors. J. Mach. Learn. Res. 2011, 12, 1955–1976. [Google Scholar]
- Wahba, G. Spline Models for Observational Data; SIAM: Philadelphia, PA, USA, 1990. [Google Scholar]
- Wang, Y. Smoothing Splines: Methods and Applications; Taylor & Francis Group: Boca Raton, FL, USA, 2011. [Google Scholar]
- Liu, A.; Qin, L.; Staudenmayer, J. M-type smoothing spline ANOVA for correlated data. J. Multivar. Anal. 2010, 101, 2282–2296. [Google Scholar] [CrossRef]
- Gao, J.; Shi, P. M-Type smoothing splines in nonparametric and semiparametric regression models. Stat. Sin. 1997, 7, 1155–1169. [Google Scholar]
- Chamidah, N.; Lestari, B.; Massaid, A.; Saifudin, T. Estimating mean arterial pressure affected by stress scores using spline nonparametric regression model approach. Commun. Math. Biol. Neurosci. 2020, 2020, 72. [Google Scholar]
- Chamidah, N.; Lestari, B.; Budiantara, I.N.; Saifudin, T.; Rulaningtyas, R.; Aryati, A.; Wardani, P.; Aydin, D. Consistency and asymptotic normality of estimator for parameters in multiresponse multipredictor semiparametric regression model. Symmetry 2022, 14, 336. [Google Scholar] [CrossRef]
- Lestari, B.; Chamidah, N.; Budiantara, I.N.; Aydin, D. Determining confidence interval and asymptotic distribution for parameters of multiresponse semiparametric regression model using smoothing spline estimator. J. King Saud Univ.-Sci. 2023, 35, 102664. [Google Scholar] [CrossRef]
- Tirosh, S.; De Ville, D.V.; Unser, M. Polyharmonic smoothing splines and the multidimensional Wiener filtering of fractal-like signals. IEEE Trans. Image Process. 2006, 15, 2616–2630. [Google Scholar] [CrossRef]
- Irizarry, R.A. Choosing Smoothness Parameters for Smoothing Splines by Minimizing an Estimate of Risk. Available online: https://www.biostat.jhsph.edu/~ririzarr/papers/react-splines.pdf (accessed on 3 February 2024).
- Adams, S.O.; Ipinyomi, R.A.; Yahaya, H.U. Smoothing spline of ARMA observations in the presence of autocorrelation error. Eur. J. Stats. Prob. 2017, 5, 1–8. [Google Scholar]
- Adams, S.O.; Yahaya, H.U.; Nasiru, O.M. Smoothing parameter estimation of the generalized cross-validation and generalized maximum likelihood. IOSR J. Math. 2017, 13, 41–44. [Google Scholar]
- Lee, T.C.M. Smoothing parameter selection for smoothing splines: A simulation study. Comput. Stats. Data Anal. 2003, 42, 139–148. [Google Scholar] [CrossRef]
- Maharani, M.; Saputro, D.R.S. Generalized cross-validation (GCV) in smoothing spline nonparametric regression models. J. Phys. Conf. Ser. 2021, 1808, 12053. [Google Scholar] [CrossRef]
- Wang, Y.; Ke, C. Smoothing spline semiparametric nonlinear regression models. J. Comp. Graph. Stats. 2009, 18, 165–183. [Google Scholar] [CrossRef]
- Gu, C. Smoothing Spline ANOVA Models; Springer: New York, NY, USA, 2002. [Google Scholar]
- Sun, X.; Zhong, W.; Ma, P. An asymptotic and empirical smoothing parameters selection method for smoothing spline ANOVA models in large samples. Biometrika 2021, 108, 149–166. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Guo, W.; Brown, M.B. Spline smoothing for bivariate data with applications to association between hormones. Stat. Sin. 2000, 10, 377–397. [Google Scholar]
- Lu, M.; Liu, Y.; Li, C.-S. Efficient estimation of a linear transformation model for current status data via penalized splines. Stat. Methods Med. Res. 2020, 29, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Berry, L.N.; Helwig, N.E. Cross-validation, information theory, or maximum likelihood? A comparison of tuning methods for penalized splines. Stats 2021, 4, 701–724. [Google Scholar] [CrossRef]
- Islamiyati, A.; Zakir, M.; Sirajang, N.; Sari, U.; Affan, F.; Usrah, M.J. The use of penalized weighted least square to overcome correlations between two responses. BAREKENG J. Ilmu Mat. Dan Terap. 2022, 16, 1497–1504. [Google Scholar] [CrossRef]
- Islamiyati, A.; Raupong; Kalondeng, A.; Sari, U. Estimating the confidence interval of the regression coefficient of the blood sugar model through a multivariable linear spline with known variance. Stat. Transit. New Ser. 2022, 23, 201–212. [Google Scholar] [CrossRef]
- Kirkby, J.L.; Leitao, A.; Nguyen, D. Nonparametric density estimation and bandwidth selection with B-spline basis: A novel Galerkin method. Comput. Stats. Data Anal. 2021, 159, 107202. [Google Scholar] [CrossRef]
- Osmani, F.; Hajizadeh, E.; Mansouri, P. Kernel and regression spline smoothing techniques to estimate coefficient in rates model and its application in psoriasis. Med. J. Islam. Repub. Iran 2019, 33, 90. [Google Scholar] [CrossRef] [PubMed]
- Lestari, B.; Chamidah, N.; Aydin, D.; Yilmaz, E. Reproducing kernel Hilbert space approach to multiresponse smoothing spline regression function. Symmetry 2022, 14, 2227. [Google Scholar] [CrossRef]
- Bilodeau, M. Fourier smoother and additive models. Can. J. Stat. 1992, 20, 257–269. [Google Scholar] [CrossRef]
- Suparti, S.; Prahutama, A.; Santoso, R.; Devi, A.R. Spline-Fourier’s Method for Modelling Inflation in Indonesia. E3S Web Conf. 2018, 73, 13003. [Google Scholar] [CrossRef]
- Mardianto, M.F.F.; Gunardi; Utami, H. An analysis about Fourier series estimator in nonparametric regression for longitudinal data. Math. Stats. 2021, 9, 501–510. [Google Scholar] [CrossRef]
- Amato, U.; Antoniadis, A.; De Feis, I. Fourier series approximation of separable models. J. Comput. Appl. Math. 2002, 146, 459–479. [Google Scholar] [CrossRef]
- Mariati, M.P.A.M.; Budiantara, I.N.; Ratnasari, V. The application of mixed smoothing spline and Fourier series model in nonparametric regression. Symmetry 2021, 13, 2094. [Google Scholar] [CrossRef]
- Aronszajn, N. Theory of reproducing kernels. Trans. Am. Math. Soc. 1950, 68, 337–404. [Google Scholar] [CrossRef]
- Kimeldorf, G.; Wahba, G. Some results on Tchebycheffian spline functions. J. Math. Anal. Appl. 1971, 33, 82–95. [Google Scholar] [CrossRef]
- Berlinet, A.; Thomas-Agnan, C. Reproducing Kernel Hilbert Spaces in Probability and Statistics; Kluwer Academic: Norwell, MA, USA, 2004. [Google Scholar]
- Paulsen, V.I. An Introduction to the Theory of Reproducing Kernel Hilbert Space. Research Report. 2009. Available online: https://www.researchgate.net/publication/255635687_AN_INTRODUCTION_TO_THE_THEORY_OF_REPRODUCING_KERNEL_HILBERT_SPACES (accessed on 24 March 2022).
- Yuan, M.; Cai, T.T. A reproducing kernel Hilbert space approach to functional linear regression. Ann. Stat. 2010, 38, 3412–3444. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis; Prentice Hall: New York, NY, USA, 1982. [Google Scholar]
- Ruppert, D.; Carroll, R. Penalized Regression Splines, Working Paper; School of Operation Research and Industrial Engineering, Cornell University: Ithaca, NY, USA, 1997. [Google Scholar]
- Wand, M.P.; Jones, M.C. Kernel Smoothing; Chapman & Hall: London, UK, 1995. [Google Scholar]
- Sen, P.K.; Singer, J.M. Large Sample in Statistics: An Introduction with Applications; Chapman & Hall: London, UK, 1993. [Google Scholar]
- Serfling, R.J. Approximation Theorems of Mathematical Statistics; John Wiley: New York, NY, USA, 1980. [Google Scholar]
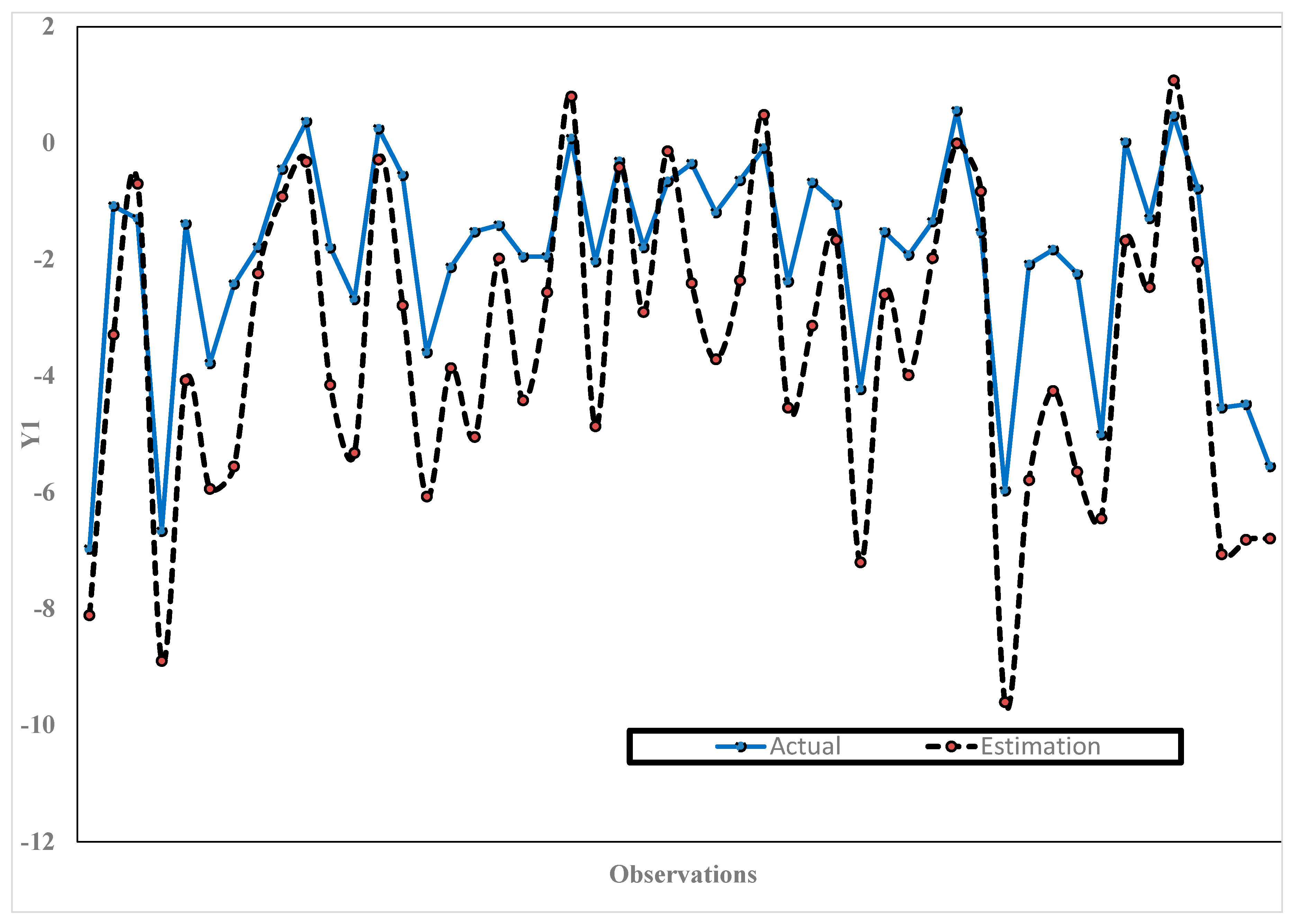
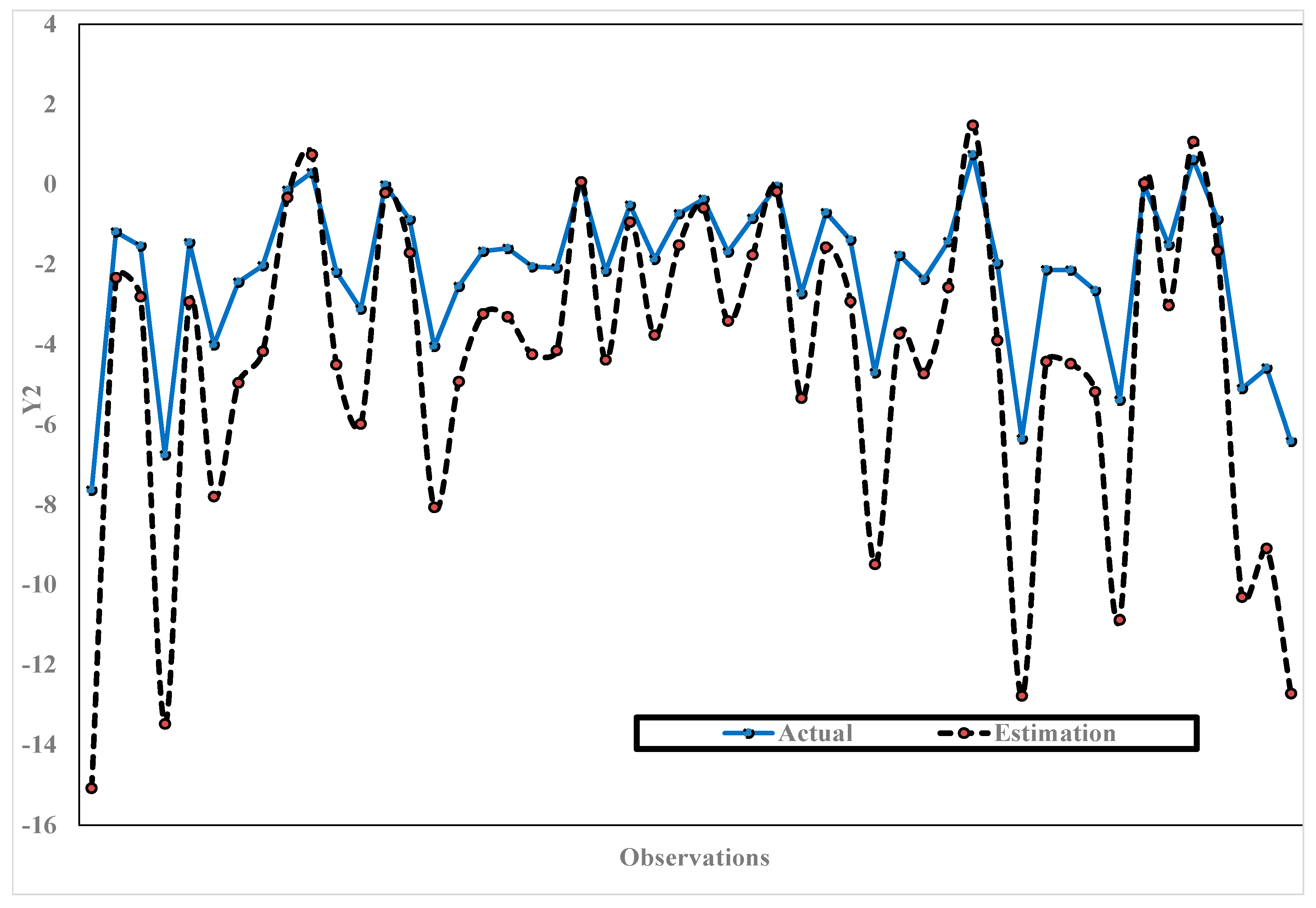

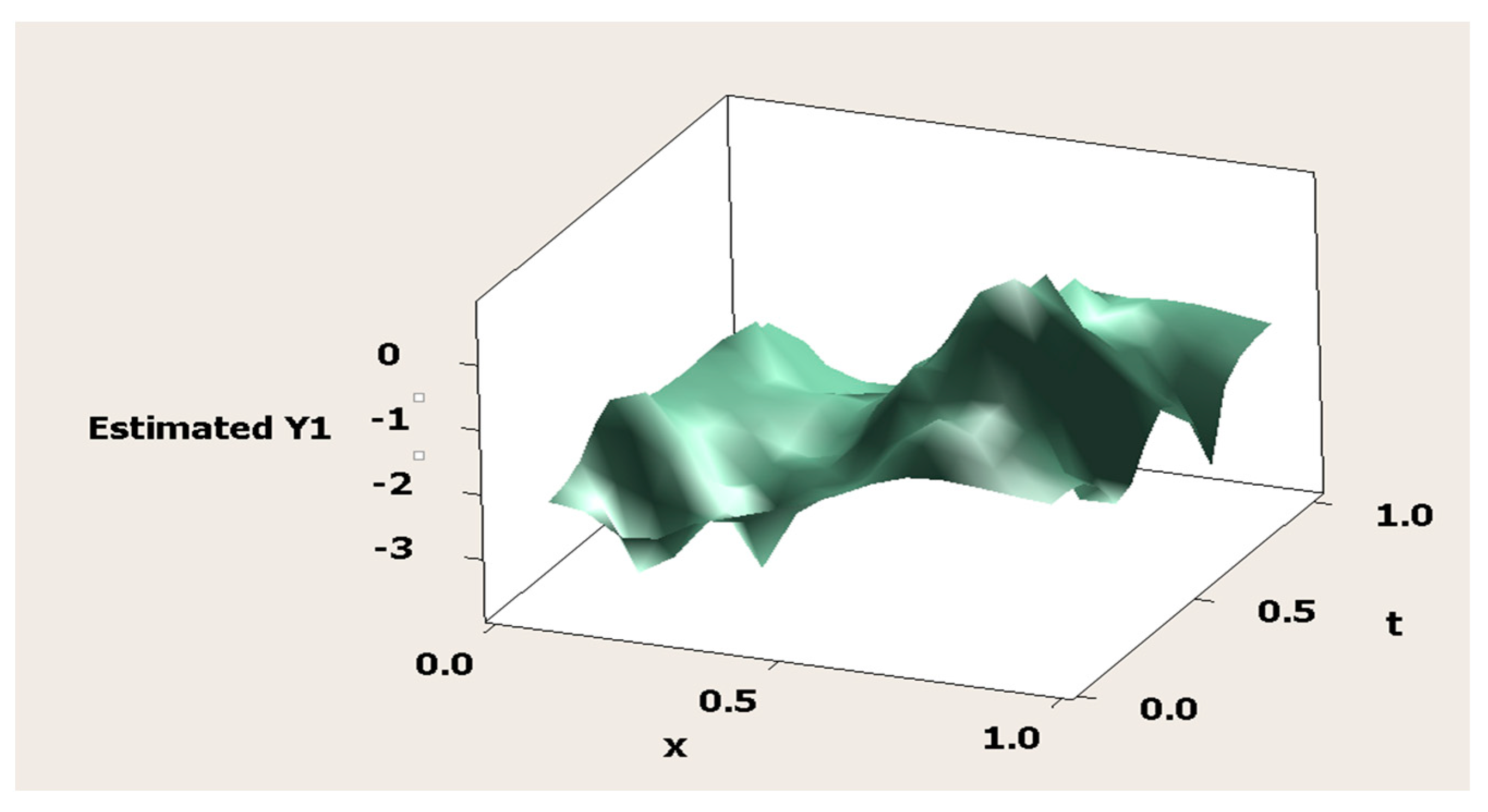

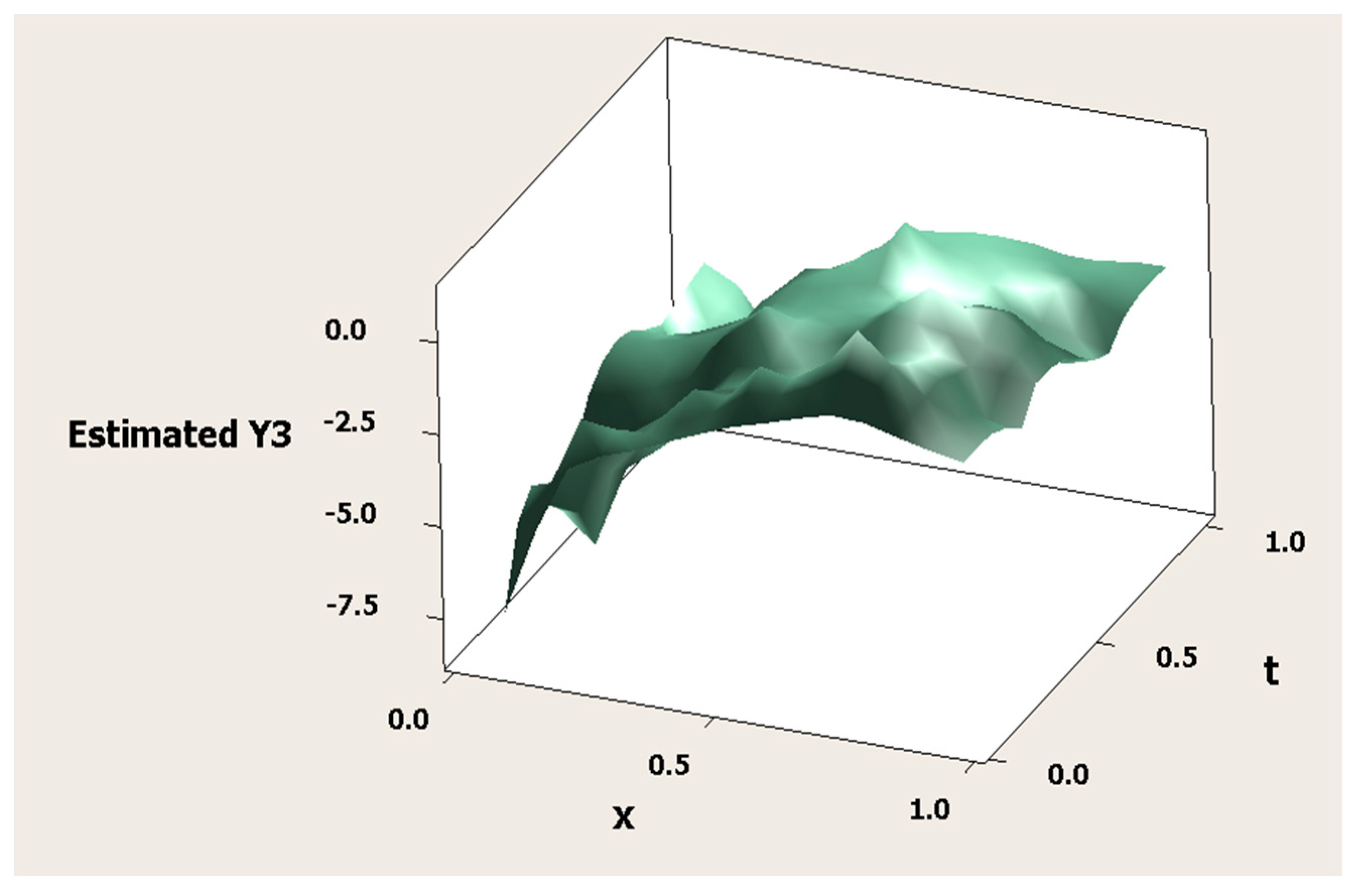
| K | MSE | Minimum GCV | λ | |
|---|---|---|---|---|
| 1 | 1.02363794 | 0.5786323 | 0.95311712 | ; . |
| 2 | 2.20132482 | 2.0945904 | 0.90018631 | ; . |
| 3 | 2.09512311 | 2.17049788 | 0.90527677 | ; . |
| 4 | 2.03215324 | 2.10132858 | 0.90769321 | ; . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamidah, N.; Lestari, B.; Budiantara, I.N.; Aydin, D. Estimation of Multiresponse Multipredictor Nonparametric Regression Model Using Mixed Estimator. Symmetry 2024, 16, 386. https://doi.org/10.3390/sym16040386
Chamidah N, Lestari B, Budiantara IN, Aydin D. Estimation of Multiresponse Multipredictor Nonparametric Regression Model Using Mixed Estimator. Symmetry. 2024; 16(4):386. https://doi.org/10.3390/sym16040386
Chicago/Turabian StyleChamidah, Nur, Budi Lestari, I Nyoman Budiantara, and Dursun Aydin. 2024. "Estimation of Multiresponse Multipredictor Nonparametric Regression Model Using Mixed Estimator" Symmetry 16, no. 4: 386. https://doi.org/10.3390/sym16040386







