Exploring the Dynamics of Dark and Singular Solitons in Optical Fibers Using Extended Rational Sinh–Cosh and Sine–Cosine Methods
Abstract
:1. Introduction
2. Solution Technique
2.1. Extended Rational Sinh–Cosh Approach
2.2. Extended Rational Sin–Cosine Approach
3. Third-Order NLS Equation and Dark/Singular Soliton Solutions
3.1. The Implementation of the Extended Rational Sinh–Cosh Technique
- Set 1:Substituting these values (13) into (8) along with (11), we obtain the following dark soliton solution:Set 2:Inserting the above expressions in (8) with (11), we obtain the following:Set 3:The corresponding solitary wave solution is given by the following:Set 4:Plugging the above expressions (19) into (8) with (11), we find the following:
3.2. The Implementation of Extended Rational Cosh–Sinh Technique
- Set 1:Inserting these values into (8) with (21), we derive the following:Set 2:Substituting the above-obtained values into (8) along with (21), the associated soliton solution is determined by the following:Set 3:Substituting these values into (8) with (21), the soliton solution is found by the following:Set 4:Plugging these set of values into (8) with (21), we obtain the following:
3.3. The Implementation of the Extended Rational Sin–Cos Approach
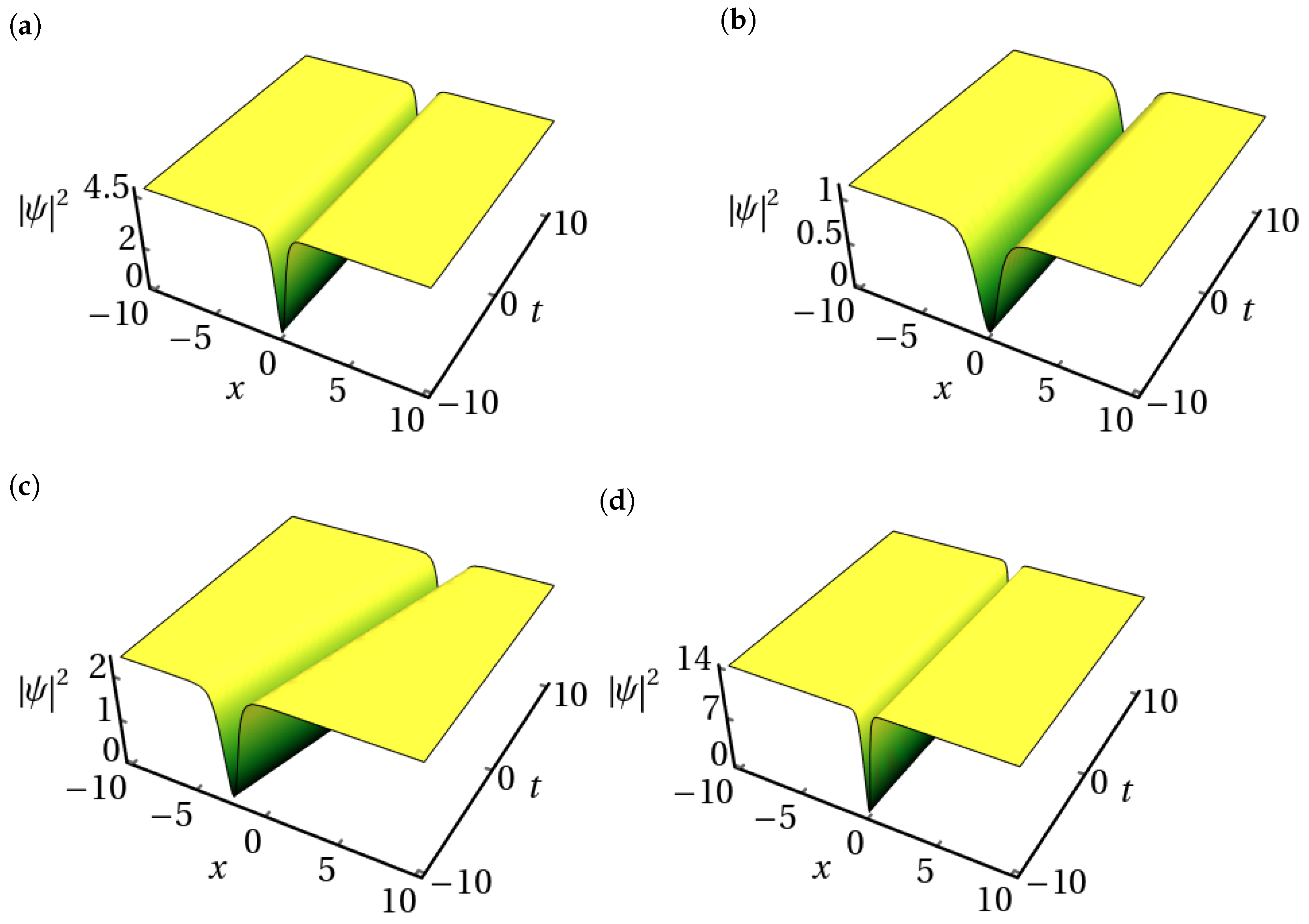
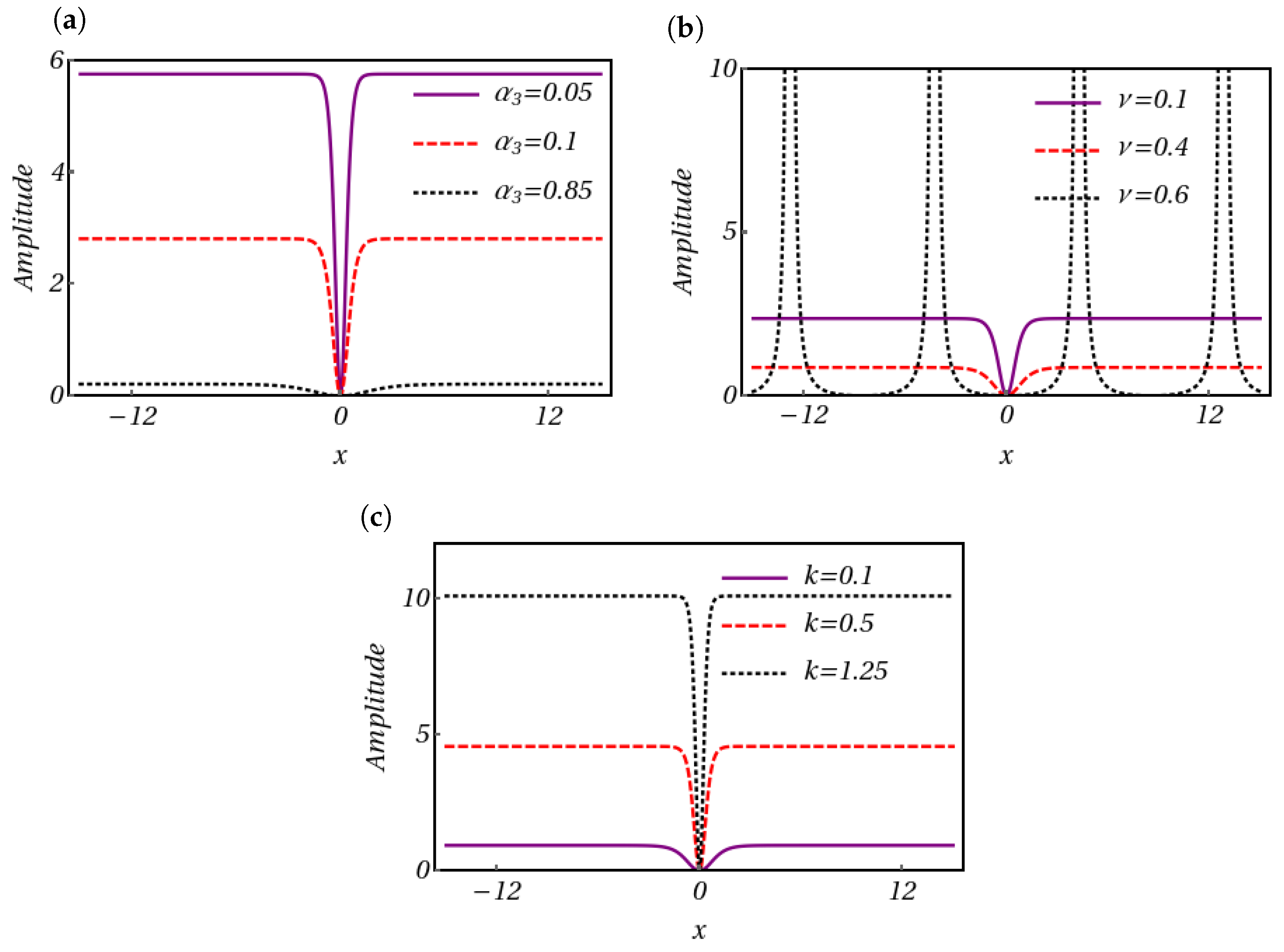
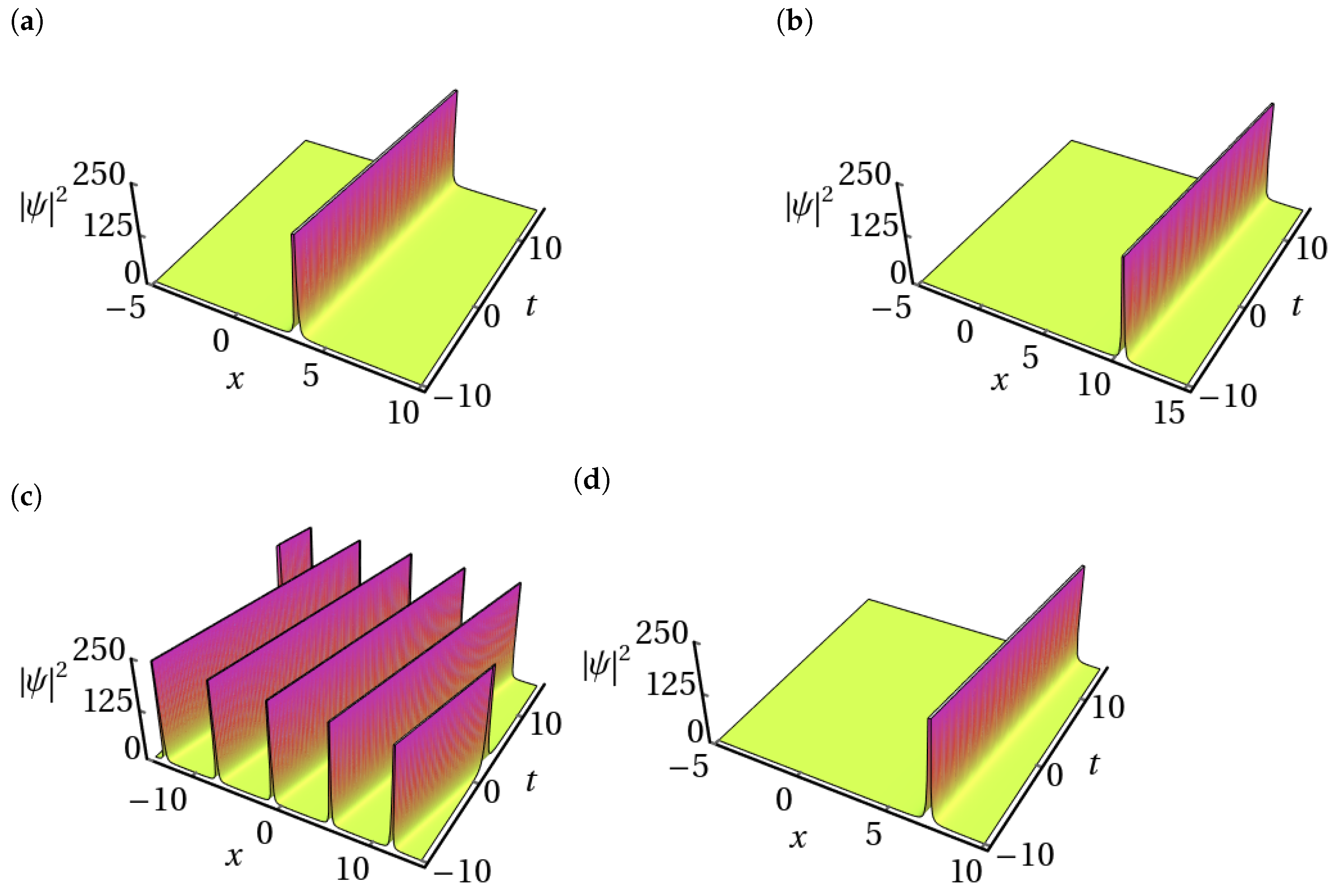
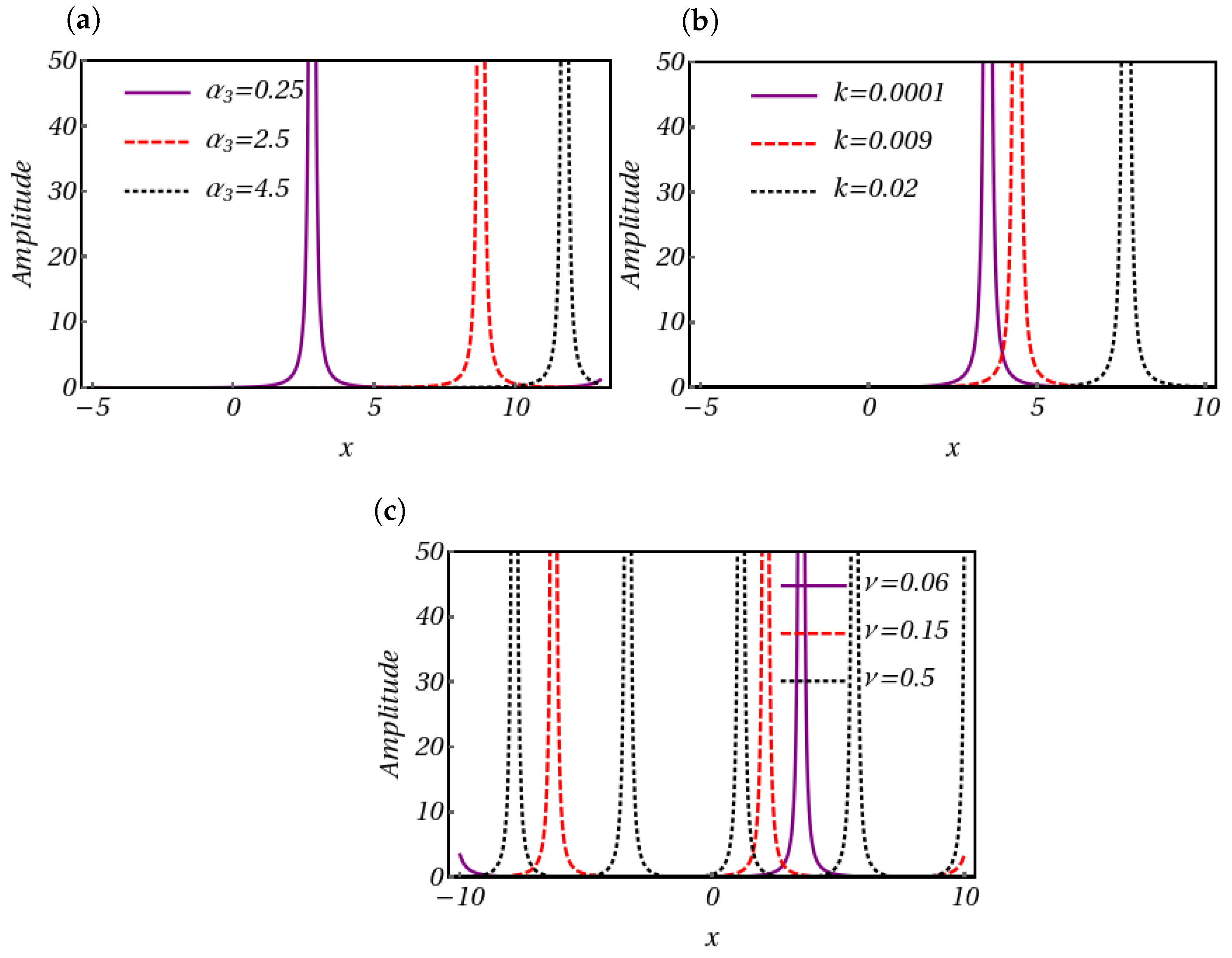
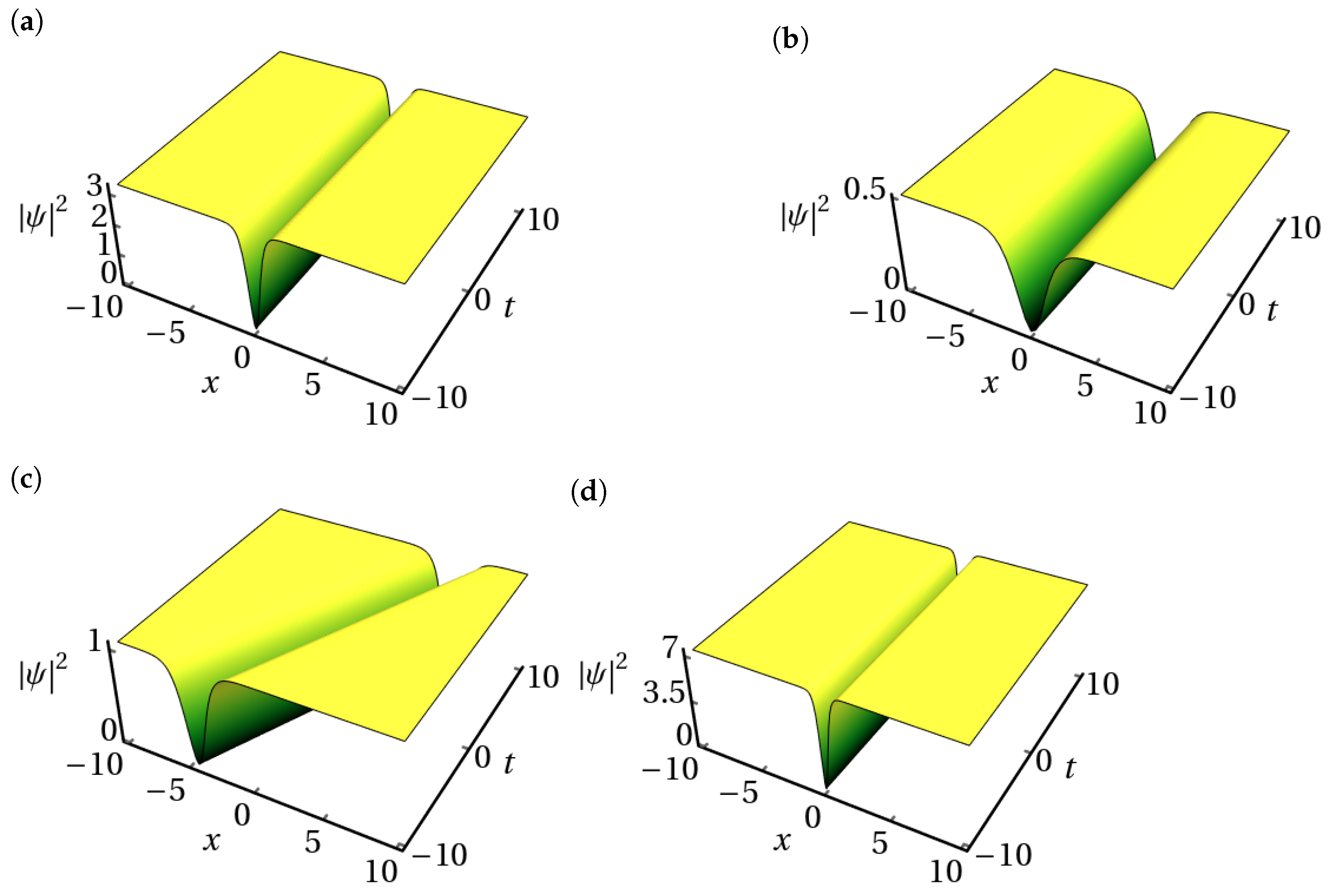
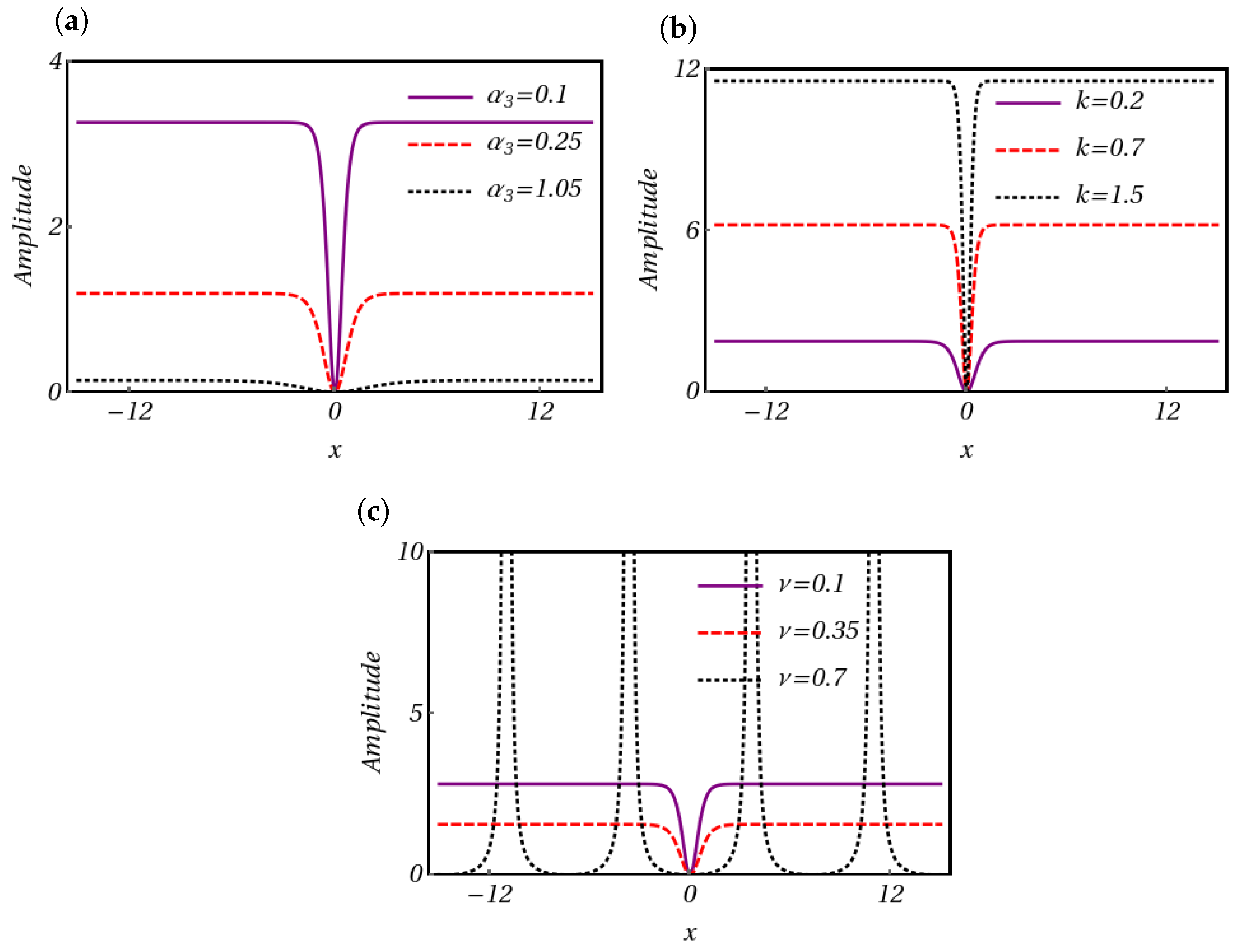
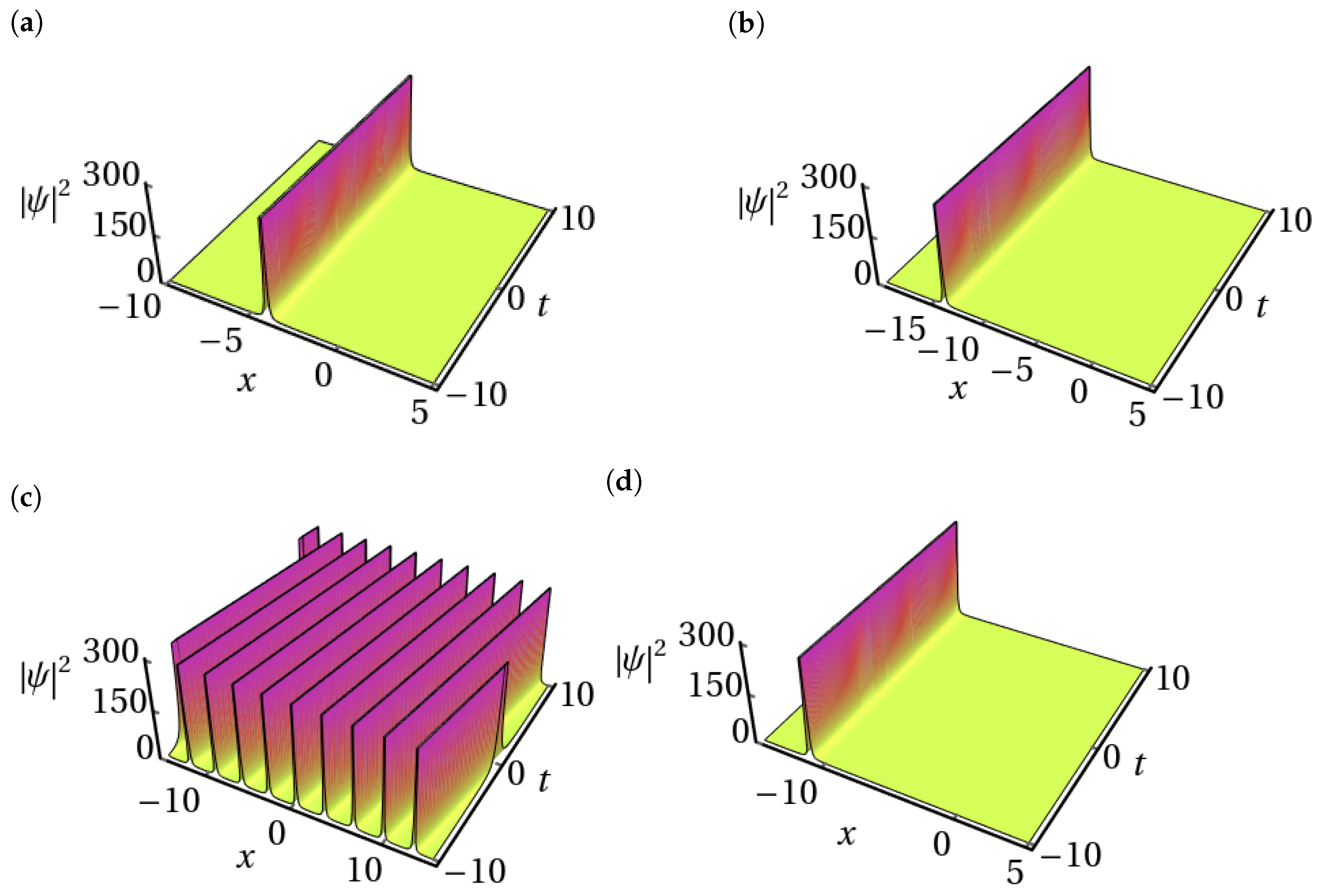
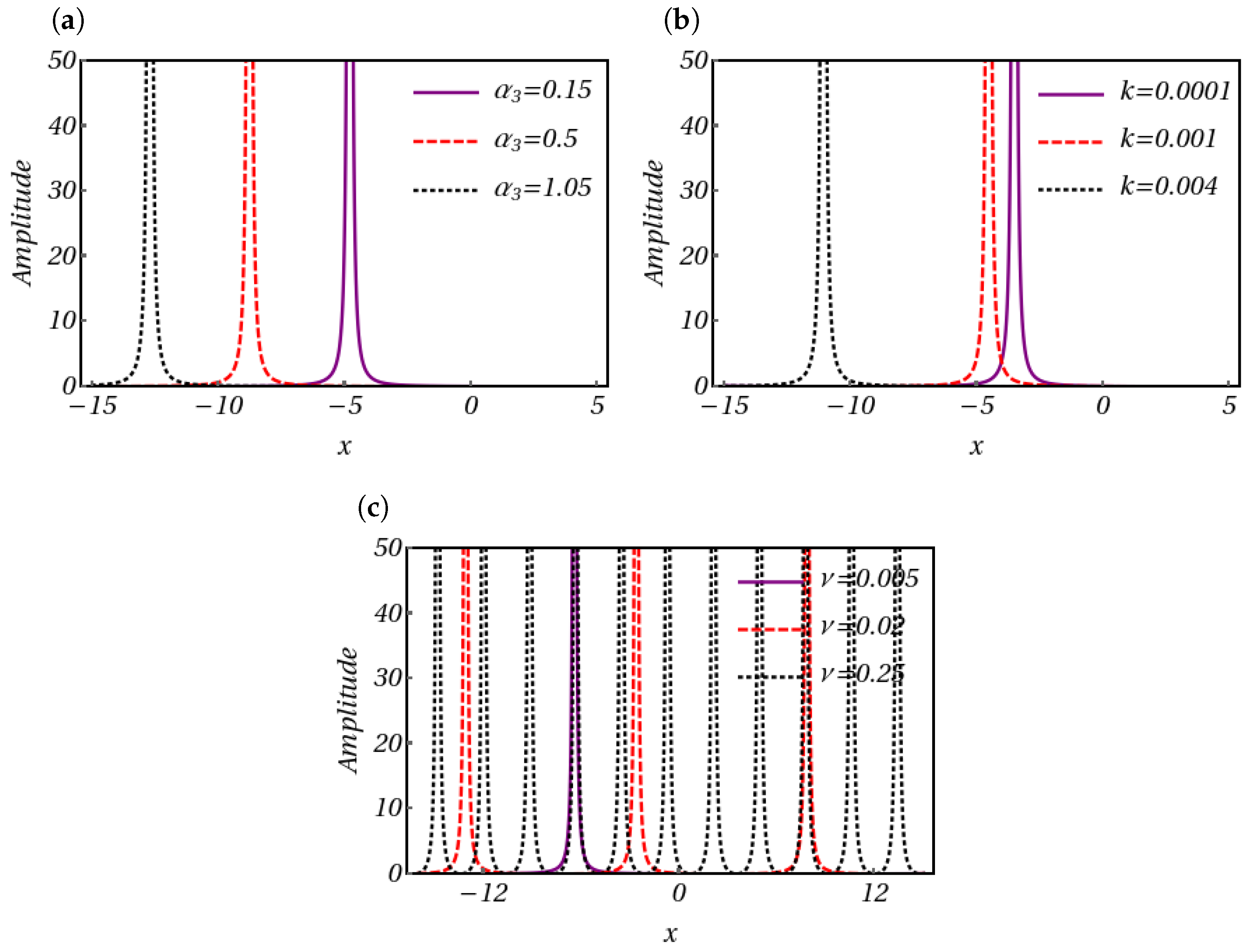
- Set 1:Plugging these sets of values into (8) along with (31), we obtain the following:Set 2:Inserting the obtained values of and in Equation (8) with Equation (31), one can derive the following soliton solution:Set 3:Substituting these forms into Equation (8) along with Equation (31), we acquire the following:Set 4:Plugging the above-obtained values into Equation (8) along with Equation (31), we obtain the following:Utilizing the parameters , , , , and , we generate an intensity profile corresponding to the dark soliton solution (34). This profile is visually represented in Figure 5a. Subsequently, as is adjusted to , a discernible shift occurs in the profile’s characteristics: the amplitude decreases, accompanied by a slight increase in width, as depicted in Figure 5b. Continuing our exploration, we investigate the impact of altering the parameter , initially set at . As demonstrated in Figure 5c, when we increase to , we see a change in the direction of the dark soliton profile along with a decrease in amplitude. Furthermore, modifying the value of k to leads to noteworthy changes in the dark soliton profile. Specifically, in Figure 5d, we witness an enhancement in the amplitude of the dark soliton profile, concomitant with a reduction in its width.
3.4. The Implementation of the Extended Rational Cos–Sin Approach
- Set 1:We construct the following dark soliton solution by substituting the above-mentioned expression into Equation (8) along with the Equation (41), namely the following:Set 2:Inserting these forms in (8) along with Equation (41), we have the following:Set 3:Plugging these expressions into Equation (8) with (41), one obtains the following soliton solution of (7):Set 4:Substituting the above-mentioned forms in Equation (8) with (41), we obtain the following:
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Porsezian, K.; Kuriakose, V.C. Optical Solitons: Theoretical and Experimental Challenges; Springer: New York, NY, USA, 2003. [Google Scholar]
- Dudley, J.M.; Finot, C.; Genty, G.; Taylor, R. Fifty years of fiber solitons. Opt. Photon. News 2023, 34, 26. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790. [Google Scholar] [CrossRef]
- Lakshmanan, M.; Rajasekar, S. Nonlinear Dynamics: Integrability, Chaos and Patterns; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Musammil, N.M.; Porsezian, K.; Nithyanandan, K.; Subha, P.A.; Tchofo Dinda, P. Ultrashort dark solitons interactions and nonlinear tunneling in the modified nonlinear Schrödinger equation with variable coefficient. Opt. Fiber Technol. 2017, 37, 11–20. [Google Scholar] [CrossRef]
- Tahir, M.; Awan, A.U. Optical dark and singular solitons to the Biswas-Arshed equation in birefringent fibers without four-wave mixing. Optik 2020, 207, 164421. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, D.Y.; Zhao, L.M.; Wu, X. Dark pulse emission of a fiber laser. Phys. Rev. A 2009, 80, 045803. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-González, R. Emergent Nonlinear Phenomena in Bose-Einstein Condensates: Theory and Experiment; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hasegawa, A.; Tappert, F.D. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett. 1973, 23, 142. [Google Scholar] [CrossRef]
- Zakharov, V.; Shabat, A. Exact theory of two dimensional self-focusing and one dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62. [Google Scholar]
- Emplit, P.; Hamaide, J.P.; Reynaud, F.; Froehly, C.; Barthelemy, A. Picosecond steps and dark pulses through nonlinear single mode fibers. Opt. Commun. 1987, 62, 374. [Google Scholar] [CrossRef]
- Liu, W.; Pang, L.; Han, H.; Tian, W.; Chen, H.; Lei, M.; Yan, P.; Wei, Z. Generation of dark solitons in erbium-doped fiber lasers based Sb2Te3 saturable absorbers. Opt. Express 2015, 23, 26023–26031. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, D.Y.; Zhao, L.M.; Knize, R.J. Vector dark domain wall solitons in a fiber ring laser. Opt. Express 2010, 18, 4428–4433. [Google Scholar] [CrossRef]
- Meng, Y.; Zhang, S.; Li, H.; Du, J.; Hao, Y.; Li, X. Bright-dark soliton pairs in a self-mode locking fiber laser. Opt. Eng. 2012, 51, 064302. [Google Scholar] [CrossRef]
- Tang, D.Y.; Li, L.; Song, Y.F.; Zhao, L.M.; Zhang, H.; Shen, D.Y. Evidence of dark solitons in all-normal-dispersion-fiber lasers. Phys. Rev. A 2013, 88, 013849. [Google Scholar] [CrossRef]
- Tang, D.; Guo, J.; Song, Y.; Zhang, H.; Zhao, L.; Shen, D. Dark soliton fiber lasers. Opt. Express 2014, 22, 19831–19837. [Google Scholar] [CrossRef] [PubMed]
- Rajan, M.; Hakkim, J.; Mahalingam, A.; Uthayakumar, A. Dispersion management and cascade compression of femtosecond nonautonomous soliton in birefringent fiber. Eur. Phys. J. D 2013, 67, 1–8. [Google Scholar] [CrossRef]
- Mahalingam, A.; Rajan, M.M. Influence of generalized external potentials on nonlinear tunneling of nonautonomous solitons: Soliton management. Opt. Fib. Technol. 2015, 25, 44–50. [Google Scholar] [CrossRef]
- Pelinovsky, D.E.; Yang, J. Stability analysis of embedded solitons in the generalized third-order nonlinear Schrödinger equation. Chaos 2005, 15, 037115. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, K.; Osman, M.S.; Mirzazadeh, M.; Rabiei, F. Investigation of different wave structures to the generalized third-order nonlinear Schrödinger equation. Optik 2020, 206, 164259. [Google Scholar] [CrossRef]
- Crabb, M.; Akhmediev, N. Doubly periodic solutions of the class-I infinitely extended nonlinear Schrödinger equation. Phys. Rev. E 2019, 99, 052217. [Google Scholar] [CrossRef] [PubMed]
- Sinthuja, N.; Manikandan, K.; Senthilvelan, M. Rogue waves on the double-periodic background in Hirota equation. Eur. Phys. J. Plus 2021, 136, 1–12. [Google Scholar] [CrossRef]
- Malomed, B.A.; Mihalache, D. Nonlinear waves in optical and matter-wave media: A topical survey of recent theoretical and experimental results. Rom. J. Phys. 2019, 64, 106. [Google Scholar]
- Mihalache, D.; Truta, N.; Crasovan, L.C. Painleve analysis and bright solitary waves of the higher-order nonlinear Schrödinger equation containing third-order dispersion and self- steepening term. Phys. Rev. E 1997, 56, 1064–1070. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Yuan, S.S. Dark soliton solutions of the defocusing Hirota equation by the binary Darboux transformation. Nonlinear Dyn. 2017, 89, 531–538. [Google Scholar] [CrossRef]
- Shaikhova, G.; Kutum, B.; Myrzakulov, R. Periodic traveling wave, bright and dark soliton solutions of the (2+1)-dimensional complex modified Korteweg-de Vries system of equations by using three different methods. AIMS Math. 2022, 7, 18948–18970. [Google Scholar] [CrossRef]
- Myrzakul, A.; Nugmanova, G.; Serikbayev, N.; Myrzakulov, R. Surfaces and curves induced by nonlinear Schrödinger-type equations and their spin systems. Symmetry 2021, 13, 1827. [Google Scholar] [CrossRef]
- Sagidullayeva, Z.; Nugmanova, G.; Myrzakulov, R.; Serikbayev, N. Integrable Kuralay equations: Geometry, solutions and generalizations. Symmetry 2022, 14, 1374. [Google Scholar] [CrossRef]
- Burdik, C.; Shaikhova, G.; Rakhimzhanov, B. Soliton solutions and traveling wave solutions of the two-dimensional generalized nonlinear Schrödinger equations. Eur. Phys. J. Plus 2021, 136, 1095. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, F.; Xu, B. Localized Symmetric and Asymmetric Solitary Wave Solutions of Fractional Coupled Nonlinear Schrödinger Equations. Symmetry 2023, 15, 1211. [Google Scholar] [CrossRef]
- Manikandan, K.; Serikbayev, N.; Vijayasree, S.P.; Aravinthan, D. Controlling Matter-Wave Smooth Positons in Bose–Einstein Condensates. Symmetry 2023, 15, 1585. [Google Scholar] [CrossRef]
- Shaikhova, G.; Kutum, B.; Syzdykova, A. Phase portraits and new exact traveling wave solutions of the (2+1)-dimensional Hirota system. Results Phys. 2023, 55, 107173. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Stefanov, A.A. Riemann–Hilbert Problems, Polynomial Lax Pairs, Integrable Equations and Their Soliton Solutions. Symmetry 2023, 15, 1933. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Seadawy, A.R.; El-Rashidy, K. Application of the extension exponential rational function method for higher-dimensional Broer–Kaup–Kupershmidt dynamical system. Mod. Phys. Lett. A 2020, 35, 1950345. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alurrfi, K.A.E. A new Jacobi elliptic function expansion method for solving a nonlinear PDE describing the nonlinear low-pass electrical lines. Chaos Solitons Fractals 2015, 78, 148–155. [Google Scholar] [CrossRef]
- Zeković, S.; Muniyappan, A.; Zdravković, S.; Kavitha, L. Employment of Jacobian elliptic functions for solving problems in nonlinear dynamics of microtubules. Chin. Phys. B 2014, 23, 020504. [Google Scholar] [CrossRef]
- Biswas, A.; Alqahtani, R.T. Chirp-free bright optical solitons for perturbed Gerdjikov–Ivanov equation by semi-inverse variational principle. Optik 2017, 147, 72–76. [Google Scholar] [CrossRef]
- Muniyappan, A.; Suruthi, A.; Monisha, B.; Sharon Leela, N.; Vijaycharles, J. Dromion-like structures in a cubic-quintic nonlinear Schrödinger equation using analytical methods. Nonlinear Dyn. 2021, 104, 1533–1544. [Google Scholar] [CrossRef]
- Qayyum, M.; Ahmad, E.; Tauseef Saeed, S.; Ahmad, H.; Askar, S. Homotopy perturbation method-based soliton solutions of the time-fractional (2+1)-dimensional Wu–Zhang system describing long dispersive gravity water waves in the ocean. Front. Phys. 2023, 11, 1178154. [Google Scholar] [CrossRef]
- Mahak, N.; Akram, G. Extension of rational sine-cosine and rational sinh-cosh techniques to extract solutions for the perturbed NLSE with Kerr law nonlinearity. Eur. Phys. J. Plus 2019, 134, 159. [Google Scholar] [CrossRef]
- Muniyappan, A.; Parasuraman, E.; Seadawy, A.R.; Sudharsan, J.B. Chirped dark soliton propagation in optical fiber under a self phase modulation and a self-steepening effect for higher order nonlinear Schrödinger equation. Opt. Quant. Electron. 2024, 56, 772. [Google Scholar] [CrossRef]
- Cinar, M.; Onder, I.; Secer, A.; Yusuf, A.; Sulaiman, T.A.; Bayram, M.; Aydin, H. The analytical solutions of Zoomeron equation via extended rational sin-cos and sinh-cosh methods. Phys. Scr. 2021, 96, 094002. [Google Scholar] [CrossRef]
- Karchi, N.A.; Ghaemi, M.B.; Vahidi, J. New exact solutions of nonlinear Schrödinger equation with extended rational sin–cos and sinh–cosh method. AIP Adv. 2022, 12, 085110. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Soto-Crespo, J.M.; Akhmediev, N. Rogue waves and rational solutions of the Hirota equation. Phys. Rev. E 2010, 81, 046602. [Google Scholar] [CrossRef] [PubMed]
- Shi, K.Z.; Ren, B.; Shen, S.F.; Wang, G.F.; Peng, J.D.; Wang, W.L. Solitons, rogue waves and interaction behaviors of a third-order nonlinear Schrödinger equation. Results Phys. 2022, 37, 105533. [Google Scholar] [CrossRef]
- Tao, Y.S.; He, J.S. Multisolitons, breathers, and rogue waves for the Hirota equation generated by the Darboux transformation. Phys. Rev. E 2012, 85, 026601. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Zhang, Q.Y.; Zhu, Z.W.; Qi, Y.Y.; Yin, P.; Ge, Y.Q.; Li, L.; Jin, L.; Zhang, L.; Zhang, H. Recent advances and challenges on dark solitons in fiber lasers. Opt. Laser Technol. 2022, 152, 108116. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Nixon, S.D.; Horikis, T.P.; Frantzeskakis, D.J. Dark solitons of the power-energy saturation model: Application to mode-locked lasers. J. Phys. A Math. Theor. 2013, 46, 095201. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Q.Y.; Li, L.; Jin, L.; Chen, S. Generation of Dark Solitons in a Self-mode-locked Tm-Ho Doped Fiber Laser. Infrared Phys. Technol. 2022, 121, 104043. [Google Scholar] [CrossRef]
- Weiner, A.M.; Heritage, J.P.; Hawkins, R.J.; Thurston, R.N.; Kirschner, E.M. Experimental Observation of the Fundamental Dark Soliton in Optical Fibers. Phys. Rev. Lett. 1988, 61, 2445–2448. [Google Scholar] [CrossRef] [PubMed]
- Emplit, P.H.; Haelterman, M.; Kashyap, R.; De Lathouwer, M. Fiber Bragg grating for optical dark soliton generation. IEEE Photonics Technol. Lett. 1997, 9, 1122–1124. [Google Scholar] [CrossRef]
- Li, H.P.; Xia, H.D.; Jing, Z.; Liao, J.K.; Tang, X.G.; Liu, Y.; Liu, Y.Z. Dark pulse generation in a dispersion-managed fiber laser. Laser Phys. 2012, 22, 261–264. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muniyappan, A.; Manikandan, K.; Saparbekova, A.; Serikbayev, N. Exploring the Dynamics of Dark and Singular Solitons in Optical Fibers Using Extended Rational Sinh–Cosh and Sine–Cosine Methods. Symmetry 2024, 16, 561. https://doi.org/10.3390/sym16050561
Muniyappan A, Manikandan K, Saparbekova A, Serikbayev N. Exploring the Dynamics of Dark and Singular Solitons in Optical Fibers Using Extended Rational Sinh–Cosh and Sine–Cosine Methods. Symmetry. 2024; 16(5):561. https://doi.org/10.3390/sym16050561
Chicago/Turabian StyleMuniyappan, Annamalai, Kannan Manikandan, Akbota Saparbekova, and Nurzhan Serikbayev. 2024. "Exploring the Dynamics of Dark and Singular Solitons in Optical Fibers Using Extended Rational Sinh–Cosh and Sine–Cosine Methods" Symmetry 16, no. 5: 561. https://doi.org/10.3390/sym16050561
APA StyleMuniyappan, A., Manikandan, K., Saparbekova, A., & Serikbayev, N. (2024). Exploring the Dynamics of Dark and Singular Solitons in Optical Fibers Using Extended Rational Sinh–Cosh and Sine–Cosine Methods. Symmetry, 16(5), 561. https://doi.org/10.3390/sym16050561





