A Systematic Formulation into Neutrosophic Z Methodologies for Symmetrical and Asymmetrical Transportation Problem Challenges
Abstract
:1. Introduction
1.1. Key Points of the Study
- This research work presents a novel approach for solving navigation problems using neutrosophic Z-numbers, which provides a unique approach to dealing with uncertainties.
- It acknowledges many unknowns inherent in travel data, including irregular travel patterns and changing demands, which are often overlooked by conventional methods.
- It shows a significant improvement in the ability to deal with uncertainties compared to traditional methods, leading to efficient and reliable solutions to transportation problems.
- We provide a practical demonstration of the proposed method by applying the developed algorithm to numerical examples, demonstrating its effectiveness in real-world situations.
1.2. Main Contributions
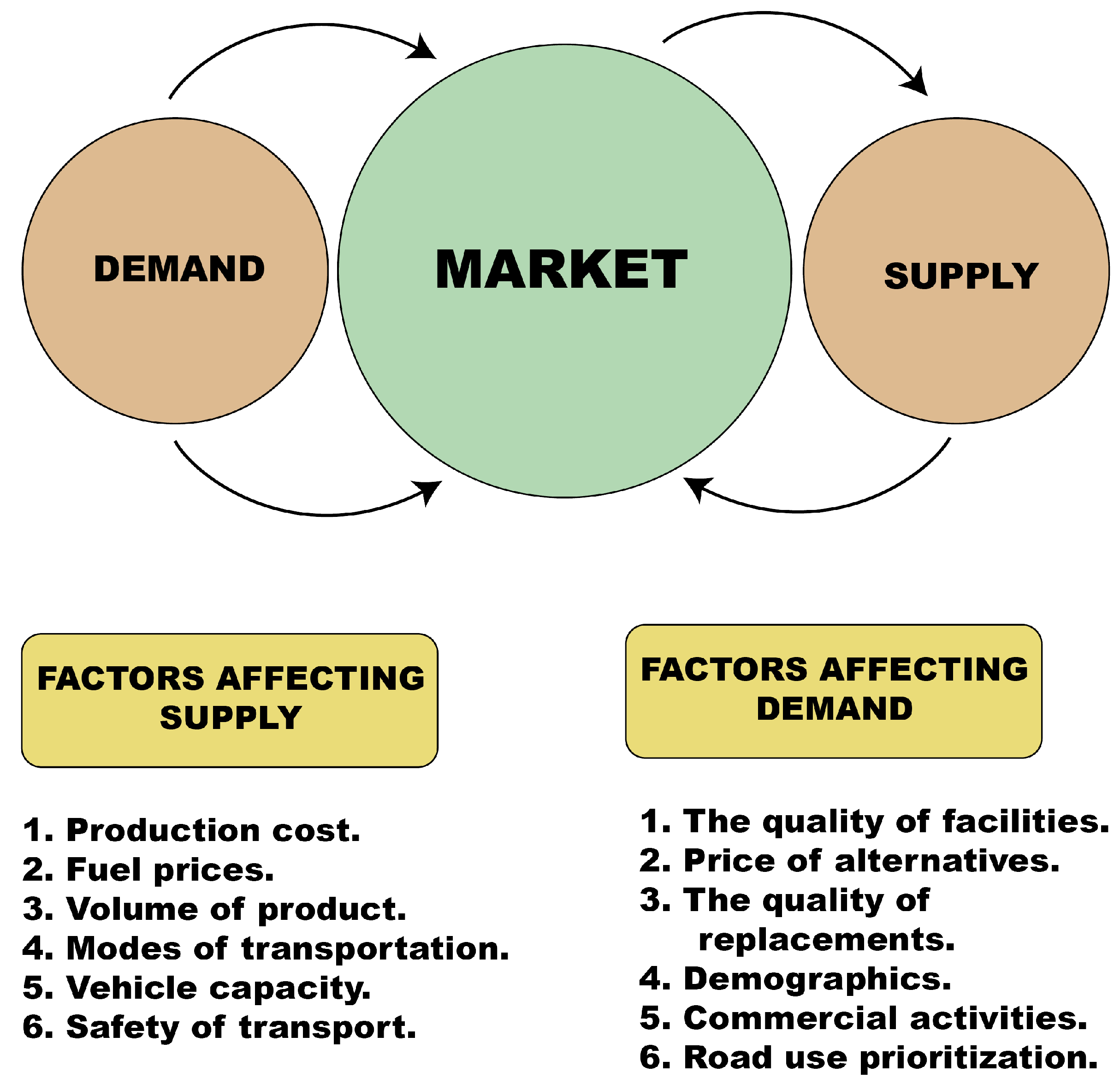
- The goal of this research is to examine how neutrosophic Z-numbers (NZNs) adapt and function in a variety of domains when faced with unpredictable situations in transportation difficulties.
- Explain the fundamental roles of algorithms in the context of NZNs and gain an understanding of the underlying ideas.
- Development of a new algorithm specifically designed for the derived set that increases the efficiency of transportation problem solving.
- Describe and analyze the algorithm in NZNs in detail, taking into account the most important aspects to obtain relevant data.
- Creation of MATLAB code to facilitate the implementation of the proposed framework, providing a user-friendly tool for researchers and professionals in the field.
- Application of the developed algorithm in mathematical models, demonstration of its practical efficacy and potential for real-world application.
- Comprehensive solutions to balanced and unbalanced transport problems, offering comprehensive strategies for dealing with a variety of situations.
Motivation
2. Preliminaries
- 1.
- iff, , , , and .
- 2.
- iff,and
- 3.
- .
- 4.
- 5.
- (Complement of )
- 6.
- 7.
- 8.
- 9.
3. Existing Model in Crisp Transportation
- How many sources are there?
- How many destinations are there?
- i The index of origin for all .
- j The index of destination for all .
- The quantity of product that we have to transport from the point of origin to the destination.
- The cost in neutrosophic Z-numbers per unit quantity that we will carry from the ith origin to the jth destination.
- The cost per unit quantity when it is expressed in the form of crisp numbers.
- The quantity which is available for supply from each source in crisp environment.
- The quantity which is available for supply from each source in NZN environment.
- The quantity which is to be demanded from each destination in crisp environment.
- The quantity which is to be demanded from each destination in NZN environment.
4. Proposed Models in NZN Environment for Transportation
4.1. Main Algorithm
- Step 1
- To begin solving the NZN transportation issue, select any model.In the transportation problem of Type 1 NZN, we have the cost value of the transportation as the neutrosophic Z-numbers while supply and demands are in crisp numbers. In this case, we will apply the score function to find the score value of each neutrosophic Z-number given in the problem either in the form of transportation cost, supply or demand.
- Step 2
- In this step, we will check whether the transportation problem is balanced or not.For this, we have to show thati.e., demand = supply.If the transportation is unbalanced, then we have to add a dummy row or column to balance the transportation problem.
- Step 3
- We are going to use Algorithm 1 to find the feasible solution of the given transportation problem.
- Step 4
- Write a clear and concise formulation of the transportation issue.
- Step 5
- For the goal function, replace all to obtain the transit cost.End.
4.2. Algorithm 1
- Step I
- We will use the table values from the first phase of the main algorithm in this stage.
- Step II
- In this step, we will find the difference between the least and next to the least transportation cost and show it in a new column and row as penalty of that column or row.
- Step III
- Find the maximum penalty and allocate the appropriate row or column of the maximum penalty to the cell with the lowest transportation cost.
- Step IV
- May the highest penalty be the same forCase 1: If there are multiple rows, choose the top row;Case 2: If there are many columns, choose the column on the left.Repeat steps III and IV until there is no supply left to fulfill and no demand left to satisfy.
5. Transportation Problems
5.1. Illustrative Examples
5.2. Balanced Transportation Problem
Type 1 NZN Model
5.3. Unbalanced Transportation Problem
Type 1 NZN Model
6. Sensitivity Analysis
6.1. Algorithm 2
- Step I
- In the first step of algorithm, we will identify the locations where no allocation has been made and obtain the initial feasible solution.
- Step II
- Starting from a vacant cell to occupied cells, draw a close loop, such that only the initial vacant cell and occupied cells are permitted locations to change direction with 90° angle in this closed path. Insert the (+) and (−) signs one after another at every location, beginning with the (+) at first empty cell. Sum up the transportation costs of every cell traced by this closed loop. The resultant value is known as net cost change. Repeat the process for every location’s transportation cost where no allotments are assigned.Note: The first positive transportation cost is the only one with no allocations, afterwards all of them which have the sign (+) or (−) are the location’s where allotments are assigned.
- Step III
- If all the net cost changes are positive then the solution is optimal. Otherwise, draw a closed loop from the vacant cell bearing the largest negative net cost change.
- Step IV
- On this closed loop, choose the cell having (−) sign and the minimum allotted value. Allot this value to the vacant cell and it becomes the occupied cell. Subtract the same value from all allocations of cells traced on this path having (−) sign and likewise add this value to the allotments of cells traced on the closed loop. From this, we will obtain a new table containing new allotments.
- Step V
- Repeat Steps II to IV until all the net cost changes we obtain are positive and hence at that moment we will achieve our optimal solution.After finding the optimal solution, repeat Steps 4 and 5 of the main algorithm to obtain the minimum value.End.
6.1.1. Optimality Test for Example 1
6.1.2. Optimality Test for Example 2
7. Limitations
- Our research focuses primarily on the application of neutrosophic group theory and Zadeh Z-numbers to navigation problems, which may limit its generalizability in other fields.
- The numerical methods used in our study can be prone to numerical complications when solving numerically, especially when dealing with large transport systems. However, researchers can minimize complexities and easily obtain the solution by using the MATLAB software.
- Although our approach provides promising results, its implementation may require significant computational resources and expertise, placing challenges on resource-limited personnel.
- Relying on numerical models and simulations to validate our methods may not fully capture the complexity and nuances of real-world navigation systems.
- The efficiency of our approach may be affected by data quality and availability, as well as by external factors such as regulatory restrictions and market trends.
8. Conclusions
- The approach provides a solution for complicated optimization problems.
- Method can manage determining the best option for many suppliers and locations.
- The study demonstrates the excellent accuracy of a suggested technique called Z-statistics.
- This strategy addresses multiple issues and uncertainty that numerical approaches for optimal solutions neglect.
- Our results undergo testing and verification, which demonstrate the dependability of our findings.
- By using cutting-edge rigorous verification techniques, we have ensured that the solutions we provide are not only correct but nearly accurate, notwithstanding some uncertainties.
- The numerical examples presented throughout verify the effectiveness of our method and highlight its practical application.
- The use of MATLAB codes provides additional accessibility and efficiency, facilitating greater adoption of our technique.
- To increase the reliability of our solutions and gain a better understanding of how uncertainty affects them, more research is required to create more reliable techniques for determining uncertainty and conducting sensitivity analyses. Work together with stakeholders and industry partners to integrate our techniques into current logistical processes so that quick and effective decision-making is possible. Examine how cutting-edge technologies like blockchain and the Internet of Things (IoT) can be combined to improve the visibility and trackability of transportation routes and to personalize and streamline our solutions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hitchcock, F.L. The distribution of a product from several sources to numerous localities. J. Math. Phys. 1941, 20, 224–230. [Google Scholar] [CrossRef]
- Balinski, M.L. Fixed-cost transportation problems. Nav. Res. Logist. Q. 1961, 8, 41–54. [Google Scholar] [CrossRef]
- Ghosh, S.; Roy, S.K.; Verdegay, J.L. Fixed-charge solid transportation problem with budget constraints based on carbon emission in neutrosophic environment. Soft Comput. 2022, 26, 11611–11625. [Google Scholar] [CrossRef]
- Korukoglu, S.; Balli, S. An improved Vogel’s approximation method for the transportation problem. Math. Comput. Appl. 2011, 16, 370–381. [Google Scholar] [CrossRef]
- Meethom, W.; Koohathongsumrit, N. A decision support system for road freight transportation route selection with new fuzzy numbers. Foresight 2020, 22, 505–527. [Google Scholar] [CrossRef]
- Dou, C.; Woldt, W.; Bogardi, I.; Dahab, M. Numerical solute transport simulation using fuzzy sets approach. J. Contam. Hydrol. 1997, 27, 107–126. [Google Scholar] [CrossRef]
- Singh, A.; Das, A.; Bera, U.K.; Lee, G.M. Prediction of transportation costs using trapezoidal neutrosophic fuzzy analytic hierarchy process and artificial neural networks. IEEE Access 2021, 9, 103497–103512. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Shukla, A.K.; Prakash, V.; Nath, R.; Muhuri, P.K. Type-2 intuitionistic fuzzy TODIM for intelligent decision-making under uncertainty and hesitancy. Soft Comput. 2023, 27, 13373–13390. [Google Scholar] [CrossRef]
- Arora, H.D.; Naithani, A. A new definition for quartic fuzzy sets with hesitation grade applied to multi-criteria decision-making problems under uncertainty. Decis. Anal. J. 2023, 7, 100239. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Majumder, P.; Das, S.; Das, R.; Tripathy, B.C. Identification of the most significant risk factor of COVID-19 in economy using cosine similarity measure under SVPNS-environment. Neutrosophic Sets Syst. 2021, 46, 112–127. [Google Scholar]
- Broumi, S.; Bakali, A.; Bahnasse, A. Neutrosophic sets: An overview. Infin. Study 2018, 2, 403–434. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single valued neutrosophic sets. Infin. Study 2010, 12, 20110. [Google Scholar]
- Das, S.; Das, R.; Tripathy, B.C. Multi-criteria group decision making model using single-valued neutrosophic set. Infin. Study 2020, 16, 421–429. [Google Scholar] [CrossRef]
- Ye, J.; Du, S.; Yong, R. Multi-criteria decision-making model using trigonometric aggregation operators of single-valued neutrosophic credibility numbers. Inf. Sci. 2023, 644, 118968. [Google Scholar] [CrossRef]
- Kamran, M.; Ismail, R.; Al-Sabri, E.H.A.; Salamat, N.; Farman, M.; Ashraf, S. An optimization strategy for MADM framework with confidence level aggregation operators under probabilistic neutrosophic hesitant fuzzy rough environment. Symmetry 2023, 15, 578. [Google Scholar] [CrossRef]
- Das, R.; Mukherjee, A.; Tripathy, B.C. Application of neutrosophic similarity measures in COVID-19. Ann. Data Sci. 2022, 9, 55–70. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Chanas, S.; Kolodziejczyk, W.; Machaj, A. A fuzzy approach to the transportation problem. Fuzzy Sets Syst. 1984, 13, 211–221. [Google Scholar] [CrossRef]
- Chanas, S.; Kuchta, D. A concept of the optimal solution of the transportation problem with fuzzy cost coefficients. Fuzzy Sets Syst. 1996, 82, 299–305. [Google Scholar] [CrossRef]
- Tada, M.; Ishii, H. An integer fuzzy transportation problem. Comput. Math. Appl. 1996, 31, 71–87. [Google Scholar] [CrossRef]
- Hashmi, N.; Jalil, S.A.; Javaid, S. A model for two-stage fixed charge transportation problem with multiple objectives and fuzzy linguistic preferences. Soft Comput. 2019, 23, 12401–12415. [Google Scholar] [CrossRef]
- Celik, E.; Akyuz, E. An interval type-2 fuzzy AHP and TOPSIS methods for decision-making problems in maritime transportation engineering: The case of ship loader. Ocean Eng. 2018, 155, 371–381. [Google Scholar] [CrossRef]
- Singh, S.K.; Yadav, S.P. A new approach for solving intuitionistic fuzzy transportation problem of type-2. Ann. Oper. Res. 2016, 243, 349–363. [Google Scholar] [CrossRef]
- Giri, B.K.; Roy, S.K. Neutrosophic multi-objective green four-dimensional fixed-charge transportation problem. Int. J. Mach. Learn. Cybern. 2022, 13, 3089–3112. [Google Scholar] [CrossRef]
- Arora, J. An algorithm for interval-valued fuzzy fractional transportation problem. Ski. Res. J. 2018, 8, 71–75. [Google Scholar]
- Bharati, S.K. Transportation problem with interval-valued intuitionistic fuzzy sets: Impact of a new ranking. Prog. Artif. Intell. 2021, 10, 129–145. [Google Scholar] [CrossRef]
- Pratihar, J.; Kumar, R.; Edalatpanah, S.A.; Dey, A. Modified Vogels approximation method for transportation problem under uncertain environment. Complex Intell. Syst. 2021, 7, 29–40. [Google Scholar] [CrossRef]
- Mondal, A.; Roy, S.K.; Midya, S. Intuitionistic fuzzy sustainable multi-objective multi-item multi-choice step fixed-charge solid transportation problem. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 6975–6999. [Google Scholar] [CrossRef]
- Bagheri, M.; Ebrahimnejad, A.; Razavyan, S.; Hosseinzadeh Lotfi, F.; Malekmohammadi, N. Fuzzy arithmetic DEA approach for fuzzy multi-objective transportation problem. Oper. Res. 2022, 22, 1479–1509. [Google Scholar] [CrossRef]
- Akram, M.; Shah, S.M.U.; Al-Shamiri, M.M.A.; Edalatpanah, S.A. Extended DEA method for solving multi-objective transportation problem with Fermatean fuzzy sets. Aims Math. 2023, 8, 924–961. [Google Scholar] [CrossRef]
- Borah, G.; Dutta, P. Aggregation operators of quadripartitioned single-valued neutrosophic Z-numbers with applications to diverse COVID-19 scenarios. Eng. Appl. Artif. Intell. 2023, 119, 105748. [Google Scholar] [CrossRef]
- Kamran, M.; Salamat, N.; Hameed, M.S. Sine Trigonometric Aggregation Operators with Single-Valued Neutrosophic Z-Numbers: Application in Business Site Selection. Neutrosophic Sets Syst. 2024, 63, 18. [Google Scholar]
- Zadeh, L.A. A note on Z-numbers. Inf. Sci. 2011, 181, 2923–2932. [Google Scholar] [CrossRef]
- Ren, Z.; Liao, H.; Liu, Y. Generalized Z-numbers with hesitant fuzzy linguistic information and its application to medicine selection for the patients with mild symptoms of the COVID-19. Comput. Ind. Eng. 2020, 145, 106517. [Google Scholar] [CrossRef] [PubMed]
- Xian, S.; Chai, J.; Li, T.; Huang, J. A ranking model of Z-mixture-numbers based on the ideal degree and its application in multi-attribute decision making. Inf. Sci. 2021, 550, 145–165. [Google Scholar] [CrossRef]
- Ye, J. Neutrosophic number linear programming method and its application under neutrosophic number environments. Soft Comput. 2018, 22, 4639–4646. [Google Scholar] [CrossRef]
- Du, S.; Ye, J.; Yong, R.; Zhang, F. Some aggregation operators of neutrosophic Z-numbers and their multicriteria decision making method. Complex Intell. Syst. 2021, 7, 429–438. [Google Scholar] [CrossRef]

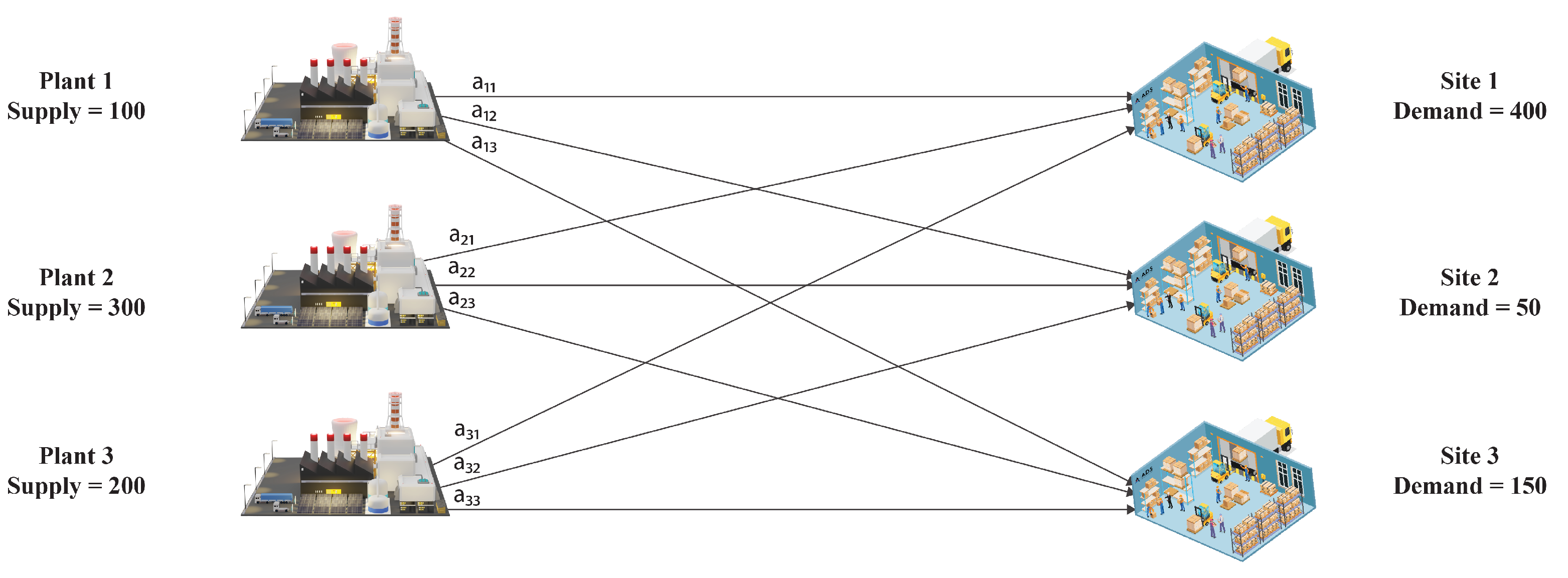

| Supply | ||||
|---|---|---|---|---|
| (0.1,0.2),(0.3,0.4),(0.5,0.6) | (0.5,0.9),(0.4,0.8),(0.3,0.7) | (0.9,0.2),(0.8,0.3),(0.7,0.4) | 100 | |
| (0.8,0.4),(0.8,0.8),(0.2,0.9) | (0.1,0.9),(0.9,0.5),(0.5,0.6) | (0.6,0.4),(0.4,0.2),(0.2,0.8) | 300 | |
| (0.8,0.5),(0.5,0.2),(0.2,0.9) | (0.9,0.8),(0.8,0.1),(0.1,0.7) | (0.7,0.53),(0.29,0.15),(0.6,0.4) | 200 | |
| Demand | 400 | 50 | 150 | 600 |
| Supply | ||||
|---|---|---|---|---|
| 0.533 | 0.64 | 0.553 | 100 | |
| 0.5 | 0.4466 | 0.666 | 300 | |
| 0.706 | 0.856 | 0.6958 | 200 | |
| Demand | 400 | 50 | 150 | 600 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.533 | 0.64 | 0.553 | 100 | 0.02 | |
| 0.5 | 0.666 | 300/250 | 0.0534 | ||
| 0.706 | 0.856 | 0.6958 | 200 | 0.0102 | |
| Demand | 400 | 50/0 | 150 | 600 | |
| Penalty | 0.033 | 0.1934 | 0.113 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.533 | 0.64 | 0.553 | 100 | 0.02 | |
| 0.666 | 300/250/0 | 0.166 | |||
| 0.706 | 0.856 | 0.6958 | 200 | 0.0102 | |
| Demand | 400/150 | 50/0 | 150 | 600 | |
| Penalty | 0.033 | - | 0.113 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.64 | 0.553 | 100/0 | 0.02 | ||
| 0.666 | 300/250/0 | - | |||
| 0.706 | 0.856 | 0.6958 | 200 | 0.0102 | |
| Demand | 400/150/50 | 50/0 | 150 | 600 | |
| Penalty | 0.173 | - | 0.1428 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.64 | 0.553 | 100/0 | - | ||
| 0.666 | 300/250/0 | - | |||
| 0.856 | 0.6958 | 200/150 | 0.0102 | ||
| Demand | 400/150/50/0 | 50/0 | 150 | 600 | |
| Penalty | 0.173 | - | 0.1428 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.64 | 0.553 | 100/0 | - | ||
| 0.666 | 300/250/0 | - | |||
| 0.856 | 200/150/0 | 0.0102 | |||
| Demand | 400/150/50/0 | 50/0 | 150/0 | 600 | |
| Penalty | - | - | 0.1428 |
| Supply | ||||
|---|---|---|---|---|
| (0.69,0.81),(0.31,0.54),(0.63,0.29) | (0.71,0.19),(0.98,0.37),(0.17,0.28) | (0.55,0.89),(0.71,0.35),(0.43,0.241) | 249 | |
| (0.43,0.21),(0.03,0.1),(0.9,0.87) | (0.05,0.97),(0.7,0.143),(0.3,0.5) | (0.879,0.71),(0.91,0.678),(0.61,0.93) | 135 | |
| (0.08,0.13),(0.24,0.35),(0.05,0.64) | (0.7,0.01),(0.897,0.34),(0.87,0.05) | (0.09,0.1),(0.2,0.256),(0.03,0.35) | 141 | |
| Demand | 200 | 250 | 100 | 645 |
| Supply | ||||
|---|---|---|---|---|
| 0.7362 | 0.5749 | 0.7124 | 249 | |
| 0.4347 | 0.5994 | 0.4799 | 135 | |
| 0.631 | 0.5528 | 0.649 | 141 | |
| Demand | 200 | 250 | 100 |
| Supply | ||||
|---|---|---|---|---|
| 0.7362 | 0.5749 | 0.7124 | 249 | |
| 0.4347 | 0.5994 | 0.4799 | 135 | |
| 0.631 | 0.5528 | 0.649 | 141 | |
| 0 | 0 | 0 | 25 | |
| Demand | 200 | 250 | 100 | 550 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.7362 | 0.5749 | 0.7124 | 249 | 0.1375 | |
| 0.4347 | 0.5994 | 0.4799 | 135 | 0.0452 | |
| 0.631 | 0.5528 | 0.649 | 141 | 0.0782 | |
| 0 | 0 | 25/0 | 0 | ||
| Demand | 200 | 250/225 | 100 | 550 | |
| Penalty | 0.4347 | 0.5528 | 0.4799 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.7362 | 0.5749 | 0.7124 | 249 | 0.1375 | |
| 0.5994 | 0.4799 | 135/0 | 0.0452 | ||
| 0.631 | 0.5528 | 0.649 | 141 | 0.0782 | |
| 0 | 0 | 25/0 | - | ||
| Demand | 200/65 | 250/225 | 100 | 550 | |
| Penalty | 0.1963 | 0.0221 | 0.1691 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.7362 | 0.7124 | 249/24 | 0.1375 | ||
| 0.5994 | 0.4799 | 135/0 | - | ||
| 0.631 | 0.5528 | 0.649 | 141 | 0.0782 | |
| 0 | 0 | 25/0 | - | ||
| Demand | 200/65 | 250/225/0 | 100 | 550 | |
| Penalty | 0.1052 | 0.0221 | 0.0634 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.7362 | 0.7124 | 249/24 | 0.0238 | ||
| 0.5994 | 0.4799 | 135/0 | - | ||
| 0.5528 | 0.649 | 141/76 | 0.018 | ||
| 0 | 0 | 25/0 | - | ||
| Demand | 200/65/0 | 250/225/0 | 100 | 550 | |
| Penalty | 0.1052 | - | 0.0634 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.7362 | 249/24/0 | 0.7124 | |||
| 0.5994 | 0.4799 | 135/0 | - | ||
| 0.5528 | 0.649 | 141/76 | 0.649 | ||
| 0 | 0 | 25/0 | - | ||
| Demand | 200/65/0 | 250/225/0 | 100/76 | 550 | |
| Penalty | - | - | 0.0634 |
| Supply | Penalty | ||||
|---|---|---|---|---|---|
| 0.7362 | 249/24/0 | - | |||
| 0.5994 | 0.4799 | 135/0 | - | ||
| 0.5528 | 141/76/0 | 0.649 | |||
| 0 | 0 | 25/0 | - | ||
| Demand | 200/65/0 | 250/225/0 | 100/76/0 | 550 | |
| Penalty | - | - | 0.649 |
| S | Supply | |||
|---|---|---|---|---|
| 0.7362 | 0.7124 | 249 | ||
| 0.5994 | 0.4799 | 135 | ||
| 0.5528 | 141 | |||
| 0 | 25 | |||
| Demand | 200 | 250 | 100 | 550 |
| S | Supply | |||
|---|---|---|---|---|
| 0.7362 | 0.7124 | 249 | ||
| 0.5994 | 0.4799 | 135 | ||
| 141 | ||||
| 0 | 0 | 25 | ||
| Demand | 200 | 250 | 100 | 550 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamran, M.; Abdalla, M.E.M.; Nadeem, M.; Uzair, A.; Farman, M.; Ragoub, L.; Cangul, I.N. A Systematic Formulation into Neutrosophic Z Methodologies for Symmetrical and Asymmetrical Transportation Problem Challenges. Symmetry 2024, 16, 615. https://doi.org/10.3390/sym16050615
Kamran M, Abdalla MEM, Nadeem M, Uzair A, Farman M, Ragoub L, Cangul IN. A Systematic Formulation into Neutrosophic Z Methodologies for Symmetrical and Asymmetrical Transportation Problem Challenges. Symmetry. 2024; 16(5):615. https://doi.org/10.3390/sym16050615
Chicago/Turabian StyleKamran, Muhammad, Manal Elzain Mohamed Abdalla, Muhammad Nadeem, Anns Uzair, Muhammad Farman, Lakhdar Ragoub, and Ismail Naci Cangul. 2024. "A Systematic Formulation into Neutrosophic Z Methodologies for Symmetrical and Asymmetrical Transportation Problem Challenges" Symmetry 16, no. 5: 615. https://doi.org/10.3390/sym16050615
APA StyleKamran, M., Abdalla, M. E. M., Nadeem, M., Uzair, A., Farman, M., Ragoub, L., & Cangul, I. N. (2024). A Systematic Formulation into Neutrosophic Z Methodologies for Symmetrical and Asymmetrical Transportation Problem Challenges. Symmetry, 16(5), 615. https://doi.org/10.3390/sym16050615








