Abstract
The pseudo-spin symmetry (PSS) provides an important angle to understand nuclear microscopic structure and the novel phenomena found in unstable nuclei. The relativistic Hartree–Fock (RHF) theory, that takes the important degrees of freedom associated with the -meson and -tensor (-T) couplings into account, provides an appropriate description of the PSS restoration in realistic nuclei, particularly for the pseudo-spin (PS) doublets with high angular momenta (). The investigations of the PSS within the RHF theory are recalled in this paper by focusing on the effects of the Fock terms. Aiming at common artificial shell closures appearing in previous relativistic mean-field calculations, the mechanism responsible for the PSS restoration of high- orbits is stressed, revealing the manifestation of nuclear in-medium effects on the PSS, and thus, providing qualitative guidance on modeling the in-medium balance between nuclear attractions and repulsions. Moreover, the essential role played by the -T coupling, that contributes mainly via the Fock terms, is introduced as combined with the relations between the PSS and various nuclear phenomena, including the shell structure and the evolution, novel halo and bubble-like phenomena, and the superheavy magicity. As the consequences of the nuclear force in complicated nuclear many-body systems, the PSS itself and the mechanism therein can not only deepen our understanding of nuclear microscopic structure and relevant phenomena, but also provide special insight into the nature of the nuclear force, which can further enrich our knowledge of nuclear physics.
Keywords:
pseudo-spin symmetry; relativistic Hartree–Fock theory; nuclear in-medium effects; artificial shell; halo structure; bubble-like structure; superheavy magicity PACS:
21.60.Jz; 24.10.Jv; 24.30.Cz; 23.40.-s
1. Introduction
The global development of new-generation radioactive-ion-beam (RIB) facilities and advanced nuclear detectors has significantly expanded the field of research in nuclear physics, extending it from a few stable nuclei to several thousand unstable ones. This has greatly enriched nuclear science [1,2,3,4,5,6]. In contrast to the stable nuclei, numerous nuclear phenomena have been observed in the unstable nuclei, including the dilute matter distributions, the halo structure [7,8,9,10]; the emergence of new magicity and the disappearance of traditional magic shells [11,12,13,14,15,16,17,18]; and the occurrence of the central density depression, the bubble-like structure [19,20,21,22,23,24,25,26,27,28,29,30,31,32]; etc. These observations challenge our conventional understanding of nuclear physics. Moreover, a significant number of unstable nuclei are involved in the rapid neutron capture process (r-process) in the synthesis of heavy elements. This indicates that the unstable nuclei play a crucial role in understanding the origin of the elements in the universe [33,34].
One of the most challenging issues in nuclear physics is the exploration of the existence limit of very heavy nuclei, which are known as the superheavy elements (SHEs), with , and the so-called stability island of superheavy nuclei (SHN). Experimentally, the discoveries of new elements up to have been reported in Refs. [35,36]. It is evident that an enhanced shell effect is observed with increasing atomic number Z, which may indicate the emergence of a proton magic shell at . This is evidenced by the increasing survival probabilities observed in SHEs from to 118 [37]. However, the current experimental conditions limit the ability to synthesize and precisely measure the expected SHN. Consequently, there is a need for pioneering theoretical studies to advance our understanding on both unstable nuclei and superheavy ones.
The pseudo-spin symmetry (PSS) [38,39] represents a significant phenomenon in nuclear structure [40,41,42,43]. It is characterized by the quasi-degeneracy of two single-particle (s.p.) orbits with the quantum numbers (n, l, j = l + 1/2) and (1, l + 2, j = l + 3/2). The pseudo-spin (PS) doublet is designated by a set of quantum numbers ( = 1, = l + 1, = j = 1/2) [38,39]. Significant research has been conducted to understand the origin of the PSS, which is recognized as a relativistic symmetry [40,42,44], and the pseudo-orbit is simply the orbital angular momentum of the lower component of the Dirac spinor [44]. According to the effective field theory, the nuclear force contains both strong attractive and repulsive components, which are described, respectively, by the exchanges of the scalar and vector mesons [45]. The exact PSS condition is then generalized as [44] or [46]. It is important to note that both conditions indicate a balance between strong attractive and repulsive nuclear interactions, which are propagated mainly by the scalar and vector mesons, respectively.
On the other hand, the delicate in-medium balance between nuclear attractions and repulsions is crucial to comprehend how a number of nucleons form a bound nucleus, a fundamental challenge in nuclear physics. The mean-field potential for nucleons in a nucleus is then approximated as a counteraction between the scalar and vector potentials, namely, . Consequently, any variation in this balance would directly influence the microscopic nuclear structure. In light of its origin, the PSS can be a valuable tool for elucidating the nature of the nuclear force and various nuclear phenomena. For instance, the pseudo-spin orbit (PSO) splitting, which measures the breaking of the PSS, can be helpful in comprehending the shell structure and the evolution [47,48,49], the halo structure [50], the superheavy nuclei [51,52], the nuclear superdeformed configurations [53,54], etc.
At the level of the mean-field approach [55], the meson-exchange diagram of the nuclear force [56] can be divided into the Hartree and Fock terms. The significant -meson contributes only via the Fock terms. The relativistic mean-field (RMF) theory [55,57], which contains only the Hartree terms, has the advantage of providing a self-consistent treatment of strong spin–orbit coupling in nuclei, in contrast to the non-relativistic Skyrme or Gogny Hartree–Fock models. The incorporation of the Bogoliubov transformation with the RMF theory, namely, the relativistic Hartree–Bogoliubov (RHB) theory [58,59,60,61,62,63], unifies the descriptions of both mean-field and pairing correlations. Furthermore, the continuum effects are taken into account automatically, which promises extensive reliability in the description of novel phenomena in unstable nuclei, such as the novel halo phenomena observed in both spherical and deformed nuclei [64,65,66,67,68]. The relativistic scheme has facilitated numerous investigations into the origin of the PSS [44,46,69], the relationship between PSS and spin-orbit effects [70], the PSS’s dynamical properties [71,72,73] and non-perturbative nature [74,75,76], the PSS in deformed nuclei [77,78,79,80,81,82,83], the PSS in hypernuclei [84,85], and the resonant states [83,86,87,88,89,90,91,92,93,94,95,96], etc.
However, limited by the Hartree approach, significant degrees of freedom associated with the -meson and -tensor (-T) couplings are missing in the RMF models. Moreover, an important ingredient of the nuclear force—the tensor force—cannot be considered efficiently either. Once the Fock terms have been implemented, the relativistic Hartree–Fock (RHF) theory [97,98,99] can introduce the -pseudo-vector (-PV) and -T couplings in a natural manner. In recent decades, RHF theory [48,100], as well as the extensive relativistic Hartree–Fock–Bogoliubov (RHFB) theory [50], has achieved comparable accuracy to the popular RMF models in describing various nuclear phenomena. Furthermore, the incorporation of Fock terms has led to significant improvements in the self-consistent description of nuclear shell evolution [49,101,102], the PSS restoration [48,100,103,104], symmetry energy [105], etc. In particular, the tensor force components can be taken into account naturally by the Fock terms [106,107,108], which is essential for extensive reliability from the stable to unstable nuclei. The RHFB theory [50], which benefits from the Bogoliubov scheme, provides a reliable description of various novel phenomena, including the bubble-like structures [31,32], halo structures [109], and new magicity [51,110,111], etc. Given these achievements, it is important to investigate systematically the relationship between the PSS and various nuclear phenomena within the RHF framework. This could provide valuable insight into the nature of the nuclear force and the properties of unstable nuclei.
For both the RMF and RHF models mentioned above, the modeling of the in-medium effects of the nuclear force is significant to ensure the accuracy in describing various nuclear phenomena, for instance, an appropriate incompressibility of nuclear matter [112]. In the RMF theory, the in-medium effects are evaluated by either collaborating with the nonlinear self-couplings of mesons [113,114,115] or by considering the density dependencies in the meson–nucleon coupling strengths [116,117,118,119]. For the RHF theory [99], theoretical accuracy can be improved by incorporating the self-couplings of the -meson or scalar fields [120,121]. Significantly, assuming the meson–nucleon coupling strengths to be density-dependent [48,50,122], the density-dependent relativistic Hartree–Fock (DDRHF) theory has been demonstrated to achieve comparable accuracy to the RMF theory in describing nuclear structures. In this review, the density dependencies of the coupling strengths will be briefly recalled in Section 2.2. In comparison to the modeling of in-medium effects via self-coupling schemes [120,121], the density dependencies in the meson–nucleon coupling strengths, as guided by ab initio calculations [116,117,119,123], are of critical importance for the theoretical consistency of the RHF approach [122].
Actually, the relativistic Brueckner–Hartree–Fock (RBHF) theory [43], which is based on a realistic nuclear force, can help us to understand the PSS. The relativistic effects, such as nucleon–antinucleon excitations, can be expressed in a non-relativistic framework in terms of a three-body force. The results of RBHF using the Bonn interaction are similar to those of non-relativistic Brueckner–Hartree–Fock containing the two- and three-body forces [124,125]. For relativistic ab initio calculations, the spin symmetry in Dirac sea is supported by the bare nucleon–nucleon interaction without three-body forces [126], and the evolution of the spin-orbit and PSO splittings in neutron drops can be explained by the tensor force [127,128]. Therefore, the RBHF calculations will provide crucial information, such as the splitting of PS partners, which is helpful when developing density functional theory. It is also interesting to study the microscopic nuclear structure by using RBHF theory with covariant chiral interactions [129].
Despite their successes, both RMF calculations and RHF ones with PKOi () can lead to the emergence of artificial shell closures = 58 and 92 [48,109], accompanied by largely overestimated binding energies around () and () [130]. In fact, these artificial shell closures correspond to large PSO splitting of the high- PS doublets near the Fermi surfaces. Fortunately, the RHF Lagrangian PKA1 [48] has been developed to address this issue. It benefits from an improved in-medium balance between nuclear attractions and repulsions due to the strong -T coupling [104]. Currently, due to the uncertainty in the decomposition of nucleon self-energy in the ab initio calculations [43] it remains challenging to constrain the density dependencies of the coupling strengths for specific channels in an efficient manner. Alternatively, suitable physical measurements, which can guide the modeling of nuclear in-medium effects, are still welcomed for both RMF and RHF models, for instance, qualitatively by the PSS restoration.
On the other hand, an increasing abundance of novelties in unstable nuclei can be taken as a new standard for testing the reliability of theoretical models which are established from the stable nuclei. It should be noted that some novel phenomena, such as the halo and bubble-like structures, are closely related to the restoration of the PSS [31,32,109]. Aiming at the role of the Fock terms in the PSS restoration, as well as the relationship between the PSS and various novel nuclear phenomena, the progress of the RHF descriptions of the PSS are reviewed. The manuscript is organized as follows. In Section 2, the RHF formalism is briefly introduced, and in Section 3 the influence of Fock terms on the PSS restoration is recalled. Then, in Section 4, the elimination of artificial shell closures and the physical mechanism responsible for the PSS restoration of the high- PS doublets are introduced. Focusing on the role of the Fock terms and their relation to the PSS, Section 5 reviews the RHF descriptions of various nuclear novelties, including the halo structure for Ce isotopes, the bubble-like structure, and the superheavy magicity. Finally, a summary is given in Section 6.
2. Relativistic Hartree–Fock Model
In order to provide a comprehensive overview of the theoretical framework, the general formalism of the RHF theory, including the effective Hamiltonian and energy functional, are recalled briefly in the following. In this review, the modeling of nuclear in-medium effects represents a significant topic. In order to address this issue, the density dependencies of the meson–nucleon coupling strengths will be introduced. These will be further detailed by analyzing the density-dependent feature of the popular RMF and RHF Lagrangians.
2.1. Hamiltonian and Energy Functional
In the context of the meson-exchange diagram [56], the nuclear force is posited to be propagated by massive virtual mesons. In the RMF and RHF approaches, two isoscalar mesons, namely, and , and two isovector ones, namely, and , are considered. These mesons, possessing the following quantum numbers (, ), are considered to be the effective fields which propagate the nucleon–nucleon interactions:
The spin, parity and isospin of selected mesons are represented by I, P, and , respectively. Specifically, the -meson, with a low mass of about 138 MeV, is responsible for the long-range part of the nucleon–nucleon () interaction. It is also thought to be the main origin of the tensor force in the relativistic framework [99]. The scalar meson , with a mass about 500 MeV, provides the intermediate-range attraction of the interaction. The repulsive inner part of the potential is thought to arise mainly from the exchange of a massive vector meson, the -meson. The repulsion can be understood by analogy with the Coulomb interaction, which is repulsive between electrons of the same charge [131]. The attraction and repulsion contributed by the - and -mesons, respectively, primarily determine the binding of a nuclear many-body system. The isovector–vector -meson is introduced to describe the isovector nature of the nucleon–nucleon interaction. The photon field accounts for the electromagnetic interactions between protons. In this review, arrows are employed to represent isovectors and bold type is used to denote the space vectors.
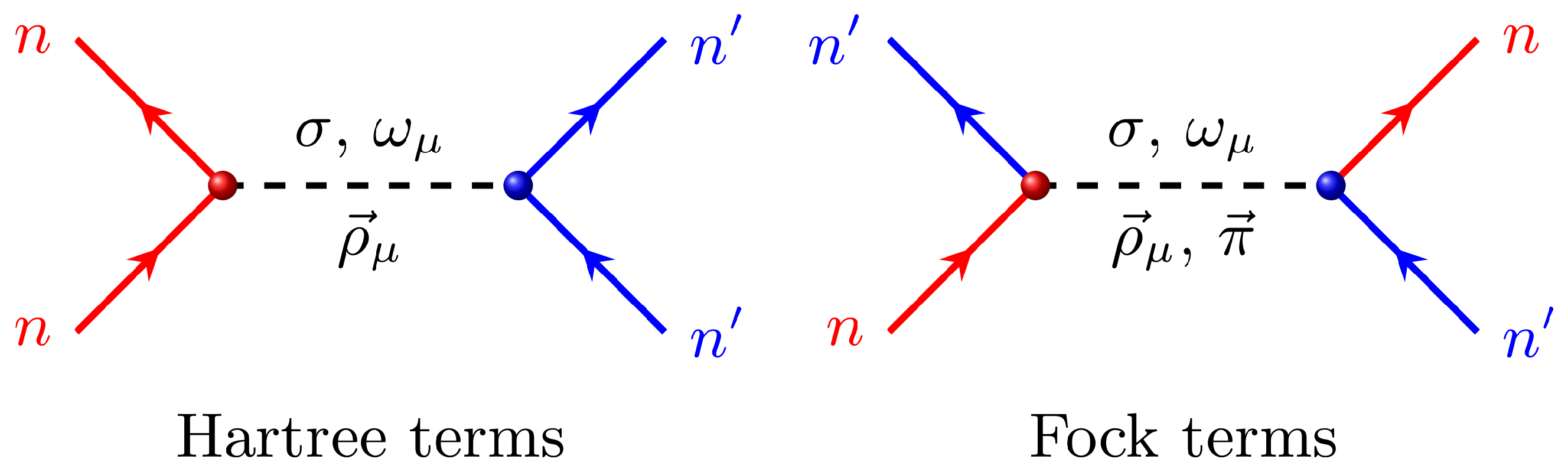
When restricting to the mean-field approach, the meson-exchange diagram of the nuclear force can be divided into the Hartree and Fock terms, as illustrated in Figure 1. Despite the fact that the two-body interactions propagated by mesons are not instantaneous, the retardation effects are ignored in the Hartree–Fock description of nuclear ground states, i.e., neglecting the time component of the four–momentum carried by the meson [99]. In fact, the masses of the -, -, and -mesons, which have several hundred MeV, are much larger than the energy transfers. Such an approximation is valid for heavy mesons, and also to a lesser extent for the -meson. Following the standard procedure as described in Ref. [99], the Hamiltonian of nuclear systems can be expressed in the following form:
where the symbol represents various two-body interaction channels, including the Lorentz scalar (-S), vector (-V, -V, A-V), tensor (-T), vector–tensor (-VT), and pseudo–vector (-PV) couplings. The corresponding vertex can be expressed in the following form:
For the meson and photon fields, the propagator is of the following form:
where . In the above expressions, M and are the masses of the nucleon and meson respectively, and the symbols () and () represent the meson–nucleon coupling strengths.
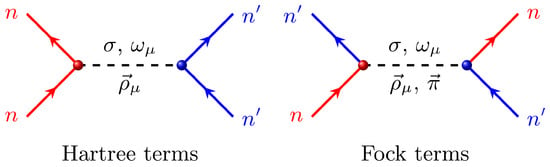
Figure 1.
Feynman diagrams of the Hartree and Fock terms under the meson-exchange picture of the nuclear force, where the solid lines with arrows represent the interacting nucleons, and the blue and red colors are used to identify the nucleons dressed by different quantum numbers.
Under the mean-field approach, the no-sea approximation is considered as usual, which amounts to neglecting the contributions from the Dirac sea [112]. Consequently, in terms of the particle creation and annihilation operators, namely, and , defined by the positive-energy solutions of the Dirac equation, the Dirac field that describes nucleons can be quantized as
where represents the Dirac spinor of positive-energy state . According to the no-sea approximations, the Hartree–Fock ground state of nuclear systems can be defined as
where the symbol represents the vacuum state, and A denotes the nuclear mass number.
Eventually, starting from the meson-exchange diagram of the nuclear force, combined with the quantization of the nucleon field (11), the expectation of the Hamiltonian (2) with respect to the Hartree–Fock ground state gives the energy functional E of nuclear systems [99,132]:
including the kinetic energy , and the Hartree and Fock terms of the potential energies from various coupling channels , named as and , respectively. In accordance with the variational principle, the single-particle Dirac equations of nucleons can be derived from the energy functional (13), which allows for the derivation of two types of self-energies, the local Hartree and non-local Fock ones [133,134]. It should be noted that in the RMF models, only the Hartree terms are considered. Consequently, the degrees of freedom associated with the -PV and -T couplings, which contribute mainly via the Fock diagrams, cannot be taken into account explicitly.
In open-shell nuclei, the pairing correlations play a significant role in determining the properties of the ground state, particularly for the nuclei situated close to the drip line [58,61,64,65,66]. In general, the pairing correlations are treated using the BCS [135] or Bogoliubov [136,137,138] methods. In particular, for unstable nuclei, the one- and/or two-nucleon separation energies may be less than 1 MeV. For such weak-bound systems it is crucial to use an appropriate treatment of pairing correlations and continuum effects. The Bogoliubov scheme offers a unified treatment of both mean fields and pairing correlations, which is a distinct advantage over the traditional BCS method. Starting from the quantization (11) and combining the Bogoliubov transformation [139], one can also quantize the Dirac spinor in the Bogoliubov quasi-particle space as follows:
where the indexes k and represent the time-reversal conjugated states, the U and V components of the Bogoliubov quasi-particle spinors are denoted by and , and is the quasi-particle energy. By considering the expectation of the Hamiltonian with respect to the Bogoliubov ground state, namely, the quasi-particle vacuum , one can obtain a unified energy functional that contains the kinetic, potential, and pairing energies:
where represents the pairing energy contributed by the coupling channel . From the full energy functional presented above, one can derive the RHFB equations by applying the variational principle.
In practice, the phenomenological pairing force was adopted, including the zero-range -force [58], and finite-range Gogny force [50,58] and separable one [140]. The details of the RHFB formalism are provided in Refs. [50,134,141]. In the following, we will focus on the RHB and RHFB calculations, with the aim of discussing novel nuclear phenomena.
2.2. Effective Lagrangian and In-Medium Effects
For both the RMF and RHF theories, the meson masses and the meson–nucleon coupling strengths in the effective Hamiltonian (2) define the effective interactions (also referred to as effective Lagrangians); these are determined by fitting the bulk properties of nuclear matter and observable nuclei, such as , , , , , , and so on. More than that, the modeling of nuclear in-medium effects is also essential for an accurate description of nuclear properties; these are evaluated by considering the nonlinear self-couplings of mesons [113,114,115,120,121] or introducing the density dependence into the meson–nucleon coupling strengths [116,117,118,119,122]. In this review, the PSS and novel nuclear phenomena will be discussed by utilizing the density-dependent effective Lagrangians.
For better understanding, the density dependence of the meson–nucleon coupling strengths is presented as follows. As shown in Equation (3), the Hamiltonian of nuclear systems includes the -S, -V, -V, -T, -VT, and -PV meson–nucleon coupling channels. The density dependencies of the coupling strengths and in the isoscalar channels -S and -V are adopted as the following form [119]:
where , and is the saturation density. For the function , it has the following explicit form:
where , , , and are the parameters determining the density dependencies of and , and the constraint conditions , , and are generally introduced to reduce the number of free parameters.
For the isovector mesons, an exponential density dependence is utilized:
In the above expression, corresponds to the free-coupling constants , , and of the -V, -T, and -PV couplings, respectively, and to the relevant density-dependent parameters.
In order to understand the difference between the density-dependent effective Lagrangians used in this review, Table 1 presents the details of the meson–nucleon coupling channel for effective Lagrangians PKA1, PKOi (i = 1, 2, 3), DD-ME2, PKDD, and DD-LZ1, respectively. One can see that the RMF effective Lagrangians DD-ME2, PKDD, and DD-LZ1 do not contain the Fock terms. Hence, the significant degrees of freedom associated with the -meson and -T couplings cannot be taken into account. For the RHF Lagrangians, PKO2 shares the same degrees of freedom as the RMF ones, whereas PKO1 and PKO3 take the -PV coupling into account, and PKA1 contains both the -PV and -T couplings, the latter of which plays an important role in the PSS restoration, in particular for the high- PS doublets.

Table 1.
Details for the density-dependent effective Lagrangians PKA1 [48], PKO1 [122], PKO2 [101], PKO3 [101], DD-ME2 [142], DD-LZ1 [143], and PKDD [115] which are used in this review.
3. The PSS and the Fock Term
Due to numerical limitations, the early RHF model does not include the -T coupling. Moreover, the energy functional contributed by the -PV coupling is relatively small compared to those contributed by the - and -couplings. Consequently, despite the implementation of the Fock terms leading to significant and remarkable differences in different meson channels [122], the sums of strong attraction (-S) and strong repulsion (-V), and the balance of attraction and repulsion will be similar to those of the RMF theory after the counteraction between the Hartree and Fock terms. According to the condition of PSS conservation, [44] or [46], the PSS restoration is less influenced by the Fock term [100].
To understand the influence of the Fock terms on the PSS, the Schrödinger-type equation deduced from the Dirac equation is quite helpful [46,100]. Under spherical symmetry, the radial Dirac equation can be derived as
where and are the radial wave functions of the upper and lower components, respectively, the quantity with , and the scalar potential and the time component of the vector potential contain the contributions from the Hartree terms and the rearrangement term due to the density dependence of the meson–nucleon couplings. The non-local integral X and Y terms can be transformed into the equivalent local contributions , , , and ; the details can be found in Ref. [100]. Thus, from the integral Equations (18) and (19), the Schrödinger-type equation for the lower component F can be derived as
where and represent the pseudo-centrifugal barrier (PCB) and pseudo-spin orbital potential (PSOP), respectively, and and are of more complicated forms than in the RMF case [46].
In the above expressions, , , with and , respectively. As indicated in Ref. [46], the PSS will be recovered under the limitation of . Compared to the RMF case, the Fock terms present new contributions, namely, the and terms in the . Moreover, the term is entirely due to the Fock term.
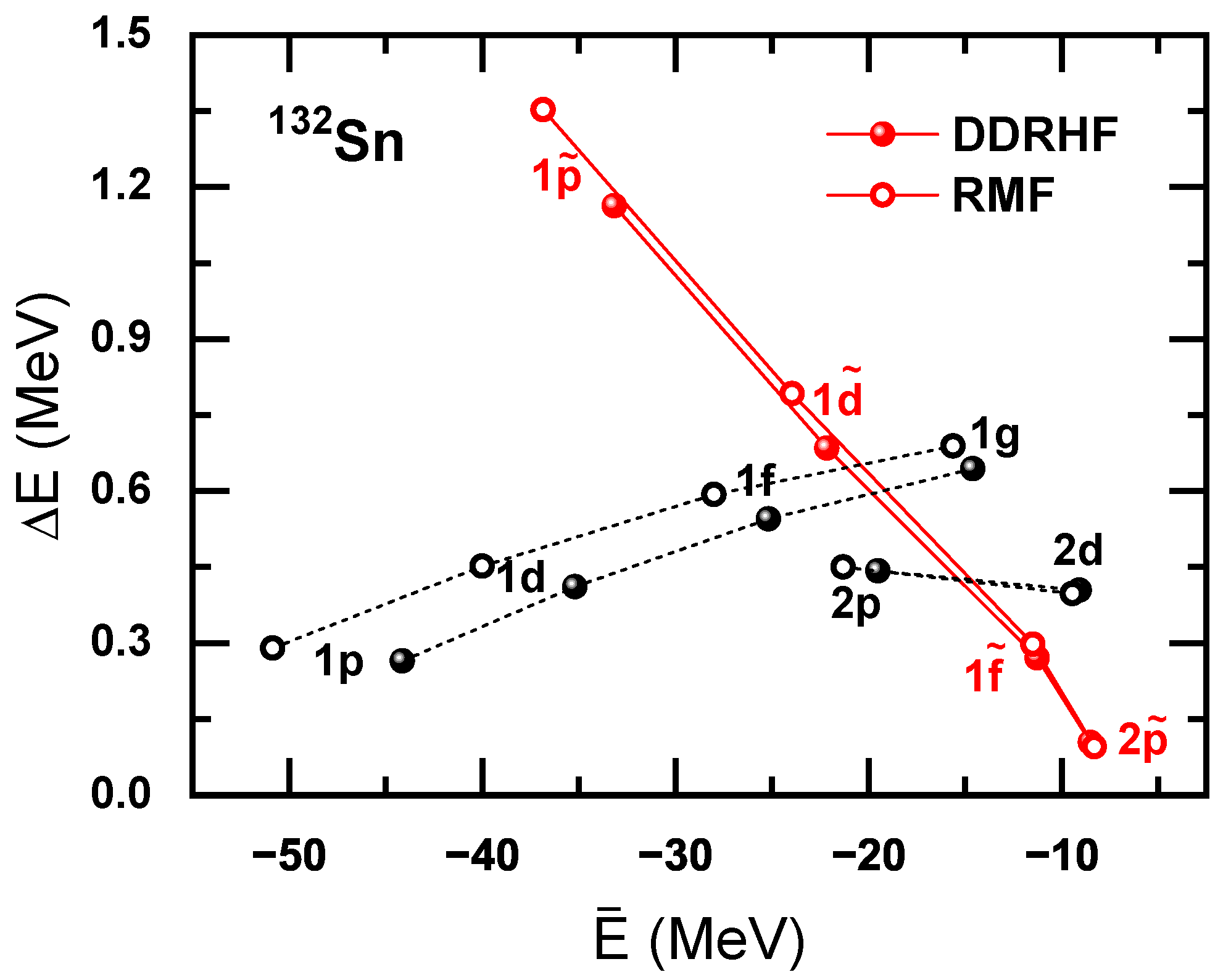
In finite nuclei, the PSO and spin-orbit (SO) splittings show some systematics with respect to the s.p. energies [46]. Coincidentally, the RHF calculations present a similar tendency as well [100]. Taking as an example, Figure 2 shows the PSO and SO splitting as functions of the average s.p. energy . Despite the minor differences in the s.p. energies, an obvious monotonous decreasing behavior of with respect to is observed for both RHF and RMF models, similar to that observed for and [46]. Compared to the , the energy dependence of is relatively weak. This is due to the fact that the in Equation (23) is divided by a smaller factor than for the SO potential [46]. Specifically, and E have the magnitude of a few tens of MeV, whereas V can be as large as several hundred MeV. It should be noted in Figure 2 that the PSO splitting is rescaled by dividing by , namely, . In the following context, the PSO splitting will not be rescaled, i.e., .
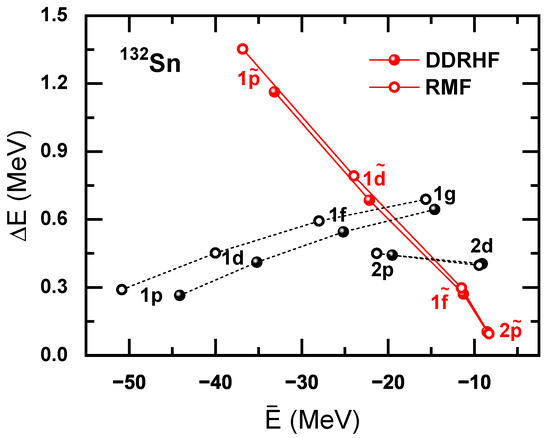
Figure 2.
The PSO splitting versus the average s.p. energy for neutron PS doublets , , , and for . The SO splitting is also given for , , , , and pairs as a function of . The results are obtained by the RHF with PKO1 (filled symbols) and the RMF with PKDD (open symbols), respectively. The figure is taken from Ref. [100].
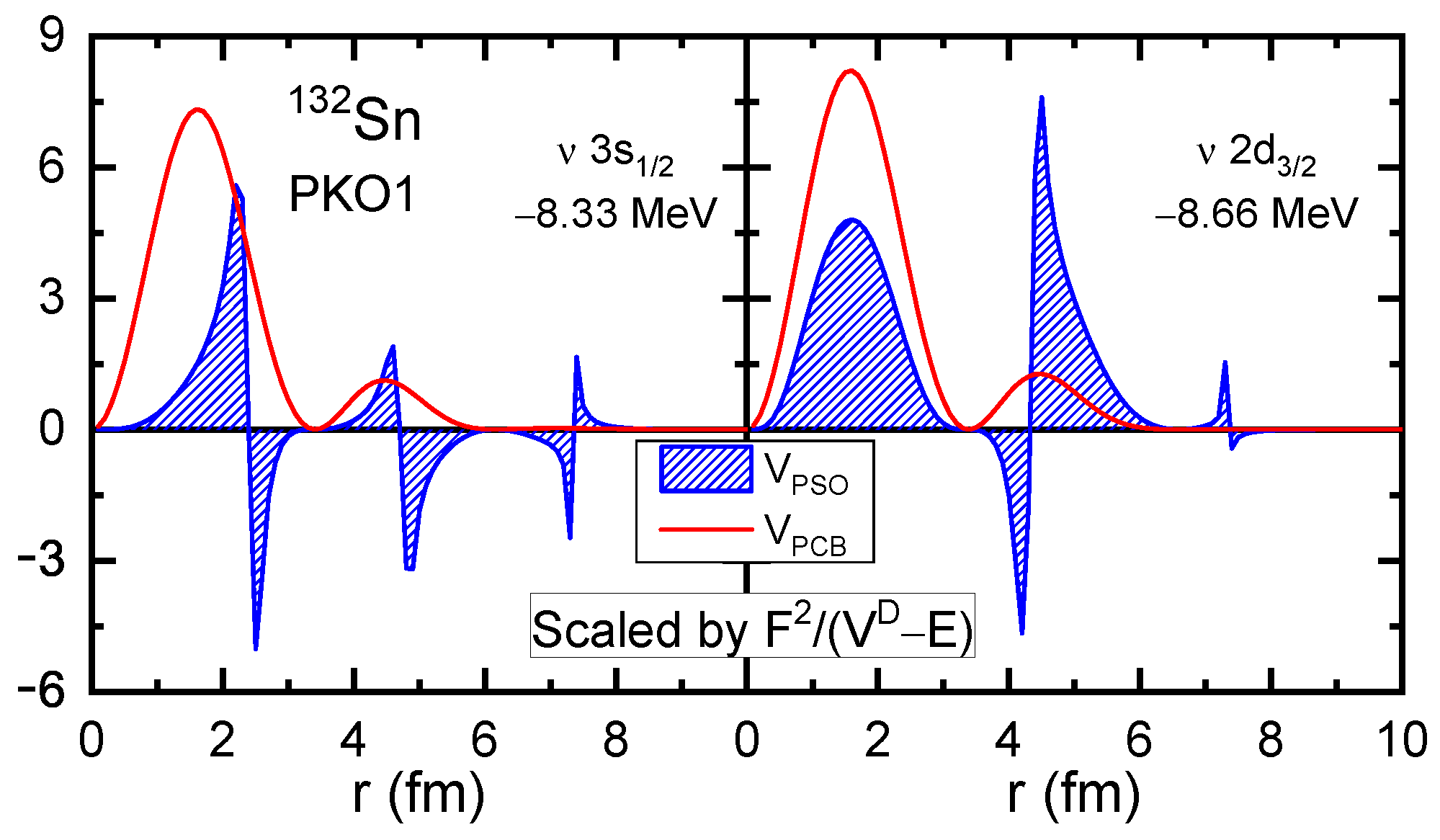
In Figure 2, it is obvious that the PSS is restored well for the PS partners in both RHF and RMF calculations. Regarding the restoration condition given by Ref. [46], Figure 3 presents the and of PS partners , both of which are scaled by the factor . For the PS partner , the PSOP is much smaller than the PCB after considering cancellation at the nodal points. However, for the partner , the PSOP becomes comparable with the PCB, even after considering the cancellation. This seems to be conflict with the conclusion drawn from the RMF calculations [46].
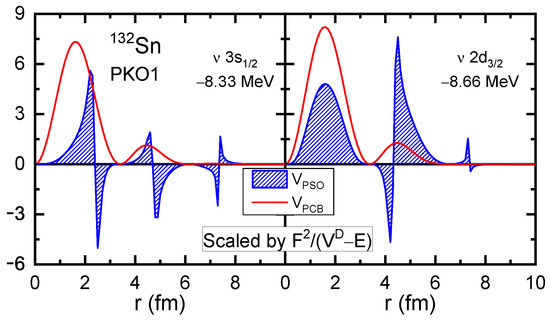
Figure 3.
The PCB and PSOP scaled by the factor for the PS partner in . The PCB contributions are shown by the red lines, while the PSOP are shown by the blue shadows. The RHF with PKO1 is used for the calculations. The figure is taken from Ref. [100].
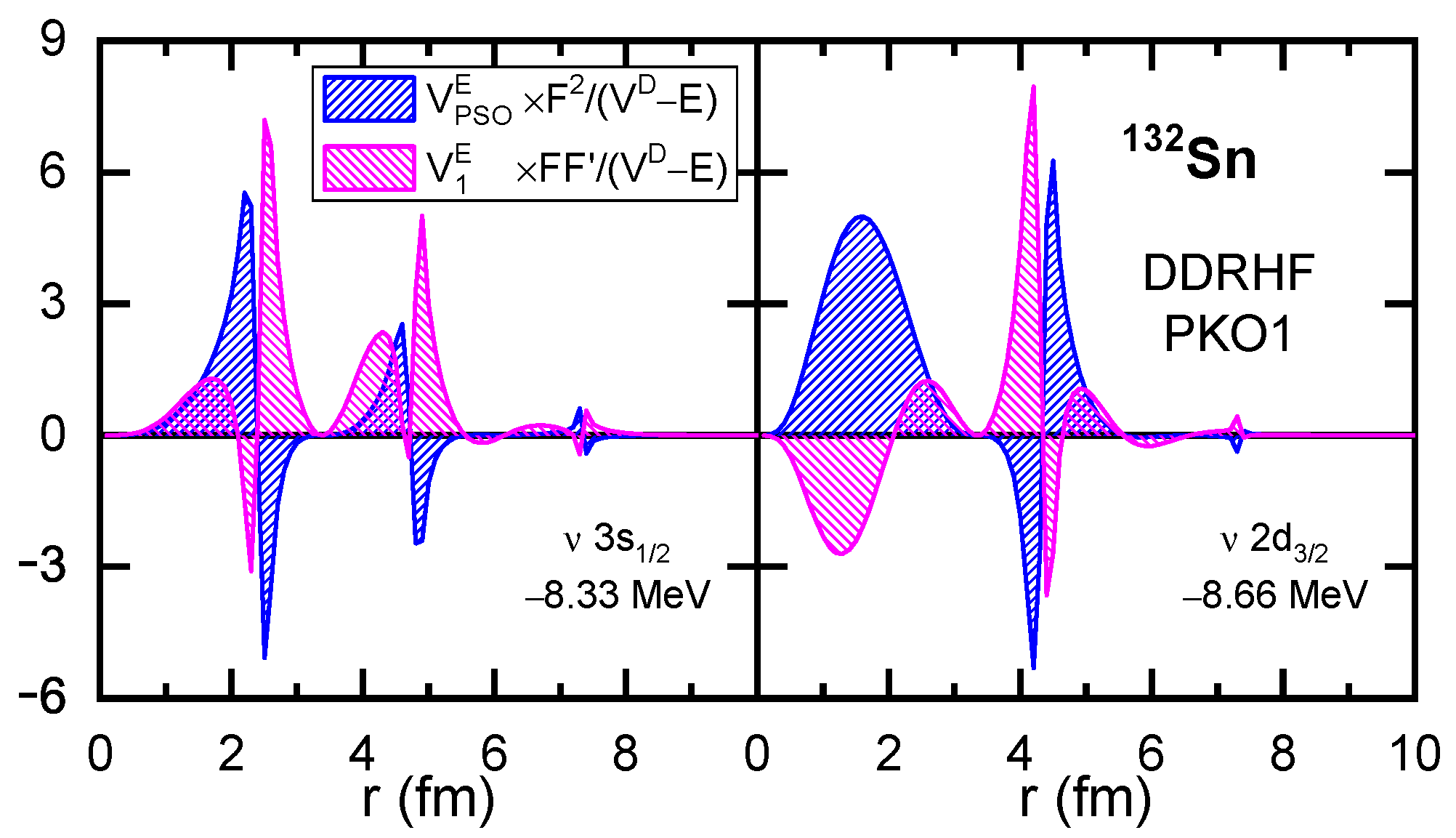
In order to understand such inconsistency, Figure 4 shows the Fock contributions to the and , namely, and , which are scaled by the factors and , respectively. It is obvious that there exist distinct cancellations for the Fock contributions and at the nodal points, which lead to tiny contributions for the PS partner . Referring to the in Figure 3, the condition becomes invalid for the PS partner due to the substantial contributions from the Fock terms. Even though, such contributions are largely canceled by the Fock contributions , particularly in the interior region; see Figure 4. Due to such counteractions among the Fock contributions, mainly in the and terms, the PSS is still properly restored for the PS partners , despite considerable PSOP originating from the Fock terms.
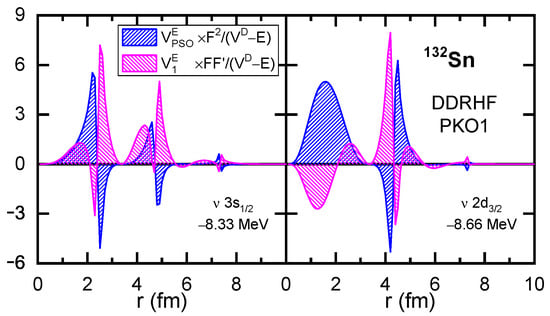
Figure 4.
The functions and given by the exchange (Fock) terms of the RHF with PKO1 for the PS partner of . The figure is taken from Ref. [100].
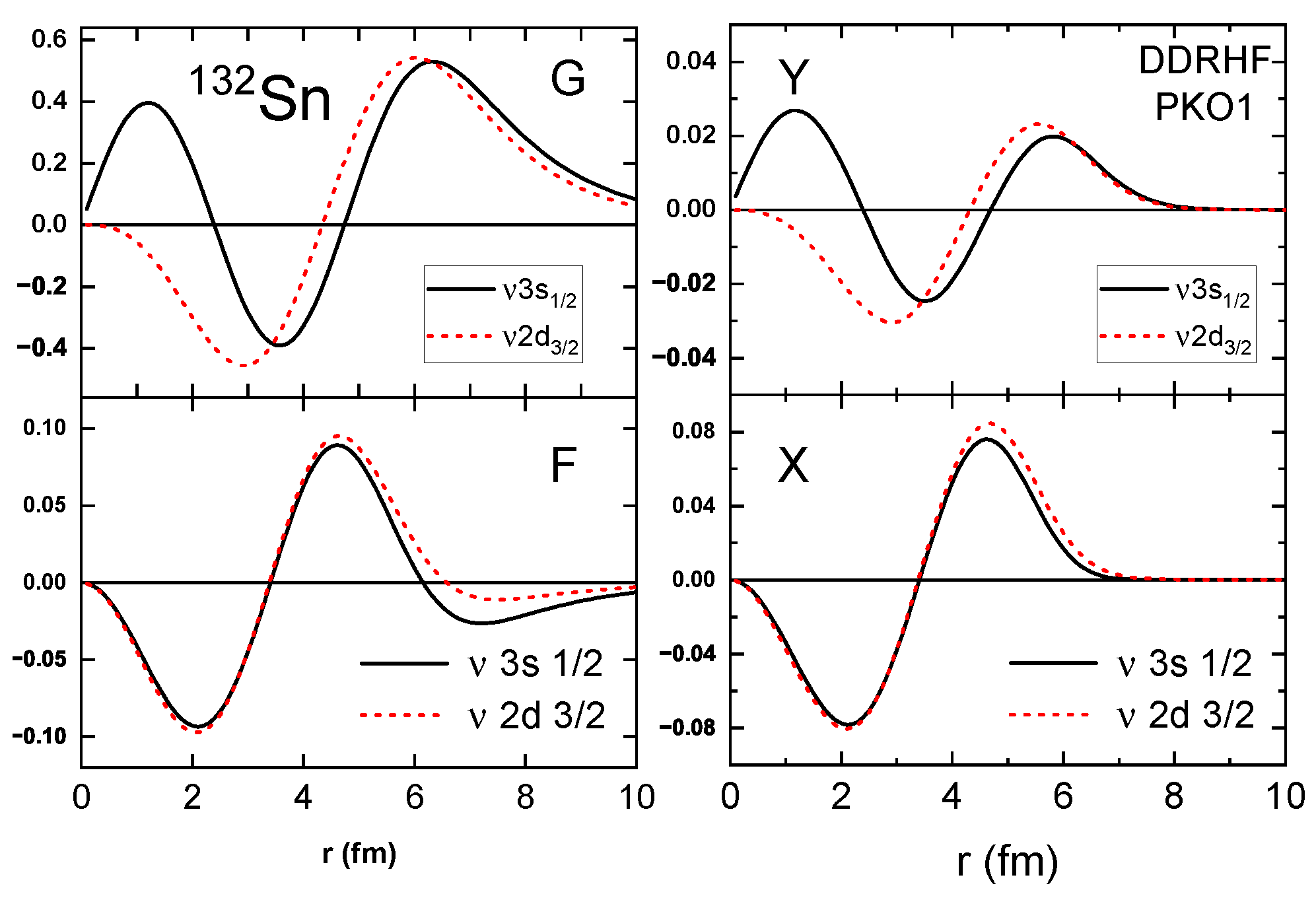
Different from the Hartree terms, the Fock terms present non-local mean-field potentials, corresponding to the non-local terms X and Y in the radial RHF Equations (18) and (19), both of which are state dependent. For explicit illustration, Figure 5 shows the radial wave functions G and F (left panels), and the Y and X terms (right panels), as functions of radial distance r. It is interesting to see that the Y (X) terms and radial wave functions G (F) have rather similar radial dependencies for both PS partners and . Thus, one can reach the approximate relations as
where the and terms can be treated as the local representations of the non-local Fock terms. In fact, it is not striking to see such a result. According to the principle of density functional theory, the contributions from the exchange correlations, here the Fock terms, can be expressed universally as the functional of local density [144,145]. Consistently, following the relation (25), the non-local RHF Equations (18) and (19) can be reduced to the equivalent local ones, which are of the same form as the radial Dirac equations in the RMF calculations [46]. From this point of view, it is not difficult to understand the approximately preserved PSS given by both RHF and RMF models, despite the fact the Fock terms present substantial contributions to the pseudo-spin orbit potentials.
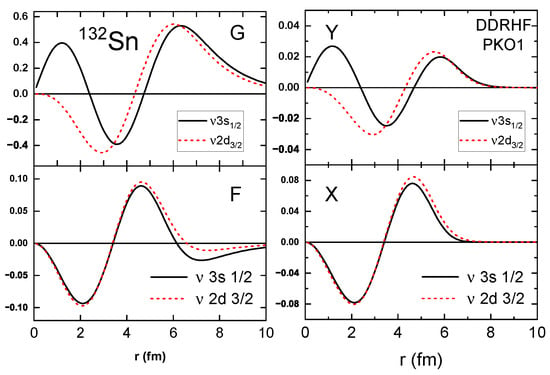
Figure 5.
The radial wave functions G and F (left panels), and the non-local terms X and Y (right panels) given by the RHF with PKO1 for the PS partner in . The figure is taken from Ref. [100].
4. The PSS and Nuclear In-Medium Effects
In realistic nuclei, the binding of the systems is ensured by the balance between the attraction and repulsion, which manifests itself as the PSS restoration. Therefore, any change in the balance will affect the microscopic nuclear structure. In the last section, the effects of Fock terms on the PSS restoration were discussed. It seems that the PSS restoration described by the RHF model is similar to the RMF one due to the significant cancellation between the Fock contributions, mainly the and terms, and the similarity between the radial wave functions and the non-local Fock terms [Y and X in Equations (18) and (19)]. Coincidentally, both RMF and RHF calculations with PKOi () suffer greatly from the notable PSS breaking of the high- PS doublets near the Fermi surfaces, which present artificial shell closures and 92 and lead to systematically overestimated binding energies for the nuclei around () and () [130].
With advances in numerical capability, -T coupling was later introduced explicitly into the RHF model. It has been shown that -T coupling contributes a rather strong attraction, which can even change the balance between the dominant -S and -V channels [48]. In addition, -T coupling contributes significant nuclear in-medium effects due to its strong density dependence [104]. Consequently, the RHF calculations with PKA1 show a rather different PSO splitting for the high- PS doublets close to the Fermi surfaces, accompanied by the disappearance of the artificial shell closures [49,51,109]. This is attributed to the implementation of the degree of freedom associated with the -T coupling. Furthermore, the calculations also benefit from this improvement, for example, in the shell structure and the evolution, in the description of novel nuclear phenomena, etc. Given these improvements, the elimination of the artificial shell closures and and the physical mechanisms behind the PSS restoration of high- PS doublets will be recalled in this section by focusing on the nuclear in-medium effects. Furthermore, the implications for the thermal properties of nuclear matter and the development of new effective Lagrangians are briefly mentioned.
4.1. Elimination of Artificial Shell Closures
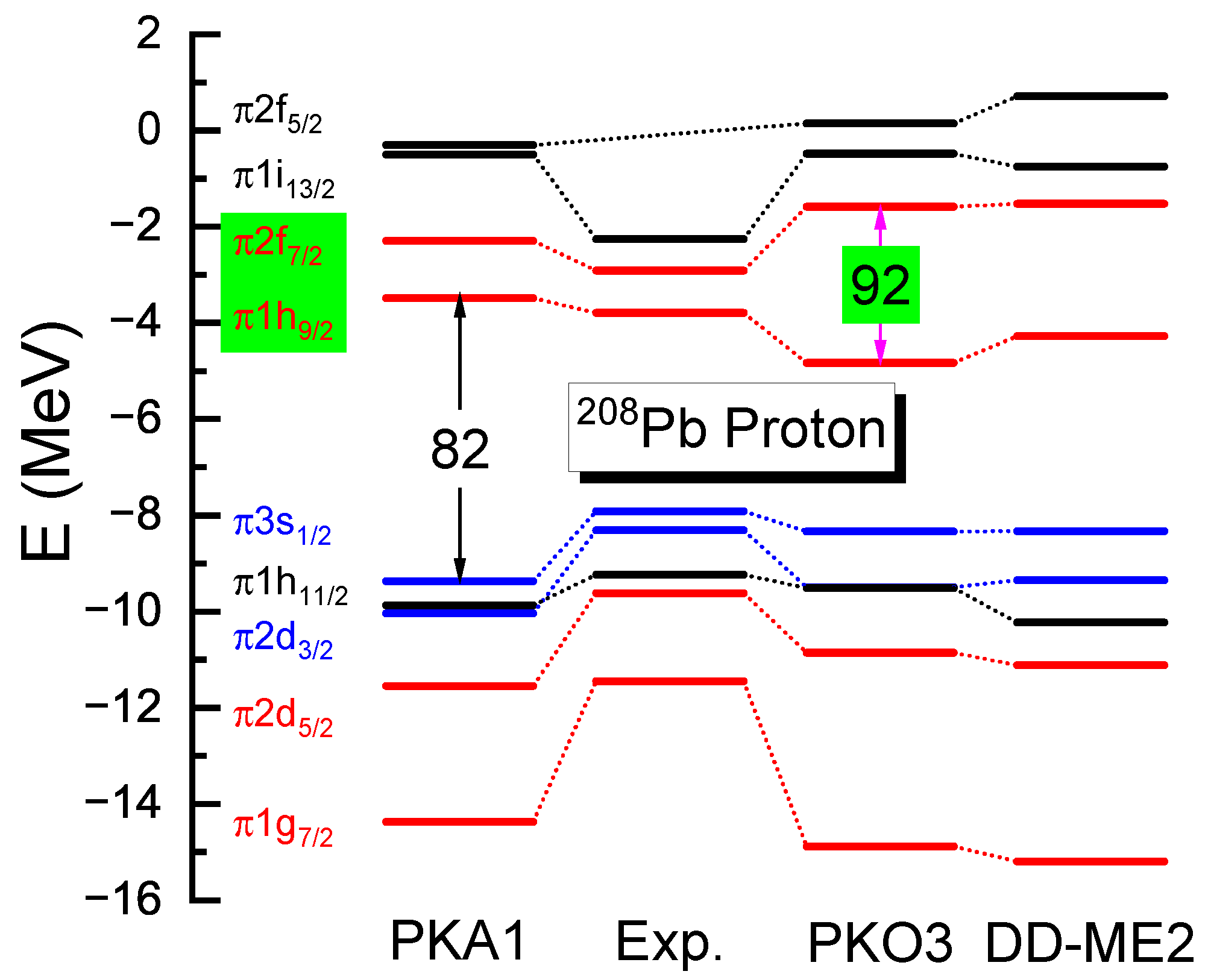
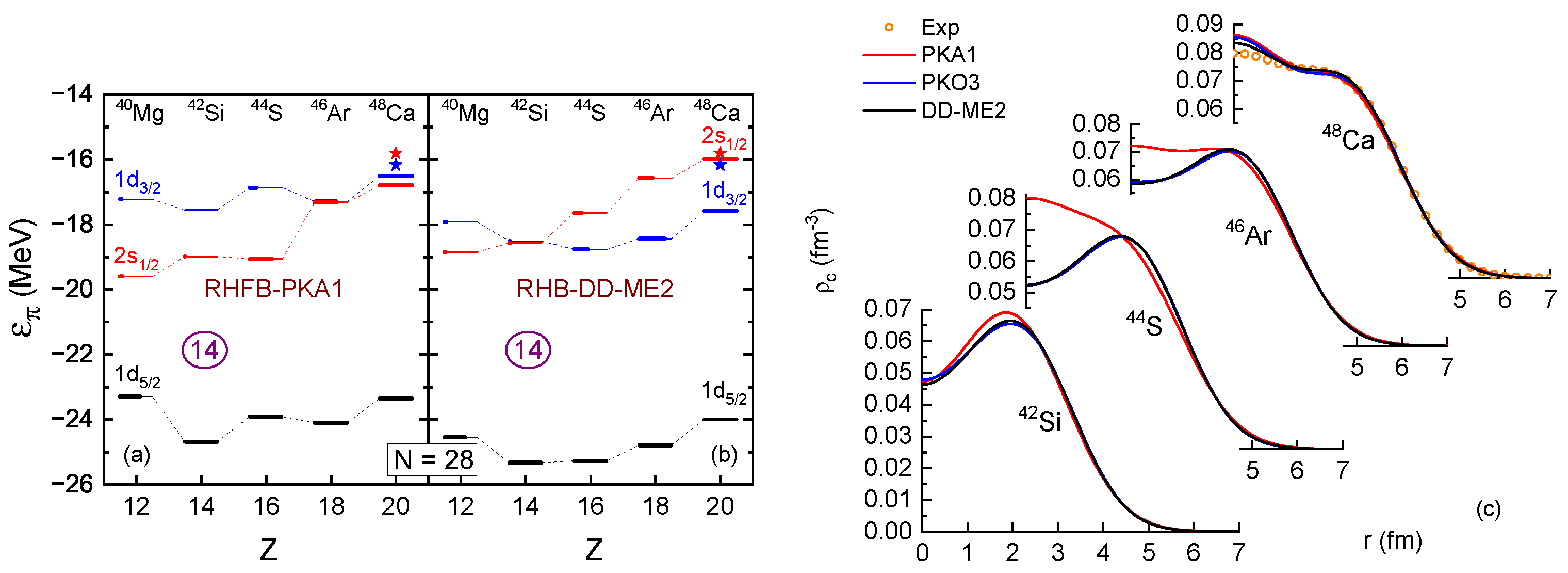
Taking the artificial shell closure as an example, Figure 6 presents the proton s.p. energy (SPE) of , by taking the RHF effective Lagrangians PKA1 [48] and PKO3 [101], and RMF’s one DD-ME2 [142], as the representatives. It can be seen that the splittings between the PS partner given by PKO3 and DD-ME2 are rather large, indicating the existence of the artificial shell that even compresses the size of the magic shell . In contrast, PKA1 provides consistent results with the experimental data, showing a properly restored PSS that eliminates the artificial shell . In fact, an experiment on the short-lived isotope has already ruled out the possibility of the sub-shell [146]. Not only for , the elimination of the artificial shell was also detailed in Ref. [48], and the relevant consequences will be introduced in the following.
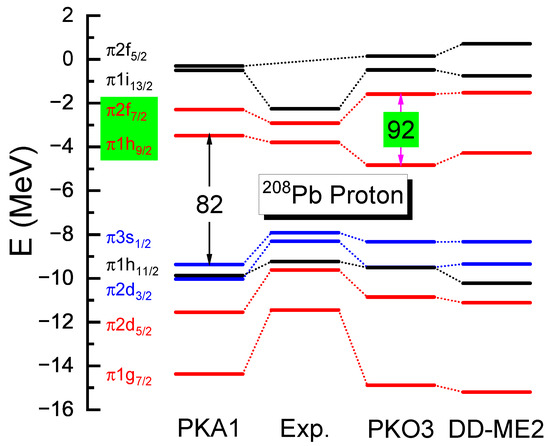
Figure 6.
Proton SPE of . The results are calculated by RHF with PKA1 and PKO3, and RMF with DD-ME2. The experimental data are from Ref. [147].
In heavy nuclei, due to the increasing s.p.-level densities, the occurrences of (semi-) magic shells can be essentially related to the PSS restoration. For instance, as shown in Figure 6, there exist two PS doublets and , above and below the magic shell , respectively, and it is already seen that the size of the shell can be affected by the PSO splittings. As another typical example, the experimentally confirmed sub-shell , which shows systematic enhancement towards along the isotonic chain of [47], can be treated as the result of the PSS restoration. However, the sub-shell is not properly described by the RMF models, which generally give an artificial shell due to the obvious PSS breaking [48,130].
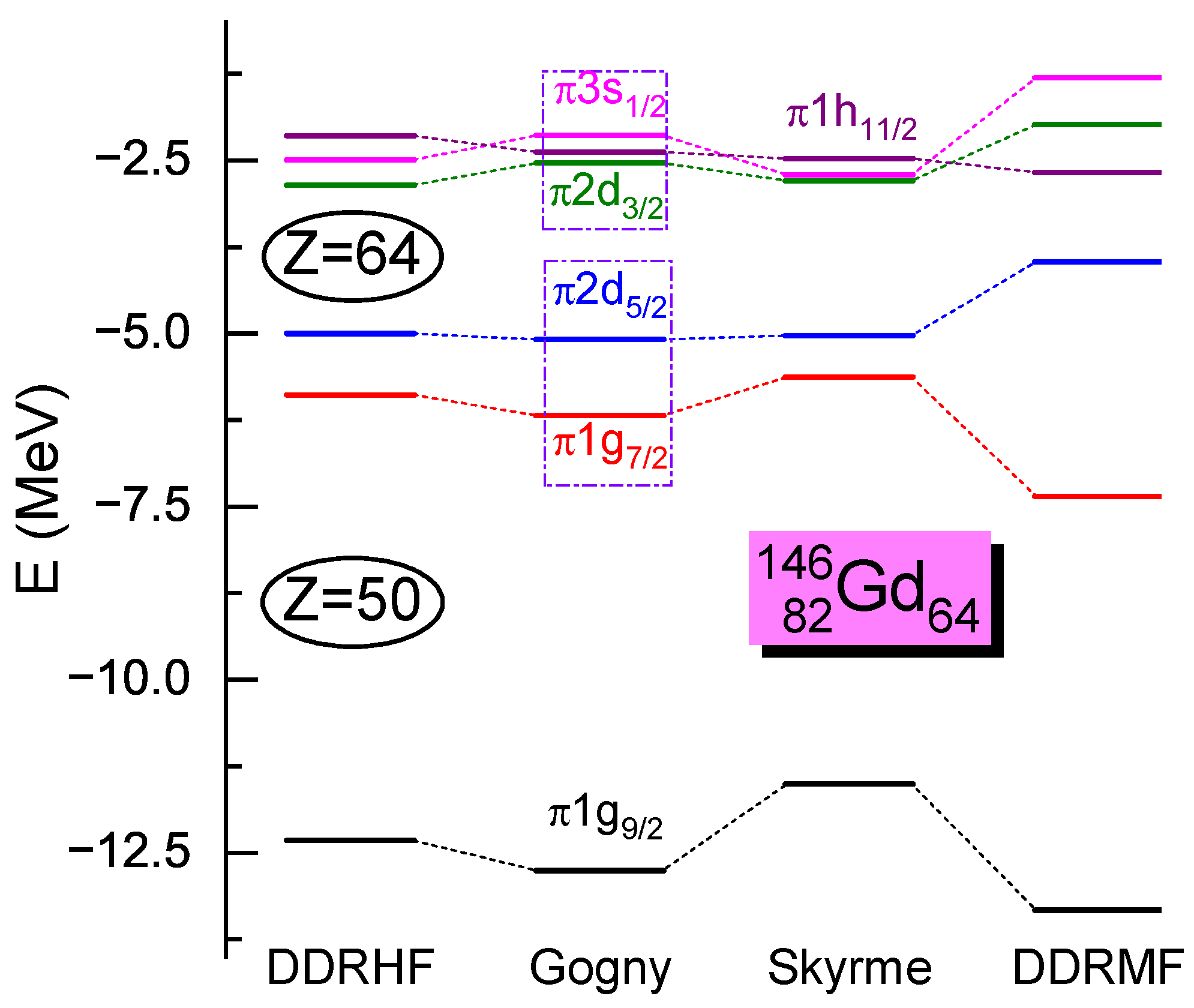
To further understand the relation between the sub-shell and artificial shell closure , is taken as an example here. Figure 7 presents the proton SPE of calculated by the RHF model with PKA1 [48], the Gogny HFB model with D1S [148], the Skyrme HF model with SLy4 [149], and the RMF model with PKDD [115]. In addition to the magic shell , the RHF, Gogny, and Skyrme models present the evident sub-shell , consistent with a properly restored PSS for the PS doublets and , which are located above and below the sub-shell, respectively. It is obvious as well that small PSO splittings are beneficial for the arising of the sub-shell . On the contrary, the RMF calculation gives an unphysically large gap between the PS doublet , leading to the artificial shell , that suppresses the emergence of the sub-shell ; see Figure 7.
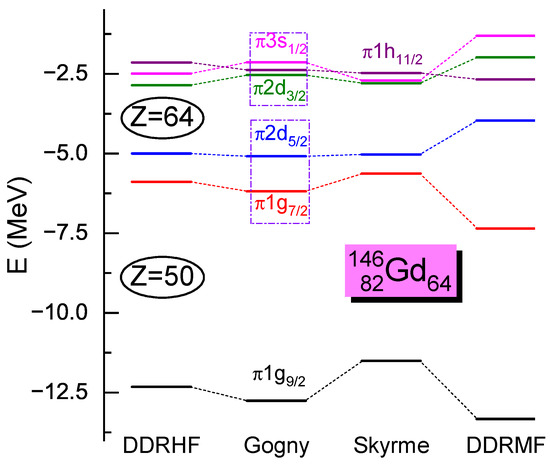
Figure 7.
Proton SPE for , calculated by RHF with PKA1 [48], Gogny HFB with D1S [148], Skyrme HF with SLy4 [149], and RMF with PKDD [115]. The figure is taken from Ref. [49]. Reprinted with permission from Ref. [49]. Copyright 2009 Elsevier.
Following the evolution of the splittings that gives the sub-shell in Figure 8a, one can see a strong enhancement in the splitting towards , and the RHF calculations with PKA1 provide the best agreement with the experimental data. More specifically, the sum of the Fock terms of isoscalar - and -couplings, and the Coulomb field, play a determining role in giving such an enhancement towards ; see Figure 8b; while the isovector - and -couplings present a tiny contribution for the enhancement in the splitting towards , due to the counteractions between the opposite tensor force contributions carried by the -PV and -T couplings, respectively. Combining the results in Figure 7 and Figure 8, it can be concluded that the PSS restoration may be essential not only for the occurrence of the sub-shell, but also for the evolution. It is worthwhile to stress that the enhancement in the splitting cannot be simply attributed to the tensor force, which indeed plays a tiny role in this case.
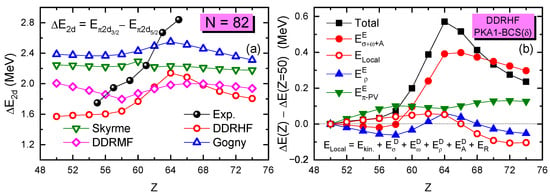
Figure 8.
(a) SO splittings of proton partner extracted from the calculations of RHF with PKA1, Gogny HFB with D1S, Skyrme HF with SLy4, and RMF with PKDD, in comparison with experimental data [47]. (b) Detailed contributions of from different channels given by the RHF calculations with PKA1. The figure is taken from Ref. [49]. Reprinted with permission from Ref. [49]. Copyright 2009 Elsevier.
4.2. New Mechanism of PSS Restoration
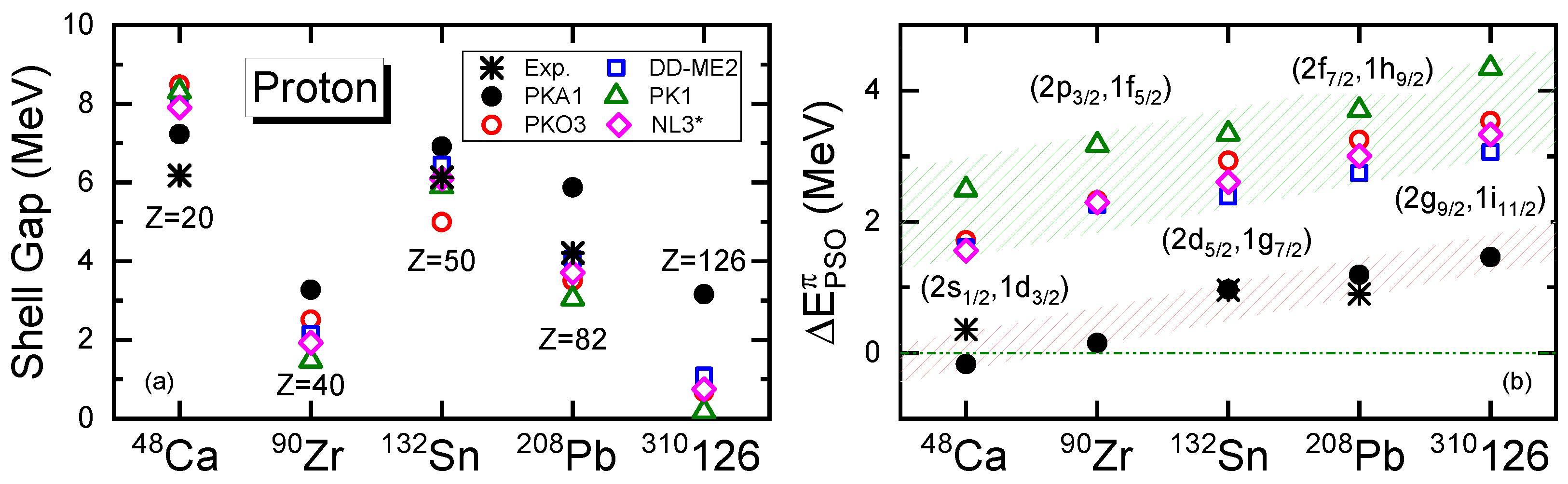
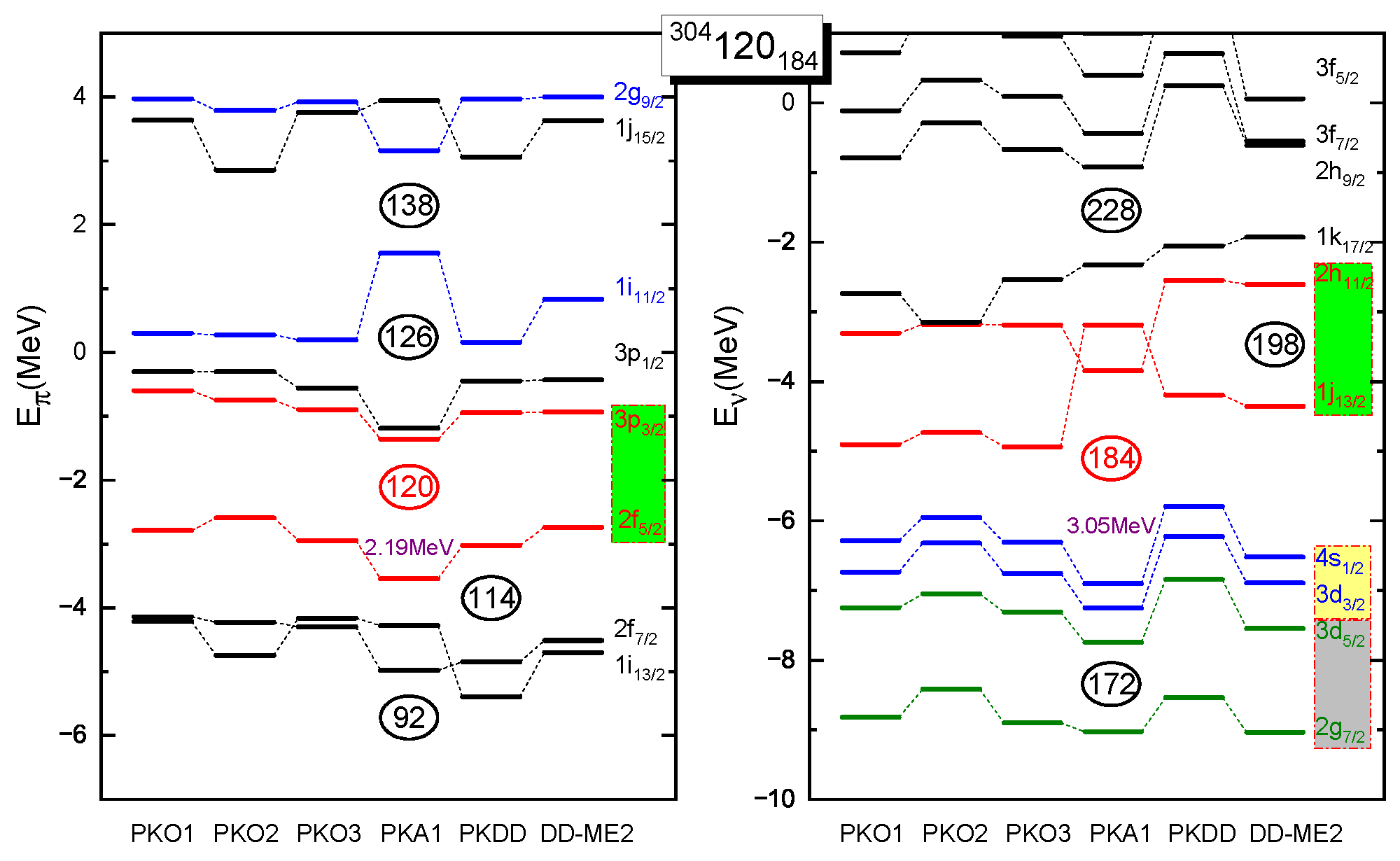
As previously, there is a systematic difference between PKA1 and other RHF/RMF effective Lagrangians in the description of the PSS restoration. This difference can be closely linked to the magic or semi-magic shells. Taking the doubly magic nuclei , , , and and the predicted superheavy one [110] as examples, Figure 9a,b illustrate the relevant proton shell gaps and the splittings of the PS doublets with high neighboring the shells, as predicted by the RHF and RMF models. When compared to experimental data [147], PKA1 shows appropriate agreements, whereas the others distinctly overestimate the PSO splittings. This has implications for the emergence of the neighboring shells in heavy nuclei. For example, less pronounced proton shells and are typically accompanied by a larger value of for the PS doublets in and in ; see Figure 9. Furthermore, the close correlation between the emergence of shell closures and the PSS is also predicted for SHN, which will be discussed in detail in Section 5.3.

Figure 9.
Proton shell gaps (MeV) (a) and the splittings of neighboring PS partners (MeV) (b) for the traditional magic nuclei , , , and , and the superheavy one . The results are calculated by PKA1, PKO3, DD-ME2, PK1 [115], and NL3* [150]. The shadow areas denote the spreading of the PSO splittings given by PKA1 and the other selected models. Experimental data are taken from Ref. [147]. The figure is taken from Ref. [104]. Reprinted with permission from Ref. [104]. Copyright 2019 American Physical Society.
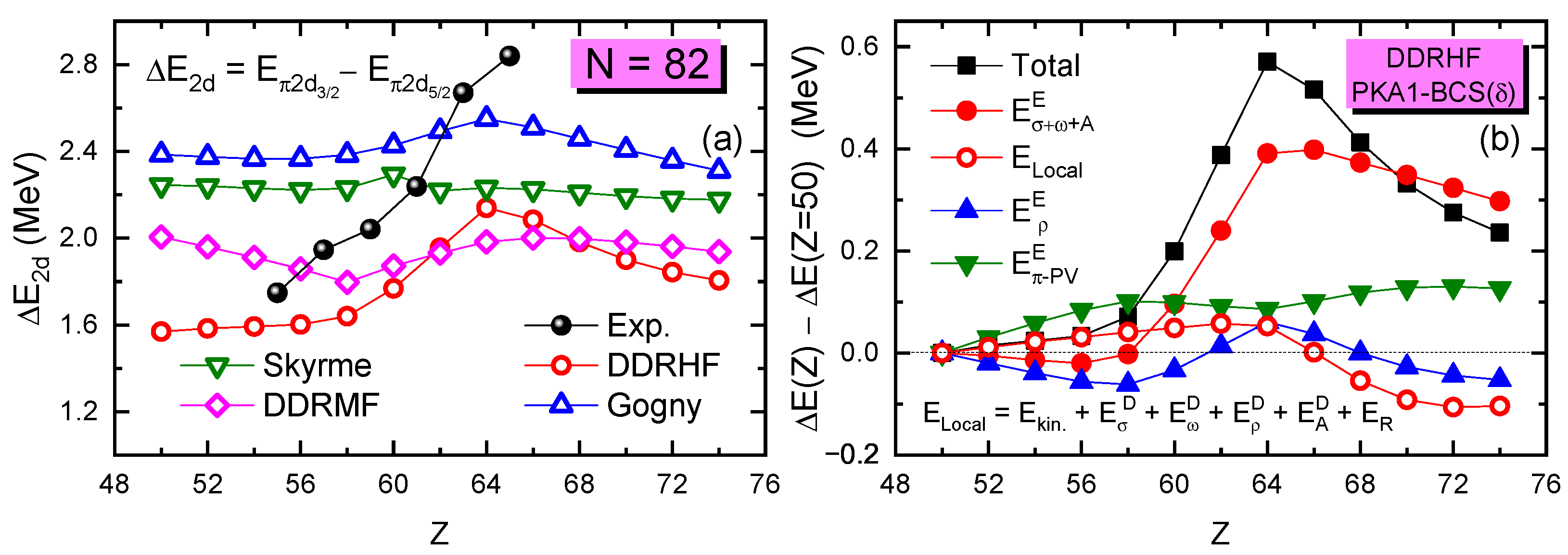
Conceptually, the condition or can preserve the PSS precisely, which cannot be satisfied in realistic nuclei. On the other hand, such a condition indeed indicates certain in-medium balance between nuclear attractions and repulsions. Taking as an example, Table 2 shows the contributions to the energy functional from the sum of kinetic energy and the isoscalar -S and -V couplings, that of the isovector and fields, and that of the electromagnetic field. Following the implementation of the Fock terms and further the -T coupling, one can observe changes from the RMF to RHF approaches on modeling the in-medium balance between nuclear attractions and repulsions.

Table 2.
Contributions to the total energy functional (MeV) of from the kinetic and isoscalar potential energies (), the isovector potential energies (), and the Coulomb ones (). The results are calculated by PKA1, PKO3, and DD-ME2. The table is taken from Ref. [104]. Reprinted with permission from Ref. [104]. Copyright 2019 American Physical Society.
As demonstrated in Table 2, all the effective Lagrangians give comparable total binding energies for , whereas the specific contributions, except , exhibit notable difference. In the RMF approach, the binding of the nucleus is primarily influenced by the counteraction between the strong attractive -S and repulsive -V couplings. The isovector contribution is notably enhanced by the Fock terms when moving from the RMF to the RHF approach. In contrast, the dominant isoscalar term is reduced in order to maintain the proper binding of . Within the RHF approach, the isovector term is considerably enhanced from PKO3 to PKA1 due to the -T coupling in PKA1, which contributes a fairly strong attraction. In contrast, the isoscalar term is significantly reduced [104].
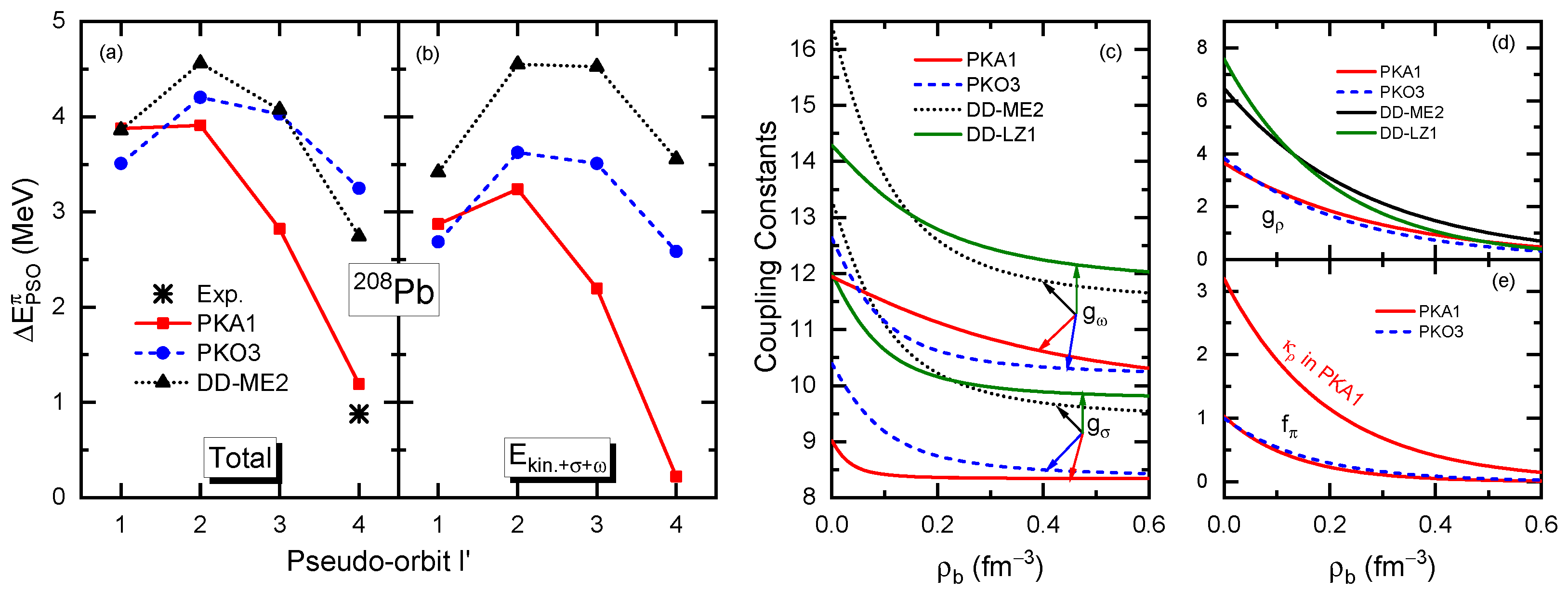
In fact, the systematic differences in the modeling of the binding of the nucleus can be manifested on the PSS restoration, not only in several doubly magic nuclei, shown in Figure 9b, but also in a single nucleus. Figure 10a shows the proton PSO splittings, , in with respect to the pseudo-orbit calculated by RHF Lagrangians PKA1 and PKO3, and the RMF one DD-ME2. In contrast to the results obtained with the PKO3 and DD-ME2, the PKA1 results show a rapid reduction with respect to and well-restored PSS for the PS doublet , which is in good agreement with the experimental data. Moreover, from a comparison of the results presented in Figure 10a,b it is evident that the sum contribution , which contains the kinetic term, and the dominant -S and -V couplings, has a significant impact on the systematic behavior of . It is thus revealed that the discrepancies in the PSS restoration are primarily due to the in-medium balance between the attractive -S and repulsive -V couplings. In particular, these balances are systematically altered from the RMF Lagrangian DD-ME2 to the RHF one PKO3 and subsequently to PKA1. This is evidenced by the reduction in the sum contributions , as shown in Figure 10b, which is consistent with the contribution of the binding energy, as shown in Table 2. It is noteworthy that the dependencies of on the exhibit a nearly parallel shift from DD-ME2 to PKO3, but undergo a significant change from PKO3 to PKA1.
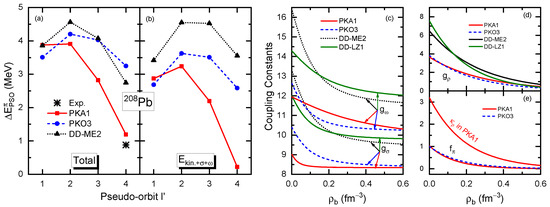
Figure 10.
Proton () PSO splittings (MeV) (a) in as functions of pseudo-orbit , and the sum contributions from kinetic energy, , and potential energies (b). The results are extracted from the calculations with PKA1, PKO3, and DD-ME2. Meson–nucleon coupling constants, namely, (c) the isoscalar and , (d) the isovector , and (e) [] and , as functions of the density () for PKA1, PKO3, DD-ME2, and DD-LZ1. The figure is taken from Refs. [104,143]. Reprinted with permission from Ref. [104]. Copyright 2019 American Physical Society. Reprinted with permission from Ref. [143]. Copyright 2020 Chinese Physical Society and the Institute of High Energy Physics of the Chinese Academy of Sciences and the Institute of Modern Physics of the Chinese Academy of Sciences and IOP Publishing Ltd.
Combining the results in Table 2 and Figure 10, the in-medium balance between nuclear attractions and repulsions can be significantly changed by the inclusion of the Fock terms, particularly in the context of the -T coupling. Consequently, it can be reasonably anticipated that these findings will have implications for the modeling of nuclear in-medium effects, as evaluated by the density dependencies of the meson–nucleon coupling strengths. As shown in Figure 10c, both the values and density dependencies of the coupling strengths and , associated with the degrees of freedom of the -S and -V couplings, respectively, are reduced from DD-ME2 to PKO3, due to the substantial contributions from the isovector channel, as evidenced in Table 2. This may also indicate that the dominant isoscalar channels (-S and -V) do not require the same strength as in the RMF approach. On the other hand, the isovector channels can be significantly enhanced by the Fock terms, which can incorporate more nuclear in-medium effects. Consequently, the density dependencies of and are reduced as well from DD-ME2 to PKO3. Even though, and still exhibit nearly parallel density-dependent behaviors from DD-ME2 to PKO3, which is common for the popular RMF Lagrangians and RHF ones PKOi (). However, this situation dramatically changes from PKO3 to PKA1. As revealed in Table 2 and Figure 10e, the -T coupling in PKA1 not only contributes fairly strong attraction, which can even affect the balance between the dominant -S and -V channels, but also takes into account much more nuclear in-medium effects than PKO3, as shown in Figure 10e. Consequently, the implementation of the -T coupling results in a further reduction in the coupling strengths and in PKA1, which no longer maintain parallel density-dependent behaviors. Further, combined with the schematic picture Figure 11, the consequence of the in-medium balance on the microscopic PSS restoration becomes more apparent.
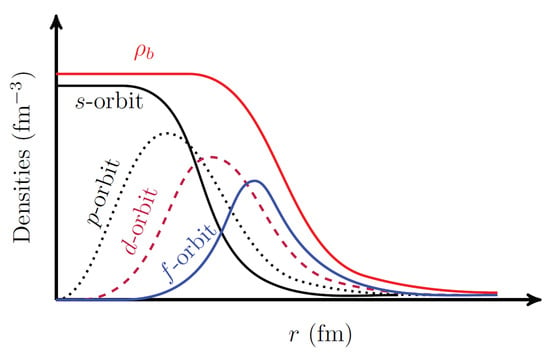
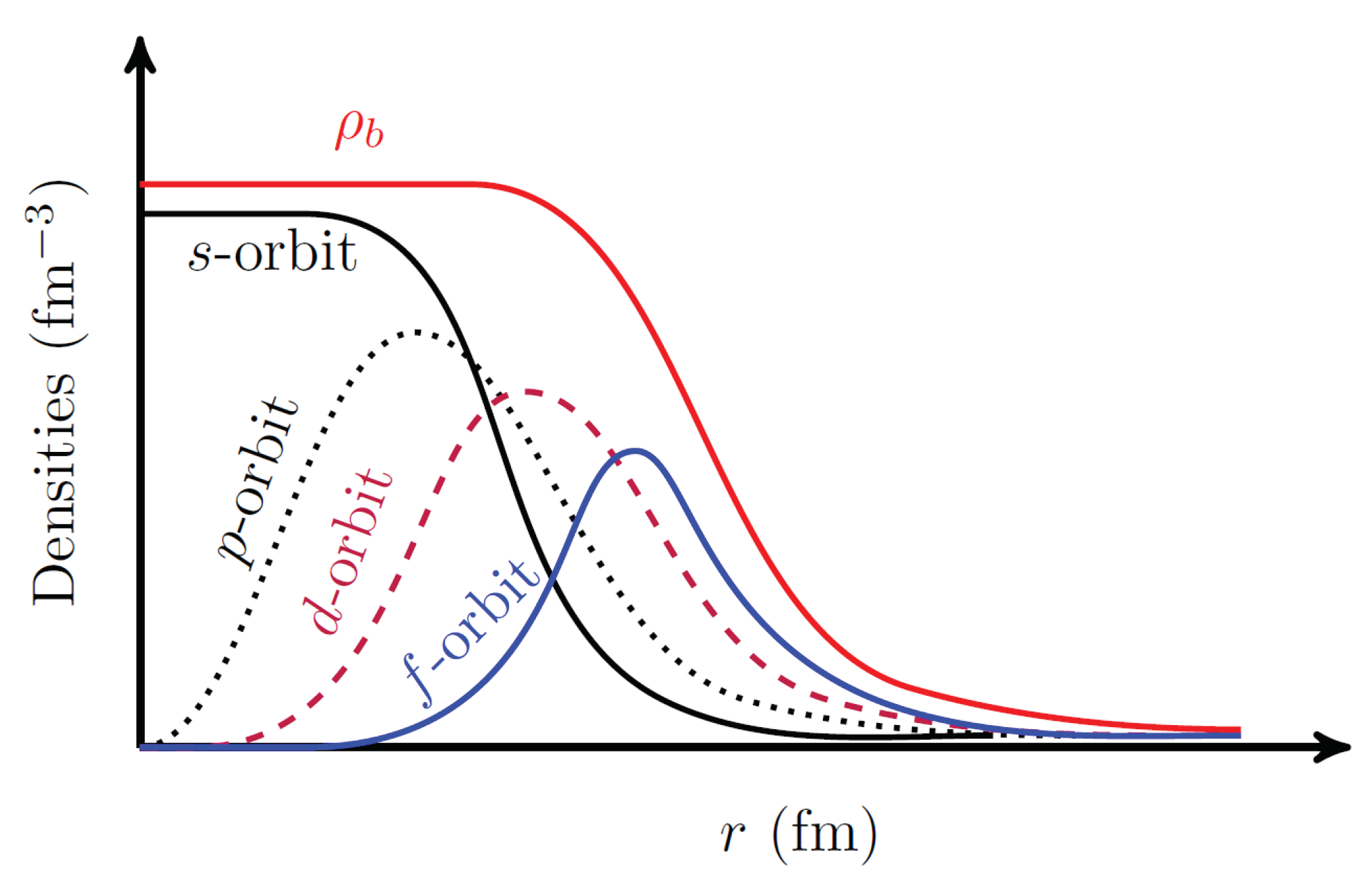
Figure 11.
Schematic diagrams of the matter density and probability densities of the s-, p-, d-, and f-orbits.
Schematically, Figure 11 shows the profiles of the matter density () and the probability densities of the s-, p-, d-, and f-orbits. Combined with the results in Figure 10c–e, Figure 11 can help us to understand the -dependence of the PSO splitting in Figure 10. As illustrated in Figure 11, the centrifugal potentials drive nucleons outwards as the angular momentum l increases. From the central region to the surface of the nucleus, the matter density gradually decreases from a near-saturated value to zero. This may result in a variation in the in-medium balance of nuclear attractions and repulsions, given that the meson–nucleon coupling strengths are density-dependent. As seen from Figure 10c, the coupling strengths and in both DD-ME2 and PKO3 exhibit near parallel density-dependent behaviors, whereas PKA1 provides a rather different modeling on the in-medium balance between nuclear attractions and repulsions. In accordance with this, the PSO splittings provided by DD-ME2 and PKO3, as well as the sum contributions , show a relatively weak angular momentum dependence. However, the PKA1 results represent a pronounced -dependence. Consequently, by combining the schematic systematics of the orbits with different l quantities in Figure 11, it is evident that the in-medium balance of nuclear attractions and repulsions can be manifested as the -dependence of the values in Figure 10, which provides a qualitative guidance to understand the nuclear in-medium effects.
4.3. The Thermal Nuclear Matter and Development of New Effective Lagrangians
The -T coupling, which may play an essential role in determining the nuclear in-medium balance, is significant not only for microscopic nuclear structure, but also for the liquid–gas (LG) phase transition of thermal nuclear matter. The LG phase transition of thermal nuclear matter has important implications for heavy-ion collisions [151,152,153,154], nuclear astrophysics [155,156,157,158,159], and so on. Numerous investigations have been devoted to the LG phase transition of thermal nuclear matter [160,161,162,163,164,165] under the RMF and RHF approaches. As illustrated in Table 3 and Figure 12, the effective Lagrangian PKA1, which exhibits a robust -T coupling, predicts distinctly different critical properties and LG phase diagrams from the other effective Lagrangians.

Table 3.
Critical parameters of LG phase transition of symmetric nuclear matter, i.e., the critical temperature (MeV), critical density (), the critical pressure (MeV ), the critical incompressibility (MeV), and the compressibility factor . The results are calculated by the RHF Lagrangians with PKA1 and PKO3, and the RMF ones with DD-ME2, PK1. The table is taken from Ref. [166]. Reprinted with permission from Ref. [166]. Copyright 2021 American Physical Society.
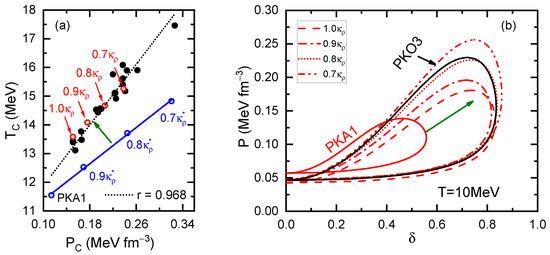
Figure 12.
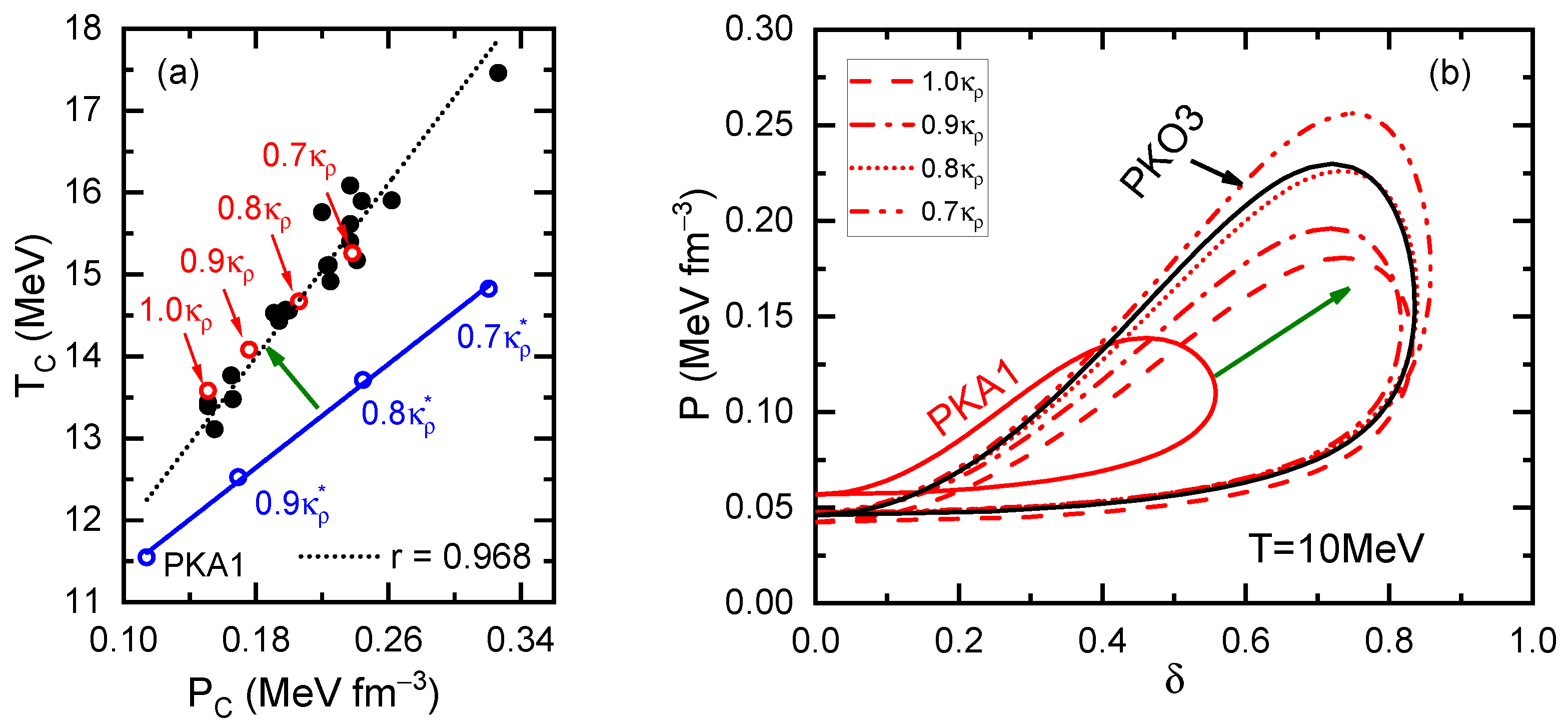
Panel (a) shows the correlation between the critical parameters (MeV) and (MeV ). The solid circles correspond to 20 selected relativistic Lagrangians from Ref. [165] and PKA1, and the open circles correspond to the testing sets , with x = 1.0 to 0.7 (in red) and with x = 0.9, 0.8, and 0.7 (in blue). As the references, the solid and dashed lines represent the linear fittings with the Pearson correlation coefficient r. Panel (b) presents LG phase diagrams of thermal nuclear matter at temperature MeV given by the sets (x = 1.0, 0.9, 0.8, and 0.7), as compared to the ones given by RHF Lagrangians PKA1 and PKO3. The figure is taken from Ref. [166]. Reprinted with permission from Ref. [166]. Copyright 2021 American Physical Society.
In order to figure out the physics behind the difference between PKA1 and other effective Lagrangians, particularly for the role of -T coupling and nuclear in-medium effects, two series of temporary parameterizations were proposed, named and [166], where means the scaling factor of the -T coupling strength . In addition, the series maintains the density dependencies of and unchanged from PKA1, whereas the series , , and share the same density dependencies, which show similar systematics as the other density-dependent effective Lagrangians. As shown in Figure 12a, nice linear correlations between the critical temperature and pressure are preserved along the series, being coincident with the selected effective Lagrangians except PKA1. On the contrary, PKA1 and the series present different linear correlations due to their different in-medium balances from the other effective Lagrangian and the series . Moreover, as shown in Figure 12b, a large expansion in the LG phase diagrams from the original PKA1 to the series is observed, and the results of set are already rather close to PKO3, that does not contain the -T coupling. From the above discussions, it is not hard to deduce that the in-medium balance of nuclear attraction and repulsion is essential for the van der Waals-like behaviors of thermal nuclear matter, in which the residual nuclear in-medium effects embedded in the balance between the dominant attractive and repulsive channels play a significant role [166].
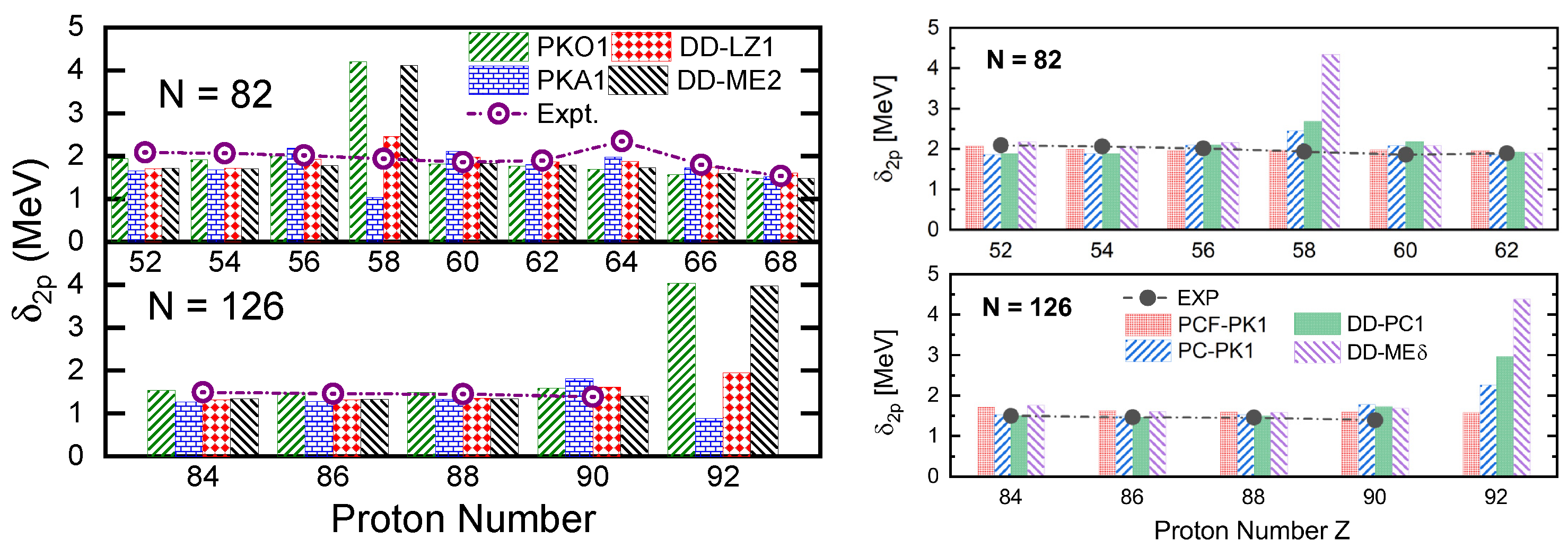
In Refs. [143,167], new RMF Lagrangians DD-LZ1 and PCF-PK1 were proposed, guided by the consistent relation between the PSS restoration and nuclear in-medium effects. In contrast to other popular RMF effective Lagrangians, the density dependences of and do not parallel each other in the case of DD-LZ1, as shown in Figure 10c. As with PKA1, DD-LZ1 addresses the common issue in previous RMF calculations, namely, the occurrence of artificial shell closures at and , as illustrated in the left panel of Figure 13. Similar to DD-LZ1, the new RMF Lagrangian PCF-PK1, which incorporates local exchange terms for the four-fermion interactions by utilizing the Fierz transformation, effectively eliminates the artificial shell closures and as well, as shown in the right panel of Figure 13, for which the unparalleled density dependences of and are essential. Moreover, DD-LZ1 and PCF-PK1 restore the PSS for the high- pseudo-spin doublets near the Fermi levels, which further corroborates the consistent relation between the PSS restoration and the nuclear in-medium balance between nuclear attraction and repulsion.
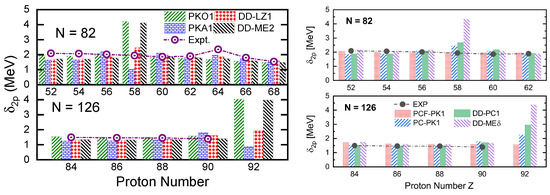
Figure 13.
Two-proton shell gap for N = 82 and 126 isotonic chains obtained from RH(F)B calculations with the new effective interaction DD-LZ1 (left panel) and PCF-PK1 (right panel). For comparison, the experimental data [168] and calculated results of PKA1, PKO1, DD-ME2, PC-PK1 [169], DD-PC1 [170], and DD-ME [123] are also given. The results of DD-LZ1 are taken from Ref. [143], and those of PCF-PK1 are taken from Ref. [167]. Reprinted with permission from Ref. [143]. Copyright 2020 Chinese Physical Society and the Institute of High Energy Physics of the Chinese Academy of Sciences and the Institute of Modern Physics of the Chinese Academy of Sciences and IOP Publishing Ltd. Reprinted with permission from Ref. [167]. Copyright 2022 American Physical Society.
5. The PSS and Novel Nuclear Phenomena
In Section 4, the mechanism of the PSS restoration for high are briefly recalled, in which the in-medium balance between nuclear attraction and repulsion plays an important role. As aforementioned, unstable nuclei exhibit plenty of novel nuclear phenomena, such as the halo and bubble-like structures, which reveal the characteristics of the microscopic structure of unstable nuclei. As one of the hottest topics in nuclear physics, the SHN are essentially stabilized by the shell effects, which may be closely related to the PSS restoration as discussed before. Therefore, in this section, the influence of PSS restoration and its breaking on novel nuclear phenomena, as well as on the emergence of superheavy magic shells, will be reviewed.
5.1. Halo Occurrence and PSS Restoration
As aforementioned, following the PSS restoration, the artificial shell closure given by the previous RMF and RHF calculations was eliminated by the RHF Lagrangian PKA1. Extending to the drip-line region, it can have a strong impact on the halo occurrence, for instance, in cerium (Ce) isotopes [109]. As one of the typical novel phenomena, a halo is characterized by an extensive matter distribution [7,8,9,10], arising from nucleons populating weakly bound low-l orbits. Due to the centrifugal barrier, the nucleons populating the neighboring high-l orbits do not contribute to the halo, but play an important role in stabilizing the dilute nucleons via the pairing correlations [64,65,109,171].
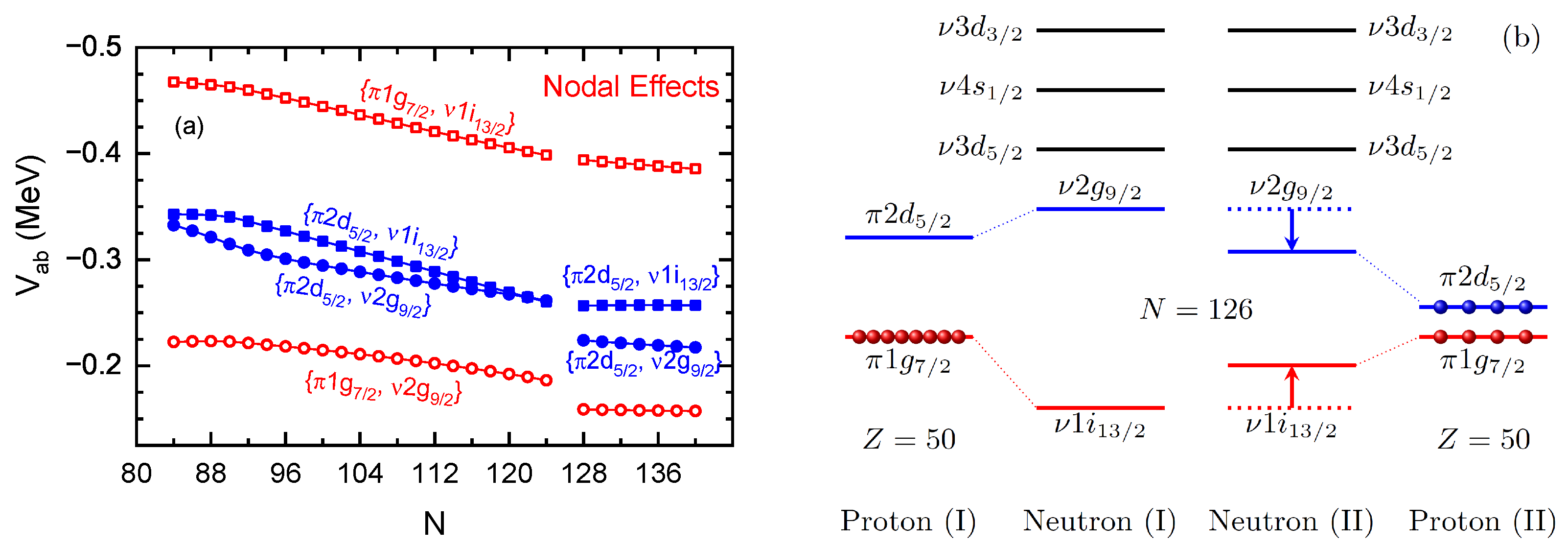
As revealed in Ref. [109], the neutron halo occurrence in the drip-line Ce isotopes is tightly connected with the PSS restoration of valence proton orbits, and such a relation is enhanced strongly by the -T coupling, which presents substantial contributions to the neutron–proton interactions via the Fock terms. From Figure 14a, the two-body interaction matrix elements between the proton PS partners and neutron orbits , one can see distinct nodal effects, i.e., that orbits with same nodal numbers present stronger couplings than those with different nodal numbers, which can be understood well following the principle of quantum mechanics.
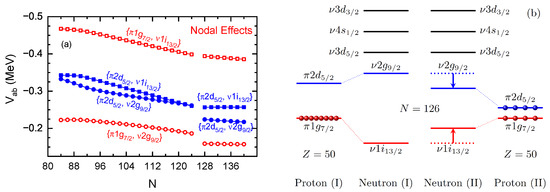
Figure 14.
(a) Two-body interaction matrix elements , where (filled symbols) and (open symbols), and and . The figure is taken from Ref. [109]. Reprinted with permission from Ref. [109]. Copyright 2010 American Physical Society. (b) Schematic diagrams of the proton–neutron configurations for the existence (I) and elimination (II) of artificial shell.
As aforementioned, large PSO splitting of gives rise to the artificial shell , and thus, the valence protons may occupy the orbit mainly, namely, the proton (I) configuration in Figure 14b. In contrast to that, following the elimination of the artificial shell with properly restored PSS, valence protons can spread over the PS partners and , which give the proton (II) configuration in Figure 14b. Regarding the fact that the shell gap is determined by the neutron orbits , it can be deduced from Figure 14 that the valence protons populating the orbit (or ) tend to enlarge (or squeeze) the shell gap due to the nodal effects. Following the PSS restoration of proton PS doublet , the shell gap is largely reduced, and thus, the Ce isotopic chain can be extended to , as predicted by PKA1, in contrast to the drip line given by other effective Lagrangians.
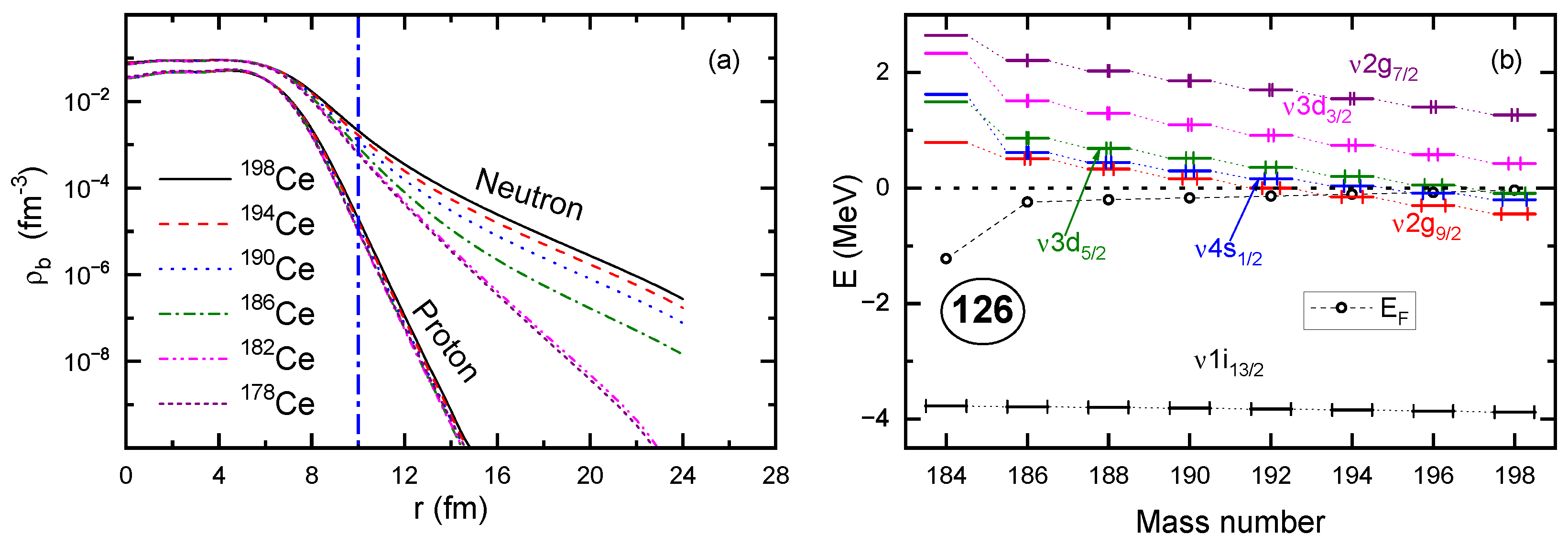
Due to the extension of the neutron drip line to , the occurrence of halos becomes possible in the Ce isotopes. As shown in Figure 15, when valence neutrons gradually occupy the low-l orbits above the shell, the neutron density distributions become more and more diffuse after the isotope (), indicating the emergence of ordinary and giant halos [109]. Moreover, as seen from Figure 15b, the continuum plays a dominant role in the formation and stabilization of the neutron halos, which are, respectively, contributed by the - and g-orbits. Combining Figure 14 and Figure 15, the squeezed shell gap following the proton PSS restoration is essential for the halo occurrence, in which the -T-enhanced neutron–proton interactions play the bridge role. It is worth mentioning that the mechanism responsible for the halo occurrences in Ce isotopes successfully interprets the experimental results of reduced PSO splitting ) approaching the shell for Cu isotopes and the neutron skin of the unstable nucleus [172].
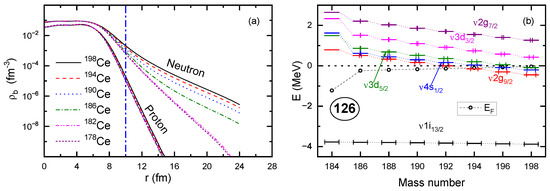
Figure 15.
(a) Neutron and proton densities; (b) neutron canonical SPE, occupation probability (x-axis error bars), and Fermi energy (open circles). Results are calculated by RHFB with PKA1 plus the Gogny pairing force D1S. The figure is taken from Ref. [109]. Reprinted with permission from Ref. [109]. Copyright 2010 American Physical Society.
5.2. Bubble-like Structure and the PSS
Since finite nuclei are complicated many-body systems; the PSS cannot be always conserved, even for the PS doublets near the Fermi surface. For example, the large PSO splitting of in has been verified experimentally [147]; see Figure 16. This may show certain impacts on the emergence of bubble-like structure, which is characterized by distinct central depressions of the matter distributions [19,20,21,22,23,24,25,26,27,28,29,30,31,32,173]. Generally speaking, the s-orbits play a decisive role in determining the central density profiles due to the vanishing of the centrifugal barrier; see Figure 11. Therefore, the absence of nucleon occupation in the s-orbits near the Fermi surface may lead to evident depression in the interior region of nuclear density profiles, giving rise to the bubble-like structure.
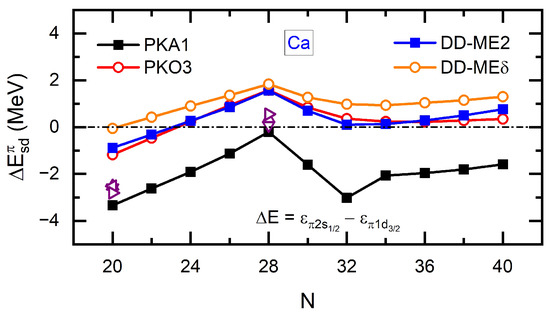
Figure 16.
Energy difference of Ca isotopes. The experimental values of and are taken from Ref. [147] (up triangle), Ref. [174] (down triangle), Ref. [175] (left triangle), and Ref. [176] (right triangle). The figure is taken from Ref. [110].
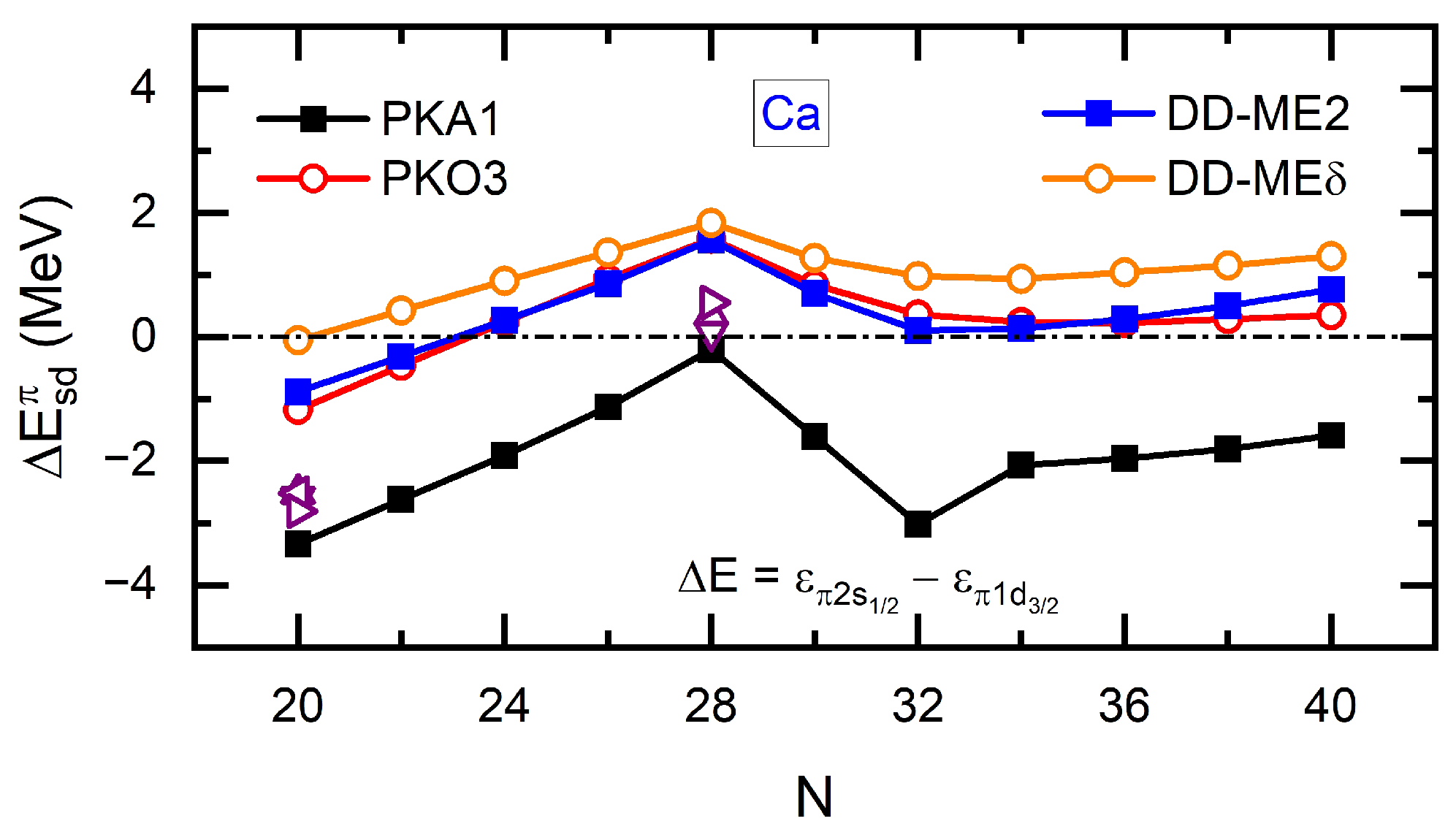
Figure 16 shows the PSO splittings between the proton PS partners and along the isotopic chain of calcium (Ca). It can be seen that only PKA1 can properly reproduce the experimental values at and , while the others show systematical deviations. As revealed in Ref. [31], such model deviations can be found consistently in describing the emergence of bubble-like structure in the isotones and Ca isotopes [111].
Figure 17 shows the proton SPE and charge density distributions of isotones. It can be seen from Figure 17c that and are predicted as the candidates with bubble-like structure by various models except PKA1. Such a model discrepancy can be traced back to the ordering of and in the proton SPE shown in Figure 17a,b. Due to large PSO splitting for the PS doublet , the RMF calculations with DD-ME2, as well as the RHF ones with PKO3, predict bubble-like structures for the isotones and , since valence protons populate mainly the orbit , instead of . However, PKA1 predicts a fairly large amount of occupation on the proton orbit , which washes out the bubble-like structures in and ; see Figure 17a,c. Combining the results in Figure 16 and Figure 17, one can see a certain relation between the PSS and the emergence of bubble-like structures in and .
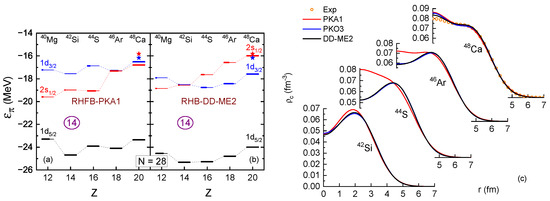
Figure 17.
Canonical proton SPE along the isotonic chain calculated by RHFB with PKA1 (a) and RHB with DD-ME2 (b). The lengths of thick bars correspond with the occupation probabilities of the proton orbits and the filled stars denote the experimental data. Charge distributions of isotones calculated by RHFB with PKA1 and PKO3, and by RHB with DD-ME2 (c). The figure is taken from Ref. [31]. Reprinted with permission from Ref. [31]. Copyright 2016 American Physical Society.
For , due to the existence of a large shell gap , all the models predict evident bubble-like structure. Similarly, both and are predicted by all the selected models to have distinct proton and neutron bubble-like structures, respectively, which is attributed to the presence of sub-shell [31]. In fact, the proton bubble-like structure in has been confirmed experimentally [177], which gives an empty proton orbit and distinct sub-shell . Moreover, the emergence of the sub-shell in is also accompanied by a neutron bubble-like structure, but due to a different mechanism from general cases [111]. Further extending to the drip line along the isotopic chain of Si and isotonic chain of simultaneously, it is interestingly to see that is predicted as a new doubly magic nucleus ( and ) with dual (neutron and proton) bubble-like structures by the RHFB calculations with PKA1 [32].
5.3. Superheavy Magicity and the PSS
As aforementioned, the appearance of magic and semi-magic shells may accompany well-restored PSS, which is also predicted for the occurrence of superheavy magicity. Taking doubly magic SHN as the example, predicted by the RHFB calculations with PKA1, one can see clear relations between the emergence of superheavy magic shells and the PSS [51]. As shown in Figure 18, the s.p. spectra of , the proton shell , originating from large splitting of the PS doublet , is commonly supported by the models. In addition, due to small PSO splitting of given by PKA1, a more pronounced superheavy shell appears, in contrast to the other model predictions. Moreover, such a model discrepancy can be also found in predicting the neutron magic shells. In the right panel of Figure 18, PKA1 predicts the most evident neutron shell . Consistent with that, both PS doublets and , above and below the shell, show well-restored PSS. However, the other selected models present large splitting for the PS doublet , which gives a fairly large shell gap . In fact, such a situation is rather similar to the results shown in Figure 6, in which the magic shell can also be squeezed by the artificial one , as well as the one in Figure 7.
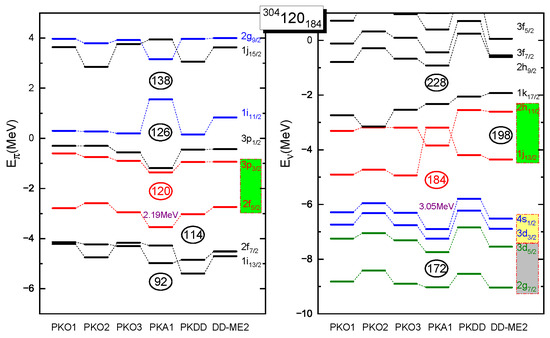
Figure 18.
Proton (left panel) and neutron (right panel) SPE of SHN . The results are extracted from RHFB calculations with PKOi () and PKA1, and compared to the RHB ones with PKDD and DD-ME2. In all cases, the pairing force is derived from the finite-range Gogny force D1S with the strength factor f = 0.9. The figure is taken from Ref. [51].
To further explore the relationship between superheavy shells ( and ) and the PSS, Figure 19 presents the proton and neutron density profiles with and calculated by PKA1 and PKO3. With the numbers of neutrons and protons increasing, the high-l orbits, such as , , , and , , are occupied. Since the nucleons populating the high-l orbits are driven towards the surface of the nucleus due to the strong centrifugal potential and large Coulomb repulsion [31,178], an obvious bubble-like structure can be commonly found in SHN, as shown in Figure 19, in particular for the ones marked in green. Following the appearance of the bubble-like structure, which can become even more extensive in SHN than in ordinary ones, the spin-orbit splittings of low-l orbits are largely squeezed. For instance, as shown in the left panel of Figure 18, fairly small splittings between the spin partners and lead to large PSO splitting for the proton PS doublet , that gives rise to the shell . The impact of the bubble-like structure on SO splitting has been introduced in Ref. [32]. Combined with the mechanism behind the PSS restoration of high- orbits, it can be concluded that reliable modeling of the in-medium balance between nuclear attractions and repulsions is essentially significant not only for ordinary nuclei but also for superheavy ones.
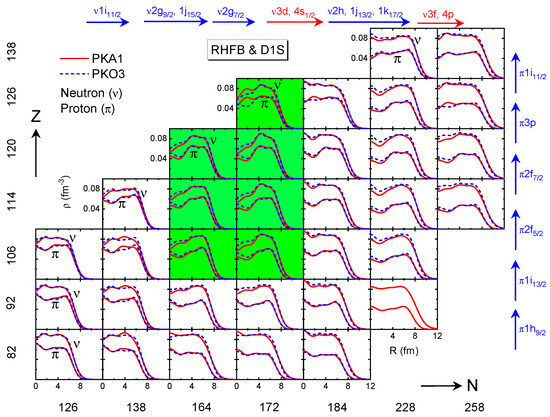
Figure 19.
The neutron () and proton () density distributions of superheavy nuclei calculated by the RHFB model with PKA1 (red line) and PKO3 (blue line).
6. Summary
In this paper, studies on the pseudo-spin symmetry (PSS) under the relativistic Hartree–Fock (RHF) theory were reviewed, including the effects of Fock terms on the PSS restoration, especially the role of -T coupling, and the relations to novel nuclear phenomena such as halo and bubble-like structures, and superheavy magicity.
Utilizing the Schrödinger-type equation, the influences of Fock terms are manifested as the cancellation within the Fock contributions, like between pseudo-spin orbit potentials and , and the RHF models with PKOi () provide a similar restoration picture as the popular RMF ones. However, when the -T coupling is incorporated into the effective Lagrangian PKA1, the PSS can also be well conserved for the high- pseudo-spin (PS) doublets, which eliminates the artificial shells and 92 appearing in the previous RMF and RHF calculations. It is found that the PSS restoration for high- PS doublets can be essentially connected with the modeling of the in-medium balance of nuclear attractions and repulsions, where -T coupling, that contributes mainly via the Fock diagram, plays an important role. This indicates that PSS restoration can provide a qualitative guidance on understanding the in-medium effects of nuclear force.
Furthermore, the impacts of PSS restoration and breaking on various nuclear phenomena are reviewed, including halos, bubble-like structure, and superheavy magicity. It was revealed that PSS restoration, that eliminates the artificial shell , can essentially be connected with the emergence of halo structures in drip-line Ce isotopes, in which the enhanced neutron–proton interactions by the -T coupling play the role of a bridge. Moreover, the PSO splitting in and the corresponding order between and can determine the prediction of bubble-like structures for and . For the superheavy nuclei, the large PSO splitting of and small one of are found to determine the emergence of superheavy magicity and , respectively.
In fact, PSS restoration or breaking has manifested the characteristics of the microscopic nuclear structure, which corresponds to the consequences of the nuclear force in complicated nuclear many-body systems. Even though, the PSS itself and the mechanism therein can provide us with a different insight to understand not only the nature of the nuclear force, that accounts for the binding of nucleus, but also various nuclear phenomena, including the shells, novel halo and bubble-like structures, superheavy magicity, etc. All these together may deepen our knowledge of nuclear physics.
Author Contributions
Conceptualization, W.L.; writing—original draft preparation, J.G. and Z.W.; writing—review and editing, J.G., Z.W., J.L. (Jia Liu), J.L. (Jiajie Li), and W.L.; investigation, J.G., J.L. (Jia Liu), J.L. (Jiajie Li), and W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Strategic Priority Research Program of Chinese Academy of Sciences under Grant No. XDB34000000, the National Natural Science Foundation of China under Grant Nos. 12275111 and 12075104, the National Key Research and Development (R&D) Program under Grant No. 2021YFA1601500, the Fundamental Research Funds for the Central Universities (lzujbky-2022-sp02), and the Supercomputing Center of Lanzhou University.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RHF | Relativistic Hartree–Fock |
| RMF | Relativistic mean field |
| RHB | Relativistic Hartree–Bogoliubov |
| DDRHF | Density-dependent relativistic Hartree–Fock |
| RHFB | Relativistic Hartree–Fock–Bogoliubov |
| -T | -tensor |
| SHE | Superheavy element |
| SHN | Superheavy nuclei |
| PSS | Pseudo-spin symmetry |
| PS | Pseudo-spin |
| SO | Spin orbit |
| PSO | Pseudo-spin orbit |
| PCB | Pseudo-centrifugal barrier |
| PSOP | Pseudo-spin orbital potential |
| s.p. | Single particle |
| SPE | Single-particle energy |
| LG | Liquid–gas |
References
- Zhan, W.; Xu, H.; Xiao, G.; Xia, J.; Zhao, H.; Yuan, Y. Progress in HIRFL-CSR. Nucl. Phys. A 2010, 834, 694c–700c. [Google Scholar] [CrossRef]
- Gales, S. SPIRAL2 at GANIL: Next Generation of ISOL Facility for Intense Secondary Radioactive Ion Beams. Nucl. Phys. A 2010, 834, 717c–723c. [Google Scholar] [CrossRef]
- Motobayashi, T. RIKEN RI Beam Factory—Recent Results and Perspectives. Nucl. Phys. A 2010, 834, 707c–712c. [Google Scholar] [CrossRef]
- Sturm, C.; Sharkov, B.; Stöcker, H. 1, 2, 3…FAIR! Nucl. Phys. A 2010, 834, 682c–687c. [Google Scholar] [CrossRef]
- Thoennessen, M. Plans for the Facility for Rare Isotope Beams. Nucl. Phys. A 2010, 834, 688c–693c. [Google Scholar] [CrossRef]
- Tshoo, K.; Kim, Y.; Kwon, Y.; Woo, H.; Kim, G.; Kim, Y.; Kang, B.; Park, S.; Park, Y.H.; Yoon, J.; et al. Experimental systems overview of the Rare Isotope Science Project in Korea. Nucl. Instr. Meth. B 2013, 317, 242–247. [Google Scholar] [CrossRef]
- Tanihata, I. Nuclear Structure Studies from Reaction Induced by Radioactive Nuclear Beams. Prog. Part. Nucl. Phys. 1995, 35, 505–575. [Google Scholar] [CrossRef]
- Casten, R.F.; Sherrill, B.M. The Study of Exotic Nuclei. Prog. Part. Nucl. Phys. 2000, 45, S171–S233. [Google Scholar] [CrossRef]
- Jensen, A.S.; Riisager, K.; Fedorov, D.V.; Garrido, E. Structure and reactions of quantum halos. Rev. Mod. Phys. 2004, 76, 215. [Google Scholar] [CrossRef]
- Jonson, B. Light dripline nuclei. Phys. Rep. 2004, 389, 1–59. [Google Scholar] [CrossRef]
- Motobayashi, T.; Ikeda, Y.; Ando, Y.; Ieki, K.; Inoue, M.; Iwasa, N.; Kikuchi, T.; Kurokawa, M.; Moriya, S.; Ogawa, S.; et al. Large deformation of the very neutron-rich nucleus 32Mg from intermediate-energy Coulomb excitation. Phys. Lett. B 1995, 346, 9–14. [Google Scholar] [CrossRef]
- Simon, H.; Aleksandrov, D.; Aumann, T.; Axelsson, L.; Baumann, T.; Borge, M.J.G.; Chulkov, L.V.; Collatz, R.; Cub, J.; Dostal, W.; et al. Direct Experimental Evidence for Strong Admixture of Different Parity States in 11Li. Phys. Rev. Lett. 1999, 83, 496–499. [Google Scholar] [CrossRef]
- Ozawa, A.; Kobayashi, T.; Suzuki, T.; Tanihata, K.Y.I. New Magic Number, N = 16, near the Neutron Drip Line. Phys. Rev. Lett. 2000, 84, 5493. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, C.R.; Baumann, T.; Bazin, D.; Brown, J.; Christian, G.; DeYoung, P.A.; Finck, J.E.; Frank, N.; Hinnefeld, J.; Howes, R.; et al. Determination of the N = 16 Shell Closure at the Oxygen Drip Line. Phys. Rev. Lett. 2008, 100, 152502. [Google Scholar] [CrossRef] [PubMed]
- Kanungo, R.; Nociforo, C.; Prochazka, A.; Aumann, T.; Boutin, D.; Cortina-Gil, D.; Davids, B.; Diakaki, M.; Farinon, F.; Geissel, H.; et al. One-Neutron Removal Measurement Reveals 24O as a New Doubly Magic Nucleus. Phys. Rev. Lett. 2009, 102, 152501. [Google Scholar] [CrossRef] [PubMed]
- Tshoo, K.; Satou, Y.; Bhang, H.; Choi, S.; Nakamura, T.; Kondo, Y.; Deguchi, S.; Kawada, Y.; Kobayashi, N.; Nakayama, Y.; et al. N = 16 Spherical Shell Closure in 24O. Phys. Rev. Lett. 2012, 109, 022501. [Google Scholar] [CrossRef] [PubMed]
- Steppenbeck, D.; Takeuchi, S.; Aoi, N.; Doornenbal, P.; Matsushita, M.; Wang, H.; Baba, H.; Fukuda, N.; Go, S.; Honma, M.; et al. Evidence for a new nuclear ’magic number’ from the level structure of 54Ca. Nature 2013, 502, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Steppenbeck, D.; Takeuchi, S.; Aoi, N.; Doornenbal, P.; Matsushita, M.; Wang, H.; Utsuno, Y.; Baba, H.; Go, S.; Lee, J.; et al. Low-Lying Structure of 50Ar and the N = 32 Subshell Closure. Phys. Rev. Lett. 2015, 114, 252501. [Google Scholar] [CrossRef] [PubMed]
- Swiatecki, W.J. Discussions with Jens Lindhard. Phys. Scr. 1983, 28, 349. [Google Scholar] [CrossRef]
- Saunier, G.; Rouben, B.; Pearson, J. Bubbles and the odd-state force. Phys. Lett. B 1974, 48, 293–296. [Google Scholar] [CrossRef]
- Campi, X.; Sprung, D. Possible bubble nuclei -36Ar and 200Hg. Phys. Lett. B 1973, 46, 291–295. [Google Scholar] [CrossRef]
- Khan, E.; Grasso, M.; Margueron, J.; Van Giai, N. Detecting bubbles in exotic nuclei. Nucl. Phys. A 2008, 800, 37–46. [Google Scholar] [CrossRef]
- Grasso, M.; Gaudefroy, L.; Khan, E.; Nikšić, T.; Piekarewicz, J.; Sorlin, O.; Giai, N.V.; Vretenar, D. Nuclear ’bubble’ structure in 34Si. Phys. Rev. C 2009, 79, 034318. [Google Scholar] [CrossRef]
- Nakada, H.; Sugiura, K.; Margueron, J. Tensor-force effects on single-particle levels and proton bubble structure around the Z or N = 20 magic number. Phys. Rev. C 2013, 87, 067305. [Google Scholar] [CrossRef]
- Todd-Rutel, B.G.; Piekarewicz, J.; Cottle, P.D. Spin-orbit splitting in low-j neutron orbits and proton densities in the nuclear interior. Phys. Rev. C 2004, 69, 021301. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Gu, J.Z.; Zhang, X.Z.; Dong, J.M. Tensor effects on the proton sd states in neutron-rich Ca isotopes and bubble structure of exotic nuclei. Phys. Rev. C 2011, 84, 044333. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Hou, Z.Y.; Zhang, Q.L.; Tian, R.L.; Gu, J.Z. Effect of a tensor force on the proton bubble structure of 206Hg. Phys. Rev. C 2015, 91, 017302. [Google Scholar] [CrossRef]
- Afanasjev, A.V.; Frauendorf, S. Central depression in nuclear density and its consequences for the shell structure of superheavy nuclei. Phys. Rev. C 2005, 71, 024308. [Google Scholar] [CrossRef]
- Pei, J.C.; Xu, F.R.; Stevenson, P.D. Density distributions of superheavy nuclei. Phys. Rev. C 2005, 71, 034302. [Google Scholar] [CrossRef]
- Dechargé, J.; Berger, J.F.; Dietrich, K.; Weiss, M. Superheavy and hyperheavy nuclei in the form of bubbles or semi-bubbles. Phys. Lett. B 1999, 451, 275–282. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Song, J.L.; Zhao, Q. Pseudospin-orbit splitting and its consequences for the central depression in nuclear density. Phys. Rev. C 2016, 93, 054312. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Margueron, J.; Giai, N.V. 48Si: An atypical nucleus? Phys. Lett. B 2019, 788, 192–197. [Google Scholar] [CrossRef]
- Kajino, T.; Aoki, W.; Balantekin, A.B.; Diehl, R.; Famiano, M.A.; Mathews, G.J. Current status of r-process nucleosynthesis. Prog. Part. Nucl. Phys. 2019, 107, 109–166. [Google Scholar] [CrossRef]
- Cowan, J.J.; Sneden, C.; Lawler, J.E.; Aprahamian, A.; Wiescher, M.; Langanke, K.; Martínez-Pinedo, G.; Thielemann, F.K. Origin of the heaviest elements: The rapid neutron-capture process. Rev. Mod. Phys. 2021, 93, 015002. [Google Scholar] [CrossRef]
- Oganessian, Y.T.; Utyonkov, V.K.; Lobanov, Y.V.; Abdullin, F.S.; Polyakov, A.N.; Sagaidak, R.N.; Shirokovsky, I.V.; Tsyganov, Y.S.; Voinov, A.A.; Gulbekian, G.G.; et al. Synthesis of the isotopes of elements 118 and 116 in the 249Cf and 245Cm + 48Ca fusion reactions. Phys. Rev. C 2006, 74, 044602. [Google Scholar] [CrossRef]
- Oganessian, Y.T.; Abdullin, F.S.; Bailey, P.D.; Benker, D.E.; Bennett, M.E.; Dmitriev, S.N.; Ezold, J.G.; Hamilton, J.H.; Henderson, R.A.; Itkis, M.G.; et al. Synthesis of a New Element with Atomic Number Z = 117. Phys. Rev. Lett. 2010, 104, 142502. [Google Scholar] [CrossRef]
- Adamian, G.G.; Antonenko, N.V.; Sargsyan, V.V. Stability of superheavy nuclei produced in actinide-based complete fusion reactions: Evidence for the next magic proton number at Z ⩾ 120. Phys. Rev. C 2009, 79, 054608. [Google Scholar] [CrossRef]
- Arima, A.; Harvey, M.; Shimizu, K. Pseudo LS coupling and pseudo SU(3) coupling schemes. Phys. Lett. B 1969, 30, 517–522. [Google Scholar] [CrossRef]
- Hecht, K.T.; Adler, A. Generalized seniority for favored J ≠ 0 pairs in mixed configurations. Nucl. Phys. A 1969, 137, 129–143. [Google Scholar] [CrossRef]
- Ginocchio, J.N. A relativistic symmetry in nuclei. Phys. Rep. 1999, 315, 231–240. [Google Scholar] [CrossRef]
- Ginocchio, J.N. Relativistic symmetries in nuclei and hadrons. Phys. Rep. 2005, 414, 165–261. [Google Scholar] [CrossRef]
- Liang, H.Z.; Meng, J.; Zhou, S.G. Hidden pseudospin and spin symmetries and their origins in atomic nuclei. Phys. Rep. 2015, 570, 1–84. [Google Scholar] [CrossRef]
- Shen, S.; Liang, H.; Long, W.H.; Meng, J.; Ring, P. Towards an ab initio covariant density functional theory for nuclear structure. Prog. Part. Nucl. Phys. 2019, 109, 103713. [Google Scholar] [CrossRef]
- Ginocchio, J.N. Pseudospin as a Relativistic Symmetry. Phys. Rev. Lett. 1997, 78, 436. [Google Scholar] [CrossRef]
- Miller, L.D.; Green, A.E.S. Relativistic self-consistent meson field theory of spherical nuclei. Phys. Rev. C 1972, 5, 241. [Google Scholar] [CrossRef]
- Meng, J.; Sugawara-Tanabe, K.; Yamaji, S.; Ring, P.; Arima, A. Pseudospin symmetry in relativistic mean field theory. Phys. Rev. C 1998, 58, R628. [Google Scholar] [CrossRef]
- Nagai, Y.; Styczen, J.; Piiparinen, M.; Kleinheinz, P.; Bazzacco, D.; Brentano, P.V.; Zell, K.O.; Blomqvist, J. Proton Single-Particle States above Z = 64. Phys. Rev. Lett. 1981, 47, 1259–1262. [Google Scholar] [CrossRef]
- Long, W.H.; Sagawa, H.; Van Giai, N.; Meng, J. Shell structure and ρ-tensor correlations in density dependent relativistic Hartree-Fock theory. Phys. Rev. C 2007, 76, 034314. [Google Scholar] [CrossRef]
- Long, W.H.; Nakatsukasa, T.; Sagawa, H.; Meng, J.; Nakada, H.; Zhang, Y. Non-local mean field effect on nuclei near sub-shell. Phys. Lett. B 2009, 680, 428–431. [Google Scholar] [CrossRef]
- Long, W.H.; Ring, P.; Giai, N.V.; Meng, J. Relativistic Hartree-Fock-Bogoliubov theory with density dependent meson-nucleon couplings. Phys. Rev. C 2010, 81, 024308. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Margueron, J.M.; Van Giai, N. Superheavy magic structures in the relativistic Hartree-Fock-Bogoliubov approach. Phys. Lett. B 2014, 732, 169–173. [Google Scholar] [CrossRef]
- Jolos, R.; Voronov, V.V. Pseudospin symmetry and structure of nuclei with Z ≥ 100. Phys. Atom. Nucl. 2007, 70, 812–817. [Google Scholar] [CrossRef][Green Version]
- Dudek, J.; Nazarewicz, W.; Szymanski, Z.; Leander, G.A. Abundance and systematics of nuclear superdeformed states; relation to the pseudospin and pseudo-SU(3) symmetries. Phys. Rev. Lett. 1987, 59, 1405–1408. [Google Scholar] [CrossRef]
- Bahri, C.; Draayer, J.P.; Moszkowski, S.A. Pseudospin symmetry in nuclear physics. Phys. Rev. Lett. 1992, 68, 2133–2136. [Google Scholar] [CrossRef] [PubMed]
- Walecka, J.D. A theory of highly condensed matter. Ann. Phys. 1974, 83, 491–529. [Google Scholar] [CrossRef]
- Yukawa, H. On the interaction of elementary particles. Proc. Phys. Math. Soc. Jpn. 1935, 17, 48–57. [Google Scholar]
- Serot, B.D.; Walecka, J.D. The relativistic nuclear many-body problem. Adv. Nucl. Phys. 1986, 16, 1–327. [Google Scholar]
- Meng, J. Relativistic continuum Hartree-Bogoliubov theory with both zero range and finite range Gogny force and their application. Nucl. Phys. A 1998, 635, 3–42. [Google Scholar] [CrossRef]
- Vretenar, D.; Afanasjev, A.V.; Lalazissis, G.A.; Ring, P. Relativistic Hartree-Bogoliubov theory: Static and dynamic aspects of exotic nuclear structure. Phys. Rep. 2005, 409, 101–259. [Google Scholar] [CrossRef]
- Zhou, S.G.; Meng, J.; Ring, P. Toward a deformed relativistic Hartree Bogoliubov model for exotic nuclei. AIP Conf. Proc. 2006, 865, 90–95. [Google Scholar]
- Meng, J.; Toki, H.; Zhou, S.G.; Zhang, S.Q.; Long, W.H.; Geng, L.S. Relativistic continuum Hartree Bogoliubov theory for ground-state properties of exotic nuclei. Prog. Part. Nucl. Phys. 2006, 57, 470–563. [Google Scholar] [CrossRef]
- Li, L.L.; Meng, J.; Ring, P.; Zhao, E.G.; Zhou, S.G. Deformed relativistic Hartree-Bogoliubov theory in continuum. Phys. Rev. C 2012, 85, 024312. [Google Scholar] [CrossRef]
- Chen, Y.; Li, L.L.; Liang, H.Z.; Meng, J. Density-dependent deformed relativistic Hartree-Bogoliubov theory in continuum. Phys. Rev. C 2012, 85, 067301. [Google Scholar] [CrossRef]
- Meng, J.; Ring, P. Relativistic Hartree-Bogoliubov Description of the Neutron Halo in 11Li. Phys. Rev. Lett. 1996, 77, 3963–3966. [Google Scholar] [CrossRef]
- Meng, J.; Ring, P. Giant halo at the neutron drip line. Phys. Rev. Lett. 1998, 80, 460–463. [Google Scholar] [CrossRef]
- Meng, J.; Tanihata, I.; Yamaji, S. The proton and neutron distributions in Na isotopes: The development of halo and shell. Phys. Lett. B 1998, 419, 1–6. [Google Scholar] [CrossRef]
- Zhou, S.G.; Meng, J.; Ring, P.; Zhao, E.G. Neutron halo in deformed nuclei. Phys. Rev. C 2010, 82, 011301. [Google Scholar] [CrossRef]
- Sun, X.X. Deformed two-neutron halo in 19B. Phys. Rev. C 2021, 103, 054315. [Google Scholar] [CrossRef]
- Liang, H.; Shen, S.; Zhao, P.; Meng, J. Pseudospin symmetry in supersymmetric quantum mechanics: Schrödinger equations. Phys. Rev. C 2013, 87, 014334. [Google Scholar] [CrossRef]
- Shen, S.; Liang, H.; Zhao, P.; Zhang, S.; Meng, J. Pseudospin symmetry in supersymmetric quantum mechanics. II. Spin-orbit effects. Phys. Rev. C 2013, 88, 024311. [Google Scholar] [CrossRef]
- Alberto, P.; Fiolhais, M.; Malheiro, M.; Delfino, A.; Chiapparini, M. Isospin Asymmetry in the Pseudospin Dynamical Symmetry. Phys. Rev. Lett. 2001, 86, 5015–5018. [Google Scholar] [CrossRef] [PubMed]
- Alberto, P.; Fiolhais, M.; Malheiro, M.; Delfino, A.; Chiapparini, M. Pseudospin symmetry as a relativistic dynamical symmetry in the nucleus. Phys. Rev. C 2002, 65, 034307. [Google Scholar] [CrossRef]
- Huang, B.; Guo, J.Y.; Chen, S.W. Investigation of pseudospin and spin symmetries in relativistic mean field theory combined with a similarity renormalization group approach. Phys. Rev. C 2022, 105, 054313. [Google Scholar] [CrossRef]
- Marcos, S.; López-Quelle, M.; Niembro, R.; Savushkin, L.; Bernardos, P. On the sufficient conditions for the pseudospin symmetry in relativistic models. Phys. Lett. B 2001, 513, 30–36. [Google Scholar] [CrossRef]
- Lisboa, R.; Malheiro, M.; Alberto, P.; Fiolhais, M.; de Castro, A.S. Spin and pseudospin symmetries in the antinucleon spectrum of nuclei. Phys. Rev. C 2010, 81, 064324. [Google Scholar] [CrossRef]
- Ginocchio, J.N. Relativistic U(3) symmetry and pseudo-U(3) symmetry of the Dirac Hamiltonian. J. Phys. Conf. Ser. 2011, 267, 012037. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Gambhir, Y.K.; Maharana, J.P.; Warke, C.S.; Ring, P. Relativistic mean field approach and the pseudospin symmetry. Phys. Rev. C 1998, 58, R45–R48. [Google Scholar] [CrossRef]
- Sugawara-Tanabe, K.; Arima, A. Hidden pseudospin symmetry in the Dirac equation. Phys. Rev. C 1998, 58, R3065–R3068. [Google Scholar] [CrossRef]
- Ginocchio, J.N. Pseudospin symmetry and relativistic mean field eigenfunctions. Phys. Rev. C 2002, 66, 064312. [Google Scholar] [CrossRef]
- Sugawara-Tanabe, K.; Yamaji, S.; Arima, A. Spin symmetry and pseudospin symmetry in the relativistic mean field with a deformed potential. Phys. Rev. C 2002, 65, 054313. [Google Scholar] [CrossRef]
- Ginocchio, J.N.; Leviatan, A.; Meng, J.; Zhou, S.G. Test of pseudospin symmetry in deformed nuclei. Phys. Rev. C 2004, 69, 034303. [Google Scholar] [CrossRef]
- Sun, T.T.; Li, B.X.; Liu, K. Probing spin and pseudospin symmetries in deformed nuclei by the Green’s function method. Phys. Rev. C 2024, 109, 014323. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, Y.X.; Liu, Q.; Guo, J.Y. Pseudospin symmetry in resonant states in deformed nuclei. Phys. Lett. B 2023, 838, 137716. [Google Scholar] [CrossRef]
- Sun, T.T.; Lu, W.L.; Zhang, S.S. Spin and pseudospin symmetries in the single-Λ spectrum. Phys. Rev. C 2017, 96, 044312. [Google Scholar] [CrossRef]
- Lu, W.L.; Liu, Z.X.; Ren, S.H.; Zhang, W.; Sun, T.T. (Pseudo)spin symmetry in the single-neutron spectrum of Λ hypernuclei. J. Phys. G Nucl. Part. Phys. 2017, 44, 125104. [Google Scholar] [CrossRef]
- Guo, J.Y.; Wang, R.D.; Fang, X.Z. Pseudospin symmetry in the resonant states of nuclei. Phys. Rev. C 2005, 72, 054319. [Google Scholar] [CrossRef]
- Guo, J.Y.; Fang, X.Z. Isospin dependence of pseudospin symmetry in nuclear resonant states. Phys. Rev. C 2006, 74, 024320. [Google Scholar] [CrossRef]
- Liu, Q.; Niu, Z.M.; Guo, J.Y. Resonant states and pseudospin symmetry in the Dirac-Morse potential. Phys. Rev. A 2013, 87, 052122. [Google Scholar] [CrossRef]
- Lu, B.N.; Zhao, E.G.; Zhou, S.G. Pseudospin Symmetry in Single Particle Resonant States. Phys. Rev. Lett. 2012, 109, 072501. [Google Scholar] [CrossRef]
- Lu, B.N.; Zhao, E.G.; Zhou, S.G. Pseudospin symmetry in single-particle resonances in spherical square wells. Phys. Rev. C 2013, 88, 024323. [Google Scholar] [CrossRef]
- Dai, H.M.; Shi, M.; Chen, S.W.; Liu, Q. Influence of different fields of mesons on the pseudospin symmetry in single-neutron resonant states. Chin. Phys. C 2021, 45, 124102. [Google Scholar] [CrossRef]
- Sun, T.T.; Lu, W.L.; Qian, L.; Li, Y.X. Green’s function method for the spin and pseudospin symmetries in the single-particle resonant states. Phys. Rev. C 2019, 99, 034310. [Google Scholar] [CrossRef]
- Xu, Q. Isospin asymmetry of the pseudospin symmetry in nuclear resonant states. Eur. Phys. J. A 2019, 55, 54. [Google Scholar] [CrossRef]
- Sun, T.T.; Li, Z.P.; Ring, P. Conservation and breaking of pseudospin symmetry. Phys. Lett. B 2023, 847, 138320. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Y.; Guo, J.Y. Pseudospin symmetry in resonant states and its dependence on the shape of potential. Phys. Lett. B 2022, 824, 136829. [Google Scholar] [CrossRef]
- Shi, X.X.; Liu, Q.; Guo, J.Y.; Ren, Z.Z. Pseudospin and spin symmetries in single particle resonant states in Pb isotopes. Phys. Lett. B 2020, 801, 135174. [Google Scholar] [CrossRef]
- Miller, L.D. Possible Validity of the Relativistic Hartree-Fock Approximation in Nuclear Physics. Phys. Rev. Lett. 1972, 28, 1281–1284. [Google Scholar] [CrossRef]
- Brockmann, R. Relativistic Hartree-Fock description of nuclei. Phys. Rev. C 1978, 18, 1510–1524. [Google Scholar] [CrossRef]
- Bouyssy, A.; Mathiot, J.F.; Giai, N.V.; Marcos, S. Relativistic description of nuclear systems in the Hartree-Fock approximation. Phys. Rev. C 1987, 36, 380–401. [Google Scholar] [CrossRef]
- Long, W.H.; Sagawa, H.; Meng, J.; Van Giai, N. Pseudo-spin symmetry in density-dependent relativistic Hartree-Fock theory. Phys. Lett. B 2006, 639, 242–247. [Google Scholar] [CrossRef]
- Long, W.H.; Sagawa, H.; Meng, J.; Van Giai, N. Evolution of nuclear shell structure due to the pion exchange potential. Europhys. Lett. 2008, 82, 12001. [Google Scholar] [CrossRef]
- Wang, L.J.; Dong, J.M.; Long, W.H. Tensor effects on the evolution of the N = 40 shell gap from nonrelativistic and relativistic mean-field theory. Phys. Rev. C 2013, 87, 047301. [Google Scholar] [CrossRef]
- Liang, H.; Long, W.H.; Meng, J.; Giai, N.V. Spin symmetry in Dirac negative-energy spectrum in density-dependent relativistic Hartree-Fock theory. Eur. Phys. J. A 2010, 44, 119–124. [Google Scholar] [CrossRef]
- Geng, J.; Li, J.J.; Long, W.H.; Niu, Y.F.; Chang, S.Y. Pseudospin symmetry restoration and the in-medium balance between nuclear attractive and repulsive interactions. Phys. Rev. C 2019, 100, 051301. [Google Scholar] [CrossRef]
- Sun, B.Y.; Long, W.H.; Meng, J.; Lombardo, U. Neutron star properties in density-dependent relativistic Hartree-Fock theory. Phys. Rev. C 2008, 78, 065805. [Google Scholar] [CrossRef]
- Jiang, L.J.; Yang, S.; Dong, J.M.; Long, W.H. Self-consistent tensor effects on nuclear matter systems within a relativistic Hartree-Fock approach. Phys. Rev. C 2015, 91, 025802. [Google Scholar] [CrossRef]
- Jiang, L.J.; Yang, S.; Sun, B.Y.; Long, W.H.; Gu, H.Q. Nuclear tensor interaction in a covariant energy density functional. Phys. Rev. C 2015, 91, 034326. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zhao, Q.; Liang, H.Z.; Long, W.H. Quantitative analysis of tensor effects in the relativistic Hartree-Fock theory. Phys. Rev. C 2018, 98, 034313. [Google Scholar] [CrossRef]
- Long, W.H.; Ring, P.; Meng, J.; Van Giai, N.; Bertulani, C.A. Nuclear halo structure and pseudospin symmetry. Phys. Rev. C 2010, 81, 031302. [Google Scholar] [CrossRef]
- Li, J.J.; Margueron, J.; Long, W.H.; Giai, N.V. Magicity of neutron-rich nuclei within relativistic self-consistent approaches. Phys. Lett. B 2016, 753, 97–102. [Google Scholar] [CrossRef]
- Liu, J.; Niu, Y.F.; Long, W.H. New magicity N = 32 and 34 due to strong couplings between Dirac inversion partners. Phys. Lett. B 2020, 806, 135524. [Google Scholar] [CrossRef]
- Reinhard, P.G. The relativistic mean-field description of nuclei and nuclear dynamics. Rep. Prog. Phys. 1989, 52, 439. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A.R. Relativistic calculation of nuclear matter and the nuclear surface. Nucl. Phys. A 1977, 292, 413–428. [Google Scholar] [CrossRef]
- Sugahara, Y.; Toki, H. Relativistic mean-field theory for unstable nuclei with non-linear σ and ω terms. Nucl. Phys. A 1994, 579, 557–572. [Google Scholar] [CrossRef]
- Long, W.H.; Meng, J.; Giai, N.V.; Zhou, S.G. New effective interactions in relativistic mean field theory with nonlinear terms and density-dependent meson-nucleon coupling. Phys. Rev. C 2004, 69, 034319. [Google Scholar] [CrossRef]
- Brockmann, R.; Toki, H. Relativistic density-dependent Hartree approcah for finite nuclei. Phys. Rev. Lett. 1992, 68, 3408. [Google Scholar] [CrossRef]
- Lenske, H.; Fuchs, C. Rearrangement in the density dependent relativistic field theory of nuclei. Phys. Lett. B 1995, 345, 355. [Google Scholar] [CrossRef]
- Fuchs, C.; Lenske, H.; Wolter, H.H. Density dependent hadron field theory. Phys. Rev. C 1995, 52, 3043. [Google Scholar] [CrossRef]
- Typel, S.; Wolter, H.H. Relativistic mean field calculations with density-dependent meson-nucleon coupling. Nucl. Phys. A 1999, 656, 331–364. [Google Scholar] [CrossRef]
- Bernardos, P.; Fomenko, V.N.; Giai, N.V.; Quelle, M.L.; Marcos, S.; Niembro, R.; Savushkin, L.N. Relativistic Hartree-Fock approximation in a nonlinear model for nuclear matter and finite nuclei. Phys. Rev. C 1993, 48, 2665–2672. [Google Scholar] [CrossRef] [PubMed]
- Marcos, S.; Savushkin, L.N.; Fomenko, V.N.; López-Quelle, M.; Niembro, R. Description of nuclear systems within the relativistic Hartree-Fock method with zero-range self-interactions of the scalar field. J. Phys. G Nucl. Part. Phys. 2004, 30, 703. [Google Scholar] [CrossRef][Green Version]
- Long, W.H.; Van Giai, N.; Meng, J. Density-dependent relativistic Hartree-Fock approach. Phys. Lett. B 2006, 640, 150–154. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Viñas, X.; Centelles, M.; Ring, P.; Schuck, P. Relativistic mean-field interaction with density-dependent meson-nucleon vertices based on microscopical calculations. Phys. Rev. C 2011, 84, 054309. [Google Scholar] [CrossRef]
- Sammarruca, F.; Chen, B.; Coraggio, L.; Itaco, N.; Machleidt, R. Dirac-Brueckner-Hartree-Fock versus chiral effective field theory. Phys. Rev. C 2012, 86, 054317. [Google Scholar] [CrossRef]
- Zuo, W.; Lejeune, A.; Lombardo, U.; Mathiot, J.F. Interplay of three-body interactions in the EOS of nuclear matter. Nucl. Phys. A 2002, 706, 418–430. [Google Scholar] [CrossRef]
- Shen, S.; Liang, H.; Meng, J.; Ring, P.; Zhang, S. Spin symmetry in the Dirac sea derived from the bare nucleon-nucleon interaction. Phys. Lett. B 2018, 781, 227–231. [Google Scholar] [CrossRef]
- Shen, S.; Liang, H.; Meng, J.; Ring, P.; Zhang, S. Effects of tensor forces in nuclear spin-orbit splittings from ab initio calculations. Phys. Lett. B 2018, 778, 344–348. [Google Scholar] [CrossRef]
- Shen, S.; Liang, H.; Meng, J.; Ring, P.; Zhang, S. Relativistic Brueckner-Hartree-Fock theory for neutron drops. Phys. Rev. C 2018, 97, 054312. [Google Scholar] [CrossRef]
- Lu, J.X.; Wang, C.X.; Xiao, Y.; Geng, L.S.; Meng, J.; Ring, P. Accurate Relativistic Chiral Nucleon-Nucleon Interaction up to Next-to-Next-to-Leading Order. Phys. Rev. Lett. 2022, 128, 142002. [Google Scholar] [CrossRef]
- Geng, L.S.; Meng, J.; Hiroshi, T.; Long, W.H.; Shen, G. Spurious Shell Closures in the relativistic mean field model. Chin. Phys. Lett. 2006, 23, 1139. [Google Scholar]
- Erkelenz, K. Current status of the relativistic two-nucleon one boson exhcange potential. Phys. Rep. 1974, 13, 191–258. [Google Scholar] [CrossRef]
- Meng, J. Relativistic Density Functional for Nuclear Structure; International Review of Nuclear Physics Volume 10; World Scientific Publishing: Singapore, 2016. [Google Scholar]
- Geng, J.; Xiang, J.; Sun, B.Y.; Long, W.H. Relativistic Hartree-Fock model for axially deformed nuclei. Phys. Rev. C 2020, 101, 064302. [Google Scholar] [CrossRef]
- Long, W.H.; Geng, J.; Liu, J.; Wang, Z.H. Relativistic Hartree-Fock model and its recent progress on the description of nuclear structure. Commun. Theor. Phys. 2022, 74, 097301. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Bogoliubov, N.N. A variation principle in the problem of many bodies. Dokl. Akad. Nauk. SSSR 1958, 119, 244–246. [Google Scholar]
- Bogoliubov, N.N.; Soloview, V.G. On a Variational Principle in the Many Body Problem. Dokl. Akad. Nauk. SSSR 1959, 124, 1011–1014. [Google Scholar]
- Valatin, J.G. Generalized Hartree-Fock Method. Phys. Rev. 1961, 122, 1012–1020. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: New York, NY, USA, 1980. [Google Scholar]
- Tian, Y.; Ma, Z.; Ring, P. A finite range pairing force for density functional theory in superfluid nuclei. Phys. Lett. B 2009, 676, 44–50. [Google Scholar] [CrossRef]
- Geng, J.; Long, W.H. Relativistic Hartree-Fock-Bogoliubov model for axially deformed nuclei. Phys. Rev. C 2022, 105, 034329. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Nikšić, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Wei, B.; Zhao, Q.; Wang, Z.H.; Geng, J.; Sun, B.Y.; Niu, Y.F.; Long, W.H. Novel relativistic mean field Lagrangian guided by pseudo-spin symmetry restoration. Chin. Rhys. C 2020, 44, 074107. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Sun, M.D.; Liu, Z.; Huang, T.H.; Zhang, W.Q.; Wang, J.G.; Liu, X.Y.; Ding, B.; Gan, Z.G.; Ma, L.; Yang, H.B.; et al. New short-lived isotope 223Np and the absence of the Z = 92 subshell closure near N = 126. Phys. Lett. B 2017, 771, 303–308. [Google Scholar] [CrossRef]
- Grawe, H.; Langanke, K.; Martínez-Pinedo, G. Nuclear structure and astrophysics. Rep. Prog. Phys. 2007, 70, 1525. [Google Scholar] [CrossRef]
- Berger, J.; Girod, M.; Gogny, D. Microscopic analysis of collective dynamics in low energy fission. Nucl. Phys. A 1984, 428, 23–36. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nucl. Phys. A 1998, 635, 231–256. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Karatzikos, S.; Fossion, R.; Arteaga, D.P.; Afanasjev, A.; Ring, P. The effective force NL3 revisited. Phys. Lett. B 2009, 671, 36–41. [Google Scholar] [CrossRef]
- Chomaz, P.; Colonna, M.; Randrup, J. Nuclear spinodal fragmentation. Phys. Rep. 2004, 389, 263–440. [Google Scholar] [CrossRef]
- Das, C.; Gupta, S.D.; Lynch, W.; Mekjian, A.; Tsang, M. The thermodynamic model for nuclear multifragmentation. Phys. Rep. 2005, 406, 1–47. [Google Scholar] [CrossRef][Green Version]
- Brown, G.E.; Holt, J.W.; Lee, C.H.; Rho, M. Vector manifestation and matter formed in relativistic heavy-ion processes. Phys. Rep. 2007, 439, 161–191. [Google Scholar] [CrossRef][Green Version]
- Li, B.A.; Chen, L.W.; Ko, C.M. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rep. 2008, 464, 113–281. [Google Scholar] [CrossRef]
- Pethick, C.J. Cooling of neutron stars. Rev. Mod. Phys. 1992, 64, 1133–1140. [Google Scholar] [CrossRef]
- Prakash, M.; Bombaci, I.; Prakash, M.; Ellis, P.J.; Lattimer, J.M.; Knorren, R. Composition and structure of protoneutron stars. Phys. Rep. 1997, 280, 1–77. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The Physics of Neutron Stars. Science 2004, 304, 536–542. [Google Scholar] [CrossRef] [PubMed]
- Lattimer, J.M.; Prakash, M. The equation of state of hot, dense matter and neutron stars. Phys. Rep. 2016, 621, 127–164. [Google Scholar] [CrossRef]
- Aloy, M.A.; Ibáñez, J.M.; Sanchis-Gual, N.; Obergaulinger, M.; Font, J.A.; Serna, S.; Marquina, A. Neutron star collapse and gravitational waves with a non-convex equation of state. Mon. Not. R. Astron. Soc. 2019, 484, 4980–5008. [Google Scholar] [CrossRef]
- Müller, H.; Serot, B.D. Phase transitions in warm, asymmetric nuclear matter. Phys. Rev. C 1995, 52, 2072–2091. [Google Scholar] [CrossRef]
- Sharma, B.K.; Pal, S. Nuclear symmetry energy effects on liquid-gas phase transition in hot asymmetric nuclear matter. Phys. Rev. C 2010, 81, 064304. [Google Scholar] [CrossRef]
- Zhang, G.H.; Jiang, W.Z. Liquid-gas phase transition in hot asymmetric nuclear matter with density-dependent relativistic mean-field models. Phys. Lett. B 2013, 720, 148–152. [Google Scholar] [CrossRef]
- Fedoseew, A.; Lenske, H. Thermal properties of asymmetric nuclear matter. Phys. Rev. C 2015, 91, 034307. [Google Scholar] [CrossRef]
- Lourenço, O.; Dutra, M.; Menezes, D.P. Critical parameters of consistent relativistic mean-field models. Phys. Rev. C 2017, 95, 065212. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, B.N.; Sun, B.Y. Critical parameters of the liquid-gas phase transition in thermal symmetric and asymmetric nuclear matter. Phys. Rev. C 2019, 100, 054314. [Google Scholar] [CrossRef]
- Yang, S.; Sun, X.D.; Geng, J.; Sun, B.Y.; Long, W.H. Liquid-gas phase transition of thermal nuclear matter and the in-medium balance between nuclear attraction and repulsion. Phys. Rev. C 2021, 103, 014304. [Google Scholar] [CrossRef]
- Zhao, Q.; Ren, Z.; Zhao, P.; Meng, J. Covariant density functional theory with localized exchange terms. Phys. Rev. C 2022, 106, 034315. [Google Scholar] [CrossRef]
- Wang, M.; Audi, G.; Kondev, F.G.; Huang, W.J.; Naimi, S.; Xu, X. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2017, 41, 030003. [Google Scholar] [CrossRef]
- Zhao, P.W.; Li, Z.P.; Yao, J.M.; Meng, J. New parametrization for the nuclear covariant energy density functional with a point-coupling interaction. Phys. Rev. C 2010, 82, 054319. [Google Scholar] [CrossRef]
- Nikšić, T.; Vretenar, D.; Ring, P. Relativistic nuclear energy density functionals: Adjusting parameters to binding energies. Phys. Rev. C 2008, 78, 034318. [Google Scholar] [CrossRef]
- Meng, J.; Toki, H.; Zeng, J.Y.; Zhang, S.Q.; Zhou, S.G. Giant halo at the neutron drip line in Ca isotopes in relativistic continuum Hartree-Bogoliubov theory. Phys. Rev. C 2002, 65, 041302. [Google Scholar] [CrossRef]
- Delafosse, C.; Verney, D.; Marević, P.; Gottardo, A.; Michelagnoli, C.; Lemasson, A.; Goasduff, A.; Ljungvall, J.; Clément, E.; Korichi, A.; et al. Pseudospin Symmetry and Microscopic Origin of Shape Coexistence in the 78Ni Region: A Hint from Lifetime Measurements. Phys. Rev. Lett. 2018, 121, 192502. [Google Scholar] [CrossRef]
- Wilson, H.A. A Spherical Shell Nuclear Model. Phys. Rev. 1946, 69, 538. [Google Scholar] [CrossRef]
- Schwierz, N.; Wiedenhover, I.; Volya, A. Parameterization of the Woods-Saxon Potential for Shell-Model Calculations. arXiv 2007, arXiv:0709.3525. [Google Scholar]
- Isakov, V.; Erokhina, K.; Mach, H.; Sanchez-Vega, M.; Fogelberg, B. On the difference between proton and neutron spin-orbit splittings in nuclei. Eur. Phys. J. A 2002, 14, 29–36. [Google Scholar] [CrossRef]
- Oros, A.-M. Study of the Coupling between Collective and Single-Particle Excitation Modes in Medium Heavy Spherical Nuclei. Ph.D. Thesis, University of Köln, Köln, Germany, 1996. [Google Scholar]
- Mutschler, A.; Lemasson, A.; Sorlin, O.; Bazin, D.; Borcea, C.; Dombrádi, Z.; Ebran, J.P.; Gade, A.; Iwasaki, H.; Khan, E.; et al. A proton density bubble in the doubly magic 34Si nucleus. Nat. Phys. 2017, 13, 152–156. [Google Scholar] [CrossRef]
- Dechargé, J.; Berger, J.F.; Girod, M.; Dietrich, K. Bubbles and semi-bubbles as a new kind of superheavy nuclei. Nucl. Phys. A 2003, 716, 55–86. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).