The Scale-Invariant Vacuum Paradigm: Main Results and Current Progress Review (Part II) †
Abstract
1. Motivation
1.1. Scale Invariance and Physical Reality
1.2. Einstein General Relativity and Weyl Integrable Geometry
2. Mathematical Framework
2.1. Weyl Integrable Geometry and Dirac Co-Calculus
2.1.1. Gauge Change and (Co-)Covariant Derivatives
2.1.2. Dirac Co-Calculus
- where the usual Christoffel symbol is replaced by
2.2. Consequences of Going beyond the EGR
2.3. Scale-Invariant Cosmology
2.3.1. The Einstein Equation for Weyl’s Geometry
2.3.2. The Scale-Invariant Vacuum Gauge at and
3. Comparisons and Applications
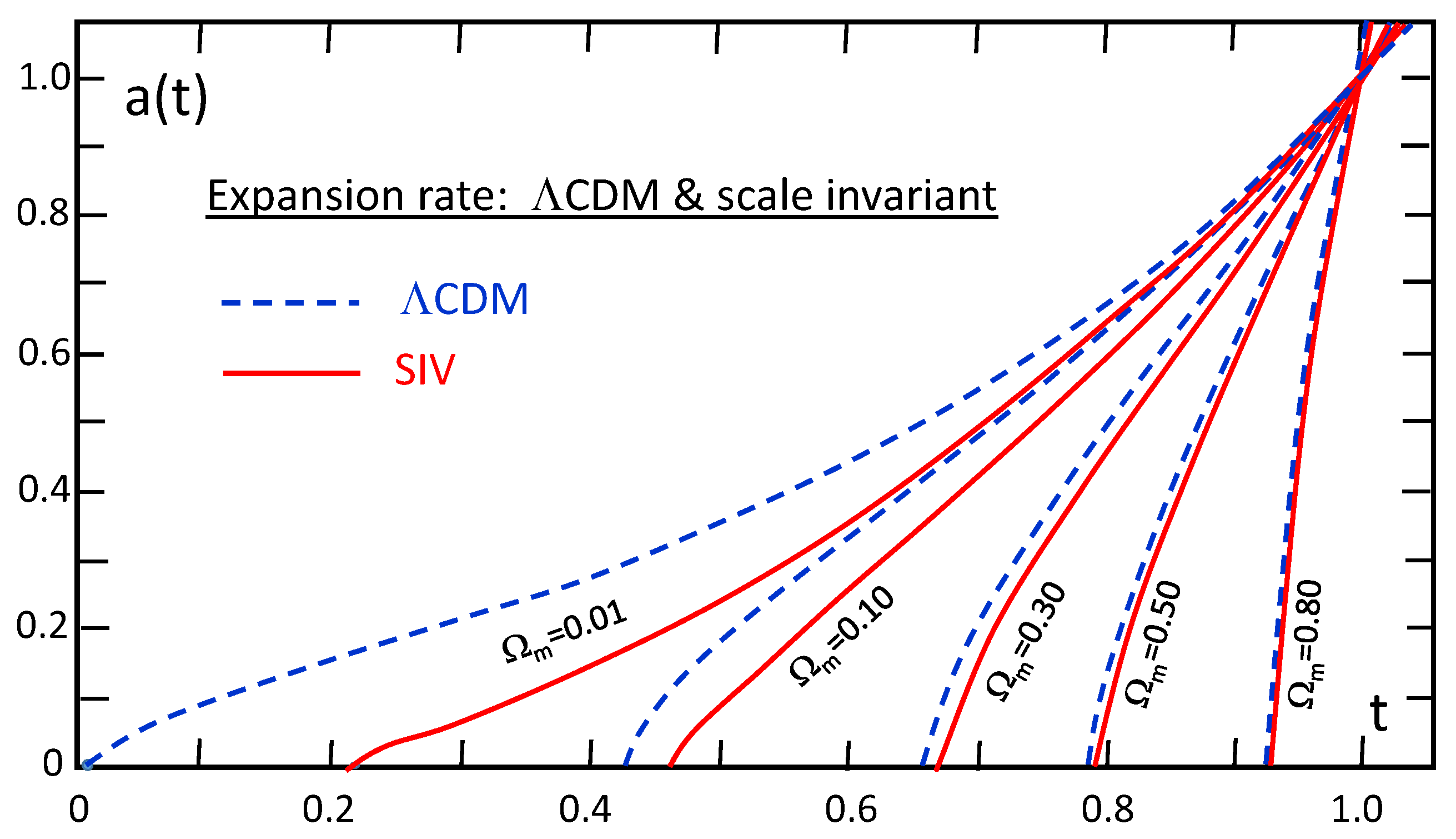
3.1. Comparing the Scale Factor within CDM and the SIV [2]
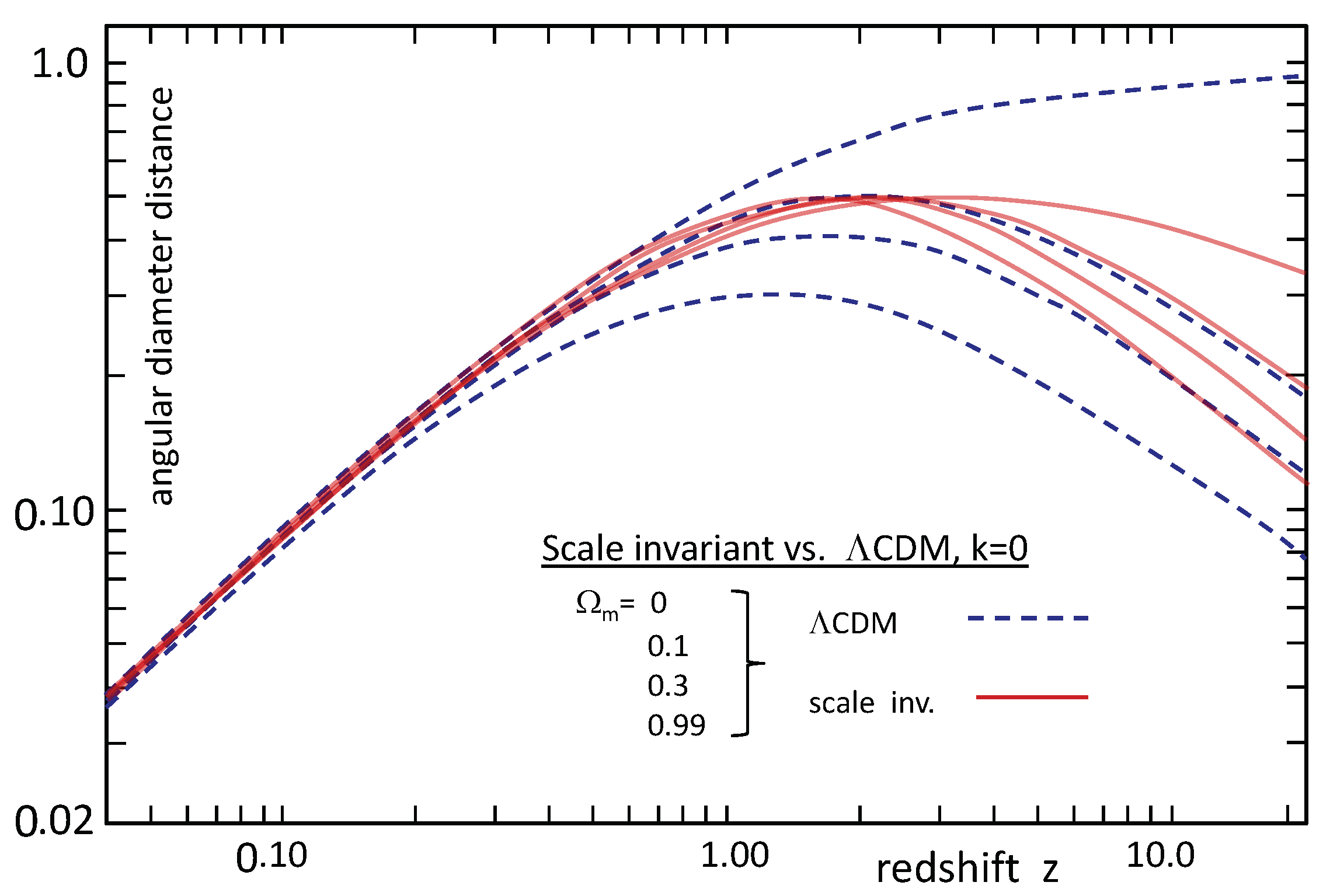
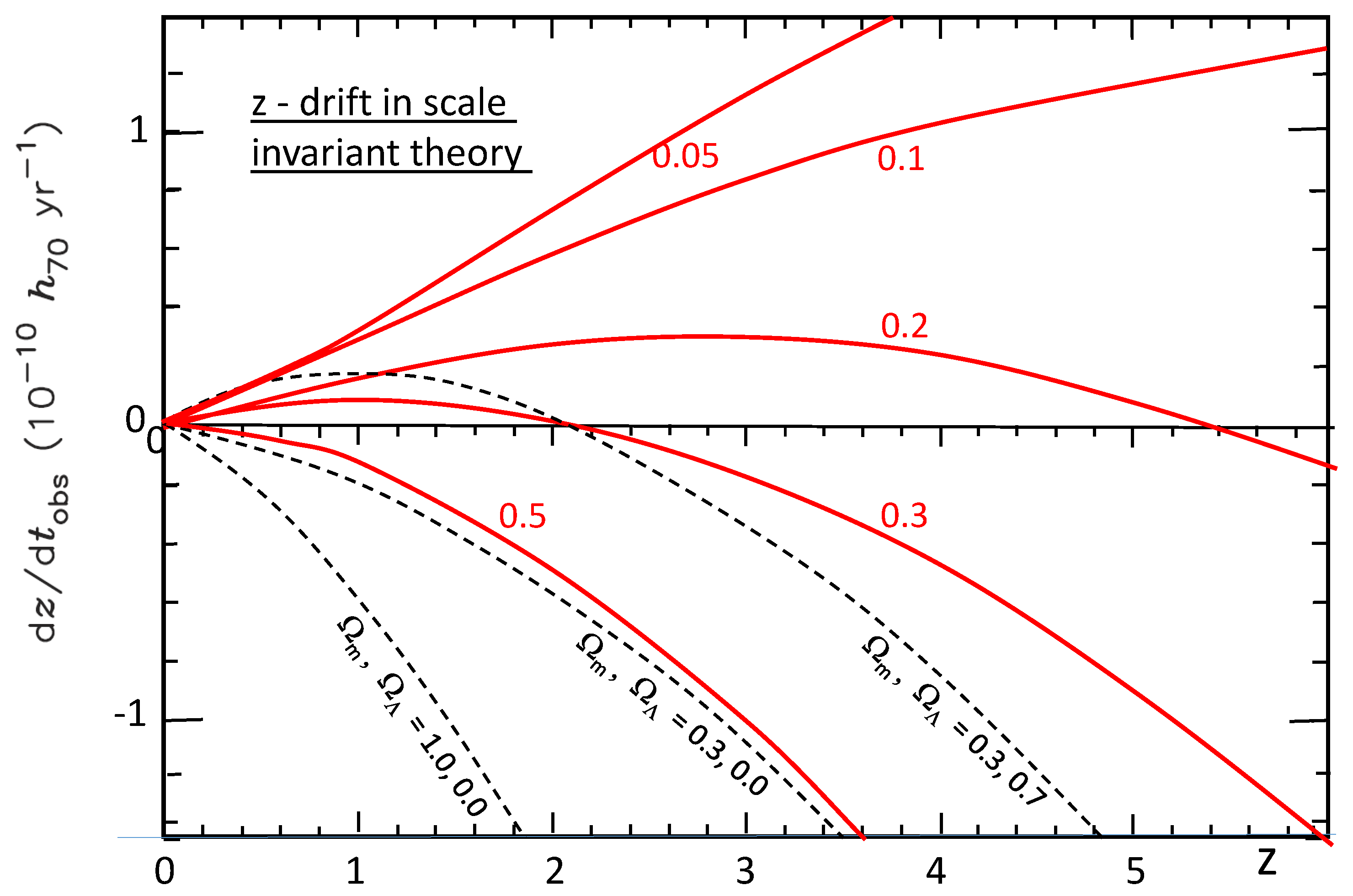
3.2. Possible Differentiators of the SIV from CDM [6]
3.3. Application to Scale-Invariant Dynamics of Galaxies [4]
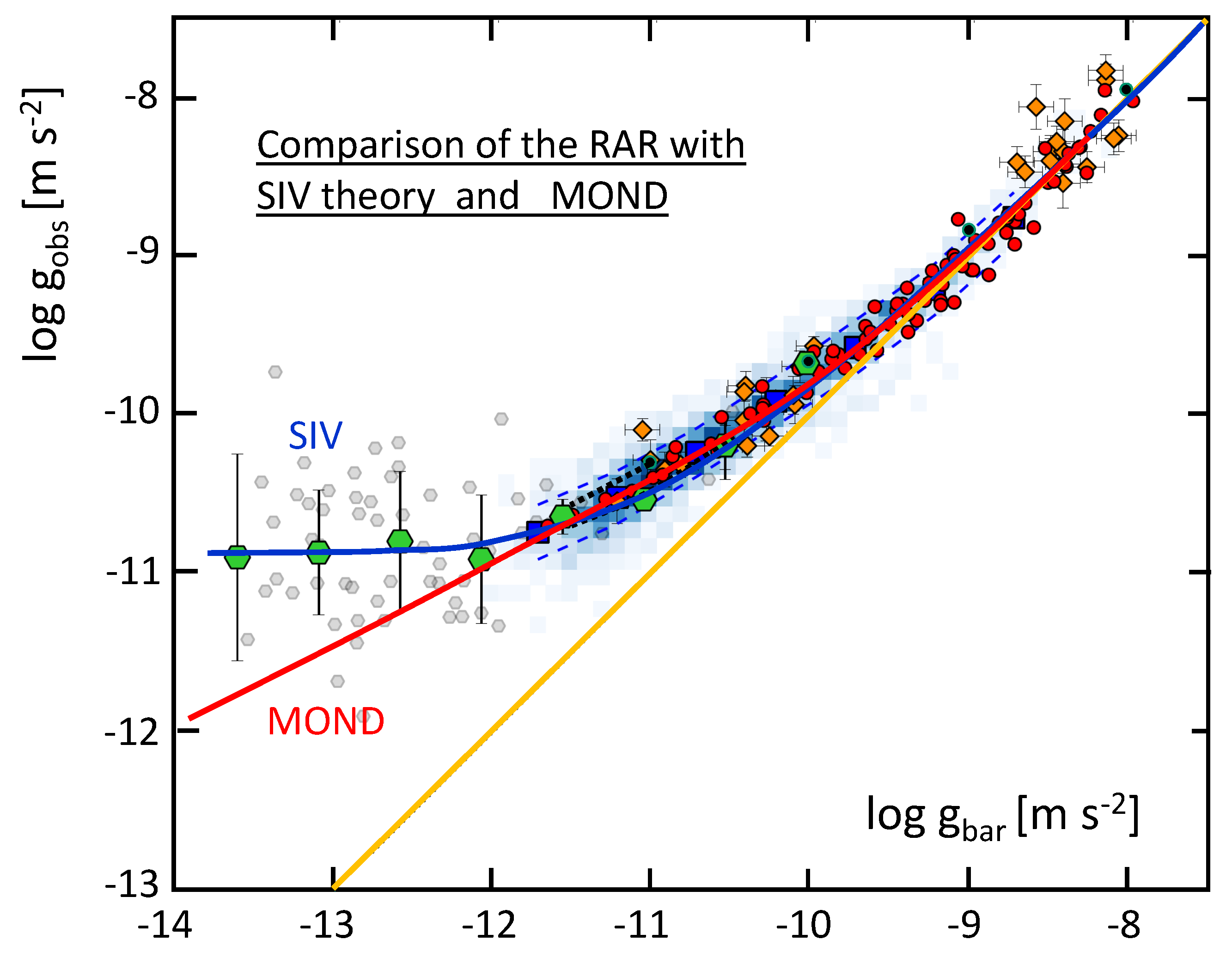
3.4. Mond as a Peculiar Case of the SIV Theory [34]
- “… as it comes out for the more general SIV theory, there are several remarks to be made on the -parameter and its meaning:
- 1.
- The equation of the deep-MOND limit is reproduced by the SIV theory both analytically and numerically if λ and M can be considered as constant. This may apply to systems with a typical dynamical timescale up to a few hundred million years.
- 2.
- Parameter is not a universal constant. It depends on the Hubble–Lemaître parameter (or the age of the universe) and on in the model universe, cf. Equation (35). The value of applies to the present epoch.
- 3.
- Parameter is defined by the condition that , i.e., when the dynamical gravity in the equation of motion (30) becomes larger than the Newtonian gravity. This situation occurs in regions at the edge of gravitational systems”.
3.5. Local Dynamical Effects within the SIV: The Lunar Recession [7]
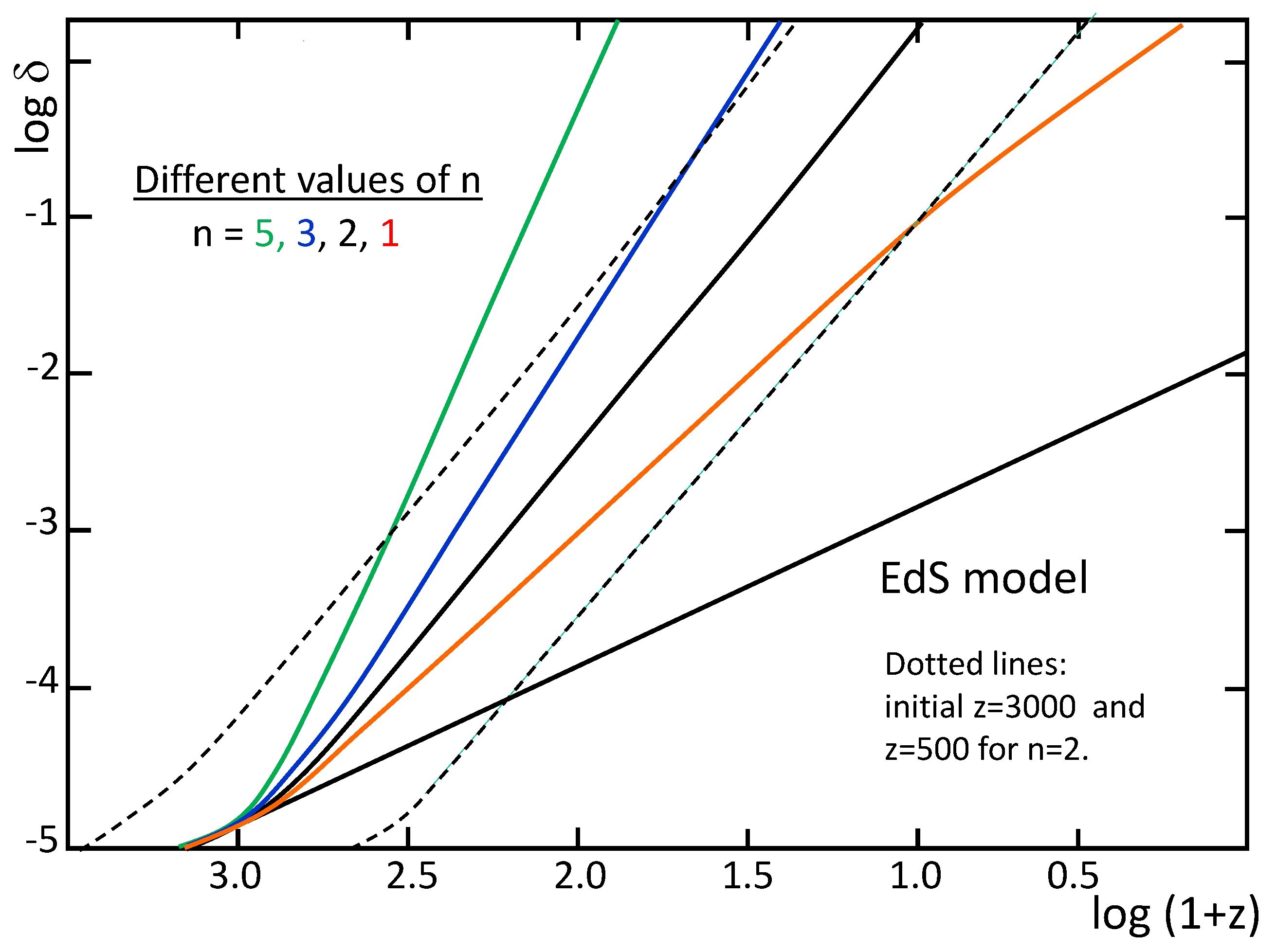
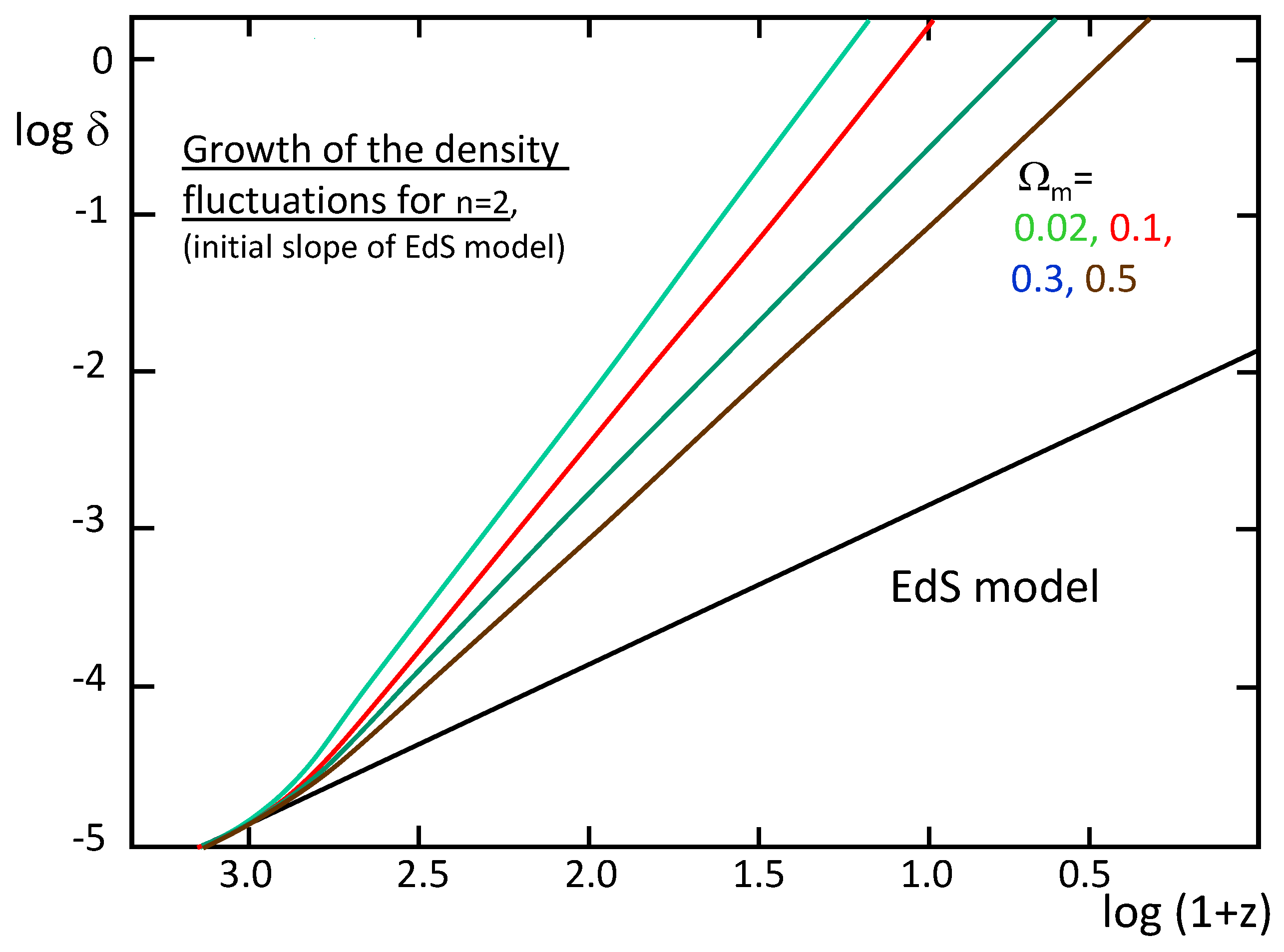
3.6. Growth of the Density Fluctuations within the SIV [3]
3.7. Big Bang Nucleosynthesis within the SIV Paradigm [8]
3.8. SIV and the Inflation of the Early Universe [5]
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. On the Error by Banik and Kroupa (2020) Concerning the Lunar Motion in the Scale-Invariant Theory
References
- Gueorguiev, V.G.; Maeder, A. The Scale Invariant Vacuum Paradigm: Main Results and Current Progress. Universe 2022, 8, 213. [Google Scholar] [CrossRef]
- Maeder, A. An Alternative to the ΛCDM Model: The Case of Scale Invariance. Apj 2017, 834, 194. [Google Scholar] [CrossRef]
- Maeder, A.; Gueorguiev, V.G. The growth of the density fluctuations in the scale-invariant vacuum theory. Phys. Dark Universe 2019, 25, 100315. [Google Scholar] [CrossRef]
- Maeder, A.; Gueorguiev, V.G. Scale-invariant dynamics of galaxies, MOND, dark matter, and the dwarf spheroidals. Mon. Not. R. Astron. Soc. 2020, 492, 2698–2708. [Google Scholar] [CrossRef]
- Maeder, A.; Gueorguiev, V.G. Scale invariance, horizons, and inflation. Mon. Not. R. Astron. Soc. 2021, 504, 4005–4014. [Google Scholar] [CrossRef]
- Maeder, A.; Gueorguiev, V.G. The Scale-Invariant Vacuum (SIV) Theory: A Possible Origin of Dark Matter and Dark Energy. Universe 2020, 6, 46. [Google Scholar] [CrossRef]
- Maeder, A.; Gueorguiev, V. Local Dynamical Effects of Scale Invariance: The Lunar Recession. arXiv 2022, arXiv:2204.13560. [Google Scholar] [CrossRef]
- Gueorguiev, V.G.; Maeder, A. Big-Bang Nucleosynthesis within the Scale Invariant Vacuum Paradigm. arXiv 2023, arXiv:2307.04269. [Google Scholar] [CrossRef]
- Maeder, A.; Gueorguiev, V.G. Action Principle for Scale Invariance and Applications (Part I). Symmetry 2023, 15, 1966. [Google Scholar] [CrossRef]
- Gueorguiev, V.G.; Maeder, A. Geometric Justification of the Fundamental Interaction Fields for the Classical Long-Range Forces. Symmetry 2021, 13, 379. [Google Scholar] [CrossRef]
- Weyl, H. Raum, Zeit, Materie. Vorlesungen über Allgemeine Relativitätstheorie; Springer: Berlin/Heidelberg, Germany, 1970. [Google Scholar]
- Brans, C.H. Jordan-Brans-Dicke Theory. Scholarpedia 2014, 9, 31358. [Google Scholar] [CrossRef]
- Faraoni, V.; Gunzig, E.; Nardone, P. Conformal transformations in classical gravitational theories and in cosmology. Fund. Cosmic Phys. 1999, 20, 121–175. [Google Scholar] [CrossRef]
- Behnke, D.; Blaschke, D.B.; Pervushin, V.N.; Proskurin, D. Description of supernova data in conformal cosmology without cosmological constant. Phys. Lett. B 2002, 530, 20–26. [Google Scholar] [CrossRef]
- Jackiw, R.; Pi, S.Y. Fake conformal symmetry in conformal cosmological models. Phys. Rev. D 2015, 91, 067501. [Google Scholar] [CrossRef]
- Tsamis, N.C.; Woodard, R.P. Gauge problems with the equations of motion. Class. Quantum Gravity 1985, 2, 841–867. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Kazanas, D. Varying-G gravity: Physical properties, asymptotic regimes, and Green’s functions, an event horizon, the vacuum energy density, and the external pressure that modifies Jeans stability. Mon. Not. R. Astron. Soc. 2023, 519, 1277–1292. [Google Scholar] [CrossRef]
- Xue, C.; Liu, J.P.; Li, Q.; Wu, J.F.; Yang, S.Q.; Liu, Q.; Shao, C.G.; Tu, L.C.; Hu, Z.K.; Luo, J. Precision measurement of the Newtonian gravitational constant. Natl. Sci. Rev. 2020, 7, 1803–1817. [Google Scholar] [CrossRef] [PubMed]
- Dirac, P.A.M. Long Range Forces and Broken Symmetries. Proc. R. Soc. Lond. Ser. A 1973, 333, 403–418. [Google Scholar] [CrossRef]
- Canuto, V.; Adams, P.J.; Hsieh, S.H.; Tsiang, E. Scale-covariant theory of gravitation and astrophysical applications. Phys. Rev. D 1977, 16, 1643–1663. [Google Scholar] [CrossRef]
- Gueorguiev, V.G.; Maeder, A. Reparametrization Invariance and Some of the Key Properties of Physical Systems. Symmetry 2021, 13, 522. [Google Scholar] [CrossRef]
- Wheeler, J.T. Weyl geometry. Gen. Relativ. Gravit. 2018, 50, 80. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Pervushin, V.N. Conformal Cosmological Model Parameters with Distant SNe ia Data: “gold” and “silver”. Int. J. Mod. Phys. D 2010, 19, 1875–1887. [Google Scholar] [CrossRef]
- Pervushin, V.N.; Arbuzov, A.B.; Zakharov, A.F. Estimation of conformal cosmological model parameters with SDSS and SNLS supernova samples. Phys. Part. Nucl. Lett. 2017, 14, 368–370. [Google Scholar] [CrossRef]
- Lee, S. Constraints on the time variation of the speed of light using Pantheon dataset. arXiv 2021, arXiv:2101.09862. [Google Scholar] [CrossRef]
- Gupta, R.P. Testing CCC+TL Cosmology with Observed Baryon Acoustic Oscillation Features. Astrophys. J. 2024, 964, 55. [Google Scholar] [CrossRef]
- Newell, D.B.; Tiesinga, E. The international system of units (SI). NIST Spec. Publ. 2019, 330, 1–138. [Google Scholar]
- Maeder, A.; Bouvier, P. Scale invariance, metrical connection and the motions of astronomical bodies. Astron. Astrophys. 1979, 73, 82–89. [Google Scholar]
- Bouvier, P.; Maeder, A. Consistency of Weyl’s Geometry as a Framework for Gravitation. Astrophys. Space Sci. 1978, 54, 497–508. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Cosmological Models and the Large Numbers Hypothesis. Proc. R. Soc. Lond. Ser. A 1974, 338, 439–446. [Google Scholar] [CrossRef]
- Gueorguiev, V.G.; Maeder, A. Revisiting the Cosmological Constant Problem within Quantum Cosmology. Universe 2020, 6, 108. [Google Scholar] [CrossRef]
- Jesus, J.F. Exact Solution for Flat Scale-Invariant Cosmology. arXiv 2017, arXiv:1712.00697. [Google Scholar] [CrossRef]
- Maeder, A. Evolution of the early Universe in the scale invariant theory. arXiv 2019, arXiv:1902.10115. [Google Scholar] [CrossRef]
- Maeder, A. MOND as a peculiar case of the SIV theory. Mon. Not. R. Astron. Soc. 2023, 520, 1447–1455. [Google Scholar] [CrossRef]
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark energy and the accelerating universe. Annu. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Lusso, E.; Piedipalumbo, E.; Risaliti, G.; Paolillo, M.; Bisogni, S.; Nardini, E.; Amati, L. Tension with the flat ΛCDM model from a high-redshift Hubble diagram of supernovae, quasars, and gamma-ray bursts. Astron. Astrophys. 2019, 628, L4. [Google Scholar] [CrossRef]
- Liske, J.; Grazian, A.; Vanzella, E.; Dessauges, M.; Viel, M.; Pasquini, L.; Haehnelt, M.; Cristiani, S.; Pepe, F.; Avila, G.; et al. Cosmic dynamics in the era of Extremely Large Telescopes. Mon. Not. R. Astron. Soc. 2008, 386, 1192–1218. [Google Scholar] [CrossRef]
- Skordis, C.; Złośnik, T. New Relativistic Theory for Modified Newtonian Dynamics. Phys. Rev. Lett. 2021, 127, 161302. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Capozziello, S.; de Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Del Popolo, A.; Chan, M.H. On the time dependency of a0. Phys. Dark Universe 2024, 43, 101415. [Google Scholar] [CrossRef]
- Milgrom, M. Cosmological variation of the MOND constant: Secular effects on galactic systems. Phys. Rev. D 2015, 91, 044009. [Google Scholar] [CrossRef]
- Feynman, R.P. Feynman Lectures on Physics; Addison-Wesley: Reading, MA, USA, 1963; Volume 1. [Google Scholar]
- Williams, J.G.; Boggs, D.H.; Ratcliff, J.T. Lunar Tidal Recession. In Proceedings of the 47th Annual Lunar and Planetary Science Conference, Woodlands, TX, USA, 21–25 March 2016; p. 1096. [Google Scholar]
- Williams, J.G.; Boggs, D.H. Secular tidal changes in lunar orbit and Earth rotation. Celest. Mech. Dyn. Astron. 2016, 126, 89–129. [Google Scholar] [CrossRef]
- Christodoulidis, D.C.; Smith, D.E.; Williamson, R.G.; Klosko, S.M. Observed Tidal Braking in the Earth/moon/sun System. J. Geophys. Res. 1988, 93, 6216–6236. [Google Scholar] [CrossRef]
- Stephenson, F.R.; Morrison, L.V.; Hohenkerk, C.Y. Measurement of the Earth’s rotation: 720 BC to AD 2015. Proc. R. Soc. Lond. Ser. A 2016, 472, 20160404. [Google Scholar] [CrossRef]
- Deines, S.D.; Williams, C.A. Earth’s Rotational Deceleration: Determination of Tidal Friction Independent of Timescales. Astron. J. 2016, 151, 103. [Google Scholar] [CrossRef]
- Stephenson, F.R.; Morrison, L.V.; Hohenkerk, C.Y. Eclipses and the Earth’s Rotation. In Proceedings of the IAU General Assembly; Cambridge University Press: Cambridge, UK, 2020; pp. 160–162. [Google Scholar] [CrossRef]
- McCarthy, D.D.; Babcock, A.K. The length of day since 1656. Phys. Earth Planet. Inter. 1986, 44, 281–292. [Google Scholar] [CrossRef]
- Sidorenkov, N.S. The effect of the El Nino Southern oscillation on the excitation of the Chandler motion of the Earth’s pole. Astron. Rep. 1997, 41, 705–708. [Google Scholar]
- Williams, J.G. Contribution to the Earth’s Obliquity Rate, Precession, and Nutation. Astron. J. 1994, 108, 711. [Google Scholar] [CrossRef]
- Maeder, A.M.; Gueorguiev, V.G. On the relation of the lunar recession and the length-of-the-day. Astrophys. Space Sci. 2021, 366, 101. [Google Scholar] [CrossRef]
- Bunker, A.J.; Saxena, A.; Cameron, A.J.; Willott, C.J.; Curtis-Lake, E.; Jakobsen, P.; Carniani, S.; Smit, R.; Maiolino, R.; Witstok, J.; et al. JADES NIRSpec Spectroscopy of GN-z11: Lyman-α emission and possible enhanced nitrogen abundance in a z = 10.60 luminous galaxy. Astron. Astrophys. 2023, 677, A88. [Google Scholar] [CrossRef]
- Pitrou, C.; Coc, A.; Uzan, J.P.; Vangioni, E. Precision big bang nucleosynthesis with improved Helium-4 predictions. Phys. Rep. 2018, 754, 1–66. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A. Lectures on inflationary cosmology. arXiv 1995, arXiv:hep-th/9410082. [Google Scholar] [CrossRef]
- Linde, A. Particle Physics and Inflationary Cosmology. arXiv 2005, arXiv:hep-th/0503203. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Skordis, C.; Mota, D.F.; Ferreira, P.G.; Bœhm, C. Large Scale Structure in Bekenstein’s Theory of Relativistic Modified Newtonian Dynamics. Phys. Rev. Lett. 2006, 96, 011301. [Google Scholar] [CrossRef]

| Co-Tensor Type | Mathematical Expression |
|---|---|
| co-scalar | , |
| co-vector | , |
| co-covector | . |
| Element | Obs. | PRMT | fit | fit* | fit* | fit | ||
|---|---|---|---|---|---|---|---|---|
| H | 0.755 | 0.753 | 0.805 | 0.755 | 0.849 | 0.75 | 0.753 | 0.755 |
| 0.245 | 0.247 | 0.195 | 0.245 | 0.151 | 0.25 | 0.247 | 0.245 | |
| 2.53 | 2.43 | 0.743 | 2.52 | 2.52 | 1.49 | 2.52 | 2.53 | |
| 3He/H × 105 | 1.1 | 1.04 | 0.745 | 1.05 | 0.825 | 0.884 | 1.05 | 1.04 |
| 7Li/H × 1010 | 1.58 | 5.56 | 11.9 | 5.24 | 6.97 | 9.65 | 5.31 | 5.42 |
| 3.01 | 3.01 | 3.01 | 3.01 | 3.01 | 3.01 | 3.01 | 3.01 | |
| 6.09 | 6.14 | 6.14 | 1.99 | 0.77 | 1.99 | 5.57 | 5.56 | |
| FRF | 1 | 1 | 1 | 1 | 1.63 | 1 | 1 | 1.02 |
| mŤ | 1 | 1 | 1 | 1 | 0.78 | 1 | 1 | 0.99 |
| Q/Ť | 1 | 1 | 1 | 1 | 1.28 | 1 | 1 | 1.01 |
| [%] | 4.9 | 4.9 | 4.9 | 1.6 | 0.6 | 1.6 | 4.4 | 4.4 |
| [%] | 31 | 31 | 31 | 5.9 | 23 | 5.9 | 86 | 95 |
| N/A | 6.84 | 34.9 | 6.11 | 14.8 | 21.9 | 6.2 | 6.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gueorguiev, V.G.; Maeder, A. The Scale-Invariant Vacuum Paradigm: Main Results and Current Progress Review (Part II). Symmetry 2024, 16, 657. https://doi.org/10.3390/sym16060657
Gueorguiev VG, Maeder A. The Scale-Invariant Vacuum Paradigm: Main Results and Current Progress Review (Part II). Symmetry. 2024; 16(6):657. https://doi.org/10.3390/sym16060657
Chicago/Turabian StyleGueorguiev, Vesselin G., and Andre Maeder. 2024. "The Scale-Invariant Vacuum Paradigm: Main Results and Current Progress Review (Part II)" Symmetry 16, no. 6: 657. https://doi.org/10.3390/sym16060657
APA StyleGueorguiev, V. G., & Maeder, A. (2024). The Scale-Invariant Vacuum Paradigm: Main Results and Current Progress Review (Part II). Symmetry, 16(6), 657. https://doi.org/10.3390/sym16060657







