Abstract
The Levenberg–Marquardt (LM) method is one of the most significant methods for solving nonlinear equations as well as symmetric and asymmetric linear equations. To improve the method, this paper proposes a new adaptive LM algorithm by modifying the LM parameter, combining the trust region technique and the non-monotone technique. It is interesting that the new algorithm is constantly optimized by adaptively choosing the LM parameter. To evaluate the effectiveness of the new algorithm, we conduct tests using various examples. To extend the convergence results, we prove the convergence of the new algorithm under the Hölderian local error bound condition rather than the commonly used local error bound condition. Theoretical analysis and numerical results show that the new algorithm is stable and effective.
1. Introduction
Nonlinear equations are widely used in key fields such as electricity, optics, mechanics, economic management, engineering technology, biomedicine, and alternative energy [1,2,3,4,5,6]. This paper discusses the following nonlinear equations:
which can be written in a vector form:
where is continuously differentiable and . We denote the solution set of Equation (1) by and assume that is nonempty.
Several promising numerical methods [7,8,9,10,11] have been proposed for solving nonlinear equations. One of the classical methods to solve Equation (1) is the Gauss–Newton method, which at each iteration computes the trial step
where , is the Jacobian matrix of at .
However, in the actual calculation, the trial step of the Gauss–Newton method may not be well defined when is singular or near-singular. To overcome this difficulty, the Levenberg–Marquardt(LM) method [10,11] was proposed. At the kth iteration, the LM method computes the trial step
where is the LM parameter and is the identity matrix. The trial step of the LM method is actually a modification of the trial step of the Gauss–Newton method, where the parameter is introduced to prevent the steps from being undefined or too large when is singular or nearly singular.
The LM method has quadratic convergence when is Lipschitz continuous and nonsingular at the solution of Equation (1) [12]. Nevertheless, the theoretical research shows that the condition of the nonsingularity of is too strong. To solve this problem, some scholars [13,14,15,16,17,18,19] have analysed the convergence of the LM method under the following local error bound condition, which is weaker than nonsingularity of :
where is a positive constant, is the distance from x to , and is some neighbourhood of . In this paper, is the 2-norm.
Although the local error bound condition is weaker than the nonsingularity of , this condition is not always satisfied with some ill-conditioned nonlinear equations in biochemical systems and certain applications. Recently, some scholars [20,21,22,23] have studied the convergence of LM method under the following Hölderian error bound condition, which is weaker than the local error bound condition:
where c is a positive constant and . Obviously, the Hölderian error bound condition (4) is a generalization of the local error bound condition (3), where the exponent of is extended to an interval . In this paper, we study the convergence of the new algorithm under the Hölderian error bound condition.
The LM parameter is vital to the efficiency of LM algorithms. Several scholars have done interesting research [13,14,15,16,17,18,19,21,22,23] on . Yamashita and Fukushima [13] took , although the disadvantage of choosing parameters in this way is that the value of may be too small to be effective when the sequence is close to the solution set of Equation (1), which affects the local convergence rate. In order to solve this disadvantage and reduce the impact, Fan and Yuan [14] chose , which is a generalization of , and extended the exponent of to an interval . The numerical results when solving some equations showed better performance when ; however, the disadvantage of choosing parameters in this way is that it may make too large and step too small when is far away from the solution set, causing the sequence to move slowly to the solution set and affecting the global convergence rate. To compensate for this flaw, Fan [17] used , where is updated every iteration by the trust region technique. Numerical results showed that this change improved the performance of the algorithm. Chen and Ma [23] took for and , finding that this improved the numerical results of the LM algorithm. Recently, Li et al. [24] proposed a new adaptive accelerated LM algorithm by choosing the LM parameter as , with numerical results showing that the algorithm is efficient for solving symmetric and asymmetric linear equations.
Inspired by the above literature, we take a new adaptive LM parameter to enhance the computing performance of the LM algorithm, as follows:
where is updated every iteration via trust region technology. When is close to a solution set, is close to 0; thus, is close to if , as used in [17]. Conversely, when is far from the solution set, the leading may be very large; thus, will be close to . This effectively regulates the range of to prevent the LM step from becoming excessively small, thereby enhancing computational efficiency. Therefore, it seems that this choice of is more effective for the LM algorithm.
The following sections outline the remaining contents of this paper. In Section 2, we propose a new algorithm with a new LM parameter in more detail and prove its global convergence. In Section 3, we analyse the convergence rate of the new algorithm. In Section 4, we present numerical results verifying that the new algorithm is effective. Finally, some key conclusions are put forward in Section 5.
2. The New Adaptive LM Algorithm and Its Global Convergence
In this section, we introduce our new adaptive algorithm and establish its global convergence.
If we define the merit function for Equation (1) as
then, at the kth iteration, the actual reduction of is provided by
and the predicted reduction of by
where is computed by Equation (2). The ratio of to is
which determines whether to accept and update . Several studies have suggested that algorithms employing non-monotone strategies outperform those with monotone strategies [18,25,26,27,28]. To carry out the non-monotone strategy, Amini et al. [18] used the following actual reduction to replace Equation (5):
where
, and is a positive integer constant. With this change, is compared with at each iteration. To combine the non-monotone strategy with the new adaptive LM parameter, we use the following ratio:
to replace the original role of the ratio in the algorithm.
Next, we present a new adaptive LM algorithm, named the ALLM algorithm (Algorithm 1).
| Algorithm 1 (ALLM Algorithm) |
| Step 1. Given , . Set . Step 2. If , stop. Otherwise let Step 3. Compute Step 4. Compute , and by Equations (9), (6) and (8). Set Step 5. Set Step 6. Choose as Step 7. Set and return to Step 2. |
To prevent excessively large steps, we impose the following condition:
where m is a positive constant.
Lemma 1.
for all .
Proof.
This proof comes from famous result in [29]. □
Lemma 2
([18]). Assume that sequence is generated by the ALLM algorithm; then, the sequence converges.
Assumption 1.
(a) is Hölderian continuous, i.e., there exists a constant such that
where the exponent .
(b) is bounded, i.e., there exists a constant such that
It follows from Equation (16) that
Thus, there exists a constant that makes
Theorem 1.
Under Assumption 1, the ALLM algorithm satisfies
Proof.
Assuming that Theorem 1 is not true, we obtain
where is a positive constant and .
If is accepted by the ALLM algorithm, then
Per Lemma 1, Equations (17) and (21) indicate that, for all ,
Then, substituting k for ,
holds for all sufficiently large k.
Per Lemma 1, we obtain
thus,
as is a positive constant, meaning that
Per Equation (19), the last equality implies that
Next, by considering the proof process of Theorem 2.4 in [18], we can prove that
Along with Equations (10), (11), (17) and (21), this implies that
Next, per Equation (18), we obtain
which yields
From Lemma 1 and Equations (17), (21), (22) and , we obtain
thus,
Combined with Equations (6), (8), (9) and (12), we obtain
In view of the ALLM algorithm, for all large k there exists a positive constant that makes , which contradicts Equation (23). Thus, Theorem 1 holds. □
3. Convergence Rate
This section discusses the convergence rate of the ALLM algorithm. Here, we let generated by ALLM algorithm lie within a neighborhood of and converge to the solution set of Equation (1).
Assumption 2.
(a) provides a Hölderian local error bound, i.e., there exist constants and that make
where the exponent , .
(b) is Hölderian continuous, i.e., there exists a constant such that
where the exponent .
Defining by satisfies
which implies that is closest to .
Next, we discuss the important property of and ; finally, we study the convergence rate of the ALLM algorithm using the singular value decomposition (SVD) technique. Without loss of generality, we assume that .
Lemma 3.
Under Assumption 2, we have
(1) If ; then, the following relationship holds:
where is a positive constant.
(2) If , then the following relationship holds:
where is a positive constant.
Proof.
(1) As , we have
thus, .
We define
It can be concluded from (11) that is the minimizer of . From (26) and , we have
If , then and . In conjunction with (15) and (24), this yields
Thus,
Setting , we obtain Equation .
(2) If , then and . Along with (19), this allows us to conclude that
Thus, there exists a constant such that
Therefore, . □
Lemma 4.
Under Assumption 2, we have the following:
(1) If , then is bounded above, i.e., there exists a positive constant such that holds for all large k.
(2) If then is bounded above, i.e., there exists a positive constant such that holds for all large k.
Proof.
(1) Considering Lemma 3.3 in [21], we can see that
thus,
This, along with Equations (6), (8), (9), and (12), yields
Considering the updating rule from (14), we can ascertain the existence of a positive constant , ensuring that holds for sufficiently large k.
(2) Consider the following two cases.
Case 1: . Per Lemma 3 (2), Equations (24), (26) and , we have
which holds for some , .
Case 2: . It follows from Equation (30) that
holds for some .
Therefore, from Equations (30) and (31), we have
which holds for some .
Because , from Equations (26) and (32) we have
thus,
This, along with Equations (6), (8), (9) and (12), yields
Therefore, there exists a positive constant such that holds for sufficiently large k. □
Next, we consider SVD technology. In view of the findings provided by Behling and Iusem in [30], without loss of generality, we set for all . Suppose that the SVD of is
where .
Correspondingly,
where .
For clearness, we let
which neglects the subscription k in , and .
Lemma 5
([21]). Under Assumption 2, the following relationship holds:
(1)
(2) .
Theorem 2.
Under the conditions of Lemma 3, we have the following:
(1) If , then the generated by the ALLM algorithm converges to the solution set of Equation (1) with order .
(2) If , then the generated by the ALLM algorithm converges to the solution set of Equation (1) with order γ.
Proof.
(1) It follows from the SVD of that
and
According to the theory of matrix perturbation [31] and Equation (25), we have
which indicates
As converges to , without loss of generality, we let hold for all large k. From Equation (34), we have
From Equations (34), (35), Lemma 5, and , we have
If , then , while from Equation (27) and Lemma 4 we have
This, along with Equation (36), yields
Letting , from Equations (24), (26), (28) and (37) we obtain
Thus,
which indicates that converges to the solution set of Equation (1) with convergence rate .
(2) The proof of is similar to the proof of . We obtain
thus, converges to the solution set of Equation (1) with order . □
Theorem 3.
Under Assumption 2, we have the following:
(1) If , , then generated by the ALLM algorithm converges to some solution of Equation (1) with order .
(2) If , then generated by the ALLM algorithm converges to some solution of Equation (1) with order γ.
Proof.
(1) If and , then from Equation (28) we obtain
It follows from and that
and
Therefore, the conditions of Lemma 4 (1) hold. In conjunction with and , this yields
Thus, converges superlinearly to .
For clearness,
In view of Equations (38) and (40), we know the existence of a constant , meaning that
holds for large k. Thus, from Equations (38), (39), (40), and (42), we have
which means that the ALLM algorithm converges with order .
(2) The proof of is similar to the proof of . We obtain
thus, ALLM algorithm converges with order . □
4. Numerical Experiments
In this section, we verify the effectiveness of the ALLM algorithm by presenting some numerical experiments. Algorithm 1 (named the AELM algorithm) from [22] is used for comparison. All algorithms were tested in the MATLAB R2022b programming environment on a personal PC with an i7-7500U CPU and 2.7 GHz. We selected the parameters of the AELM algorithm as follows: , . We selected the parameters of the ALLM algorithm as follows: All algorithms were terminated when or when the number of iterations surpassed 1000.
Example 1.
We consider four special functions [22] to verify that the ALLM algorithm satisfies more theoretical applications. Functions 1–4 satisfy the Hölderian local error bound condition around the zero point but do not satisfy the local error bound condition. Here, the for Functions 3–4 are Hölderian continuous but not Lipschitz continuous, while the for Functions 1–2 are both Lipschitz continuous and Hölderian continuous.
Function 1
Initial point: , zero point: .
Function 2
Initial point: , zero point: .
Function 3
Initial point: , zero point: .
Function 4
Initial point: , zero point: .
We tested each function for three starting points, and , to study the global convergence of the ALLM algorithm. Table 1 lists the numerical results achieved by the AELM and ALLM algorithms on the four test functions. The symbols in Table 1 have the following meanings:
- NF: The number of function calculations.
- NJ: The number of Jacobian calculations.
- NT: We generally use the ‘’ to indicate the total computations.

Table 1.
Numerical results of the AELM and ALLM algorithms with various choices of and .
Table 1.
Numerical results of the AELM and ALLM algorithms with various choices of and .
| AELM | ALLM | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Function | |||||||||
| NF/NJ/NT | NF/NJ/NT | NF/NJ/NT | NF/NJ/NT | NF/NJ/NT | NF/NJ/NT | NF/NJ/NT | |||
| 1 | 4 | 1 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 |
| 10 | 13/13/65 | 13/13/65 | 13/13/65 | 13/13/65 | 13/13/65 | 13/13/65 | 13/13/65 | ||
| 100 | 16/16/80 | 16/16/80 | 16/16/80 | 16/16/80 | 16/16/80 | 16/16/80 | 16/16/80 | ||
| 2 | 2 | 1 | 8/8/24 | 8/8/24 | 8/8/24 | 8/8/24 | 8/8/24 | 8/8/24 | 8/8/24 |
| 10 | 11/11/33 | 11/11/33 | 11/11/33 | 11/11/33 | 11/11/33 | 11/11/33 | 11/11/33 | ||
| 100 | 15/15/45 | 15/15/45 | 15/15/45 | 15/15/45 | 15/15/45 | 15/15/45 | 15/15/45 | ||
| 3 | 4 | 1 | 8/8/40 | 8/8/40 | 8/8/40 | 8/8/40 | 8/8/40 | 8/8/40 | 8/8/40 |
| 10 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | 10/10/50 | ||
| 100 | 12/12/60 | 12/12/60 | 12/12/60 | 12/12/60 | 12/12/60 | 12/12/60 | 12/12/60 | ||
| 4 | 4 | 1 | 13/13/65 | 7/7/35 | 7/7/35 | 7/7/35 | 7/7/35 | 7/7/35 | 7/7/35 |
| 10 | 16/16/80 | 9/9/45 | 9/9/45 | 9/9/45 | 9/9/45 | 9/9/45 | 9/9/45 | ||
| 100 | 61/50/261 | 11/11/55 | 11/11/55 | 11/11/55 | 11/11/55 | 11/11/55 | 11/11/55 |
As can be seen from Table 1, the ALLM algorithm is obviously superior to the AELM algorithm for the numerical results of Function 4, while the two algorithms are the same for the numerical results of Functions 1–3.
Example 2.
We consider some singular problems which are created by the following form [32]:
where the test function is provided by Moré, Garbow, and Hillstrom in [33], is the root of , and has full column rank. It is clear that the Jacobian of is
with rank and . Similar to [33], we choose
which implies .
Next, we ran all test problems for three starting points: , and , where derives from [33]. Table 2 and Table 3 display the numerical results achieved by the algorithms for all test functions. The meanings of the symbols in Table 2 and Table 3 are as follows:
- Iter: Number of iterations.
- F: Final value of the norm of the function.
- Time: CPU time in seconds.
From Table 2 and Table 3, it is evident that the ALLM algorithm generally outperforms the AELM algorithm in terms of CPU time across most test functions. Compared with the AELM algorithm, the performance of the ALLM algorithm exhibits superior performance when and , dominating approximately 90% of the CPU time results; about of the results of iterations of the two algorithms are the same. In particular, for certain test functions it can be seen that the ALLM algorithm consistently outperforms the AELM algorithm in terms of both iteration count and CPU time when the initial point is distant from the solution set. From Table 2, for the extended helical valley function, when and the initial point is , the number of iterations and the CPU time of the ALLM algorithm are better than those of the AELM algorithm. From Table 3, for the discrete boundary value function, when and the initial point is or or or or , the number of iterations and CPU time of the ALLM algorithm are better than those of the AELM algorithm.
To compare the numerical performance profile of the AELM and ALLM algorithms, we chose the performance analysis method proposed by Dolan [34]. As can be seen from Figure 1, when and , the ALLM algorithm demonstrates the best performance in terms of iteration count, while when and , the performance in terms of the number of iterations for both algorithms. As can be seen from Figure 2, when and , the CPU time of the ALLM algorithm has the best performance, while when and take other values the ALLM algorithm maintains advantages in CPU time performance.
In general, the ALLM algorithm proves more effective in solving nonlinear equations compared to the AELM algorithm. In particular, when is larger and is smaller, the ALLM algorithm demonstrates superior performance. According to the needs of practical applications, the selection of is continuously optimized by changing the values of and .


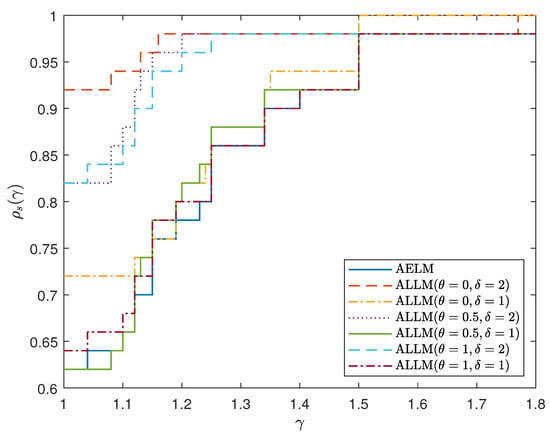
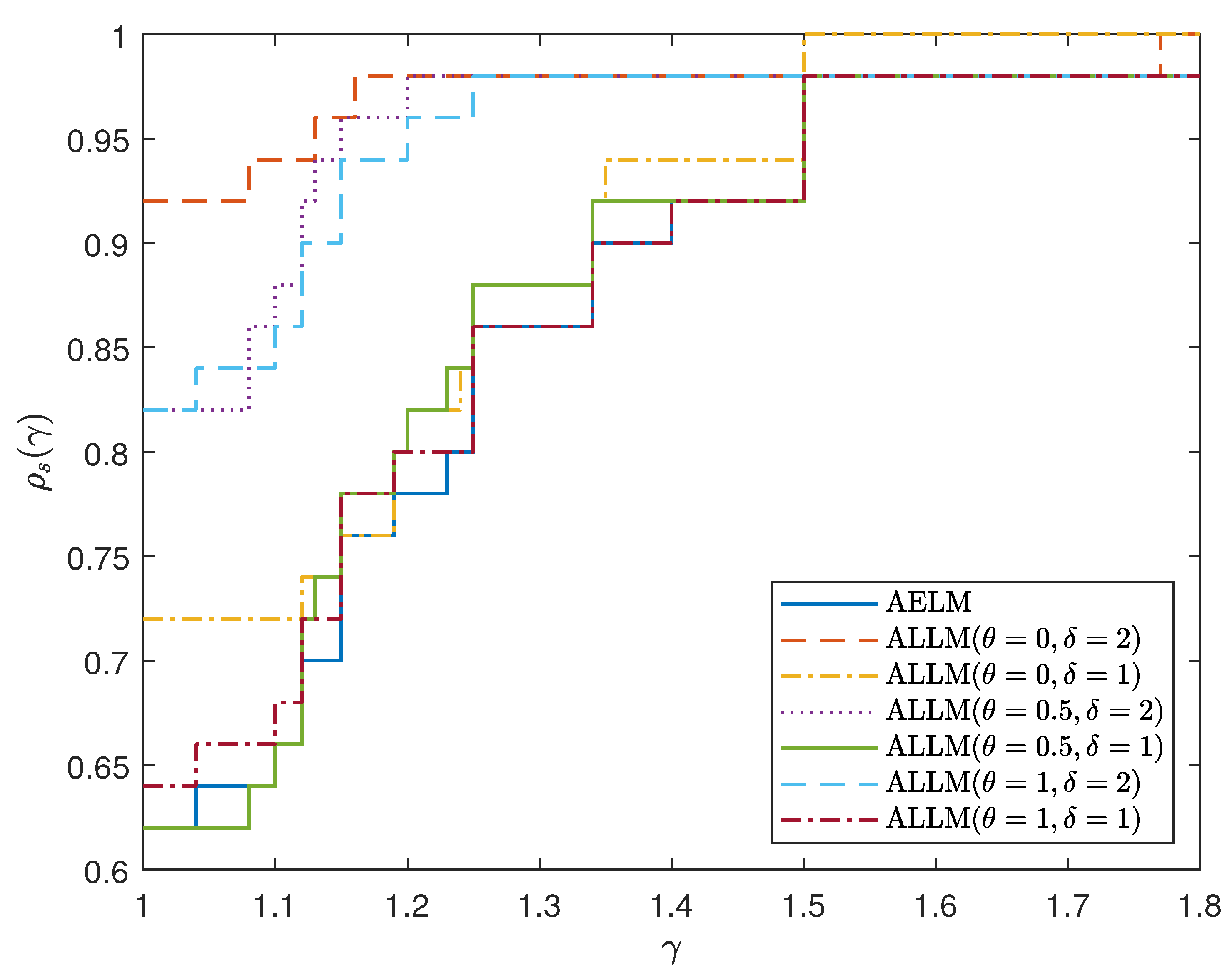
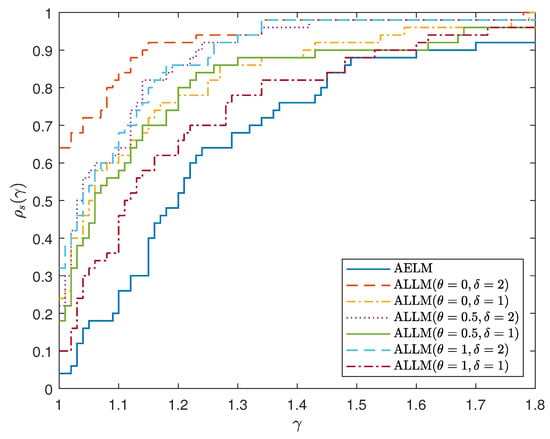
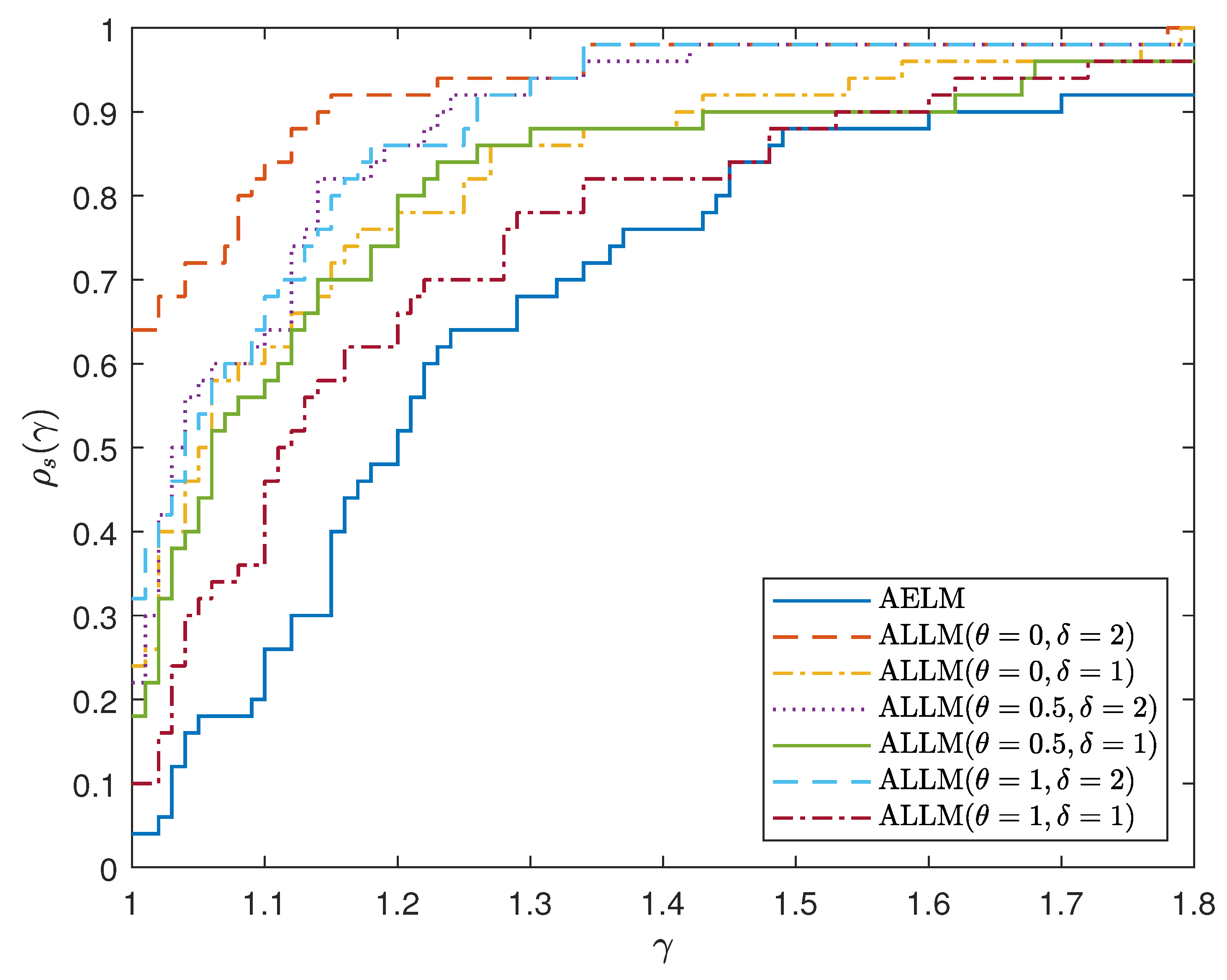

Table 2.
Numerical results of the AELM and ALLM algorithms with and various choices of .
Table 2.
Numerical results of the AELM and ALLM algorithms with and various choices of .
| AELM | ALLM | |||||
|---|---|---|---|---|---|---|
| Function | ||||||
| Iters/F/Time | Iters/F/Time | Iters/F/Time | Iters/F/Time | |||
| Extended Rosenbrock | 500 | −10 | 19/2.7631 × 10−7/0.30 | 19/2.7858 × 10−7/0.27 | 19/2.7744 × 10−7/0.29 | 19/2.7631 × 10−7/0.28 |
| −1 | 16/1.7341 × 10−7/0.23 | 14/2.5509 × 10−7/0.19 | 15/3.3852 × 10−7/0.20 | 16/1.7341 × 10−7/0.25 | ||
| 1 | 17/2.2186 × 10−7/0.24 | 17/1.9553 × 10−7/0.25 | 17/2.0901 × 10−7/0.22 | 17/2.2186 × 10−7/0.23 | ||
| 10 | 19/3.9252 × 10−7/0.29 | 19/3.8895 × 10−7/0.25 | 19/3.9066 × 10−7/0.27 | 19/3.9252 × 10−7/0.29 | ||
| 100 | 23/1.3154 × 10−7/0.42 | 23/1.3142 × 10−7/0.30 | 23/1.3150 × 10−7/0.34 | 23/1.3154 × 10−7/0.37 | ||
| 1000 | −10 | 19/3.9156 × 10−7/1.63 | 19/3.9442 × 10−7/1.52 | 19/3.9299 × 10−7/1.53 | 19/3.9156 × 10−7/1.64 | |
| −1 | 16/2.5034 × 10−7/1.43 | 14/3.8204 × 10−7/1.10 | 16/1.2047 × 10−7/1.28 | 16/2.5034 × 10−7/1.34 | ||
| 1 | 17/3.1868 × 10−7/1.46 | 17/2.8057 × 10−7/1.40 | 17/2.9943 × 10−7/1.36 | 17/3.1868 × 10−7/1.46 | ||
| 10 | 20/1.3911 × 10−7/1.67 | 20/1.3781 × 10−7/1.93 | 20/1.3866 × 10−7/1.65 | 20/1.3911 × 10−7/1.57 | ||
| 100 | 23/1.8652 × 10−7/2.06 | 23/1.8646 × 10−7/1.90 | 23/1.8638 × 10−7/1.90 | 23/1.8652 × 10−7/1.98 | ||
| Extended Helical valley | 501 | −10 | 42/1.3356 × 10−6/0.68 | 3/5.1316 × 10−7/0.03 | 13/3.7044 × 10−7/0.17 | 14/3.2573 × 10−7/0.23 |
| −1 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | ||
| 1 | 8/3.1758 × 10−7/0.13 | 8/1.4137 × 10−7/0.09 | 8/2.1648 × 10−7/0.10 | 8/3.1758 × 10−7/0.12 | ||
| 10 | 8/1.8981 × 10−9/0.12 | 8/8.0024 × 10−10/0.10 | 8/1.2568 × 10−9/0.10 | 8/1.8981 × 10−9/0.11 | ||
| 100 | 8/5.9124 × 10−10/0.12 | 8/3.9747 × 10−10/0.11 | 8/4.8399 × 10−10/0.11 | 8/5.9124 × 10−10/0.12 | ||
| 1000 | −10 | 7/2.3766 × 10−13/0.53 | 6/3.0134 × 10−13/0.45 | 6/1.5143 × 10−9/0.44 | 7/2.3766 × 10−13/0.55 | |
| −1 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | ||
| 1 | 8/1.8337 × 10−8/0.69 | 8/7.2043 × 10−9/0.68 | 8/1.1804 × 10−8/0.62 | 8/1.8337 × 10−8/0.67 | ||
| 10 | 8/1.6817 × 10−11/0.66 | 8/1.0758 × 10−11/0.61 | 8/1.4744 × 10−11/0.60 | 8/1.6817 × 10−11/0.65 | ||
| 100 | 26/9.3824 × 10−13/2.51 | 35/1.0739 × 10−7/3.29 | 26/6.6675 × 10−8/2.18 | 26/6.9835 × 10−11/2.16 | ||
| Discrete boundary value | 500 | −10 | 6/3.3487 × 10−3/0.11 | 6/3.3666 × 10−3/0.07 | 6/3.3631 × 10−3/0.09 | 6/3.3487 × 10−3/0.12 |
| −1 | 4/1.2234 × 10−3/0.06 | 4/1.2579 × 10−3/0.04 | 4/1.2417 × 10−3/0.05 | 4/1.2234 × 10−3/0.04 | ||
| 1 | 3/3.5633 × 10−4/0.04 | 3/3.6008 × 10−4/0.03 | 3/3.5823 × 10−4/0.03 | 3/3.5633 × 10−4/0.03 | ||
| 10 | 5/6.7290 × 10−3/0.08 | 5/6.7739 × 10−3/0.06 | 5/6.7614 × 10−3/0.06 | 5/6.7290 × 10−3/0.08 | ||
| 100 | 12/1.3651 × 10−4/0.23 | 13/1.3834 × 10−5/0.16 | 12/1.5752 × 10−4/0.17 | 12/1.3651 × 10−4/0.16 | ||
| 1000 | −10 | 6/3.6656 × 10−3/0.52 | 6/3.6804 × 10−3/0.50 | 6/3.6780 × 10−3/0.47 | 6/3.6656 × 10−3/0.48 | |
| −1 | 4/1.4253 × 10−3/0.30 | 4/1.4669 × 10−3/0.30 | 4/1.4474 × 10−3/0.30 | 4/1.4253 × 10−3/0.31 | ||
| 1 | 3/1.3022 × 10−4/0.22 | 3/1.3092 × 10−4/0.20 | 3/1.3058 × 10−4/0.21 | 3/1.3022 × 10−4/0.21 | ||
| 10 | 5/6.5900 × 10−3/0.40 | 5/6.6346 × 10−3/0.38 | 5/6.6209 × 10−3/0.35 | 5/6.5900 × 10−3/0.39 | ||
| 100 | 13/9.9458 × 10−5/1.09 | 13/1.0869 × 10−4/1.06 | 13/1.0505 × 10−4/1.07 | 13/9.9458 × 10−5/1.08 | ||
| Discrete integral equation | 500 | −10 | 12/1.2304 × 10−5/1.06 | 12/1.2171 × 10−5/1.03 | 12/1.2238 × 10−5/1.04 | 12/1.2304 × 10−5/1.06 |
| −1 | 9/1.5928 × 10−5/0.76 | 9/1.4153 × 10−5/0.76 | 9/1.5162 × 10−5/0.75 | 9/1.5928 × 10−5/0.76 | ||
| 1 | 7/1.3357 × 10−5/0.59 | 7/1.3770 × 10−5/0.58 | 7/1.3592 × 10−5/0.58 | 7/1.3357 × 10−5/0.58 | ||
| 10 | 10/9.3502 × 10−6/0.86 | 8/9.0151 × 10−6/0.67 | 9/1.5419 × 10−5/0.76 | 10/9.3502 × 10−6/0.86 | ||
| 100 | 10/4.5155 × 10−9/0.91 | 10/4.5463 × 10−9/0.89 | 10/4.5306 × 10−9/0.88 | 10/4.5155 × 10−9/0.91 | ||
| 1000 | −10 | 12/1.7452 × 10−5/4.50 | 12/1.7265 × 10−5/4.48 | 12/1.7358 × 10−5/4.50 | 12/1.7452 × 10−5/4.51 | |
| −1 | 10/6.0308 × 10−6/3.71 | 10/5.2005 × 10−6/3.73 | 10/5.6998 × 10−6/3.70 | 10/6.0308 × 10−6/3.67 | ||
| 1 | 8/5.1495 × 10−6/2.86 | 8/5.3838 × 10−6/2.90 | 8/5.2754 × 10−6/2.50 | 8/5.1495 × 10−6/2.86 | ||
| 10 | 10/1.4251 × 10−5/3.73 | 9/5.0675 × 10−6/3.30 | 10/5.7297 × 10−6/3.59 | 10/1.4251e × 10−5/3.66 | ||
| 100 | 10/6.3828 × 10−9/3.86 | 10/6.4261 × 10−9/3.83 | 10/6.4040 × 10−9/3.81 | 10/6.3828 × 10−9/3.83 | ||
| Broyden banded | 500 | −10 | 10/3.8446 × 10−12/0.17 | 10/3.9166 × 10−12/0.16 | 10/4.3882 × 10−12/0.14 | 10/3.8446 × 10−12/0.17 |
| −1 | 26/6.9212 × 10−6/0.52 | 31/1.2468 × 10−5/0.53 | 28/1.6756 × 10−5/0.50 | 25/1.2128 × 10−5/0.50 | ||
| 1 | 12/1.5063 × 10−5/0.20 | 12/1.5060 × 10−5/0.20 | 12/1.5061 × 10−5/0.19 | 12/1.5063 × 10−5/0.20 | ||
| 10 | 18/1.7636 × 10−5/0.33 | 18/1.7636 × 10−5/0.30 | 18/1.7636 × 10−5/0.28 | 18/1.7636 × 10−5/0.28 | ||
| 100 | 24/1.0280 × 10−5/0.44 | 24/1.0280 × 10−5/0.36 | 24/1.0280 × 10−5/0.37 | 24/1.0280 × 10−5/0.37 | ||
| 1000 | −10 | 10/3.5499 × 10−12/0.90 | 10/3.8124 × 10−12/0.91 | 10/4.6220 × 10−12/0.90 | 10/3.5499 × 10−12/0.99 | |
| −1 | 33/9.9927 × 10−6/3.35 | 27/9.6110 × 10−6/2.54 | 33/2.6949 × 10−5/3.04 | 28/9.7912 × 10−6/2.62 | ||
| 1 | 12/2.1201 × 10−5/1.22 | 12/2.1196 × 10−5/1.08 | 12/2.1199 × 10−5/1.09 | 12/2.1201 × 10−5/1.17 | ||
| 10 | 18/2.4886 × 10−5/1.82 | 18/2.4886 × 10−5/1.59 | 18/2.4886 × 10−5/1.68 | 18/2.4886 × 10−5/1.68 | ||
| 100 | 24/1.4499 × 10−5/2.80 | 24/1.4499 × 10−5/2.42 | 24/1.4499 × 10−5/2.37 | 24/1.4499 × 10−5/2.54 | ||

Table 3.
Numerical results of the AELM and ALLM algorithms with and various choices of .
Table 3.
Numerical results of the AELM and ALLM algorithms with and various choices of .
| AELM | ALLM | |||||
|---|---|---|---|---|---|---|
| Function | ||||||
| Iters/F/Time | Iters/F/Time | Iters/F/Time | Iters/F/Time | |||
| Extended Rosenbrock | 500 | −10 | 19/2.7631 × 10−7/0.30 | 19/2.7841 × 10−7/0.26 | 19/2.7734 × 10−7/0.26 | 19/2.7635 × 10−7/0.30 |
| −1 | 16/1.7341 × 10−7/0.23 | 14/1.7729 × 10−7/0.17 | 15/3.2343 × 10−7/0.21 | 16/1.7288 × 10−7/0.20 | ||
| 1 | 17/2.2186 × 10−7/0.24 | 17/1.8677 × 10−7/0.25 | 17/2.0435 × 10−7/0.25 | 17/2.2121 × 10−7/0.22 | ||
| 10 | 19/3.9252 × 10−7/0.29 | 19/3.8875 × 10−7/0.24 | 19/3.9061 × 10−7/0.26 | 19/3.9243 × 10−7/0.25 | ||
| 100 | 23/1.3154 × 10−7/0.42 | 23/1.3134 × 10−7/0.29 | 23/1.3145 × 10−7/0.33 | 23/1.3149 × 10−7/0.33 | ||
| 1000 | −10 | 19/3.9156 × 10−7/1.63 | 19/3.9423 × 10−7/1.50 | 19/3.9284 × 10−7/1.54 | 19/3.9140 × 10−7/1.56 | |
| −1 | 16/2.5034 × 10−7/1.43 | 14/2.3878 × 10−7/1.05 | 15/4.5237 × 10−7/1.24 | 16/2.4969 × 10−7/1.32 | ||
| 1 | 17/3.1868 × 10−7/1.46 | 17/2.7048 × 10−7/1.33 | 17/2.9369 × 10−7/1.36 | 17/3.1809 × 10−7/1.33 | ||
| 10 | 20/1.3911 × 10−7/1.67 | 20/1.3786 × 10−7/1.53 | 20/1.3857 × 10−7/1.57 | 20/1.3919e × 10−7/1.59 | ||
| 100 | 23/1.8652 × 10−7/2.06 | 23/1.8649 × 10−7/1.83 | 23/1.8655 × 10−7/1.80 | 23/1.8633 × 10−7/1.81 | ||
| Extended Helical valley | 501 | −10 | 42/1.3356 × 10−6/0.68 | 3/7.5853 × 10−13/0.04 | 13/1.7643 × 10−7/0.18 | 14/2.0341 × 10−7/0.19 |
| −1 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | 1/0.0000 × 100/0.01 | ||
| 1 | 8/3.1758 × 10−7/0.13 | 8/1.0595 × 10−7/0.11 | 8/1.9230 × 10−7/0.11 | 8/3.2101 × 10−7/0.09 | ||
| 10 | 8/1.8981 × 10−9/0.12 | 8/4.7841 × 10−10/0.11 | 8/9.5278 × 10−10/0.10 | 8/1.6935 × 10−9/0.10 | ||
| 100 | 8/5.9124 × 10−10/0.12 | 8/2.0055 × 10−10/0.10 | 8/3.2729 × 10−10/0.13 | 8/4.9161 × 10−10/0.13 | ||
| 1000 | −10 | 7/2.3766 × 10−13/0.53 | 5/7.4481 × 10−10/0.36 | 6/1.7998 × 10−12/0.51 | 6/4.6416 × 10−7/0.42 | |
| −1 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | 1/0.0000 × 100/0.04 | ||
| 1 | 8/1.8337 × 10−8/0.69 | 8/4.1226 × 10−9/0.59 | 8/9.1462 × 10−9/0.62 | 8/1.7753 × 10−8/0.63 | ||
| 10 | 8/1.6817 × 10−11/0.66 | 8/2.2703 × 10−11/0.59 | 8/3.2386 × 10−11/0.60 | 8/4.0803 × 10−11/0.64 | ||
| 100 | 26/9.3824 × 10−13/2.51 | 46/2.6770 × 10−11/3.70 | 26/8.5493 × 10−9/2.09 | 26/2.8466 × 10−10/2.15 | ||
| Discrete boundary value | 500 | −10 | 6/3.3487 × 10−3/0.11 | 4/3.1555 × 10−3/0.04 | 4/4.2613 × 10−3/0.04 | 4/4.7919 × 10−3/0.05 |
| −1 | 4/1.2234 × 10−3/0.06 | 3/7.2588 × 10−4/0.03 | 3/7.1034 × 10−4/0.03 | 3/6.9394 × 10−4/0.04 | ||
| 1 | 3/3.5633 × 10−4/0.04 | 3/4.1479 × 10−6/0.03 | 3/4.1402 × 10−6/0.04 | 3/4.1324 × 10−6/0.04 | ||
| 10 | 5/6.7290 × 10−3/0.08 | 4/2.4328 × 10−3/0.05 | 4/ 3.0758 × 10−3/0.05 | 4/3.4218 × 10−3/0.05 | ||
| 100 | 12/1.3651 × 10−4/0.23 | 11/4.2188 × 10−5/0.16 | 12/1.5591 × 10−5/0.18 | 12/1.3814 × 10−5/0.18 | ||
| 1000 | −10 | 6/3.6656 × 10−3/0.52 | 4/3.5180 × 10−3/0.29 | 4/4.5349 × 10−3/0.29 | 4/5.0429 × 10−3/0.28 | |
| −1 | 4/1.4253 × 10−3/0.30 | 3/9.3230 × 10−4/0.21 | 3/9.1090 × 10−4/0.21 | 3/8.8813 × 10−4/0.23 | ||
| 1 | 3/1.3022 × 10−4/0.22 | 2/2.6311 × 10−4/0.13 | 2/2.6303 × 10−4/0.13 | 2/2.6296 × 10−4/0.13 | ||
| 10 | 5/6.5900 × 10−3/0.40 | 4/2.5604 × 10−3/0.29 | 4/3.0932 × 10−3/0.30 | 4/3.4004 × 10−3/0.27 | ||
| 100 | 13/9.9458 × 10−5/1.09 | 11/1.2743 × 10−4/0.88 | 11/2.1884 × 10−4/0.93 | 11/2.1536 × 10−4/0.85 | ||
| Discrete integral equation | 500 | −10 | 12/1.2304 × 10−5/1.06 | 12/1.2047 × 10−5/1.03 | 12/1.2171 × 10−5/1.05 | 12/1.2294 × 10−5/1.04 |
| −1 | 9/1.5928 × 10−5/0.76 | 9/1.0655 × 10−5/0.75 | 9/1.2735 × 10−5/0.76 | 9/ 1.4195 × 10−5/0.76 | ||
| 1 | 7/1.3357 × 10−5/0.59 | 7/1.0869 × 10−5/0.57 | 7/1.0772 × 10−5/0.58 | 7/1.0633 × 10−5/0.57 | ||
| 10 | 10/9.3502 × 10−6/0.86 | 9/4.8669 × 10−6/0.75 | 9/1.3758 × 10−5/0.76 | 10/9.7578 × 10−6/0.84 | ||
| 100 | 10/4.5155 × 10−9/0.91 | 10/4.5453 × 10−9/0.89 | 10/4.5300 × 10−9/0.90 | 10/4.5154 × 10−9/0.88 | ||
| 1000 | −10 | 12/1.7452 × 10−5/4.50 | 12/1.7133 × 10−5/4.41 | 12/1.7285 × 10−5/4.46 | 12/1.7441 × 10−5/4.47 | |
| −1 | 10/6.0308 × 10−6/3.71 | 9/1.5092 × 10−5/3.25 | 9/1.8533 × 10−5/3.27 | 10/5.2150 × 10−6/3.66 | ||
| 1 | 8/5.1495 × 10−6/2.86 | 7/1.5749 × 10−5/2.48 | 7/1.5610 × 10−5/2.50 | 7/1.5367 × 10−5/2.62 | ||
| 10 | 10/1.4251 × 10−5/3.73 | 9/8.5398 × 10−6/3.25 | 10/5.1845 × 10−6/3.62 | 10/1.4626 × 10−5/3.71 | ||
| 100 | 10/6.3828 × 10−9/3.86 | 10/6.4246 × 10−9/3.76 | 10/6.4031 × 10−9/3.79 | 10/6.3825 × 10−9/3.77 | ||
| Broyden banded | 500 | −10 | 10/3.8446 × 10−12/0.17 | 10/3.795 × 10−12/0.16 | 10/4.3814 × 10−12/0.17 | 10/3.8105 × 10−12/0.16 |
| −1 | 26/6.9212 × 10−6/0.52 | 29/6.5177 × 10−6/0.45 | 28/1.6459 × 10−5/0.44 | 25/1.1907 × 10−5/0.42 | ||
| 1 | 12/1.5063 × 10−5/0.20 | 12/1.5059 × 10−5/0.20 | 12/1.5061 × 10−5/0.20 | 12/1.5063 × 10−5/0.18 | ||
| 10 | 18/1.7636 × 10−5/0.33 | 18/1.7636 × 10−5/0.30 | 18/1.7636 × 10−5/0.33 | 18/1.7636 × 10−5/0.31 | ||
| 100 | 24/1.0280 × 10−5/0.44 | 24/1.0280 × 10−5/0.36 | 24/1.0280 × 10−5/0.40 | 24/1.0280 × 10−5/0.36 | ||
| 1000 | −10 | 10/3.5499 × 10−12/0.90 | 10/4.5936 × 10−12/0.86 | 10/3.810 × 10−12/0.89 | 10/5.7143 × 10−12/0.93 | |
| −1 | 33/9.9927 × 10−6/3.35 | 29/1.5374 × 10−5/2.76 | 31/1.8408 × 10−5 /2.84 | 28/9.7968 × 10−6/2.61 | ||
| 1 | 12/2.1201 × 10−5/1.22 | 12/2.1194 × 10−5/1.07 | 12/2.1198 × 10−5/1.08 | 12/2.1201 × 10−5/1.13 | ||
| 10 | 18/2.4886 × 10−5/1.82 | 18/2.4886 × 10−5/1.69 | 18/2.4886 × 10−5/1.64 | 18/2.4886 × 10−5/1.65 | ||
| 100 | 24/1.4499 × 10−5/2.80 | 24/1.4499 × 10−5/2.30 | 24/1.4499 × 10−5/2.33 | 24/1.4499 × 10−5/2.51 | ||

Figure 1.
Performance profile of AELM and ALLM based on number of iterations for example 1–10.
Figure 1.
Performance profile of AELM and ALLM based on number of iterations for example 1–10.


Figure 2.
Performance profile of AELM and ALLM based on CPU time for example 1–10.
Figure 2.
Performance profile of AELM and ALLM based on CPU time for example 1–10.

5. Conclusions
In this paper, inspired by the Hölderian local error bound condition, we studied the convergence properties of our ALLM algorithm under different conditions. We used the new modified adaptive LM parameter and incorporated the non-monotone technique to modify the Levenberg–Marquardt algorithm. The numerical results show that our new algorithm is efficient and stable.
Author Contributions
Conceptualization, Y.H. and S.R.; methodology, Y.H. and S.R.; Software, Y.H.; validation, Y.H. and S.R.; formal analysis, Y.H. and S.R.; investigation, Y.H. and S.R.; resources, Y.H. and S.R.; data curation, Y.H. and S.R.; Writing—original draft, Y.H.; writing—review and editing, Y.H. and S.R.; visualization, Y.H.; supervision, S.R.; project administration, S.R.; funding acquisition, S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of the Anhui Higher Education Institutions of China, 2023AH050348.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank S.R. and everyone for their valuable comments and suggestions which helped us improve the quality of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Leonov, E.; Polbin, A. Numerical Search for a Global Solution in a Two-Mode Economy Model with an Exhaustible Resource of Hydrocarbons. Math. Model. Comput. Simul. 2022, 14, 213–223. [Google Scholar] [CrossRef]
- Xu, D.; Bai, Z.; Jin, X.; Yang, X.; Chen, S.; Zhou, M. A mean-variance portfolio optimization approach for high-renewable energy hub. Appl. Energy 2022, 325, 119888. [Google Scholar] [CrossRef]
- Manzoor, Z.; Iqbal, M.S.; Hussain, S.; Ashraf, F.; Inc, M.; Tarar, M.A.; Momani, S. A study of propagation of the ultra-short femtosecond pulses in an optical fiber by using the extended generalized Riccati equation mapping method. Opt. Quantum Electron. 2023, 55, 717. [Google Scholar] [CrossRef]
- Vu, D.T.S.; Gharbia, I.B.; Haddou, M.; Tran, Q.H. A new approach for solving nonlinear algebraic systems with complementarity conditions. Application to compositional multiphase equilibrium problems. Math. Comput. Simul. 2021, 190, 1243–1274. [Google Scholar] [CrossRef]
- Maia, L.; Nornberg, G.; Pacella, F. A dynamical system approach to a class of radial weighted fully nonlinear equations. Commun. Partial Differ. Equ. 2021, 46, 573–610. [Google Scholar] [CrossRef]
- Vasin, V.V.; Skorik, G.G. Two-stage method for solving systems of nonlinear equations and its applications to the inverse atmospheric sounding problem. In Doklady Mathematics; Springer: New York, NY, USA, 2020; Volume 102, pp. 367–370. [Google Scholar]
- Luo, X.l.; Xiao, H.; Lv, J.h. Continuation Newton methods with the residual trust-region time-stepping scheme for nonlinear equations. Numer. Algorithms 2022, 89, 223–247. [Google Scholar] [CrossRef]
- Waziri, M.Y.; Ahmed, K. Two descent Dai-Yuan conjugate gradient methods for systems of monotone nonlinear equations. J. Sci. Comput. 2022, 90, 1–53. [Google Scholar] [CrossRef]
- Pes, F.; Rodriguez, G. A doubly relaxed minimal-norm Gauss–Newton method for underdetermined nonlinear least-squares problems. Appl. Numer. Math. 2022, 171, 233–248. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 1999. [Google Scholar]
- Yamashita, N.; Fukushima, M. On the rate of convergence of the Levenberg-Marquardt method. In Topics in Numerical Analysis: With Special Emphasis on Nonlinear Problems; Springer: New York, NY, USA, 2001; pp. 239–249. [Google Scholar]
- Fan, J.Y.; Yuan, Y.X. On the quadratic convergence of the Levenberg-Marquardt method without nonsingularity assumption. Computing 2005, 74, 23–39. [Google Scholar] [CrossRef]
- Fischer, A. Local behavior of an iterative framework for generalized equations with nonisolated solutions. Math. Program. 2002, 94, 91–124. [Google Scholar] [CrossRef]
- Ma, C.; Jiang, L. Some research on Levenberg–Marquardt method for the nonlinear equations. Appl. Math. Comput. 2007, 184, 1032–1040. [Google Scholar] [CrossRef]
- Fan, J.Y. A modified Levenberg-Marquardt algorithm for singular system of nonlinear equations. J. Comput. Math. 2003, 625–636. [Google Scholar]
- Amini, K.; Rostami, F.; Caristi, G. An efficient Levenberg–Marquardt method with a new LM parameter for systems of nonlinear equations. Optimization 2018, 67, 637–650. [Google Scholar] [CrossRef]
- Rezaeiparsa, Z.; Ashrafi, A. A new adaptive Levenberg–Marquardt parameter with a nonmonotone and trust region strategies for the system of nonlinear equations. Math. Sci. 2023, 1–13. [Google Scholar] [CrossRef]
- Ahookhosh, M.; Aragón Artacho, F.J.; Fleming, R.M.; Vuong, P.T. Local convergence of the Levenberg–Marquardt method under Hölder metric subregularity. Adv. Comput. Math. 2019, 45, 2771–2806. [Google Scholar] [CrossRef]
- Wang, H.Y.; Fan, J.Y. Convergence rate of the Levenberg-Marquardt method under Hölderian local error bound. Optim. Methods Softw. 2020, 35, 767–786. [Google Scholar] [CrossRef]
- Zeng, M.; Zhou, G. Improved convergence results of an efficient Levenberg–Marquardt method for nonlinear equations. J. Appl. Math. Comput. 2022, 68, 3655–3671. [Google Scholar] [CrossRef]
- Chen, L.; Ma, Y. A modified Levenberg–Marquardt method for solving system of nonlinear equations. J. Appl. Math. Comput. 2023, 69, 2019–2040. [Google Scholar] [CrossRef]
- Li, R.; Cao, M.; Zhou, G. A New Adaptive Accelerated Levenberg–Marquardt Method for Solving Nonlinear Equations and Its Applications in Supply Chain Problems. Symmetry 2023, 15, 588. [Google Scholar] [CrossRef]
- Grippo, L.; Lampariello, F.; Lucidi, S. A nonmonotone line search technique for Newton’s method. SIAM J. Numer. Anal. 1986, 23, 707–716. [Google Scholar] [CrossRef]
- Ahookhosh, M.; Amini, K. A nonmonotone trust region method with adaptive radius for unconstrained optimization problems. Comput. Math. Appl. 2010, 60, 411–422. [Google Scholar] [CrossRef][Green Version]
- Ahookhosh, M.; Amini, K. An efficient nonmonotone trust-region method for unconstrained optimization. Numer. Algorithms 2012, 59, 523–540. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, D. A derivative-free affine scaling trust region methods based on probabilistic models with new nonmonotone line search technique for linear inequality constrained minimization without strict complementarity. Int. J. Comput. Math. 2019, 96, 663–691. [Google Scholar] [CrossRef]
- Powell, M.J.D. Convergence properties of a class of minimization algorithms. In Nonlinear Programming 2; Elsevier: Amsterdam, The Netherlands, 1975; pp. 1–27. [Google Scholar]
- Behling, R.; Iusem, A. The effect of calmness on the solution set of systems of nonlinear equations. Math. Program. 2013, 137, 155–165. [Google Scholar] [CrossRef]
- Stewart, G.; Sun, J. Matrix Perturbation Theory; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]
- Schnabel, R.B.; Frank, P.D. Tensor methods for nonlinear equations. SIAM J. Numer. Anal. 1984, 21, 815–843. [Google Scholar] [CrossRef]
- Moré, J.J.; Garbow, B.S.; Hillstrom, K.E. Testing unconstrained optimization software. ACM Trans. Math. Softw. (TOMS) 1981, 7, 17–41. [Google Scholar] [CrossRef]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
