Timelike Constant Axis Ruled Surface Family in Minkowski 3-Space
Abstract
:1. Introduction
2. Basic Concepts
3. Main Results
3.1. Hamilton and Mannheim Formulae
- (1)
- can be distinguished as .
- (2)
- If is a point on the , then
3.2. Timelike Cylindroid
- A:
- If , that is, the - movement is not a pure turnover, then there are two isotropic rulings crossing through the point .
- B:
- If , that is, the - movement is a pure turnover, then there are two isotropic lines , detected by
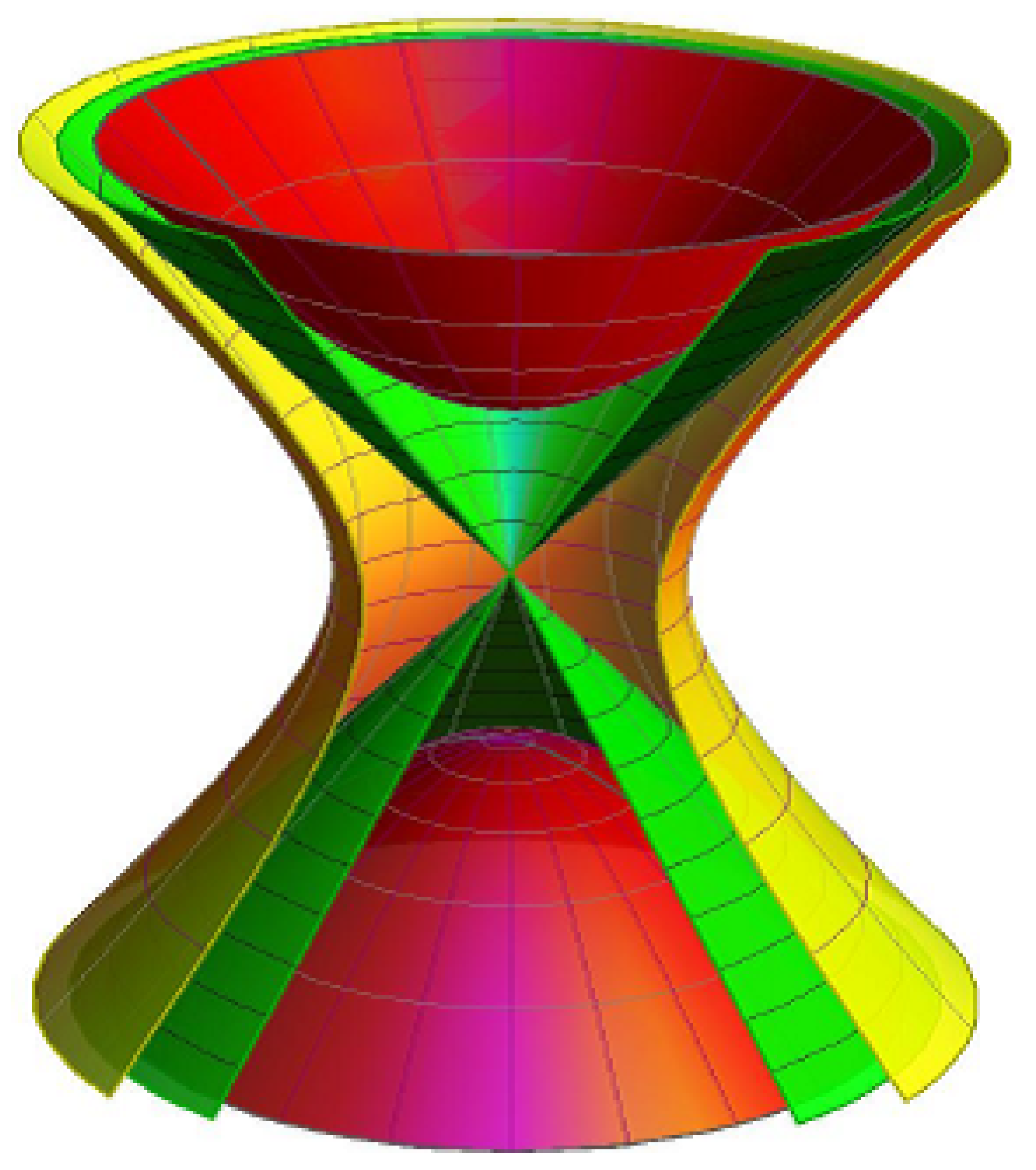
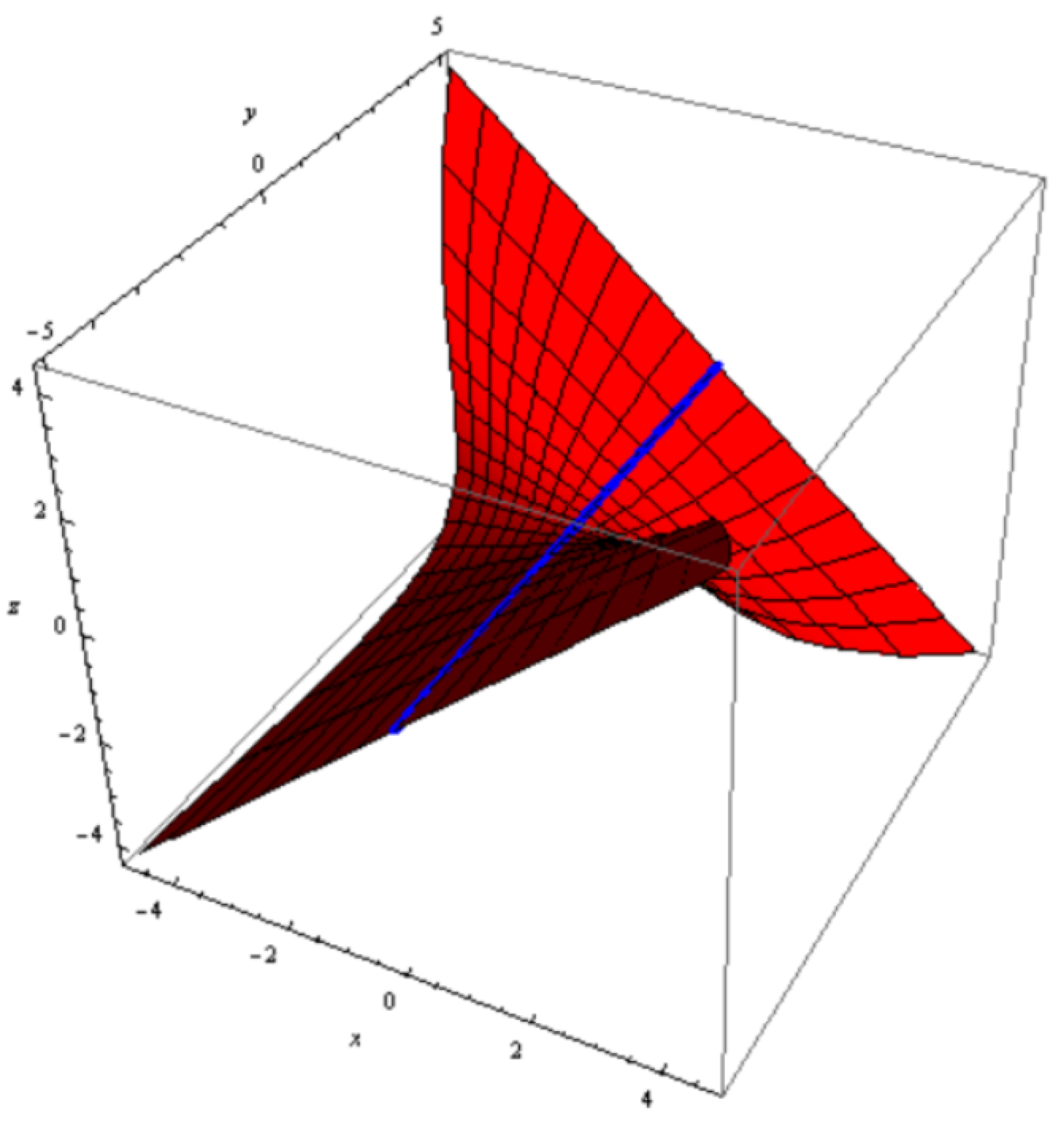
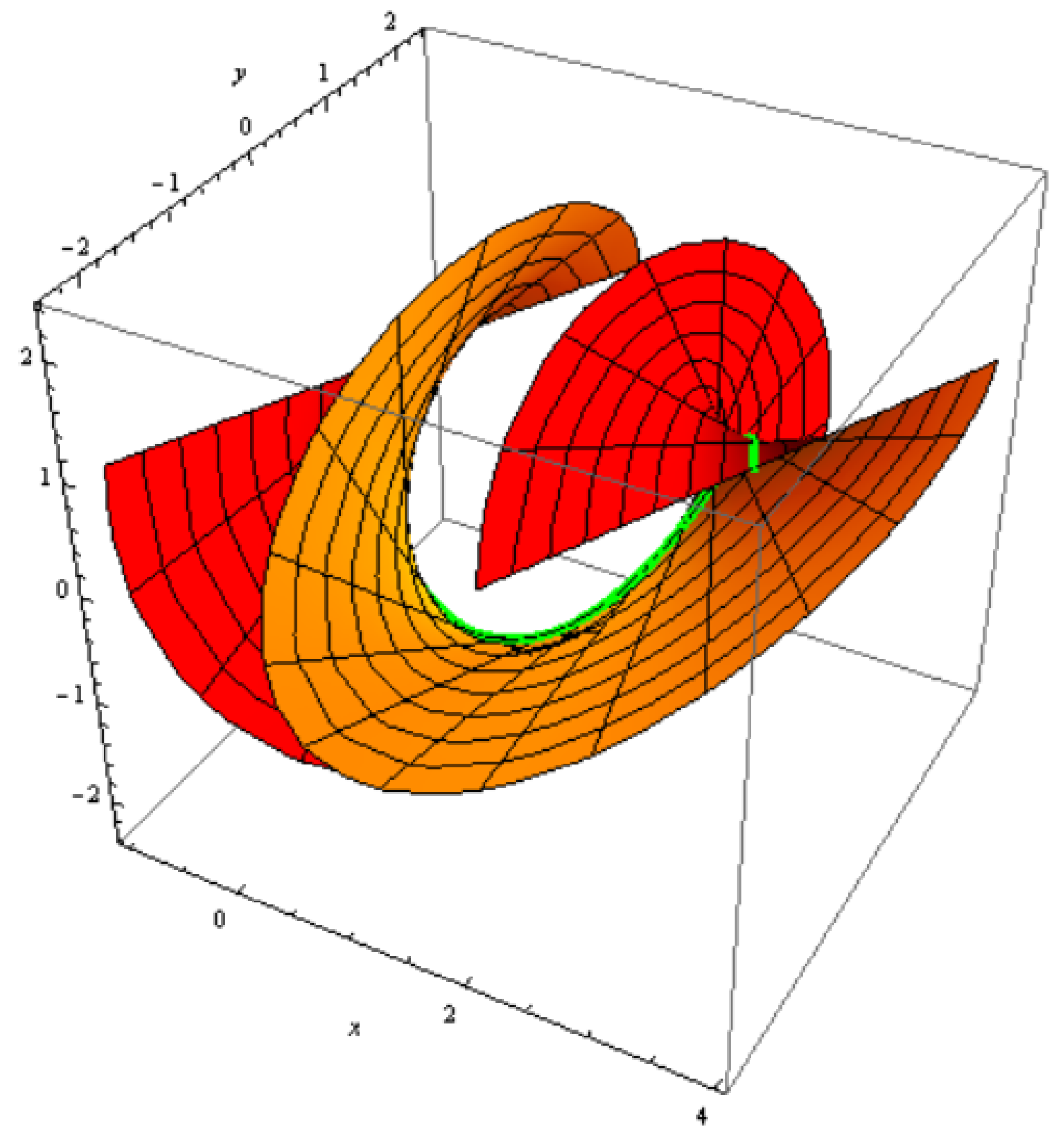
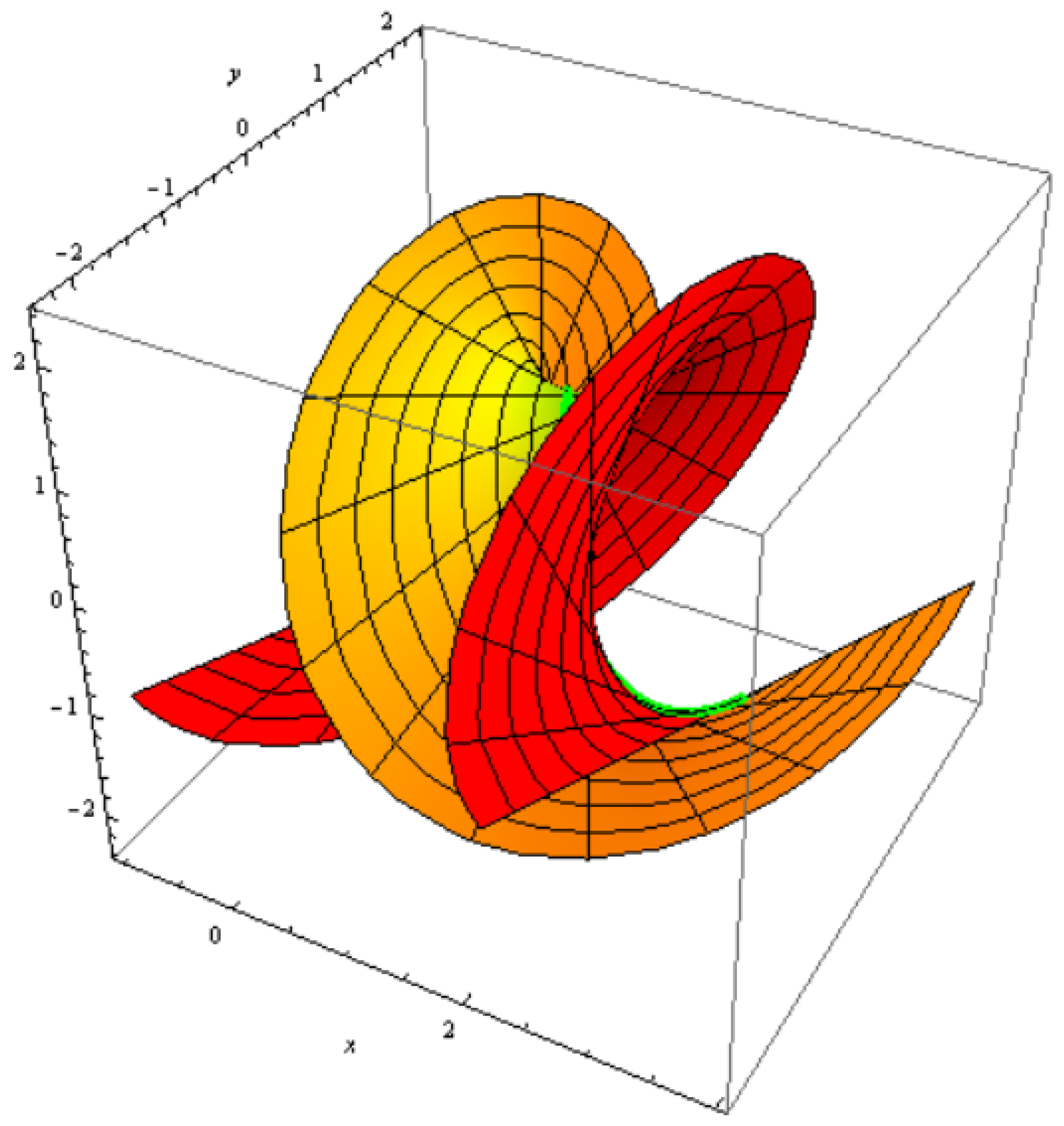
3.3. Timelike Constant Axis Ruled Surface Family
Height Functions
- i.
- will be invariant in the first evaluation if ,, that is,for some dual numbers and .
- ii.
- will be invariant in the second evaluation if is an evolute of , that is,
- iii.
- will be invariant in the third evaluation if is an evolute of , that is,
- iv.
- will be invariant in the fourth evaluation if is an evolute of , that is,
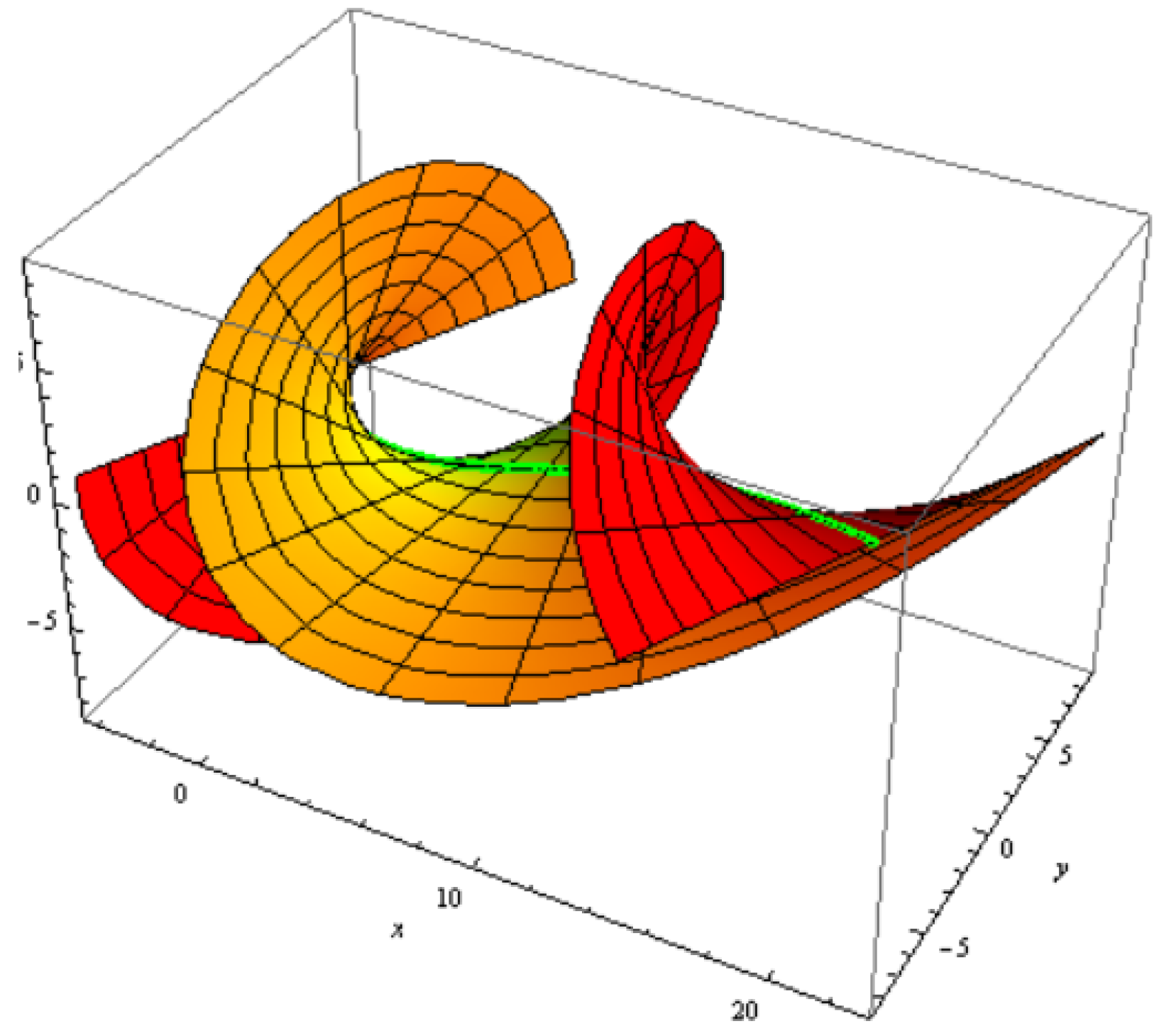
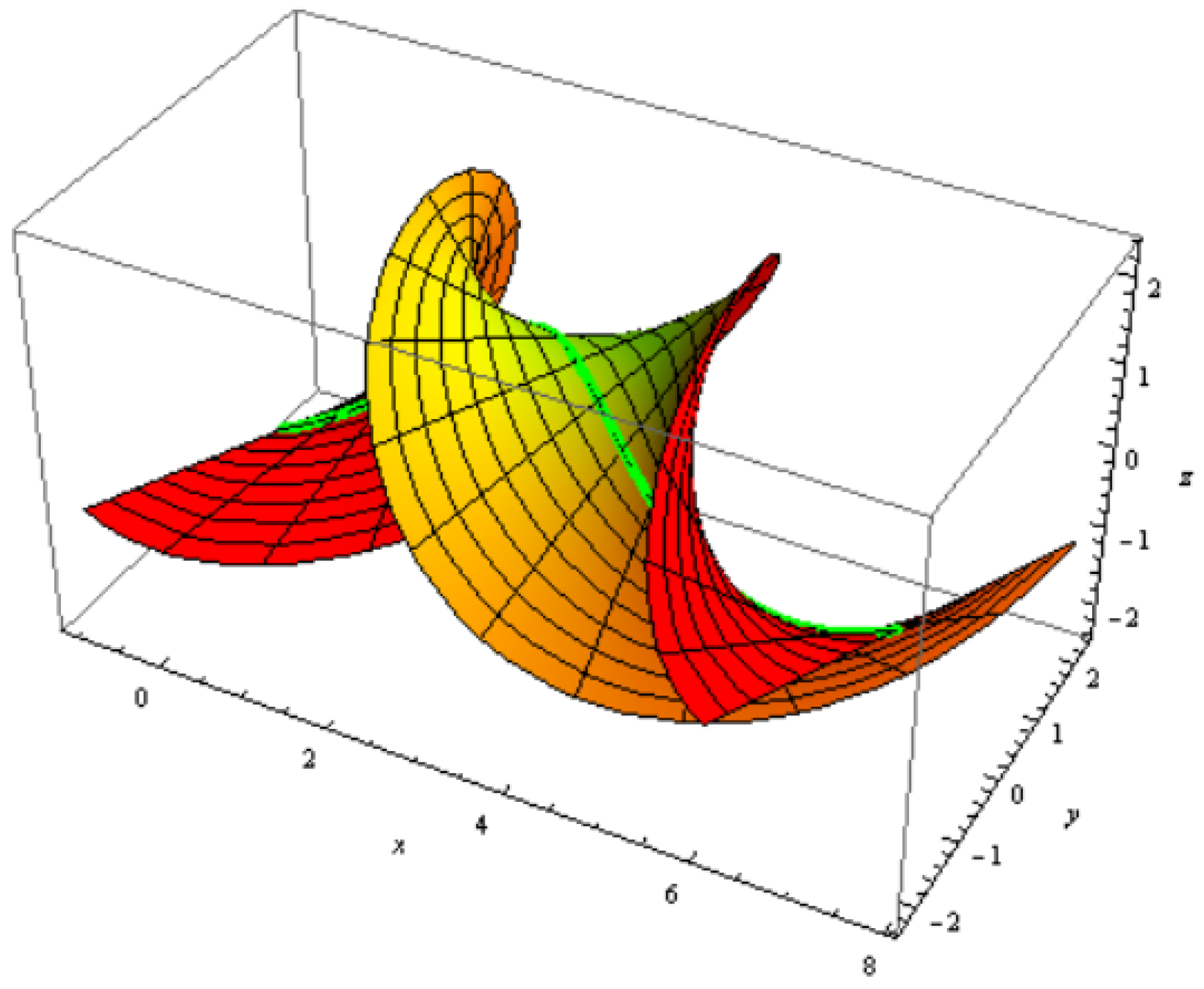
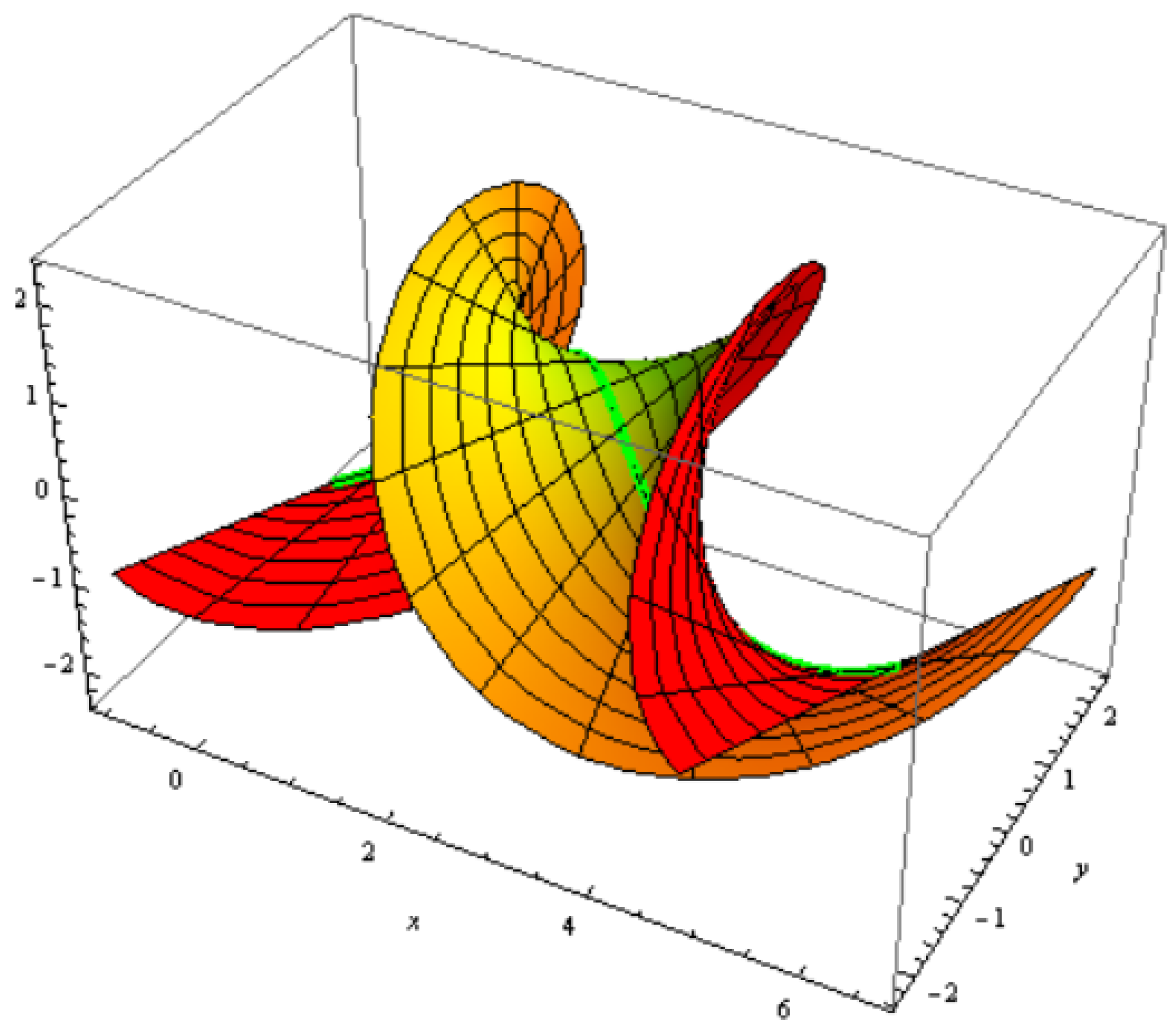
3.4. Construction of the Constant Axis Family
3.5. Organizations among a Constant Axis and Its Striction Curve
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bottema, O.; Roth, B. Theoretical Kinematics; North-Holland Press: New York, NY, USA, 1979. [Google Scholar]
- Karger, A.; Novak, J. Space Kinematics and Lie Groups; Gordon and Breach Science Publishers: New York, NY, USA, 1985. [Google Scholar]
- Pottman, H.; Wallner, J. Computational Line Geometry; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Köse, Ö.; Sarıoglu, C.C.; Karabey, B.; Karakılıç, I. Kinematic differential geometry of a rigid body in spatial motion using dual vector calculus: Part-II. Appl. Math. 2006, 182, 333–358. [Google Scholar] [CrossRef]
- Jafari, M.; Yayli, Y. The E. Study map of circule on dual elliptical unit sphere. BEU J. Sci. 2015, 4, 12–20. [Google Scholar]
- Turhan, T.; Ayyıldız, N. A study on geometry of spatial kinematics in Lorentzian space. Süleyman Demirel Üniversitesi Fen Bilimleri Enstitüsü Dergisi 2017, 21, 808–811. [Google Scholar] [CrossRef]
- Ali, A.T. A constant angle ruled surfaces. Int. J. Geom. 2018, 7, 69–80. [Google Scholar]
- Alluhaibi, N.; Abdel-Baky, R.A. On the one-parameter Lorentzian spatial motions. Int. Geom. Methods Mod. Phys. 2019, 16, 1950197. [Google Scholar] [CrossRef]
- Gilani, S.M.; Abazari, N.; Yayli, Y. Characterizations of dual curves and dual focal curves in dual Lorentzian space D13. Turk. J. Math. 2020, 44, 1561–1577. [Google Scholar] [CrossRef]
- Aslan, M.C.; Sekerci, G.A. Dual curves associated with the Bonnet ruled surfaces. Int. Geom. Methods Mod. Phys. 2020, 17, 2050204. [Google Scholar] [CrossRef]
- Alluhaibi, N.S.; Abdel-Baky, R.A. Kinematic geometry of timelike ruled surfaces in Minkowski 3-space E13. Symmetry 2022, 14, 749. [Google Scholar] [CrossRef]
- Mofarreh, F. Timelike ruled and developable surfaces in Minkowski 3-space E13. Front. Phys. 2022, 10, 838957. [Google Scholar] [CrossRef]
- Abdel-Baky, R.A.; Unluturk, Y. A new construction of timelike ruled surfaces with stationarfy Disteli-axis. Honam Math. J. 2020, 42, 551–568. [Google Scholar]
- Bruce, J.W.; Giblin, P.J. Curves and Singularities, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Li, Y.L.; Zhu, Y.S.; Sun, Q.Y. Singularities and dualities of pedal curves in pseudo-hyperbolic and de Sitter space. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150008. [Google Scholar] [CrossRef]
- Li, Y.L.; Nazra, S.; Abdel-Baky, R.A. Singularities Properties of timelike sweeping surface in Minkowski 3-Space. Symmetry 2022, 14, 1996. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, L.; Li, P.; Chang, Y. Singularities of Osculating Developable Surfaces of Timelike Surfaces along Curves. Symmetry 2022, 14, 2251. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almoneef, A.A.; Abdel-Baky, R.A. Timelike Constant Axis Ruled Surface Family in Minkowski 3-Space. Symmetry 2024, 16, 677. https://doi.org/10.3390/sym16060677
Almoneef AA, Abdel-Baky RA. Timelike Constant Axis Ruled Surface Family in Minkowski 3-Space. Symmetry. 2024; 16(6):677. https://doi.org/10.3390/sym16060677
Chicago/Turabian StyleAlmoneef, Areej A., and Rashad A. Abdel-Baky. 2024. "Timelike Constant Axis Ruled Surface Family in Minkowski 3-Space" Symmetry 16, no. 6: 677. https://doi.org/10.3390/sym16060677




