Dynamical Analysis and Synchronization of Complex Network Dynamic Systems under Continuous-Time
Abstract
:1. Introduction
2. Construction of Mathematical Model of Complex Network Dynamic System
2.1. Problem Description
2.2. Stability Analysis of Complete Synchronization of Complex Dynamic Networks
3. State Estimation of Dynamic Systems with Multilayer Complex Networks
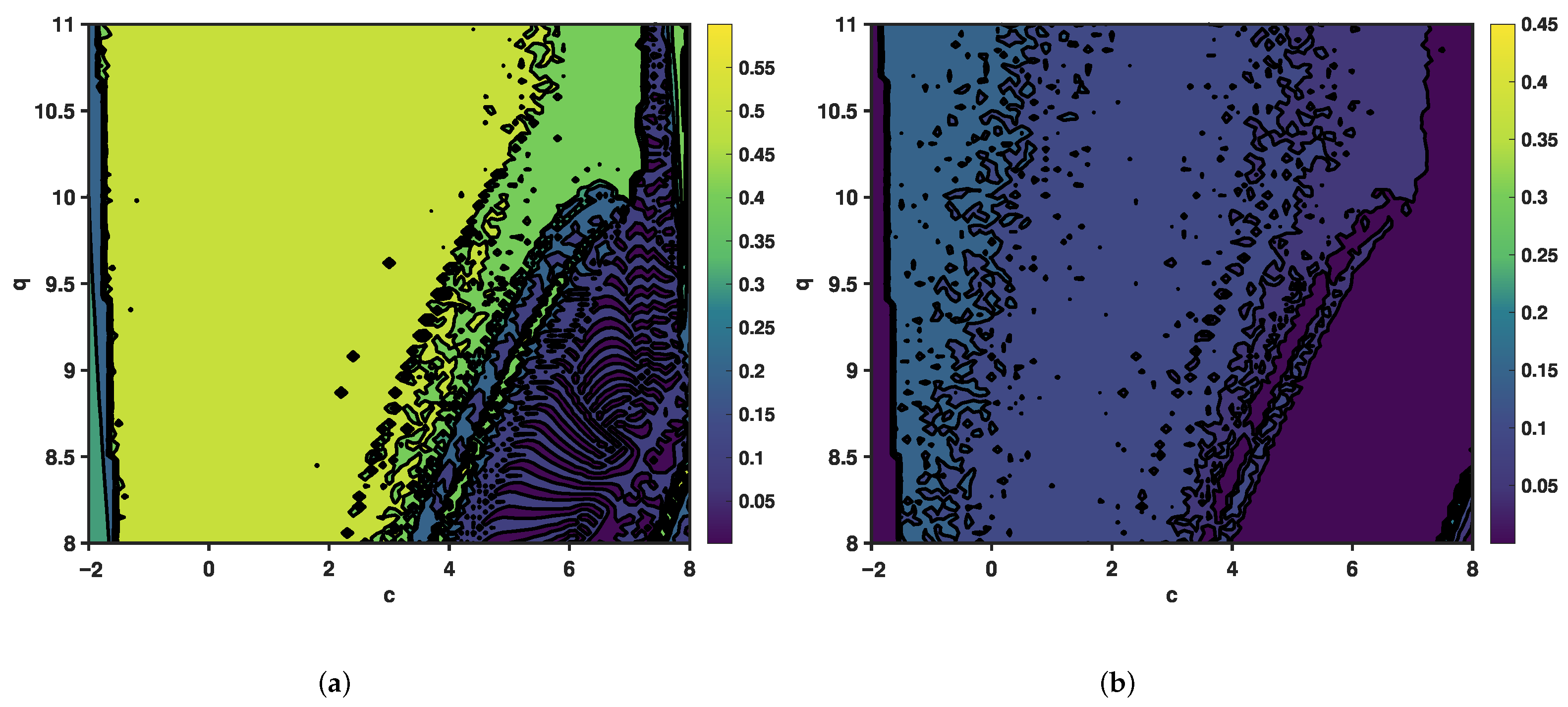
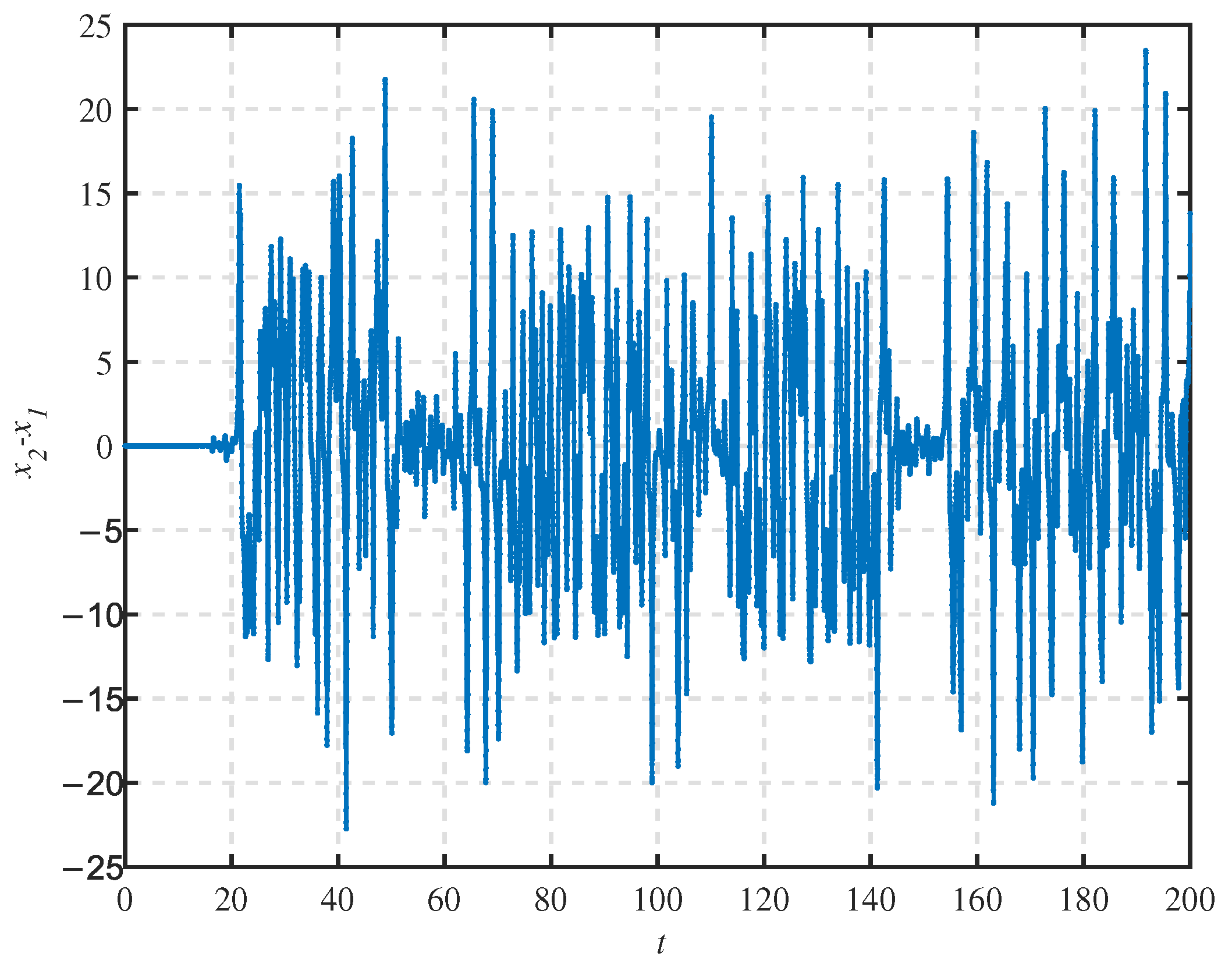
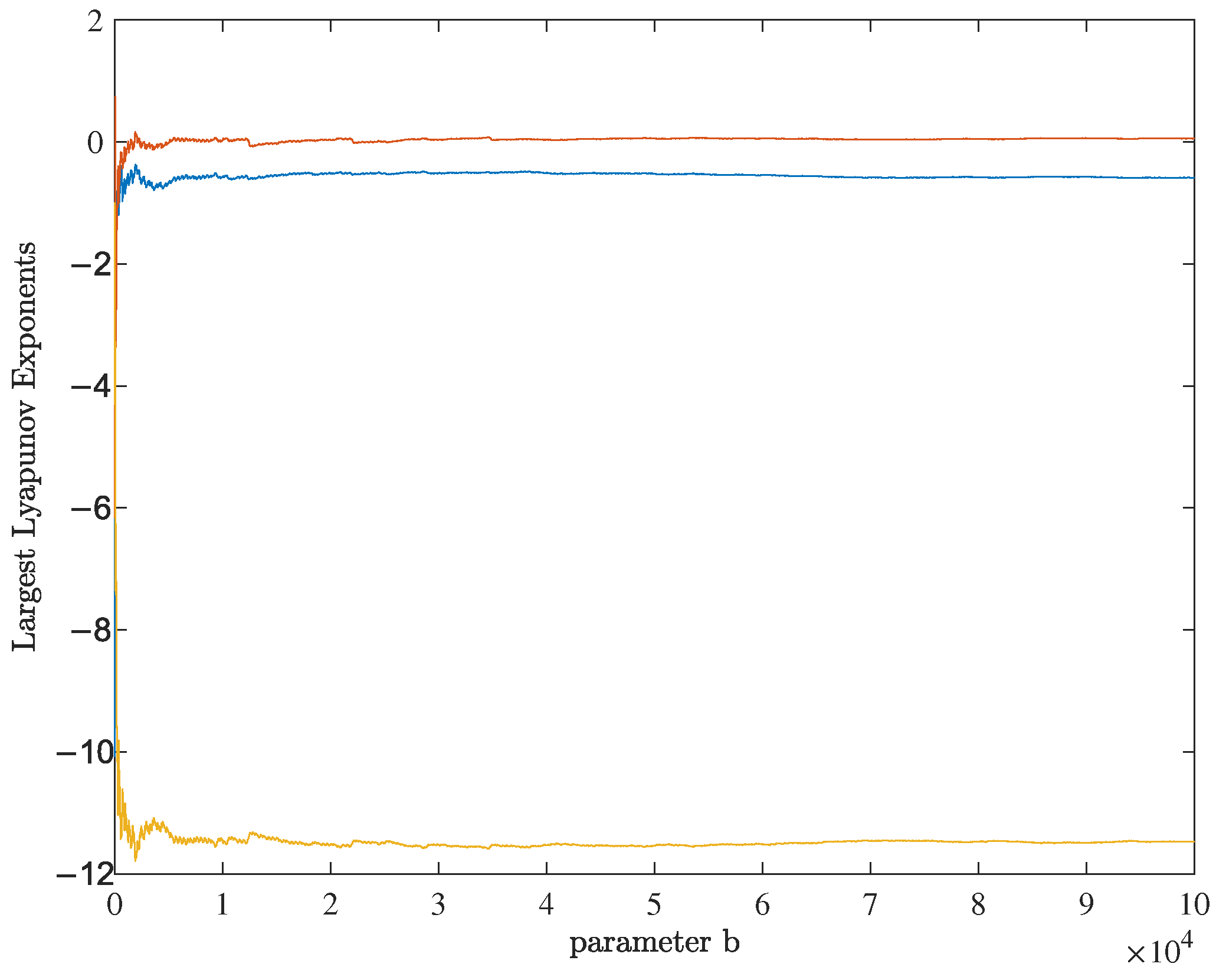
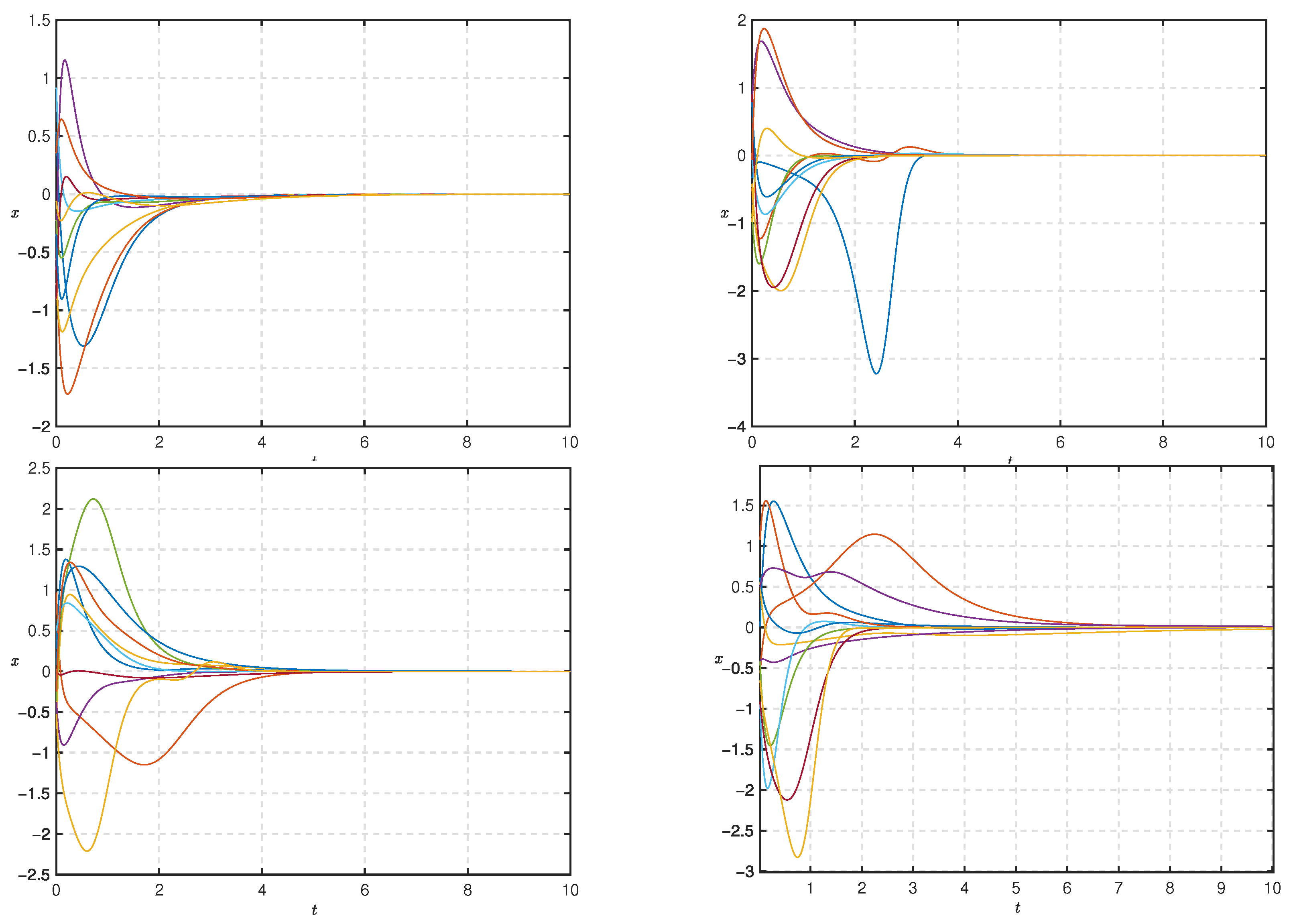
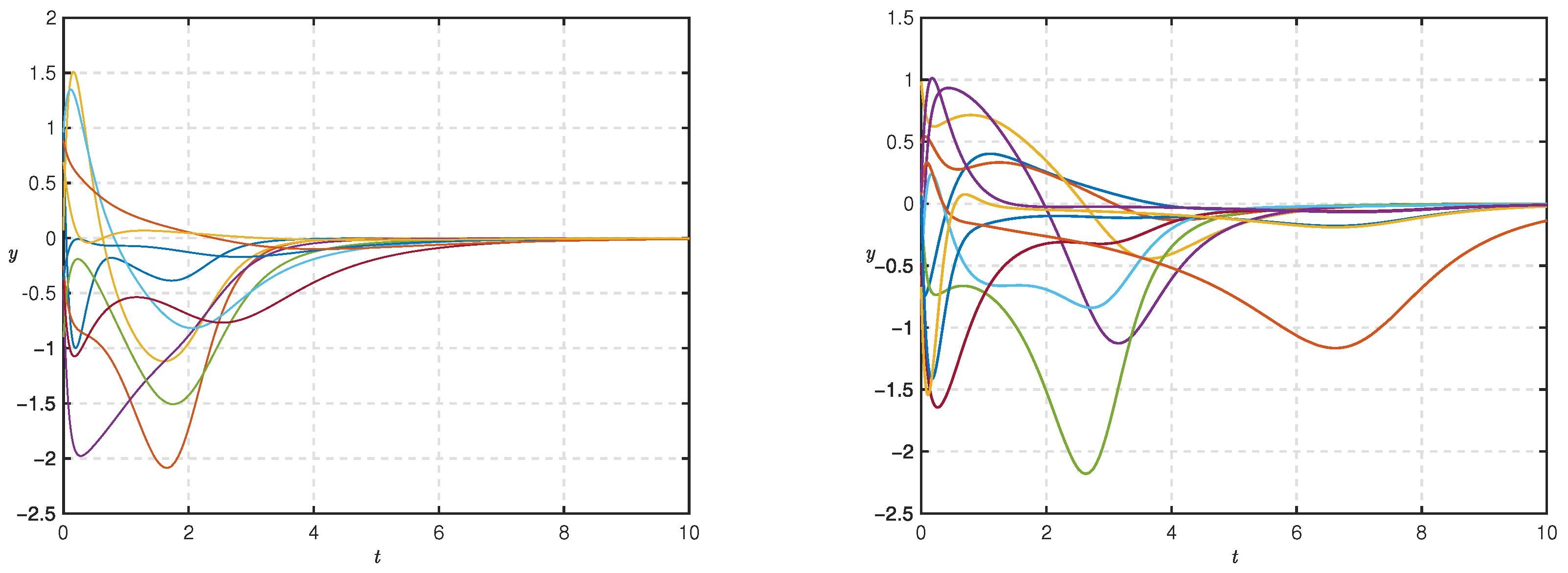
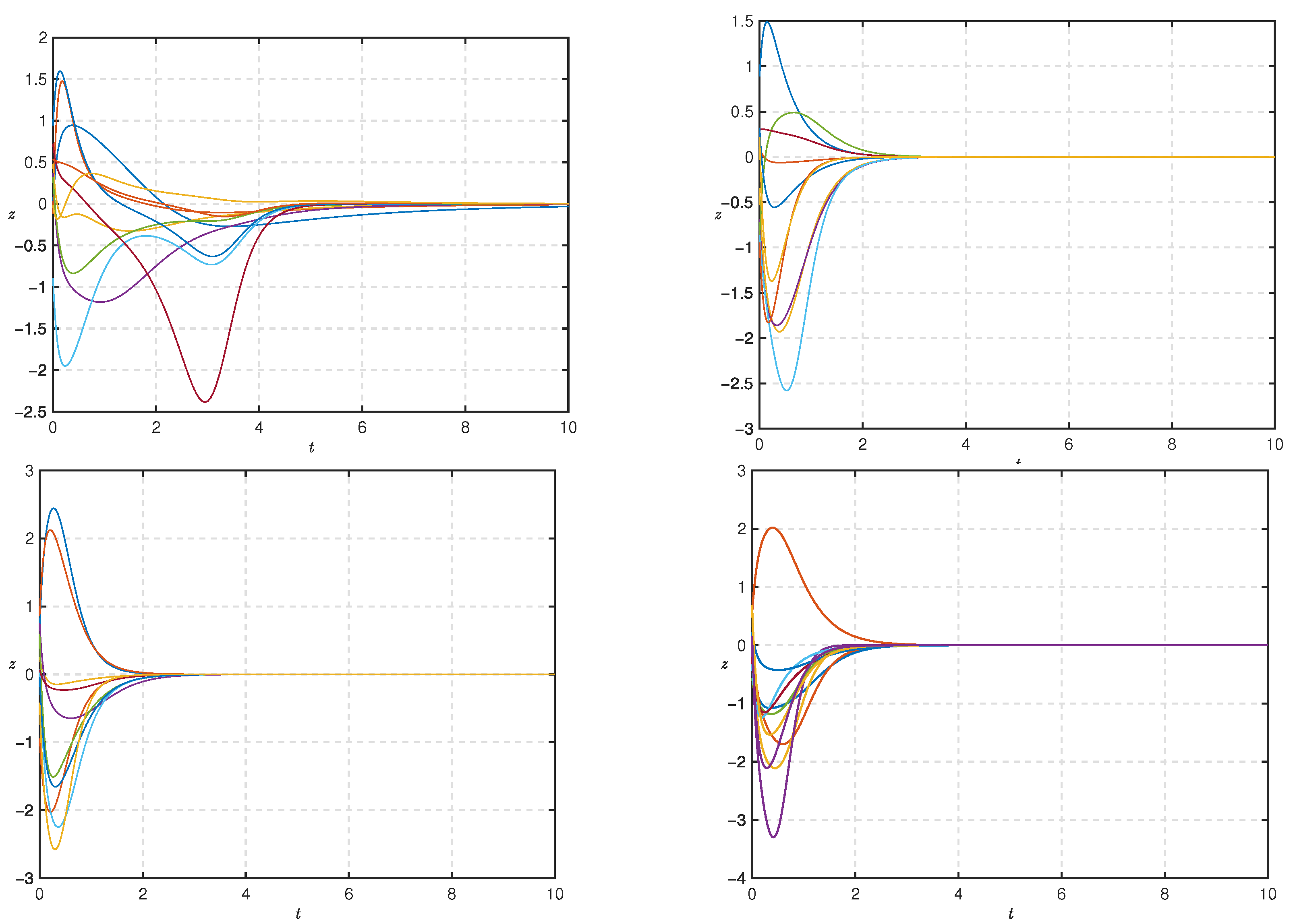
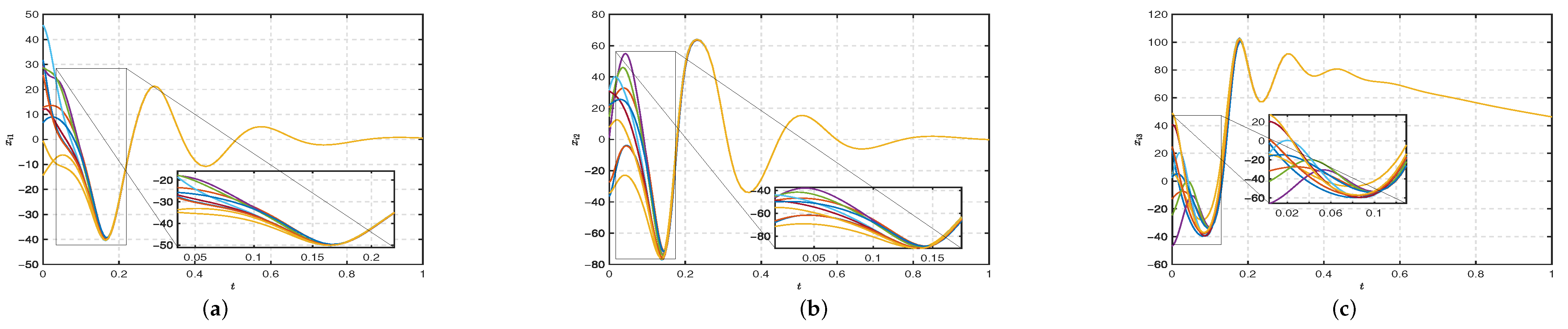
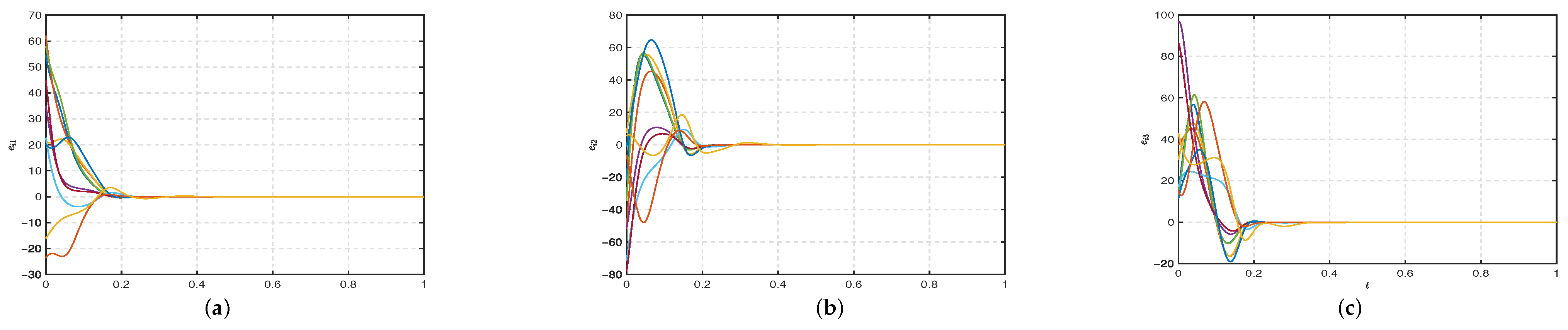
4. Simulation and Result Analysis
5. Conclusions
6. Use of AI Tools Declaration
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, L.; Li, Z.; Giua, A. Containment of rumor spread in complex social networks. Inf. Sci. 2020, 506, 113–130. [Google Scholar] [CrossRef]
- Ullah, A.; Shao, J.; Yang, Q.; Khan, N.; Bernard, C.M.; Kumar, R. LSS: A locality-based structure system to evaluate the spreader’s importance in social complex networks. Expert Syst. Appl. 2023, 228, 120326. [Google Scholar] [CrossRef]
- Alexandridis, A.T.; Papageorgiou, P.C. A complex network deployment suitable for modern power distribution analysis at the primary control level. IFAC-PapersOnLine 2017, 50, 9186–9191. [Google Scholar] [CrossRef]
- Xia, Y.; Kanna, S.; Mandic, D.P. Diffusion Augmented Complex Extended Kalman Filtering for Adaptive Frequency Estimation in Distributed Power Networks. In Cooperative and Graph Signal Processing; Elsevier: Amsterdam, The Netherlands, 2018; pp. 735–755. [Google Scholar]
- Dehdarian, A.; Tucci, C.L. A complex network approach for analyzing early evolution of smart grid innovations in Europe. Appl. Energy 2021, 298, 117143. [Google Scholar] [CrossRef]
- Schimit, P.H.; Pereira, F.H. Disease spreading in complex networks: A numerical study with Principal Component Analysis. Expert Syst. Appl. 2018, 97, 41–50. [Google Scholar] [CrossRef]
- Sun, Y.F.; Sun, Z.Y. Target observation of complex networks. Phys. A Stat. Mech. Its Appl. 2019, 517, 233–245. [Google Scholar] [CrossRef]
- Medina, P.; Carrasco, S.; Correa-Burrows, P.; Rogan, J.; Valdivia, J.A. Nontrivial and anomalous transport on weighted complex networks. Commun. Nonlinear Sci. Numer. Simul. 2022, 114, 106684. [Google Scholar] [CrossRef]
- Ji, P.; Ye, J.; Mu, Y.; Lin, W.; Tian, Y.; Hens, C.; Perc, M.; Tang, Y.; Sun, J.; Kurths, J. Signal propagation in complex networks. Phys. Rep. 2023, 1017, 1–96. [Google Scholar]
- Dramsch, J.S.; Lüthje, M.; Christensen, A.N. Complex-valued neural networks for machine learning on non-stationary physical data. Comput. Geosci. 2021, 146, 104643. [Google Scholar] [CrossRef]
- Qiao, H.H.; Deng, Z.H.; Li, H.J.; Hu, J.; Song, Q.; Gao, L. Research on historical phase division of terrorism: An analysis method by time series complex network. Neurocomputing 2021, 420, 246–265. [Google Scholar] [CrossRef]
- Rocha, R.V.; de Souza Filho, F.D.A. Stream gauge clustering and analysis for non-stationary time series through complex networks. J. Hydrol. 2023, 616, 128773. [Google Scholar] [CrossRef]
- Räz, T. Euler’s Königsberg: The explanatory power of mathematics. Eur. J. Philos. Sci. 2018, 8, 331–346. [Google Scholar] [CrossRef]
- Cohen, R.; Havlin, S. Scale-free networks are ultrasmall. Phys. Rev. Lett. 2003, 90, 058701. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Saleh, M.; Esa, Y.; Mohamed, A. Applications of complex network analysis in electric power systems. Energies 2018, 11, 1381. [Google Scholar] [CrossRef]
- Targui, B.; Frikel, M.; M’saad, M.; Safi, S. Observer design for the state estimation of a class of communication networks. In Proceedings of the 18th Mediterranean Conference on Control and Automation, MED’10, Marrakech, Morocco, 23–25 June 2010; IEEE: New York, NY, USA, 2010; pp. 495–499. [Google Scholar]
- Fan, C.X.; Wan, Y.H.; Jiang, G.P. Topology identification for a class of complex dynamical networks using output variables. Chin. Phys. B 2012, 21, 020510. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, G.P.; Wang, X. State estimation for general complex dynamical networks with packet loss. IEEE Trans. Circuits Syst. II Express Briefs 2017, 65, 1753–1757. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, J.; Liu, H.; Yu, X.; Liu, F. Recursive state estimation for time-varying complex networks subject to missing measurements and stochastic inner coupling under random access protocol. Neurocomputing 2019, 346, 48–57. [Google Scholar] [CrossRef]
- Hu, B.; Song, Q.; Zhao, Z. Robust state estimation for fractional-order complex-valued delayed neural networks with interval parameter uncertainties: LMI approach. Appl. Math. Comput. 2020, 373, 125033. [Google Scholar] [CrossRef]
- Alsaadi, F.E.; Wang, Z.; Wang, D.; Alsaadi, F.E.; Alsaade, F.W. Recursive fusion estimation for stochastic discrete time-varying complex networks under stochastic communication protocol: The state-saturated case. Inf. Fusion 2020, 60, 11–19. [Google Scholar] [CrossRef]
- Hu, W.X.; Ruan, Z.H.; Xiao, X.Y.; Xiong, X.Y.; Wang, J.Q. A novel voltage sag state estimation method based on complex network analysis. Int. J. Electr. Power Energy Syst. 2022, 140, 108119. [Google Scholar] [CrossRef]
- Lü, L.; Zhou, T. Link prediction in complex networks: A survey. Phys. A Stat. Mech. Its Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Yu, G.; Wan, Y.; Jiang, C. Complex network analysis on provincial innovation development in China. Appl. Math. Comput. 2023, 455, 128103. [Google Scholar] [CrossRef]
- Laumann, F.; von Kügelgen, J.; Uehara, T.H.K.; Barahona, M. Complex interlinkages, key objectives, and nexuses among the Sustainable Development Goals and climate change: A network analysis. Lancet Planet. Health 2022, 6, e422–e430. [Google Scholar] [CrossRef] [PubMed]
- Lü, L.; Li, C.; Bai, S.; Li, G.; Rong, T.; Gao, Y.; Yan, Z. Synchronization of uncertain time-varying network based on sliding mode control technique. Phys. A Stat. Mech. Its Appl. 2017, 482, 808–817. [Google Scholar] [CrossRef]
- Tong, L.; Liang, J.; Liu, Y. Generalized cluster synchronization of Boolean control networks with delays in both the states and the inputs. J. Frankl. Inst. 2022, 359, 206–223. [Google Scholar] [CrossRef]
- Aadhithiyan, S.; Raja, R.; Zhu, Q.; Alzabut, J.; Niezabitowski, M.; Lim, C.P. Exponential synchronization of nonlinear multi-weighted complex dynamic networks with hybrid time varying delays. Neural Process. Lett. 2021, 53, 1035–1063. [Google Scholar] [CrossRef]
- He, X.; Zhang, H. Exponential synchronization of complex networks via feedback control and periodically intermittent noise. J. Frankl. Inst. 2022, 359, 3614–3630. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Z.; Zhang, P.; Chen, M.; Wang, Y. Dynamic analysis and robust control of a chaotic system with hidden attractor. Complexity 2021, 2021, 8865522. [Google Scholar] [CrossRef]
- Li, X.; Wu, H.; Cao, J. Synchronization in finite time for variable-order fractional complex dynamic networks with multi-weights and discontinuous nodes based on sliding mode control strategy. Neural Netw. 2021, 139, 335–347. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Z.; Zhang, H.; Cao, Z.; Zhang, P. Dynamical analysis and fixed-time synchronization of a chaotic system with hidden attractor and a line equilibrium. Eur. Phys. J. Spec. Top. 2022, 231, 2455–2466. [Google Scholar] [CrossRef]
- Wang, Z.; Veeman, D.; Zhang, M.; Natiq, H.; Yang, R.; Hussain, I. A symmetric oscillator with multi-stability and chaotic dynamics: Bifurcations, circuit implementation, and impulsive control. Eur. Phys. J. Spec. Top. 2022, 231, 2153–2161. [Google Scholar] [CrossRef]
- Tian, H.; Liu, J.; Wang, Z.; Xie, F.; Cao, Z. Characteristic Analysis and Circuit Implementation of a Novel Fractional-Order Memristor-Based Clamping Voltage Drift. Fractal Fract. 2022, 7, 2. [Google Scholar] [CrossRef]
- Soudbakhsh, D.; Chakrabortty, A.; Annaswamy, A.M. A delay-aware cyber-physical architecture for wide-area control of power systems. Control Eng. Pract. 2017, 60, 171–182. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Zhang, G.; Xu, L. Dynamic spatio-temporal graph network with adaptive propagation mechanism for multivariate time series forecasting. Expert Syst. Appl. 2023, 216, 119374. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, Z.; Bohner, M.; Cao, J. Impulsive boundedness for nonautonomous dynamic complex networks with constraint nonlinearity. Appl. Math. Model. 2023, 115, 853–867. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Liu, L. Model Following Adaptive Control for a Class of Complex Dynamic Networks Based on the Dynamics of Links. Int. J. Control Autom. Syst. 2022, 20, 2202–2210. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, J.; Zhang, X.; Xiao, Z.; Tao, J.; Wang, X. Dynamic event-triggered synchronization of complex networks with switching topologies: Asynchronous observer-based case. Appl. Math. Comput. 2022, 435, 127413. [Google Scholar] [CrossRef]
- Wan, X.; Li, Y.; Li, Y.; Wu, M. Finite-time H state estimation for two-time-scale complex networks under stochastic communication protocol. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 25–36. [Google Scholar] [CrossRef]
- Hongsri, A.; Botmart, T.; Weera, W.; Junsawang, P. New delay-dependent synchronization criteria of complex dynamical networks with time-varying coupling delay based on sampled-data control via new integral inequality. IEEE Access 2021, 9, 64958–64971. [Google Scholar] [CrossRef]
- Motter, A.E. Networkcontrology. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 097621. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Wang, X.; Jiang, G.P. State estimation for multi-layer complex dynamical networks with time-varying delay. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; IEEE: New York, NY, USA, 2021; pp. 717–723. [Google Scholar]
- Wu, Y.; Wang, X.; Jiang, G.P.; Gu, M. Target layer state estimation in multilayer complex dynamical networks using functional observability. J. Frankl. Inst. 2023, 360, 8178–8199. [Google Scholar] [CrossRef]
- Berner, R.; Mehrmann, V.; Scholl, E.; Yanchuk, S. The multiplex decomposition: An analytic framework for multilayer dynamical networks. SIAM J. Appl. Dyn. Syst. 2021, 20, 1752–1772. [Google Scholar] [CrossRef]
- Liu, L.; Feng, M.; Xia, C.; Zhao, D.; Perc, M. Epidemic trajectories and awareness diffusion among unequals in simplicial complexes. Chaos Solitons Fractals 2023, 173, 113657. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Tian, H.; Wang, Z.; Wang, W.; Zhang, Y. Dynamical Analysis and Synchronization of Complex Network Dynamic Systems under Continuous-Time. Symmetry 2024, 16, 687. https://doi.org/10.3390/sym16060687
Yang R, Tian H, Wang Z, Wang W, Zhang Y. Dynamical Analysis and Synchronization of Complex Network Dynamic Systems under Continuous-Time. Symmetry. 2024; 16(6):687. https://doi.org/10.3390/sym16060687
Chicago/Turabian StyleYang, Rui, Huaigu Tian, Zhen Wang, Wei Wang, and Yang Zhang. 2024. "Dynamical Analysis and Synchronization of Complex Network Dynamic Systems under Continuous-Time" Symmetry 16, no. 6: 687. https://doi.org/10.3390/sym16060687




