Study of Non-Smooth Symmetry Collision of Rolling Bodies of Localized Functional-Slot Cage-Less Ball Bearings Considering Lubrication Flow
Abstract
1. Introduction
2. Modeling of Non-Smooth Bumper Vibration Considering Symmetry Collision of Neighboring Rolling Bodies with Oil Film Flow
2.1. Rolling Body Oil Film Flow Characterization
2.2. Modeling of Non-Smooth Vibrations of Adjacent Rolling Bodies
3. Dynamic Characterization of Rolling Bodies Considering Oil Film Flow
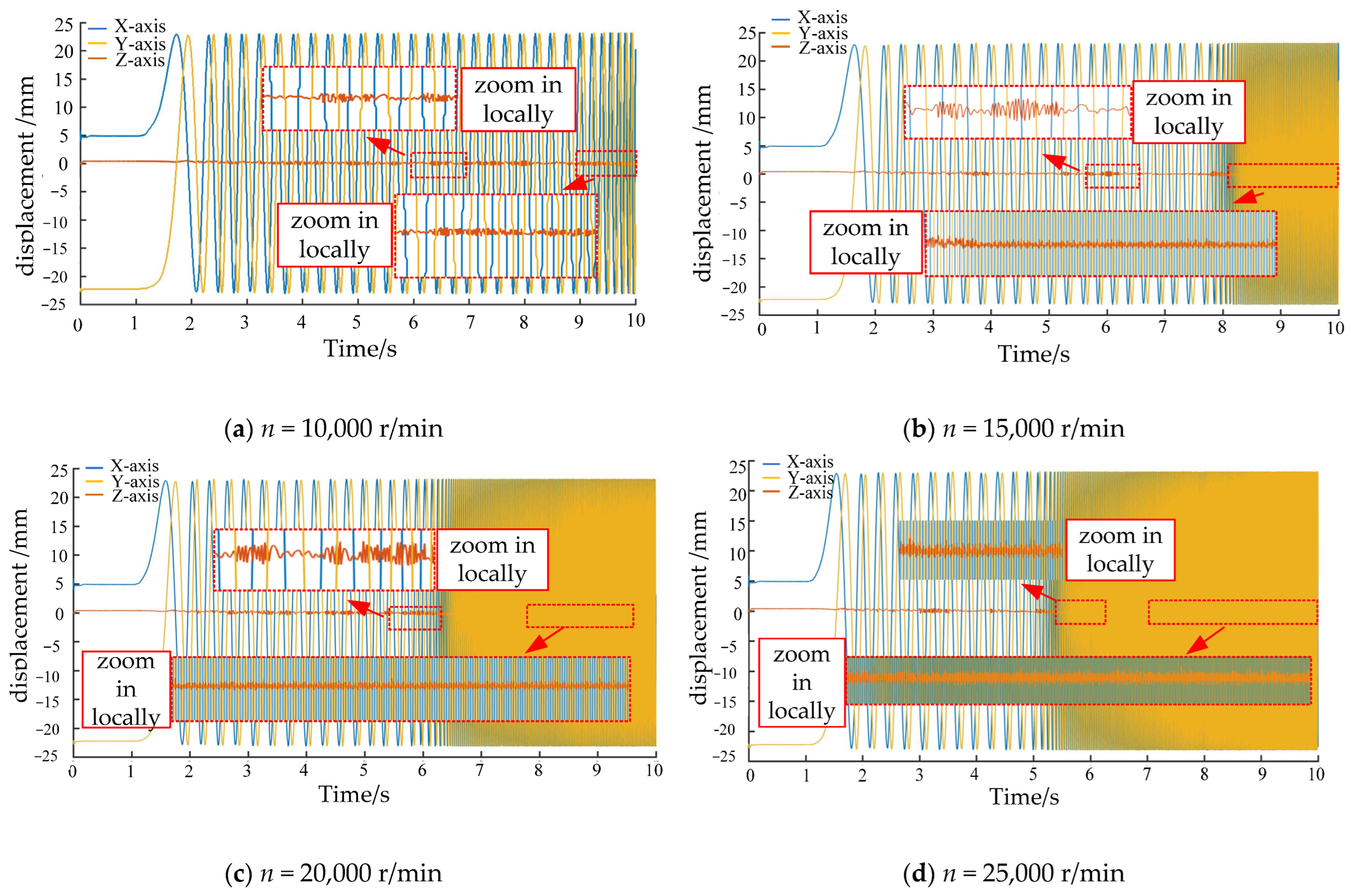
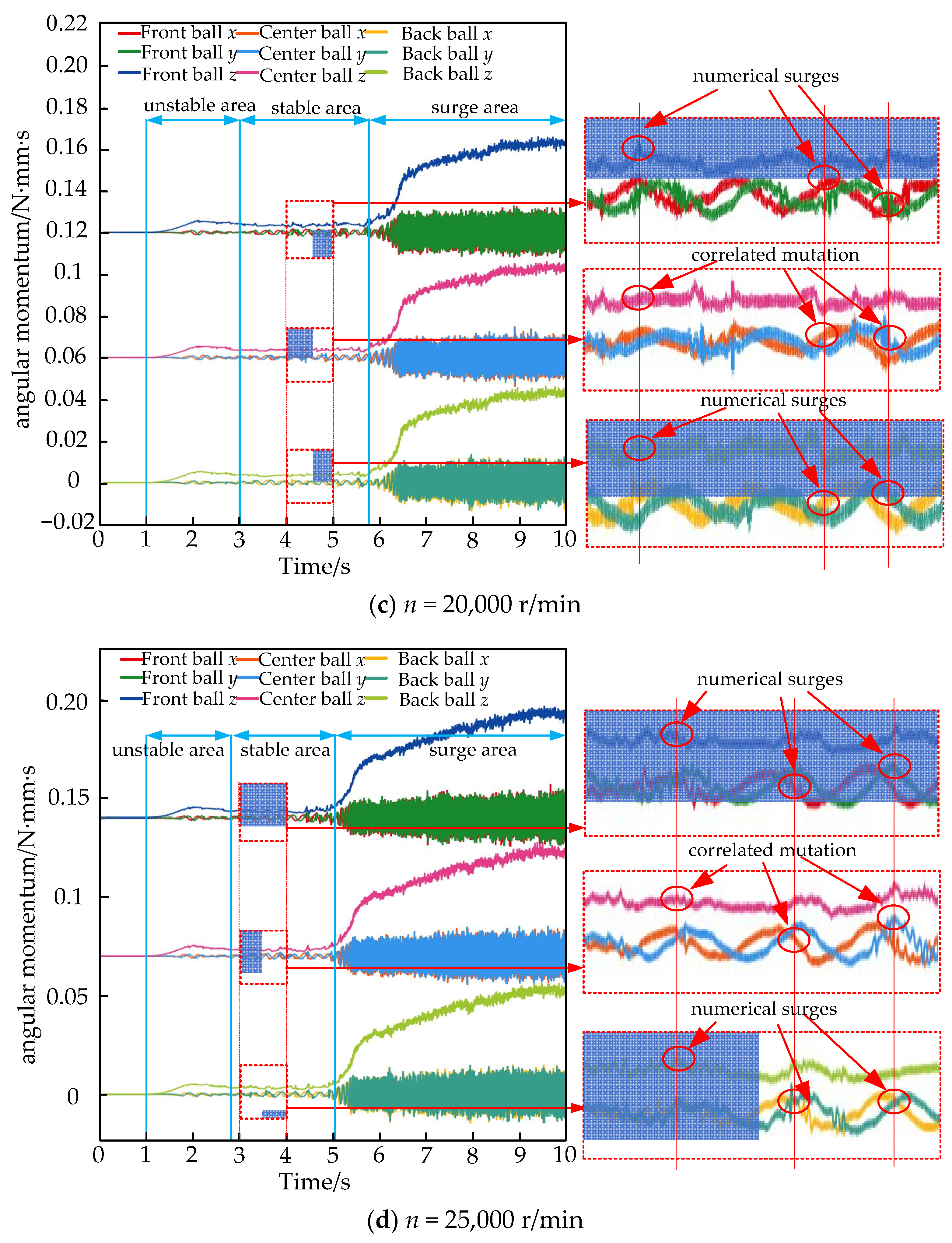
3.1. Rolling Body Displacement and Angular Attitude Analysis
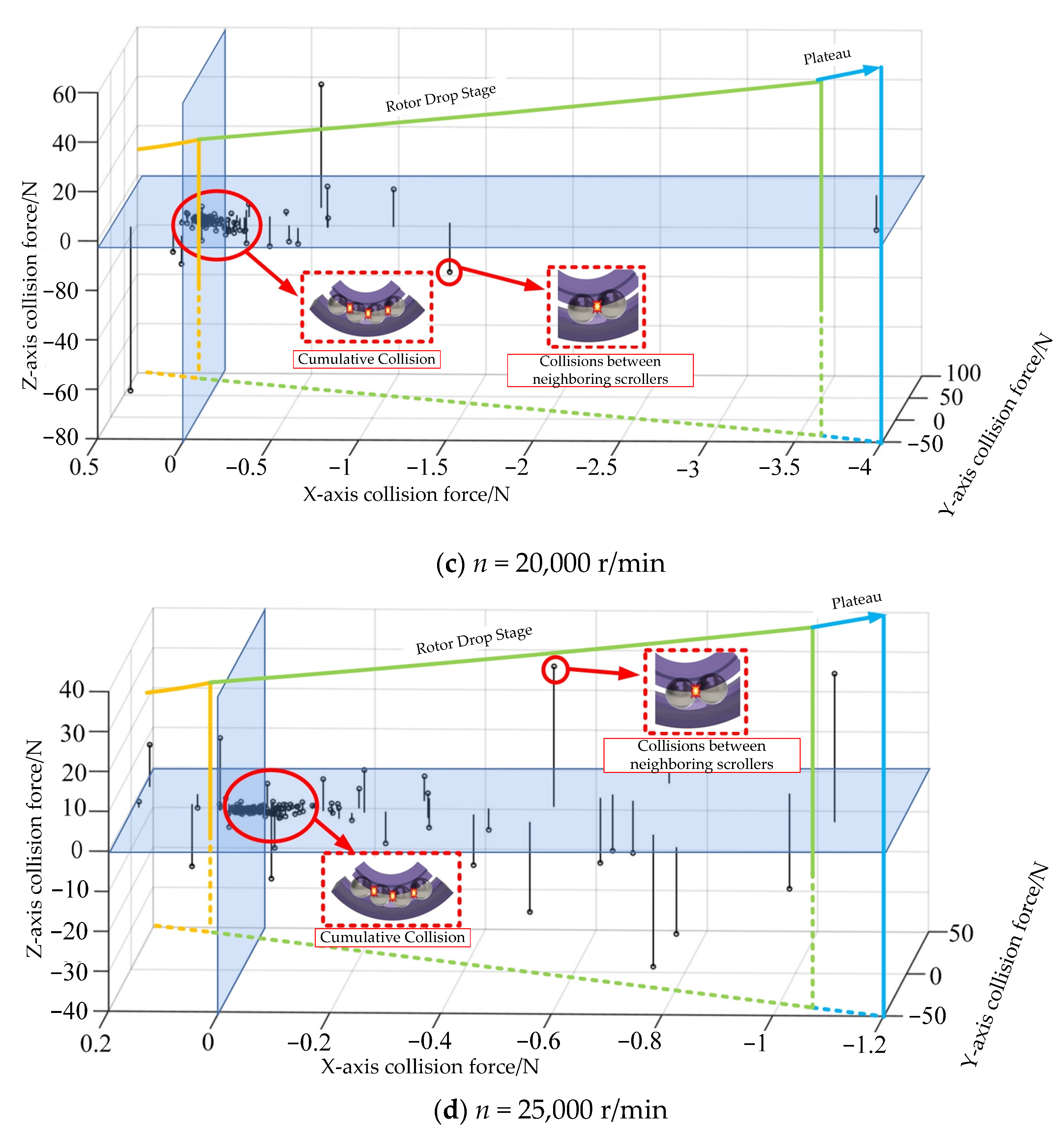
3.2. Rolling Body Overall Collision Form Analysis
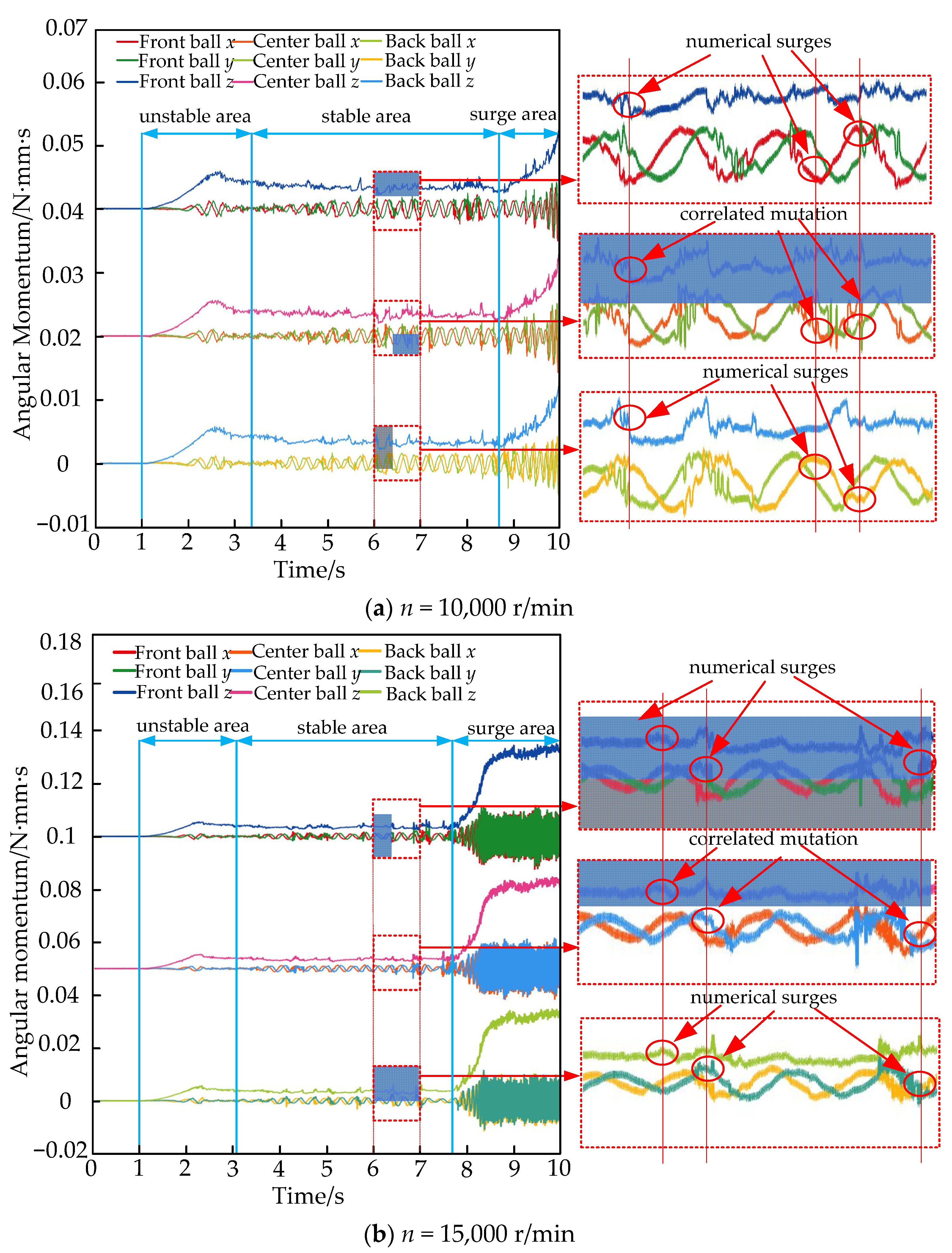
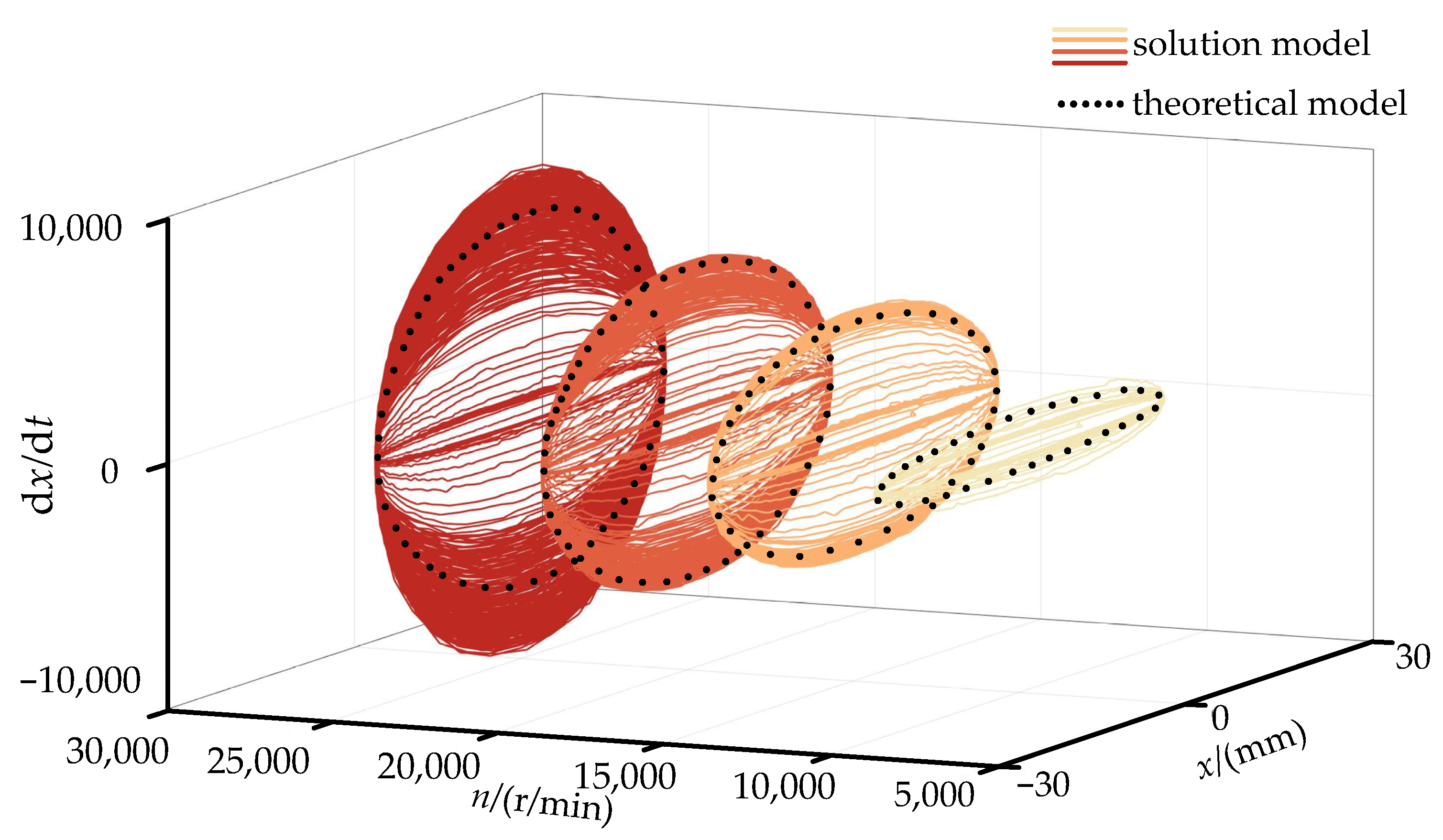
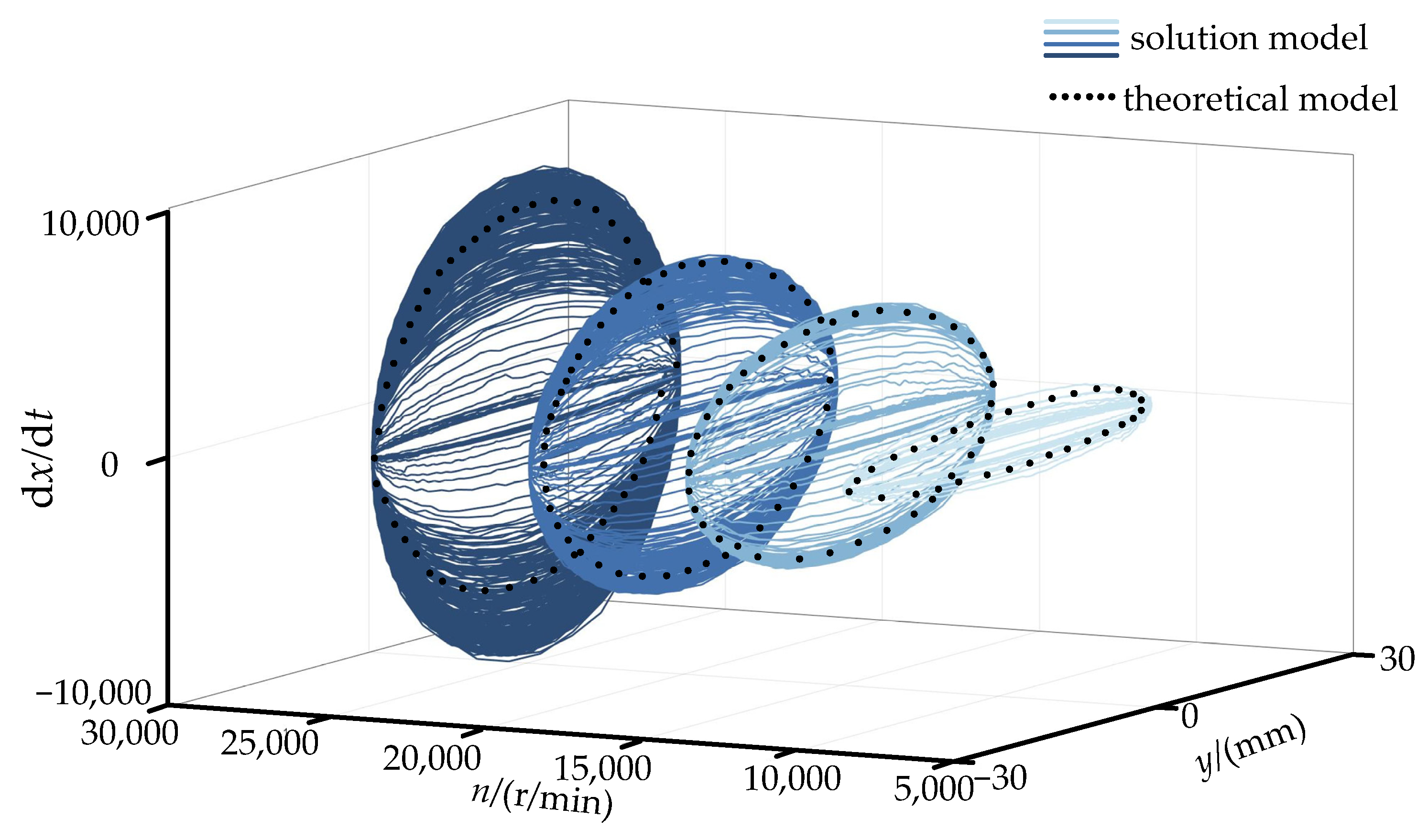
3.3. Chaotic Characterization of Rolling Body Motion
4. Experimental Study of Vibration Response of Adjacent Rolling Bodies
4.1. Vibration Response Experimental Program Design
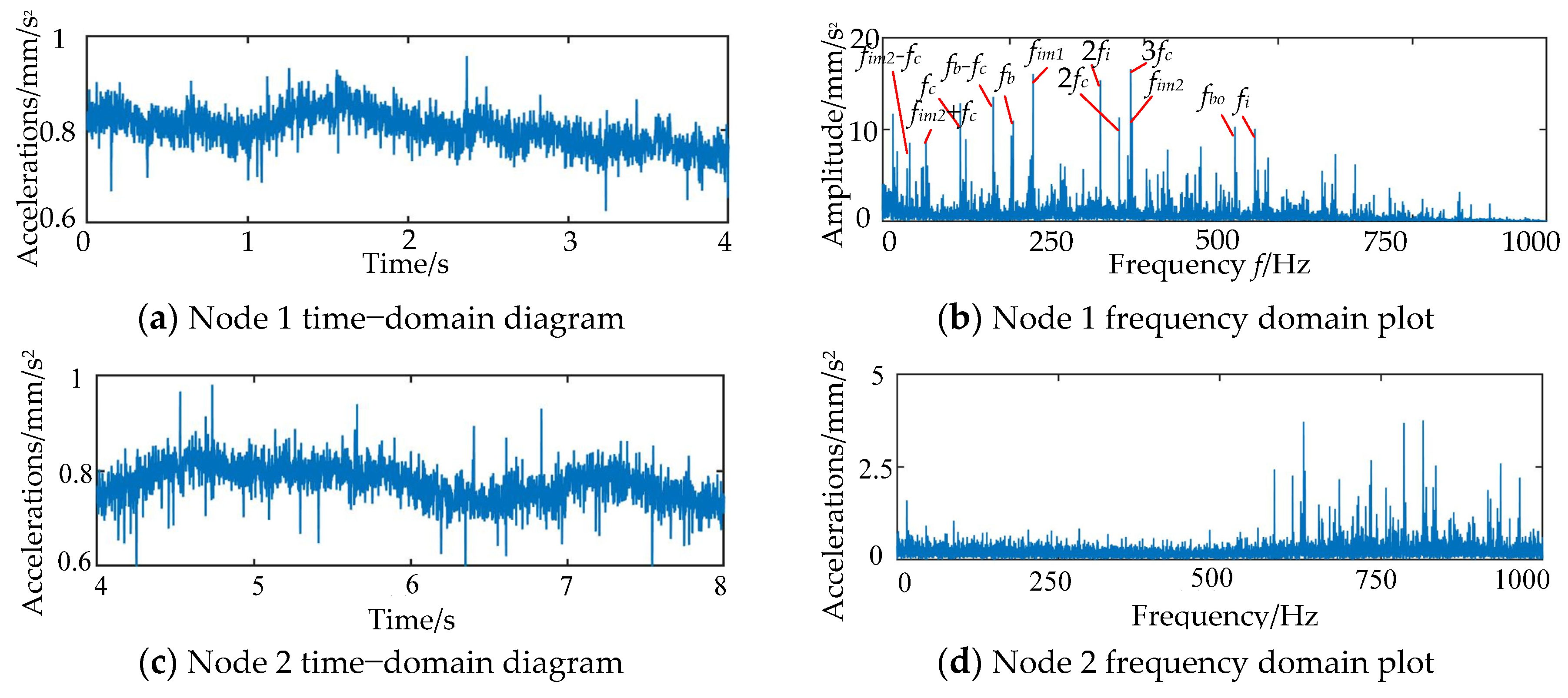
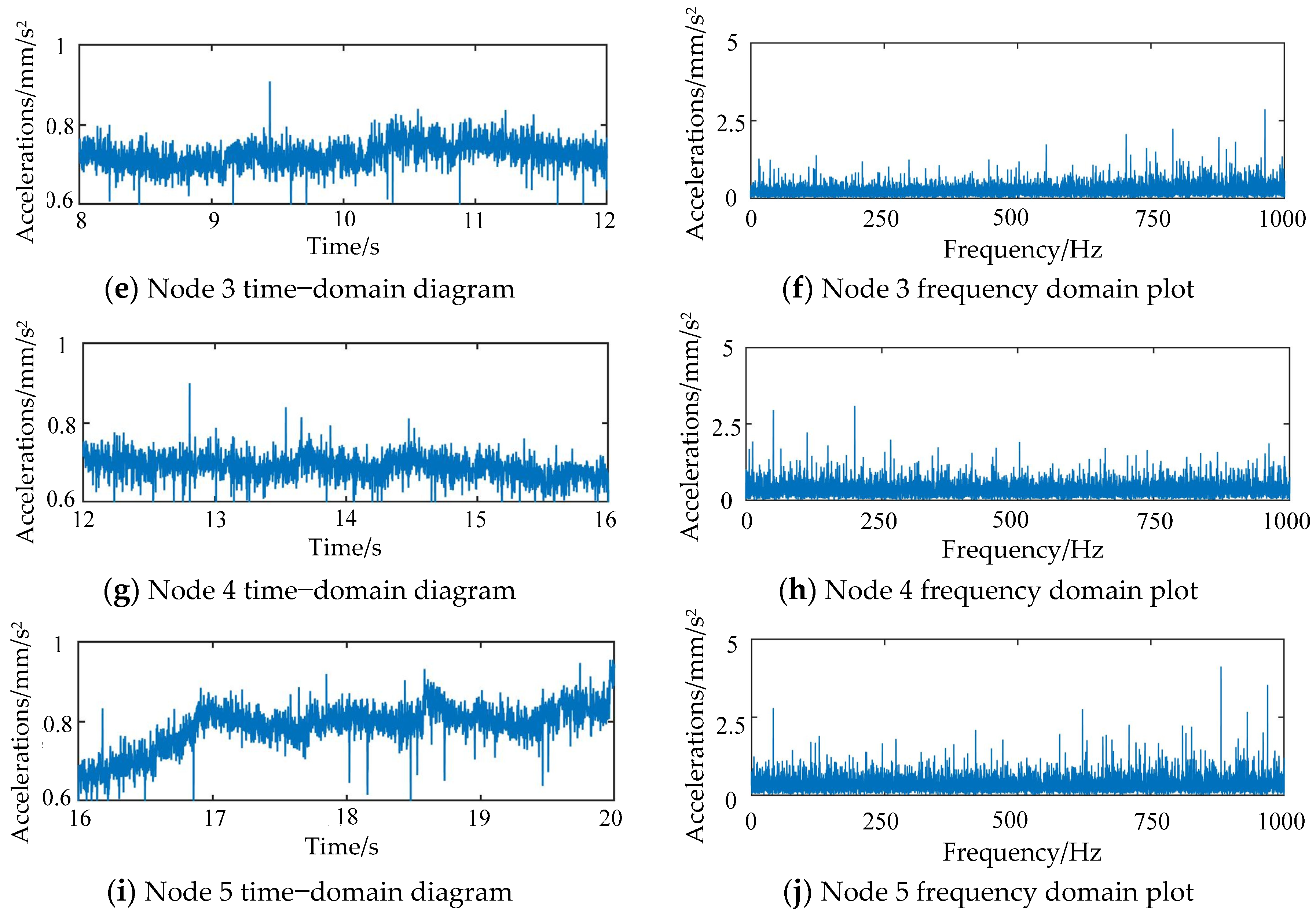
4.2. Analysis of Non-Smooth Vibration Response to Collision of Neighboring Rolling Bodies
5. Conclusions
- The characteristics of oil film flow were studied, along with the change in pressure of the oil film flow when two adjacent rolling bodies collided. This led to the creation of a multi-degree-of-freedom vibration model. The multi-degree-of-freedom vibration model was oriented and solved to describe the total collision, as well as the collision area and time of the two adjacent rolling bodies.
- Using the chaotic description of the non-smooth collision of rolling bodies, it was discovered that the effects of non-smooth collisions in different conditions on bearing operation can be described by a mix of motion chaos description and regular vibration experiments. At 25,000 r/min, the centrifugal force on the rolling body’s movement rises because the value goes up. This, in turn, determines how the change in rotor drop speed affects the collision that is not smooth.
- We looked into how stable the bearing operation is when the rolling body collides with it in a way that is not smooth. Experiments were performed, and the results showed that the bearing start-up stage has a higher frequency of characteristics. The rolling body will slip because of the cumulative collision, but as the speed goes up, the rolling body can gradually increase the speed of collision. As the speed goes up, the rolling bodies can be spread out more slowly and evenly, and the inner ring action is more stable.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Helfert, M. Analysis of anti-friction bearings by means of high-speed videography. Experimental analysis of the retainer bearing behavior after touchdown of a magnetically suspended rotor. Tribol. Und Schmier. 2008, 55, 10–15. [Google Scholar]
- Kawashima, S. Rolling Device and Using Method Thereof. U.S. Patent 8,783,958, 22 July 2014. [Google Scholar]
- Nie, A.; Li, Y.; Xia, W.; Qiu, M.; Huang, K. Study on the collision characteristics of protection bearings in active magnetic levitation bearing systems. Bearing 2022, 6, 30–37. [Google Scholar] [CrossRef]
- Halminen, O.; Aceituno, J.F.; Escalona, J.L.; Sopanen, J.; Mikkola, A. Models for dynamic analysis of backup ball bearings of an AMB-system. Mech. Syst. Signal Proc. 2017, 95, 324–344. [Google Scholar] [CrossRef]
- Halminen, O.; Kärkkäinen, A.; Sopanen, J.; Mikkola, A. Active magnetic bearing-supported rotor with misaligned cageless backup bearings: A dropdown event simulation model. Mech. Syst. Signal Process. 2015, 50, 692–705. [Google Scholar] [CrossRef]
- Kärkkäinen, A.; Sopanen, J.; Mikkola, A. Dynamic simulation of a flexible rotor during drop on retainer bearings. J. Sound Vibr. 2007, 306, 601–617. [Google Scholar] [CrossRef]
- Neisi, N.; Sikanen, E.; Heikkinen, J.E.; Sopanen, J. Stress analysis of a touchdown bearing having an artificial crack. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017; p. V008T012A034. [Google Scholar]
- Sun, G.; Palazzolo, A.; Provenza, A.; Montague, G. Detailed ball bearing model for magnetic suspension auxiliary service. J. Sound Vibr. 2004, 269, 933–963. [Google Scholar] [CrossRef]
- Jarroux, C.; Mahfoud, J.; Dufour, R.; Legrand, F.; Defoy, B.; Alban, T. Investigations on the dynamic behaviour of an on-board rotor-AMB system with touchdown bearing contacts: Modelling and experimentation. Mech. Syst. Signal Proc. 2021, 159, 107787. [Google Scholar] [CrossRef]
- Jarroux, C.; Dufour, R.; Mahfoud, J.; Defoy, B.; Alban, T.; Delgado, A. Touchdown bearing models for rotor-AMB systems. J. Sound Vibr. 2019, 440, 51–69. [Google Scholar] [CrossRef]
- Cole, M.; Keogh, P.; Burrows, C. The dynamic behavior of a rolling element auxiliary bearing following rotor impact. J. Trib. 2002, 124, 406–413. [Google Scholar] [CrossRef]
- Peta, K.; Bartkowiak, T.; Rybicki, M.; Galek, P.; Mendak, M.; Wieczorowski, M.; Brown, C.A. Scale-dependent wetting behavior of bioinspired lubricants on electrical discharge machined Ti6Al4V surfaces. Tribol. Int. 2024, 194, 109562. [Google Scholar] [CrossRef]
- Zhil’nikov, E.; Balyakin, V.; Lavrin, A. A method for calculating the frictional moment in cageless bearings. J. Frict. Wear 2018, 39, 400–404. [Google Scholar] [CrossRef]
- Townsend, D.P.; Allen, C.W.; Zaretsky, E.V. Friction losses in a lubricated thrust-loaded cageless angular-contract bearing. U.S. Patent NASA-TN-D-7356, 1 July 1973. [Google Scholar]
- Jones, W. Long Term Performance of a Retainerless Bearing Cartridge with an Oozing Flow Lubricator for Spacecraft Applications; TM-1074921997; NASA: Washington, DC, USA, 1997.
- Kingsbury, E. Ball-ball load carrying capacity in retainerless angular-contact bearings. J. Lubr. Technol. ASME 1982, 104, 327–329. [Google Scholar] [CrossRef]
- Li, Y.; Mo, J.; Zeng, J.; Xu, T.; Xu, S. Pure rolling design and dynamic characterization of a new type of cage-free ball bearing. J. Mech. Eng. 2023, 59, 256–269. [Google Scholar]
- Yang, J.; Tian, J.; Yu, J. Friction dynamics of water-lubricated bearings under transverse vibration. Lubr. Seal. 2023, 48, 95–104. [Google Scholar]
- Liu, T.; Li, R.; Zhang, S. Theoretical and experimental study on thermal fluid lubrication characteristics of woven dynamic bearing. China Surf. Eng. 2023, 36, 156–167. [Google Scholar]
- Zhang, G.; Zhao, Y.; Chen, X. Optimized design of anti-resonance thrust bearing and analysis of nonlinear effects of friction. Chinese Society of Vibration Engineering. In Proceedings of the 14th National Vibration Theory and Application Conference (NVTA2021), Tianjin, China, 22–24 October 2021. [Google Scholar] [CrossRef]
- Li, Z.; Pang, X.; Yan, Z.; Zhang, L. Study on the wear characteristics of rolling bearings due to rolling-sliding motion. Mech. Transm. 2021, 45, 10–17. [Google Scholar] [CrossRef]
- Adamczak, S.; Zmarzły, P. Research of the Influence of the 2d and 3d Surface Roughness Parameters of Bearing Raceways on the Vibration Level. J. Phys. Conf. Ser. 2019, 1183, 012001. [Google Scholar] [CrossRef]
- Zheng, G. Research on Surface Damage and Diagnosis Methods of Rolling Bearings; Southwest Jiaotong University: Chengdu, China, 2022. [Google Scholar]
- Yang, J.; Bu, J.; Tong, W. Research on the Spalling and Expansion Characteristics of Outer Ring of Ball Bearings Based on Abrasion Particle Analysis. J. Aerodyn. 2024, 39, 1–8. [Google Scholar] [CrossRef]
- Luo, M.; Guo, Y.; Wu, X. Dynamic modeling of the double impact phenomenon of peeling defects on the outer ring of ball bearings considering impact force. Vib. Shock. 2019, 38, 48–54. [Google Scholar]
- Jamadar, I.M.; Suresha, B.; Samal, P.K.; Bellary, S.A.I. Dimensional Amplitude Response Analysis of Vibrations Produced by Defects in Rolling Contact Bearings. Sound Vib. 2022, 56, 165–191. [Google Scholar] [CrossRef]
- Lu, Y. Dynamic modeling and simulation of peeling fault in deep slot ball bearings. J. Hubei Univ. Technol. 2023, 38, 34–38+54. [Google Scholar]
- McFadden, P.; Smith, J. Model for the Vibration Produced by a Single Point Defect in a Rolling Element Bearing. J. Sound Vib. 1984, 96, 69–82. [Google Scholar] [CrossRef]
- Fan, J.; Cui, W.; Han, Q. Vibration Signal Modeling of a Localized Defective Rolling Bearing under Unbalanced Force Excitations. J. Vibroeng. 2017, 19, 5009–5019. [Google Scholar] [CrossRef]
- Behzad, M.; Bastami, A.R.; Mba, D. A New Model for Estimating Vibrations Generated in the Defective Rolling Element Bearings. J. Vib. Acoust. 2011, 133, 041011. [Google Scholar] [CrossRef]
- Liu, J.; Shao, Y.; Zhu, W. A New Model for the Relationship between Vibration Characteristics Caused by the Time-Varying Contact Stiffness of a Deep slot Ball Bearing and Defect Sizes. J. Tribol. 2015, 137, 031101. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Zhou, E. Research on multi-body dynamic model of automatic discrete system for protection bearing without cage. Nonlinear Dyn. 2023, 111, 20869–20897. [Google Scholar] [CrossRef]
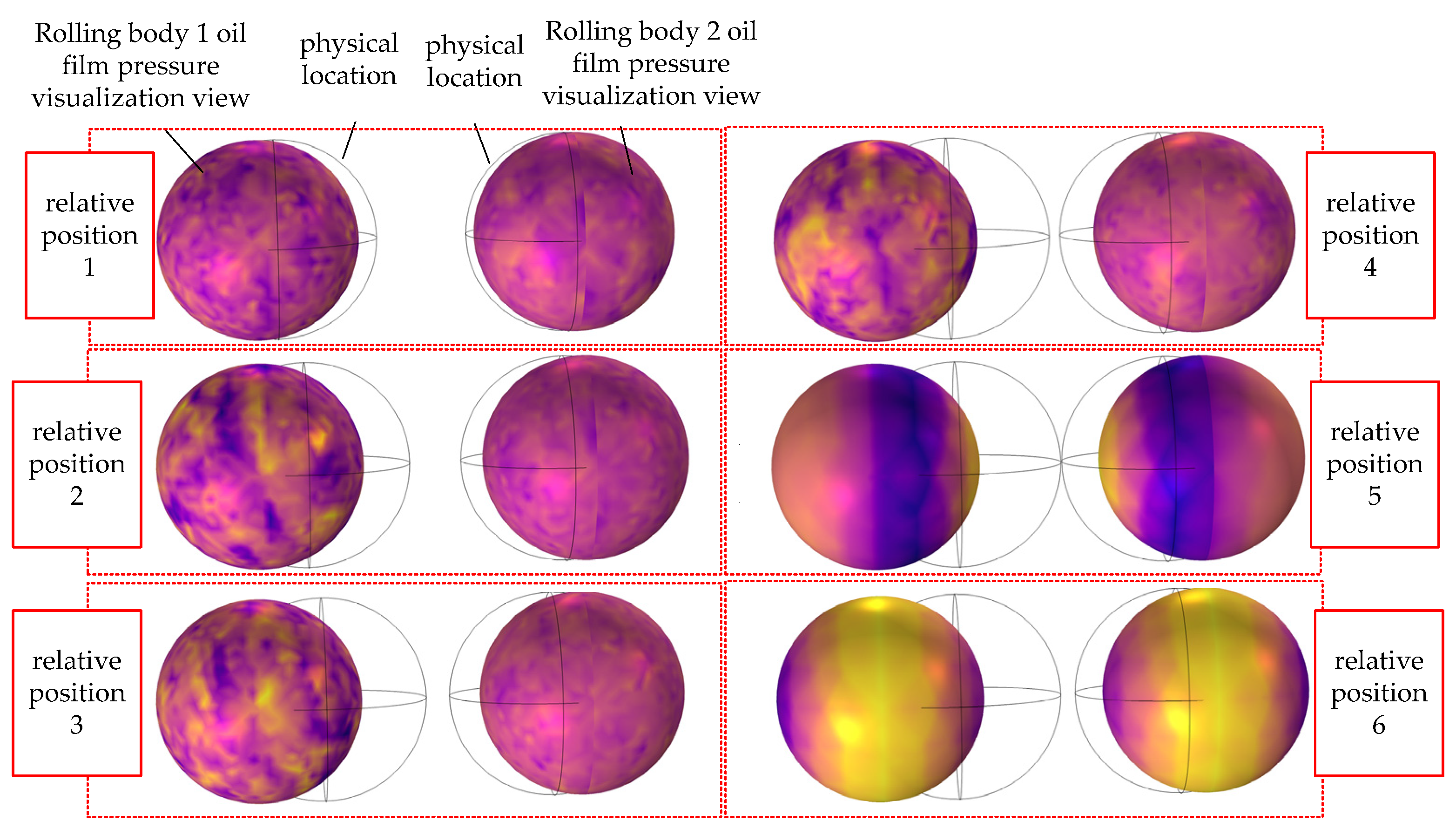
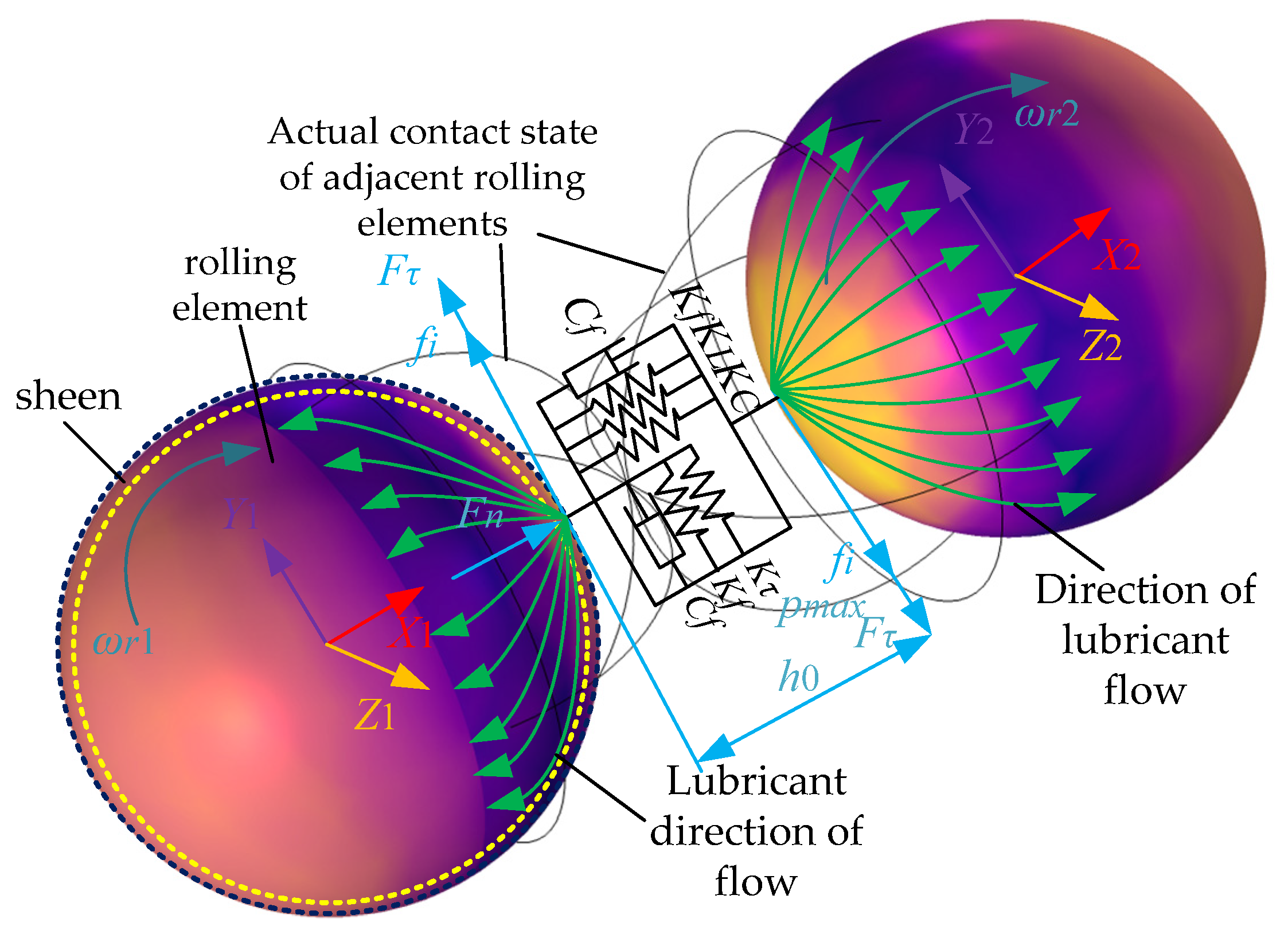




| Parameters | Numerical Value |
|---|---|
| Rolling body 1 modulus of elasticity E1/GPa | 207 |
| Rolling body 2 modulus of elasticity E2/GPa | 207 |
| Initial lubricant viscosity η0/Pa·s | 0.050 |
| Lubricant viscous pressure coefficient α/m2/N | 1.85 × 10−8 |
| Poisson’s ratio for rolling stock υ1 | 0.29 |
| Initial lubricant density ρ0/kg/m3 | 992 |
| Parameters | Numerical Value |
|---|---|
| Poisson’s ratio for rolling stock/υ1 | 0.29 |
| Number of scrollers/Z | 14 |
| Inside diameter d/mm | 30 |
| Outer diameter D/mm | 62 |
| Height B/mm | 16 |
| Rolling body radius r/mm | 4.7625 |
| Rolling body mass m/kg | 0.01 |
| Radial load Fr/N | 2000 |
| Axial load Fa/N | 200 |
| Rotation speed n/(r/min) | 10,000/15,000/20,000/25,000 |
| Poisson’s ratio for rolling stock µ1 | 0.29 |
| Poisson’s ratio of inner and outer ring µ2 | 0.3 |
| Localized functional slot Poisson’s ratio µ3 | 0.3 |
| Initial lubricant density ρ0 | 992 kg/m3 |
| Initial lubricant viscosity η0 | 0.050 Pa·s |
| Modulus of elasticity of a rolling body E | 207 GPa |
| Modulus of elasticity of inner and outer ring E/Mpa | 208,000 |
| Lubricant viscous pressure coefficient α | 1.85 × 10−8 m2/N |
| Orientations | 10,000 r/min | 15,000 r/min | 20,000 r/min | 25,000 r/min |
|---|---|---|---|---|
| x-directional | 4.5933 | 4.2011 | 3.9126 | 3.9158 |
| y-directional | 4.6431 | 4.2613 | 3.9350 | 3.9094 |
| z-directional | 7.6814 | 7.9442 | 7.9972 | 8.6271 |
| Expressed Symbol | Designation | Numerical Value | Unit |
|---|---|---|---|
| Z | Number of rolling bodies | 14 | number |
| Wu | Local function slot width | 3.5 | mm |
| Lu | Local function slot length | 11.5 | mm |
| Hu | Local function slot depth | 1 | mm |
| Dm | Pitch circle diameter | 46.005 | mm |
| Di | Inner ring slot bottom diameter | 36.48 | mm |
| ri | Radius of curvature of inner ring slot bottom | 4.905 | mm |
| Dw | Rolling body diameter | 9.525 | mm |
| Do | Outer ring slot bottom diameter | 55.53 | mm |
| ro | Radius of curvature of outer ring slot bottom | 4.953 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, Y.; Guan, L.; Zhang, Y.; Yang, S. Study of Non-Smooth Symmetry Collision of Rolling Bodies of Localized Functional-Slot Cage-Less Ball Bearings Considering Lubrication Flow. Symmetry 2024, 16, 741. https://doi.org/10.3390/sym16060741
Zhang J, Wang Y, Guan L, Zhang Y, Yang S. Study of Non-Smooth Symmetry Collision of Rolling Bodies of Localized Functional-Slot Cage-Less Ball Bearings Considering Lubrication Flow. Symmetry. 2024; 16(6):741. https://doi.org/10.3390/sym16060741
Chicago/Turabian StyleZhang, Jingwei, Yibo Wang, Linting Guan, Yuan Zhang, and Shanping Yang. 2024. "Study of Non-Smooth Symmetry Collision of Rolling Bodies of Localized Functional-Slot Cage-Less Ball Bearings Considering Lubrication Flow" Symmetry 16, no. 6: 741. https://doi.org/10.3390/sym16060741
APA StyleZhang, J., Wang, Y., Guan, L., Zhang, Y., & Yang, S. (2024). Study of Non-Smooth Symmetry Collision of Rolling Bodies of Localized Functional-Slot Cage-Less Ball Bearings Considering Lubrication Flow. Symmetry, 16(6), 741. https://doi.org/10.3390/sym16060741





