Study on Neutrosophic Graph with Application on Earthquake Response Center in Japan
Abstract
:1. Introduction
1.1. Motivation
- The goal of creating a new mathematical technique for the fusion is to provide a more adaptable method for solving real-time issues.
- Graph theory and neutrosophic sets are used to improve the knowledge by constructing s, which opens up new avenues for using mathematical techniques.
- By investigating ideas such as union, join, and composition of and sophisticated homeomorphisms, difficult situations can be handled more easily, offering useful information for real-world issue resolution.
- Japan’s placement near the Pacific Ring of Fire makes it vulnerable to earthquakes. To lessen the effects of a disaster, efficient earthquake response centers must be established. In these areas, neutrophilic graph theory helps improve the modeling and analysis of complex networks by taking uncertainty in decision-making processes, communication pathways, and resource allocation into account.
1.2. Need
- While rough sets, fuzzy sets, and other generalizations of fuzzy sets are most important and often used in various applications, neutrosophic sets and neutrosophic graphs are especially well-suited for addressing the problems associated with ambiguity, indeterminacy, and uncertainty in specific contexts, such as earthquake response planning, because of their special qualities.
- In Japan’s earthquake response centers, MADM models, especially those based on neutrosophic logic, are crucial because they give decision-makers a methodical framework for assessing difficult choices in the face of uncertainty, taking stakeholder preferences into account, weighing trade-offs, and supporting adaptive decision-making. Response centers can improve their capacity to efficiently handle and lessen the effects of earthquakes on impacted areas by utilizing these techniques.
1.3. Advantages and Limitations
- Neutrosophic graphs, as opposed to conventional crisp or fuzzy graphs, can depict uncertainty in a more subtle way. They make it possible to explicitly describe information that is true, untrue, or uncertain, which helps decision-makers more correctly model and reason about uncertain relationships.
- By grading graph elements according to degrees of truth, indeterminacy, and falsity, neutrosophic graphs offer a detailed depiction of uncertainty. Because of its granularity, decision-makers are better equipped to analyze and make decisions by capturing even the smallest differences in the degree of uncertainty.
- Neutrosophic graph analysis can be computationally demanding and complicated, especially in large-scale systems with many interconnected parts. Non-experts may not be able to analyze or understand neutrosophic graph topologies due to the need for certain knowledge and experience.
- Neutronosophic graph models can be difficult to validate and verify for accuracy and reliability, especially when benchmark datasets or ground truth are lacking. Conducting sensitivity studies and establishing strong validation procedures are crucial for evaluating the effectiveness and real-world applications of neutrosophic graph-based methods.
1.4. Contributions of the Study
2. Neutrosophic Graph
- 1.
- The functions and are mappings from V to the closed interval , signifying the degrees of true, intermediate, and false membership, in that order for each element . It holds that , for all .
- 2.
- Moreover, in the context of G, the functions and are mappings from to the closed interval [0, 1], representing the degrees of true, intermediate, and false membership, in that order for each edge .
- 1.
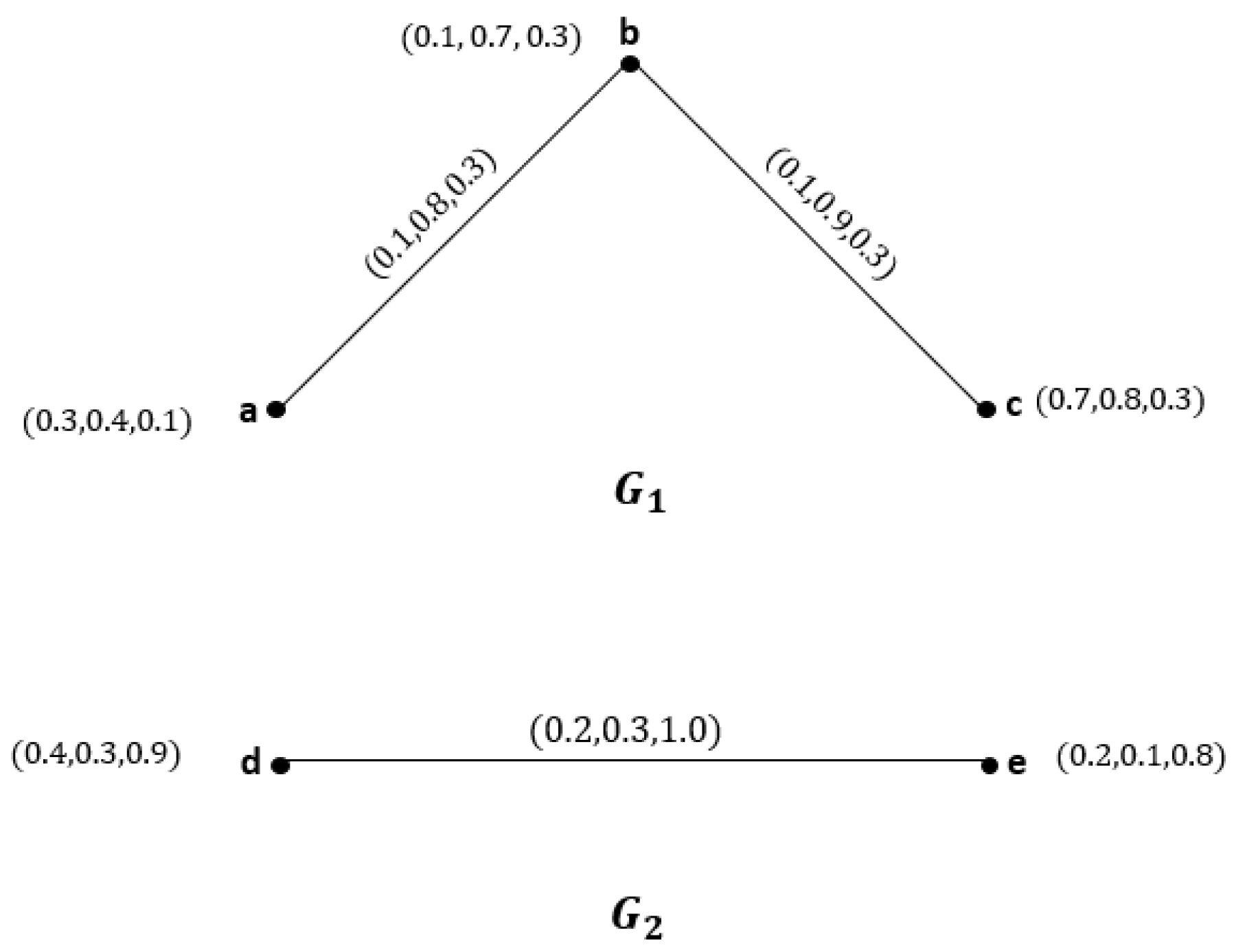
- Figure 1 is a , as may be observed from basic computations.
- 2.
- 3.
- Each vertex in G has a degree of
- D(a) = (0.2, 1.0, 1.2)
- D(b) = (0.4, 1.4, 0.8)
- D(c) = (0.4, 1.0, 0.7)
- D(d) = (0.1, 0.3, 0.6)
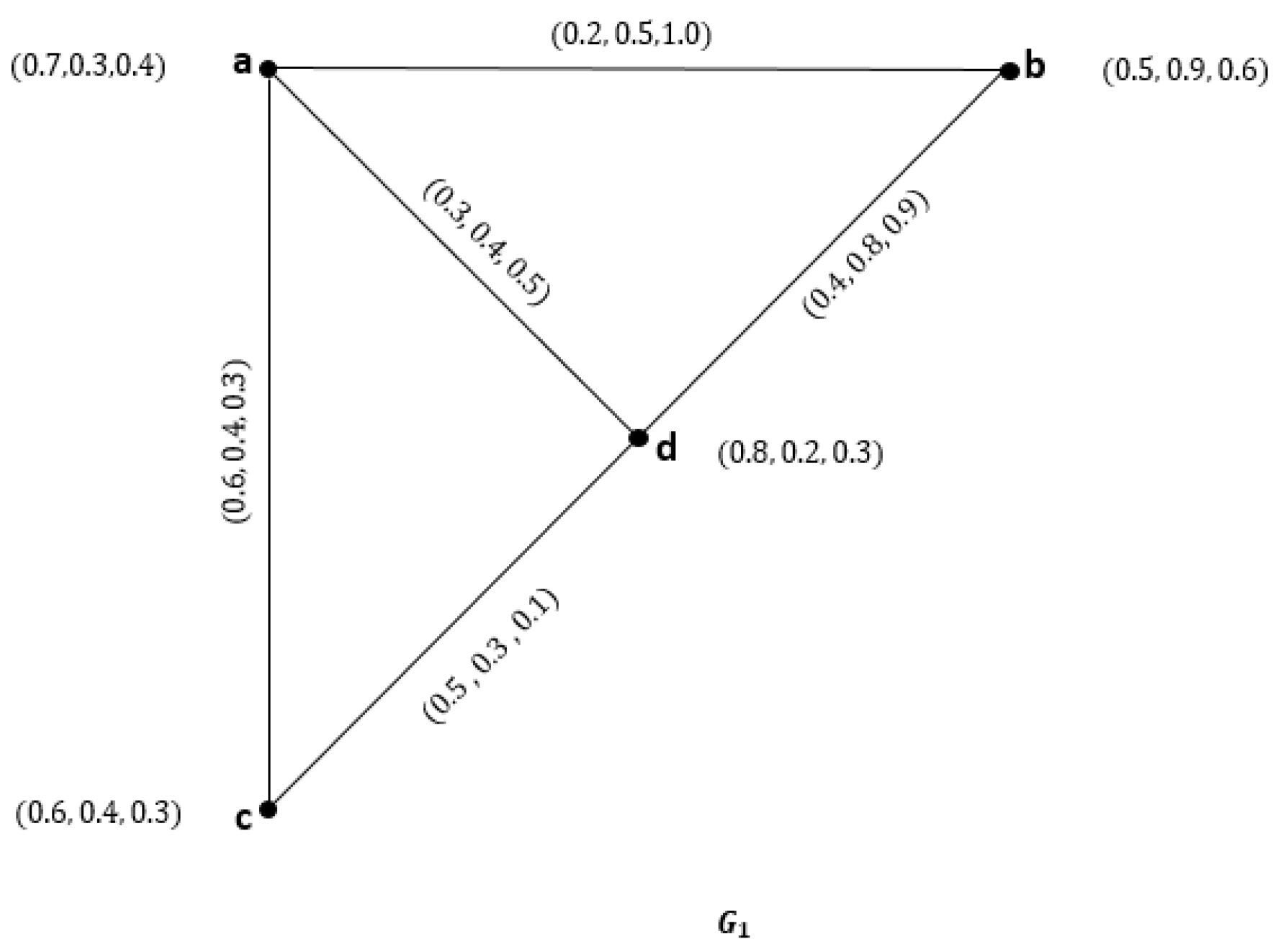
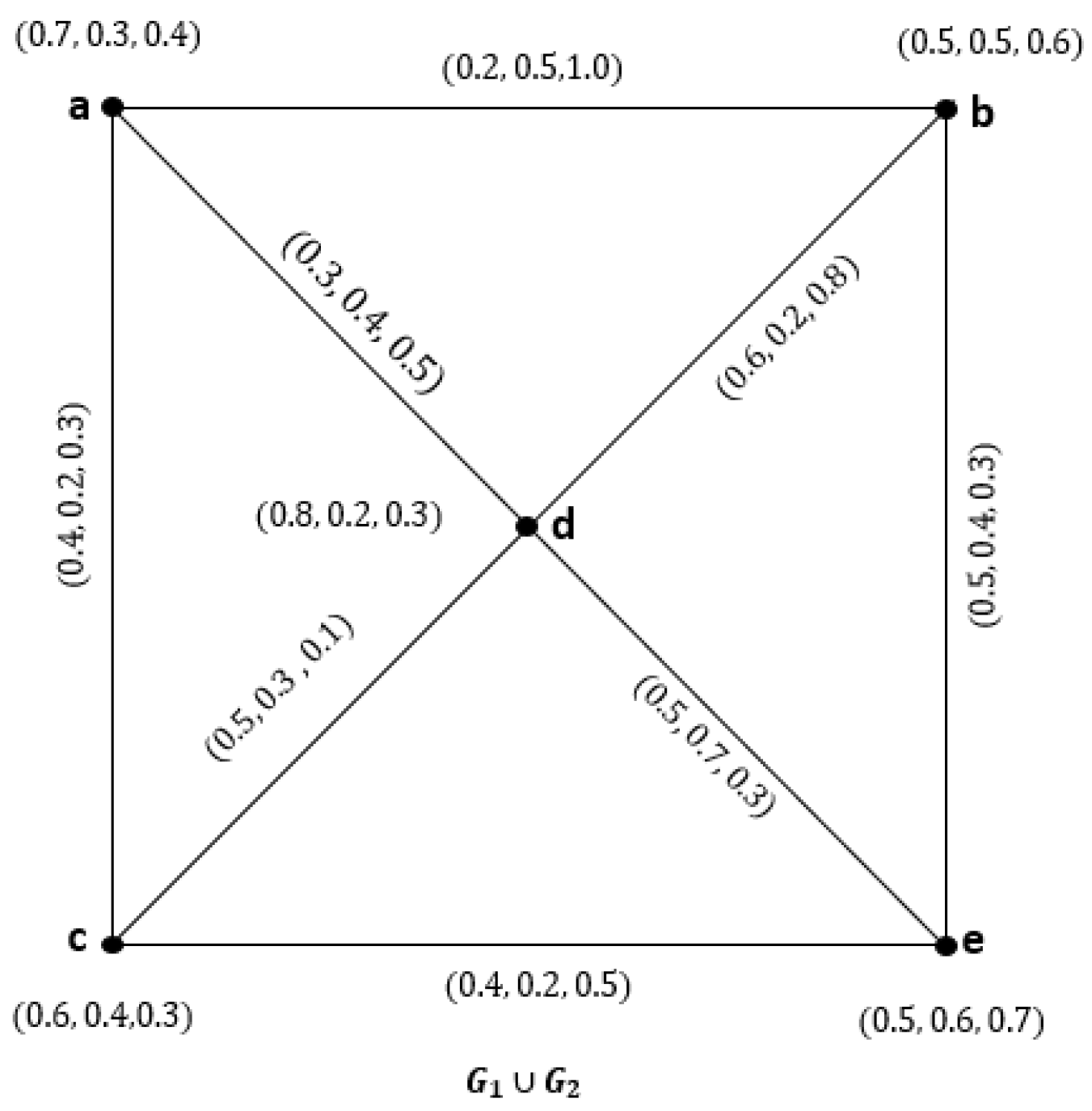
- 1.
- , for & .
- 2.
- , for & .
- 3.
- .
- 4.
- , for & .
- 5.
- , for & .
- 6.
- .
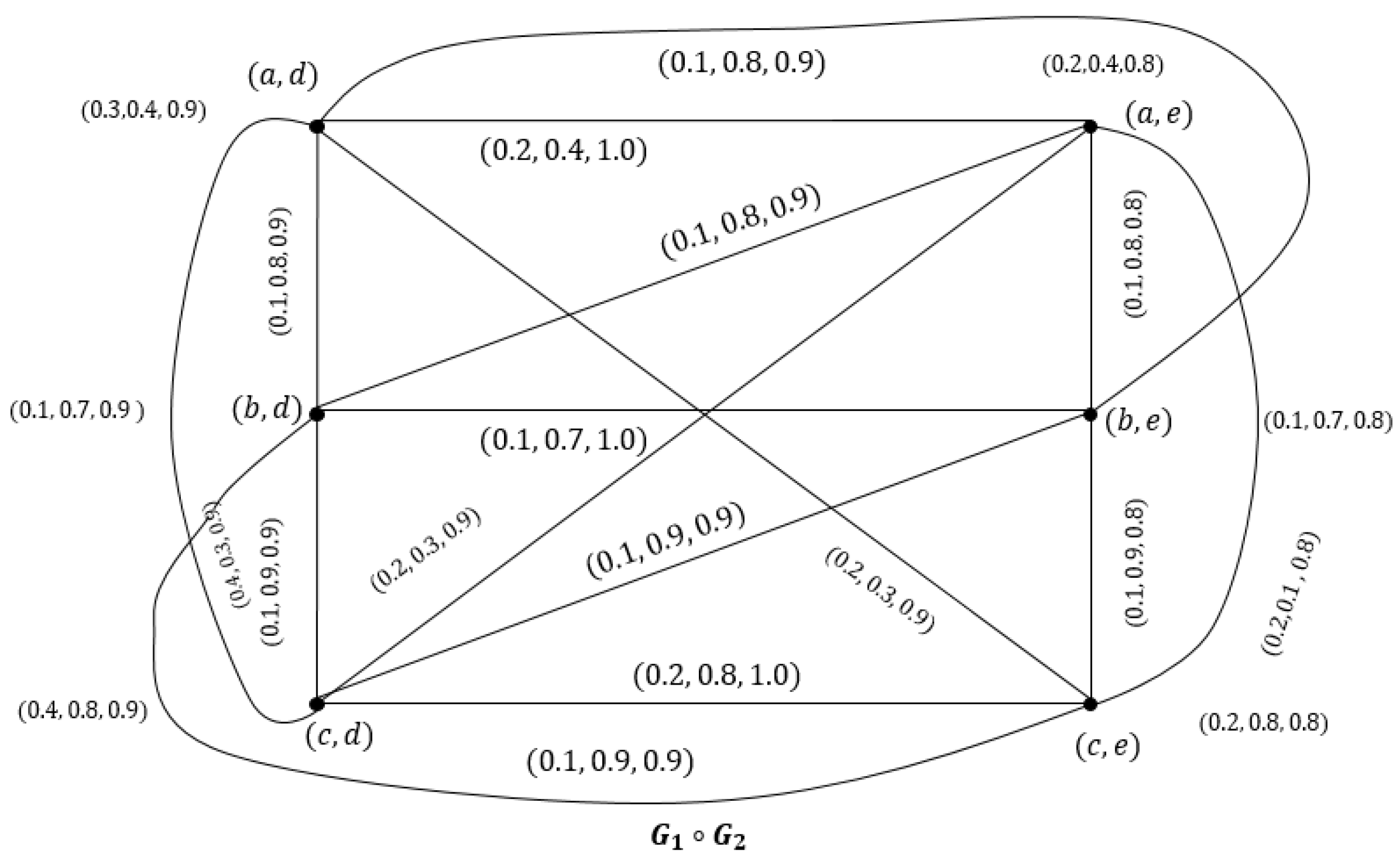
- 1.
- , if .
- 2.
- , for .
- 3.
- , if . Where E is the collection of all edges connecting & vertices.
3. Isomorphism of s
- 1.
- 2.
- A bijective homomorphism with the property
- 3.
- is called a week isomorphism.A bijective homomorphism with the property
- 4.
- is called a strong co-isomorphism. A bijective mapping satisfying 3 and 4 is called an isomorphism.
4. Complement of s
- 1.
- 2.
- 3.
5. Application
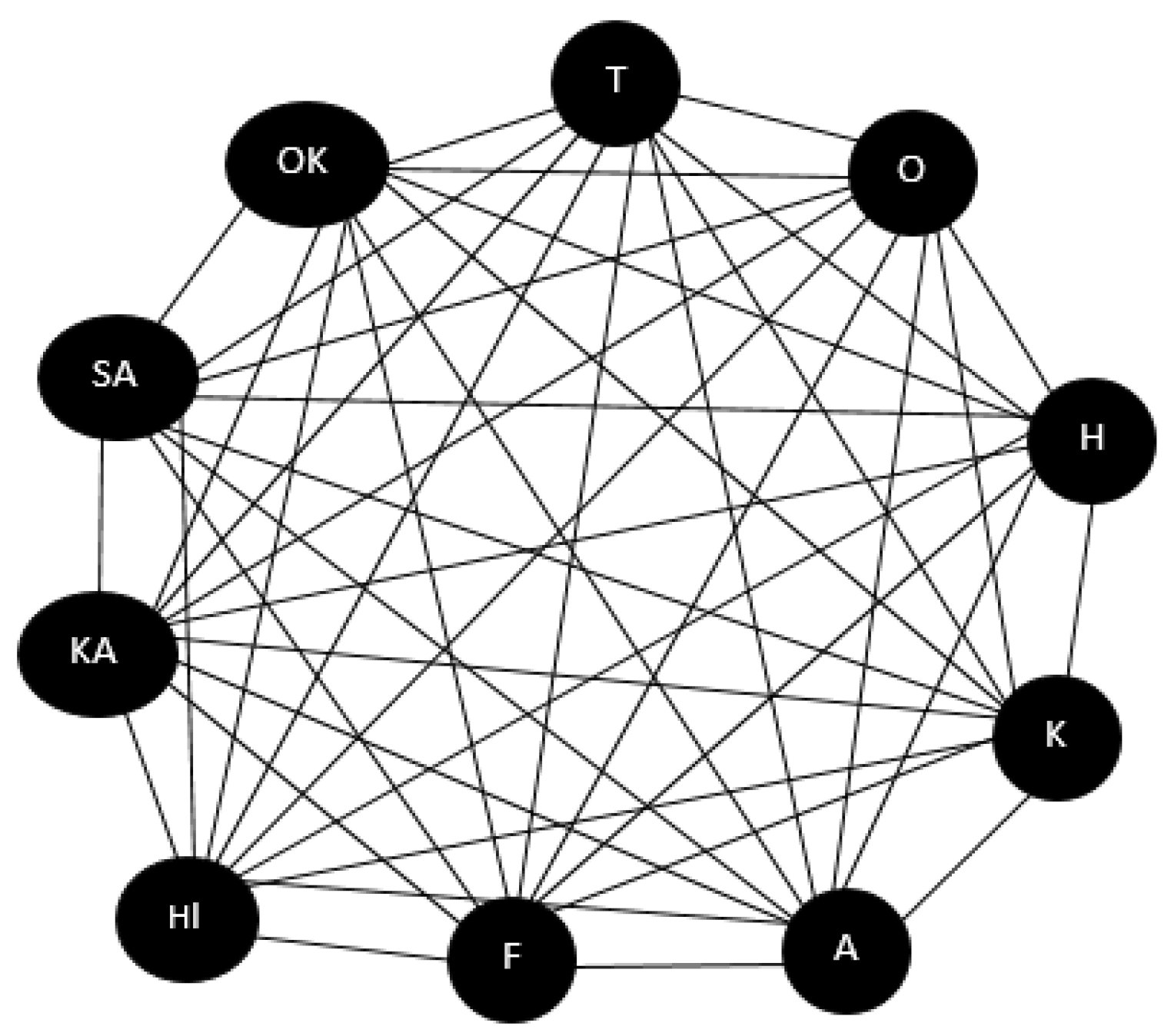
- Situation (i): Building Earthquake-Resistant Facilities in 10 Chosen Regions
- Situation (ii): Building an intermediary earthquake response center between any two chosen Regions.
5.1. Comparative Analysis
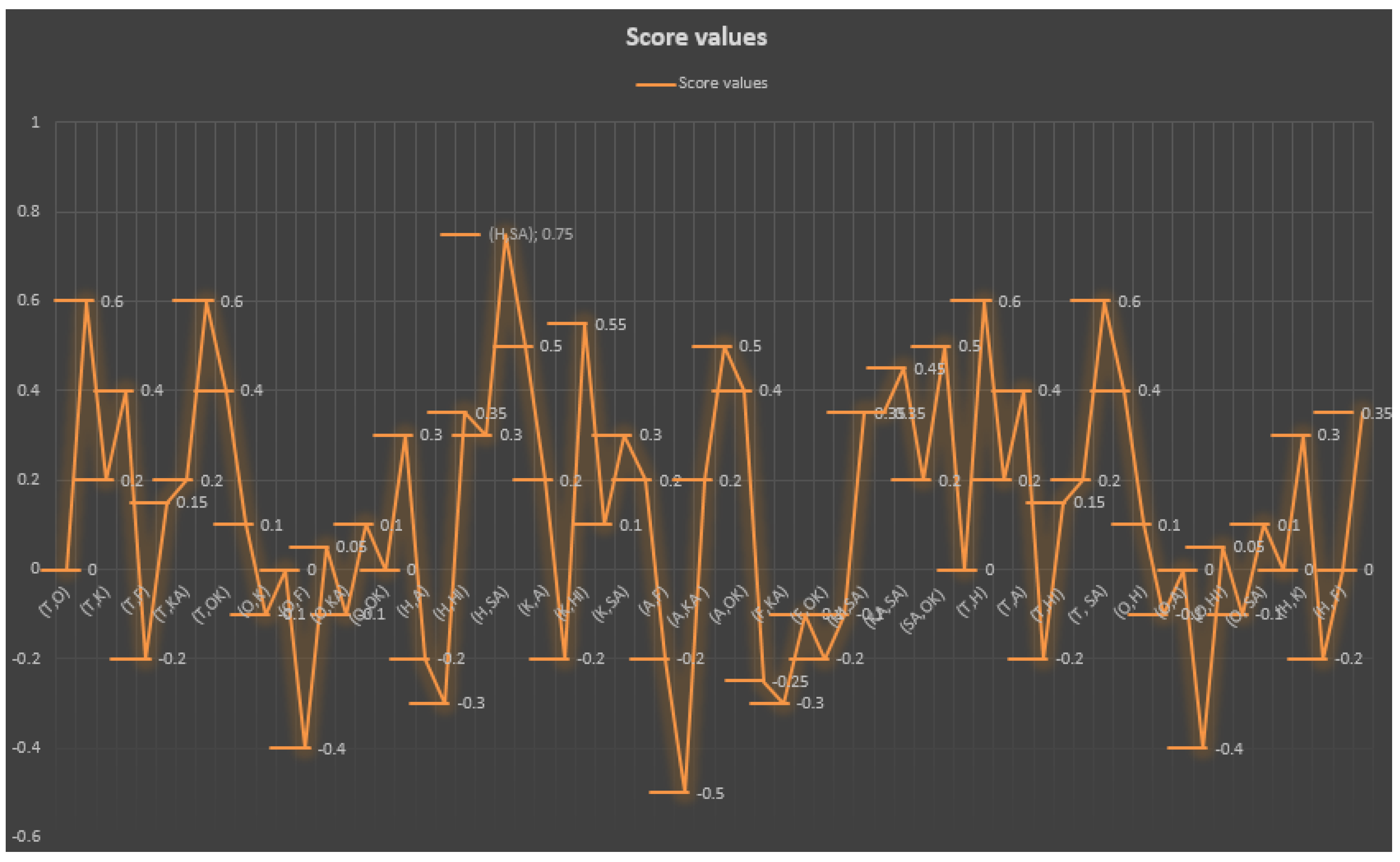
5.2. Connections and Discussions of the Results
6. Conclusions
- Certain types of super hyper s.
- Dominating energy in hyper s
- Maximal product of super hyper and its real time applications.
- Operation of super hyper .
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov Krassimir, T. Intuitionistic fuzzy sets. In Intuitionistic Fuzzy Sets; Springer: New York, NY, USA, 2019; pp. 1–137. [Google Scholar]
- Smarandache, F. A unifying field in logics: Neutrosophic logic. In Philosophy; American Research Press: New York, NY, USA, 1999; pp. 1–141. [Google Scholar]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability and Statistics, 6th ed.; InfoLearnQuest: Philadelphia, PA, USA, 2007. [Google Scholar]
- Borzooei, R.A.; Rashmanlou, H.; Samanta, S.; Pal, M. Regularity of vague graphs. J. Intell. Fuzzy Syst. 2016, 30, 3681–3689. [Google Scholar] [CrossRef]
- Waseem, N.; Dudek, W.A. Certain types of edge m-polar fuzzy graphs. Iran. J. Fuzzy Syst. 2017, 14, 27–50. [Google Scholar]
- Ghorai, G.; Pal, M. Certain types of product bipolar fuzzy graphs. Int. J. Appl. Comput. Math. 2017, 3, 605–619. [Google Scholar] [CrossRef]
- Naz, S.; Rashmanlou, H.; Malik, M.A. Operations on single valued ℵGs with application. J. Intell. Fuzzy Syst. 2017, 32, 2137–2151. [Google Scholar] [CrossRef]
- Sahoo, S.; Pal, M. Different types of products on intuitionistic fuzzy graphs. Pac. Sci. Rev. A Nat. Sci. Eng. 2015, 17, 87–96. [Google Scholar] [CrossRef]
- Yang, H.-L.; Guo, Z.-L.; She, Y.; Liao, X. On single valued neutrosophic relations. J. Intell. Fuzzy Syst. 2006, 30, 1045–1056. [Google Scholar] [CrossRef]
- Ye, J. Single-valued neutrosophic minimum spanning tree and its clustering method. J. Intell. Syst. 2014, 23, 311–324. [Google Scholar] [CrossRef]
- Shannon, A.; Atanassov, K. On a generalization of intuitionistic fuzzy graphs. NIFS 2006, 12, 24–29. [Google Scholar]
- Parvathi, R.; Karunambigai, M.G. Intuitionistic fuzzy graphs. In Computational Intelligence, Theory and Applications; Springer: New York, NY, USA, 2006; pp. 139–150. [Google Scholar]
- Parvathi, R.; Karunambigai, M.G.; Atanassov, K.T. Operations on intuitionistic fuzzy graphs. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju, Republic of Korea, 20–24 August 2009; pp. 1396–1401. [Google Scholar]
- Parvathi, R.; Thamizhendhi, G. Domination in intuitionistic fuzzy graphs. Notes Intuit Fuzzy Sets 2010, 16, 39–49. [Google Scholar]
- Rashmanlou, H.; Borzooei, R.A.; Samanta, S.; Pal, M. Properties of interval valued intuitionistic (s, t)–fuzzy graphs. Pac. Sci. Rev. A Nat. Sci. Eng. 2016, 18, 30–37. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Samanta, S.; Pal, M.; Borzooei, R.A. Bipolar fuzzy graphs with categorical properties. Int. J. Comput. Intell. Syst. 2015, 8, 808–818. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Samanta, S.; Pal, M.; Borzooei, R.A. Intuitionistic fuzzy graphs with categorical properties. Fuzzy Inf. Eng. 2015, 7, 317–334. [Google Scholar] [CrossRef]
- Smarandache, F. Extension of hypergraph to n-superhypergraph and to plithogenic n-superhypergraph, and extension of hyperalgebra to n-ary hyperalgebra. Neutrosophic Sets Syst. 2020, 33, 290–296. [Google Scholar]
- Akram, M. Certain bipolar neutrosophic competition graphs. J. Indones. Math. Soc. 2017, 24, 1–25. [Google Scholar] [CrossRef]
- Akram, M.; Akmal, R. Operations on intuitionistic fuzzy graph structures. Fuzzy Inf. Eng. 2016, 8, 389–410. [Google Scholar] [CrossRef]
- Akram, M.; Dar, J.M.; Naz, S. Certain graphs under pythagorean fuzzy environment. Complex Intell. Syst. 2019, 5, 127–144. [Google Scholar] [CrossRef]
- Akram, M.; Habib, A.; Ilyas, F.; Dar, J.M. Specific types of pythagorean fuzzy graphs and application to decision-making. Math. Comput. Appl. 2018, 23, 42. [Google Scholar] [CrossRef]
- Akram, M.; Naz, S. Energy of pythagorean fuzzy graphs with applications. Mathematics 2018, 6, 136. [Google Scholar] [CrossRef]
- Akram, M.; Siddique, S. Neutrosophic competition graphs with applications. J. Intell. Fuzzy Syst. 2017, 33, 921–935. [Google Scholar] [CrossRef]
- Karaaslan, F.; Hayat, K.; Jana, C. The Determinant and Adjoint of an Interval-Valued Neutrosophic Matrix. In Neutrosophic Operational Research; Smarandache, F., Abdel-Basset, M., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Hayat, K.; Cao, B.-Y.; Ali, M.I.; Karaaslan, F.; Qin, Z. Characterizations of Certain Types of Type 2 Soft Graphs. Discret. Dyn. Nat. Soc. 2018, 2018, 8535703. [Google Scholar] [CrossRef]
- Karaaslan, F.; Hayat, K. Some new operations on single-valued neutrosophic matrices and their applications in multi-criteria group decision making. Appl. Intell. 2018, 48, 4594–4614. [Google Scholar] [CrossRef]
- Majeed, A.S.; Arif, N.E. Topological indices of certain neutrosophic graphs. Aip Conf. Proc. 2023, 2845, 060024. [Google Scholar]
- Kaviyarasu, M. On r-Edge Regular Neutrosophic Graphs. Neutrosophic Sets Syst. 2023, 53, 239–250. [Google Scholar]
- AL-Omeri, W.F.; Kaviyarasu, M.; Rajeshwari, M. Identifying Internet Streaming Services using Max Product of Complement in Neutrosophic Graphs. Int. J. Neutrosophic Sci. 2024, 3, 257–272. [Google Scholar] [CrossRef]
- Yaqoob, N.; Gulistan, M.; Kadry, S.; Wahab, H.A. Complex Intuitionistic Fuzzy Graphs with Application in Cellular Network Provider Companies. Mathematics 2019, 7, 35. [Google Scholar] [CrossRef]
- Mahapatra, R.; Samanta, S.; Pal, M.; Xin, Q. Link Prediction in Social Networks by Neutrosophic Graph. Int. J. Comput. Intell. Syst. 2020, 13, 1699–1713. [Google Scholar] [CrossRef]
- Srisarkun, V.; Jittawiriyanukoon, C. An approximation of balanced score in neutrosophic graphs with weak edge weights. Int. J. Electr. Comput. Eng. 2021, 11, 5286–5291. [Google Scholar] [CrossRef]
- Mahapatra, R.; Samanta, S.; Pal, M. Edge Colouring of Neutrosophic Graphs and Its Application in Detection of Phishing Website. Discret. Dyn. Nat. Soc. 2022, 2022, 1149724. [Google Scholar] [CrossRef]
- Quek, S.G.; Selvachandran, G.; Ajay, D.; Chellamani, P.; Taniar, D.; Fujita, H.; Duong, P.; Son, L.H.; Giang, N.L. New concepts of pentapartitioned neutrosophic graphs and applications for determining safest paths and towns in response to COVID-19. Comp. Appl. Math. 2022, 41, 151. [Google Scholar] [CrossRef]
- Alqahtani, M.; Kaviyarasu, M.; Al-Masarwah, A.; Rajeshwari, M. Application of Complex Neutrosophic Graphs in Hospital Infrastructure Design. Mathematics 2024, 12, 719. [Google Scholar] [CrossRef]
- Wang, J.-q.; Wang, J.; Chen, Q.-h.; Zhang, H.-y.; Chen, X.-h. An outranking approach for multi-criteria decision-making with hesitant fuzzy linguistic term sets. Inf. Sci. 2014, 280, 338–351. [Google Scholar] [CrossRef]
- Şahin, R. Multi-criteria neutrosophic decision making method based on score and accuracy functions under neutrosophic environment. Inf. Sci. 2014, 280, 338–351. [Google Scholar]
- Broumi, S.; Sundareswaran, R.; Shanmugapriya, M.; Bakali, A.; Talea, M. Theory and Applications of Fermatean Neutrosophic Graphs. Neutrosophic Sets Syst. 2002, 50, 248–286. [Google Scholar]




| Reference | Year | Techniques | Solved Problem |
|---|---|---|---|
| [32] | 2018 | Complex Intuitionistic Fuzzy Graphs | Cellular network provider companies for the testing of our approach. |
| [33] | 2020 | graph | Modified RSM index |
| [34] | 2021 | Find weak edge weights | |
| [35] | 2022 | Edge Colouring of | To identify the phishing website |
| [36] | 2022 | Pentapartitioned | Determining safest paths |
| [37] | 2024 | Complex | Hospital Infrastructure Design |
| Present | 2024 | Decision-Making and the Proposal for an Earthquake Response Center in Japan |
| Locations | Neutrosophic Membership Values | Locations | Neutrosophic Membership Values |
|---|---|---|---|
| |T-O| | (0.5, 0.2, 0.3) | |T-H| | (0.8, 0.1, 0.1) |
| |T-K| | (0.6, 0.2, 0.2) | |T-A| | (0.7, 0.2, 0.1 |
| |T-F| | (0.4, 0.2, 0.4) | |T-HI| | (0.5, 0.15, 0.5) |
| |T-KA| | (0.6, 0.2, 0.2) | |T-SA| | (0.8, 0.1, 0.1) |
| |T-OK| | (0.7, 0.2, 0.1) | |O-H| | (0.5, 0.1, 0.3) |
| |O-K| | (0.5, 0.3, 0.3) | |O-A| | (0.5, 0.2, 0.3) |
| |O-F| | (0.4, 0.4, 0.4) | |O-HI| | (0.5, 0.15, 0.3) |
| |O-KA| | (0.5, 0.3, 0.3) | |O-SA| | (0.5, 0.1, 0.3) |
| |O-OK| | (0.5, 0.2, 0.3) | |H-K| | (0.6, 0.1, 0.2) |
| |H-A| | (0.4, 0.1, 0.5) | |H-F| | (0.4, 0.1, 0.8) |
| |H-HI| | (0.5, 0.1, 0.05) | |H-KA| | (0.6, 0.1, 0.2) |
| |H-SA| | (0.9, 0.1, 0.05) | |H-OK| | (0.7, 0.1, 0.1) |
| |K-A| | (0.6, 0.2, 0.2) | |K-F| | (0.4, 0.2, 0.4) |
| |K-HI| | (0.5, 0.15, 0.2) | |K-KA| | (0.6, 0.3, 0.2) |
| |K-SA| | (0.6, 0.1, 0.2) | |K-OK| | (0.6, 0.2, 0.2) |
| |A-F| | (0.4, 0.2, 0.4) | |A-HI| | (0.5, 0.15, 0.4) |
| |A-KA| | (0.6, 0.2, 0.2) | |A-SA| | (0.7, 0.1, 0.1) |
| |A-OK| | (0.7,0.2, 0.1) | |F-HI| | (0.4, 0.15, 0.5) |
| |F-KA| | (0.4, 0.3, 0.4) | |F-SA| | (0.4, 0.1, 0.4) |
| |F-OK| | (0.4, 0.2, 0.4) | |HI-KA| | (0.5, 0.1, 0.5) |
| |HI-SA| | (0.5, 0.1, 0.05) | |HI-OK| | (0.5, 0.1, 0.05) |
| |KA-SA| | (0.6, 0.1, 0.05) | |KA-OK| | (0.6, 0.2, 0.2) |
| |SA-OK| | (0.7, 0.1, 0.1) | - | - |
| Edges | Score Functions | Edges | Score Functions |
|---|---|---|---|
| S(T-O) | 0 | S(T,H) | 0.6 |
| S(T-K) | 0.2 | S(T,A) | 0.4 |
| S(T-F) | −0.2 | S(T,HI) | 0.15 |
| S(T-KA) | 0.2 | S(T,SA) | 0.6 |
| S(T-OK) | 0.4 | S (O,H) | 0.1 |
| S(O-K) | −0.1 | S(O,A) | 0 |
| S(O-F) | −0.4 | S(O,HI) | 0.05 |
| S(O-KA) | −0.1 | S(O,SA) | 0.1 |
| S(O-OK) | 0 | S(H,K) | 0.3 |
| S(H-A) | −0.2 | S(H,F) | −0.3 |
| (H-HI) | 0.35 | S(H,KA) | 0.3 |
| S(H-SA) | 0.75 | S(H,OK) | 0.5 |
| S(K-A) | 0.2 | S(K,F) | −0.2 |
| S(K-HI) | 0.55 | S(K,KA) | 0.1 |
| S(K-SA) | 0.3 | S(K,OK) | 0.2 |
| S(A-F) | −0.2 | S(A,HI) | −0.5 |
| S(A-KA) | 0.2 | S(A,SA) | 0.5 |
| S(A-OK) | 0.4 | S(F,HI) | −0.25 |
| S(F-KA) | −0.3 | S(F,SA) | 0.1 |
| S(F-OK) | −0.2 | S(HI,KA) | −0.1 |
| S(HI-SA) | 0.35 | S(HI,OK) | 0.35 |
| S(KA-SA) | 0.45 | S(KA,OK) | 0.2 |
| S(SA-OK) | 0.5 | – | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AL-Omeri, W.F.; Kaviyarasu, M. Study on Neutrosophic Graph with Application on Earthquake Response Center in Japan. Symmetry 2024, 16, 743. https://doi.org/10.3390/sym16060743
AL-Omeri WF, Kaviyarasu M. Study on Neutrosophic Graph with Application on Earthquake Response Center in Japan. Symmetry. 2024; 16(6):743. https://doi.org/10.3390/sym16060743
Chicago/Turabian StyleAL-Omeri, Wadei Faris, and M. Kaviyarasu. 2024. "Study on Neutrosophic Graph with Application on Earthquake Response Center in Japan" Symmetry 16, no. 6: 743. https://doi.org/10.3390/sym16060743






