Cloud Manufacturing Service Composition Optimization Based on Improved Chaos Sparrow Search Algorithm with Time-Varying Reliability and Credibility Evaluation
Abstract
:1. Introduction
2. Related Work
3. Cloud Manufacturing Service Composition Modeling
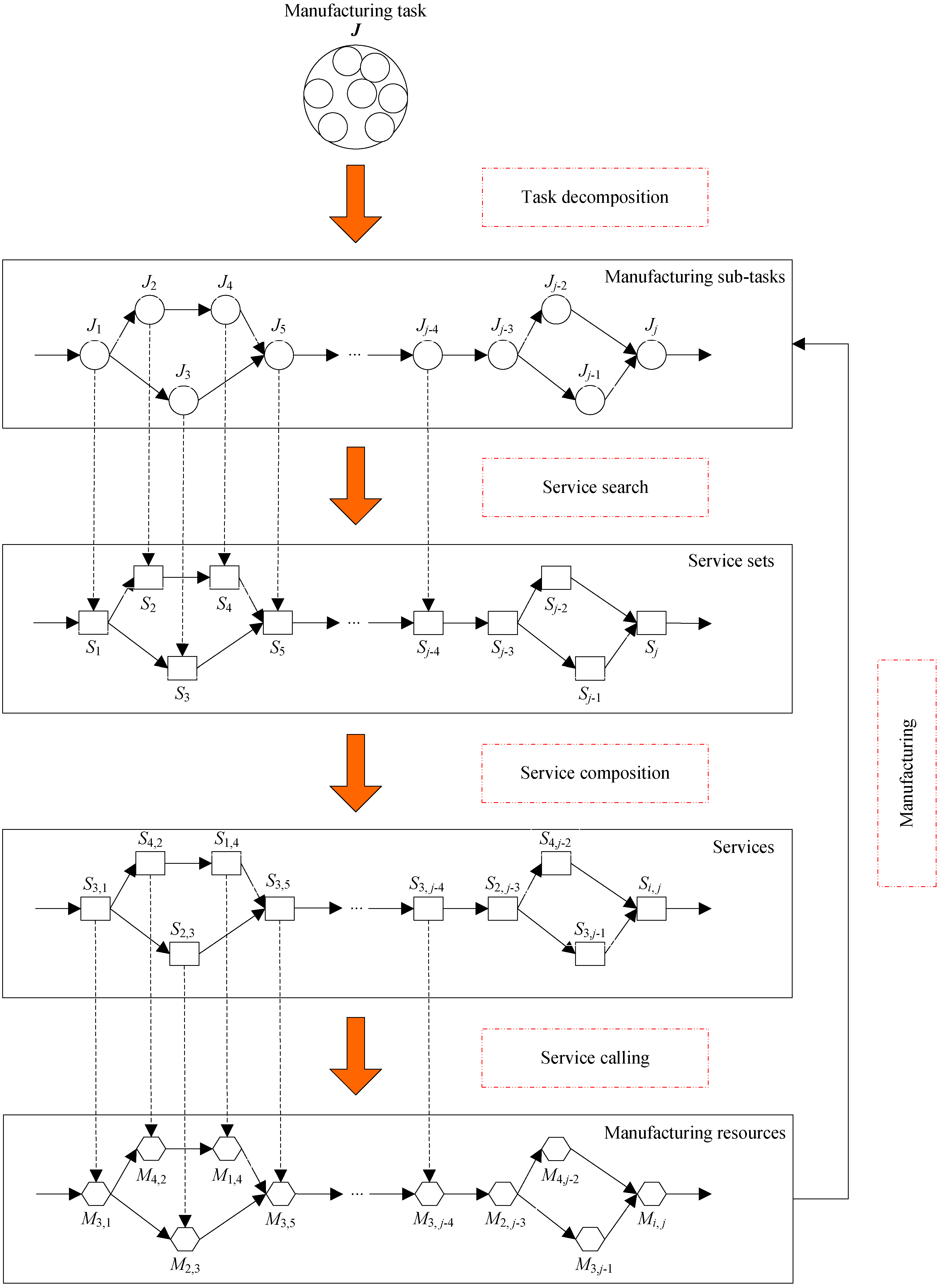
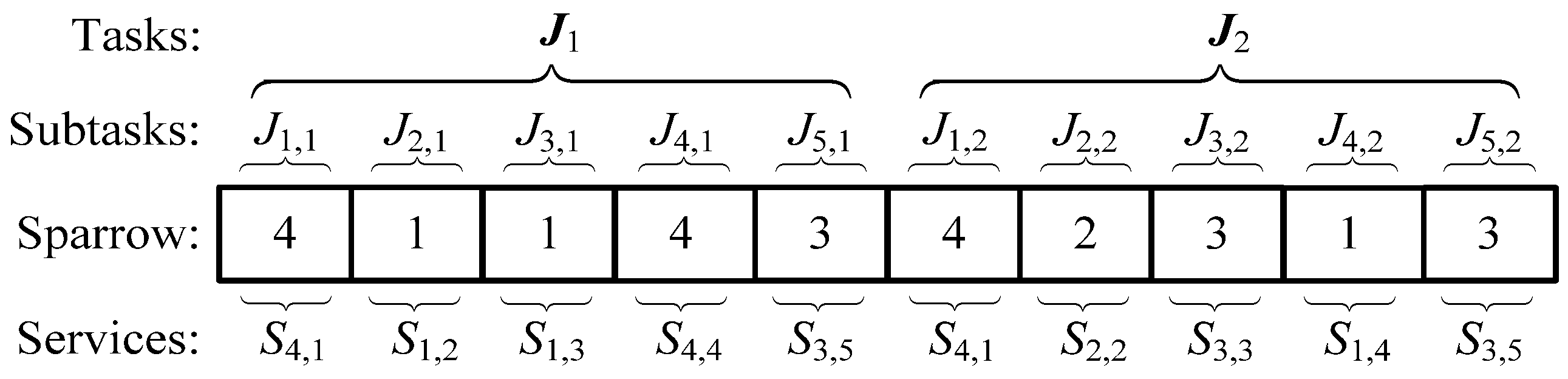
3.1. Task Decomposition
3.2. SvcComp Process
3.3. SvcComp Evaluation Factors
3.3.1. Time-Varying Service Credibility
3.3.2. Composition Synergy Degree
3.3.3. Time-Varying Service Reliability
3.3.4. Composition Complexity
3.3.5. Execution Time
3.3.6. Execution Cost
3.4. Multi-Objective Optimization Model of CMfg SvcComp
4. Improved Chaos Sparrow Search Algorithm
4.1. Basic Sparrow Search Algorithm
4.2. Improved Chaos Sparrow Search Algorithm
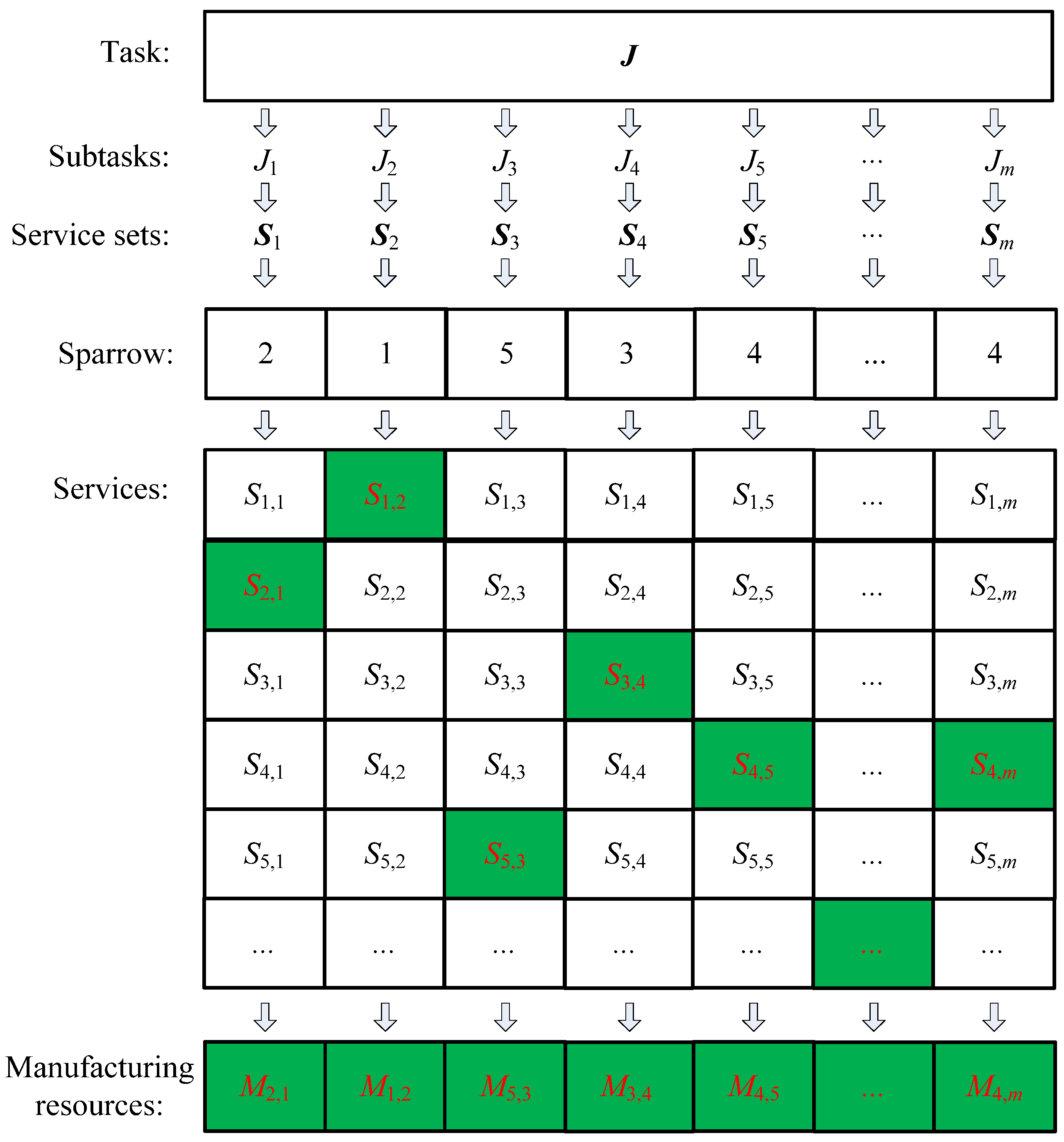
4.2.1. SvcComp Coding Method
4.2.2. Fitness Function Construction
4.2.3. Improve the Position Formula of the Explorer Sparrow
4.2.4. Improve the Position Formula of the Follower Sparrow
4.2.5. Improve the Position Formula of the Scouter Sparrow
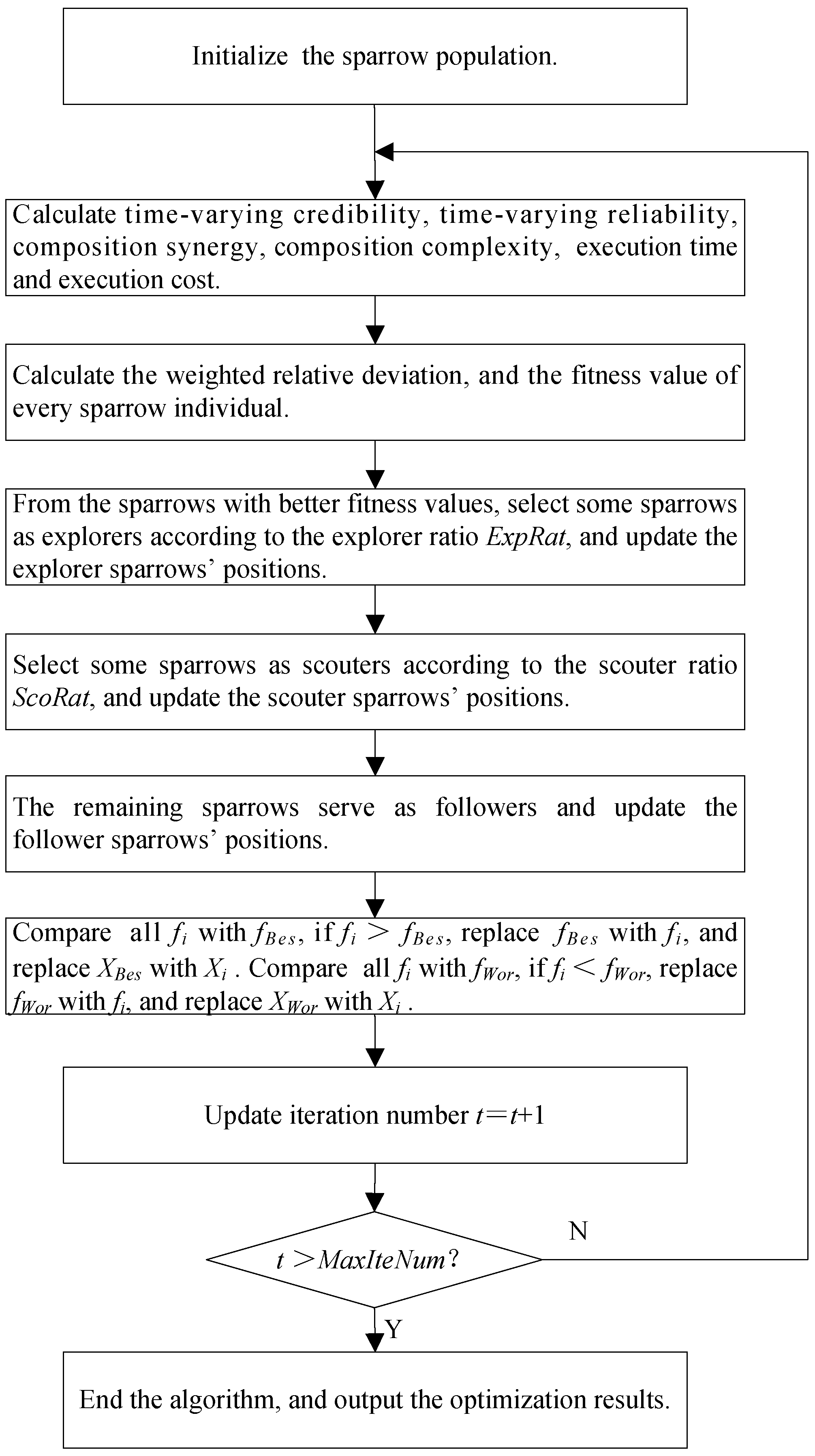
4.3. Algorithm Steps
5. Simulation Experiments and Analysis
5.1. Experimental Condition Setting
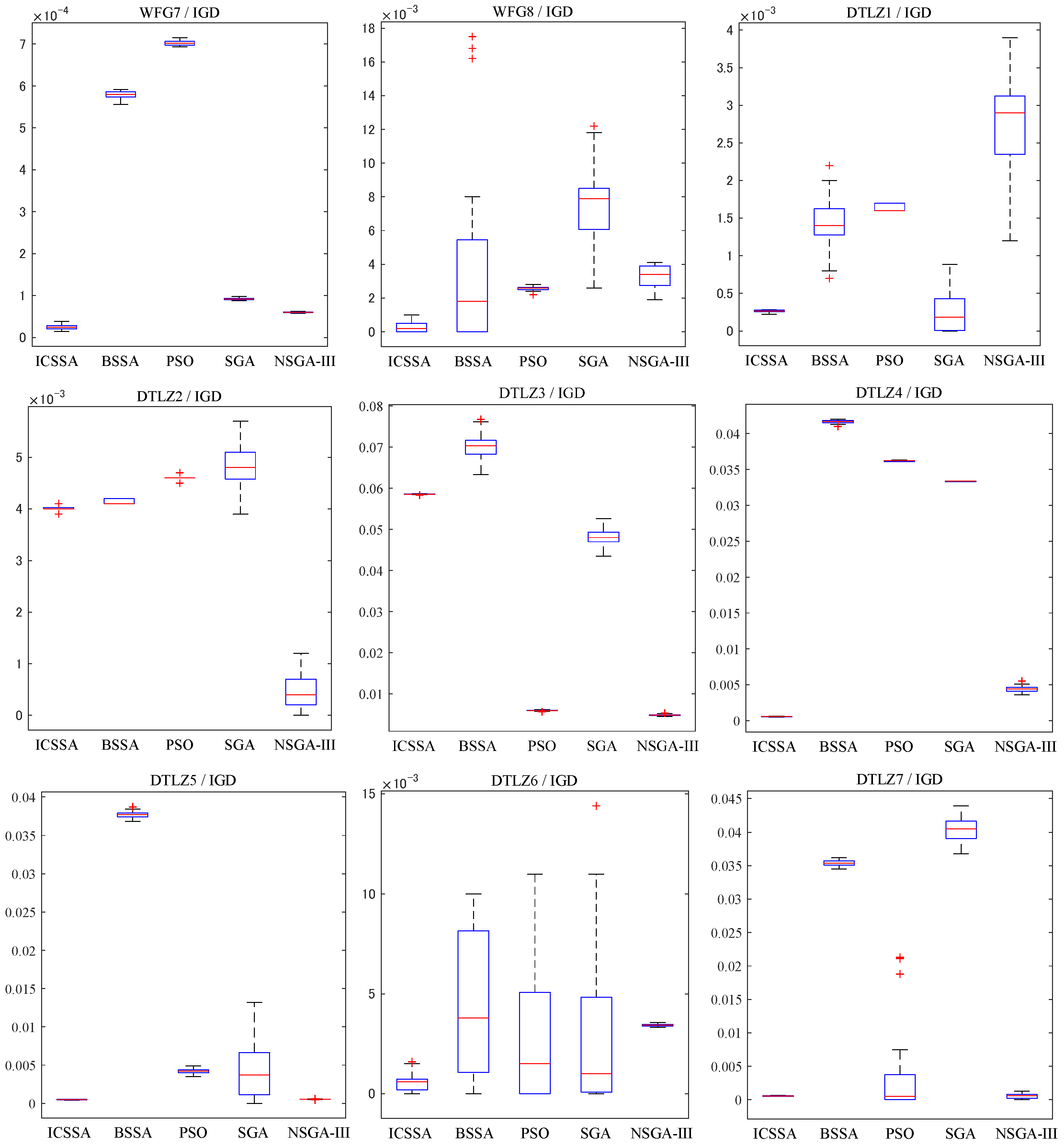
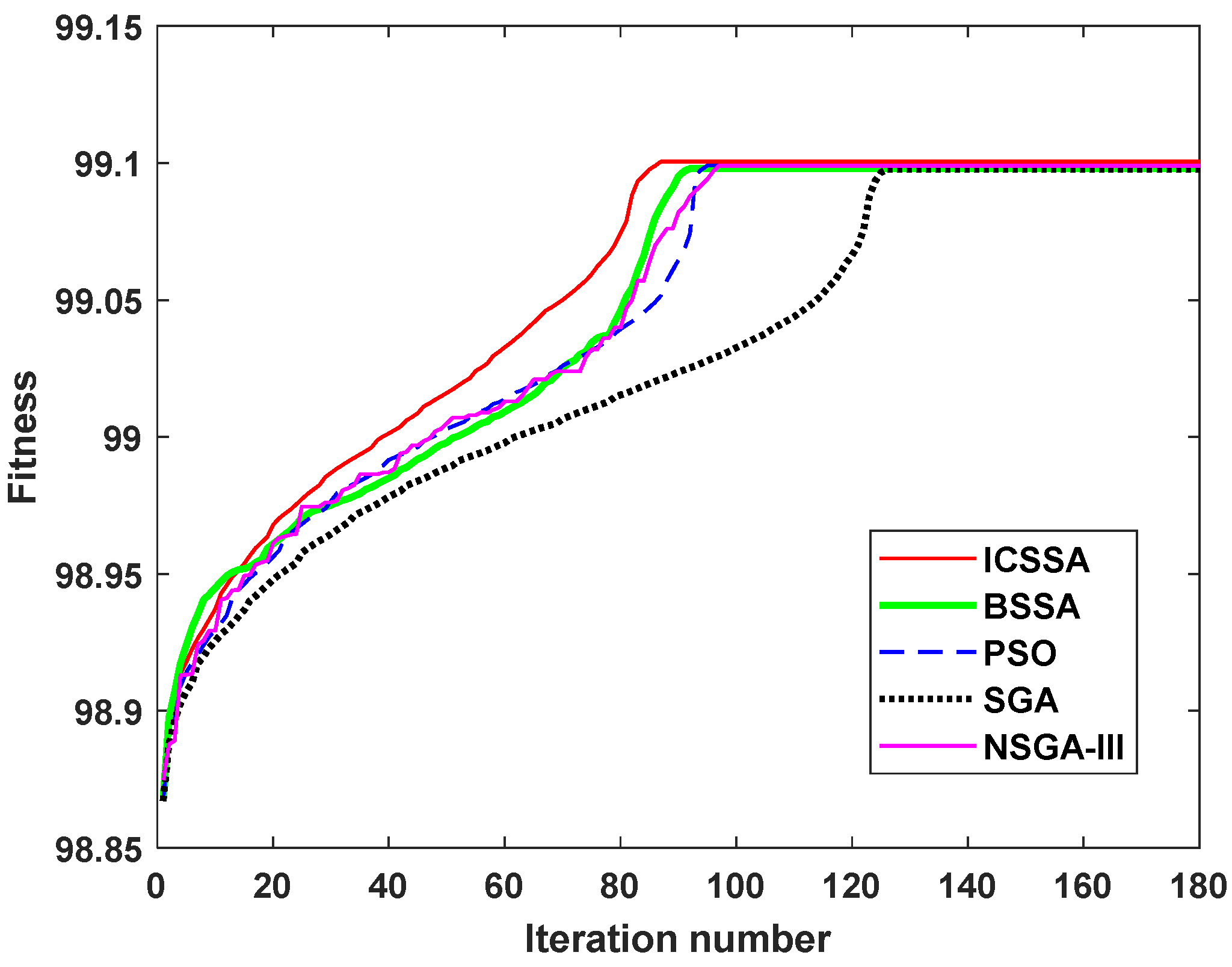
5.2. Analysis of Experimental Results
6. Application Example
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.; Gao, L.; Lu, C.; Yao, X. Transfer learning assisted batch optimization of jobs arriving dynamically in manufacturing cloud. J. Manuf. Syst. 2022, 65, 44–58. [Google Scholar] [CrossRef]
- Yin, C.; Li, S.; Li, X. An optimization method of cloud manufacturing service composition based on matching-collaboration degree. Int. J. Adv. Manuf. Technol. 2024, 131, 343–353. [Google Scholar] [CrossRef]
- Ali, M.T.N.; Mirsaeid, S.H.; Homayun, M. Reliability-aware web service composition with cost minimization perspective: A multi-objective particle swarm optimization model in multi-cloud scenarios. Soft Comput. 2023, 28, 5173–5196. [Google Scholar]
- Delaram, J.; Houshamand, M.; Ashtiani, F.; Fatahi Valilai, O. Development of public cloud manufacturing markets: A mechanism design approach. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2079751. [Google Scholar] [CrossRef]
- Jin, H.; Jiang, C.; Lv, S. A hybrid whale optimization algorithm for quality of service-aware manufacturing cloud service composition. Symmetry 2023, 16, 46. [Google Scholar] [CrossRef]
- Zhao, Q.-Y.; Wei, L.; Shu, H.-P. Research on credibility support mechanism of manufacturing cloud service based on classified QoS. In Proceedings of the 5th International Asia Conference on Industrial Engineering and Management Innovation (IEMI2014); Atlantis Press: Paris, France, 2015; Volume 1, pp. 67–70. [Google Scholar]
- Aamir, T.; Dong, H.; Bouguettaya, A. Stance and credibility based trust in social-sensor cloud services. Web Inf. Syst. Eng. 2018, 11234, 178–189. [Google Scholar]
- Tang, R.; Yue, Y.; Ding, X.; Qiu, Y. Credibility-based cloud media resource allocation algorithm. J. Netw. Comput. Appl. 2014, 46, 315–321. [Google Scholar] [CrossRef]
- Wang, S.; Lu, W.; Du, Z. A approach of credibility-based trust management service in cloud environments. Adv. Mechatron. Control Eng. 2013, 278–280, 1771–1778. [Google Scholar] [CrossRef]
- Qu, L.; Wang, Y.; Orgun, M.; Wong, D.S.; Bouguettaya, A. Evaluating cloud users’ credibility of providing subjective assessment or objective assessment for cloud services. Serv.-Oriented Comput. 2014, 8831, 453–461. [Google Scholar]
- Cai, X.; Zhang, M.; Hu, J.; Wu, Q. A reputation revision method based on the credibility for cloud services. In Proceedings of the 3rd Internatioinal Conference on Mechatronics and Industrial Informatics, Zhuhai, China, 30–31 October 2015; Volume 31, pp. 581–586. [Google Scholar]
- Mubarok, K.; Xu, X.; Ye, X.; Zhong, R.Y.; Lu, Y. Manufacturing service reliability assessment in cloud manufacturing. Procedia CIRP 2018, 72, 940–946. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y. A personalized clustering-based and reliable trust-aware QoS prediction approach for cloud service recommendation in cloud manufacturing. Knowl.-Based Syst. 2019, 174, 43–56. [Google Scholar] [CrossRef]
- Jing, S.K.; Jiang, H.; Xu, W.T.; Zhou, J.T. Cloud manufacturing service composition considering execution reliability. J. Comput.-Aided Des. Comput. Graph. 2014, 26, 392–400. [Google Scholar]
- Jiang, C.; Qiu, H.; Gao, L.; Wang, D.; Yang, Z.; Chen, L. Real-time estimation error-guided active learning Kriging method for time-dependent reliability analysis. Appl. Math. Model. 2019, 77, 82–98. [Google Scholar] [CrossRef]
- Junejo, A.K.; Jokhio, I.A.; Jan, T. A multi-dimensional and multi-factor trust computation framework for cloud services. Electronics 2022, 11, 1932. [Google Scholar] [CrossRef]
- Wan, Z.; Chen, J.; Li, J.; Ang, A.H.-S. An efficient new PDEM-COM based approach for time-variant reliability assessment of structures with monotonically deteriorating materials. Struct. Saf. 2019, 82, 101878. [Google Scholar] [CrossRef]
- Qian, H.-M.; Huang, H.-Z.; Li, Y.-F. A novel single-loop procedure for time-variant reliability analysis based on Kriging model. Appl. Math. Model. 2019, 75, 735–748. [Google Scholar] [CrossRef]
- Li, H.-S.; Wang, T.; Yuan, J.-Y.; Zhang, H. A sampling-based method for high-dimensional time-variant reliability analysis. Mech. Syst. Signal Process. 2019, 126, 505–520. [Google Scholar] [CrossRef]
- Ping, M.; Han, X.; Jiang, C.; Xiao, X. A time-variant extreme-value event evolution method for time-variant reliability analysis. Mech. Syst. Signal Process. 2019, 130, 333–348. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Q.; Ling, L. Cloud manufacturing task decomposition method based on HTN. China Mech. Eng. 2017, 28, 924–929. [Google Scholar]
- Liu, A.; Pfund, M.; Fowler, J. Scheduling optimization of task allocation in integrated manufacturing system based on task decomposition. J. Syst. Eng. Electron. 2016, 27, 422–433. [Google Scholar] [CrossRef]
- Yi, S.; Tan, M.; Guo, Z.; Wen, P.; Zhou, J. Manufacturing task decomposition optimization in cloud manufacturing service platform. Comput. Integr. Manuf. Syst. 2015, 21, 2201–2212. [Google Scholar]
- Dmitriy, K.; Baruch, S.; Hadas, S. Flexible resource allocation to interval jobs. Algorithmica 2019, 81, 3217–3244. [Google Scholar]
- Thekinen, J.; Panchal, J.H. Resource allocation in cloud-based design and manufacturing: A mechanism design approach. J. Manuf. Syst. 2017, 43, 327–338. [Google Scholar] [CrossRef]
- Morariu, O.; Borangiu, T.; Morariu, C.; Răileanu, S. Service oriented mechanisms for smart resource allocation in private manufacturing clouds. Explor. Serv. Sci. 2016, 247, 367–383. [Google Scholar]
- Lin, Y.-K.; Chong, C.S. Fast GA-based project scheduling for computing resources allocation in a cloud manufacturing system. J. Intell. Manuf. 2017, 28, 1189–1201. [Google Scholar] [CrossRef]
- Sheng, B.; Zhang, C.; Yin, X.; Lu, Q.; Cheng, Y.; Xiao, T.; Liu, H. Common intelligent semantic matching engines of cloud manufacturing service based on OWL-S. Int. J. Adv. Manuf. Technol. 2016, 84, 103–118. [Google Scholar] [CrossRef]
- Tao, F.; Cheng, J.; Cheng, Y.; Gu, S.; Zheng, T.; Yang, H. SDMSim: A manufacturing service supply–demand matching simulator under cloud environment. Robot. Comput.-Integr. Manuf. 2017, 45, 34–46. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, X. Two-sided matching model of cloud service based on QoS in cloud manufacturing environment. Comput. Integr. Manuf. Syst. 2016, 22, 104–112. [Google Scholar]
- Lu, Y.; Xu, X. A semantic web-based framework for service composition in a cloud manufacturing environment. J. Manuf. Syst. 2017, 42, 69–81. [Google Scholar] [CrossRef]
- Lartigau, J.; Xu, X.; Nie, L.; Zhan, D. Cloud manufacturing service composition based on QoS with geo-perspective transportation using an improved artificial bee colony optimization algorithm. Int. J. Prod. Res. 2015, 53, 4380–4404. [Google Scholar] [CrossRef]
- Pisching, M.A.; Junqueira, F.; Filho, D.J.S.; Miyagi, P.E. Service composition in the cloud-based manufacturing focused on the industry 4.0. In Technological Innovation for Cloud-Based Engineering Systems; Springer International Publishing: Cham, Switzerland, 2015; Volume 450, pp. 65–72. [Google Scholar]
- Xiao, Y.; Li, C.; Song, L.; Yang, J.; Su, J. A multidimensional information fusion-based matching decision method for manufacturing service resource. IEEE Access 2021, 2021, 39839–39851. [Google Scholar] [CrossRef]
- Bouzary, H.; Frank Chen, F. A hybrid grey wolf optimizer algorithm with evolutionary operators for optimal QoS-aware service composition and optimal selection in cloud manufacturing. Int. J. Adv. Manuf. Technol. 2019, 101, 2771–2784. [Google Scholar] [CrossRef]
- Fazeli, M.M.; Farjami, Y.; Nickray, M. An ensemble optimisation approach to service composition in cloud manufacturing. Int. J. Comput. Integr. Manuf. 2019, 32, 83–91. [Google Scholar] [CrossRef]
- He, K.; Zhu, D. Quality evaluation of cloud manufacturing service. Comput. Integr. Manuf. Syst. 2018, 24, 53–62. [Google Scholar]
- Wang, S.; Liu, Z.; Sun, Q.; Zou, H.; Yang, F. Towards an accurate evaluation of quality of cloud service in service-oriented cloud computing. J. Intell. Manuf. 2014, 25, 283–291. [Google Scholar] [CrossRef]
- Wang, X.; Sheng, B.; Zhang, C.; Xiao, Z.; Wang, H.; Zhao, F. An effective application of 3D cloud printing service quality evaluation in BM-MOPSO. Concurr. Comput. Pract. Exp. 2018, 30, e4977. [Google Scholar] [CrossRef]
- Ye, Y. Study the evaluation system about E-government quality of service based on the customer perception. In Proceedings of the 2016 6th International Conference on Information Technology for Manufacturing Systems; DEStech Publications Inc.: Lancaster, PA, USA, 2016; pp. 323–327. [Google Scholar]
- Hu, Y.; Pan, L.; Lv, W.; Wang, Z. Optimal selection of cloud manufacturing resources based on bacteria foraging optimization. Int. J. Comput. Integr. Manuf. 2024, 37, 165–182. [Google Scholar] [CrossRef]
- Li, Y.; Yao, X.; Zhou, J. Multi-objective optimization of cloud manufacturing service composition with cloud-entropy enhanced genetic algorithm. Stroj. Vestn.-J. Mech. Eng. 2016, 62, 577–590. [Google Scholar] [CrossRef]
- Xu, W.; Tian, S.; Liu, Q.; Xie, Y.; Zhou, Z.; Pham, D.T. An improved discrete bees algorithm for correlation-aware service aggregation optimization in cloud manufacturing. Int. J. Adv. Manuf. Technol. 2016, 84, 17–28. [Google Scholar] [CrossRef]
- Onaizah, N.A.; Aljanabi, R.M. Modelling of African vulture optimization algorithm with deep learning-based object classification for intelligent manufacturing systems. J. Smart Internet Things 2023, 2023, 62–83. [Google Scholar] [CrossRef]
- Tavana, M.; Shahdi-Pashaki, S.; Teymourian, E.; Santos-Arteaga, F.J.; Komaki, M. A discrete cuckoo optimization algorithm for consolidation in cloud computing. Comput. Ind. Eng. 2018, 115, 495–511. [Google Scholar] [CrossRef]
- Seghir, F.; Khababa, A. A hybrid approach using genetic and fruit fly optimization algorithms for QoS-aware cloud service composition. J. Intell. Manuf. 2018, 29, 1773–1792. [Google Scholar] [CrossRef]
- Wei, X.; Liu, H. A cloud manufacturing resource allocation model based on ant colony optimization algorithm. Int. J. Grid Distrib. Comput. 2015, 8, 55–66. [Google Scholar] [CrossRef]
- Que, Y.; Zhong, W.; Chen, H.; Chen, X.; Ji, X. Improved adaptive immune genetic algorithm for optimal QoS-aware service composition selection in cloud manufacturing. Int. J. Adv. Manuf. Technol. 2018, 96, 4455–4465. [Google Scholar] [CrossRef]
- Jiang, H.; Yi, J.; Chen, S.; Zhu, X. A multi-objective algorithm for task scheduling and resource allocation in cloud-based disassembly. J. Manuf. Syst. 2016, 41, 239–255. [Google Scholar] [CrossRef]
- Vila, S.; Guirado, F.; Lerida, J.L.; Cores, F. Energy-saving scheduling on IaaS HPC cloud environments based on a multi-objective genetic algorithm. J. Supercomput. 2019, 75, 1483–1495. [Google Scholar] [CrossRef]
- Li, T.; Yin, Y.; Yang, B.; Hou, J.; Zhou, K. A self-learning bee colony and genetic algorithm hybrid for cloud manufacturing services. Computing 2022, 104, 1977–2003. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, S.; Yang, B.; Wang, Y.; Chen, R. A novel hybrid algorithm for large-scale composition optimization problems in cloud manufacturing. Int. J. Comput. Integr. Manuf. 2021, 34, 898–919. [Google Scholar] [CrossRef]
- Gad, A.G.; Sallam, K.M.; Chakrabortty, R.K.; Ryan, M.J.; Abohany, A.A. An improved binary sparrow search algorithm for feature selection in data classification. Neural Comput. Appl. 2022, 34, 15705–15752. [Google Scholar] [CrossRef]
- Ruiz-Vélez, A.; García, J.; Alcalá, J.; Yepes, V. Enhancing robustness in precast modular frame optimization: Integrating NSGA-II, NSGA-III, and RVEA for sustainable infrastructure. Mathematics 2024, 12, 1478. [Google Scholar] [CrossRef]

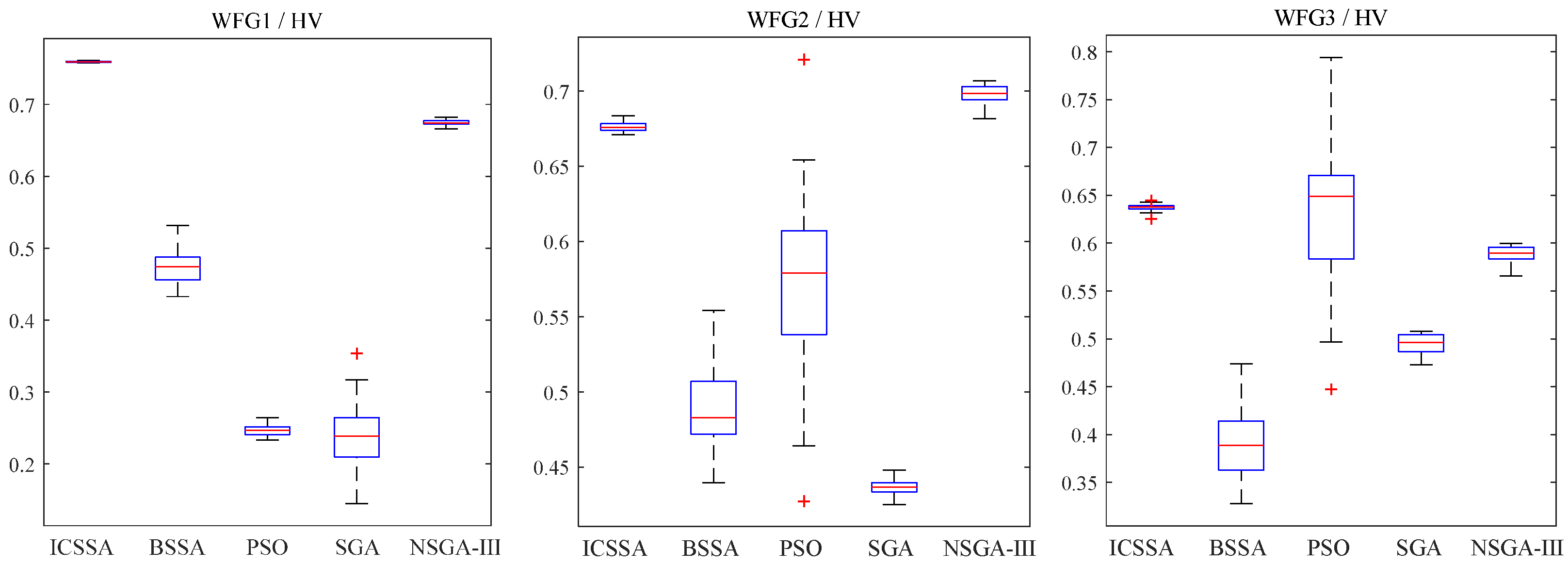
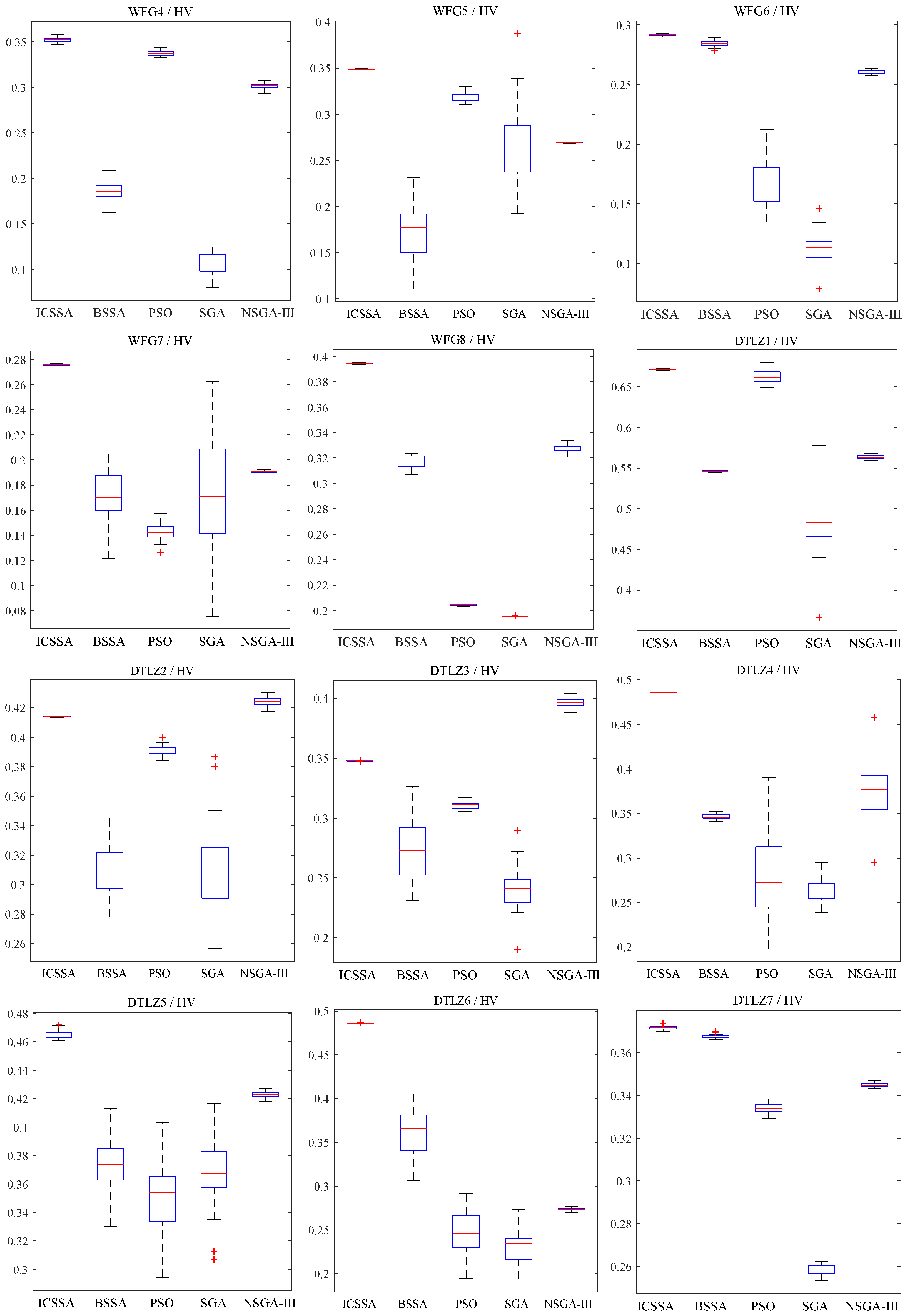

| Issues | ICSSA | BSSA | PSO | SGA | NSGA-III |
|---|---|---|---|---|---|
| WFG1 | 1.703 × 10−5 (8.064 × 10−7) | 3.149 × 10−4 (9.586 × 10−6) + | 5.941 × 10−5 (1.874 × 10−5) + | 3.205 × 10−5 (9.363 × 10−3) + | 2.261 × 10−5 (9.501 × 10−6) + |
| WFG2 | 1.964 × 10−4 (1.655 × 10−6) | 4.734 × 10−4 (7.681 × 10−6) = | 5.906 × 10−5 (3.765 × 10−6) − | 3.813 × 10−4 (3.522 × 10−6) = | 8.584 × 10−5 (3.203 × 10−5) − |
| WFG3 | 8.575 × 10−5 (1.322 × 10−7) | 8.264 × 10−4 (3.959 × 10−5) + | 7.942 × 10−5 (4.092 × 10−6) − | 9.545 × 10−4 (3.565 × 10−6) + | 3.938 × 10−4 (8.723 × 10−6) + |
| WFG4 | 3.379 × 10−5 (1.906 × 10−6) | 8.905 × 10−4 (2.652 × 10−6) + | 9.182 × 10−5 (1.652 × 10−5) + | 2.930 × 10−4 (2.689 × 10−4) + | 6.045 × 10−5 (2.102 × 10−5) + |
| WFG5 | 3.141 × 10−5 (3.407 × 10−6) | 1.781 × 10−4 (4.809 × 10−5) + | 3.332 × 10−5 (1.307 × 10−5) + | 2.130 × 10−4 (6.643 × 10−4) + | 2.494 × 10−4 (1.328 × 10−4) + |
| WFG6 | 8.399 × 10−5 (6.465 × 10−7) | 9.779 × 10−5 (9.534 × 10−7) = | 1.207 × 10−4 (1.722 × 10−5) + | 2.408 × 10−4 (2.481 × 10−6) + | 9.473 × 10−5 (2.138 × 10−6) + |
| WFG7 | 2.460 × 10−5 (5.745 × 10−6) | 5.795 × 10−4 (8.552 × 10−6) + | 7.018 × 10−4 (5.826 × 10−6) + | 9.184 × 10−5 (2.293 × 10−6) = | 6.010 × 10−5 (1.285 × 10−6) = |
| WFG8 | 2.695 × 10−4 (5.953 × 10−4) | 3.798 × 10−3 (8.123 × 10−3) + | 2.583 × 10−3 (1.219 × 10−4) + | 7.405 × 10−3 (2.149 × 10−3) + | 3.240 × 10−3 (6.775 × 10−4) + |
| DTLZ1 | 2.643 × 10−4 (1.493 × 10−5) | 1.462 × 10−3 (3.399 × 10−4) + | 1.635 × 10−3 (3.678 × 10−5) + | 2.723 × 10−4 (4.843 × 10−4) + | 2.787 × 10−3 (7.211 × 10−4) + |
| DTLZ2 | 4.005 × 10−3 (5.898 × 10−5) | 4.139 × 10−3 (3.628 × 10−5) = | 4.612 × 10−3 (4.231 × 10−5) = | 4.813 × 10−3 (4.499 × 10−4) + | 4.930 × 10−4 (3.695 × 10−4) − |
| DTLZ3 | 5.853 × 10−2 (7.844 × 10−5) | 7.013 × 10−2 (3.185 × 10−3) + | 5.909 × 10−3 (1.328 × 10−4) − | 4.810 × 10−2 (2.163 × 10−3) + | 4.828 × 10−3 (1.861 × 10−4) − |
| DTLZ4 | 5.570 × 10−4 (3.397 × 10−5) | 4.165 × 10−2 (2.467 × 10−4) + | 3.617 × 10−2 (4.615 × 10−5) + | 3.335 × 10−2 (4.039 × 10−5) + | 4.408 × 10−3 (4.548 × 10−4) + |
| DTLZ5 | 4.940 × 10−4 (3.773 × 10−5) | 3.769 × 10−2 (4.194 × 10−4) + | 4.198 × 10−3 (3.428 × 10−4) + | 4.782 × 10−3 (4.258 × 10−3) + | 5.352 × 10−4 (2.529 × 10−5) = |
| DTLZ6 | 5.549 × 10−4 (4.494 × 10−4) | 4.323 × 10−3 (3.594 × 10−3) + | 3.097 × 10−3 (4.938 × 10−3) + | 3.119 × 10−3 (4.119 × 10−3) + | 3.437 × 10−3 (5.678 × 10−4) + |
| DTLZ7 | 5.578 × 10−4 (3.963 × 10−5) | 3.537 × 10−2 (4.887 × 10−4) + | 3.571 × 10−3 (9.137 × 10−3) + | 4.034 × 10−2 (1.673 × 10−3) + | 5.320 × 10−4 (3.449 × 10−4) + |
| (+/=/−) | (12/3/0) | (11/1/3) | (13/2/0) | (10/2/3) |
| Issues | ICSSA | BSSA | PSO | SGA | NSGA-III |
|---|---|---|---|---|---|
| WFG1 | 7.590 × 10−1 (8.111 × 10−4) | 4.736 × 10−1 (2.388 × 10−2) + | 2.469 × 10−1 (7.416 × 10−3) + | 2.404 × 10−1 (4.654 × 10−2) + | 6.746 × 10−1 (3.979 × 10−3) + |
| WFG2 | 6.766 × 10−1 (3.528 × 10−3) | 4.906 × 10−1 (3.027 × 10−2) + | 5.709 × 10−1 (6.061 × 10−2) + | 4.365 × 10−1 (5.437 × 10−3) = | 6.983 × 10−1 (6.015 × 10−3) = |
| WFG3 | 6.370 × 10−1 (3.876 × 10−3) | 3.953 × 10−1 (4.129 × 10−2) + | 6.317 × 10−1 (8.259 × 10−2) + | 4.943 × 10−1 (1.114 × 10−2) + | 5.885 × 10−1 (8.532 × 10−3) = |
| WFG4 | 3.523 × 10−1 (2.559 × 10−3) | 1.859 × 10−1 (1.099 × 10−2) + | 3.374 × 10−1 (2.504 × 10−3) = | 1.058 × 10−1 (1.387 × 10−2) + | 3.017 × 10−1 (3.641 × 10−3) = |
| WFG5 | 3.488 × 10−1 (2.708 × 10−4) | 1.735 × 10−1 (2.628 × 10−2) + | 3.193 × 10−1 (4.418 × 10−3) + | 2.658 × 10−1 (4.681 × 10−2) + | 2.695 × 10−1 (2.974 × 10−4) = |
| WFG6 | 2.915 × 10−1 (7.222 × 10−4) | 2.842 × 10−1 (2.648 × 10−3) + | 1.683 × 10−1 (1.972 × 10−2) + | 1.131 × 10−1 (1.321 × 10−2) + | 2.605 × 10−1 (1.625 × 10−3) + |
| WFG7 | 2.758 × 10−1 (4.446 × 10−4) | 1.691 × 10−1 (2.186 × 10−2) + | 1.429 × 10−1 (7.218 × 10−3) + | 1.763 × 10−1 (4.688 × 10−2) + | 1.907 × 10−1 (6.864 × 10−4) = |
| WFG8 | 3.943 × 10−1 (4.296 × 10−4) | 3.167 × 10−1 (5.194 × 10−3) + | 2.043 × 10−1 (4.644 × 10−4) = | 1.953 × 10−1 (1.543 × 10−4) = | 3.272 × 10−1 (3.027 × 10−3) + |
| DTLZ1 | 6.713 × 10−1 (4.638 × 10−4) | 5.462 × 10−1 (9.202 × 10−4) = | 6.623 × 10−1 (7.853 × 10−3) = | 4.873 × 10−1 (4.116 × 10−2) + | 5.635 × 10−1 (2.581 × 10−3) + |
| DTLZ2 | 4.139 × 10−1 (2.033 × 10−4) | 3.112 × 10−1 (1.829 × 10−2) + | 3.912 × 10−1 (3.245 × 10−3) + | 3.103 × 10−1 (3.074 × 10−2) + | 4.240 × 10−1 (3.452 × 10−3) + |
| DTLZ3 | 3.478 × 10−1 (1.699 × 10−4) | 2.743 × 10−1 (2.648 × 10−2) + | 3.109 × 10−1 (2.923 × 10−3) + | 2.410 × 10−1 (1.953 × 10−2) + | 3.963 × 10−1 (3.787 × 10−3) + |
| DTLZ4 | 4.860 × 10−1 (2.452 × 10−4) | 3.465 × 10−1 (2.696 × 10−3) + | 2.857 × 10−1 (5.425 × 10−2) + | 2.635 × 10−1 (1.502 × 10−2) + | 3.728 × 10−1 (3.345 × 10−2) + |
| DTLZ5 | 4.652 × 10−1 (3.106 × 10−3) | 3.729 × 10−1 (1.933 × 10−2) + | 3.488 × 10−1 (2.715 × 10−2) + | 3.672 × 10−1 (2.738 × 10−2) + | 4.230 × 10−1 (2.243 × 10−3) = |
| DTLZ6 | 4.859 × 10−1 (4.424 × 10−4) | 3.613 × 10−1 (2.763 × 10−2) + | 2.477 × 10−1 (2.306 × 10−2) + | 2.309 × 10−1 (1.858 × 10−2) + | 2.737 × 10−1 (1.825 × 10−3) + |
| DTLZ7 | 3.718 × 10−1 (7.866 × 10−4) | 3.677 × 10−1 (8.731 × 10−4) = | 3.340 × 10−1 (2.417 × 10−3) + | 2.584 × 10−1 (2.627 × 10−3) + | 3.450 × 10−1 (8.816 × 10−4) = |
| (+/=/−) | (13/2/0) | (12/3/0) | (13/2/0) | (8/7/0) |
| Jj | J1 | J2 | J3 | J4 | J5 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sj | S1 | S2 | S3 | S4 | S5 | |||||||||||||
| Si,j | S1,1 | S2,1 | S3,1 | S4,1 | S1,2 | S2,2 | S1,3 | S2,3 | S3,3 | S1,4 | S2,4 | S3,4 | S4,4 | S5,4 | S1,5 | S2,5 | S3,5 | S4,5 |
| FF | 0.4 | 0.4 | 0.2 | 0.8 | 0.8 | 0.6 | 0.8 | 0.4 | 0.2 | 0.8 | 0.4 | 0.2 | 0.6 | 0.8 | 0.6 | 0.4 | 0.8 | 0.2 |
| SF | 0.5 | 0.8 | 0.6 | 0.8 | 0.8 | 0.8 | 0.9 | 0.7 | 0.7 | 0.3 | 0.6 | 0.4 | 0.6 | 0.9 | 0.8 | 0.3 | 0.8 | 0.6 |
| DF | 0.4 | 0.8 | 0.4 | 0.8 | 0.8 | 0.4 | 1 | 0.8 | 1 | 0.8 | 0.4 | 0.4 | 1 | 1 | 0.8 | 0.4 | 1 | 0.4 |
| SR | 0.43 | 0.64 | 0.38 | 0.80 | 0.80 | 0.60 | 0.81 | 0.77 | 0.83 | 0.65 | 0.46 | 0.32 | 0.72 | 0.89 | 0.72 | 0.37 | 0.86 | 0.38 |
| RRi | 139 | 140 | 119 | 145 | 144 | 150 | 144 | 111 | 146 | 114 | 150 | 146 | 110 | 142 | 126 | 148 | 150 | 129 |
| DRi | 5 | 3 | 5 | 3 | 3 | 2 | 2 | 2 | 1 | 5 | 6 | 3 | 4 | 4 | 5 | 3 | 4 | 4 |
| VNi | 221 | 215 | 182 | 216 | 200 | 220 | 223 | 188 | 225 | 213 | 212 | 193 | 217 | 216 | 248 | 183 | 215 | 195 |
| SSi | 0.663 | 0.667 | 0.653 | 0.472 | 0.693 | 0.700 | 0.467 | 0.733 | 0.800 | 0.733 | 0.622 | 0.576 | 0.792 | 0.558 | 0.773 | 0.538 | 0.867 | 0.625 |
| SHi | 0.965 | 0.979 | 0.960 | 0.980 | 0.980 | 0.987 | 0.986 | 0.982 | 0.993 | 0.958 | 0.962 | 0.980 | 0.965 | 0.973 | 0.962 | 0.980 | 0.974 | 0.970 |
| VRi | 1.000 | 0.973 | 0.824 | 0.977 | 0.909 | 1.000 | 0.991 | 0.837 | 1.000 | 0.982 | 0.977 | 0.889 | 1.000 | 0.995 | 1.000 | 0.738 | 0.867 | 0.786 |
| SC | 0.885 | 0.884 | 0.827 | 0.827 | 0.873 | 0.905 | 0.832 | 0.864 | 0.937 | 0.898 | 0.865 | 0.832 | 0.924 | 0.855 | 0.917 | 0.775 | 0.910 | 0.811 |
| ET | 99 | 91 | 58 | 63 | 60 | 70 | 45 | 47 | 48 | 74 | 89 | 80 | 74 | 88 | 75 | 87 | 67 | 90 |
| LET | 7 | 4 | 7 | 4 | 4 | 7 | 2 | 4 | 2 | 4 | 7 | 7 | 2 | 2 | 4 | 7 | 2 | 7 |
| PET | 23 | 27 | 33 | 27 | 28 | 33 | 32 | 23 | 22 | 33 | 27 | 33 | 27 | 19 | 27 | 23 | 29 | 21 |
| AET | 3 | 1 | 2 | 3 | 3 | 1 | 2 | 2 | 3 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 2 | 3 |
| UC | 47 | 40 | 64 | 55 | 60 | 46 | 41 | 46 | 44 | 50 | 55 | 50 | 51 | 45 | 57 | 66 | 65 | 65 |
| PEC | 5 | 5 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 5 | 5 | 5 | 3 | 5 | 3 | 5 | 3 | 5 |
| USh,i | S1,1 | S2,1 | S3,1 | S4,1 | S1,2 | S2,2 | S1,3 | S2,3 | S3,3 | S1,4 | S2,4 | S3,4 | S4,4 | S5,4 | S1,5 | S2,5 | S3,5 | S4,5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| US1 | 2 | 3 | 3 | 2 | 5 | 4 | 2 | 3 | 4 | 3 | 4 | 3 | 5 | 1 | 3 | 2 | 5 | 3 |
| US2 | 3 | 2 | 3 | 3 | 3 | 3 | 3 | 4 | 5 | 2 | 3 | 2 | 3 | 3 | 4 | 3 | 4 | 3 |
| US3 | 2 | 3 | 4 | 4 | 3 | 2 | 2 | 3 | 5 | 3 | 2 | 1 | 4 | 2 | 5 | 5 | 4 | 5 |
| US4 | 3 | 3 | 2 | 1 | 2 | 3 | 1 | 5 | 3 | 4 | 2 | 1 | 2 | 4 | 5 | 4 | 4 | 2 |
| US5 | 5 | 5 | 5 | 2 | 4 | 4 | 2 | 5 | 5 | 4 | 2 | 2 | 4 | 3 | 4 | 1 | 3 | 2 |
| US6 | 5 | 4 | 3 | 3 | 5 | 5 | 1 | 4 | 3 | 5 | 2 | 4 | 5 | 3 | 5 | 3 | 5 | 2 |
| US7 | 3 | 5 | 4 | 4 | 4 | 5 | 3 | 2 | 5 | 3 | 2 | 3 | 5 | 2 | 5 | 2 | 5 | 3 |
| US8 | 4 | 5 | 2 | 2 | 4 | 5 | 2 | 4 | 5 | 3 | 3 | 5 | 4 | 2 | 5 | 3 | 5 | 4 |
| US9 | 4 | 2 | 4 | 1 | 3 | 4 | 1 | 3 | 5 | 4 | 5 | 4 | 3 | 1 | 5 | 2 | 4 | 4 |
| US10 | 2 | 5 | 2 | 2 | 2 | 3 | 1 | 5 | 4 | 5 | 4 | 3 | 3 | 5 | 5 | 3 | 2 | 3 |
| US11 | 2 | 2 | 4 | 3 | 1 | 2 | 2 | 5 | 3 | 5 | 5 | 1 | 4 | 4 | 2 | 4 | 5 | 5 |
| US12 | 3 | 1 | 3 | 3 | 4 | 1 | 3 | 4 | 2 | 5 | 4 | 3 | 5 | 3 | 4 | 2 | 4 | 4 |
| US13 | 4 | 3 | 5 | 2 | 3 | 2 | 5 | 4 | 4 | 1 | 1 | 2 | 4 | 3 | 1 | 4 | 5 | 1 |
| US14 | 3 | 5 | 4 | 1 | 3 | 3 | 4 | 3 | 5 | 2 | 3 | 4 | 4 | 2 | 4 | 2 | 5 | 2 |
| US15 | 5 | 4 | 3 | 2 | 5 | 3 | 3 | 3 | 5 | 5 | 2 | 3 | 2 | 1 | 3 | 1 | 5 | 4 |
| US16 | 3 | 3 | 2 | 1 | 5 | 5 | 2 | 2 | 3 | 3 | 5 | 3 | 4 | 3 | 4 | 2 | -- | 2 |
| US17 | -- | 2 | 4 | 2 | 4 | 4 | 2 | 5 | 4 | 4 | 2 | 5 | 5 | 4 | 3 | 2 | -- | 3 |
| US18 | -- | 3 | 3 | 3 | 5 | 4 | 3 | 2 | 3 | 5 | 5 | -- | 5 | 3 | 4 | 4 | -- | 5 |
| US19 | -- | -- | 4 | 2 | 3 | 5 | 2 | 4 | 2 | 4 | -- | -- | 4 | 4 | 3 | 3 | -- | 3 |
| US20 | -- | -- | 3 | 4 | 3 | 4 | 2 | 3 | 5 | 5 | -- | -- | 3 | -- | 2 | 4 | -- | 2 |
| US21 | -- | -- | 1 | 4 | 2 | 3 | 3 | 3 | 4 | 2 | -- | -- | 5 | -- | 5 | 3 | -- | 4 |
| US22 | -- | -- | 5 | 2 | 2 | 2 | -- | 4 | 3 | -- | -- | -- | 5 | -- | 5 | 5 | -- | 2 |
| US23 | -- | -- | 2 | 3 | 4 | 3 | -- | 3 | 4 | -- | -- | -- | 4 | -- | 4 | 1 | -- | 3 |
| US24 | -- | -- | 3 | 1 | 4 | 4 | -- | 4 | 5 | -- | -- | -- | 3 | -- | 5 | 3 | -- | 4 |
| US25 | -- | -- | 4 | 2 | 3 | 5 | -- | 5 | 5 | -- | -- | -- | -- | -- | 5 | 2 | -- | -- |
| US26 | -- | -- | 4 | -- | 4 | 4 | -- | 4 | 4 | -- | -- | -- | -- | -- | 5 | 1 | -- | -- |
| US27 | -- | -- | 3 | -- | 5 | 3 | -- | 3 | 5 | -- | -- | -- | -- | -- | 1 | 2 | -- | -- |
| US28 | -- | -- | 3 | -- | 2 | 2 | -- | 4 | 3 | -- | -- | -- | -- | -- | 1 | 4 | -- | -- |
| US29 | -- | -- | 2 | -- | 3 | 3 | -- | 5 | 2 | -- | -- | -- | -- | -- | 5 | 1 | -- | -- |
| US30 | -- | -- | 4 | -- | 4 | 5 | -- | 2 | 5 | -- | -- | -- | -- | -- | 4 | -- | -- | -- |
| Si,j | S1,1 | S2,1 | S3,1 | S4,1 | S1,2 | S2,2 | S1,3 | S2,3 | S3,3 | S1,4 | S2,4 | S3,4 | S4,4 | S5,4 | S1,5 | S2,5 | S3,5 | S4,5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1,1 | 1.000 | 1.919 | 1.586 | 1.636 | 1.606 | 1.707 | 1.000 | 1.000 | 1.000 | 1.747 | 1.899 | 1.808 | 1.747 | 1.889 | 1.758 | 1.879 | 1.677 | 1.833 |
| S2,1 | 1.919 | 1.000 | 1.637 | 1.692 | 1.659 | 1.769 | 1.000 | 1.000 | 1.000 | 1.813 | 1.978 | 1.879 | 1.813 | 1.967 | 1.824 | 1.956 | 1.736 | 1.967 |
| S3,1 | 1.586 | 1.637 | 1.000 | 1.921 | 1.967 | 1.829 | 1.000 | 1.000 | 1.000 | 1.784 | 1.652 | 1.725 | 1.784 | 1.659 | 1.773 | 1.667 | 1.866 | 1.744 |
| S4,1 | 1.636 | 1.692 | 1.921 | 1.000 | 1.952 | 1.900 | 1.000 | 1.000 | 1.000 | 1.851 | 1.708 | 1.788 | 1.851 | 1.716 | 1.840 | 1.724 | 1.940 | 1.822 |
| S1,2 | 1.606 | 1.659 | 1.967 | 1.952 | 1.000 | 1.857 | 1.000 | 1.000 | 1.000 | 1.811 | 1.674 | 1.750 | 1.811 | 1.682 | 1.800 | 1.690 | 1.896 | 1.989 |
| S2,2 | 1.707 | 1.769 | 1.829 | 1.900 | 1.857 | 1.000 | 1.000 | 1.000 | 1.000 | 1.946 | 1.787 | 1.875 | 1.946 | 1.795 | 1.933 | 1.805 | 1.957 | 1.889 |
| S1,3 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.957 | 1.938 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| S2,3 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.957 | 1.000 | 1.979 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| S3,3 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.938 | 1.979 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| S1,4 | 1.747 | 1.813 | 1.784 | 1.851 | 1.811 | 1.946 | 1.000 | 1.000 | 1.000 | 1.000 | 1.831 | 1.925 | 2.000 | 1.841 | 1.987 | 1.851 | 1.905 | 1.989 |
| S2,4 | 1.899 | 1.978 | 1.652 | 1.708 | 1.674 | 1.787 | 1.000 | 1.000 | 1.000 | 1.831 | 1.000 | 1.899 | 1.831 | 1.989 | 1.843 | 1.978 | 1.753 | 1.644 |
| S3,4 | 1.808 | 1.879 | 1.725 | 1.788 | 1.750 | 1.875 | 1.000 | 1.000 | 1.000 | 1.925 | 1.899 | 1.000 | 1.925 | 1.909 | 1.938 | 1.920 | 1.838 | 1.700 |
| S4,4 | 1.747 | 1.813 | 1.784 | 1.851 | 1.811 | 1.946 | 1.000 | 1.000 | 1.000 | 2.000 | 1.831 | 1.925 | 1.000 | 1.841 | 1.987 | 1.851 | 1.905 | 1.677 |
| S5,4 | 1.889 | 1.967 | 1.659 | 1.716 | 1.682 | 1.795 | 1.000 | 1.000 | 1.000 | 1.841 | 1.989 | 1.909 | 1.841 | 1.000 | 1.852 | 1.989 | 1.761 | 1.778 |
| S1,5 | 1.758 | 1.824 | 1.773 | 1.840 | 1.800 | 1.933 | 1.000 | 1.000 | 1.000 | 1.987 | 1.843 | 1.938 | 1.987 | 1.852 | 1.000 | 1.862 | 1.893 | 1.500 |
| S2,5 | 1.879 | 1.956 | 1.667 | 1.724 | 1.690 | 1.805 | 1.000 | 1.000 | 1.000 | 1.851 | 1.978 | 1.920 | 1.851 | 1.989 | 1.862 | 1.000 | 1.770 | 1.522 |
| S3,5 | 1.677 | 1.736 | 1.866 | 1.940 | 1.896 | 1.957 | 1.000 | 1.000 | 1.000 | 1.905 | 1.753 | 1.838 | 1.905 | 1.761 | 1.893 | 1.770 | 1.000 | 1.533 |
| S4,5 | 1.833 | 1.967 | 1.744 | 1.822 | 1.989 | 1.889 | 1.000 | 1.000 | 1.000 | 1.989 | 1.644 | 1.700 | 1.677 | 1.778 | 1.500 | 1.522 | 1.533 | 1.000 |
| Algorithm | Run Time | Iterations | SvcComp Optimization Results | SRsum | CCsum | SCsum | CSsum | ETsum | ECsum | |
|---|---|---|---|---|---|---|---|---|---|---|
| ICSSA | 18.73 s | 87 | {S4,1, S1,2, S1,3, S4,4, S3,5, S4,1, S2,2, S3,3, S1,4, S3,5,} | 6.161 | 8.81 | 7.085 | 40.854 | 182 | 33921 | −0.101 |
| BSSA | 19.25 s | 92 | {S3,1, S1,2, S3,3, S1,4, S1,5, S1,1, S4,2, S4,3, S2,4, S3,5,} | 5.663 | 9.143 | 6.919 | 40.686 | 123 | 34088 | −0.098 |
| PSO | 19.81 s | 95 | {S4,1, S1,2, S1,3, S1,4, S3,5, S2,1, S2,2, S3,3, S4,4, S1,5,} | 5.978 | 9.694 | 7.188 | 40.627 | 139 | 34018 | −0.099 |
| SGA | 26.68 s | 126 | {S1,1, S1,2, S4,3, S1,4, S1,5, S3,1, S4,2, S2,3, S2,4, S3,5,} | 5.978 | 9.694 | 7.188 | 40.367 | 139 | 34018 | −0.098 |
| NSGA-III | 20.54 s | 97 | {S4,1, S1,2, S1,3, S4,4, S3,5, S2,1, S2,2, S3,3, S1,4, S1,5,} | 5.978 | 8.907 | 7.188 | 40.627 | 139 | 34018 | −0.099 |
| METSC | — | — | {S3,1, S1,2, S2,3, S1,4, S3,5, S4,1, S2,2, S1,3, S4,4, S1,5,} | 5.482 | 9.102 | 6.711 | 40.686 | 122 | 34138 | −0.085 |
| MECSC | — | — | {S4,1, S2,2, S1,3, S1,4, S1,5, S4,1, S2,2, S1,3, S1,4, S1,5,} | 5.51 | 8.536 | 6.78 | 38.914 | 240 | 33042 | −0.034 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yao, X.; Wei, S.; Xiao, W.; Yin, Z. Cloud Manufacturing Service Composition Optimization Based on Improved Chaos Sparrow Search Algorithm with Time-Varying Reliability and Credibility Evaluation. Symmetry 2024, 16, 772. https://doi.org/10.3390/sym16060772
Li Y, Yao X, Wei S, Xiao W, Yin Z. Cloud Manufacturing Service Composition Optimization Based on Improved Chaos Sparrow Search Algorithm with Time-Varying Reliability and Credibility Evaluation. Symmetry. 2024; 16(6):772. https://doi.org/10.3390/sym16060772
Chicago/Turabian StyleLi, Yongxiang, Xifan Yao, Shanxiang Wei, Wenrong Xiao, and Zongming Yin. 2024. "Cloud Manufacturing Service Composition Optimization Based on Improved Chaos Sparrow Search Algorithm with Time-Varying Reliability and Credibility Evaluation" Symmetry 16, no. 6: 772. https://doi.org/10.3390/sym16060772
APA StyleLi, Y., Yao, X., Wei, S., Xiao, W., & Yin, Z. (2024). Cloud Manufacturing Service Composition Optimization Based on Improved Chaos Sparrow Search Algorithm with Time-Varying Reliability and Credibility Evaluation. Symmetry, 16(6), 772. https://doi.org/10.3390/sym16060772







