Stability and Numerical Simulation of a Nonlinear Hadamard Fractional Coupling Laplacian System with Symmetric Periodic Boundary Conditions

Abstract

The Hadamard fractional derivative and integral are important parts of fractional calculus which have been widely used in engineering, biology, neural networks, control theory, and so on. In addition, the periodic boundary conditions are an important class of symmetric two-point boundary conditions for differential equations and have wide applications. Therefore, this article considers a class of nonlinear Hadamard fractional coupling $(p_1,p_2)$-Laplacian systems with periodic boundary value conditions. Based on nonlinear analysis methods and the contraction mapping principle, we obtain some new and easily verifiable sufficient criteria for the existence and uniqueness of solutions to this system. Moreover, we further discuss the generalized Ulam–Hyers (GUH) stability of this problem by using some inequality techniques. Finally, three examples and simulations explain the correctness and availability of our main results.

1. Introduction

In this article, we consider the following nonlinear Hadamard fractional coupling $(p_1,p_2)$-Laplacian system with periodic boundary value conditions

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{ }^H{\mathcal{D}}_{1^{+}}^{{\alpha }_1}\left[{\Phi }_{p_1}\left({ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_1}{u}_1\left(t\right)\right)\right]=f_1(t,u_1\left(t\right),u_2\left(t\right)),t\in (1,e],\hfill \\ { }^H{\mathcal{D}}_{1^{+}}^{{\alpha }_2}\left[{\Phi }_{p_2}\left({ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_2}{u}_2\left(t\right)\right)\right]=f_2(t,u_1\left(t\right),u_2\left(t\right)),t\in (1,e],\hfill \\ u_1\left(1\right)=u_1\left(e\right),{ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_1}{u}_1\left(1\right)={ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_1}{u}_1\left(e\right),\hfill \\ u_2\left(1\right)=u_2\left(e\right),{ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_2}{u}_2\left(1\right)={ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_2}{u}_2\left(e\right).\hfill \end{array}\right.\end{array}$$

(1)

where $1<{\alpha }_i\le 2$, $1<{\beta }_i\le 2$, $p_i>1,{ }^H{\mathcal{D}}_{1^{+}}^{*}$ represents the Hadamard fractional derivative of $*$-order and ${\Phi }_{p_i}\left(x\right)={\left|x\right|}^{p_i-2}x$ are $p_i$-Lapacian operators with inverses ${\Phi }_{p_i}^{-1}={\Phi }_{q_i}$, provided that $\frac{1}{p_i}+\frac{1}{q_i}=1$, $f_i\in C([1,e]\times {\mathbb{R}}^2,\mathbb{R})$, $i=1,2$.

Hadamard [1] first proposed Hadamard fractional calculus in 1892. Hadamard fractional calculus has some obvious differences compared to Riemann–Liouville fractional calculus. The most direct manifestation is that the kernel function $k_H(t,s)={\left(\log \frac{t}{s}\right)}^{\alpha -1}$ of Hadamard fractional calculus is different from the kernel function $k_R(t,s)={(t-s)}^{\alpha -1}$ of Riemann–Liouville fractional calculus. Moreover, $\forall \mu >0$, $k_H(\mu t,\mu s)=k_H(t,s)$ and $k_R(\mu t,\mu s)={\mu }^{\alpha -1}{k}_R(t,s)\ne k_R(t,s)$, which is also different. For more details on Hadamard fractional calculus, we refer the reader to [2,3,4,5,6] and the references therein. In recent years, the study of Hadamard fractional differential equations has attracted the attention of many scholars, mainly focusing on the existence, stability and approximation of solutions (see [7,8,9,10,11,12,13,14,15,16,17,18,19]). For example, Huang et al. [9] applied a nonlinear alternative of Leray–Schauder to study the existence of solutions to a nonlinear coupled Hadamard fractional system.

To describe the turbulence problem in porous media, Leibenson [20] proposed the following p-Laplacian differential equation model in 1983

$${\Phi }_p\left(x^{\prime }\left(t\right)\right)=f(t,x\left(t\right)),t\in (0,1],$$

where the p-Laplacian operator is defined by ${\Phi }_p\left(z\right)={\left|z\right|}^{p-2}z$ $(p>1)$; its inverse is ${\Phi }_p^{-1}={\Phi }_q$ when $\frac{1}{p}+\frac{1}{q}=1$. Because it can describe the basic mechanical structure of turbulence problems, many scholars have begun to focus on the dynamics of nonlinear fractional differential equations with the p-Laplacian. In recent years, many excellent results (see [21,22,23,24,25,26]) have been obtained in the study of nonlinear fractional differential equations with the p-Laplacian. For example, Zhao [21] studied a nonlinear Hadamard fractional differential equation with the p-Laplacian. He defined two different distances in a metric space to discuss the solvability, approximation and stability of this system. Compared to this article, our system (1) is a coupled system of equations, and we study the solvability and stability of the system in a Banach space. In terms of norm definition and estimation, coupled systems are more complex and more difficult to solve than the single equation. In [26], Li et al. studied the existence of at least triple positive solutions of fractional-delay differential equations with a p-Laplacian operator using the Avery–Peterson theorem.

Hyers and Ulam [27,28] raised the Ulam–Hyers (UH) stability in the 1940s. On this basis, many UH-type stability concepts have been proposed successively, such as the generalized UH stability, Ulam–Hyers–Rassias stability and generalized Ulam–Hyers–Rassias stability. Recently, the study of UH-type stability has still been very popular, especially for fractional-order differential systems. There are many papers dealing with UH-type stability of nonlinear fractional differential systems (see [21,22,25,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45], among others). However, the UH-type stability of Hadamard fractional differential coupling systems is rarely studied because the study of the former is much more difficult than that of a single differential equation. To the best of our knowledge, there are no papers focusing on nonlinear Hadamard fractional coupling Laplacian systems with periodic boundary value conditions, which are an interesting and challenging problem.

The purpose of this article is to investigate the solvability, GUH stability and simulation of solutions for system (1). Our main contributions are as follows: (i) Since there are few papers dealing with nonlinear Hadamard fractional coupling Laplacian systems with periodic boundary value conditions, we first consider system (1) to fill this gap. (ii) We obtain some novel sufficient conditions for the existence, uniqueness and GUH stability of solutions to system (1). (iii) Based on the integral equation and differential equation, we have obtained the numerical solution and simulation of system (1) using the appropriate ODE toolbox in MATLAB.

The structure of this paper is as follows. Section 2 mainly introduces some necessary information and lemmas about Hadamard fractional calculus. In Section 3, some sufficient conditions on the existence and uniqueness of a solution are obtained by the contraction mapping principle. We prove the GUH stability of Hadamard fractional coupling Laplacian system (1) by applying nonlinear analysis methods and inequality techniques in Section 4. Section 5 provides the numerical solutions and simulations for three examples, illustrating the correctness and validity of our main results. Finally, we present a simple conclusion in Section 6.

2. Preliminaries

In this section, we introduce some important concepts and lemmas of Hadamard fractional calculus.

Definition 1

([3]). For $a>0$, the left-sided Hadamard fractional integral of order $\alpha >0$ for a function $f:[a,\infty )\to \mathbb{R}$ is defined by

$${ }^H{\mathcal{J}}_{a^{+}}^{\alpha }f\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^t{\left(\log \frac{t}{s}\right)}^{\alpha -1}f\left(s\right)\frac{ds}{s},$$

provided the integral exists, where $\Gamma \left(\alpha \right)={\int }_0^{\infty }{t}^{\alpha -1}{e}^{-t}dt$ and $\log (·)={\log }_e(·)$.

Definition 2

([3]). For $a,\alpha >0$ and $f\in C^n[a,\infty )$, the α-order left-sided Hadamard fractional derivative is defined by

$${ }^H{\mathcal{D}}_{a^{+}}^{\alpha }f\left(t\right)=\frac{1}{\Gamma (n-\alpha )}{\left(t\frac{d}{dt}\right)}^n{\int }_a^t{\left(\log \frac{t}{s}\right)}^{n-\alpha -1}f\left(s\right)\frac{ds}{s},$$

where $n-1<\alpha \le n,n=\left[\alpha \right]+1$ and $[·]$ is the Gaussian function.

Lemma 1

([3]). Let $a,b,\alpha >0$ and $f\in C^n(a,b)\cap L^1(a,b)$, then

$${ }^H{\mathcal{J}}_{a^{+}}^{\alpha }{(}^H{\mathcal{D}}_{a^{+}}^{\alpha }f\left(t\right))=f\left(t\right)+\sum _{i=1}^n{d}_i{\left(\log \frac{t}{a}\right)}^{\alpha -i},$$

where $d_1,d_2,\dots ,d_n$ are some real constants, and $n=\left[\alpha \right]+1$.

Lemma 2

([21]). Let $p>1$. The p-laplacian operator ${\Phi }_p\left(z\right)={\left|z\right|}^{p-2}z$ admits the properties as follows:

$\left(\mathrm{i}\right)$

If $z\ge 0$, then ${\Phi }_p\left(z\right)=z^{p-1}$, and ${\Phi }_p\left(z\right)$ is increasing with respect to z;

$\left(\mathrm{ii}\right)$

For all $z,w\in \mathbb{R}$, ${\Phi }_p\left(zw\right)={\Phi }_p\left(z\right){\Phi }_p\left(w\right)$;

$\left(\mathrm{iii}\right)$

If $\frac{1}{p}+\frac{1}{q}=1$, then ${\Phi }_q\left[{\Phi }_p\left(z\right)\right]={\Phi }_p\left[{\Phi }_q\left(z\right)\right]=z$, for all $z\in \mathbb{R}$;

$\left(\mathrm{iv}\right)$

For all $z,w\ge 0$, $z\le w\iff {\Phi }_q\left(z\right)={\Phi }_q\left(w\right)$;

$\left(\mathrm{v}\right)$

$0\le z\le {\Phi }_q^{-1}\left(w\right)\iff 0\le {\Phi }_q\left(z\right)\le w$;

$\left(\mathrm{vi}\right)$

$|{\Phi }_q\left(z\right)-{\Phi }_q\left(w\right)|\le (q-1){\overline{M}}^{q-2}|z-w|,q\ge 2,0\le z,w\le \overline{M}$;

$\left(\mathrm{vii}\right)$

$|{\Phi }_q\left(z\right)-{\Phi }_q\left(w\right)|\le (q-1){\underline{M}}^{q-2}|z-w|,1<q<2,z,w\ge \underline{M}\ge 0$.

Lemma 3

([46]). Let $\mathbb{X}$ be a Banach space and $\varnothing \ne \mathbb{E}\subset \mathbb{X}$ be closed. If $\mathcal{T}:\mathbb{E}\to \mathbb{E}$ is contracted, then $\mathcal{T}$ admits a unique fixed point $x^{*}\in \mathbb{E}$.

Lemma 4.

Assume that $1<{\alpha }_i\le 2$, $1<{\beta }_i\le 2$, and $p_i>1$ are some constants, $f_i\in C([1,e]\times {\mathbb{R}}^2,\mathbb{R})$, $i=1,2$. Then, BVP (1) is equivalent to the following integral equation

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_1\left(t\right)=-B_{1u}\left(e\right){\left(\log t\right)}^{{\beta }_1-1}+B_{1u}\left(t\right),\hfill \\ u_2\left(t\right)=-B_{2u}\left(e\right){\left(\log t\right)}^{{\beta }_2-1}+B_{2u}\left(t\right).\hfill \end{array}\right.\end{array}$$

(2)

where $B_{iu}\left(t\right)={ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}\left({\Phi }_{q_i}[-A_{iu}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}+A_{iu}\left(t\right)]\right),A_{iu}\left(t\right)={ }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i}{f}_i(t,u_1\left(t\right),u_2\left(t\right)),$$i=1,2$.

We can obtain Equation (2) using the method in reference [21], so we omitted the proof of Lemma 4.

3. Existence and Uniqueness of Solutions

We take $\mathbb{X}=C\left(\right[1,e],\mathbb{R})\times C\left(\right[1,e],\mathbb{R})$. For all $u=(u_1,u_2)\in \mathbb{X}$, define the norm $\parallel u\parallel =\parallel (u_1,u_2)\parallel =max\{{sup}_{t\in [1,e]}|u_1\left(t\right)|,{sup}_{t\in [1,e]}|u_2\left(t\right)\left|\right\}$, then $(\mathbb{X},\parallel ·\parallel )$ is a Banach space. Subsequently, we will inquire into the existence and stability of (1.1) on $(\mathbb{X},\parallel ·\parallel )$. In addition, we need the following underlying assumptions in the whole paper.

$\left({\mathrm{H}}_1\right)$

$1<{\alpha }_i\le 2,1<{\beta }_i\le 2$ and $1<p_i\le 2$ are some constants, $f_i\in C([1,e]\times {\mathbb{R}}^2,\mathbb{R})$, $i=1,2$;

$\left({\mathrm{H}}_2\right)$

There are two constants $M_i>0(i=1,2)$, such that for all $t\in [1,e],(u_1,u_2)\in {\mathbb{R}}^2$, $0\le f_i(t,u_1\left(t\right),u_2\left(t\right))\le M_i$;

$\left({\mathrm{H}}_3\right)$

There exist some continuous functions $l_{ij}\left(t\right)\ge 0(i,j=1,2)$, such that for all $t\in [1,e]$, $u_1,u_2$, ${\overline{u}}_1,{\overline{u}}_2\in \mathbb{R}$, $|f_i(t,u_1,u_2)-f_i(t,{\overline{u}}_1,{\overline{u}}_2)|\le l_{i1}\left(t\right)|u_1-{\overline{u}}_1|+l_{i2}\left(t\right)|u_2-{\overline{u}}_2|$;

$\left({\mathrm{H}}_4\right)$

$max\{{\kappa }_1,{\kappa }_2\}<1$, where ${\kappa }_i=\frac{4(q_i-1)}{\Gamma ({\alpha }_i+{\beta }_i+1)}{\left[\frac{M_i}{\Gamma ({\alpha }_i+1)}\right]}^{q_i-2}{\displaystyle \sum _{j=1}^2}\parallel l_{ij}{\parallel }_e,{\parallel l_{ij}\parallel }_e=\underset{1\le t\le e}{max}\left\{l_{ij}\left(t\right)\right\}$, $i=1,2$.

Theorem 1.

If $\left({\mathrm{H}}_1\right)$–$\left({\mathrm{H}}_4\right)$ are true, then system (1) has a unique solution $(u_1^{*}\left(t\right),u_2^{*}\left(t\right))\in \mathbb{X}$.

Proof. 

For all $u=(u_1\left(t\right),u_2\left(t\right))\in \mathbb{X}$, based on Lemma 4, we define the vector operator $\mathcal{L}:\mathbb{X}\to \mathbb{X}$ as

$$\begin{array}{c}\hfill \mathcal{L}(u_1\left(t\right),u_2\left(t\right))=({\mathcal{L}}_1(u_1\left(t\right),u_2\left(t\right)),{\mathcal{L}}_2(u_1\left(t\right),u_2\left(t\right))),\end{array}$$

(3)

where

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{L}}_1(u_1\left(t\right),u_2\left(t\right))=-B_{1u}\left(e\right){\left(\log t\right)}^{{\beta }_1-1}+B_{1u}\left(t\right),\hfill \\ {\mathcal{L}}_2(u_1\left(t\right),u_2\left(t\right))=-B_{2u}\left(e\right){\left(\log t\right)}^{{\beta }_2-1}+B_{2u}\left(t\right).\hfill \end{array}\right.\end{array}$$

(4)

By $\left({\mathrm{H}}_2\right)$, we have

$$0\le { }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i}{f}_i(t,u_1\left(t\right),u_2\left(t\right))\le \frac{M_i}{\Gamma ({\alpha }_i+1)},t\in [1,e],i=1,2.$$

(5)

According to $\left({\mathrm{H}}_2\right)$ and $A_{iu}\left(t\right)={ }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i}\left[f_i(t,u_1\left(t\right),u_2\left(t\right))\right](i=1,2)$, for all $t\in [1,e]$, we know that

$$\begin{array}{cc}\hfill & {\left[\frac{A_{iu}\left(t\right)}{{\left(\log t\right)}^{{\alpha }_i-1}}\right]}^{\prime }={\left[\frac{1}{\Gamma \left({\alpha }_i\right)}{\int }_1^t{\left(1-\frac{\log s}{\log t}\right)}^{{\alpha }_i-1}{f}_i(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}\right]}^{\prime }\hfill \\ \hfill =& \frac{({\alpha }_i-1)}{\Gamma \left({\alpha }_i\right)}\frac{1}{t}{\int }_1^t{\left(1-\frac{\log s}{\log t}\right)}^{{\alpha }_i-2}\frac{\log s}{{\left(\log t\right)}^2}{f}_i(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}>0,\hfill \end{array}$$

(6)

which implies that $\frac{A_{iu}\left(t\right)}{{\left(\log t\right)}^{{\alpha }_i-1}}(i=1,2)$ is monotonically increasing with respect to $t\in [1,e]$. So, we have

$$\begin{array}{c}\hfill 0<A_{iu}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}-A_{iu}\left(t\right)<\frac{M_i}{\Gamma ({\alpha }_i+1)},i=1,2.\end{array}$$

(7)

For all $u=(u_1,u_2)$, $\overline{u}=({\overline{u}}_1,{\overline{u}}_2)$$\in \mathbb{X}$, $t\in [1,e]$, we derive from (vi) in Lemma 2, $\left({\mathrm{H}}_3\right)$ and (5) that

$$\begin{array}{cc}\hfill & { }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|A_{iu}\left(t\right)-A_{i\overline{u}}\left(t\right)|\hfill \\ \hfill =& { }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|{ }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i}\left[f_i(t,u_1\left(t\right),u_2\left(t\right))\right]-{ }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i}\left[f_i(t,{\overline{u}}_1\left(t\right),{\overline{u}}_2\left(t\right))\right]|\hfill \\ \hfill \le & { }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i+{\beta }_i}|f_i(t,u_1\left(t\right),u_2\left(t\right))-f_i(t,{\overline{u}}_1\left(t\right),{\overline{u}}_2\left(t\right))|\hfill \\ \hfill \le & { }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i+{\beta }_i}[l_{i1}\left(t\right)|u_1\left(t\right)-{\overline{u}}_1\left(t\right)|+l_{i2}\left(t\right)|u_2\left(t\right)-{\overline{u}}_2\left(t\right)|]\hfill \\ \hfill \le & \frac{1}{\Gamma ({\alpha }_i+{\beta }_i+1)}\sum _{j=1}^2\parallel l_{ij}{\parallel }_e·\parallel u-\overline{u}\parallel ,i=1,2,\hfill \end{array}$$

(8)

and

$$\begin{array}{cc}\hfill & |B_{iu}\left(t\right)-B_{i\overline{u}}\left(t\right)|\hfill \\ \hfill =& \left|{ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}\left({\Phi }_{q_i}[-A_{iu}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}+A_{iu}\left(t\right)]-{\Phi }_{q_i}[-A_{i\overline{u}}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}+A_{i\overline{u}}\left(t\right)]\right)\right|\hfill \\ \hfill \le & { }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|{\Phi }_{q_i}[A_{iu}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}-A_{iu}\left(t\right)]-{\Phi }_{q_i}[A_{i\overline{u}}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}-A_{i\overline{u}}\left(t\right)]|\hfill \\ \hfill \le & (q_i-1){\left[\frac{M_i}{\Gamma ({\alpha }_i+1)}\right]}^{q_i-2}{ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|(A_{iu}\left(e\right)-A_{i\overline{u}}\left(e\right)){\left(\log t\right)}^{{\alpha }_1-1}-(A_{iu}\left(t\right)-A_{i\overline{u}}\left(t\right))|\hfill \\ \hfill \le & (q_i-1){\left[\frac{M_i}{\Gamma ({\alpha }_i+1)}\right]}^{q_i-2}\left({ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|A_{iu}\left(e\right)-A_{i\overline{u}}\left(e\right)|+{ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|A_{iu}\left(t\right)-A_{i\overline{u}}\left(t\right)|\right)\hfill \\ \hfill \le & \frac{2(q_i-1)}{\Gamma ({\alpha }_i+{\beta }_i+1)}{\left[\frac{M_i}{\Gamma ({\alpha }_i+1)}\right]}^{q_i-2}\sum _{j=1}^2\parallel l_{ij}{\parallel }_e\parallel u-\overline{u}\parallel ,i=1,2.\hfill \end{array}$$

(9)

It follows from (4) and (9) that

$$\begin{array}{cc}\hfill & |{\mathcal{L}}_1(u_1\left(t\right),u_2\left(t\right))-{\mathcal{L}}_1({\overline{u}}_1\left(t\right),{\overline{u}}_2\left(t\right))|=|(B_{1u}\left(e\right)-B_{1\overline{u}}\left(e\right)){\left(\log t\right)}^{{\beta }_1-1}-(B_{1u}\left(t\right)-B_{1\overline{u}}\left(t\right))|\hfill \\ \hfill \le & \frac{4(q_1-1)}{\Gamma ({\alpha }_1+{\beta }_1+1)}{\left[\frac{M_1}{\Gamma ({\alpha }_1+1)}\right]}^{q_1-2}\sum _{j=1}^2\parallel l_{1j}{\parallel }_e\parallel u-\overline{u}\parallel ={\kappa }_1\parallel u-\overline{u}\parallel ,\hfill \end{array}$$

(10)

and

$$\begin{array}{cc}\hfill & |{\mathcal{L}}_2(u_1\left(t\right),u_2\left(t\right))-{\mathcal{L}}_2({\overline{u}}_1\left(t\right),{\overline{u}}_2\left(t\right))|=|(B_{2u}\left(e\right)-B_{2\overline{u}}\left(e\right)){\left(\log t\right)}^{{\beta }_2-1}-(B_{2u}\left(t\right)-B_{2\overline{u}}\left(t\right))|\hfill \\ \hfill \le & \frac{4(q_2-1)}{\Gamma ({\alpha }_2+{\beta }_2+1)}{\left[\frac{M_2}{\Gamma ({\alpha }_2+1)}\right]}^{q_2-2}\sum _{j=1}^2\parallel l_{2j}{\parallel }_e\parallel u-\overline{u}\parallel ={\kappa }_2\parallel u-\overline{u}\parallel .\hfill \end{array}$$

(11)

By (10) and (11), we obtain

$$\begin{array}{c}\hfill \parallel \mathcal{L}(u_1\left(t\right),u_2\left(t\right))-\mathcal{L}({\overline{u}}_1\left(t\right),{\overline{u}}_2\left(t\right))\parallel \le max\{{\kappa }_1,{\kappa }_2\}·\parallel u-\overline{u}\parallel .\end{array}$$

(12)

Due to $0<max\{{\kappa }_1,{\kappa }_2\}<1$, (12) means that the operator $\mathcal{L}:\mathbb{X}\to \mathbb{X}$ is contractive. Hence, it follows from Lemma 3 that $\mathcal{L}$ has a unique fixed point $(u_1^{*}\left(t\right),u_2^{*}\left(t\right))\in \mathbb{X}$, which is the unique solution of system (1). The proof is complete. □

4. GUH Stability

In this section, we mainly discuss the GUH stability of problem (1) using direct analysis methods for $u=(u_1,u_2)\in \mathbb{X}$ and $ϵ>0$. Consider the following inequality

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{ }^H{\mathcal{D}}_{1^{+}}^{{\alpha }_1}\left[{\Phi }_{p_1}{(}^H{\mathcal{D}}_{1^{+}}^{{\beta }_1}{u}_1\left(t\right))\right]-f_1(t,u_1\left(t\right),u_2\left(t\right))\le ϵ,t\in (1,e],\hfill \\ { }^H{\mathcal{D}}_{1^{+}}^{{\alpha }_2}\left[{\Phi }_{p_2}{(}^H{\mathcal{D}}_{1^{+}}^{{\beta }_2}{u}_2\left(t\right))\right]-f_2(t,u_1\left(t\right),u_2\left(t\right))\le ϵ,t\in (1,e],\hfill \\ u_1\left(1\right)=u_1\left(e\right),{ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_1}{u}_1\left(1\right)={ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_1}{u}_1\left(e\right),\hfill \\ u_2\left(1\right)=u_2\left(e\right),{ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_2}{u}_2\left(1\right)={ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_2}{u}_2\left(e\right).\hfill \end{array}\right.\end{array}$$

(13)

Definition 3.

Suppose that for all $ϵ>0$ and $u=(u_1,u_2)\in \mathbb{X}$ satisfying (13), there is a unique $\overline{u}=({\overline{u}}_1,{\overline{u}}_2)\in \mathbb{X}$ satisfying (1) such that

$$\parallel u\left(t\right)-\overline{u}\left(t\right)\parallel \le \omega ϵ,$$

where $\omega >0$ is a constant. Then, problem (1) is said to be Ulam–Hyers stable.

Definition 4.

Suppose that for all $ϵ>0$ and $u=(u_1,u_2)\in \mathbb{X}$ satisfying (13), there is a unique $\overline{u}=({\overline{u}}_1,{\overline{u}}_2)\in \mathbb{X}$ satisfying (1) such that

$$\parallel u\left(t\right)-\overline{u}\left(t\right)\parallel \le \varpi \left(ϵ\right),$$

where $\varpi \in C(\mathbb{R},{\mathbb{R}}^{+})$ with $\varpi \left(0\right)=0$. Then, problem (1) is said to be GUH stable.

Remark 1.

$u=(u_1,u_2)\in \mathbb{X}$ is a solution of inequality (13) iff there exist $\phi =({\phi }_1,{\phi }_2)\in \mathbb{X}$ such that

(1)

$|{\phi }_1\left(t\right)|\le ϵ$ and $|{\phi }_2\left(t\right)|\le ϵ,1<t\le e$;

(2)

${ }^H{\mathcal{D}}_{1^{+}}^{{\alpha }_1}\left[{\Phi }_{p_1}\left({ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_1}{u}_1\left(t\right)\right)\right]=f_1(t,u_1\left(t\right),u_2\left(t\right))+{\phi }_1\left(t\right)$, $1<t\le e$;

(3)

${ }^H{\mathcal{D}}_{1^{+}}^{{\alpha }_2}\left[{\Phi }_{p_2}\left({ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_2}{u}_2\left(t\right)\right)\right]=f_2(t,u_1\left(t\right),u_2\left(t\right))+{\phi }_2\left(t\right)$, $1<t\le e$;

(4)

$u_1\left(1\right)=u_1\left(e\right),{ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_1}{u}_1\left(1\right)={ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_1}{u}_1\left(e\right),u_2\left(1\right)=u_2\left(e\right),{ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_2}{u}_2\left(1\right)={ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_2}{u}_2\left(e\right)$.

Theorem 2.

If $\left({\mathrm{H}}_1\right)$–$\left({\mathrm{H}}_4\right)$ are satisfied, then problem (13) is GUH stable.

Proof. 

On the basis of Lemma 4 and Remark 1, the inequality (13) is solved by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_1\left(t\right)=-B_{1u}^{\phi }\left(e\right){\left(\log t\right)}^{{\beta }_1-1}+B_{1u}^{\phi }\left(t\right),\hfill \\ u_2\left(t\right)=-B_{2u}^{\phi }\left(e\right){\left(\log t\right)}^{{\beta }_2-1}+B_{2u}^{\phi }\left(t\right).\hfill \end{array}\right.\end{array}$$

(14)

where $B_{iu}^{\phi }\left(t\right)={ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}\left({\Phi }_{q_i}[-A_{iu}^{\phi }\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}+A_{iu}^{\phi }\left(t\right)]\right)$, $A_{iu}^{\phi }\left(t\right)={ }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i}[f_i(t,u_1\left(t\right),u_2\left(t\right))+{\phi }_i\left(t\right)]$, $i=1,2.$

According to Theorem 1 and Lemma 4, the unique solution $u^{*}=(u_1^{*},u_2^{*})\in \mathbb{X}$ of system (1) is

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_1^{*}\left(t\right)=-B_{1u^{*}}\left(e\right){\left(\log t\right)}^{{\beta }_1-1}+B_{1u^{*}}\left(t\right),\hfill \\ u_2^{*}\left(t\right)=-B_{2u^{*}}\left(e\right){\left(\log t\right)}^{{\beta }_2-1}+B_{2u^{*}}\left(t\right).\hfill \end{array}\right.\end{array}$$

(15)

where $B_{i{u}^{*}}\left(t\right)={ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}\left({\Phi }_{q_i}[-A_{i{u}^{*}}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}+A_{i{u}^{*}}\left(t\right)]\right)$, $A_{i{u}^{*}}\left(t\right)={ }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i}\left[f_i(t,u_1^{*}\left(t\right),u_2^{*}\left(t\right))\right]$, $i=1,2$.

Similar to (8) and (9), we have

$$\begin{array}{cc}\hfill & { }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|A_{iu}^{{\phi }_i}\left(t\right)-A_{i{u}^{*}}\left(t\right)|\hfill \\ \hfill =& { }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|{ }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i}[f_i(t,u_1\left(t\right),u_2\left(t\right))+{\phi }_i\left(t\right)]-{ }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i}\left[f_i(t,u_1^{*}\left(t\right),u_2^{*}\left(t\right))\right]|\hfill \\ \hfill \le & { }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i+{\beta }_i}\left[\right|f_i(t,u_1\left(t\right),u_2\left(t\right))-f_i(t,u_1^{*}\left(t\right),u_2^{*}\left(t\right))|+|{\phi }_i\left(t\right)\left|\right]\hfill \\ \hfill \le & { }^H{\mathcal{J}}_{1^{+}}^{{\alpha }_i+{\beta }_i}[l_{i1}\left(t\right)|u_1\left(t\right)-u_1^{*}\left(t\right)|+l_{i2}\left(t\right)|u_2\left(t\right)-u_2^{*}\left(t\right)|+|{\phi }_i\left(t\right)\left|\right]\hfill \\ \hfill \le & \frac{1}{\Gamma ({\alpha }_i+{\beta }_i+1)}\left[\sum _{j=1}^2\parallel l_{ij}{\parallel }_e·\parallel u-\overline{u}\parallel +ϵ\right],i=1,2,\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill & |B_{iu}^{{\phi }_i}\left(t\right)-B_{i{u}^{*}}\left(t\right)|\hfill \\ \hfill =& \left|{ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}\left({\Phi }_{q_i}[-A_{iu}^{{\phi }_i}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}+A_{iu}^{{\phi }_i}\left(t\right)]-{\Phi }_{q_i}[-A_{i{u}^{*}}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}+A_{i{u}^{*}}\left(t\right)]\right)\right|\hfill \\ \hfill \le & { }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|{\Phi }_{q_i}[A_{iu}^{{\phi }_i}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}-A_{iu}^{{\phi }_i}\left(t\right)]-{\Phi }_{q_i}[A_{i{u}^{*}}\left(e\right){\left(\log t\right)}^{{\alpha }_i-1}-A_{i{u}^{*}}\left(t\right)]|\hfill \\ \hfill \le & (q_i-1){\left[\frac{M_i+ϵ}{\Gamma ({\alpha }_i+1)}\right]}^{q_i-2}{ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|(A_{iu}^{{\phi }_i}\left(e\right)-A_{i{u}^{*}}\left(e\right)){\left(\log t\right)}^{{\alpha }_i-1}-(A_{iu}^{{\phi }_i}\left(t\right)-A_{i{u}^{*}}\left(t\right))|\hfill \\ \hfill \le & (q_i-1){\left[\frac{M_i+ϵ}{\Gamma ({\alpha }_i+1)}\right]}^{q_i-2}\left({ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|A_{iu}^{{\phi }_i}\left(e\right)-A_{i{u}^{*}}\left(e\right)|+{ }^H{\mathcal{J}}_{1^{+}}^{{\beta }_i}|A_{iu}^{{\phi }_i}\left(t\right)-A_{i{u}^{*}}\left(t\right)|\right)\hfill \\ \hfill \le & \frac{2(q_i-1)}{\Gamma ({\alpha }_i+{\beta }_i+1)}{\left[\frac{M_i+ϵ}{\Gamma ({\alpha }_i+1)}\right]}^{q_i-2}\left[\sum _{j=1}^2\parallel l_{ij}{\parallel }_e·\parallel u-\overline{u}\parallel +ϵ\right],i=1,2.\hfill \end{array}$$

(17)

By the same manner as (10) and (11), we apply (14)–(17) to obtain

$$\begin{array}{cc}\hfill |u_i\left(t\right)-u_i^{*}\left(t\right)|=& |(B_{iu}^{{\phi }_i}\left(e\right)-B_{i{u}^{*}}\left(e\right)){\left(\log t\right)}^{{\beta }_i-1}-(B_{iu}^{{\phi }_i}\left(t\right)-B_{i{u}^{*}}\left(t\right))|\hfill \\ \hfill \le & |B_{iu}^{{\phi }_i}\left(e\right)-B_{i{u}^{*}}\left(e\right)|+|B_{iu}^{{\phi }_i}\left(t\right)-B_{i{u}^{*}}\left(t\right)|\hfill \\ \hfill \le & \frac{4(q_i-1)}{\Gamma ({\alpha }_i+{\beta }_i+1)}{\left[\frac{M_i+ϵ}{\Gamma ({\alpha }_i+1)}\right]}^{q_i-2}\left[\sum _{j=1}^2\parallel l_{ij}{\parallel }_e·\parallel u-\overline{u}\parallel +ϵ\right]\hfill \\ \hfill =& {\kappa }_i\left(ϵ\right)\parallel u-u^{*}\parallel +{\lambda }_i\left(ϵ\right)ϵ,i=1,2,\hfill \end{array}$$

(18)

where ${\kappa }_i\left(ϵ\right)=\frac{4(q_i-1)}{\Gamma ({\alpha }_i+{\beta }_i+1)}{\left[\frac{M_i+ϵ}{\Gamma ({\alpha }_i+1)}\right]}^{q_i-2}{\displaystyle \sum _{j=1}^2}{\parallel l_{ij}\parallel }_e$, ${\lambda }_i\left(ϵ\right)=\frac{4(q_i-1)}{\Gamma ({\alpha }_i+{\beta }_i+1)}{\left[\frac{M_i+ϵ}{\Gamma ({\alpha }_i+1)}\right]}^{q_i-2}$, $i=1,2$.

We know from (18) that

$$\begin{array}{c}\hfill \parallel u-u^{*}\parallel \le max\{{\kappa }_1\left(ϵ\right),{\kappa }_2\left(ϵ\right)\}\parallel u-u^{*}\parallel +max\{{\lambda }_1\left(ϵ\right),{\lambda }_2\left(ϵ\right)\}ϵ.\end{array}$$

(19)

For all $ϵ>0$ ($ϵ$ small enough), condition $\left({\mathrm{H}}_4\right)$ ensures that $0<max\{{\kappa }_1\left(ϵ\right),{\kappa }_2\left(ϵ\right)\}<1$. Then, it follows from (19) that

$$\begin{array}{c}\hfill \parallel u-u^{*}\parallel \le \frac{max\{{\lambda }_1\left(ϵ\right),{\lambda }_2\left(ϵ\right)\}ϵ}{1-max\{{\kappa }_1\left(ϵ\right),{\kappa }_2\left(ϵ\right)\}}=\varpi \left(ϵ\right).\end{array}$$

(20)

Obviously, when $ϵ>0$, $\varpi \left(ϵ\right)>0$ and $\varpi \left(0\right)=0$. Therefore, we know from (20) and Definition 4 that problem (1) is GUH stable. The proof is complete. □

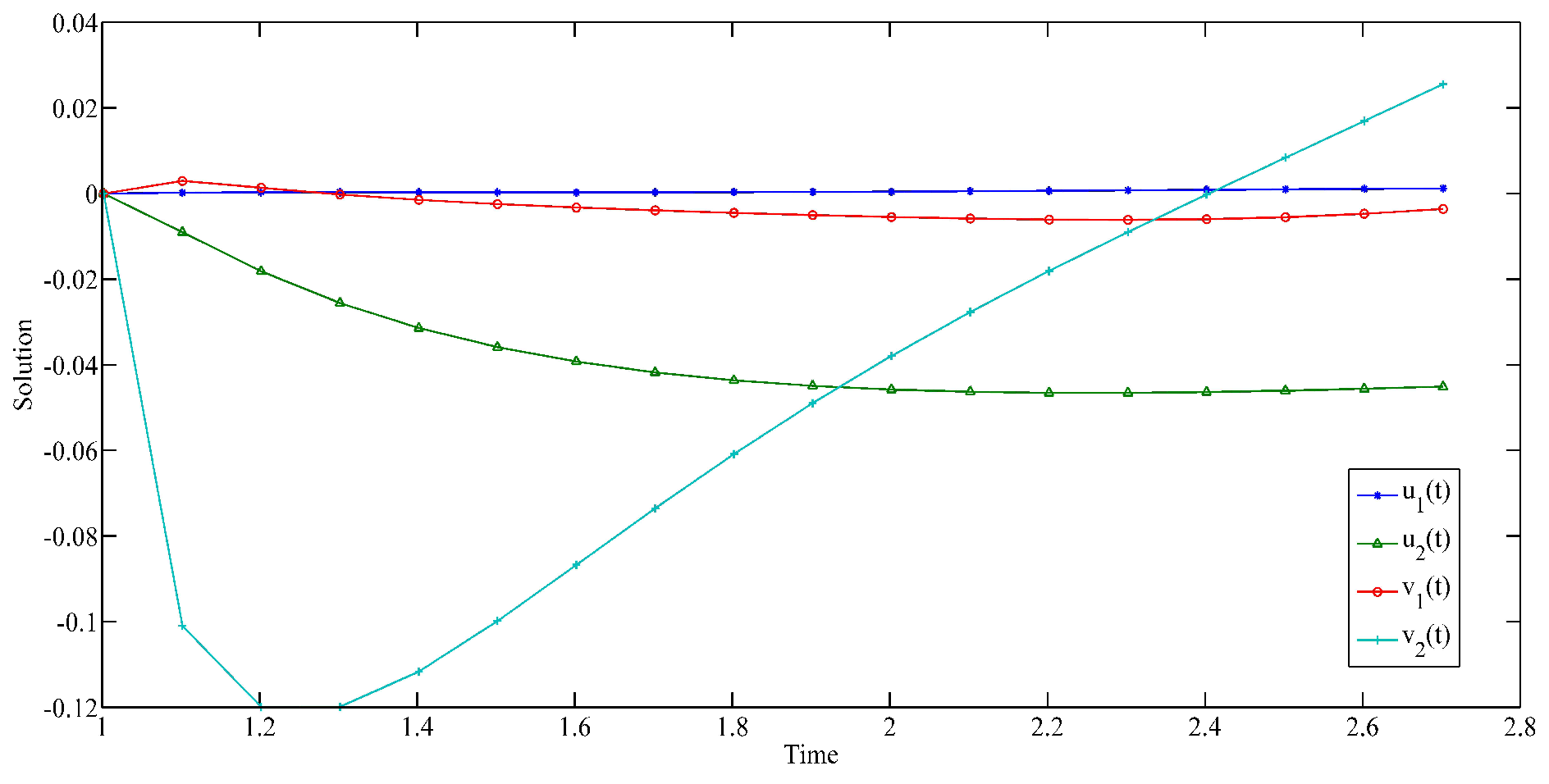
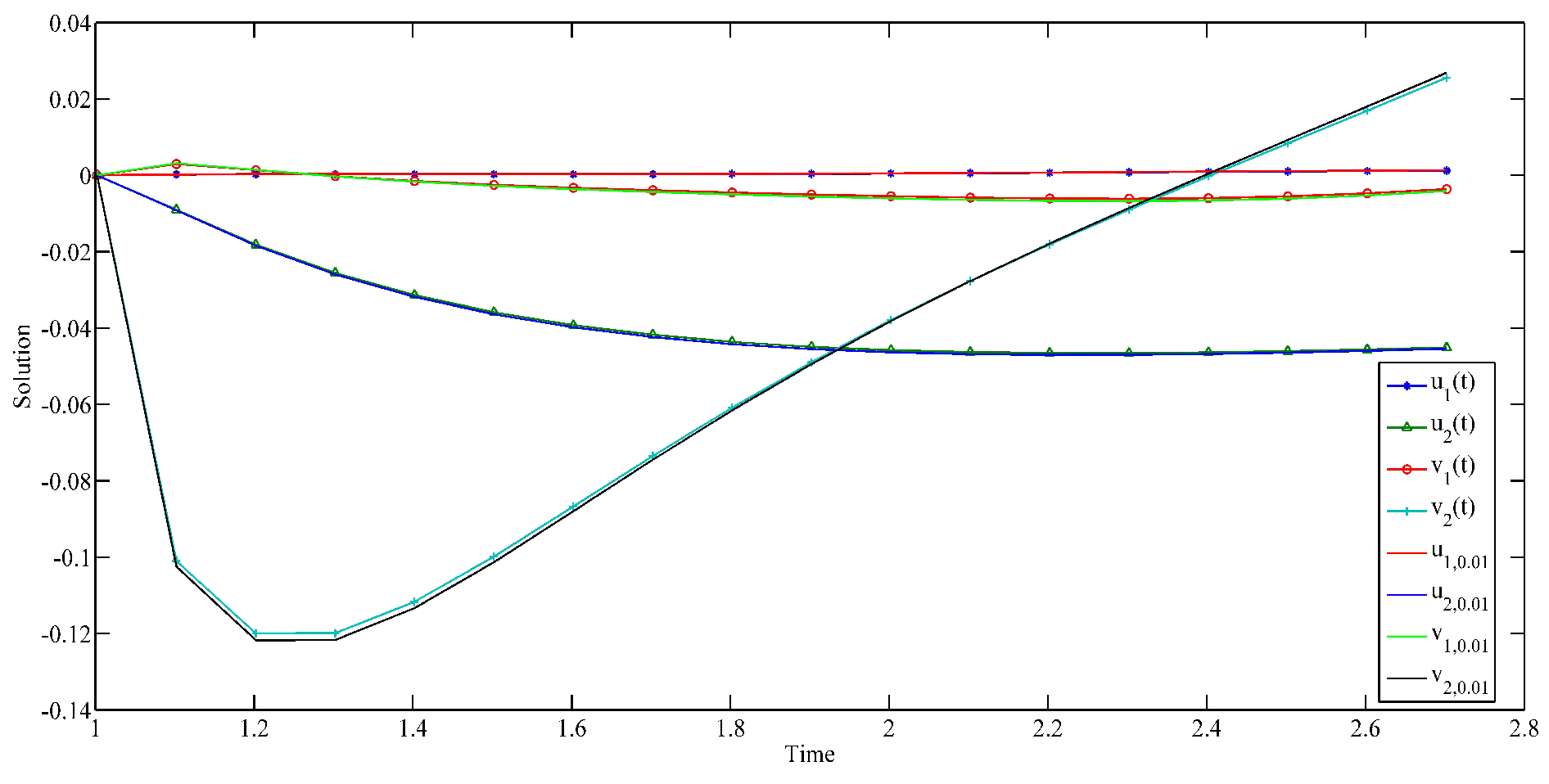
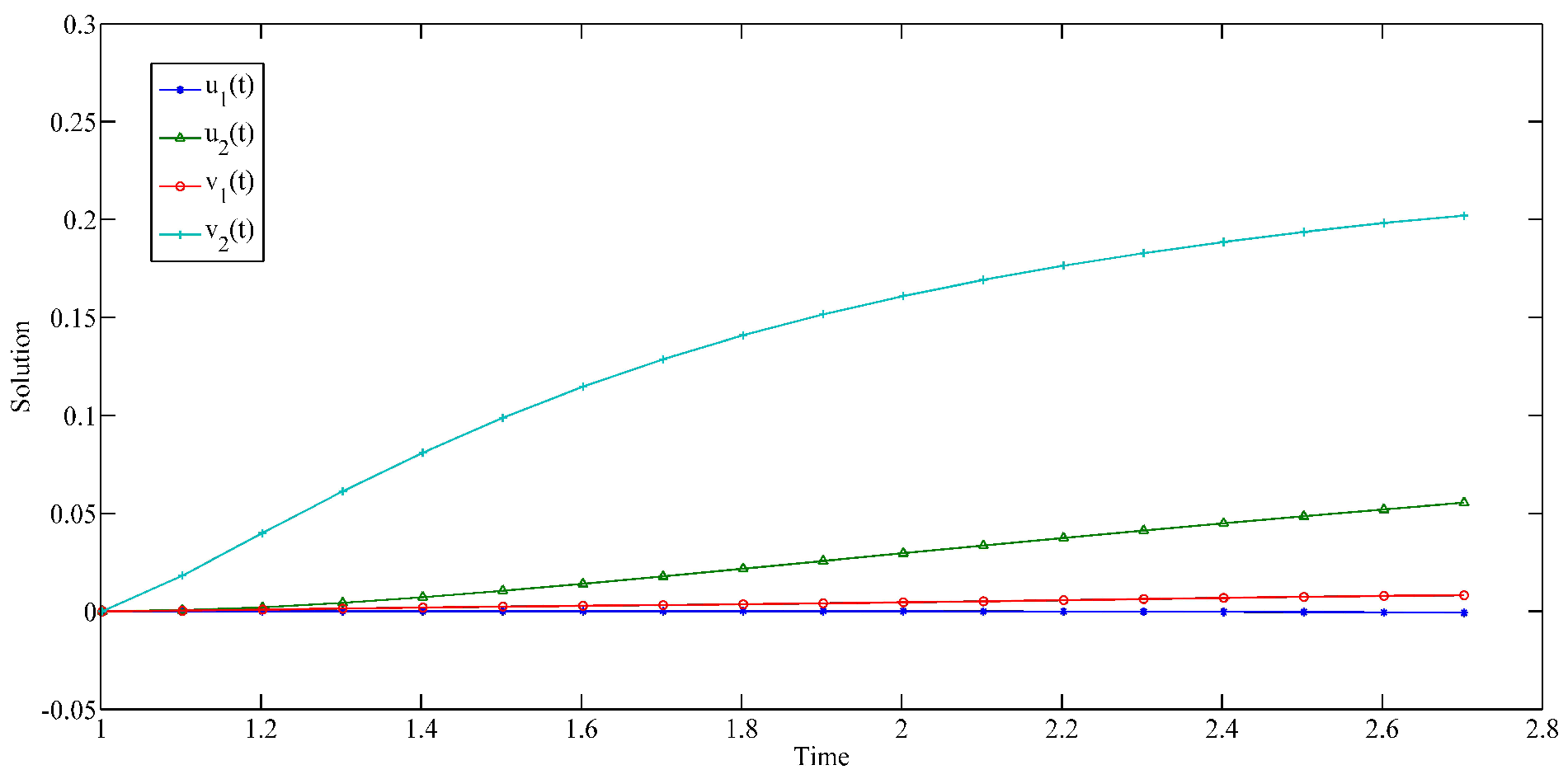
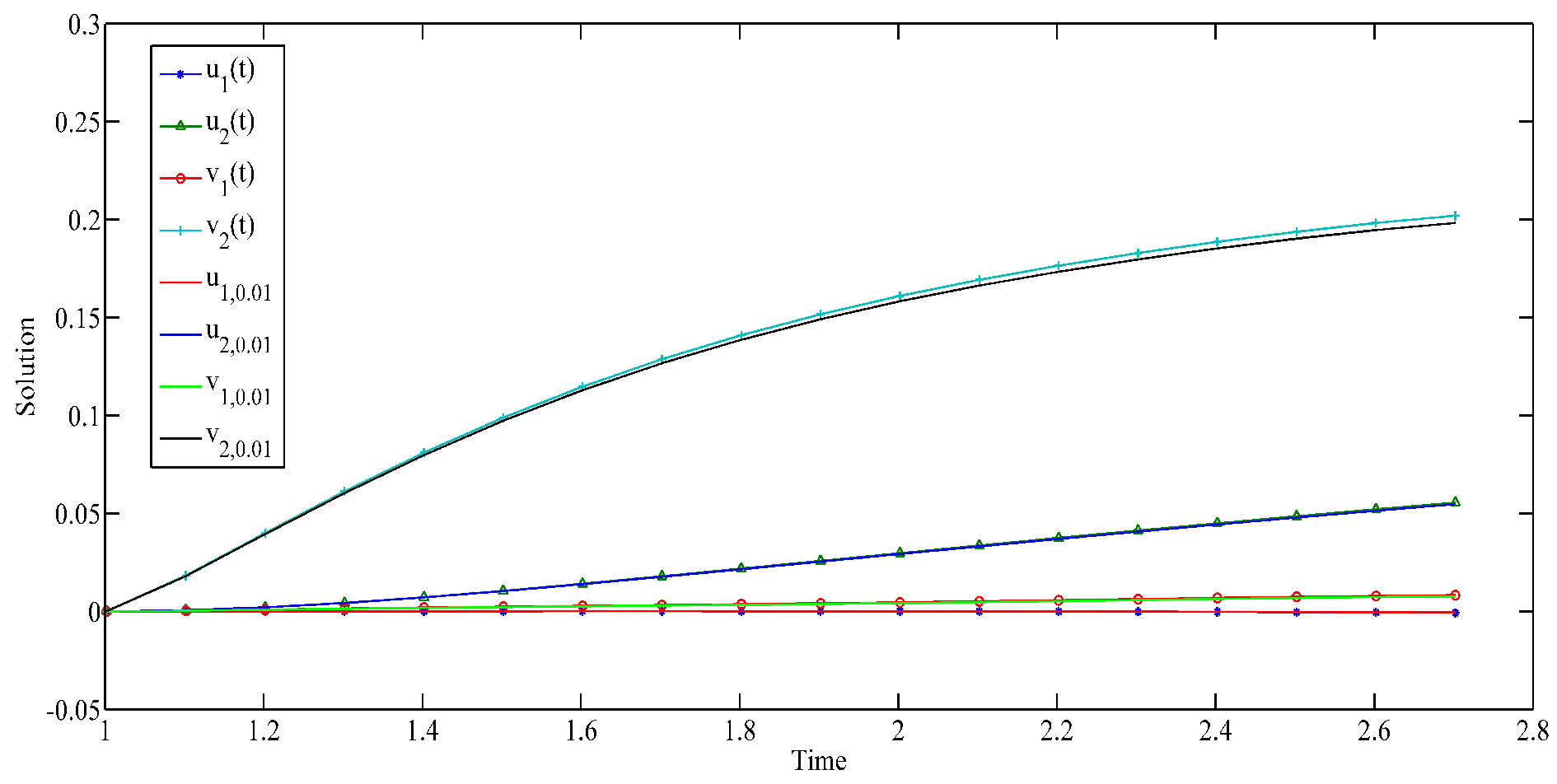
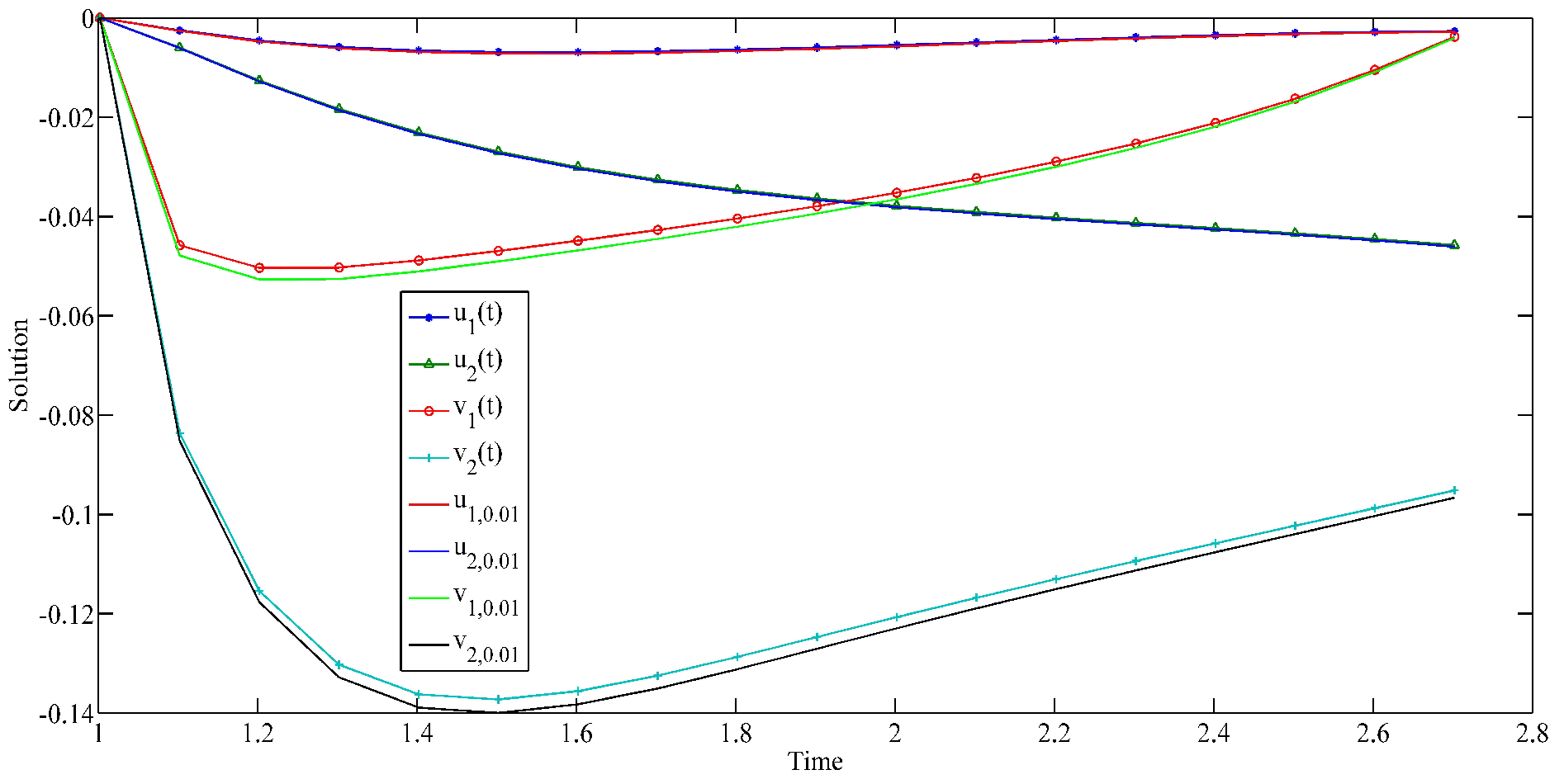
5. Three Examples and Simulations

This section provides three examples to verify the validity and correctness of our main results.

Example 1.

In (1), we take ${\alpha }_1=1.2$, ${\alpha }_2=1.4$, ${\beta }_1=1.8$, ${\beta }_2=1.6$, $p_1=\frac{3}{2}$, $p_2=\frac{7}{4}$, $f_1(t,u_1,u_2)=\frac{2+cos\left(2t\right)}{20}[\frac{5\pi }{4}+arctan\left(u_1\left(t\right)\right)+arctan\left(u_2\left(t\right)\right)]$, $f_2(t,u_1,u_2)=\frac{4+sin\left(2t\right)}{30}[\frac{7\pi }{4}+arctan\left(u_1\left(t\right)\right)+2arctan\left(u_2\left(t\right)\right)]$. By a simple calculation, we have

$$\begin{array}{c}\hfill \frac{\pi }{80}<f_1(t,u_1,u_2)<\frac{27\pi }{80},\frac{\pi }{80}<f_2(t,u_1,u_2)<\frac{13\pi }{24},\end{array}$$

$$\begin{array}{cc}\hfill & |f_1(t,u_1,u_2)-f_1(t,{\overline{u}}_1,{\overline{u}}_2)|<\frac{2+cos\left(2t\right)}{20}\left[\right|u_1-{\overline{u}}_1|+|u_2-{\overline{u}}_2\left|\right],\hfill \\ \hfill & |f_2(t,u_1,u_2)-f_2(t,{\overline{u}}_1,{\overline{u}}_2)|<\frac{4+sin\left(2t\right)}{30}|u_1-{\overline{u}}_1|+\frac{4+sin\left(2t\right)}{15}|u_2-{\overline{u}}_2|.\hfill \end{array}$$

Thus, the conditions $\left({\mathrm{H}}_1\right)$–$\left({\mathrm{H}}_3\right)$ are true. Consequently, $M_1=\frac{27\pi }{80}$, $M_2=\frac{13\pi }{24}$, $\parallel l_{11}{\parallel }_e={\parallel l_{12}\parallel }_e\le \frac{3}{20}$, $\parallel l_{21}{\parallel }_e\le \frac{1}{6}$, $\parallel l_{22}{\parallel }_e\le \frac{1}{3}$. When $p_1=\frac{3}{2}$, $p_2=\frac{7}{4}$, then $q_1=3>2$, $q_2=\frac{7}{3}>2$, and

$$\begin{array}{cc}\hfill & {\kappa }_1=\frac{4(q_1-1)}{\Gamma ({\alpha }_1+{\beta }_1+1)}{\left[\frac{M_1}{\Gamma ({\alpha }_1+1)}\right]}^{q_1-2}\sum _{j=1}^2{\parallel l_{1j}\parallel }_e\le 0.3849<1,\hfill \\ \hfill & {\kappa }_2=\frac{4(q_2-1)}{\Gamma ({\alpha }_2+{\beta }_2+1)}{\left[\frac{M_2}{\Gamma ({\alpha }_2+1)}\right]}^{q_2-2}\sum _{j=1}^2{\parallel l_{2j}\parallel }_e\le 0.4936<1.\hfill \end{array}$$

Thus, $\left({\mathrm{H}}_4\right)$ holds. From Theorems 1 and 2, we claim that system (1) in Example 1 has a unique solution, which is GUH stable.

Remark 2.

In Example 1, ${\alpha }_i$, ${\beta }_i$$(i=1,2)$ are all rational numbers. ${\alpha }_1=1.2$ is close to 1, ${\beta }_1=1.8$ is close to 2, and ${\alpha }_2=1.4$ and ${\beta }_2=1.6$ are close to 1.5. To further verify the correctness of our results and the sensitivity of the numerical simulation to the parameters, we set ${\alpha }_i$ and ${\beta }_i$ close to 2 in Example 2.

Example 2.

In (1), assume ${\alpha }_1=1.9$, ${\alpha }_2=1.95$, ${\beta }_1=1.95$, ${\beta }_2=1.9$, $p_1$, $p_2$, $f_1(t,u_1,u_2)$ and $f_2(t,u_1,u_2)$ are the same as in Example 1. Then, conditions $\left({\mathrm{H}}_1\right)$–$\left({\mathrm{H}}_3\right)$ hold. We simply perform some calculations to obtain

$$\begin{array}{cc}\hfill & {\kappa }_1=\frac{4(q_1-1)}{\Gamma ({\alpha }_1+{\beta }_1+1)}{\left[\frac{M_1}{\Gamma ({\alpha }_1+1)}\right]}^{q_1-2}\sum _{j=1}^2{\parallel l_{1j}\parallel }_e\le 0.0725<1,\hfill \\ \hfill & {\kappa }_2=\frac{4(q_2-1)}{\Gamma ({\alpha }_2+{\beta }_2+1)}{\left[\frac{M_2}{\Gamma ({\alpha }_2+1)}\right]}^{q_2-2}\sum _{j=1}^2{\parallel l_{2j}\parallel }_e\le 0.1337<1.\hfill \end{array}$$

Thus, $\left({\mathrm{H}}_4\right)$ also holds. It follows from Theorems 1 and 2 that system (1) in Example 2 has a unique solution, which is GUH stable.

Remark 3.

In Examples 1 and 2, $p_1$ and $p_2$ are all rational numbers. To further verify the correctness of our results and the sensitivity of the numerical simulation to the parameters, we chose some irrational numbers $p_1$ and $p_2$ satisfying $1<p_1,p_2<2$ in Example 3.

Example 3.

In (1), assume $p_1=\sqrt{3}$, $p_2=\sqrt{2.5}$, ${\alpha }_1$, ${\alpha }_2$, ${\beta }_1$, ${\beta }_2$, $f_1(t,u_1,u_2)$ and $f_2(t,u_1,u_2)$ are the same as in Example 1. Then, conditions $\left({\mathrm{H}}_1\right)$–$\left({\mathrm{H}}_3\right)$ hold. When $p_1=\sqrt{3}$ and $p_2=\sqrt{2.5}$, then $q_1=2.366>2$ and $q_2=2.7208>2$. A simple computation gives that

$$\begin{array}{cc}\hfill & {\kappa }_1=\frac{4(q_1-1)}{\Gamma ({\alpha }_1+{\beta }_1+1)}{\left[\frac{M_1}{\Gamma ({\alpha }_1+1)}\right]}^{q_1-2}\sum _{j=1}^2{\parallel l_{1j}\parallel }_e\le 0.2694<1,\hfill \\ \hfill & {\kappa }_2=\frac{4(q_2-1)}{\Gamma ({\alpha }_2+{\beta }_2+1)}{\left[\frac{M_2}{\Gamma ({\alpha }_2+1)}\right]}^{q_2-2}\sum _{j=1}^2{\parallel l_{2j}\parallel }_e\le 0.7197<1.\hfill \end{array}$$

Thus, $\left({\mathrm{H}}_4\right)$ also holds. We conclude from Theorems 1 and 2 that system (1) in Example 3 has a unique solution, which is GUH stable.

To complete the numerical simulations of Examples 1–3, we present a concise algorithm below. Let $(v_1\left(t\right),v_2\left(t\right))=({ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_1}{u}_1\left(t\right),{ }^H{\mathcal{D}}_{1^{+}}^{{\beta }_2}{u}_2\left(t\right))$; then, system (1) can be rewritten as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_1\left(t\right)=\frac{1}{\Gamma \left({\beta }_1\right)}\left[{\int }_1^e{\left(\log \frac{e}{s}\right)}^{{\beta }_1-1}{v}_1\left(s\right)\frac{ds}{s}·{\left(\log t\right)}^{{\beta }_1-1}-{\int }_1^t{\left(\log \frac{t}{s}\right)}^{{\beta }_1-1}{v}_1\left(s\right)\frac{ds}{s}\right],\hfill \\ u_2\left(t\right)=\frac{1}{\Gamma \left({\beta }_2\right)}\left[{\int }_1^e{\left(\log \frac{e}{s}\right)}^{{\beta }_2-1}{v}_2\left(s\right)\frac{ds}{s}·{\left(\log t\right)}^{{\beta }_2-1}-{\int }_1^t{\left(\log \frac{t}{s}\right)}^{{\beta }_2-1}{v}_2\left(s\right)\frac{ds}{s}\right],\hfill \\ v_1\left(t\right)=[\frac{1}{\Gamma \left({\alpha }_1\right)}{\int }_1^t{\left(\log \frac{t}{s}\right)}^{{\alpha }_1-1}{f}_1(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}\hfill \\ -\frac{1}{\Gamma \left({\alpha }_1\right)}{\int }_1^e{\left(\log \frac{e}{s}\right)}^{{\alpha }_1-1}{f}_1(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}·{\left(\log t\right)}^{{\alpha }_1-1}{]}^{q_1-1},\hfill \\ v_2\left(t\right)=[\frac{1}{\Gamma \left({\alpha }_2\right)}{\int }_1^t{\left(\log \frac{t}{s}\right)}^{{\alpha }_2-1}{f}_2(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}\hfill \\ -\frac{1}{\Gamma \left({\alpha }_2\right)}{\int }_1^e{\left(\log \frac{e}{s}\right)}^{{\alpha }_2-1}{f}_2(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}·{\left(\log t\right)}^{{\alpha }_2-1}{]}^{q_2-1}.\hfill \end{array}\right.\end{array}$$

(21)

Taking the derivative on both sides of system (21), we get

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{d{u}_1\left(t\right)}{dt}=\frac{{\beta }_1-1}{\Gamma \left({\beta }_1\right)t}\left[{\int }_1^e{\left(\log \frac{e}{s}\right)}^{{\beta }_1-1}{v}_1\left(s\right)\frac{ds}{s}·{\left(\log t\right)}^{{\beta }_1-2}-{\int }_1^t{\left(\log \frac{t}{s}\right)}^{{\beta }_1-2}{v}_1\left(s\right)\frac{ds}{s}\right],\hfill \\ \frac{d{u}_2\left(t\right)}{dt}=\frac{{\beta }_2-1}{\Gamma \left({\beta }_2\right)t}\left[{\int }_1^e{\left(\log \frac{e}{s}\right)}^{{\beta }_2-1}{v}_2\left(s\right)\frac{ds}{s}·{\left(\log t\right)}^{{\beta }_2-2}-{\int }_1^t{\left(\log \frac{t}{s}\right)}^{{\beta }_2-2}{v}_2\left(s\right)\frac{ds}{s}\right],\hfill \\ \frac{d{v}_1\left(t\right)}{dt}=(q_1-1)[\frac{1}{\Gamma \left({\alpha }_1\right)}{\int }_1^t{\left(\log \frac{t}{s}\right)}^{{\alpha }_1-1}{f}_1(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}\hfill \\ -\frac{1}{\Gamma \left({\alpha }_1\right)}{\int }_1^e{\left(\log \frac{e}{s}\right)}^{{\alpha }_1-1}{f}_1(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}·{\left(\log t\right)}^{{\alpha }_1-1}{]}^{q_1-2}\hfill \\ \times \frac{{\alpha }_1-1}{\Gamma \left({\alpha }_1\right)t}[{\int }_1^t{\left(\log \frac{t}{s}\right)}^{{\alpha }_1-2}{f}_1(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}\hfill \\ -{\int }_1^e{\left(\log \frac{e}{s}\right)}^{{\alpha }_1-1}{f}_1(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}·{\left(\log t\right)}^{{\alpha }_1-2}],\hfill \\ \frac{d{v}_2\left(t\right)}{dt}=(q_2-1)[\frac{1}{\Gamma \left({\alpha }_2\right)}{\int }_1^t{\left(\log \frac{t}{s}\right)}^{{\alpha }_2-1}{f}_2(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}\hfill \\ -\frac{1}{\Gamma \left({\alpha }_2\right)}{\int }_1^e{\left(\log \frac{e}{s}\right)}^{{\alpha }_2-1}{f}_2(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}·{\left(\log t\right)}^{{\alpha }_2-1}{]}^{q_2-2}\hfill \\ \times \frac{{\alpha }_2-1}{\Gamma \left({\alpha }_2\right)t}[{\int }_1^t{\left(\log \frac{t}{s}\right)}^{{\alpha }_2-2}{f}_2(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}\hfill \\ -{\int }_1^e{\left(\log \frac{e}{s}\right)}^{{\alpha }_2-1}{f}_2(s,u_1\left(s\right),u_2\left(s\right))\frac{ds}{s}·{\left(\log t\right)}^{{\alpha }_2-2}].\hfill \end{array}\right.\end{array}$$

(22)

We can use the appropriate ODE toolbox in MATLAB to complete numerical simulations of (22). Based on the above analysis, we employ the ODE113 toolbox in MATLAB R2017b on the three examples to present numerical simulations of their solutions and GUH stability. The simulation diagrams are shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6.

6. Conclusions

The Hadamard fractional derivative and integral are important parts of fractional calculus which have been widely used in engineering, biology, neural networks, control theory, and so on. Compared with a single Hadamard fractional system, Hadamard fractional coupling systems have a more complex structure and a wide range of applications. As far as we know, there are no works dealing with nonlinear Hadamard fractional coupling Laplacian systems with periodic boundary value conditions. So, we investigated system (1) to fill this gap. In this article, we consider a class of nonlinear Hadamard fractional coupling $(p_1$, $p_2)$-Laplacian systems with periodic boundary value conditions. Based on nonlinear analysis methods and contraction mapping principle, we obtain some new and easily verifiable sufficient criteria of the existence, uniqueness and GUH stability of solutions of system (1). Examples 1–3 and their simulations demonstrate the correctness and availability of our main results. Meanwhile, Figure 2, Figure 4 and Figure 6 also indicate that the solution of (1) is sensitive and dependent on parameters $p_i$, ${\alpha }_i$ and ${\beta }_i$, $i=1,2.$ In addition, inspired by recently published papers [9,47,48], we will investigate the Lyapunov stability of fractional differential equations, the coincidence theory of fractional differential equations, and fractional differential equations involving fractional derivative impulses in the future.