Simulation of Dynamic Path Planning of Symmetrical Trajectory of Mobile Robots Based on Improved A* and Artificial Potential Field Fusion for Natural Resource Exploration
Abstract
:1. Introduction
- (1)
- Improving the heuristic function: The heuristic function plays a significant role in determining the direction of search expansion. By enhancing the heuristic function, the accuracy and efficiency of the search can be improved;
- (2)
- Enhancing the weighting coefficients of the estimation function: The weighting coefficients determine whether the search process tends more towards breadth or depth. Optimizing these coefficients can better guide the search direction;
- (3)
- Optimizing the search domain: Reducing the search domain in special cases can significantly decrease the number of search nodes, thereby enhancing search efficiency;
- (4)
- Path curve optimization: Smoothing the path to make it more suitable for robot movement, reducing the problems of redundant path nodes and non-smooth turning angles;
- (5)
- Improving search strategies: Introducing strategies such as bidirectional search and jump point search (JPS) can significantly accelerate search efficiency.
- (1)
- Improving the repulsive force function to ensure that the target point lies at the global potential energy minimum of the attractive and repulsive fields;
- (2)
- Introducing global planning by combining with global path planning algorithms such as the A* algorithm to avoid falling into local optima;
- (3)
- Dynamically adjusting parameters based on real-time environmental information to adapt the potential field function and parameters to different scenarios;
- (4)
- Smoothing the generated paths to enhance robot mobility efficiency.
2. Materials and Methods
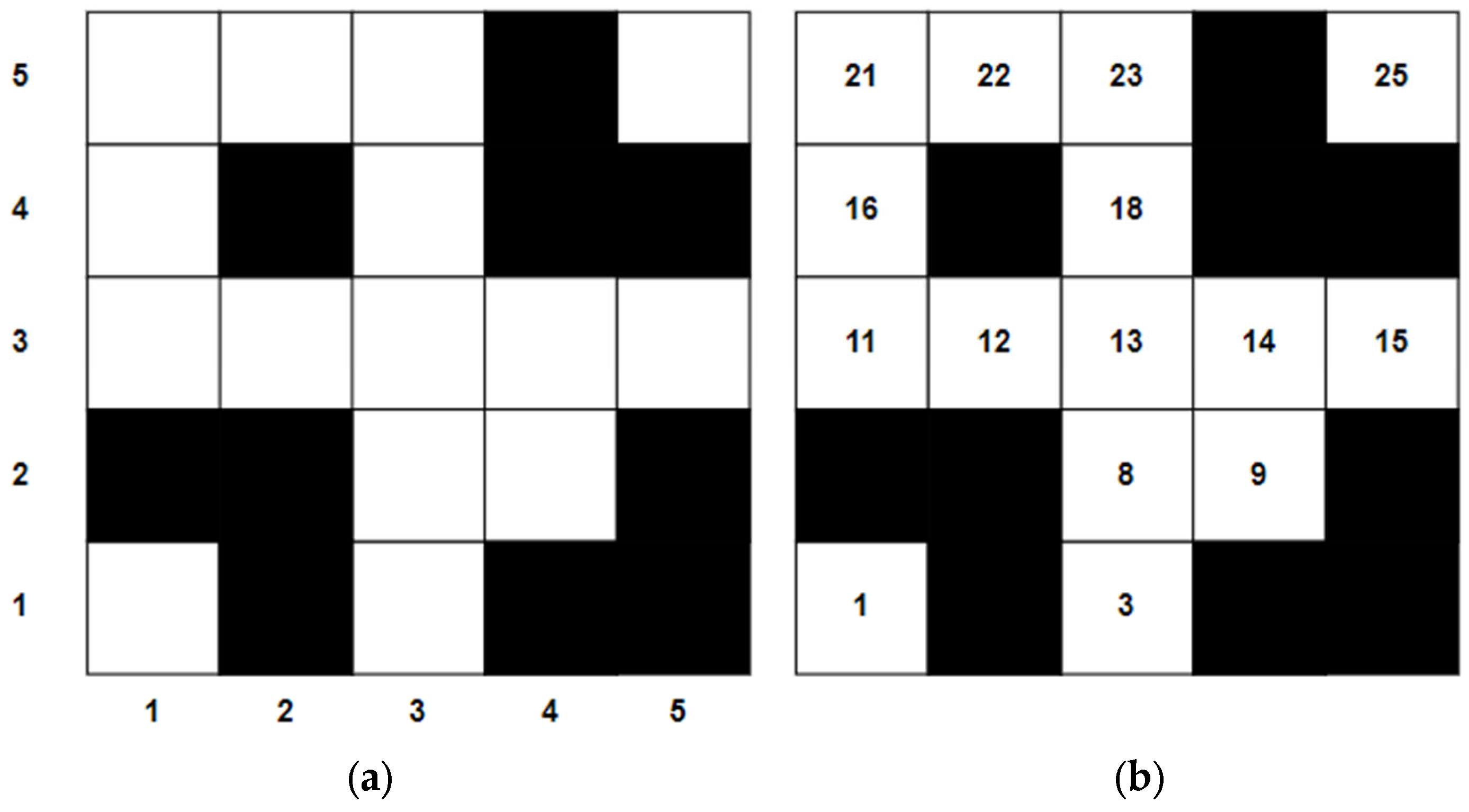
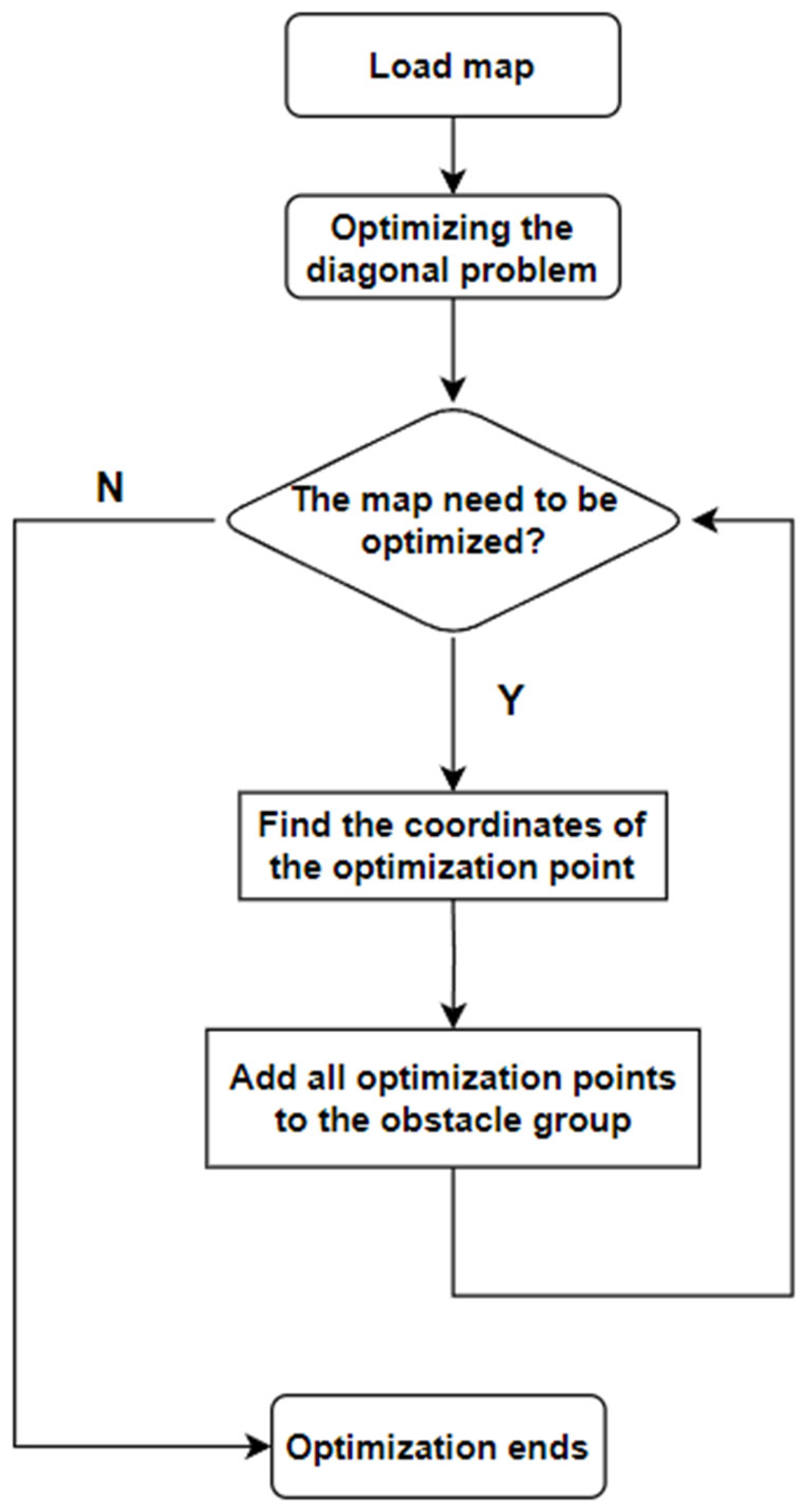
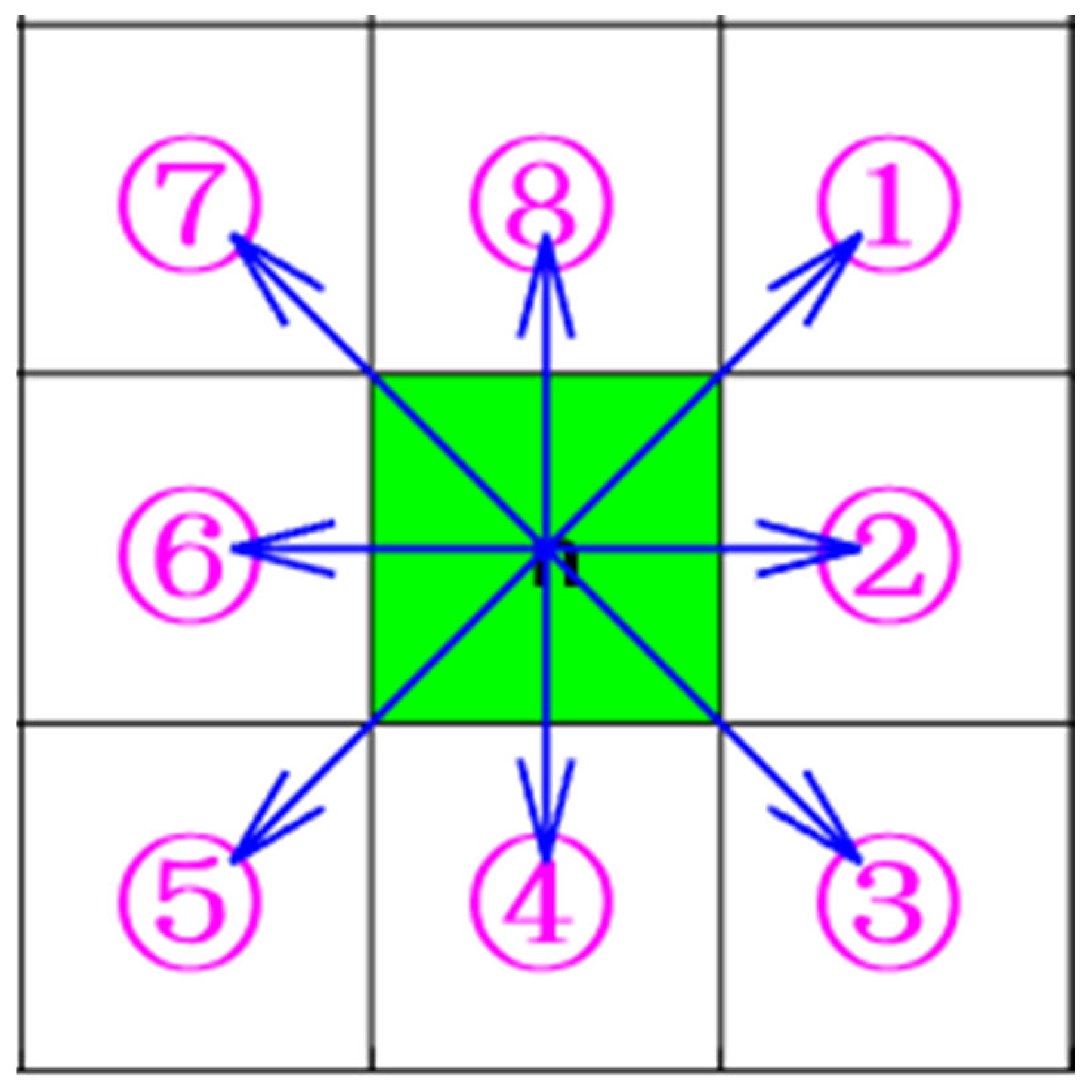
- Map creation and optimization;
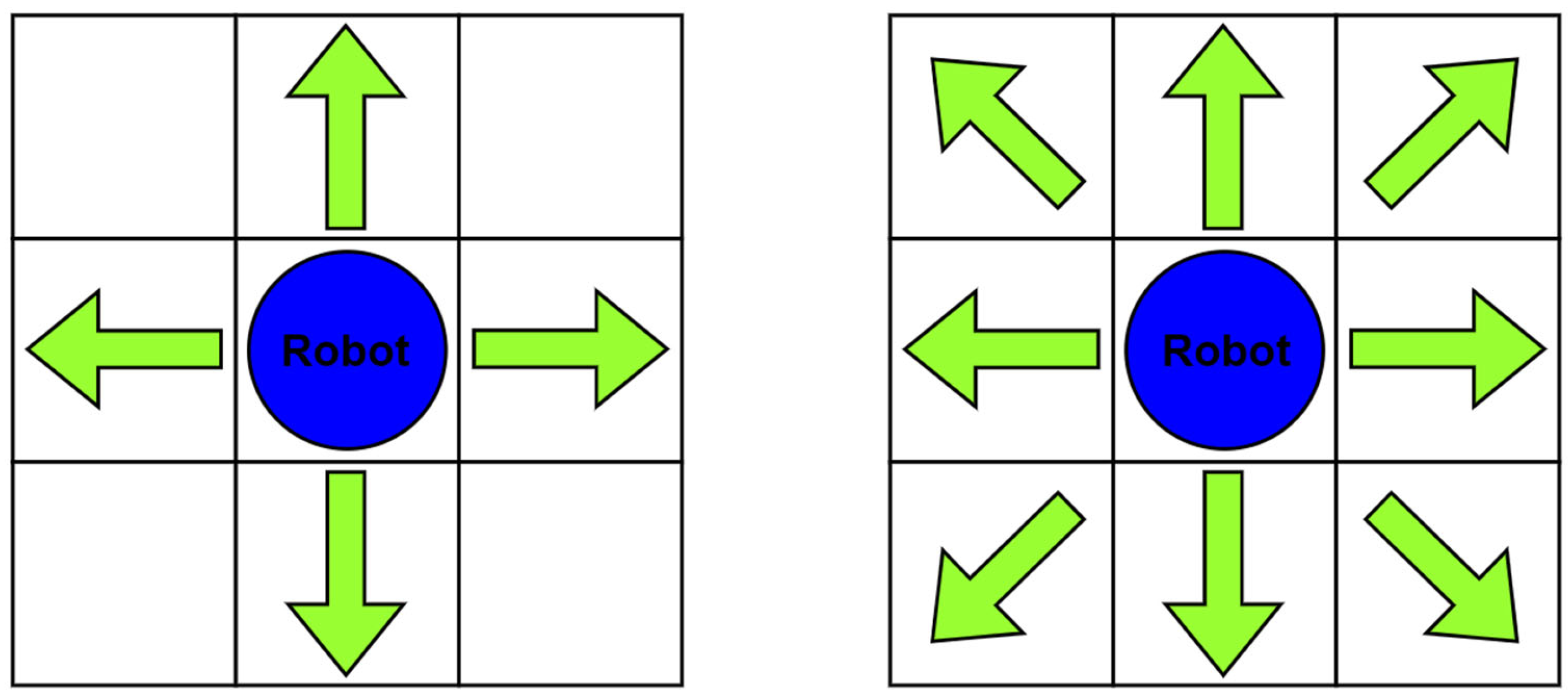
- The A* algorithm and its optimization;
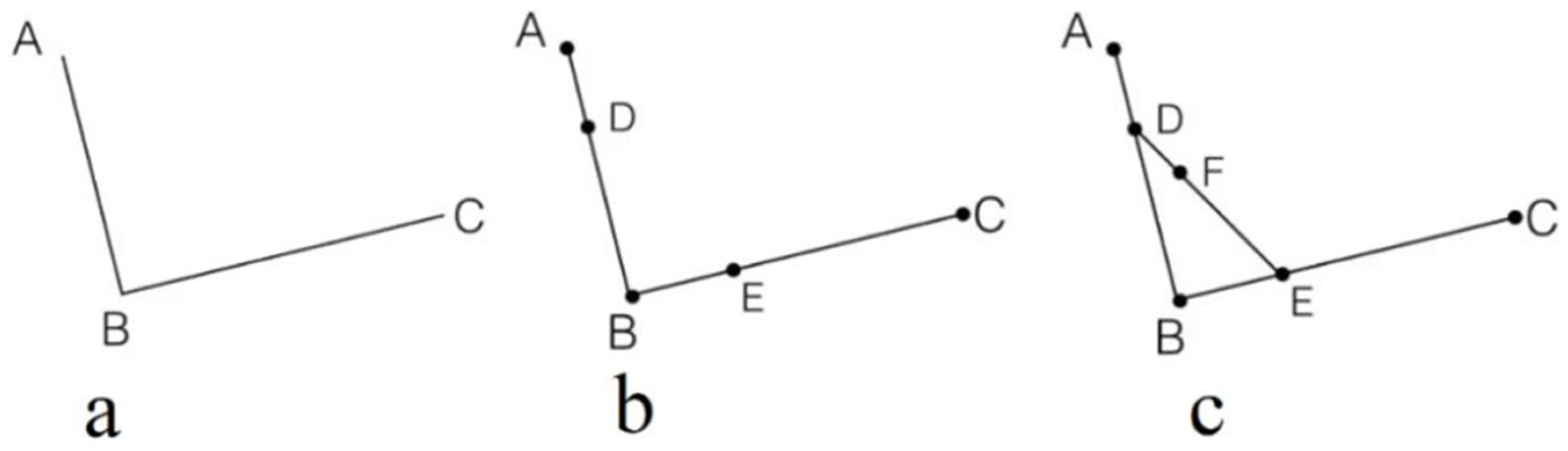
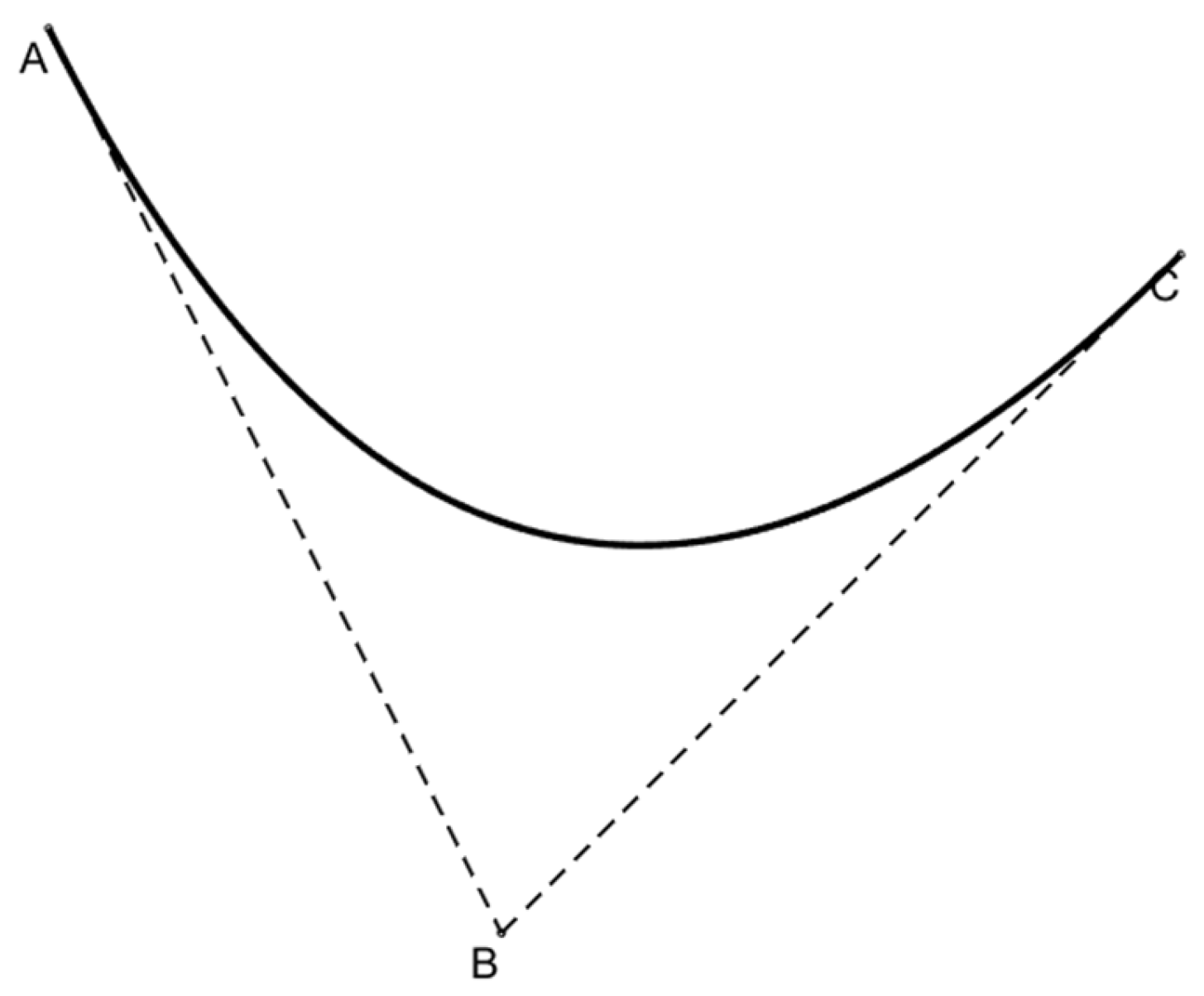
- Bézier curve optimization;
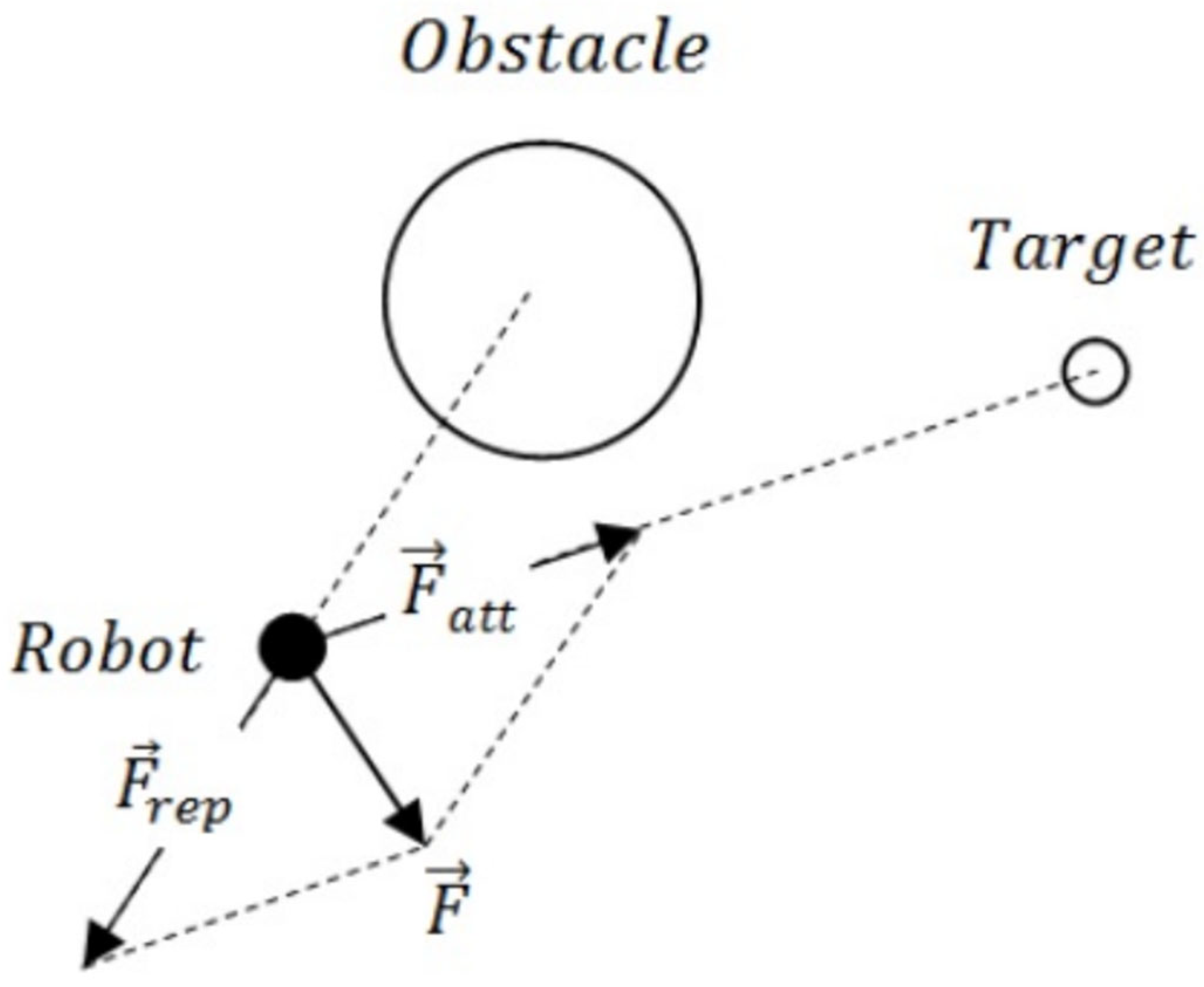
- The Artificial Potential Field Method (APF) and its Optimization;
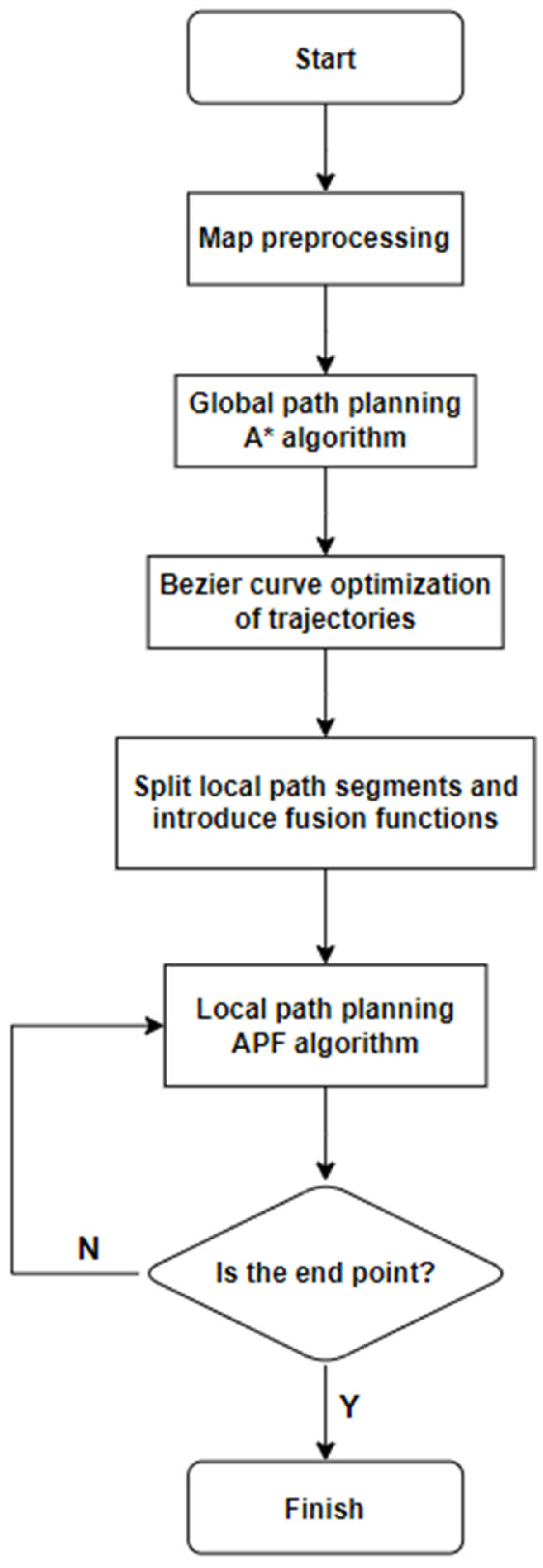
- Algorithm combination process;
3. Experiments and Results
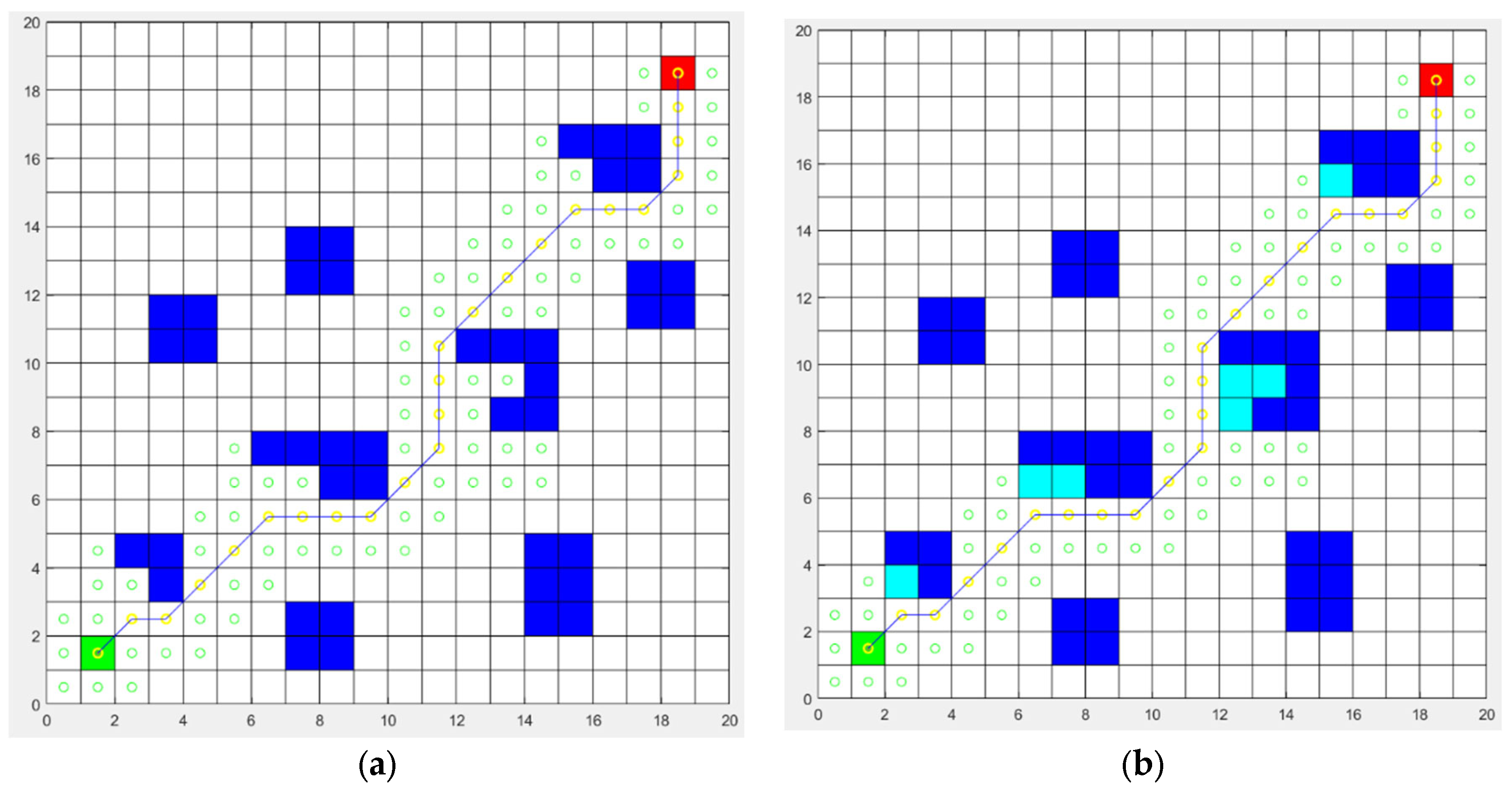
3.1. Experiment 1: Map Preprocessing Optimization Experiment
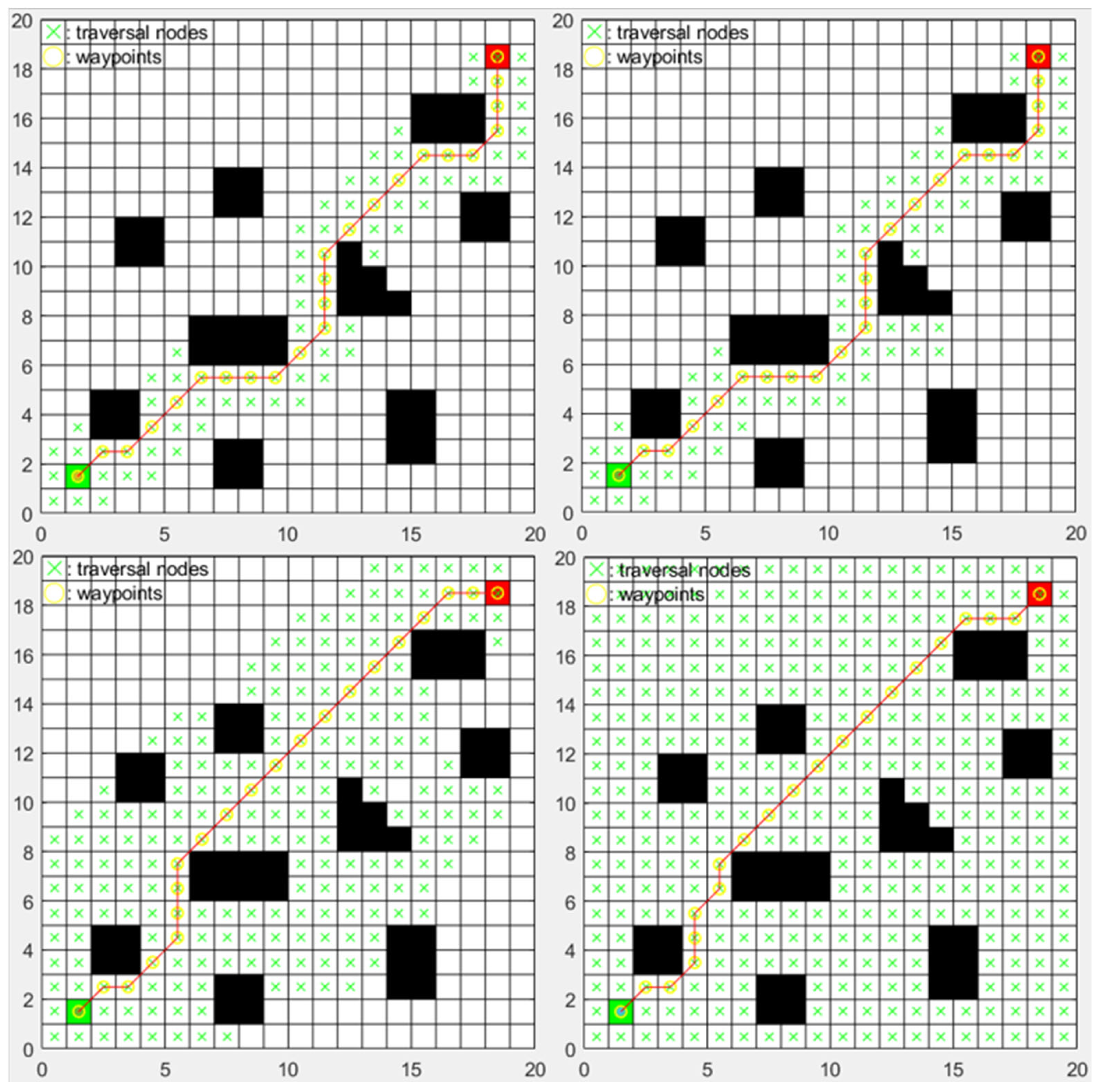
3.2. Experiment 2: A* Algorithm Parameter Analysis
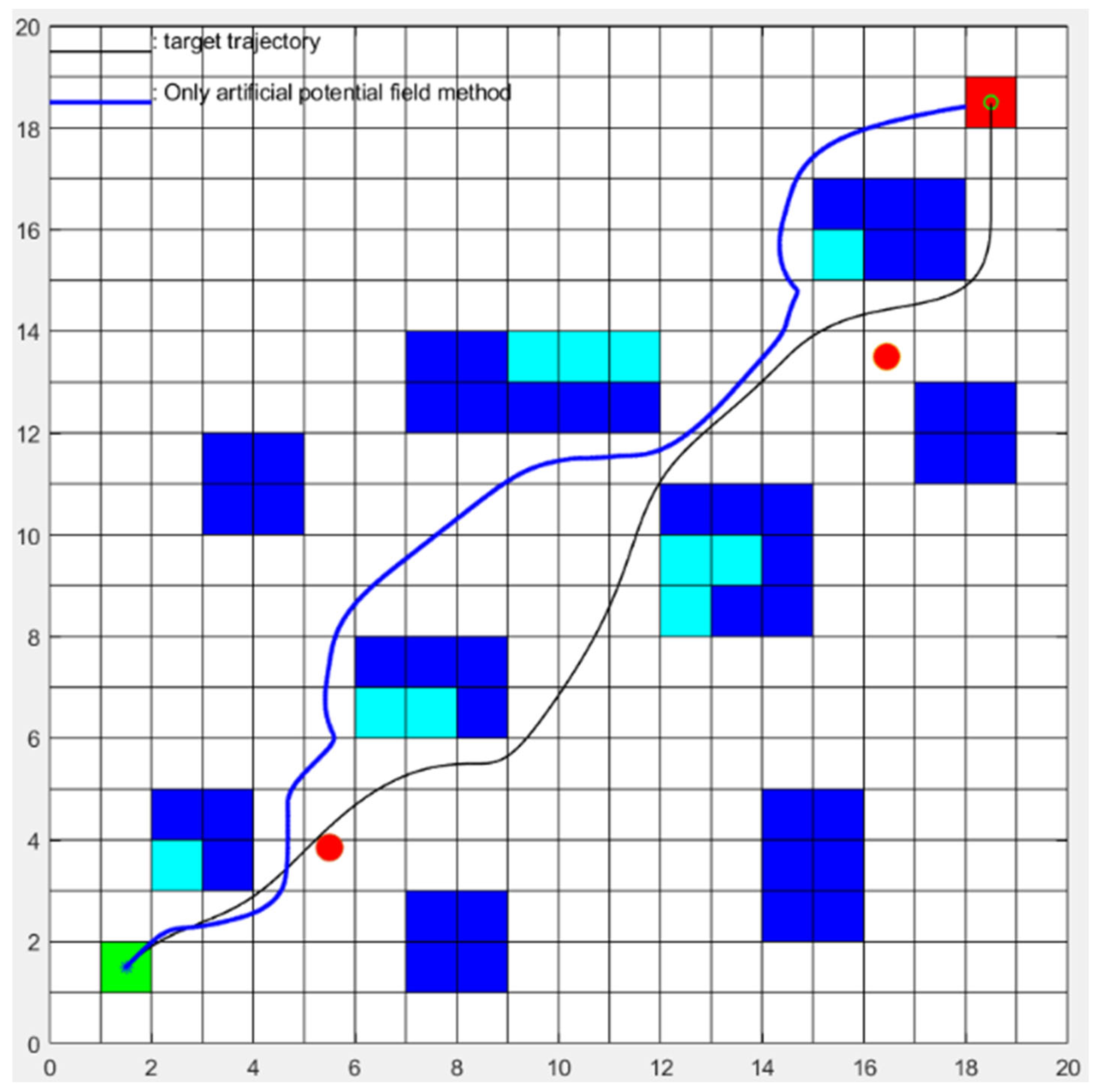
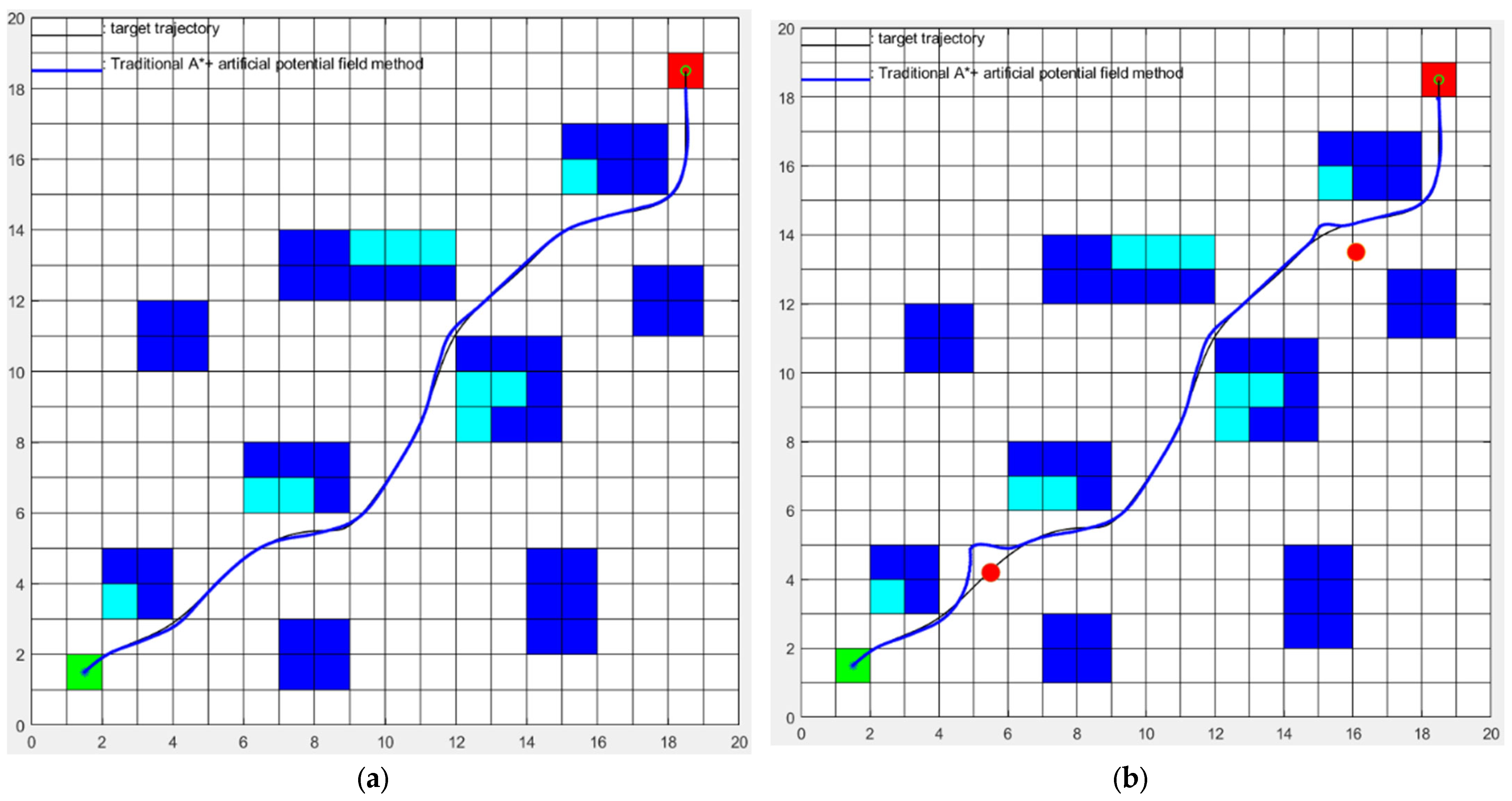
3.3. Experiment 3: Simulation Analysis of Hybrid Path Planning
4. Discussion
- In this study, a method of preprocessing grid maps is proposed to improve the efficiency of path planning and optimize path results. This method encloses the internal space of concave obstacles, which can effectively reduce the number of grid nodes searched by the A* algorithm during path planning, thereby improving the efficiency of path search. It also effectively solves the practical application problems caused by the robot’s own volume problem in path planning, such as the situation where the diagonal position is unreachable. Through this preprocessing method, a more reliable map foundation can be provided in the global path planning and local path planning stages, and it is expected to achieve more efficient and optimized path planning;
- For the issues in the A* algorithm used for global path planning, such as excessive node traversal, low search efficiency, redundant path nodes, and non-smooth turning angles, an improved heuristic function and weight coefficients are proposed. Additionally, the n-order Bézier curve method is introduced for trajectory optimization and removal of redundant nodes. Simulation results demonstrate that the improved algorithm outperforms the A* algorithm in terms of planning efficiency, number of turns, path smoothness, and path length;
- Regarding the problems in the artificial potential field method used for local path planning, including local minima and unreachable target points, an improved artificial potential field method is proposed. It combines with the A* algorithm to optimize trajectories and eliminate local minima and unreachable target points. Simulation results show that the proposed algorithm not only successfully solves the problems of local minima and unreachable target points but also achieves a higher planning success rate, shorter average path length, shorter planning time, and lower total turning angle;
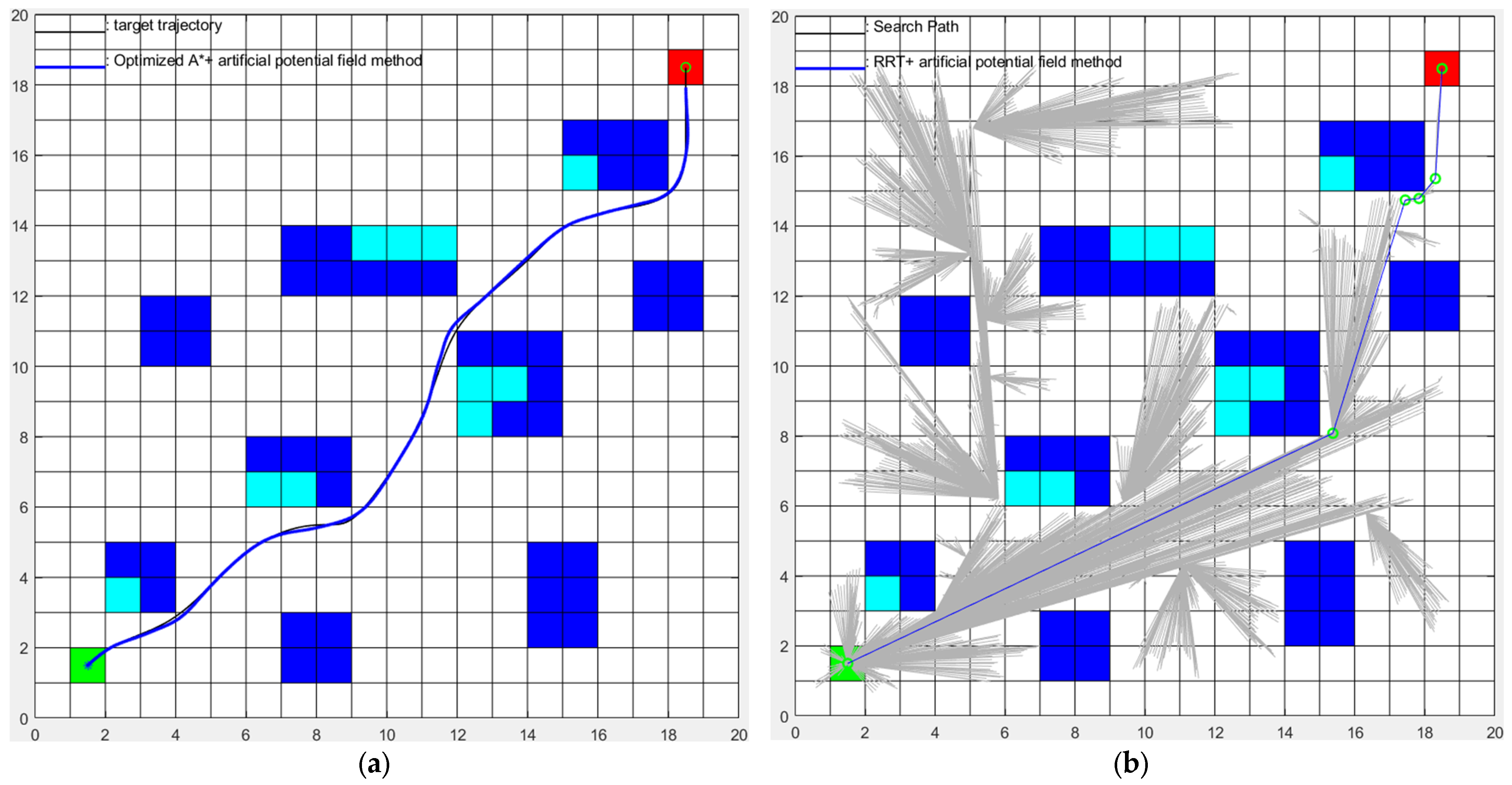
- Considering the limitations of global path planning algorithms in dynamic environments and the tendency of local path planning algorithms to fall into local minima, a hybrid path planning algorithm based on the A* algorithm and artificial potential field method is proposed. This algorithm utilizes the A* algorithm to plan the globally optimal path and then conducts Bézier curve optimization and designs the gravitational potential field for the tracking effect. Meanwhile, it employs the improved artificial potential field for local dynamic obstacle avoidance. Simulation results demonstrate that the proposed hybrid algorithm effectively addresses the issues of global path planning algorithms’ inability to dynamically avoid obstacles and local path planning algorithms’ susceptibility to local minima.
- The algorithms proposed in this paper are only designed for single robots and do not consider coordination and obstacle avoidance among multiple robots. Therefore, future research efforts could focus on the coordination of multiple robots and the optimization of obstacle avoidance strategies in multi-robot scenarios;
- This paper primarily addresses the obstacle avoidance problem in two-dimensional plane environments and does not account for variations in ground elevation. To better reflect real-world applications, further research is needed to investigate the complexity of ground environments and extend the scope of study to three-dimensional spaces.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cai, X.; Ning, H.; Dhelim, S.; Zhou, R.; Zhang, T.; Xu, Y.; Wan, Y. Robot and its living space: A roadmap for robot development based on the view of living space. Digit. Commun. Netw. 2021, 7, 505–517. [Google Scholar] [CrossRef]
- Fu, B.; Chen, L.; Zhou, Y.; Zheng, D.; Wei, Z.; Dai, J.; Pan, H. An improved A* algorithm for the industrial robot path planning with high success rate and short length. Robot. Auton. Syst. 2018, 106, 26–37. [Google Scholar] [CrossRef]
- Regev, C.; Jiang, Z.; Kasher, R.; Miller, Y. Distinct Antifouling Mechanisms on Different Chain Densities of Zwitterionic Polymers. Molecules 2022, 27, 7394. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Yang, Y.; Liu, Y.; Li, Q.; Cao, F.; Feng, M.; Wu, H.; Li, W.; Kang, Y. Development Status and Multilevel Classification Strategy of Medical Robots. Electronics 2021, 10, 1278. [Google Scholar] [CrossRef]
- Islamov, S.; Grigoriev, A.; Beloglazov, I.; Savchenkov, S.; Gudmestad, O.T. Research Risk Factors in Monitoring Well Drilling—A Case Study Using Machine Learning Methods. Symmetry 2021, 13, 1293. [Google Scholar] [CrossRef]
- Vaussard, F.; Fink, J.; Bauwens, V.; Rétornaz, P.; Hamel, D.; Dillenbourg, P.; Mondada, F. Lessons learned from robotic vacuum cleaners entering the home ecosystem. Robot. Auton. Syst. 2014, 62, 376–391. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.L.; Kovalchuk, M.S.; Batueva, D.E.; Senchilo, N.D. Development of an Algorithm for Regulating the Load Schedule of Educational Institutions Based on the Forecast of Electric Consumption within the Framework of Application of the Demand Response. Sustainability 2021, 13, 13801. [Google Scholar] [CrossRef]
- Ajeil, F.H.; Ibraheem, I.K.; Sahib, M.A.; Humaidi, A.J. Multi-objective path planning of an autonomous mobile robot using hybrid PSO-MFB optimization algorithm. Appl. Soft Comput. 2020, 89, 106076. [Google Scholar] [CrossRef]
- Qing, G.; Zheng, Z.; Yue, X. Path-planning of automated guided vehicle based on improved Dijkstra algorithm. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 7138–7143. [Google Scholar]
- Beloglazov, I.I.; Plaschinsky, V.A. Development MPC for the Grinding Process in SAG Mills Using DEM Investigations on LinerWear. Materials 2024, 17, 795. [Google Scholar] [CrossRef]
- Enayattabar, M.; Ebrahimnejad, A.; Motameni, H. Dijkstra algorithm for shortest path problem under interval-valued Pythagorean fuzzy environment. Complex Intell. Syst. 2019, 5, 93–100. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Brigadnov, I.; Lutonin, A.; Bogdanova, K. Error State Extended Kalman Filter Localization for Underground Mining Environments. Symmetry 2023, 15, 344. [Google Scholar] [CrossRef]
- Zhang, H.-M.; Li, M.-L.; Yang, L. Safe Path Planning of Mobile Robot Based on Improved A* Algorithm in Complex Terrains. Algorithms 2018, 11, 44. [Google Scholar] [CrossRef]
- Pandini, M.M.; Spacek, A.D.; Neto, J.M.; Ando, O. Design of a Didatic Workbench of Industrial Automation Systems for Engineering Education. IEEE Lat. Am. Trans. 2017, 15, 1384–1391. [Google Scholar] [CrossRef]
- Yang, D.; Xu, B.; Rao, K.; Sheng, W. Passive Infrared (PIR)-Based Indoor Position Tracking for Smart Homes Using Accessibility Maps and A-Star Algorithm. Sensors 2018, 18, 332. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.L.; Koshenkova, A.A.; Vorobieva, V.A.; Raspunin, D.L. Assessment of the Impact of Technological Development and Scenario Forecasting of the Sustainable Development of the Fuel and Energy Complex. Energies 2023, 16, 3185. [Google Scholar] [CrossRef]
- Orozco-Rosas, U.; Montiel, O.; Sepúlveda, R. Mobile robot path planning using membrane evolutionary artificial potential field. Appl. Soft Comput. 2019, 77, 236–251. [Google Scholar] [CrossRef]
- Doostie, S.; Hoshiar, A.; Nazarahari, M.; Lee, S.; Choi, H. Optimal path planning of multiple nanoparticles in continuous environment using a novel Adaptive Genetic Algorithm. Precis. Eng. 2018, 53, 65–78. [Google Scholar] [CrossRef]
- Lamini, C.; Benhlima, S.; Elbekri, A. Genetic Algorithm Based Approach for Autonomous Mobile Robot Path Planning. Procedia Comput. Sci. 2018, 127, 180–189. [Google Scholar] [CrossRef]
- Zakharov, L.; Martyushev, D.; Ponomareva, I.N. Predicting dynamic formation pressure using artificial intelligence methods. J. Min. Inst. 2022, 253, 23–32. [Google Scholar] [CrossRef]
- Li, K.; Hu, Q.; Liu, J. Path planning of mobile robot based on improved multi-objective genetic algorithm. Wirel. Commun. Mob. Comput. 2021, 2021, 8836615. [Google Scholar] [CrossRef]
- Candeloro, M.; Lekkas, A.M.; Sørensen, A.J. A Voronoi-diagram-based dynamic path-planning system for underactuated marine vessels. Control. Eng. Pr. 2017, 61, 41–54. [Google Scholar] [CrossRef]
- Matrokhina, K.V.; Trofimets, V.Y.; Mazakov, E.B.; Makhovikov, A.B.; Khaykin, M.M. Development of methodology for scenario analysis of investment projects of enterprises of the mineral resource complex. J. Min. Inst. 2023, 259, 112–124. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Chen, Z.; Xiong, G.; Liu, S. A Robot Path Planning Method Based on Improved Genetic Algorithm and Improved Dynamic Window Approach. Sustainability 2023, 15, 4656. [Google Scholar] [CrossRef]
- Filippov, V.; Zakharov, L.A.; Martyushev, D.A.; Ponomareva, I.N. Reproduction of reservoir pressure by machine learning methods and study of its influence on the cracks formation process in hydraulic fracturing. J. Min. Inst. 2022, 258, 924–932. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Z.; Tao, Y.; Chen, W.; Chen, B.; Wang, Q.; Yan, X.; Wang, G. Improvement in EEG Source Imaging Accuracy by Means of Wavelet Packet Transform and Subspace Component Selection. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 650–661. [Google Scholar] [CrossRef]
- Sychev, Y.; Zimin, R. Improving the quality of electricity in the power supply systems of the mineral resource complex with hybrid filter-compensating devices. J. Min. Inst. 2021, 247, 132–140. [Google Scholar] [CrossRef]
- Kozhubaev, Y.; Belyaev, V.; Murashov, Y.; Prokofev, O. Controlling of Unmanned Underwater Vehicles Using the Dynamic Planning of Symmetric Trajectory Based on Machine Learning for Marine Resources Exploration. Symmetry 2023, 15, 1783. [Google Scholar] [CrossRef]
- Muniteja, M.; Bee, M.K.M.; Suresh, V. Detection and classification of Melanoma image of skin cancer based on Convolutional Neural Network and comparison with Coactive Neuro Fuzzy Inference System. In Proceedings of the 2022 International Conference on Cyber Resilience (ICCR), Dubai, United Arab Emirates, 6–7 October 2022; pp. 1–5. [Google Scholar]
- Sychev, Y.A.; Aladin, M.E.; Aleksandrovich, S.V. Developing a hybrid filter structure and a control algorithm for hybrid power supply. Int. J. Power Electron. Drive Syst. 2022, 13, 1625–1634. [Google Scholar] [CrossRef]
- Alqobali, R.; Alshmrani, M.; Alnasser, R.; Rashidi, A.; Alhmiedat, T.; Alia, O.M. A Survey on Robot Semantic Navigation Systems for Indoor Environments. Appl. Sci. 2024, 14, 89. [Google Scholar] [CrossRef]
- Nowakowski, M.; Kurylo, J.; Braun, J.; Berger, G.S.; Mendes, J.; Lima, J. Using LiDAR Data as Image for AI to Recognize Objects in the Mobile Robot Operational Environment. In Optimization, Learning Algorithms and Applications; Pereira, A.I., Mendes, A., Fernandes, F.P., Pacheco, M.F., Coelho, J.P., Lima, J., Eds.; OL2A 2023. Communications in Computer and Information Science; Springer: Cham, Switzerland, 2024; Volume 1982. [Google Scholar] [CrossRef]
- Miao, H.; Chen, J.; Qi, B.; Li, Y.; Li, C. Path planning algorithm based on improved RRT and artificial potential field method. Autom. Instrum. 2023, 9–14. [Google Scholar] [CrossRef]
- Kramer, J.; Scheutz, M. Development environments for autonomous mobile robots: A survey. Auton. Robot. 2007, 22, 101–132. [Google Scholar] [CrossRef]



| Group | Preprocessing Map | Number of Nodes | Search Time (s) | Optimization Effect | |
|---|---|---|---|---|---|
| Number of Nodes | Search Time | ||||
| 1 | no | 95 | 0.1921 | 11 (11.6%) | 0.035 (18.6%) |
| 2 | yes | 84 | 0.1563 | ||
| Weight Coefficient w | Total Number of Search Nodes | Number of Trajectory Nodes | Search Time (s) |
|---|---|---|---|
| 0 | 80 | 22 | 0.2425 |
| 0.5 | 84 | 22 | 0.2705 |
| 0.75 | 207 | 19 | 0.9437 |
| 1 | 351 | 19 | 2.5598 |
| Parameter | Numerical Value |
|---|---|
| Map size | 20 × 20 |
| of the estimation function | 0.5 |
| 20 | |
| for the force of repulsion from obstacles | 20 |
| for the force of attraction of the trajectory points | 3 |
| 2 | |
| of the trajectory point | 1 |
| 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozhubaev, Y.; Yang, R. Simulation of Dynamic Path Planning of Symmetrical Trajectory of Mobile Robots Based on Improved A* and Artificial Potential Field Fusion for Natural Resource Exploration. Symmetry 2024, 16, 801. https://doi.org/10.3390/sym16070801
Kozhubaev Y, Yang R. Simulation of Dynamic Path Planning of Symmetrical Trajectory of Mobile Robots Based on Improved A* and Artificial Potential Field Fusion for Natural Resource Exploration. Symmetry. 2024; 16(7):801. https://doi.org/10.3390/sym16070801
Chicago/Turabian StyleKozhubaev, Yuriy, and Ruide Yang. 2024. "Simulation of Dynamic Path Planning of Symmetrical Trajectory of Mobile Robots Based on Improved A* and Artificial Potential Field Fusion for Natural Resource Exploration" Symmetry 16, no. 7: 801. https://doi.org/10.3390/sym16070801
APA StyleKozhubaev, Y., & Yang, R. (2024). Simulation of Dynamic Path Planning of Symmetrical Trajectory of Mobile Robots Based on Improved A* and Artificial Potential Field Fusion for Natural Resource Exploration. Symmetry, 16(7), 801. https://doi.org/10.3390/sym16070801






