Solving a Novel System of Time-Dependent Nuclear Reactor Equations of Fractional Order
Abstract
:1. Introduction
2. The Physical Phenomena
3. Preliminaries
4. The Nuclear Reactor Equations Analytical Solution
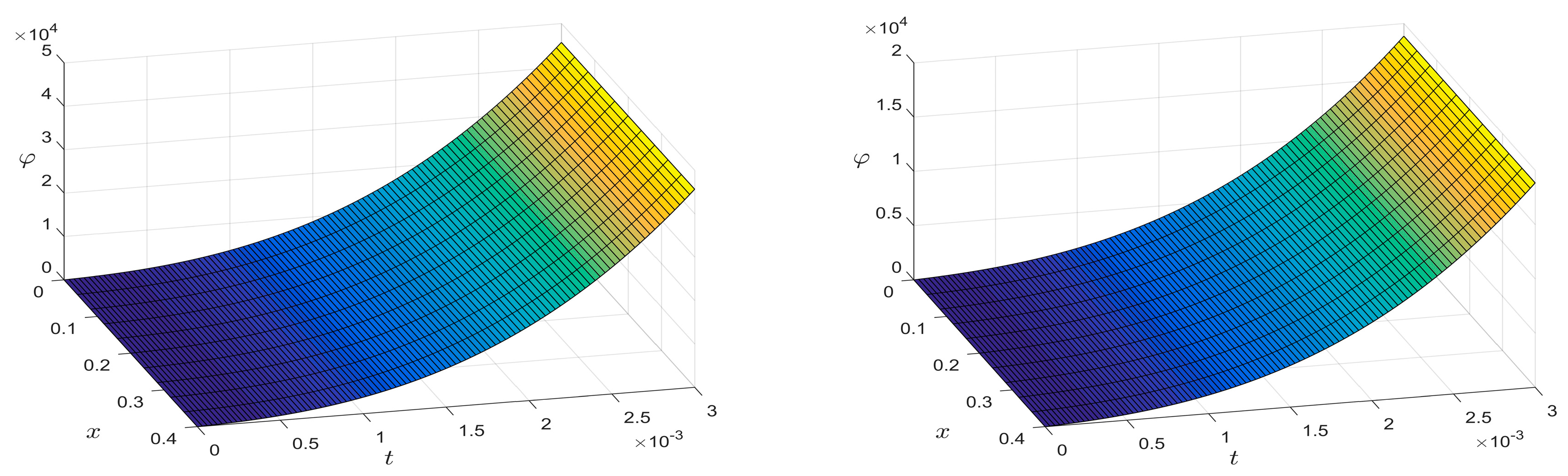
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stacey, W.M. Nuclear Reactor Physics; John Wiley & Sons: Boston, MA, USA, 2001. [Google Scholar]
- Duderstadt, J.J.; Hamilton, L.J. Nuclear Reactor Analysis; John Wiley & Sons: Boston, MA, USA, 1976. [Google Scholar]
- Lamarsh, J.R. Introduction to Nuclear Engineering, 2nd ed.; Addison-Wesley: Boston, MA, USA, 1983. [Google Scholar]
- Khasawneh, K.; Dababneh, S.; Odibat, Z. A solution of the neutron diffusion equation in hemispherical symmetry using the homotopy perturbation method. Ann. Nucl. Energy 2009, 36, 1711–1717. [Google Scholar] [CrossRef]
- Dababneh, S.; Khasawneh, K.; Odibat, Z. An alternative solution of the neutron diffusion equation in cylindrical symmetry. Ann. Nucl. Energy 2010, 38, 1140–1143. [Google Scholar] [CrossRef]
- El-Ajou, A.; Shqair, M.; Ghabar, I.; Burqan, A.; Saadeh, R. A solution for the neutron diffusion equation in the spherical and hemispherical reactors using the residual power series. Front. Phys. 2023, 11, 1229142. [Google Scholar] [CrossRef]
- Alquran, M.; Ali, M.; Alsukhour, M.; Jaradat, I. Promoted residual power series technique with Laplace transform to solve some time-fractional problems arising in physics. Results Phys. 2020, 19, 103667. [Google Scholar] [CrossRef]
- Alaroud, M. Application of Laplace residual power series method for approximate solutions of fractional IVP’s. Alex. Eng. J. 2022, 61, 1585–1595. [Google Scholar] [CrossRef]
- Vyawahare, V.; Nataraj, P. Fractional-Order Modeling of Nuclear Reactor: From Subdiffusive Neutron Transport to Control-Oriented Models; Springer Nature: Singapore, 2018. [Google Scholar]
- Ray, S. Fractional Calculus with Applications for Nuclear Reactor Dynamics; CRC Press: Broken, NW, USA, 2016. [Google Scholar]
- Aboanber, A.; Nahla, A.; Aljawazneh, S. Fractional two energy groups matrix representation for nuclear reactor dynamics with an external source. Ann. Nucl. Energy 2021, 153, 108062. [Google Scholar] [CrossRef]
- Sardar, T.; Ray, S.; Bera, R. The solution of coupled fractional neutron diffusion equations with delayed neutrons. Int. J. Nuclear Energy Sci. Technol. 2010, 5, 105–133. [Google Scholar] [CrossRef]
- Khaled, S. Exact solution of the one-dimensional neutron diffusion kinetic equation with one delayed precursor concentration in Cartesian geometry. AIMS Math. 2022, 7, 12364–12373. [Google Scholar] [CrossRef]
- Sarhan, A.; Burqan, A.; Saadeh, R.; Al-Zhour, Z. Analytical Solutions of the Nonlinear Time-Fractional Coupled Boussinesq-Burger Equations Using Laplace Residual Power Series Technique. Fractal Fract. 2022, 6, 631. [Google Scholar] [CrossRef]
- Kazem, S. Exact solution of some linear fractional differential equations by Laplace transform. Int. J. Nonlinear Sci. 2013, 16, 3–11. [Google Scholar]
- Yavuz, M.; Özdemir, N. Numerical inverse Laplace homotopy technique for fractional heat equations. Therm. Sci. 2018, 22, 185–194. [Google Scholar] [CrossRef]
- Wang, Q. Numerical solutions for fractional KdV–Burgers equation by Adomian decomposition method. Appl. Math. Comput. 2006, 182, 1048–1055. [Google Scholar] [CrossRef]
- Cao, Y.; Nikan, O.; Avazzadeh, Z. A localized meshless technique for solving 2D nonlinear integro-differential equation with multi-term kernels. Appl. Numer. Math. 2023, 183, 140–156. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Ali, A. A numerical study on time fractional Fisher equation using an extended cubic B-spline approximation. J. Math. Comput. Sci. 2021, 22, 85–96. [Google Scholar] [CrossRef]
- Oderinu, R.A.; Owolabi, J.A.; Taiwo, M. Approximate solutions of linear time-fractional differential equations. J. Math. Comput. Sci. 2023, 29, 60–72. [Google Scholar] [CrossRef]
- Ali, A.; Abbas, M.; Akram, T. New group iterative schemes for solving the two-dimensional anomalous fractional sub-diffusion equation. J. Math. Comput. Sci. 2021, 22, 119–127. [Google Scholar] [CrossRef]
- Liao, H.; Zhang, D.; Zhao, Y. Sharp error estimate of a nonuniform L1 formula for time-fractional reaction subdiffusion equations. SIAM J. Numer. Anal. 2018, 56, 1122–1133. [Google Scholar] [CrossRef]
- Lyu, P.; Vong, S. A symmetric fractional-order reduction method for direct nonuniform approximations of semilinear diffusion-wave equations. J. Sci. Comput. 2022, 93, 34. [Google Scholar] [CrossRef]
- Eriqat, T.; El-Ajou, A.; Moa’ath, N.O.; Al-Zhour, Z.; Momani, S. A new attractive analytic approach for solutions of linear and nonlinear neutral fractional pantograph equations. Chaos Solitons Fractals 2020, 138, 109957. [Google Scholar] [CrossRef]
- Batiha, I.; Shqair, M.; Abu-Sei’leek, M.H.; Alshorm, S.; Abd El-Azeem, S.; Momani, S. Two Energy Groups Neutron Diffusion Model in Spherical Reactors. Results Nonlinear Anal. 2024, 7, 160–173. [Google Scholar]
- Burqan, A.; Shqair, M.; El-Ajou, A.; Ismaeel, S.M.E.; AlZhour, Z. Analytical solutions to the coupled fractional neutron diffusion equations with delayed neutrons system using Laplace transform method. AIMS Math. 2023, 8, 19297–19312. [Google Scholar] [CrossRef]


| . |
| t | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.00010 | 1.0001 × 1014 | 2.3998 × 1012 | 5.1358 × 1010 | 1.0172 × 109 | 1.9570 × 107 | 409,582 | 12,938.5 | 1069.01 | 218.945 | 67.1205 |
| 0.00039 | 1.7233 × 1014 | 7.1214 × 1012 | 2.6187 × 1011 | 8.8447 × 109 | 2.8255 × 108 | 8.93672 × 106 | 311,117 | 15,528 | 1642 | 366.761 |
| 0.00068 | 2.1524 × 1014 | 1.1106 × 1013 | 5.0966 × 1011 | 2.1440 × 1010 | 8.4808 × 108 | 3.26117 × 107 | 1.30286 × 106 | 63,492.3 | 5186.97 | 887.538 |
| 0.00097 | 2.4809 × 1014 | 1.4753 × 1013 | 7.7999 × 1011 | 3.7766 × 1010 | 1.7145 × 109 | 7.50461 × 107 | 3.32891 × 106 | 167,752 | 12,286.8 | 1733.47 |
| 0.00126 | 2.7544 × 1014 | 1.8184 × 1013 | 1.0671 × 1011 | 5.7313 × 1010 | 2.8813 × 109 | 1.38975 × 108 | 6.69906 × 106 | 352,590 | 24,648.1 | 3033.51 |
| 0.00155 | 2.9923 × 1014 | 2.1459 × 1013 | 1.3677 × 1012 | 7.9754 × 1010 | 4.3478 × 109 | 2.26674 × 108 | 1.17040 × 107 | 643,464 | 44,222.3 | 4941.57 |
| 0.00184 | 3.2047 × 1014 | 2.4613 × 1013 | 1.6798 × 1012 | 1.0485 × 1011 | 6.1139 × 109 | 3.40119 × 108 | 1.86209 × 107 | 1.0668 × 106 | 73,184.9 | 7636.5 |
| 0.00213 | 3.3979 × 1014 | 2.7669 × 1013 | 2.0019 × 1012 | 1.3244 × 1011 | 8.1791 × 109 | 4.81079 × 108 | 2.77163 × 107 | 1.64988 × 106 | 113,920 | 11,322.1 |
| 0.00242 | 3.5758 × 1014 | 3.0642 × 1013 | 2.3329 × 1012 | 1.6236 × 1011 | 1.0543 × 1010 | 6.51161 × 108 | 3.92481 × 107 | 2.42072 × 106 | 169,007 | 16,227.1 |
| 0.00271 | 3.7414 × 1014 | 3.3544 × 1013 | 2.6718 × 1012 | 1.9451 × 1011 | 1.3206 × 1010 | 8.51847 × 108 | 5.34675 × 107 | 3.40801 × 106 | 241,213 | 22,605.1 |
| 0.00300 | 3.8966 × 1014 | 3.6384 × 1013 | 3.0181 × 1012 | 2.2879 × 1011 | 1.6168 × 1010 | 1.08452 × 109 | 7.06193 × 107 | 4.64106 × 106 | 333,482 | 30,734.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filali, D.; Shqair, M.; Alghamdi, F.A.; Ismaeel, S.; Hagag, A. Solving a Novel System of Time-Dependent Nuclear Reactor Equations of Fractional Order. Symmetry 2024, 16, 831. https://doi.org/10.3390/sym16070831
Filali D, Shqair M, Alghamdi FA, Ismaeel S, Hagag A. Solving a Novel System of Time-Dependent Nuclear Reactor Equations of Fractional Order. Symmetry. 2024; 16(7):831. https://doi.org/10.3390/sym16070831
Chicago/Turabian StyleFilali, Doaa, Mohammed Shqair, Fatemah A. Alghamdi, Sherif Ismaeel, and Ahmed Hagag. 2024. "Solving a Novel System of Time-Dependent Nuclear Reactor Equations of Fractional Order" Symmetry 16, no. 7: 831. https://doi.org/10.3390/sym16070831
APA StyleFilali, D., Shqair, M., Alghamdi, F. A., Ismaeel, S., & Hagag, A. (2024). Solving a Novel System of Time-Dependent Nuclear Reactor Equations of Fractional Order. Symmetry, 16(7), 831. https://doi.org/10.3390/sym16070831







