Investigation of Partition Function Transformation for the Potts Model into a Dichromatic Knot Polynomial 74
Abstract
:1. Introduction
2. The Partition Function of the Potts Model
3. Finding the Dichromatic Polynomial by Constructing a Planar Graph
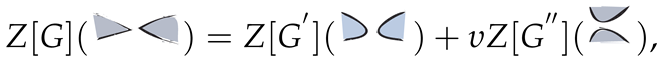

4. Potts Brackets

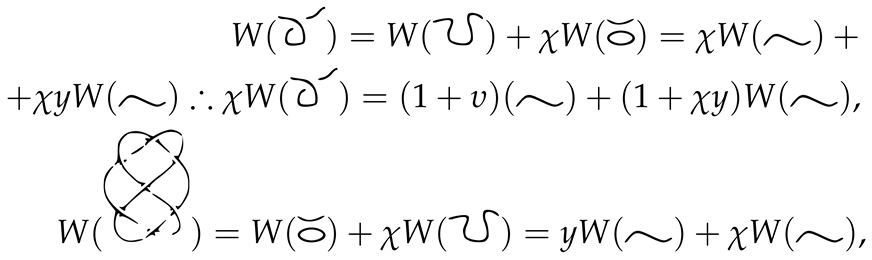
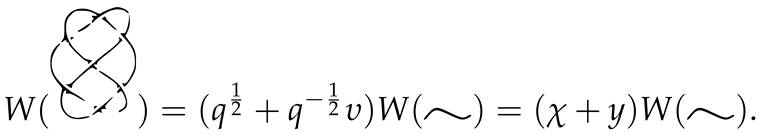

5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Landau, L.D.; Lifshitz, E.M. Statistical Physics; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Jones, V.F.R. On knot invariants related to some statistical mechanical models. Pacific J. Math. 1989, 137, 311–334. [Google Scholar] [CrossRef]
- Banica, T. Hopf algebras and subfactors associated to vertex models. J. Funct. Anal. 1998, 159, 243–266. [Google Scholar] [CrossRef]
- Kauffman, L.H. Remarks on Khovanov Homology and the Potts Model. In Perspectives in Analysis, Geometry, and Topology; Springer: Berlin/Heidelberg, Germany, 2012; Volume 296, pp. 130–163. [Google Scholar]
- Stosic, M. New Categorifications of the Chromatic and the Dichromatic Polynomials for Graphs. Fundam. Math. 2005, 190, 231–243. [Google Scholar] [CrossRef]
- Chmutov, S. Topological Tutte Polynomial. arXiv 2017, arXiv:1708.08132. [Google Scholar]
- Forge, D.; Zaslavsky, T. Lattice points in orthotopes and a huge polynomial Tutte invariant of weighted gain graphs. J. Comb. Theory Ser. B 2016, 118, 186–227. [Google Scholar] [CrossRef]
- Krajewski, T.; Moffatt, I.; Tanasa, A. Hopf algebras and Tutte polynomials. Adv. Appl. Math. 2018, 95, 271–330. [Google Scholar] [CrossRef]
- Helme-Guizon, L.; Rong, Y. Graph Cohomologies from Arbitrary Algebras. arXiv 2005, arXiv:math/0506023. [Google Scholar]
- Stosic, M. Categorification of the Dichromatic Polynomial for Graphs. J. Knot Theory Its Ramif. 2005, 17, 31–45. [Google Scholar] [CrossRef]
- Khovanov, M. A categorification of the Jones polynomial. Duke Math. J. 2000, 101, 359–426. [Google Scholar] [CrossRef]
- Helme-Guizon, L.; Rong, Y. A categorification for the chromatic polynomial. Algebr. Geom. Topol. 2006, 5, 1365–1388. [Google Scholar] [CrossRef]
- Jasso-Hernandez, E.; Rong, Y. A categorification of the Tutte polynomial. Algebr. Geom. Topol. 2006, 6, 2031–2049. [Google Scholar] [CrossRef]
- Kauffman, L.H. Remarks on Khovanov Homology and the Potts Model. Geom. Topol. 2009, 3, 237–262. [Google Scholar]
- Helme-Guizon, L.; Przytycki, J.H.; Rong, Y. Torsion in Graph Homology. Fundam. Math. 2006, 190, 139–177. [Google Scholar] [CrossRef]
- Viro, O. Khovanov homology, its definitions and ramifications. Fund. Math. 2004, 184, 317–342. [Google Scholar] [CrossRef]
- King, C.; Wu, F.Y. New Correlation Duality Relations for the Planar Potts Model. J. Stat. Phys. 2002, 107, 919–940. [Google Scholar] [CrossRef]
- Drinfeld, V.G. Quantum groups. Proc. Int. Congr. Math. 1986, 155, 18–49. [Google Scholar]
- Woronowicz, S.L. Compact matrix pseudogroups. Comm. Math. Phys. 1987, 111, 613–665. [Google Scholar] [CrossRef]
- Chari, V.; Pressley, A. A Guide to Quantum Groups; Cambridge University: Cambridge, UK, 1995. [Google Scholar]
- Sahin, A.; Kopuzlu, A.; Ugur, T. Tutte Polynomials of (2, N)-Torus Knots. Appl. Math. Sci. 2015, 9, 747–759. [Google Scholar] [CrossRef]
- Abdulgani, S. Dichromatic polynomial for graph of a (2, n)-torus knot. Appl. Math. Nonlinear Sci. 2021, 9, 397–402. [Google Scholar]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Wu, F.-Y. The Potts model. Rev. Mod. Phys. 1988, 54, 253–268. [Google Scholar]
- Wu, F.-Y. Potts model and graph theory. J. Stat. Phys 1988, 52, 99–112. [Google Scholar] [CrossRef]
- Cipra, B.A. An introduction to the Ising model. Am. Math. Mon. 1987, 94, 937–959. [Google Scholar] [CrossRef]
- Martin, P. Potts Models and Related Problems in Statistical Mechanics, 2nd ed.; World Scientific: Singapore, 1991; pp. 158–191. [Google Scholar]
- Welsh, D.J.; Merino, C. The Potts model and the Tutte polynomial. J. Math. Phys. 2000, 41, 1127–1152. [Google Scholar] [CrossRef]
- Shrock, R. Chromatic polynomials and their zeros and asymptotic limits for families of graphs. Discret. Math. 2001, 231, 421–446. [Google Scholar] [CrossRef]
- Chang, S.-C.; Jacobsen, J.; Salas, R. Exact Potts model partition functions for strips of the triangular lattice. J. Stat. Phys. 2004, 114, 768–823. [Google Scholar] [CrossRef]
- Sokal, A.D. Chromatic polynomials, Potts models and all that. Physica A 2000, 279, 324–332. [Google Scholar] [CrossRef]
- Sokal, A.D. The Multivariate Tutte Polynomial (Alias Potts Model) for Graphs and Matroids; Cambridge University Press: Cambridge, UK, 2005; Volume 279, pp. 173–226. [Google Scholar]
- Farr, G.E. Tutte—Whitney Polynomials: Some History and Generalizations; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Brightwell, G.R.; Winkler, P. Graph homomorphisms and phase transitions. J. Combin. Theory Ser. B 1999. [Google Scholar] [CrossRef]
- Shrock, R. T = 0 partition functions for Potts antiferromagnets on Mobius strips and effects of graph topology. Phys. Lett. A 1999, 32, 57–62. [Google Scholar] [CrossRef]
- Biggs, N.L.; Shrock, R. T = 0 partition functions for Potts antiferromagnets on square lattice strips with (twisted) periodic boundary conditions. J. Phys. A (Lett.) 1999, 32, L489–L493. [Google Scholar] [CrossRef]
- Chang, S.-C.; Shrock, R. Zeros of Jones polynomials for families of knots and links. Physica A 2001, 301, 196–218. [Google Scholar] [CrossRef]
- Sokal, A.D. A personal list of unsolved problems concerning lattice gases and antiferromagnetic Potts models. Markov Process Relat. Fields 2001, 7, 21–38. [Google Scholar]
- Gimenez, O.; Hlineny, P.; Noy, M. Computing the Tutte polynomial on graphs of bounded clique-width. SIAM J. Discret. Math. 2006, 20, 932–946. [Google Scholar] [CrossRef]
- Woodall, D. Tutte polynomials for 2-separable graphs. Discret. Math. 2001, 247, 201–213. [Google Scholar] [CrossRef]
- Traldi, L. Chain polynomials and Tutte polynomials. Discret. Math. 2002, 248, 279–282. [Google Scholar] [CrossRef]
- Traldi, L. On the colored Tutte polynomial of a graph of bounded treewidth. Discret. Appl. Math. 2006, 154, 1032–1036. [Google Scholar] [CrossRef]
- Jin, X.A.; Zhang, F. Oriented state model of the Jones polynomial and its connection to the dichromatic polynomial. J. Knot Theory Its Ramifi. 2010, 19, 81–92. [Google Scholar] [CrossRef]
- Jaeger, F.; Vertigen, D.; Welsh, D. On the Computational Complexity of the Jones’ and Tutte polynomials. Math. Proc. Camb. Philos. Soc. 1990, 108, 35–53. [Google Scholar] [CrossRef]
- Kassenova, T.K.; Tsyba, P.Y.; Razina, O.V. Eight-vertex model over Grassmann algebra. J. Phys. Conf. Ser. 2019, 1391, 012035. [Google Scholar] [CrossRef]
- Martin, P.P.; Zakaria, S.F. Zeros of the 3-state Potts model partition function for the square lattice revisited. J. Stat. Mech. Theory Exp. 2019, 19, 86–105. [Google Scholar] [CrossRef]
- Yin, J. Phase diagram and critical behavior of the square-lattice Ising model with competing nearest-neighbor and next-nearest-neighbor interactions. Phys. Rev. E 2009, 80, 51–117. [Google Scholar] [CrossRef]
- Kalz, A.; Honecker, A.; Fuchs, S.; Pruschke, T. Monte Carlo studies of the Ising square lattice with competing interactions. J. Phys. Conf. Ser. 2009, 145, 12–51. [Google Scholar] [CrossRef]
- Malakis, A.; Kalozoumis, P.; Tyraskis, N. onte Carlo studies of the square Ising model with next-nearest-neighbor interactions. The European Physical Journal B-Condensed Matter and Complex Systems. Eur. Phys. J. B 2006, 50, 63–67. [Google Scholar] [CrossRef]
- Kassenova, T.K. Parametrized eight-vertex model and knot invariant 10136. Eurasian Phys. Tech. J. 2022, 19, 39. [Google Scholar] [CrossRef]
- Kassenova, T.K.; Tsyba, P.Y.; Razina, O.V.; Myrzakulov, R. Three-partite vertex model and knot invariants. Physica A 2022, 597, 127–283. [Google Scholar] [CrossRef]
- Kassenova, T.K. Quantum solution of the relationship between the 19-vertex model and the Jones polynomial. J. Phys. Conf. Ser. 2024, 2701, 012127. [Google Scholar] [CrossRef]
- Tutte, W.T. A ring in graph theory. Math. Proc. Camb. Philos. Soc. 1947, 43, 26–40. [Google Scholar] [CrossRef]
- Tutte, W.T. A Contribution to the Theory of Chromatic Polynomials. Cand. J. Math. 1953, 6, 80–81. [Google Scholar] [CrossRef]
- Rolfsen, D. Knots and Links; American Mathematical Soc.: Providence, RI, USA, 2003; pp. 256–307. [Google Scholar]
- Adams, C.C.; Crawford, T.; DeMeo, B.; Landry, M.; Lin, A.T.; Montee, M.; Park, S.; Venkatesh, S.; Yhee, F. Knot projections with a single multi-crossing. J. Knot Theory Its Ramifi. 2015, 24, 30. [Google Scholar] [CrossRef]
- Beaudin, L.; Ellis-Monaghan, J.; Pangborn, G.; Shrock, R. A little statistical mechanics for the graph theorist. Discret. Math. 2010, 310, 2037–2053. [Google Scholar] [CrossRef]
- Jablan, S.; Sazdanovic, R. Linknot: Knot Theory by Computer; World Scientific: Singapore, 2007; pp. 172–191. [Google Scholar]
- Adams, C.C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots; American Mathematical Soc.: Providence, RI, USA, 1994; pp. 238–305. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kassenova, T.; Tsyba, P.; Razina, O. Investigation of Partition Function Transformation for the Potts Model into a Dichromatic Knot Polynomial 74. Symmetry 2024, 16, 842. https://doi.org/10.3390/sym16070842
Kassenova T, Tsyba P, Razina O. Investigation of Partition Function Transformation for the Potts Model into a Dichromatic Knot Polynomial 74. Symmetry. 2024; 16(7):842. https://doi.org/10.3390/sym16070842
Chicago/Turabian StyleKassenova, Tolkyn, Pyotr Tsyba, and Olga Razina. 2024. "Investigation of Partition Function Transformation for the Potts Model into a Dichromatic Knot Polynomial 74" Symmetry 16, no. 7: 842. https://doi.org/10.3390/sym16070842





