An Analytical Study of the Mikhailov–Novikov–Wang Equation with Stability and Modulation Instability Analysis in Industrial Engineering via Multiple Methods
Abstract
:1. Introduction
2. Mathematical Approach
2.1. Improved Sardar Subequation Approach
2.2. The (, ) Approach
- Substitute the determined value of into Equation (30) and then substitute in Equation (4), along with Equations (22), (23) and (25). This transformation yields a polynomial in the left-hand side of Equation (30), incorporating terms and .
- Formulate a system of algebraic equations by equating the coefficients of terms with corresponding powers within the polynomial to 0. These equations include parameters such as , , , , , and others.
- Any symbolic calculation tools can solve these algebraic equations, thereby determining the values of the involved parameters.
- Substitute the obtained parameter values into Equation (30), expressed in trigonometric, hyperbolic, and rational functions that are the exact solution of Equation (1).
3. Method’s Application
3.1. The Improved Sardar Subequation Method
3.2. The (, ) Approach
4. Analyses
4.1. Stability Analysis
4.2. Modulation Instability
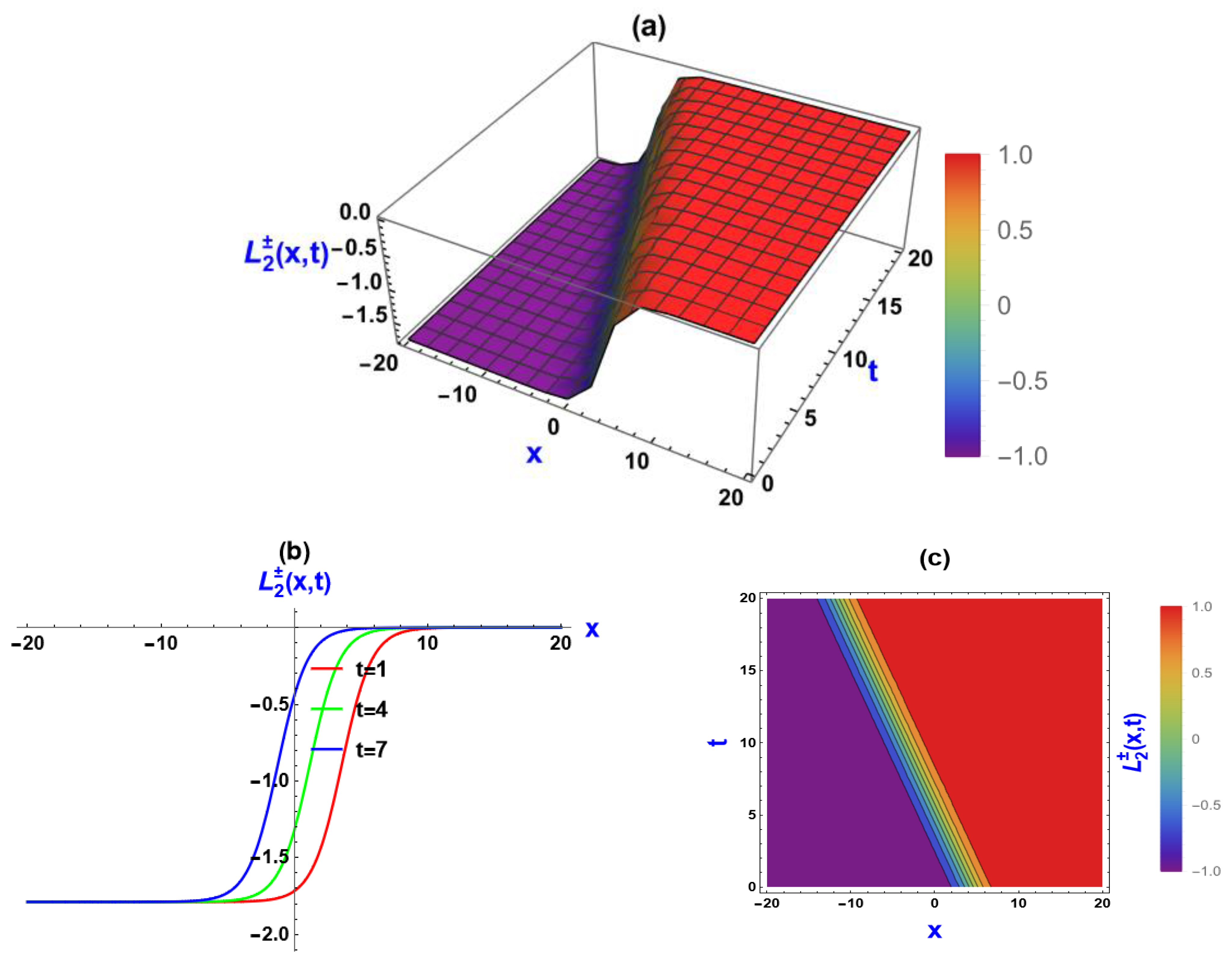
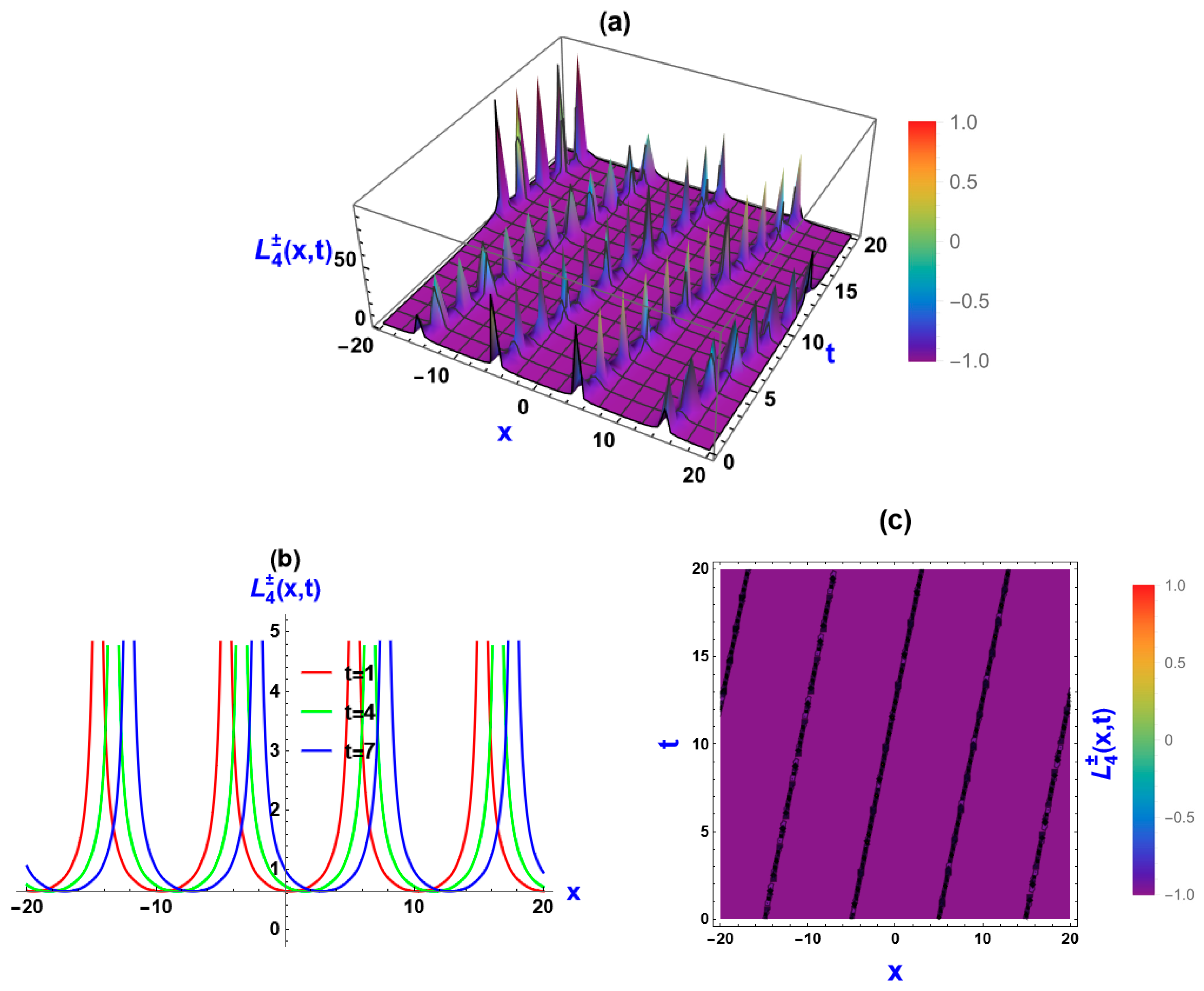
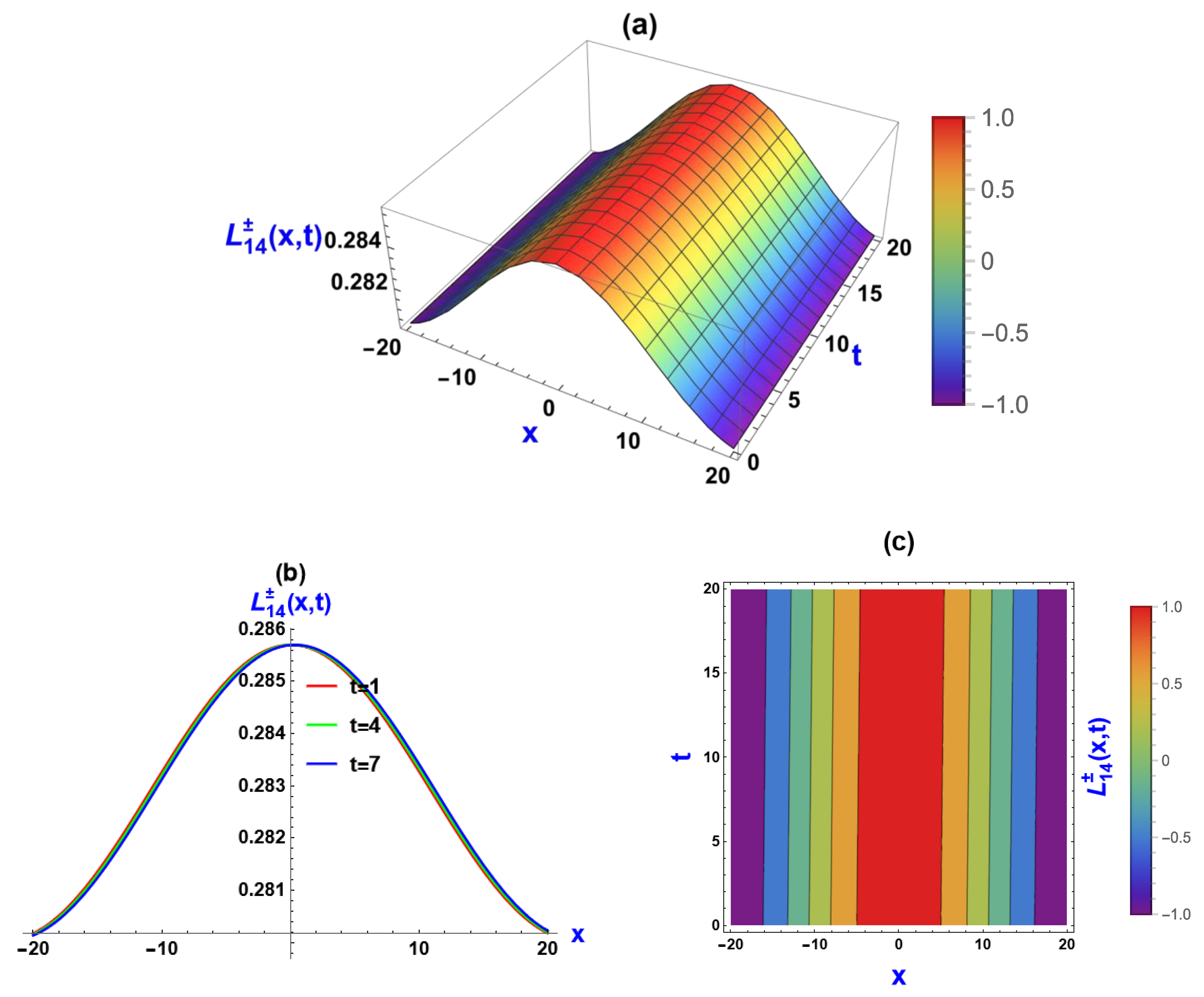
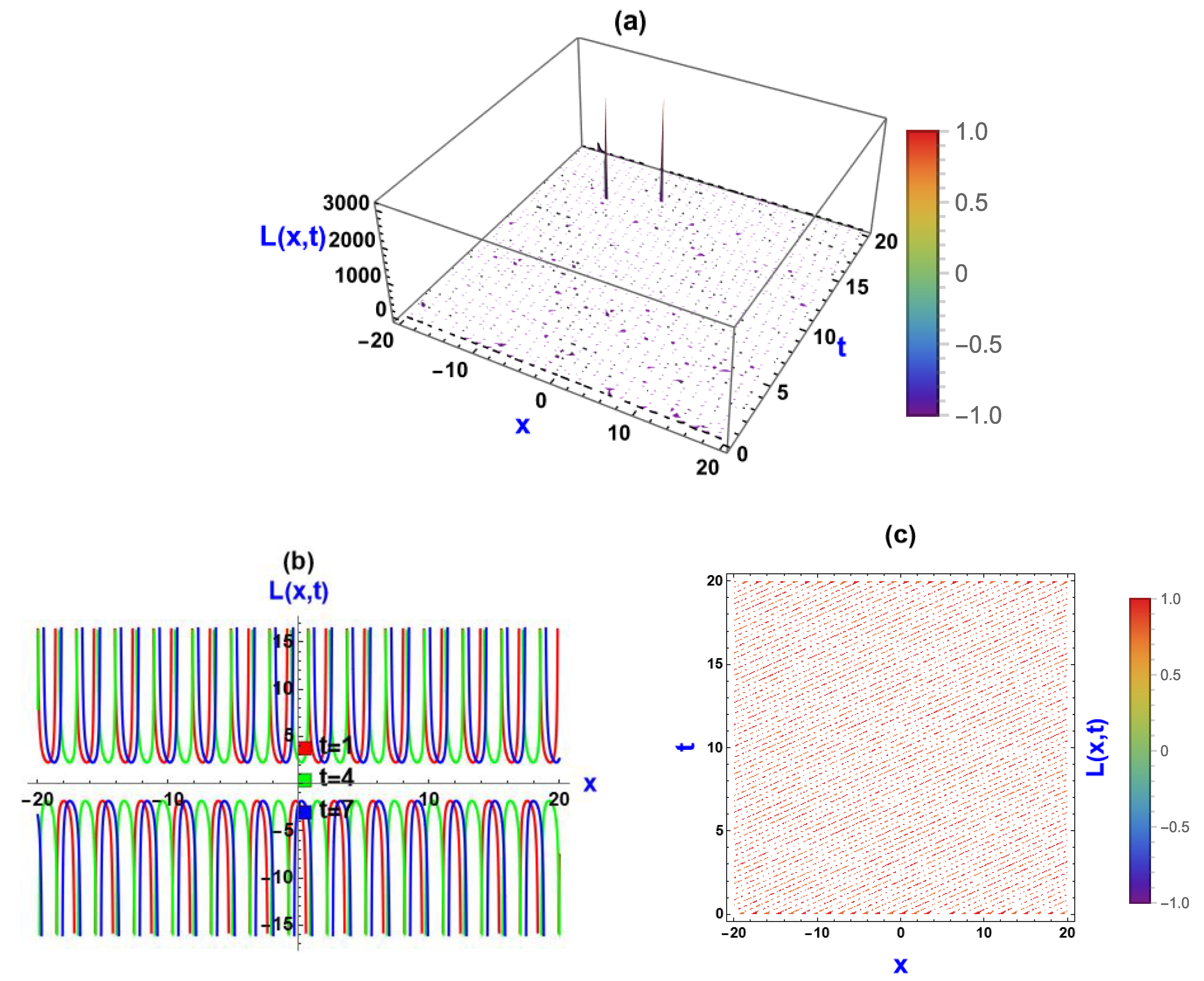
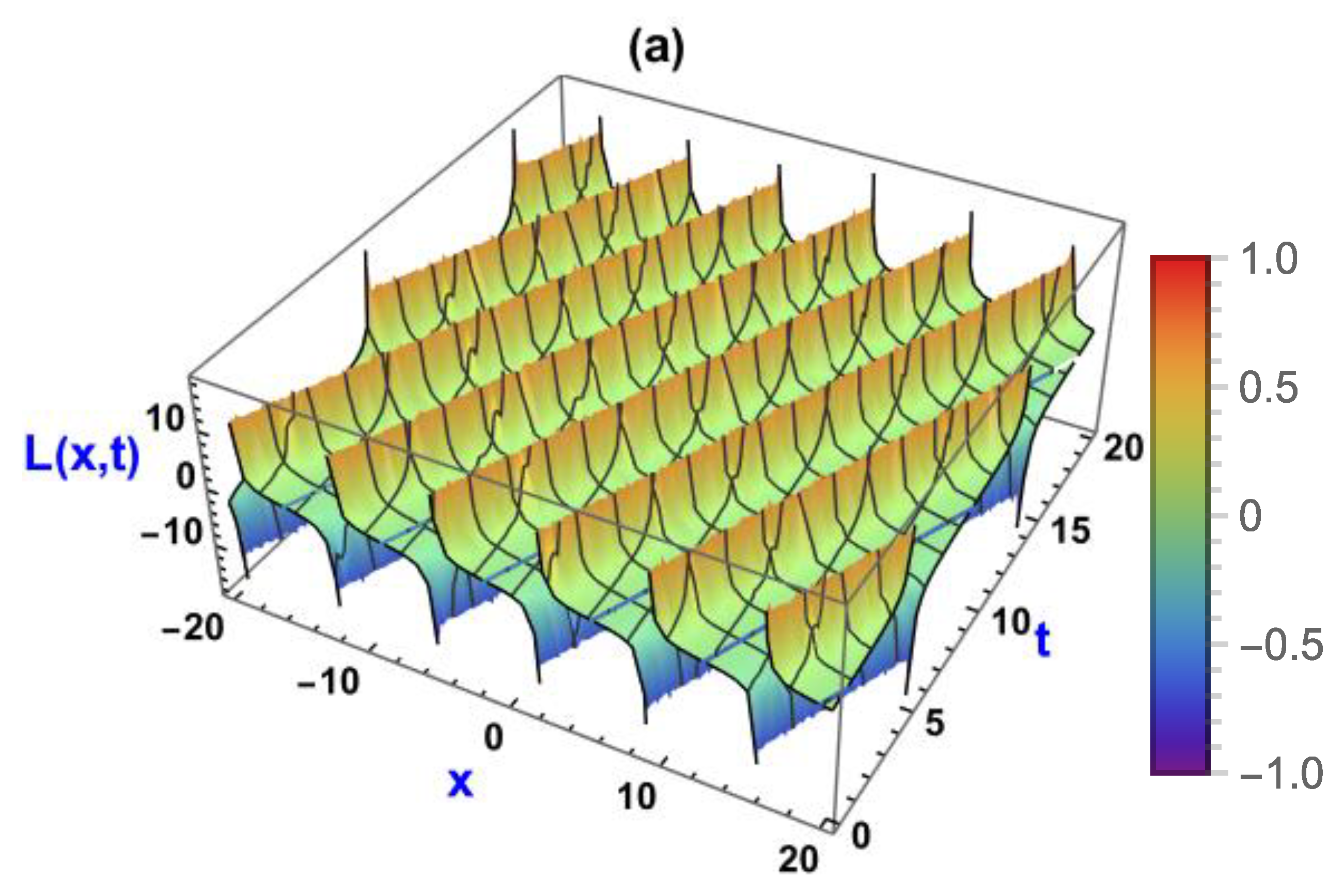
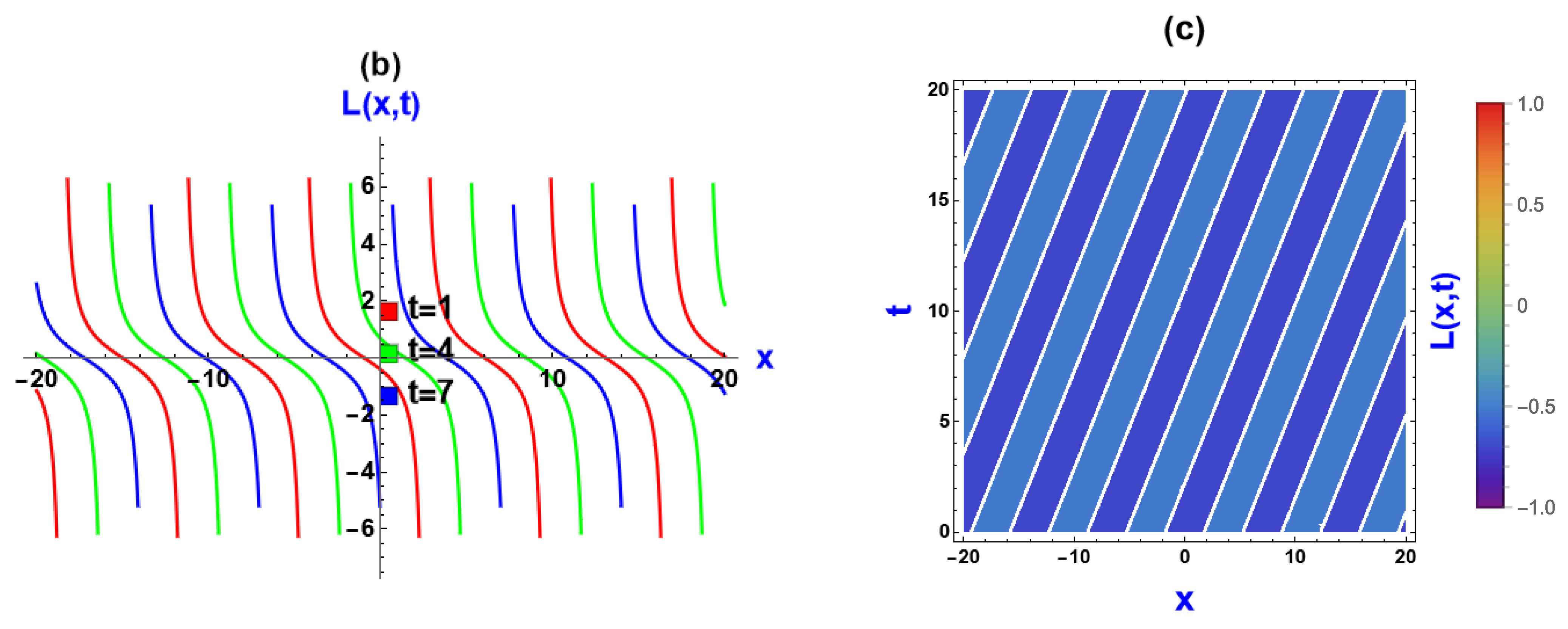
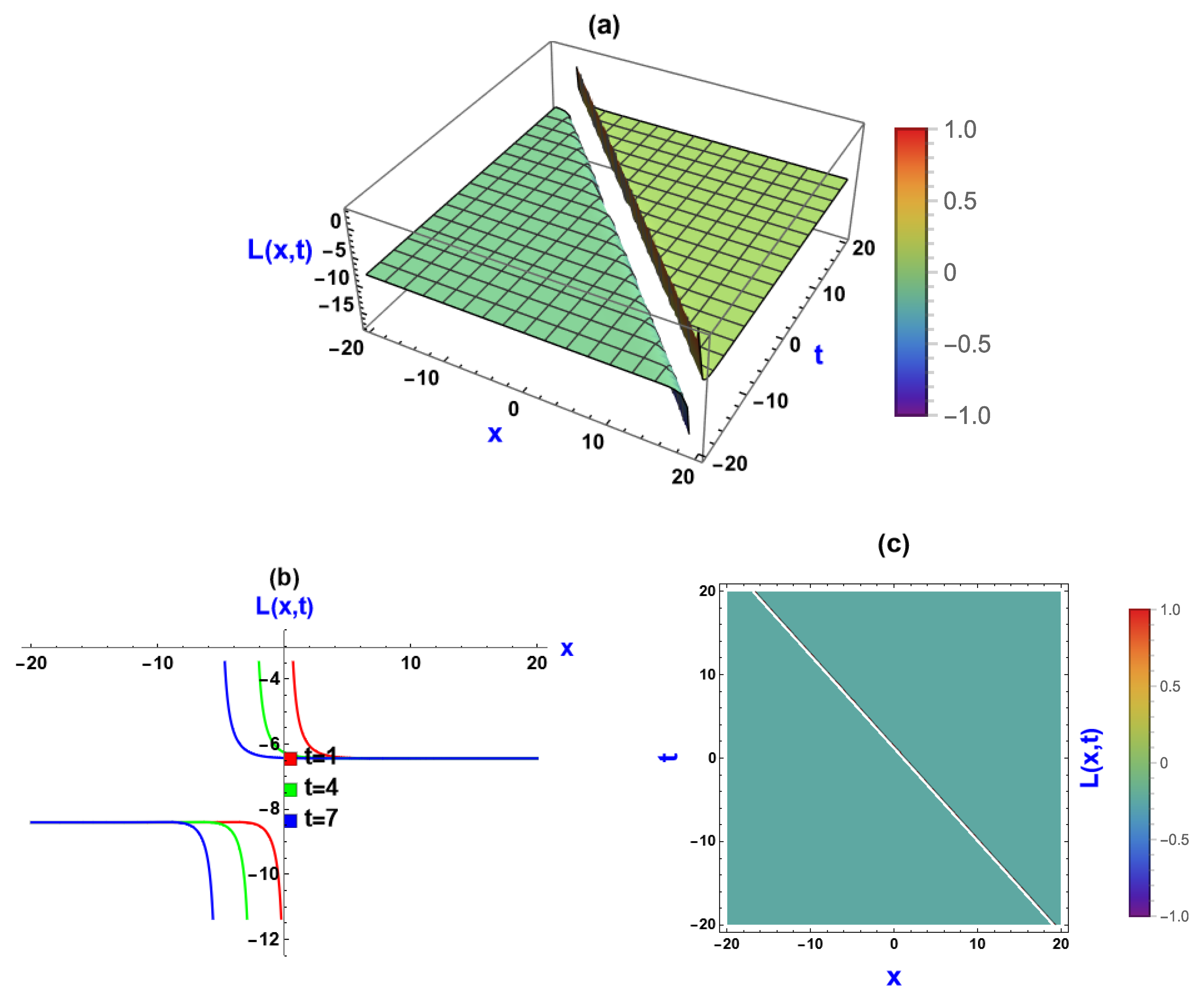
5. Visual Representation of the Exact Solutions
5.1. Visualization via Improved Sardar Subeqaution Method
5.2. Visualization via (, ) Approach
5.3. Discussions of the Graphs
6. Comparison
6.1. Unities
- (a)
- Both this study and previous studies focus on the MNW equation, a pivotal nonlinear model utilized for analyzing solitary wave dynamics.
- (b)
- The primary objective of both studies is to attain precise exact solutions through the utilization of analytical techniques.
- (c)
- Both studies have discovered a shared soliton type, specifically the kink soliton.
6.2. Variation and Uniqueness
- (a)
- In this study, two versatile methods were employed: the improved Sardar subequation method (involving one variable) and the (, ) method (utilizing two variables). Conversely, other studies utilized diverse methodologies, such as the (G′/G)-expansion method by [8], simplified Hirota’s method by [12], singular manifold method, exp(−(ξ))-expansion method, and generalized projective Riccati equations method by [11].
- (b)
- While the previous studies primarily yielded kink, anti-kink, bright, and periodic solitons, our investigation encompasses a broader range of soliton patterns. We have identified breather, singular, kink, anti-kink, bell, and hyperbolic-shaped solitons, among which singular, breather, bell, and hyperbolic-shaped solitons are entirely novel.
- (c)
- This study addresses both stability and modulation stability, whereas these critical aspects were overlooked in other studies.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Zafar, A.; Raheel, M.; Ali, K.K.; Razzaq, W. On Optical Soliton Solutions of New Hamiltonian Amplitude Equation via Jacobi Elliptic Functions. Eur. Phys. J. Plus 2020, 135, 674. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Hamid, A.; Osman, G.M.S. Discovering New Abundant Optical Solutions for the Resonant Nonlinear Schrödinger Equation Using an Analytical Technique. Opt. Quantum Electron. 2024, 56, 847. [Google Scholar] [CrossRef]
- Borhan, J.R.M.; Ganie, A.H.; Miah, M.M.; Iqbal, M.A.; Seadawy, A.R.; Mishra, N.K. A Highly Effective Analytical Approach to Innovate the Novel Closed Form Soliton Solutions of the Kadomtsev–Petviashivili Equations with Applications. Opt. Quantum Electron. 2024, 56, 938. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Iqbal, M. Dispersive Propagation of Optical Solitions and Solitary Wave Solutions of Kundu-Eckhaus Dynamical Equation via Modified Mathematical Method. Appl. Math. 2023, 38, 16–26. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Iqbal, M.; Althobaiti, S.; Sayed, S. Wave Propagation for the Nonlinear Modified Kortewege–de Vries Zakharov–Kuznetsov and Extended Zakharov–Kuznetsov Dynamical Equations Arising in Nonlinear Wave Media. Opt. Quantum Electron. 2021, 53, 85. [Google Scholar] [CrossRef]
- Khater, M.M.A. Soliton Propagation under Diffusive and Nonlinear Effects in Physical Systems; (1+1)–Dimensional MNW Integrable Equation. Phys. Lett. A 2023, 480, 128945. [Google Scholar] [CrossRef]
- Iqbal, M.; Lu, D.; Seadawy, A.R.; Ashraf, M.; Albaqawi, H.S.; Khan, K.A.; Chou, D. Investigation of Solitons Structures for Nonlinear Ionic Currents Microtubule and Mikhaillov-Novikov-Wang Dynamical Equations. Opt. Quantum Electron. 2024, 56, 361. [Google Scholar] [CrossRef]
- Bekir, A.; Shehata, M.S.M.; Zahran, E.H.M. Comparison between the New Exact and Numerical Solutions of the Mikhailov–Novikov–Wang Equation. Numer. Methods Partial Differ. Equ. 2024, 40, e22775. [Google Scholar] [CrossRef]
- Akbulut, A.; Kaplan, M.; Kaabar, M.K.A. New Exact Solutions of the Mikhailov-Novikov-Wang Equation via Three Novel Techniques. J. Ocean Eng. Sci. 2023, 8, 103–110. [Google Scholar] [CrossRef]
- Mikhailov, B.A.V.; Novikov, V.S.; Wang, J.P. On Classification of Integrable Davey-Stewartson Type Equations. Stud. Appl. Math. 2007, 118, 419–457. [Google Scholar] [CrossRef]
- Raza, N.; Seadawy, A.R.; Arshed, S.; Rafiq, M.H. A Variety of Soliton Solutions for the Mikhailov-Novikov-Wang Dynamical Equation via Three Analytical Methods. J. Geom. Phys. 2022, 176, 104515. [Google Scholar] [CrossRef]
- Ray, S.S.; Singh, S. New Various Multisoliton Kink-Type Solutions Ofthe (1 + 1)-Dimensional Mikhailov–Novikov–Wang Equation. Math. Methods Appl. Sci. 2021, 44, 14690–14702. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, S. Dynamic Nature of Analytical Soliton Solutions of the (1+1)-Dimensional Mikhailov-Novikov-Wang Equation Using the Unified Approach. Int. J. Math. Comput. Eng. 2023, 1, 217–228. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Iqbal, M. Propagation Ofthe Nonlinear Damped Korteweg-de Vries Equation in an Unmagnetized Collisional Dusty Plasma via Analytical Mathematical Methods. Math Meth Appl Sci. 2021, 44, 737–748. [Google Scholar] [CrossRef]
- Mia, R.; Mamun Miah, M.; Osman, M.S. A New Implementation of a Novel Analytical Method for Finding the Analytical Solutions of the (2+1)-Dimensional KP-BBM Equation. Heliyon 2023, 9, e15690. [Google Scholar] [CrossRef] [PubMed]
- Shakeel, M.; Attaullah; Shah, N.A.; Chung, J.D. Modified Exp-Function Method to Find Exact Solutions of Microtubules Nonlinear Dynamics Models. Symmetry 2023, 15, 360. [Google Scholar] [CrossRef]
- Ma, W.X. N-Soliton Solutions and the Hirota Conditions in (1 + 1) -Dimensions. Int. J. Nonlinear Sci. Numer. Simul. 2022, 23, 123–133. [Google Scholar] [CrossRef]
- Elsayed, M.E.Z.; Khaled, A.E.A. The Generalized Projective Riccati Equations Method and Its Applications for Solving Two Nonlinear PDEs Describing Microtubules. Int. J. Phys. Sci. 2015, 10, 391–402. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Kravchenko, O.V.; Deka, M.K.; Dev, A.N.; Churikov, D.V. The Exact Solutions of the 2+1–Dimensional Kadomtsev–Petviashvili Equation with Variable Coefficients by Extended Generalized [Formula Presented]-Expansion Method. J. King Saud Univ.-Sci. 2023, 35, 102358. [Google Scholar] [CrossRef]
- Shakeel, M.; Attaullah; Kbiri Alaoui, M.; Zidan, A.M.; Shah, N.A.; Weera, W. Closed-Form Solutions in a Magneto-Electro-Elastic Circular Rod via Generalized Exp-Function Method. Mathematics 2022, 10, 3400. [Google Scholar] [CrossRef]
- Babajanov, B.; Abdikarimov, F. The Application of the Functional Variable Method for Solving the Loaded Non-Linear Evaluation Equations. Front. Appl. Math. Stat. 2022, 8, 912674. [Google Scholar] [CrossRef]
- Tandel, P.; Patel, H.; Patel, T. Tsunami Wave Propagation Model: A Fractional Approach. J. Ocean Eng. Sci. 2022, 7, 509–520. [Google Scholar] [CrossRef]
- Iqbal, M.; Seadawy, A.R.; Lu, D.; Zhang, Z. Computational Approach and Dynamical Analysis of Multiple Solitary Wave Solutions for Nonlinear Coupled Drinfeld–Sokolov–Wilson Equation. Results Phys. 2023, 54, 107099. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Zahed, H.; Iqbal, M. Solitary Wave Solutions for the Higher Dimensional Jimo-Miwa Dynamical Equation via New Mathematical Techniques. Mathematics 2022, 10, 1011. [Google Scholar] [CrossRef]
- Taghizadeh, N.; Mirzazadeh, M. The First Integral Method to Some Complex Nonlinear Partial Differential Equations. J. Comput. Appl. Math. 2011, 235, 4871–4877. [Google Scholar] [CrossRef]
- Islam, Z.; Sheikh, M.A.N.; Roshid, H.O.; Hossain, M.A.; Taher, M.A.; Abdeljabbar, A. Stability and Spin Solitonic Dynamics of the HFSC Model: Effects of Neighboring Interactions and Crystal Field Anisotropy Parameters. Opt. Quantum Electron. 2024, 56, 190. [Google Scholar] [CrossRef]
- Kumar, A.; Pankaj, R.D. Tanh–Coth Scheme for Traveling Wave Solutions for Nonlinear Wave Interaction Model. J. Egypt. Math. Soc. 2015, 23, 282–285. [Google Scholar] [CrossRef]
- Islam, S.; Khan, K.; Arnous, A.H. Generalized Kudryashov Method for Solving Some. New Trends Math. Sci. 2015, 57, 46–57. [Google Scholar]
- Abdel-Gawad, H.I.; Osman, M. On Shallow Water Waves in a Medium with Time-Dependent Dispersion and Nonlinearity Coefficients. J. Adv. Res. 2015, 6, 593–599. [Google Scholar] [CrossRef]
- Shakeel, M.; Manan, A.; Bin Turki, N.; Shah, N.A.; Tag, S.M. Novel Analytical Technique to Find Diversity of Solitary Wave Solutions for Wazwaz-Benjamin-Bona Mahony Equations of Fractional Order. Results Phys. 2023, 51, 106671. [Google Scholar] [CrossRef]
- Iqbal, I.; Rehman, H.U.; Mirzazadeh, M.; Hashemi, M.S. Retrieval of Optical Solitons for Nonlinear Models with Kudryashov’s Quintuple Power Law and Dual-Form Nonlocal Nonlinearity. Opt. Quantum Electron. 2023, 55, 588. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Inc, M.; Baleanu, D. New Solitary Wave Solutions for Variants of (3+1)-Dimensional Wazwaz-Benjamin-Bona-Mahony Equations. Front. Phys. 2020, 8, 332. [Google Scholar] [CrossRef]
- Rehman, H.U.; Iqbal, I.; Subhi Aiadi, S.; Mlaiki, N.; Saleem, M.S. Soliton Solutions of Klein–Fock–Gordon Equation Using Sardar Subequation Method. Mathematics 2022, 10, 3377. [Google Scholar] [CrossRef]
- Ibrahim, S.; Ashir, A.M.; Sabawi, Y.A.; Baleanu, D. Realization of Optical Solitons from Nonlinear Schrödinger Equation Using Modified Sardar Sub-Equation Technique. Opt. Quantum Electron. 2023, 55, 617. [Google Scholar] [CrossRef]
- Cinar, M.; Secer, A.; Ozisik, M.; Bayram, M. Derivation of Optical Solitons of Dimensionless Fokas-Lenells Equation with Perturbation Term Using Sardar Sub-Equation Method. Opt. Quantum Electron. 2022, 54, 402. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Alosaimi, M.; Alsharif, F.; Kanan, M. Exploring Novel Soliton Solutions to the Time-Fractional Coupled Drinfel’d–Sokolov–Wilson Equation in Industrial Engineering Using Two Efficient Techniques. Fractal Fract. 2024, 8, 352. [Google Scholar] [CrossRef]
- Sadaf, M.; Arshed, S.; Ghazala Akram, I. Exact Soliton and Solitary Wave Solutions to the Fokas System Using Two Variables (G′/G,1/G)-Expansion Technique and Generalized Projective Riccati Equation Method. Opt.-Int. J. Light Electron Opt. 2022, 268, 169713. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Akram, G.; Sadaf, M.; Arshed, S.; Rehan, K.; Farooq, K. Traveling Wave Behavior of New (2+1)-Dimensional Combined KdV–MKdV Equation. Results Phys. 2023, 45, 106244. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alurrfi, K.A.E. The (G’/G, 1/G)-Expansion Method and Its Applications for Solving Two Higher Order Nonlinear Evolution Equations. Math. Probl. Eng. 2014, 2014, 746538. [Google Scholar] [CrossRef]
- Sirisubtawee, S.; Koonprasert, S.; Sungnul, S. Some Applications of the (G’/G, 1/G)-Expansion Method for Finding Exact Traveling Wave Solutions of Nonlinear Fractional Evolution Equations. Symmetry 2019, 11, 952. [Google Scholar] [CrossRef]
- Hossain, M.N.; Alsharif, F.; Miah, M.M.; Kanan, M. Abundant New Optical Soliton Solutions to the Biswas–Milovic Equation with Sensitivity Analysis for Optimization. Mathematics 2024, 12, 1585. [Google Scholar] [CrossRef]
- Younis, M.; Sulaiman, T.A.; Bilal, M.; Rehman, S.U.; Younas, U. Modulation Instability Analysis, Optical and Other Solutions to the Modified Nonlinear Schrödinger Equation. Commun. Theor. Phys. 2020, 72, 065001. [Google Scholar] [CrossRef]
- Rahman, M.; Sun, M.; Boulaaras, S.; Baleanu, D. Bifurcations, Chaotic Behavior, Sensitivity Analysis, and Various Soliton Solutions for the Extended Nonlinear Schrödinger Equation. Bound. Value Probl. 2024, 2024, 15. [Google Scholar] [CrossRef]
- Hossain, M.N.; El Rashidy, K.; Alsharif, F.; Kanan, M.; Ma, W.-X.; Miah, M.M. New Optical Soliton Solutions to the Biswas–Milovic Equations with Power Law and Parabolic Law Nonlinearity Using the Sardar-Subequation Method. Opt. Quantum Electron. 2024, 56, 1163. [Google Scholar] [CrossRef]
- Yasin, S.; Khan, A.; Ahmad, S.; Osman, M.S. New Exact Solutions of (3+1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation by Sardar-Subequation Method. Opt. Quantum Electron. 2024, 56, 90. [Google Scholar] [CrossRef]
- Li, L.X.; Li, E.Q.; Wang, M.L. The (G′/G, 1/G)-Expansion Method and Its Application to Travelling Wave Solutions of the Zakharov Equations. Appl. Math. 2010, 25, 454–462. [Google Scholar] [CrossRef]
- Shakeel, M.; Mohyud-Din, S.T. Soliton Solutions for the Positive Gardner-KP Equation by (G′/G, 1/G)—Expansion Method. Ain Shams Eng. J. 2014, 5, 951–958. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Duraihem, F.Z.; Rehman, S.; Ma, W.-X. Chaotic Behavior, Bifurcations, Sensitivity Analysis, and Novel Optical Soliton Solutions to the Hamiltonian Amplitude Equation in Optical Physics. Phys. Scr. 2024, 99, 075231. [Google Scholar] [CrossRef]
- Bilal, M.; Shafqat-Ur-Rehman; Ahmad, J. Stability Analysis and Diverse Nonlinear Optical Pluses of Dynamical Model in Birefringent Fibers without Four-Wave Mixing. Opt. Quantum Electron. 2022, 54, 277. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Duraihem, F.Z.; Rehman, S. Stability, Modulation Instability, and Analytical Study of the Confirmable Time Fractional Westervelt Equation and the Wazwaz Kaur Boussinesq Equation. Opt. Quantum Electron. 2024, 56, 948. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.N.; Miah, M.M.; Abbas, M.S.; El-Rashidy, K.; Borhan, J.R.M.; Kanan, M. An Analytical Study of the Mikhailov–Novikov–Wang Equation with Stability and Modulation Instability Analysis in Industrial Engineering via Multiple Methods. Symmetry 2024, 16, 879. https://doi.org/10.3390/sym16070879
Hossain MN, Miah MM, Abbas MS, El-Rashidy K, Borhan JRM, Kanan M. An Analytical Study of the Mikhailov–Novikov–Wang Equation with Stability and Modulation Instability Analysis in Industrial Engineering via Multiple Methods. Symmetry. 2024; 16(7):879. https://doi.org/10.3390/sym16070879
Chicago/Turabian StyleHossain, Md Nur, M. Mamun Miah, M. S. Abbas, K. El-Rashidy, J. R. M. Borhan, and Mohammad Kanan. 2024. "An Analytical Study of the Mikhailov–Novikov–Wang Equation with Stability and Modulation Instability Analysis in Industrial Engineering via Multiple Methods" Symmetry 16, no. 7: 879. https://doi.org/10.3390/sym16070879
APA StyleHossain, M. N., Miah, M. M., Abbas, M. S., El-Rashidy, K., Borhan, J. R. M., & Kanan, M. (2024). An Analytical Study of the Mikhailov–Novikov–Wang Equation with Stability and Modulation Instability Analysis in Industrial Engineering via Multiple Methods. Symmetry, 16(7), 879. https://doi.org/10.3390/sym16070879








