A New Latin Hypercube Sampling with Maximum Diversity Factor for Reliability-Based Design Optimization of HLM
Abstract
:1. Introduction
2. Latin Hypercube Sampling with Maximum Diversity Factor (LHSMDF)
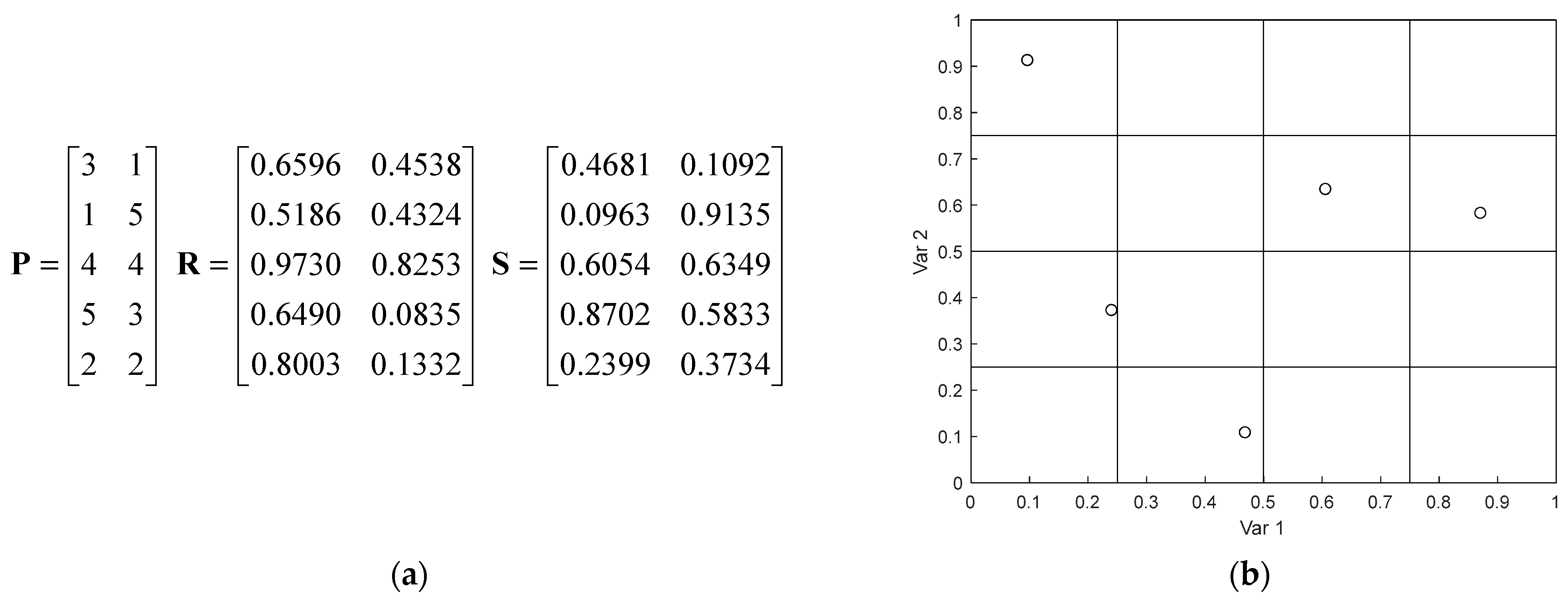
2.1. LHS
2.2. LHSMDF
2.2.1. Improving of Euclidean Norm with k-Nearest
2.2.2. LHS with Maximum Diversity Factor
- (1)
- Sampling of random variables (X) multiple times.
- (2)
- Finding the minimum (Df), with the best minimum being selected from the random variable sets.
- (3)
- Conducting numerical experiments to find output Y.
- (4)
- Performing statistical analysis of output Y.
2.3. Motion Analysis of a High-Lift Mechanism
2.4. Motion Generation of Six-Bar Linkage
2.5. Reliability-Based Design Optimization
3. Numerical Experiment
3.1. Test Problems
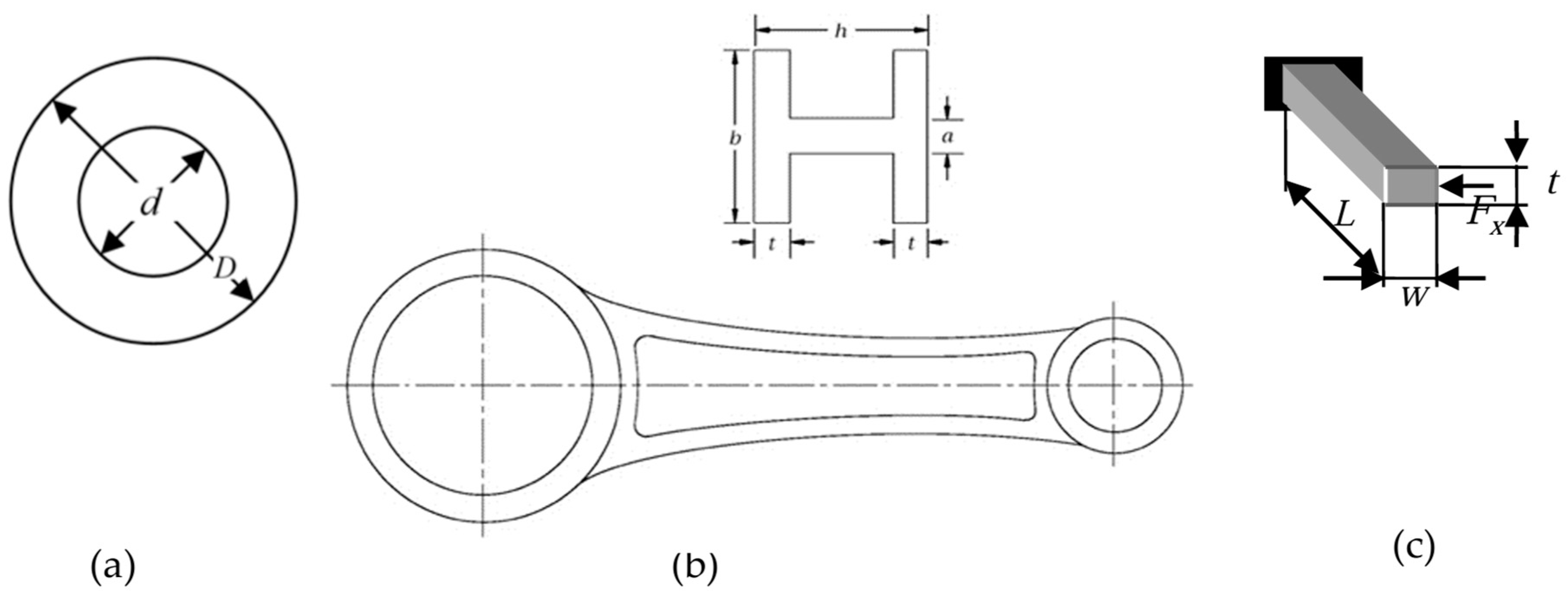
3.2. Reliability-Based Design of a High-Lift Mechanism
4. Design Results
4.1. Test Problem Results
4.2. HLM Synthesis Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Wan, H.; Gao, W.; Tong, F.; Li, H. Reliability based multidisciplinary design optimization of cooling turbine blade considering uncertainty data statistics. Struct. Multidiscipl. Optim. 2019, 59, 659–673. [Google Scholar] [CrossRef]
- Elishakoff, I.; Colombi, P. Combination of probabilistic and convex models of uncertainty when scare knowledge is present on acoustic excitation parameters. Comput. Methods Appl. Mech. Eng. 1993, 104, 187–209. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. Multi-objective reliability-based topology Optimization of Structures Using a Fuzzy Set Model. J. Mech. Sci. Technol. 2020, 34, 3973–3980. [Google Scholar] [CrossRef]
- Kang, Z.; Luo, Y.; Li, A. On non-probabilistic reliability-based design optimization of structures with uncertain-but-bounded parameters. Struct. Saf. 2011, 33, 196–205. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. Multi-Objective, Reliability-Based Design Optimization of a Steering Linkage. Appl. Sci. 2020, 10, 5748. [Google Scholar] [CrossRef]
- Enevoldsen, I.; Sørensen, J. Reliability-based optimization in structural engineering. Struct. Saf. 1994, 15, 169–196. [Google Scholar] [CrossRef]
- Tu, J.; Choi, K.K.; Park, Y.H. A New Study on Reliability-Based Design Optimization. J. Mech. Des. 1999, 121, 557–564. [Google Scholar] [CrossRef]
- Youn, B.D.; Choi, K.K.; Park, Y.H. Hybrid Analysis Method for Reliability-Based Design Optimization. J. Mech. Des. 2003, 125, 221–232. [Google Scholar] [CrossRef]
- Du, X.; Chen, W. Sequential Optimization and Reliability Assessment Method for Efficient Probabilistic Design. J. Mech. Des. 2004, 126, 225–233. [Google Scholar] [CrossRef]
- Zou, T.; Mahadevan, S. A direct decoupling approach for efficient reliability-based design optimization. Struct. Multidiscip. Optim. 2006, 31, 190–200. [Google Scholar] [CrossRef]
- Shan, S.; Wang, G.G. Reliable design space and complete single-loop reliability-based design optimization. Reliab. Eng. Syst. Saf. 2008, 93, 1218–1230. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Song, J.; Paulino, G.H. Single-Loop System Reliability-Based Design Optimization Using Matrix-Based System Reliability Method: Theory and Applications. J. Mech. Des. 2009, 132, 011005. [Google Scholar] [CrossRef]
- Chun, J.; Paulino, G.H.; Song, J. Reliability-based topology optimization by ground structure method employing a discrete filtering technique. Struct. Multidiscip. Optim. 2019, 60, 1035–1058. [Google Scholar] [CrossRef]
- Chun, J.; Song, J.; Paulino, G.H. System-reliability-based design and topology optimization of structures under constraints on first-passage probability. Struct. Saf. 2019, 76, 81–94. [Google Scholar] [CrossRef]
- Chun, J. Reliability-Based Design Optimization of Structures Using Complex-Step Approximation with Sensitivity Analysis. Appl. Sci. 2021, 11, 4708. [Google Scholar] [CrossRef]
- Fang, J.; Smith, S.M.; Elishakoffk, I. Combination of anti-optimization and fuzzy-set-based analyses for structural optimization under uncertainty. Math. Prob. Eng. 1998, 4, 187–200. [Google Scholar] [CrossRef]
- Moller, B.; Graf, W.; Beer, M. Fuzzy structural analysis using α-level optimization. Comput. Mech. 2000, 26, 547–565. [Google Scholar] [CrossRef]
- Tang, Z.C.; Lu, Z.Z.; Hu, J.X. An efficient approach for design optimization of structures involving fuzzy variables. Fuzzy Sets Syst. 2014, 255, 52–73. [Google Scholar] [CrossRef]
- Yin, H.; Yu, D.; Xia, R. Reliability-based topology optimization for structures using fuzzy set model. Comput. Methods Appl. Mech. Eng. 2018, 333, 197–217. [Google Scholar] [CrossRef]
- Luo, Y.; Zhan, J.; Xing, J.; Kang, Z. Non-probabilistic uncertainty quantification and response analysis of structures with a bounded field model. Comput. Methods Appl. Mech. Eng. 2019, 347, 663–678. [Google Scholar] [CrossRef]
- Zhang, L.; Qiu, Z. Multidisciplinary non-probabilistic reliability optimization based on collaborative optimization method. J. Nanjing Univ. Aeronaut. Astronaut. 2010, 42, 267–271. [Google Scholar]
- Mostafa, M.N.; Morteza, T. Robust data envelopment analysis with Monte Carlo simulation model for optimization the energy consumption in agriculture. Energy Sources Part A: Recovery Util. Environ. Eff. 2020, 42, 1–15. [Google Scholar]
- Peng, H.; Peng, Z. A Practical Method for Redesigning Statistical Tolerances Using Monte Carlo Simulation. In Proceedings of the 9th International Conference on Mechanical and Aerospace Engineering, Budapest, Hungary, 10–13 July 2018; pp. 213–218. [Google Scholar]
- Abyani, M.; Bahaari, R.M. A comparative reliability study of corroded pipelines based on Monte Carlo Simulation and Latin Hypercube Sampling methods. Int. J. Press. Vessel. Pip. 2020, 181, 104079. [Google Scholar] [CrossRef]
- Champasak, P.; Panagant, N.; Pholdee, N.; Vio, G.; Bureerat, S.; Yıldız, B.; Yıldız, A. Aircraft conceptual design using metaheuristic-based reliability optimization. Aerosp. Sci. Technol. 2022, 129, 107803. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, Y.; Liu, J. Reliability sensitivity analysis using axis orthogonal importance Latin hypercube sampling method. Adv. Mech. Eng. 2019, 11, 1–13. [Google Scholar]
- Minasny, B.; McBratney, A.B. A conditioned latin hypercube method for sampling in the presence of ancillary information. Comput. Geosci. 2006, 32, 1378–1388. [Google Scholar] [CrossRef]
- Le, V.H.; Vargas, R. An autocorrelated conditioned Latin hypercube method for temporal or spatial sampling and predictions. Comput. Geosci. 2024, 184, 105539. [Google Scholar] [CrossRef]
- Johnson, M.E.; Moore, L.M.; Ylvisaker, D. Minimax and maximin distance designs. J. Stat. Plan. Inference 1990, 26, 131–148. [Google Scholar] [CrossRef]
- Deutsch, J.L.; Deutsch, C.V. Latin hypercube sampling with multidimensional uniformity. J. Stat. Plan. Inference 2012, 142, 763–772. [Google Scholar] [CrossRef]
- Erten, O.; Pereira, F.P.L.; Deutsch, C.V. Projection Pursuit Multivariate Sampling of Parameter Uncertainty. Appl. Sci. 2022, 12, 9668. [Google Scholar] [CrossRef]
- Morris, M.D.; Mitchell, T.J. Exploratory Designs for Computational Experiments. J. Stat. Plan. Inference 1995, 43, 381–402. [Google Scholar] [CrossRef]
- Zhu, H.G.; Liu, L.; Long, T.; Peng, L. A Novel Algorithm of Maximin Latin Hypercube Design Using Successive Local Enumeration. Eng. Optim. 2012, 44, 551–564. [Google Scholar] [CrossRef]
- Li, G.; Yang, J.; Wu, Z.; Zhang, W.; Okolo, P.; Zhang, D. A Sequential Optimal Latin Hypercube Design Method Using an Efficient Recursive Permutation Evolution Algorithm. Eng. Optim. 2022, 56, 179–198. [Google Scholar] [CrossRef]
- Liaw, H.C.; Shirinzadeh, B. Constrained Motion Tracking Control of Piezo-Actuated Flexure-Based Four-Bar Mechanisms for Micro/Nano Manipulation. IEEE Trans. Autom. Sci. Eng. 2010, 7, 699–705. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. Optimization of a High-Lift Mechanism Motion Generation Synthesis Using MHS. In Advances in Swarm Intelligence; Tan, Y., Shi, Y., Eds.; ICSI 2021; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2021; p. 12689. [Google Scholar]
- Promphan, P.; Suvisuthikasame, J.; Kaewmongkol, M.; Chanpichitwanich, W.; Sleesongsom, S. Optimal Synthesis of a Motion Generation Six-Bar Linkage. In Advances in Swarm Intelligence; Tan, Y., Shi, Y., Niu, B., Eds.; ICSI 2022; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2022; p. 13345. [Google Scholar]
- Promphan, P.; Suvisuthikasame, J.; Kaewmongkol, M.; Chanpichitwanich, W.; Sleesongsom, S. Optimal synthesis of a six-bar linkage. AIP Conf. Proc. 2023, 2601, 020029. [Google Scholar]
- Gordon, R.; Pennock, A. Kinematic analysis and synthesis of an adjustable six-bar linkage. Mech. Mach. Theory 2009, 44, 306–323. [Google Scholar]
- Erkin, G.; Pyung-Hun, C.; Ahmet, F.A. Synthesis of a Watt II six-bar linkage in the design of a hand rehabilitation robot. Mech. Mach. Theory 2016, 104, 177–189. [Google Scholar]
- Gogate, G.R.; Matekar, S.B. Unified synthesis of Watt-I six-link mechanisms using evolutionary optimization. J. Mech. Sci. Technol. 2014, 28, 3075–3086. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. Four-bar linkage path generation through self-adaptive population size teaching-learning based optimization. Knowl.-Based Syst. 2017, 135, 180–191. [Google Scholar] [CrossRef]
- Bureerat, S.; Sleesongsom, S. Constraint handling technique for four-bar linkage path generation using self-adaptive teaching–learning-based optimization with a diversity archive. Eng. Optim. 2020, 53, 513–530. [Google Scholar] [CrossRef]
- McKay, M.D.; Conover, W.J.; Beckman, R.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On Latin hypercube sampling for structural reliability analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- Cioppa, T.; Lucas, T. Efficient nearly orthogonal and space-filling Latin hypercubes. Technometrics 2007, 49, 45–55. [Google Scholar] [CrossRef]
- Chanu, S.; Wattanathorn, A.; Senpong, M.; Sleesongsom, S. Reliability analysis in design of mechanical components. AIP Conf. Proc. 2023, 2601, 020030. [Google Scholar]
- Sleesongsom, S.; Winyangkul, S.; Bureerat, S. Multiobjective reliability-based design of an aircraft wing using a fuzzy-based metaheuristic. In Proceedings of the ASME 2021 International Mechanical Engineering Congress and Exposition, Virtual, 1–5 November 2021; Volume 13: Safety Engineering, Risk, and Reliability Analysis, Research Posters, V013T14A016; ASME: New York, NY, USA, 2021. [Google Scholar]



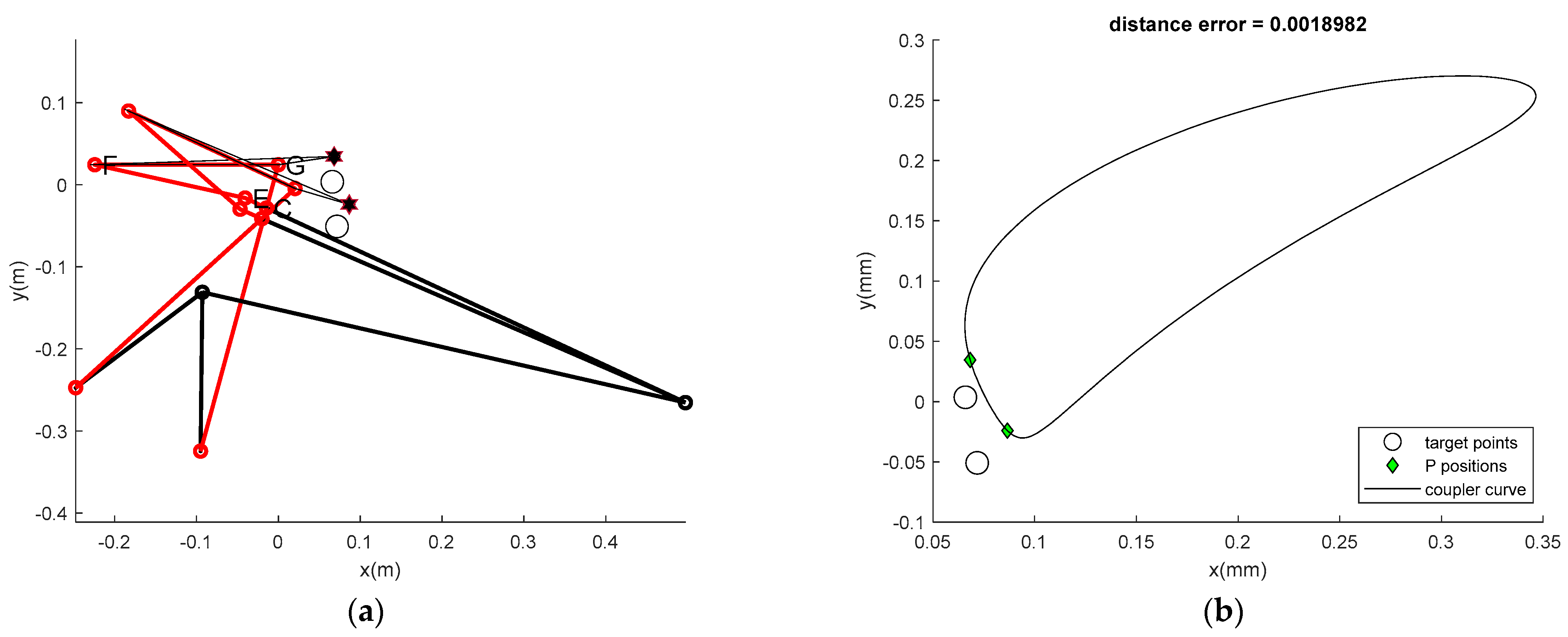
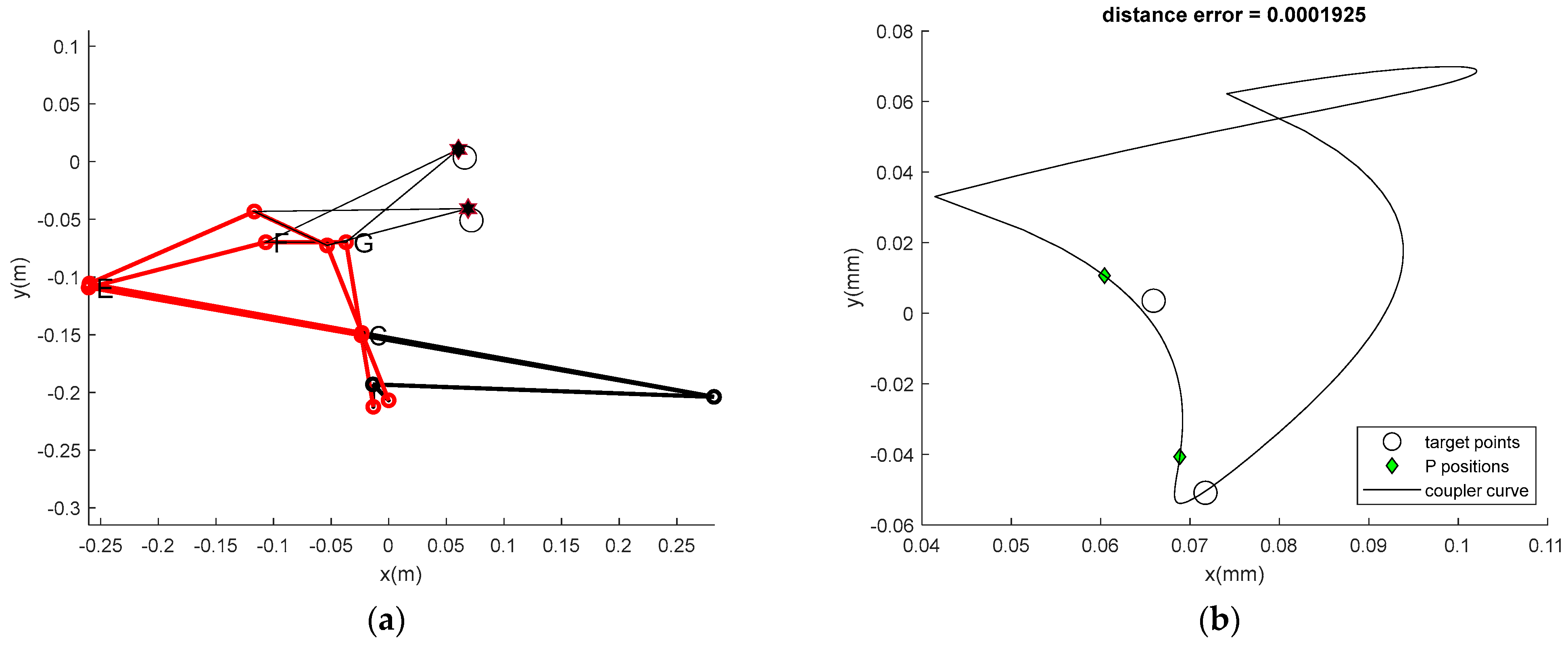
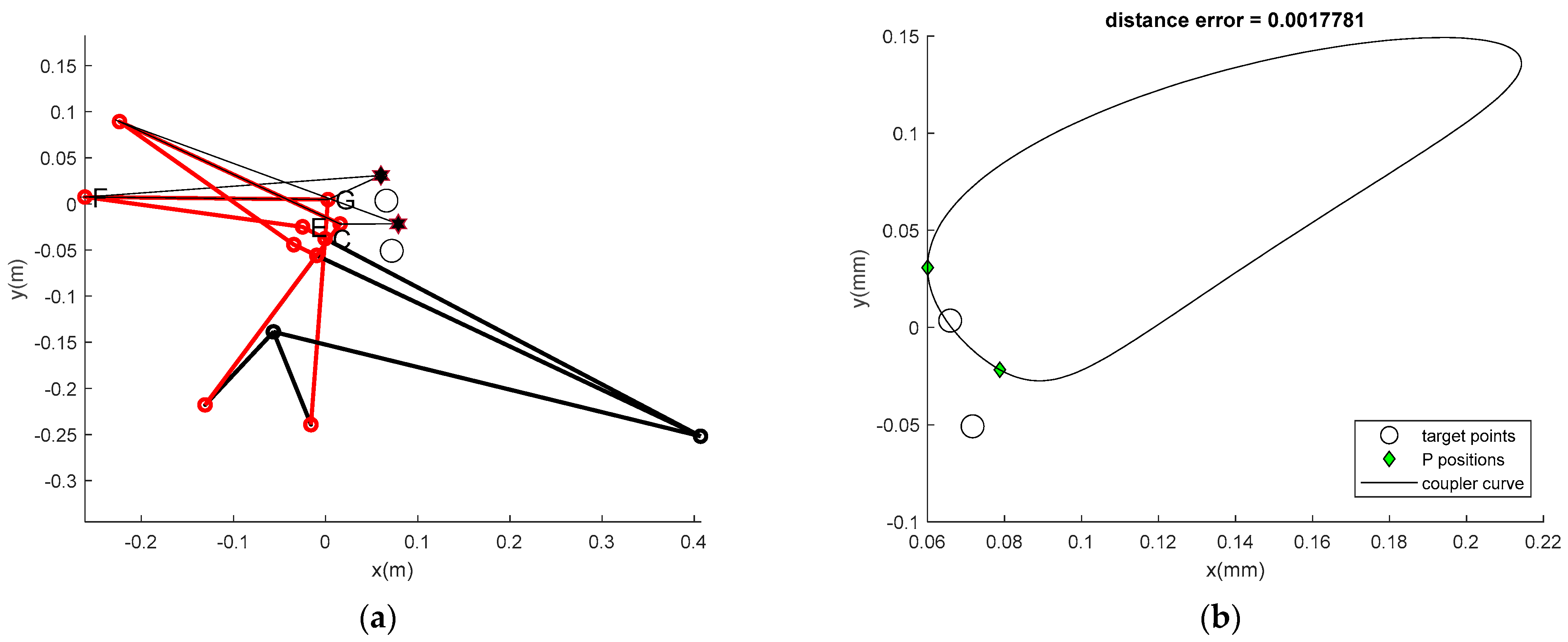
| Sampling Number (n) | 20 | 103 | 104 | 105 | 106 | |
|---|---|---|---|---|---|---|
| LHS | pf | 0 | 0.0060 | 0.0030 | 0.0026 | 0.0023 |
| R | 1 | 0.994 | 0.997 | 0.9974 | 0.9977 | |
| Rand. samp. (s) | 0.00812 | 0.01049 | 0.02210 | 0.04230 | 0.36420 | |
| Statistic test (s) | 0.00288 | 0.00596 | 0.01146 | 0.02527 | 0.21685 | |
| n | 20 | 103 | 104 | 2 × 104 | 5 × 104 | |
| LHSMDF | pf | 0 | 0 | 0.0010 | 0.0015 | 0.0027 |
| R | 1 | 1 | 0.999 | 0.9985 | 0.9973 | |
| Rand. samp. (s) | 0.08524 | 0.07039 | 12.50720 | 153.52924 | 2516.02090 | |
| Statistic test(s) | 0.00565 | 0.00735 | 0.01510 | 0.02231 | 0.06244 | |
| n | 20 | 102 | 103 | 2 × 103 | 5 × 103 | |
| OLHS | pf | 0 | 0 | 0.007 | 0.0075 | 2.0 × 10−4 |
| R | 1 | 1 | 0.993 | 0.9925 | 0.9998 | |
| Rand. samp. (s) | 0.33351 | 6.15665 | 590.78005 | 2193.59261 | 10,215.09658 | |
| Statistic test(s) | 0.01823 | 0.00364 | 0.01957 | 0.01446 | 0.38352 | |
| Sampling Number (n) | 20 | 103 | 104 | 105 | 106 | |
|---|---|---|---|---|---|---|
| LHS | pf | 0.0500 | 0.0910 | 0.0929 | 0.0928 | 0.0923 |
| R | 0.9500 | 0.9090 | 0.9071 | 0.9072 | 0.9077 | |
| Rand. samp. (s) | 0.00809 | 0.01061 | 0.01274 | 0.05724 | 0.46319 | |
| Statistic test(s) | 0.00512 | 0.00497 | 0.00698 | 0.01607 | 0.09077 | |
| n | 20 | 103 | 104 | 2 × 104 | 5 × 104 | |
| LHSMDF | pf | 0.1000 | 0.0800 | 0.0920 | 0.0935 | 0.0947 |
| R | 0.9000 | 0.9200 | 0.9080 | 0.9065 | 0.9053 | |
| Rand. samp. (s) | 0.03783 | 0.06768 | 14.34204 | 179.43832 | 3006.86080 | |
| Statistic test(s) | 0.00533 | 0.00433 | 0.00699 | 0.00535 | 0.00423 | |
| n | 20 | 102 | 103 | 2 × 103 | 5 × 103 | |
| OLHS | pf | 0.1000 | 0.1800 | 0.083 | 0.08 | 0.0978 |
| R | 0.9000 | 0.82000 | 0.917 | 0.92 | 0.9022 | |
| Rand. samp. (s) | 0.2725 | 4.93440 | 522.91080 | 1771.68530 | 9448.59657 | |
| Statistic test(s) | 0.04570 | 0.00194 | 0.00592 | 0.03291 | 0.00301 | |
| Sampling Number (n) | 20 | 103 | 104 | 105 | 106 | |
|---|---|---|---|---|---|---|
| LHS | pf | 0.9000 | 0.9270 | 0.9204 | 0.9251 | 0.9246 |
| R | 0.100 | 0.0796 | 0.0796 | 0.0749 | 0.0754 | |
| Rand. samp. (s) | 0.00612 | 0.00661 | 0.00774 | 0.03763 | 0.16724 | |
| Statistic test (s) | 0.00211 | 0.00249 | 0.00426 | 0.01976 | 0.11857 | |
| n | 20 | 103 | 104 | 2 × 104 | 5 × 104 | |
| LHSMDF | pf | 0.9000 | 0.9100 | 0.9310 | 0.9216 | 0.9256 |
| R | 0.1000 | 0.0900 | 0.0690 | 0.0784 | 0.0744 | |
| Rand. samp. (s) | 0.03716 | 0.04131 | 4.99398 | 60.95796 | 1038.02087 | |
| Statistic test(s) | 0.00328 | 0.00274 | 0.00597 | 0.01041 | 0.02588 | |
| n | 20 | 102 | 103 | 2 × 103 | 5 × 103 | |
| OLHS | pf | 0.9000 | 0.8600 | 0.8920 | 0.8790 | 0.893 |
| R | 0.1000 | 0.1400 | 0.1080 | 0.1210 | 0.106999 | |
| Rand. samp. (s) | 0.34223 | 6.12404 | 624.30990 | 2197.04548 | 9804.15560 | |
| Statistic test(s) | 0.00246 | 0.00234 | 0.00349 | 0.00695 | 0.02253 | |
| Parameters | Flap Take-Off Condition | ||||
|---|---|---|---|---|---|
| pfmax | 1 | 0.01 | 0.001 | ||
| DTM | LHSMDF | MCS | LHSMDF | MCS | |
| r1 (m) | 0.4993 | 0.2963 | 0.3660 | 0.4771 | 0.6052 |
| r2 (m) | 0.4157 | 0.0194 | 0.1949 | 0.1085 | 0.1935 |
| r3 (m) | 0.4913 | 0.0628 | 0.2839 | 0.2023 | 0.3069 |
| r3,2 (m) | 0.0150 | 0.0817 | 0.0519 | 0.0425 | 0.0547 |
| r4 (m) | 0.5692 | 0.3106 | 0.3047 | 0.4604 | 0.5638 |
| r4,2 (m) | 0.0400 | 0.2403 | 0.0176 | 0.0274 | 0.0290 |
| r5 (m) | 0.0133 | 0.1602 | 0.1074 | 0.2564 | 0.2121 |
| r6 (m) | 0.0240 | 0.0696 | 0.0985 | 0.2637 | 0.2242 |
| rpx (m) | −0.0604 | −0.0976 | 9.0807 × 10−4 | −0.0572 | −0.0682 |
| rpy (m) | 0.0477 | 0.0804 | 0.0120 | 0.0266 | 0.0101 |
| x0 (m) | 0.0759 | −0.0138 | −0.0692 | −0.0567 | −0.0929 |
| y0 (m) | −0.1056 | −0.1930 | −0.1119 | −0.1387 | −0.1310 |
| θ0 (rad) | −0.0318 | −0.0367 | −0.3662 | −0.2395 | −0.2240 |
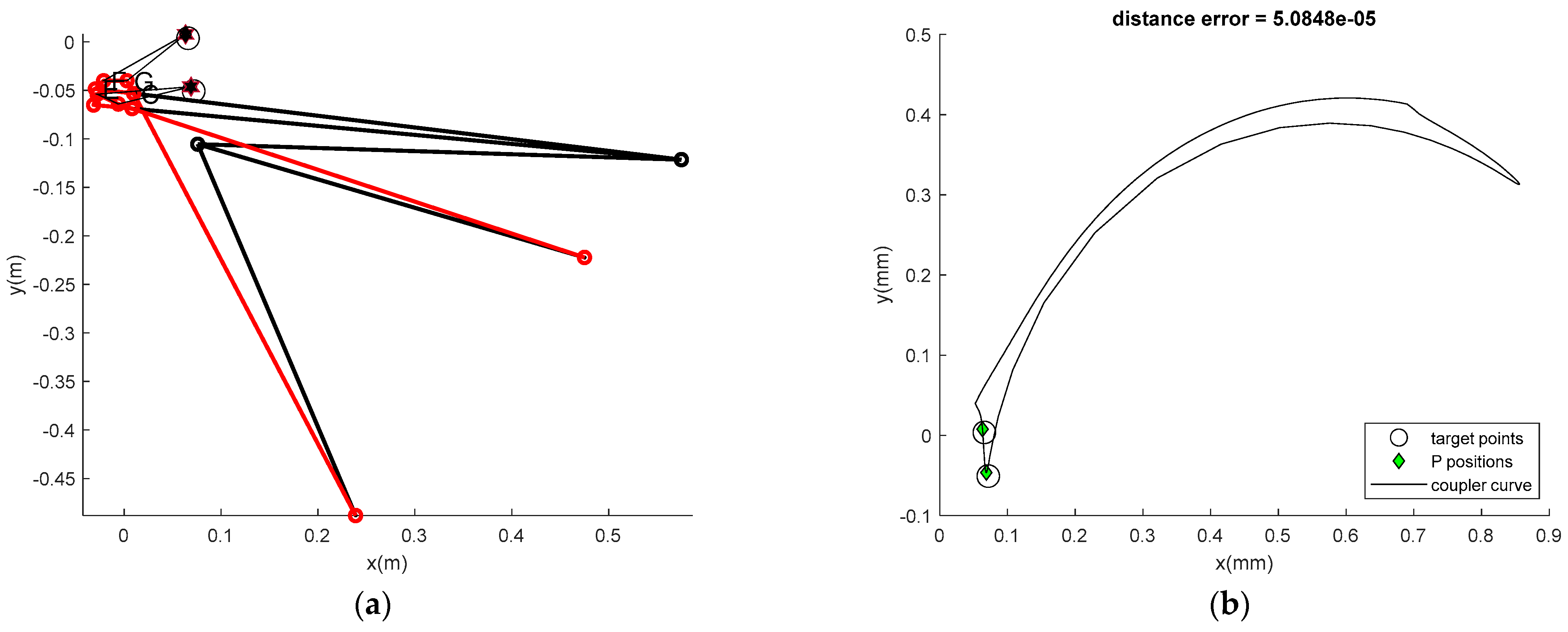
| Mean fobj | 3.90 × 10−2 | 8.66 × 10−3 | 1.77 × 10−2 | 9.09 × 10−3 | 1.91 × 10−2 |
| β | 0.8981 | 5.1114 | 4.7652 | 13.5966 | 12.6165 |
| pf | 0.1846 | 1.60 × 10−7 | 9.43 × 10−7 | 0 | 0 |
| Best min | 5.0848× 10−5 | 1.93 × 10−4 | 1.51 × 10−4 | 0.0018 | 0.0019 |
| Compt. (s) | 28.6467 | 256.4276 | 832.0085 | 256.8591 | 788.8039 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phromphan, P.; Suvisuthikasame, J.; Kaewmongkol, M.; Chanpichitwanich, W.; Sleesongsom, S. A New Latin Hypercube Sampling with Maximum Diversity Factor for Reliability-Based Design Optimization of HLM. Symmetry 2024, 16, 901. https://doi.org/10.3390/sym16070901
Phromphan P, Suvisuthikasame J, Kaewmongkol M, Chanpichitwanich W, Sleesongsom S. A New Latin Hypercube Sampling with Maximum Diversity Factor for Reliability-Based Design Optimization of HLM. Symmetry. 2024; 16(7):901. https://doi.org/10.3390/sym16070901
Chicago/Turabian StylePhromphan, Pakin, Jirachot Suvisuthikasame, Metas Kaewmongkol, Woravech Chanpichitwanich, and Suwin Sleesongsom. 2024. "A New Latin Hypercube Sampling with Maximum Diversity Factor for Reliability-Based Design Optimization of HLM" Symmetry 16, no. 7: 901. https://doi.org/10.3390/sym16070901






