Comparing the Numerical Solution of Fractional Glucose–Insulin Systems Using Generalized Euler Method in Sense of Caputo, Caputo–Fabrizio and Atangana–Baleanu
Abstract
1. Introduction
2. Preliminaries and Definitions
3. Euler Method Involving Caputo, Caputo–Fabrizio, and Atangana–Baleanu Operators
4. Properties of the Solutions
4.1. Existence, Uniqueness, Non-Negativity, and Boundedness
4.2. Stability of the Proposed Model Locally and Globally
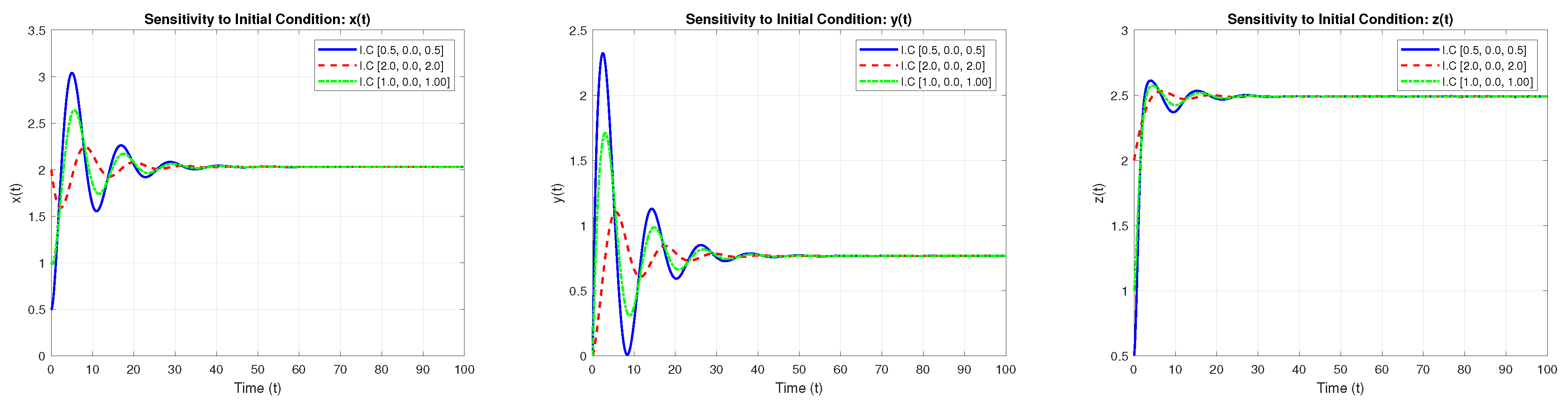
4.3. Sensitivity to Initial Values
5. Hyers-Ulam Stability
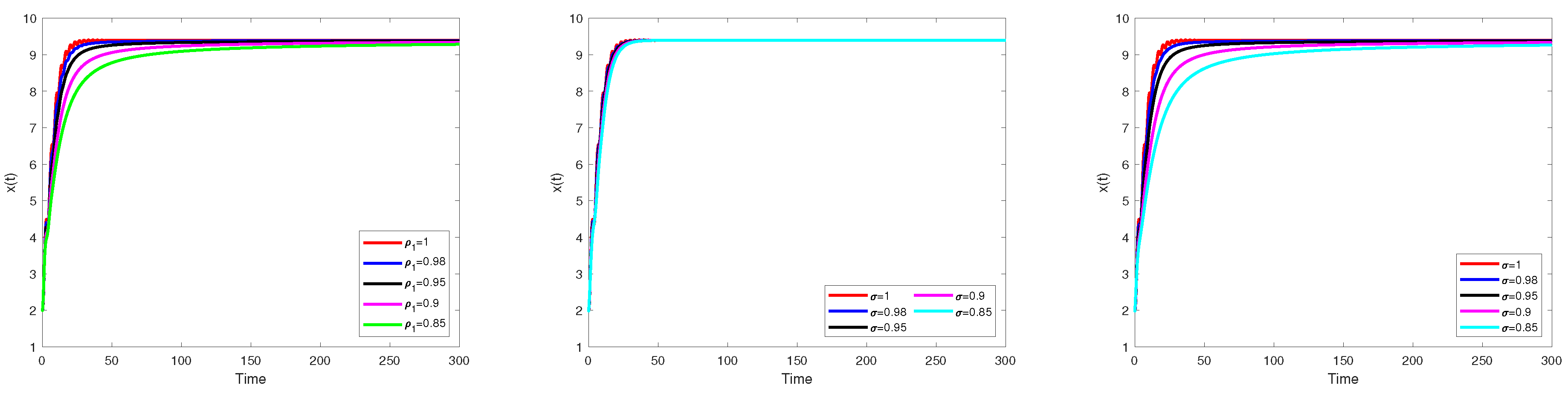
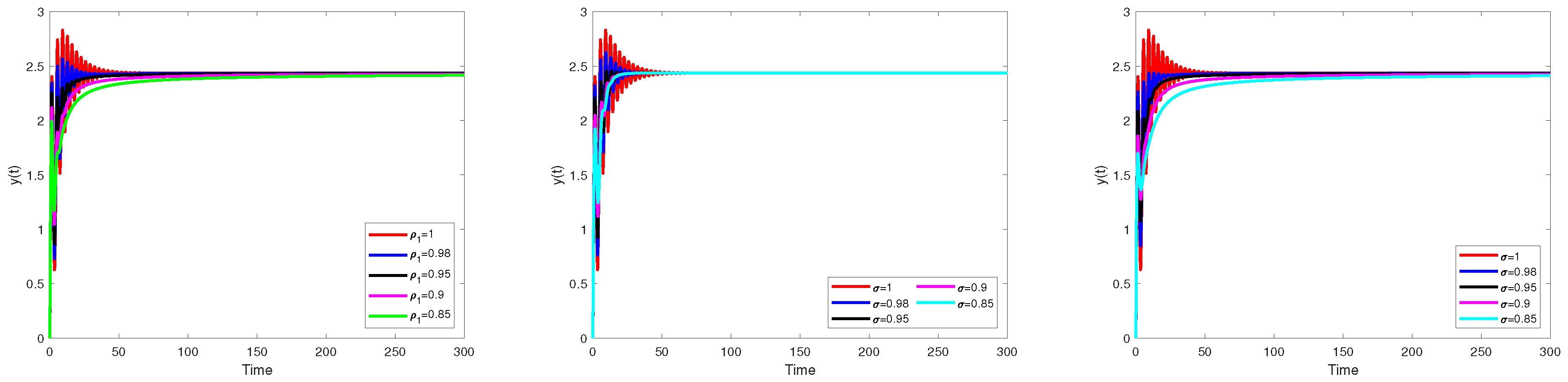
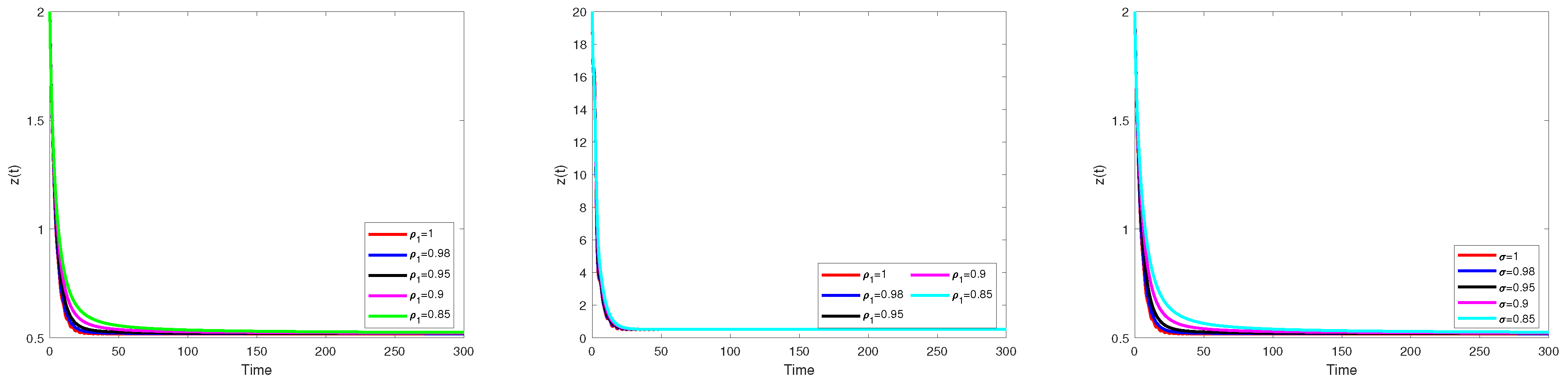
Numerical Simulation
6. Discussion
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ackerman, E.; Rosevear, J.W.; Mcguckin, W.F. A mathematical model of the glucose-tolerance test. Phys. Med. Biol. 1964, 9, 203–213. [Google Scholar] [CrossRef]
- Molnar, G.D.; Taylor, W.F.; Langworthy, A.L. Langworthy, Plasma immunoreactive insulin patterns in insulin-treated diabetics. Mayo Clin. Proc. 1972, 47, 709–719. [Google Scholar] [PubMed]
- Bajaj, J.S.; Rao, G.S. A mathematical model for insulin kinetics and its application to protein-deficient (malnutrition-related) Diabetes Mellitus (PDDM). J. Theoret. Biol. 1987, 129, 491–503. [Google Scholar] [CrossRef] [PubMed]
- Saber, S.; Bashier, E.B.M.; Alzahrani, S.M.; Noaman, I.A. A Mathematical Model of Glucose-Insulin Interaction with Time Delay. J. Appl. Computat. Math. 2018, 7, 416. [Google Scholar]
- Lenbury, Y.; Kumnungkit, K.; Novaprateep, B. Detection a slow-fast limit cycles in a model for electrical activity in the pancreatic β-cell. IMA J. Math. Appl. Med. Biol. 1996, 13, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Turner, R.C.; Holman, R.R.; Matthews, D.R.; Hockaday, T.D.R.; Peto, J. Insulin deficiency and insulin resistance interaction in diabeties: Estimation of their relative contribution by feedback analysis from basal plasma insulin and glucose concentrations. Metabolism 1979, 28, 1086–1096. [Google Scholar] [CrossRef]
- Lenbury, Y.; Ruktamatakul, S.; Amornsamarnkul, S. Modeling insulin kinetics: Responses to a single oral glucose adminstration or ambulatory-fed conditions. BioSystems 2001, 59, 15–25. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Singh, J.; Kumar, D.; Baleanu, D. On the analysis of fractional diabetes model with exponential law. Adv. Differ. Equ. 2018, 2018, 231. [Google Scholar] [CrossRef]
- Rocco, A.; West, B.J. Fractional calculus and the evolution of fractal phenomena. Physica A 1999, 265, 535. [Google Scholar] [CrossRef]
- Chaurasia, V.B.L.; Dubey, R.S.; Belgacem, F.B.M. Fractional radial diffusion equation analytical solution via hankel and Sumudu transforms. Math. Eng. Sci. Aerosp. 2012, 3, 179–188. [Google Scholar]
- Dubey, R.S.; Goswami, P.; Belgacem, F.B.M. Generalized time-fractional telegraph equation analytical solution by Sumudu and Fourier transforms. J. Fract. Calc. Appl. 2014, 5, 52–58. [Google Scholar]
- Matouk, A.E. Chaos, feedback control and synchronization of a fractional-order modified autonomous Van der Pol-Duffing circuit. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 975–986. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; El-Mesiry, A.; El-Saka, H. On the fractional-order logistic equation. Appl. Math. Lett. 2007, 20, 817–823. [Google Scholar] [CrossRef]
- Agarwal, R.P.; El-Sayed, A.M.A.; Salman, S.M. Fractional-order Chua’s system: Discretization, bifurcation and chaos. Adv. Differ. Equ. 2013, 2013, 320. [Google Scholar] [CrossRef]
- Alshehri, M.H.; Duraihem, F.Z.; Alalyani, A.; Saber, S. A Caputo (discretization) fractional-order model of glucose-insulin interaction: Numerical solution and comparisons with experimental data. J. Taibah Univ. Sci. 2021, 15, 26–36. [Google Scholar] [CrossRef]
- Alshehri, M.H.; Saber, S.; Duraihem, F.Z. Dynamical analysis of fractional-order of IVGTT glucose–insulin interaction. Int. J. Nonlin. Sci. Num. 2023, 24, 1123–1140. [Google Scholar] [CrossRef]
- Saber, S. Control of chaos in the Burke-Shaw system of fractal-fractional order in the sense of Caputo-Fabrizio. J. Appl. Math. Comput. Mech. 2024, 23, 83–96. [Google Scholar] [CrossRef]
- Ahmed, K.I.A.; Adam, H.D.S.; Almutairi, N.; Saber, S. Analytical solutions for a class of variable-order fractional Liu system under time-dependent variable coefficients. Results Phys. 2024, 56, 107311. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S. Existence of chaos and the approximate solution of the Lorenz–Lü–Chen system with the Caputo fractional operator. AIP Adv. 2024, 14, 015112. [Google Scholar] [CrossRef]
- Ahmed, K.I.A.; Adam, H.D.S.; Youssif, M.Y.; Saber, S. Different strategies for diabetes by mathematical modeling: Modified Minimal Model. Alex. Eng. J. 2023, 80, 74–87. [Google Scholar] [CrossRef]
- Ahmed, K.I.A.; Adam, H.D.S.; Youssif, M.Y.; Saber, S. Different strategies for diabetes by mathematical modeling: Applications of fractal–fractional derivatives in the sense of Atangana–Baleanu. Results Phys. 2023, 52, 106892. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S.; Hijaz, A. The fractal-fractional Atangana-Baleanu operator for pneumonia disease: Stability, statistical and numerical analyses. AIMS Math. 2023, 8, 29382–29410. [Google Scholar] [CrossRef]
- Choi, S.K.; Kang, B.; Koo, N. Stability for Caputo fractional differential systems. Abstr. Appl. Anal. 2014, 2014, 631419. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Li, H.L.; Zhang, L.; Hu, C.; Jiang, Y.L.; Teng, Z. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 2017, 54, 435–449. [Google Scholar] [CrossRef]
- Atangana, A.; Alabaraoye, E. Solving a system of fractional partial differential equations arising in the model of HIV infection of CD4+ cells and attractor one-dimensional Keller-Segel equations. Adv. Differ. Equ. 2013, 2013, 94. [Google Scholar] [CrossRef]
- Saber, S.; Alalyani, A. Stability analysis and numerical simulations of IVGTT glucose-insulin interaction models with two time delays. Math. Model. Anal. 2022, 27, 383–407. [Google Scholar] [CrossRef]
- Alalyani, A.; Saber, S. Stability analysis and numerical simulations of the fractional COVID-19 pandemic model. Int. J. Nonlin. Sci. Num. 2023, 24, 989–1002. [Google Scholar] [CrossRef]
- Ahmeda, E.; Elgazzar, A.S. On fractional order differential equations model for nonlocal epidemics. Physica A 2007, 379, 607–614. [Google Scholar] [CrossRef]
- Ucar, E.; Özdemir, N.; Altun, E. Fractional order model of immune cells influenced by cancer cells. Math. Model. Nat. Phenom. 2019, 14, 308. [Google Scholar] [CrossRef]
- Moore, E.J.; Sirisubtawee, S.; Koonprasert, S. A Caputo–Fabrizio fractional differential equation model for HIV/AIDS with treatment compartment. Adv. Differ. Equ. 2019, 2019, 200. [Google Scholar] [CrossRef]
- Carvalho, A.R.; Pinto, C.M.; Baleanu, D. HIV/HCV coinfection model: A fractional-order perspective for the effect of the HIV viral load. Adv. Differ. Equ. 2018, 2018, 2. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. The finite difference methods for fractional ordinary differential equations. Num. Func. Anal. Opt. 2013, 34, 149–179. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Saber, S.; Alghamdi, A.M.; Ahmed, G.A.; Alshehri, K.M. Mathematical modelling and optimal control of pneumonia disease in sheep and goats in Al-Baha region with cost-effective strategies. AIMS Math. 2022, 7, 12011–12049. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S. Application of a time-fractal fractional derivative with a power-law kernel to the Burke-Shaw system based on Newton’s interpolation polynomials. MethodsX 2023, 2023, 102510. [Google Scholar] [CrossRef] [PubMed]
- Almutairi, N.; Saber, S. On chaos control of nonlinear fractional Newton-Leipnik system via fractional Caputo-Fabrizio derivatives. Sci. Rep. 2023, 13, 22726. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.B.; Jang, B. A High-Order Predictor-Corrector Method for Solving Nonlinear Differential Equations of Fractional Order. Fract. Calc. Appl. Anal. 2017, 20, 447–476. [Google Scholar] [CrossRef]
- Boukhouima, A.; Hattaf, K.; Yousfi, N. Dynamics of a fractional order HIV infection model with specific functional response and cure rate. Int. J. Differ. Equ. 2017, 2017, 8372140. [Google Scholar] [CrossRef]
- Hurwitz, A. On the conditions under which an equation has only roots with negative real parts. In Selected Papers on Mathematical Trends in Control Theory; Ballman, R.T., Ed.; Dover: New York, NY, USA, 1964. [Google Scholar]
- Ulam, S.M. A Collection of Mathematical Problems; Interscience Publishing: New York, NY, USA, 1960. [Google Scholar]
- Ulam, S.M. Problems in Modern Mathematics; Courier Corporation: North Chelmsford, MA, USA, 2004. [Google Scholar]
- He, S.; Wang, H.; Sun, K. Solutions and memory effect of fractional-order chaotic system: A review. Chin. Phys. B 2022, 31, 060501. [Google Scholar] [CrossRef]
| Parameters | Description |
|---|---|
| The rate at which insulin concentrations increase as blood glucose levels rise | |
| Insulin reduction rate | |
| Loss of -cells rate | |
| Glucose level decreases as a result of insulin production | |
| The rate at which -cells divide in response to blood glucose | |
| -cell growth rate due to dividing and non-dividing cells | |
| The rate at which -cells decrease as a result of its current level | |
| An increase in x at a constant rate | |
| An increase in y at a constant rate | |
| T | The total number of dividing and non-dividing cells |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhazmi, M. Comparing the Numerical Solution of Fractional Glucose–Insulin Systems Using Generalized Euler Method in Sense of Caputo, Caputo–Fabrizio and Atangana–Baleanu. Symmetry 2024, 16, 919. https://doi.org/10.3390/sym16070919
Alhazmi M. Comparing the Numerical Solution of Fractional Glucose–Insulin Systems Using Generalized Euler Method in Sense of Caputo, Caputo–Fabrizio and Atangana–Baleanu. Symmetry. 2024; 16(7):919. https://doi.org/10.3390/sym16070919
Chicago/Turabian StyleAlhazmi, Muflih. 2024. "Comparing the Numerical Solution of Fractional Glucose–Insulin Systems Using Generalized Euler Method in Sense of Caputo, Caputo–Fabrizio and Atangana–Baleanu" Symmetry 16, no. 7: 919. https://doi.org/10.3390/sym16070919
APA StyleAlhazmi, M. (2024). Comparing the Numerical Solution of Fractional Glucose–Insulin Systems Using Generalized Euler Method in Sense of Caputo, Caputo–Fabrizio and Atangana–Baleanu. Symmetry, 16(7), 919. https://doi.org/10.3390/sym16070919





