Comparing the Numerical Solution of Fractional Glucose–Insulin Systems Using Generalized Euler Method in Sense of Caputo, Caputo–Fabrizio and Atangana–Baleanu
Abstract
:1. Introduction
2. Preliminaries and Definitions
3. Euler Method Involving Caputo, Caputo–Fabrizio, and Atangana–Baleanu Operators
4. Properties of the Solutions
4.1. Existence, Uniqueness, Non-Negativity, and Boundedness
4.2. Stability of the Proposed Model Locally and Globally
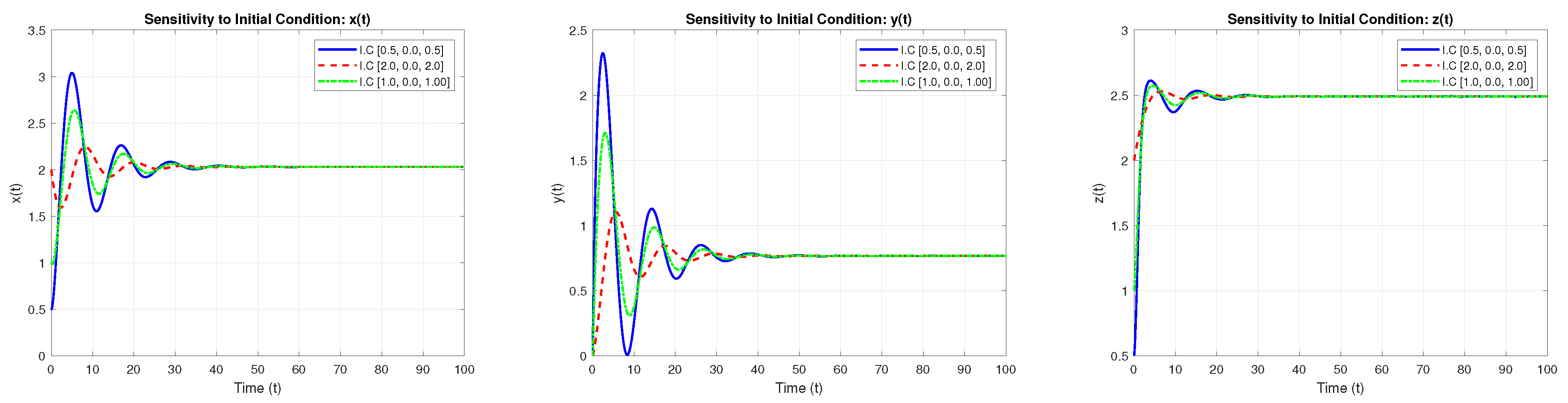
4.3. Sensitivity to Initial Values
5. Hyers-Ulam Stability
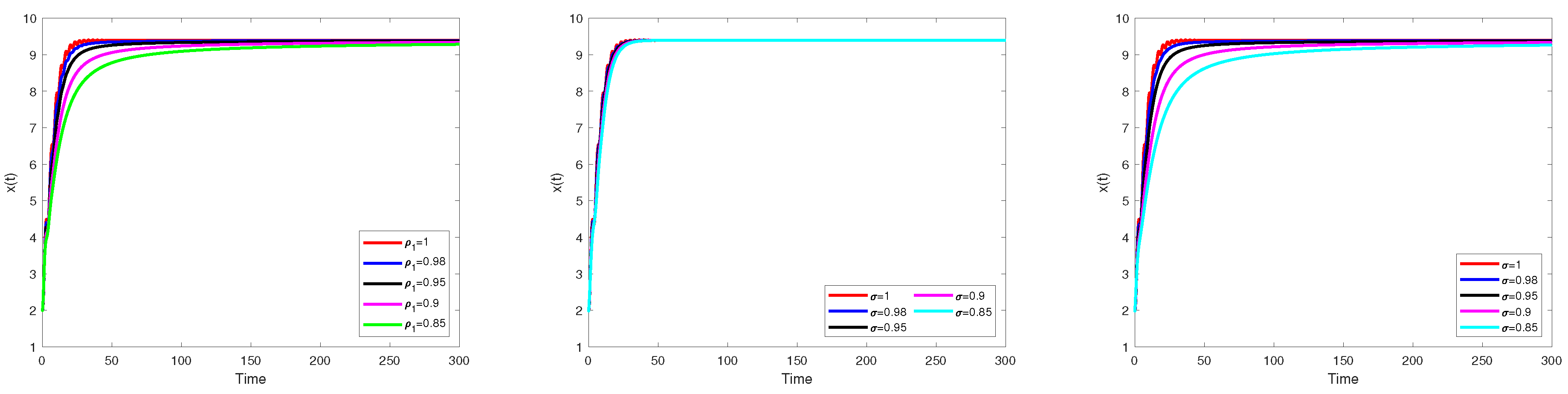
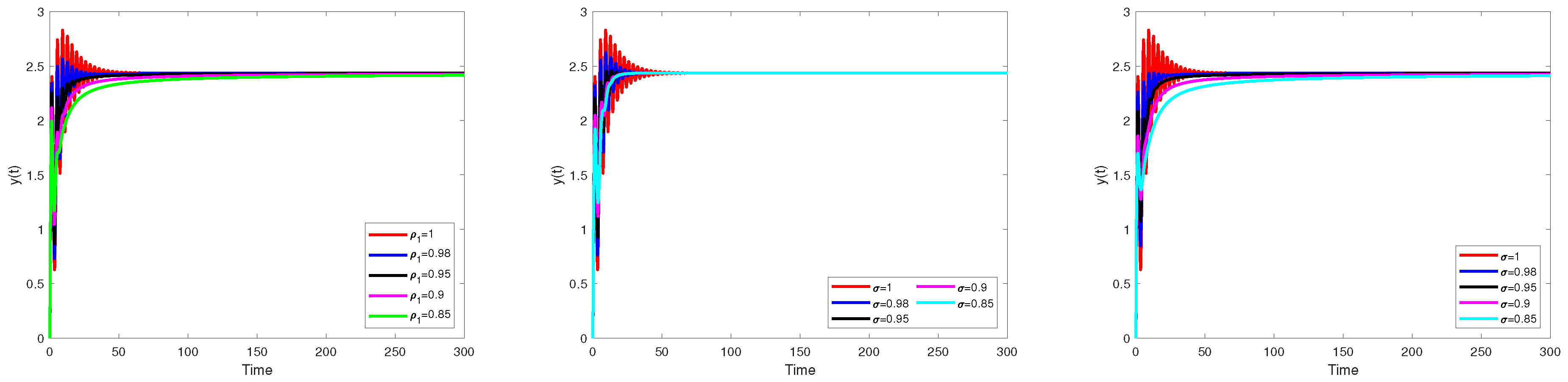
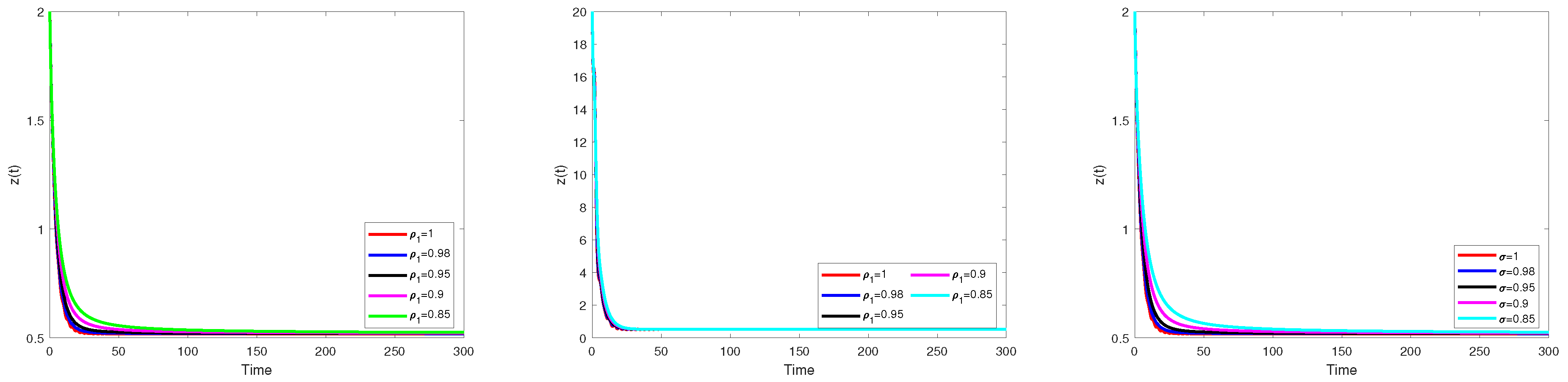
Numerical Simulation
6. Discussion
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ackerman, E.; Rosevear, J.W.; Mcguckin, W.F. A mathematical model of the glucose-tolerance test. Phys. Med. Biol. 1964, 9, 203–213. [Google Scholar] [CrossRef]
- Molnar, G.D.; Taylor, W.F.; Langworthy, A.L. Langworthy, Plasma immunoreactive insulin patterns in insulin-treated diabetics. Mayo Clin. Proc. 1972, 47, 709–719. [Google Scholar] [PubMed]
- Bajaj, J.S.; Rao, G.S. A mathematical model for insulin kinetics and its application to protein-deficient (malnutrition-related) Diabetes Mellitus (PDDM). J. Theoret. Biol. 1987, 129, 491–503. [Google Scholar] [CrossRef] [PubMed]
- Saber, S.; Bashier, E.B.M.; Alzahrani, S.M.; Noaman, I.A. A Mathematical Model of Glucose-Insulin Interaction with Time Delay. J. Appl. Computat. Math. 2018, 7, 416. [Google Scholar]
- Lenbury, Y.; Kumnungkit, K.; Novaprateep, B. Detection a slow-fast limit cycles in a model for electrical activity in the pancreatic β-cell. IMA J. Math. Appl. Med. Biol. 1996, 13, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Turner, R.C.; Holman, R.R.; Matthews, D.R.; Hockaday, T.D.R.; Peto, J. Insulin deficiency and insulin resistance interaction in diabeties: Estimation of their relative contribution by feedback analysis from basal plasma insulin and glucose concentrations. Metabolism 1979, 28, 1086–1096. [Google Scholar] [CrossRef]
- Lenbury, Y.; Ruktamatakul, S.; Amornsamarnkul, S. Modeling insulin kinetics: Responses to a single oral glucose adminstration or ambulatory-fed conditions. BioSystems 2001, 59, 15–25. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Singh, J.; Kumar, D.; Baleanu, D. On the analysis of fractional diabetes model with exponential law. Adv. Differ. Equ. 2018, 2018, 231. [Google Scholar] [CrossRef]
- Rocco, A.; West, B.J. Fractional calculus and the evolution of fractal phenomena. Physica A 1999, 265, 535. [Google Scholar] [CrossRef]
- Chaurasia, V.B.L.; Dubey, R.S.; Belgacem, F.B.M. Fractional radial diffusion equation analytical solution via hankel and Sumudu transforms. Math. Eng. Sci. Aerosp. 2012, 3, 179–188. [Google Scholar]
- Dubey, R.S.; Goswami, P.; Belgacem, F.B.M. Generalized time-fractional telegraph equation analytical solution by Sumudu and Fourier transforms. J. Fract. Calc. Appl. 2014, 5, 52–58. [Google Scholar]
- Matouk, A.E. Chaos, feedback control and synchronization of a fractional-order modified autonomous Van der Pol-Duffing circuit. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 975–986. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; El-Mesiry, A.; El-Saka, H. On the fractional-order logistic equation. Appl. Math. Lett. 2007, 20, 817–823. [Google Scholar] [CrossRef]
- Agarwal, R.P.; El-Sayed, A.M.A.; Salman, S.M. Fractional-order Chua’s system: Discretization, bifurcation and chaos. Adv. Differ. Equ. 2013, 2013, 320. [Google Scholar] [CrossRef]
- Alshehri, M.H.; Duraihem, F.Z.; Alalyani, A.; Saber, S. A Caputo (discretization) fractional-order model of glucose-insulin interaction: Numerical solution and comparisons with experimental data. J. Taibah Univ. Sci. 2021, 15, 26–36. [Google Scholar] [CrossRef]
- Alshehri, M.H.; Saber, S.; Duraihem, F.Z. Dynamical analysis of fractional-order of IVGTT glucose–insulin interaction. Int. J. Nonlin. Sci. Num. 2023, 24, 1123–1140. [Google Scholar] [CrossRef]
- Saber, S. Control of chaos in the Burke-Shaw system of fractal-fractional order in the sense of Caputo-Fabrizio. J. Appl. Math. Comput. Mech. 2024, 23, 83–96. [Google Scholar] [CrossRef]
- Ahmed, K.I.A.; Adam, H.D.S.; Almutairi, N.; Saber, S. Analytical solutions for a class of variable-order fractional Liu system under time-dependent variable coefficients. Results Phys. 2024, 56, 107311. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S. Existence of chaos and the approximate solution of the Lorenz–Lü–Chen system with the Caputo fractional operator. AIP Adv. 2024, 14, 015112. [Google Scholar] [CrossRef]
- Ahmed, K.I.A.; Adam, H.D.S.; Youssif, M.Y.; Saber, S. Different strategies for diabetes by mathematical modeling: Modified Minimal Model. Alex. Eng. J. 2023, 80, 74–87. [Google Scholar] [CrossRef]
- Ahmed, K.I.A.; Adam, H.D.S.; Youssif, M.Y.; Saber, S. Different strategies for diabetes by mathematical modeling: Applications of fractal–fractional derivatives in the sense of Atangana–Baleanu. Results Phys. 2023, 52, 106892. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S.; Hijaz, A. The fractal-fractional Atangana-Baleanu operator for pneumonia disease: Stability, statistical and numerical analyses. AIMS Math. 2023, 8, 29382–29410. [Google Scholar] [CrossRef]
- Choi, S.K.; Kang, B.; Koo, N. Stability for Caputo fractional differential systems. Abstr. Appl. Anal. 2014, 2014, 631419. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Li, H.L.; Zhang, L.; Hu, C.; Jiang, Y.L.; Teng, Z. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 2017, 54, 435–449. [Google Scholar] [CrossRef]
- Atangana, A.; Alabaraoye, E. Solving a system of fractional partial differential equations arising in the model of HIV infection of CD4+ cells and attractor one-dimensional Keller-Segel equations. Adv. Differ. Equ. 2013, 2013, 94. [Google Scholar] [CrossRef]
- Saber, S.; Alalyani, A. Stability analysis and numerical simulations of IVGTT glucose-insulin interaction models with two time delays. Math. Model. Anal. 2022, 27, 383–407. [Google Scholar] [CrossRef]
- Alalyani, A.; Saber, S. Stability analysis and numerical simulations of the fractional COVID-19 pandemic model. Int. J. Nonlin. Sci. Num. 2023, 24, 989–1002. [Google Scholar] [CrossRef]
- Ahmeda, E.; Elgazzar, A.S. On fractional order differential equations model for nonlocal epidemics. Physica A 2007, 379, 607–614. [Google Scholar] [CrossRef]
- Ucar, E.; Özdemir, N.; Altun, E. Fractional order model of immune cells influenced by cancer cells. Math. Model. Nat. Phenom. 2019, 14, 308. [Google Scholar] [CrossRef]
- Moore, E.J.; Sirisubtawee, S.; Koonprasert, S. A Caputo–Fabrizio fractional differential equation model for HIV/AIDS with treatment compartment. Adv. Differ. Equ. 2019, 2019, 200. [Google Scholar] [CrossRef]
- Carvalho, A.R.; Pinto, C.M.; Baleanu, D. HIV/HCV coinfection model: A fractional-order perspective for the effect of the HIV viral load. Adv. Differ. Equ. 2018, 2018, 2. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. The finite difference methods for fractional ordinary differential equations. Num. Func. Anal. Opt. 2013, 34, 149–179. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Saber, S.; Alghamdi, A.M.; Ahmed, G.A.; Alshehri, K.M. Mathematical modelling and optimal control of pneumonia disease in sheep and goats in Al-Baha region with cost-effective strategies. AIMS Math. 2022, 7, 12011–12049. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S. Application of a time-fractal fractional derivative with a power-law kernel to the Burke-Shaw system based on Newton’s interpolation polynomials. MethodsX 2023, 2023, 102510. [Google Scholar] [CrossRef] [PubMed]
- Almutairi, N.; Saber, S. On chaos control of nonlinear fractional Newton-Leipnik system via fractional Caputo-Fabrizio derivatives. Sci. Rep. 2023, 13, 22726. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.B.; Jang, B. A High-Order Predictor-Corrector Method for Solving Nonlinear Differential Equations of Fractional Order. Fract. Calc. Appl. Anal. 2017, 20, 447–476. [Google Scholar] [CrossRef]
- Boukhouima, A.; Hattaf, K.; Yousfi, N. Dynamics of a fractional order HIV infection model with specific functional response and cure rate. Int. J. Differ. Equ. 2017, 2017, 8372140. [Google Scholar] [CrossRef]
- Hurwitz, A. On the conditions under which an equation has only roots with negative real parts. In Selected Papers on Mathematical Trends in Control Theory; Ballman, R.T., Ed.; Dover: New York, NY, USA, 1964. [Google Scholar]
- Ulam, S.M. A Collection of Mathematical Problems; Interscience Publishing: New York, NY, USA, 1960. [Google Scholar]
- Ulam, S.M. Problems in Modern Mathematics; Courier Corporation: North Chelmsford, MA, USA, 2004. [Google Scholar]
- He, S.; Wang, H.; Sun, K. Solutions and memory effect of fractional-order chaotic system: A review. Chin. Phys. B 2022, 31, 060501. [Google Scholar] [CrossRef]
| Parameters | Description |
|---|---|
| The rate at which insulin concentrations increase as blood glucose levels rise | |
| Insulin reduction rate | |
| Loss of -cells rate | |
| Glucose level decreases as a result of insulin production | |
| The rate at which -cells divide in response to blood glucose | |
| -cell growth rate due to dividing and non-dividing cells | |
| The rate at which -cells decrease as a result of its current level | |
| An increase in x at a constant rate | |
| An increase in y at a constant rate | |
| T | The total number of dividing and non-dividing cells |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhazmi, M. Comparing the Numerical Solution of Fractional Glucose–Insulin Systems Using Generalized Euler Method in Sense of Caputo, Caputo–Fabrizio and Atangana–Baleanu. Symmetry 2024, 16, 919. https://doi.org/10.3390/sym16070919
Alhazmi M. Comparing the Numerical Solution of Fractional Glucose–Insulin Systems Using Generalized Euler Method in Sense of Caputo, Caputo–Fabrizio and Atangana–Baleanu. Symmetry. 2024; 16(7):919. https://doi.org/10.3390/sym16070919
Chicago/Turabian StyleAlhazmi, Muflih. 2024. "Comparing the Numerical Solution of Fractional Glucose–Insulin Systems Using Generalized Euler Method in Sense of Caputo, Caputo–Fabrizio and Atangana–Baleanu" Symmetry 16, no. 7: 919. https://doi.org/10.3390/sym16070919
APA StyleAlhazmi, M. (2024). Comparing the Numerical Solution of Fractional Glucose–Insulin Systems Using Generalized Euler Method in Sense of Caputo, Caputo–Fabrizio and Atangana–Baleanu. Symmetry, 16(7), 919. https://doi.org/10.3390/sym16070919





