The Pedal Curves Generated by Alternative Frame Vectors and Their Smarandache Curves
Abstract
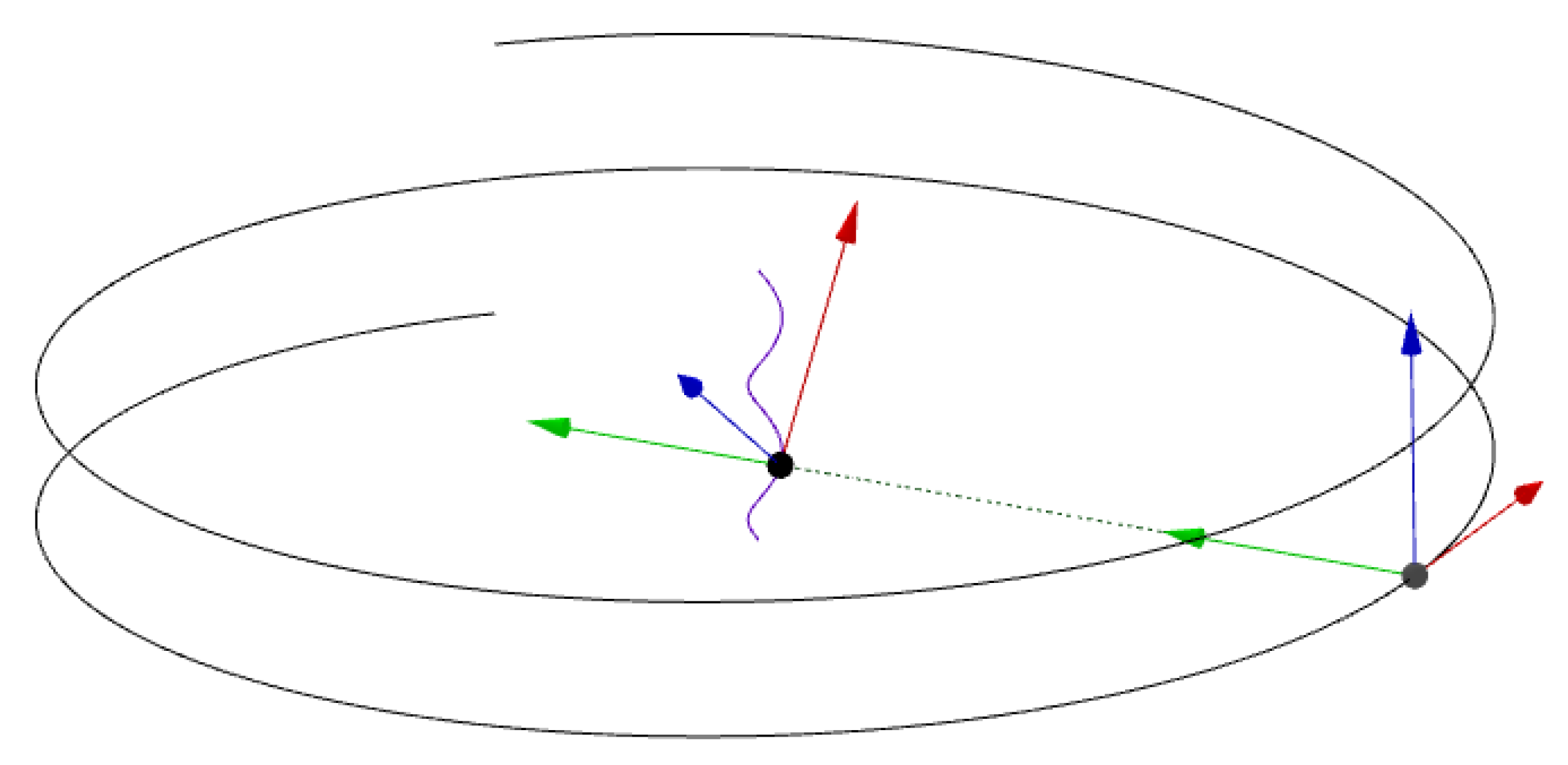
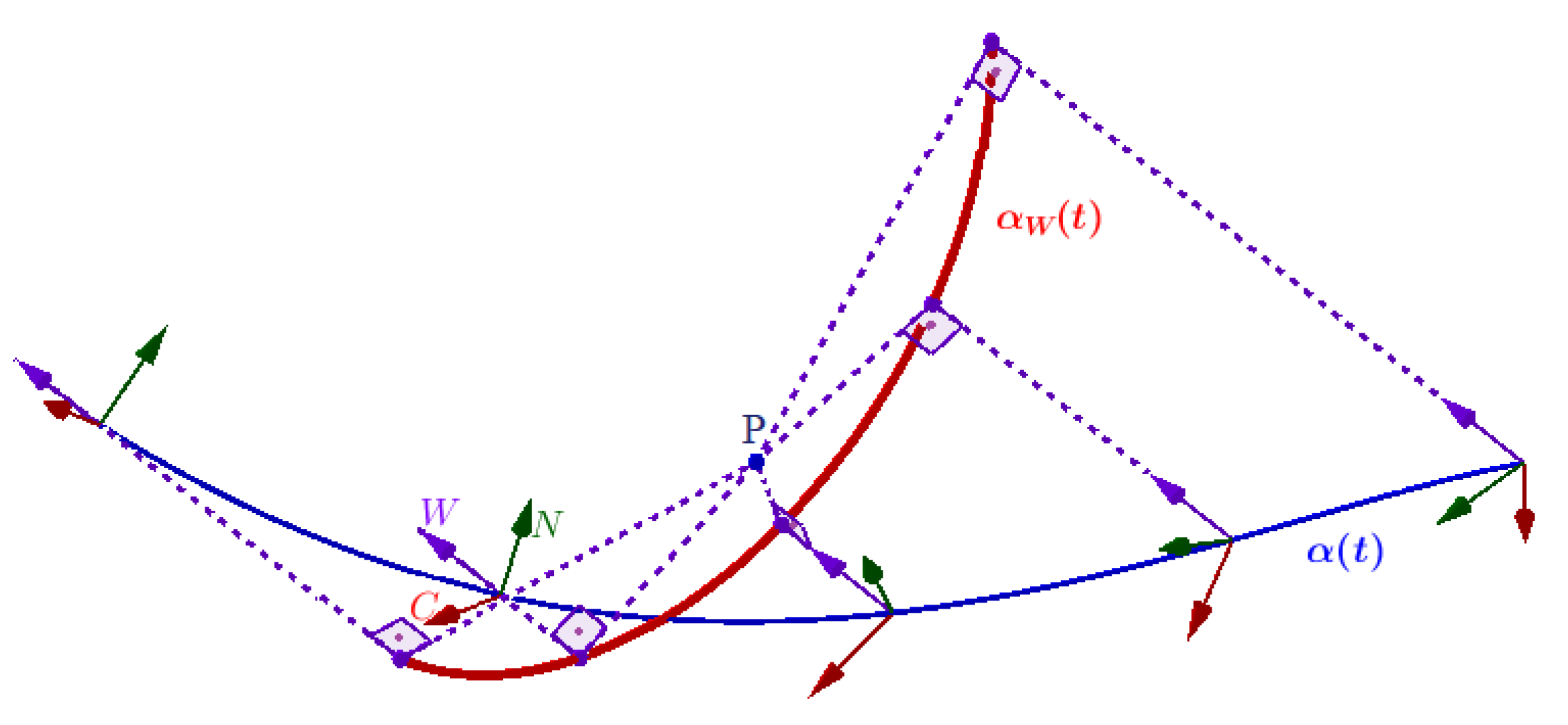
1. Introduction
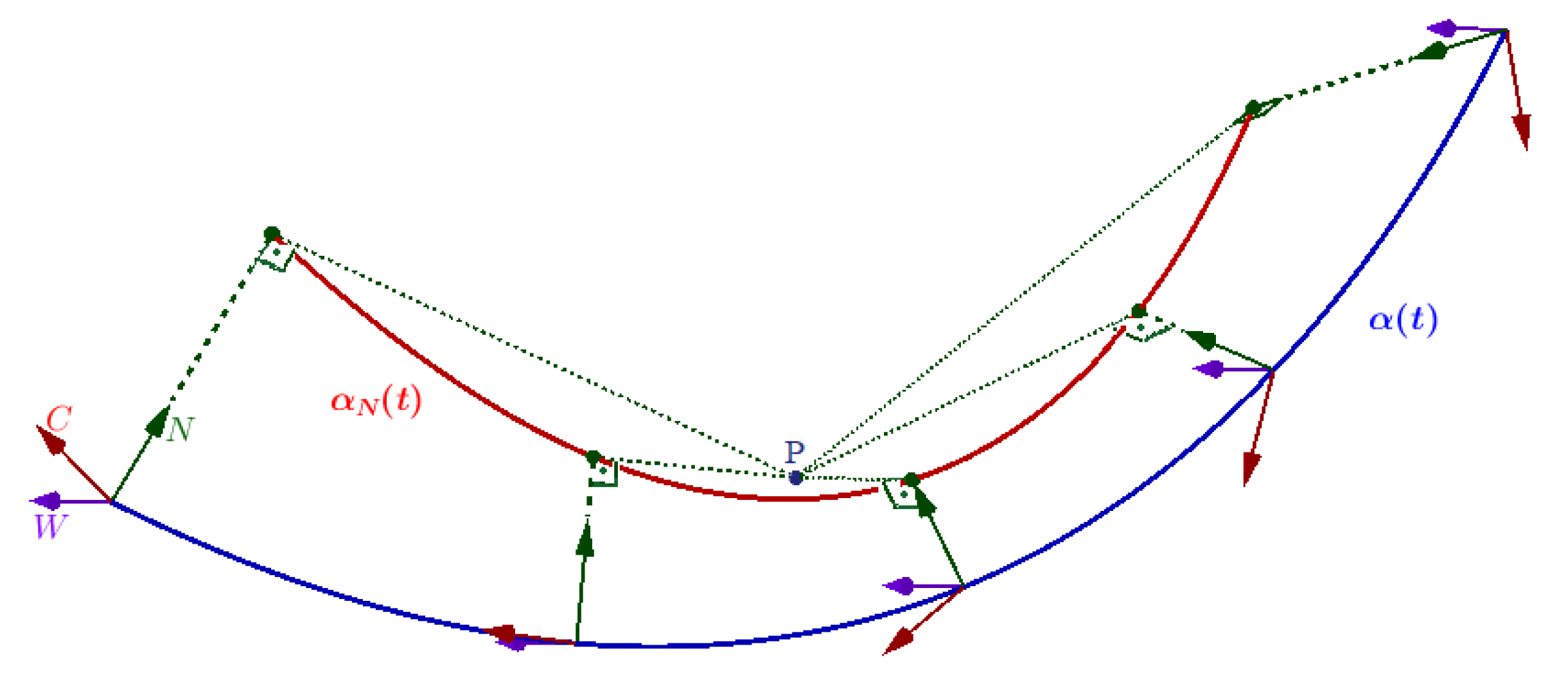
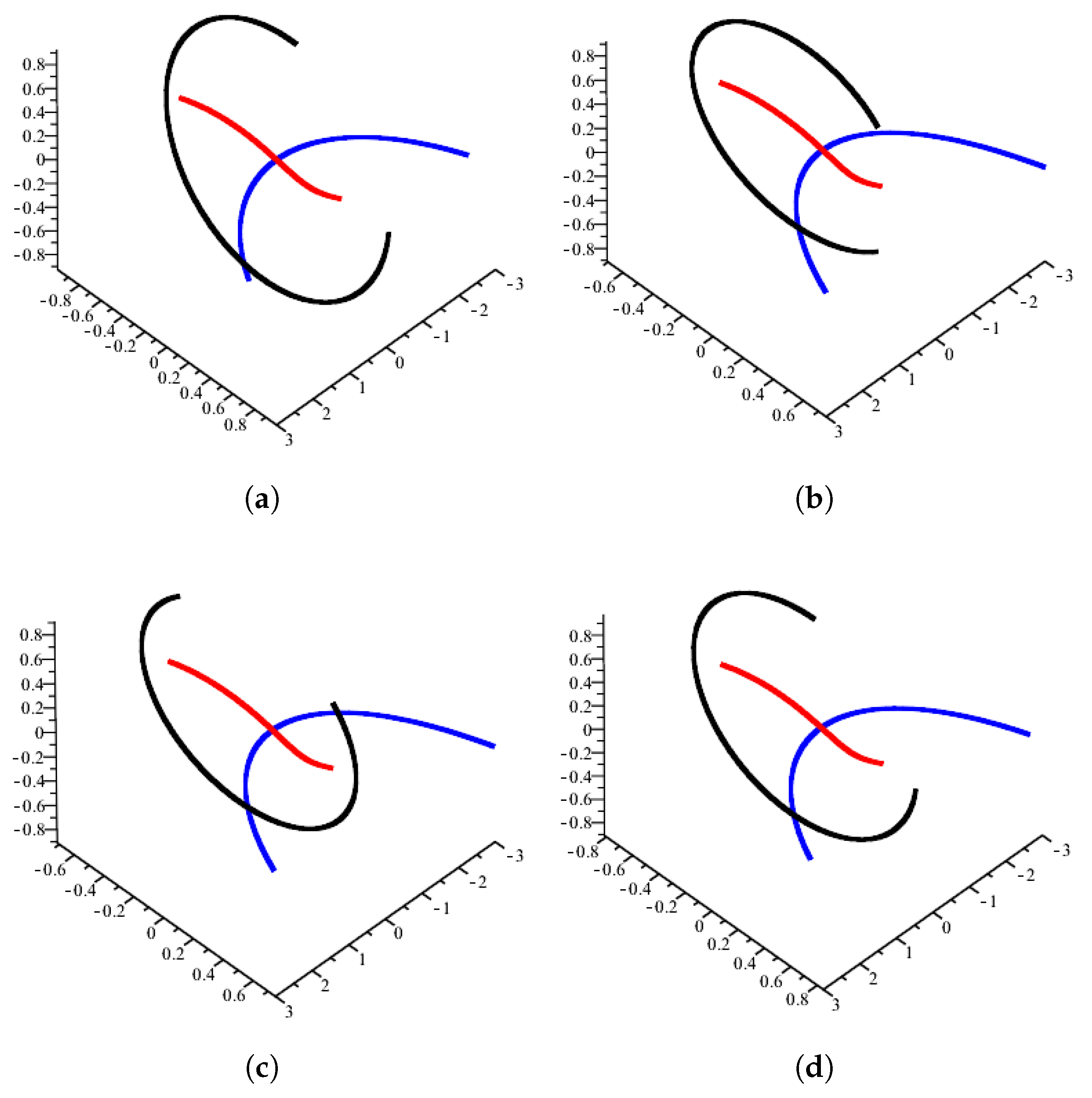
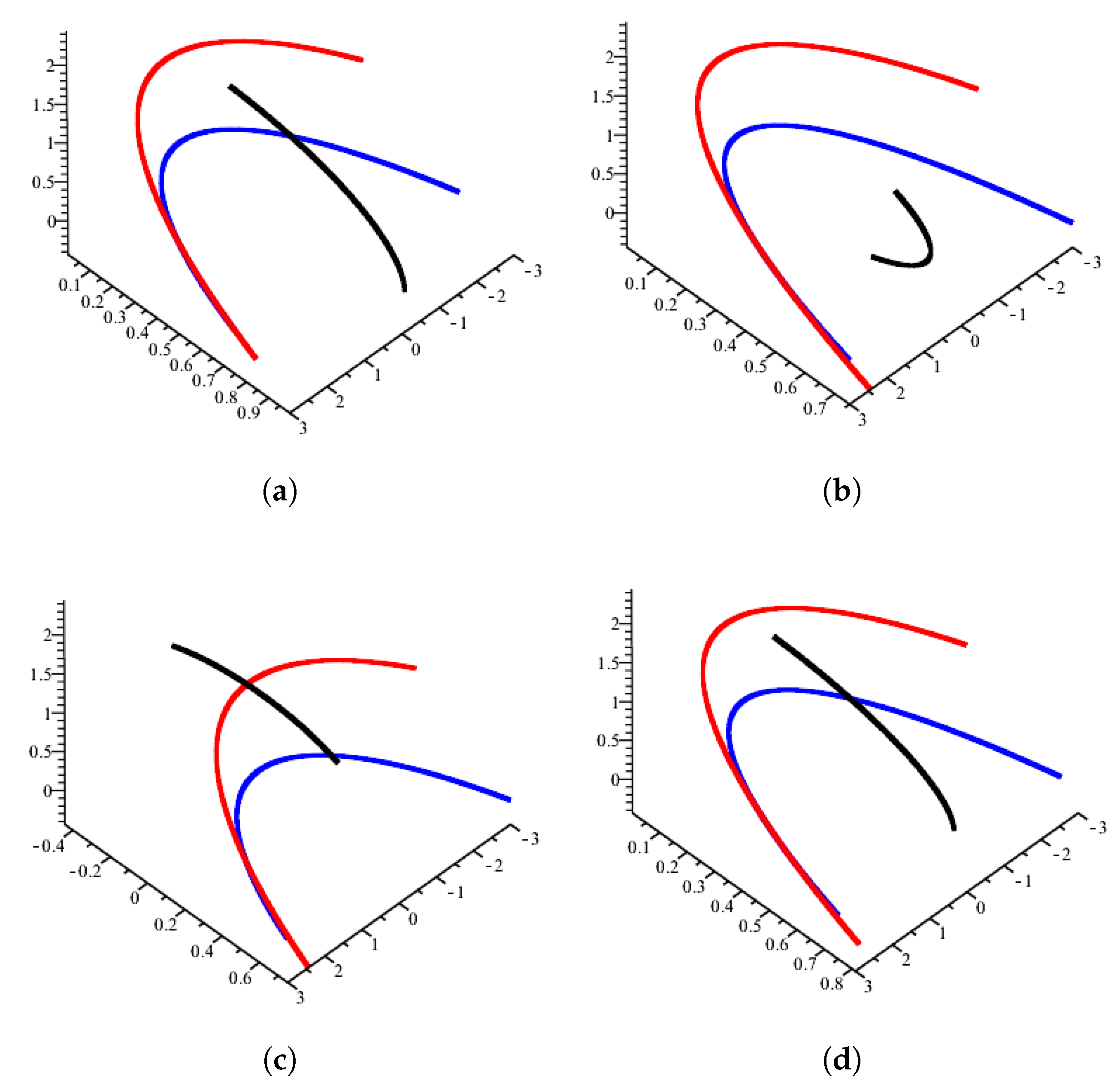
2. The Alternative -Pedal Curve and Its Smarandache Curves
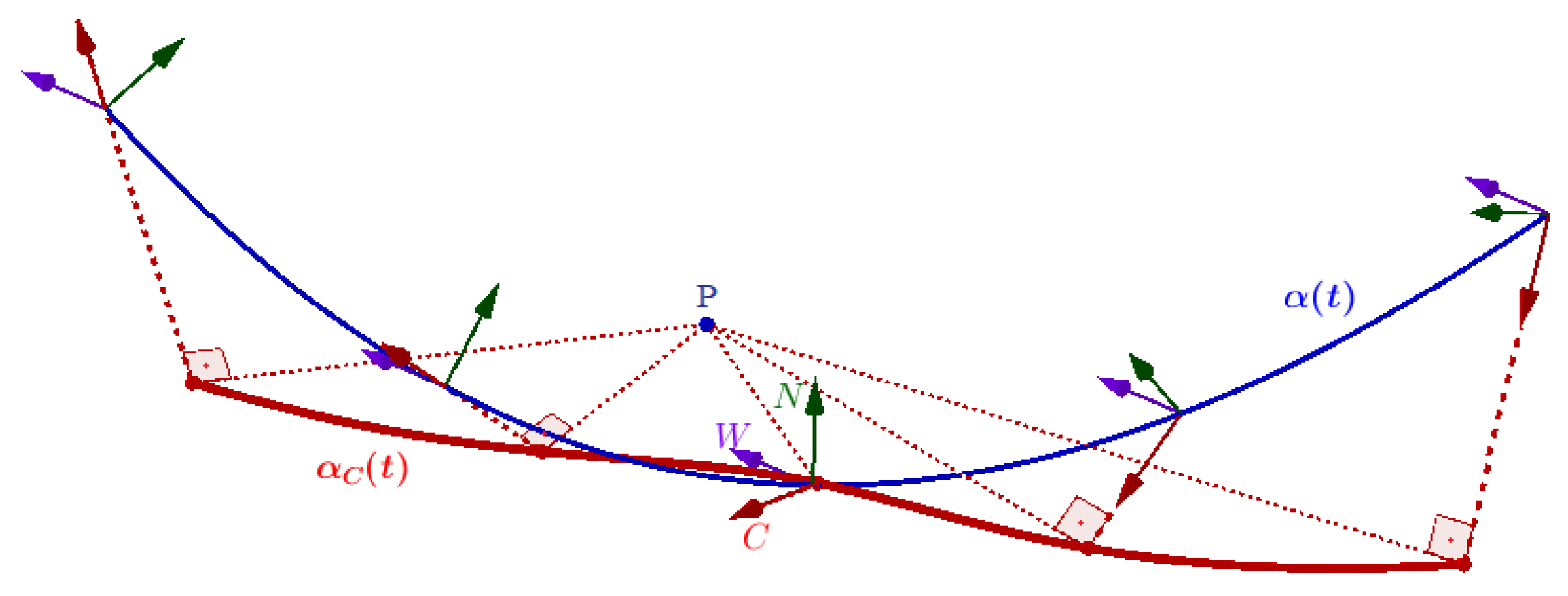
3. The Alternative -Pedal Curve and Its Smarandache Curves
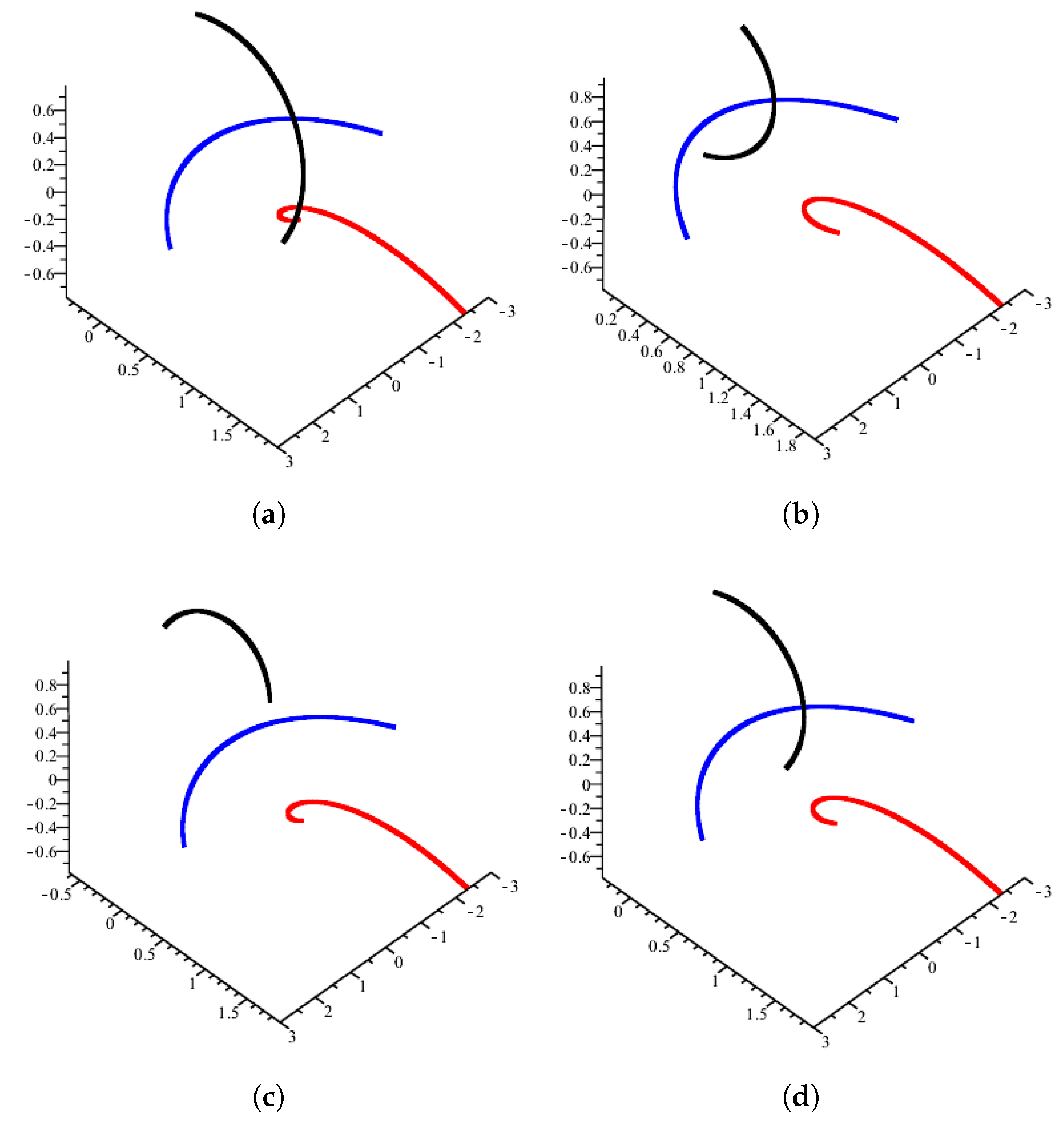
4. The Alternative -Pedal Curve and Its Smarandache Curves
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Monterde, J. Salkowski curves revisited: A family of curves with constant curvature and non-constant torsion. Comput. Aided Geom. Des. 2009, 26, 271–278. [Google Scholar] [CrossRef]
- Mazlum, S.G.; Şenyurt, S.; Bektaş, M. Salkowski curves and their modified orthogonal frames in E3. J. New Theory 2022, 40, 12–26. [Google Scholar] [CrossRef]
- Li, M.; Yao, K.; Li, P.; Pei, D. Pedal curves of non-lightlike curves in Minkowski 3-space. Symmetry 2022, 14, 59. [Google Scholar] [CrossRef]
- Şenyurt, S.; Canlı, D.; Ayvacı, K.H. Associated curves from a different point of view in E3. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2022, 71, 826–845. [Google Scholar] [CrossRef]
- Ali, A.T. Special Smarandache curves in the Euclidean space. Int. J. Math. Combin. 2010, 2, 30–36. [Google Scholar]
- Turgut, M.; Yılmaz, S. Smarandache curves in Minkowski space-time. Int. J. Math. Combin. 2008, 3, 51–55. [Google Scholar]
- Şenyurt, S.; Sivas, S. An application of Smarandache curve. Ordu Univ. J. Sci. Tech. 2013, 3, 46–60. [Google Scholar]
- Ceylan, A.Y.; Kara, M. On pedal and contrapedal curves of Bezier curves. Konuralp J. Math. 2021, 9, 217–221. [Google Scholar]
- As, E.; Sarıoğlugil, A. On the pedal surfaces of 2-d surfaces with the constant support function in E4. Pure Math. Sci. 2015, 4, 105–120. [Google Scholar] [CrossRef]
- Carmo, M.P. Differential Geometry of Curves and Surfaces; Prentice Hall: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Kuruoğlu, N.; Sarıoğlugil, A. On the characteristic properties of the a-Pedal surfaces in the euclidean space E3. Commun. Fac. Sci. Univ. Ank. Series A 1993, 42, 19–25. [Google Scholar] [CrossRef]
- Tuncer, O.O.; Ceyhan, H.; Gök, I.; Ekmekci, F.N. Notes on pedal and contrapedal curves of fronts in the Euclidean plane. Math. Methods Appl. Sci. 2018, 41, 5096–5111. [Google Scholar] [CrossRef]
- Li, Y.; Pei, D. Pedal curves of fronts in the sphere. J. Nonlinear Sci. Appl. 2016, 9, 836–844. [Google Scholar] [CrossRef]
- Li, Y.; Pei, D. Pedal curves of frontals in the Euclidean plane. Math. Methods Appl. Sci. 2018, 41, 1988–1997. [Google Scholar] [CrossRef]
- Li, Y.; Tuncer, O.O. On (contra)pedals and (anti)orthotomics of frontals in de Sitter 2-space. Math. Methods Appl. Sci. 2023, 46, 11157–11171. [Google Scholar] [CrossRef]
- Şenyurt, S.; Kaya, F.E.; Canlı, D. Pedal curves obtained from Frenet vector of a space curve and Smarandache curves belonging to these curves. AIMS Math. 2024, 9, 20136–20162. [Google Scholar] [CrossRef]
- Abbena, E.; Salamon, S.; Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica; Chapman and Hall/CRC: New York, NY, USA, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Canlı, D.; Şenyurt, S.; Ertem Kaya, F.; Grilli, L. The Pedal Curves Generated by Alternative Frame Vectors and Their Smarandache Curves. Symmetry 2024, 16, 1012. https://doi.org/10.3390/sym16081012
Canlı D, Şenyurt S, Ertem Kaya F, Grilli L. The Pedal Curves Generated by Alternative Frame Vectors and Their Smarandache Curves. Symmetry. 2024; 16(8):1012. https://doi.org/10.3390/sym16081012
Chicago/Turabian StyleCanlı, Davut, Süleyman Şenyurt, Filiz Ertem Kaya, and Luca Grilli. 2024. "The Pedal Curves Generated by Alternative Frame Vectors and Their Smarandache Curves" Symmetry 16, no. 8: 1012. https://doi.org/10.3390/sym16081012
APA StyleCanlı, D., Şenyurt, S., Ertem Kaya, F., & Grilli, L. (2024). The Pedal Curves Generated by Alternative Frame Vectors and Their Smarandache Curves. Symmetry, 16(8), 1012. https://doi.org/10.3390/sym16081012







