Rational Solutions for Two Nonautonomous Lattice Korteweg–de Vries Type Equations
Abstract
:1. Introduction
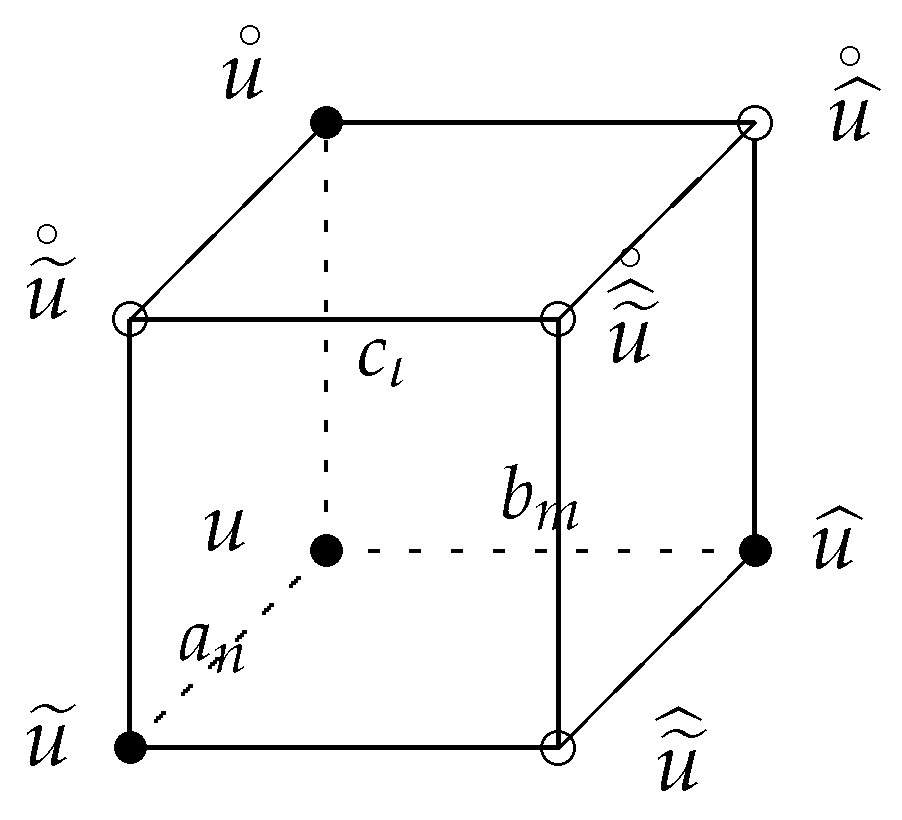
2. Bilinearization and Casoratian Solutions
3. Some Examples of Solutions
3.1. Soliton Solutions
3.2. Jordan-Block Solutions
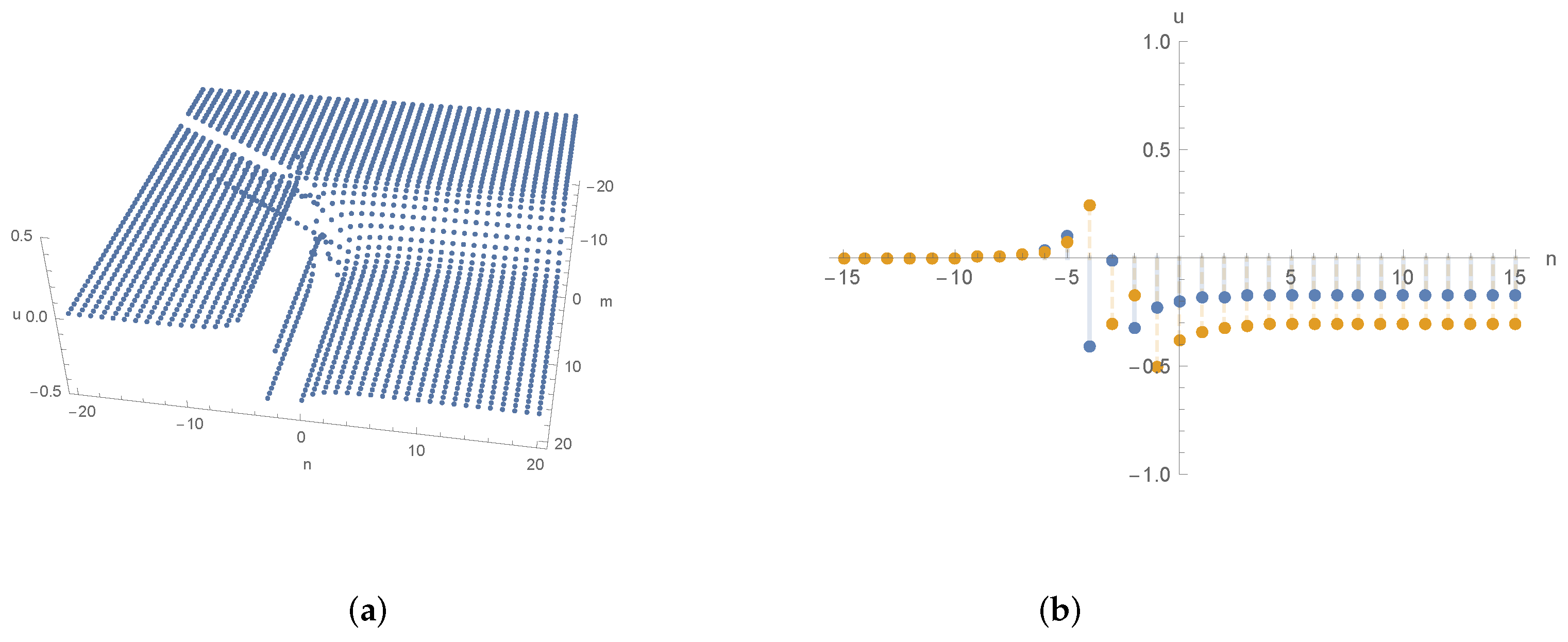
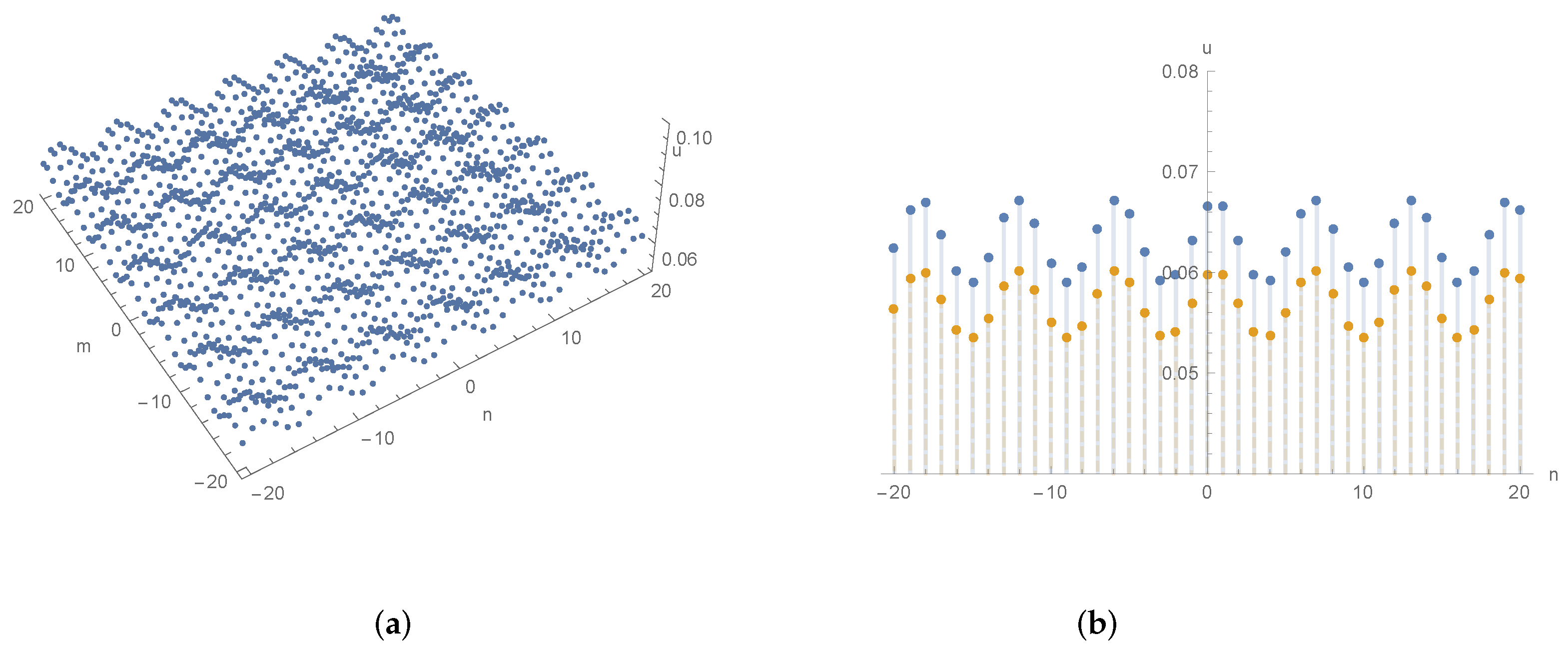
3.3. Rational Solutions
4. Dynamics of Rational Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. MDC Property of the Equation (3)
References
- Sahadevan, R.; Capel, H.W. Complete integrability and singularity confinement of nonautonomous modified Korteweg–de Vries and sine-Gordon mappings. Phys. A Stat. Mech. Appl. 2003, 330, 373–390. [Google Scholar] [CrossRef]
- Sahadevan, R.; Rasin, O.G.; Hydon, P.E. Integrability conditions for nonautonomous quad-graph equations. J. Math. Anal. Appl. 2007, 3310, 712–726. [Google Scholar] [CrossRef]
- Willox, R.; Tokihiro, T.; Satsuma, J. Darboux and binary Darboux transformations for the nonautonomous discrete KP equation. J. Math. Phys. 1997, 38, 6455–6469. [Google Scholar] [CrossRef]
- Willox, R.; Tokihiro, T.; Satsuma, J. Nonautonomous discrete integrable systems. Chaos Solitons Fract. 2000, 11, 121–135. [Google Scholar] [CrossRef]
- Hay, H. Casorati Determinant Solutions to The Nonautonomous Cross-Ratio Equation. 2010. Available online: http://lsec.cc.ac.cn/~icnwta2/postersession/hay.pdf (accessed on 26 June 2010).
- Kajiwara, K.; Mukaihira, A. Soliton solutions for the non-autonomous discrete-time Toda lattice equation. J. Phys. A Math. Gen. 2005, 38, 6363–6370. [Google Scholar] [CrossRef]
- Kajiwara, K.; Ohta, Y. Bilinearization and Casorati determinant solution to the non-autonomous discrete KdV equation. J. Phys. Soc. Jpn. 2008, 77, 054004. [Google Scholar] [CrossRef]
- Kajiwara, K.; Ohta, Y. Bilinearization and Casorati determinant solutions to non-autonomous 1+1 dimensional discrete soliton equations. RIMS Kôkyûroku Bessatsu 2009, B13, 53–73. [Google Scholar]
- Shi, Y.; Zhang, D.J.; Zhao, S.L. Solutions to the nonautonomous ABS lattice equations: Casoratians and bilinearization. Sci. Sin. Math. 2014, 44, 37–54. (In Chinese) [Google Scholar] [CrossRef]
- Grammaticos, B.; Ramani, A. Singularity confinement property for the (non-autonomous) Adler–Bobenko–Suris integrable lattice equations. Lett. Math. Phys. 2010, 92, 33–45. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, D.J.; Zhao, S.L. Solutions to non-autonomous ABS lattice equations: Generalized Cauchy matrix approach. Commun. Appl. Math. Comput. 2018, 3, 1–25. [Google Scholar]
- Nijhoff, F.W.; Walker, A.J. The discrete and continuous Painlevé hierarchy and the Garnier system. Glasgow Math. J. 2001, 43A, 109–123. [Google Scholar] [CrossRef]
- Bobenko, A.I.; Suris, Y.B. Integrable systems on quad-graphs. Int. Math. Res. Notices 2002, 11, 573–611. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Taki, M. Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 2009, 373, 675–678. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Satsuma, J. Solitons and rational solutions of nonlinear evolution equations. J. Math. Phys. 1978, 19, 2180–2187. [Google Scholar] [CrossRef]
- Zhang, D.J. Notes on solutions in Wronskian form to soliton equations: KdV-type. arXiv 2006, arXiv:nlin.SI/0603008. [Google Scholar]
- Zhang, D.-J.; Zhao, S.-L.; Sun, Y.-Y.; Zhou, J. Solutions to the modified Korteweg–de Vries equation. Rev. Math. Phys. 2014, 26, 1430006. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, D.J. Rational solutions of the H3 and Q1 models in the ABS lattice list. SIGMA 2011, 7, 046. [Google Scholar] [CrossRef]
- Nong, L.-J.; Zhang, D.-J.; Shi, Y.; Zhang, W.-Y. Parameter extension and the quasi-rational solution of a lattice Boussinesq equation. Chin. Phys. Lett. 2013, 30, 040201. [Google Scholar] [CrossRef]
- Maruno, K.; Kajiwara, K.; Nakao, S.; Oikawa, M. Bilinearization of discrete soliton equations and singularity confinement. Phys. Lett. A 1997, 229, 173–182. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, S.; Shi, Y. Rational solutions for lattice potential KdV equation and two semi-discrete lattice potential KdV equations. Z. Naturforsch. 2016, 71, 121–128. [Google Scholar] [CrossRef]
- Zhang, D.D.; Zhang, D.J. Rational solutions to the ABS list: Transformation approach. SIGMA 2017, 13, 078. [Google Scholar] [CrossRef]
- Zhao, S.L.; Zhang, D.J. Rational solutions to Q3δ in the Adler–Bobenko–Suris list and degenerations. J. Nonlinear Math. Phys. 2019, 26, 107–132. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Freeman, N.C.; Nimmo, J.J.C. Soliton solutions of the KdV and KP equations: The Wronskian technique. Phys. Lett. A 1983, 95, 1–3. [Google Scholar] [CrossRef]
- Ma, W.X.; You, Y.C. Rational solutions of the Toda lattice equation in Casoratian form. Chaos Solitons Fract. 2004, 22, 395–406. [Google Scholar] [CrossRef]
- Zhang, D.J.; Hietarinta, J. Generalized solutions for the H1 model in ABS list of lattice equations. In Nonlinear and Modern Mathematical Physics, Proceedings of the First International Workshop on AIP Conference Proceedings 1212, Beijing, China, 15–21 July 2009; Ma, W.X., Hu, X.B., Liu, Q.P., Eds.; American Institute of Physics: Melville, NY, USA, 2010; pp. 154–161. [Google Scholar]
- Adler, V.E.; Bobenko, A.I.; Suris, Y.B. Classification of integrable equations on quad-graphs. The consistency approach. Commun. Math. Phys. 2003, 233, 513–543. [Google Scholar] [CrossRef]
- Nijhoff, F.W. Lax pair for the Adler (lattice Krichever–Novikov) system. Phys. Lett. A 2002, 297, 49–58. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, M.; Zhao, S.; Feng, W. Rational Solutions for Two Nonautonomous Lattice Korteweg–de Vries Type Equations. Symmetry 2024, 16, 1037. https://doi.org/10.3390/sym16081037
Ma M, Zhao S, Feng W. Rational Solutions for Two Nonautonomous Lattice Korteweg–de Vries Type Equations. Symmetry. 2024; 16(8):1037. https://doi.org/10.3390/sym16081037
Chicago/Turabian StyleMa, Mingyu, Songlin Zhao, and Wei Feng. 2024. "Rational Solutions for Two Nonautonomous Lattice Korteweg–de Vries Type Equations" Symmetry 16, no. 8: 1037. https://doi.org/10.3390/sym16081037




