Structured Light from Classical to Quantum Perspectives
Abstract
:1. Introduction
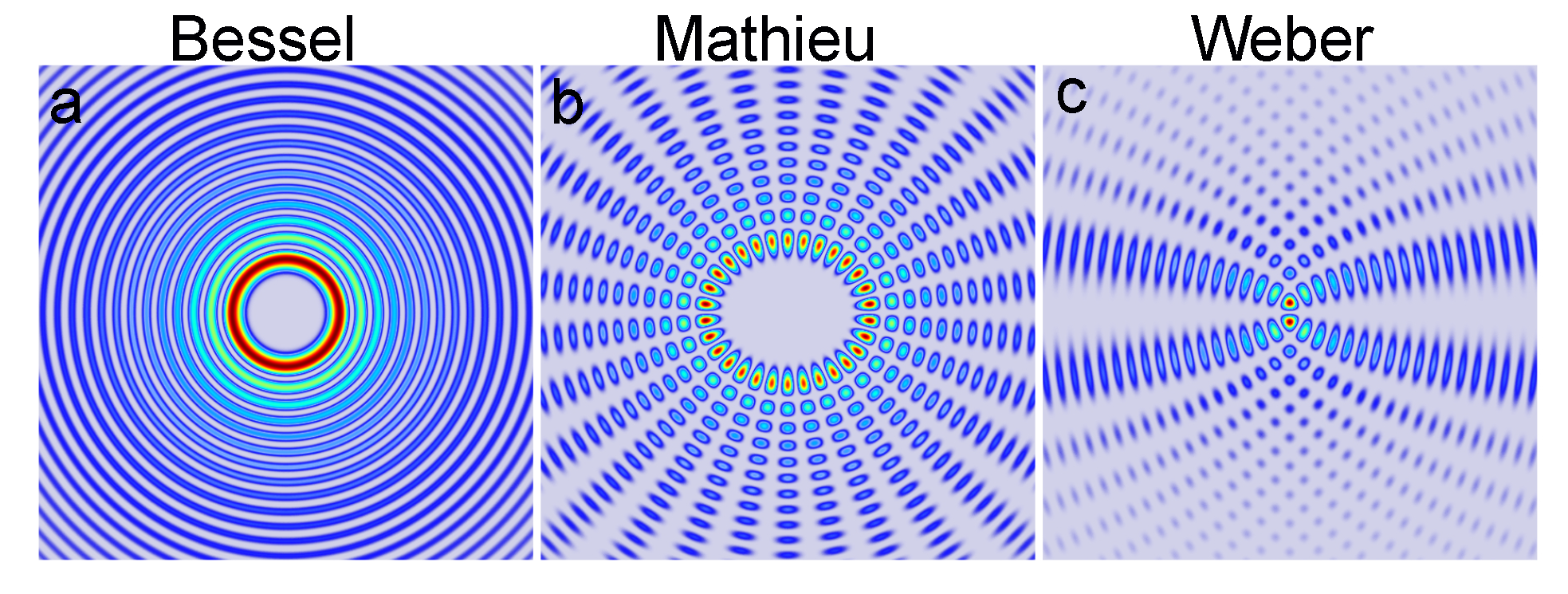
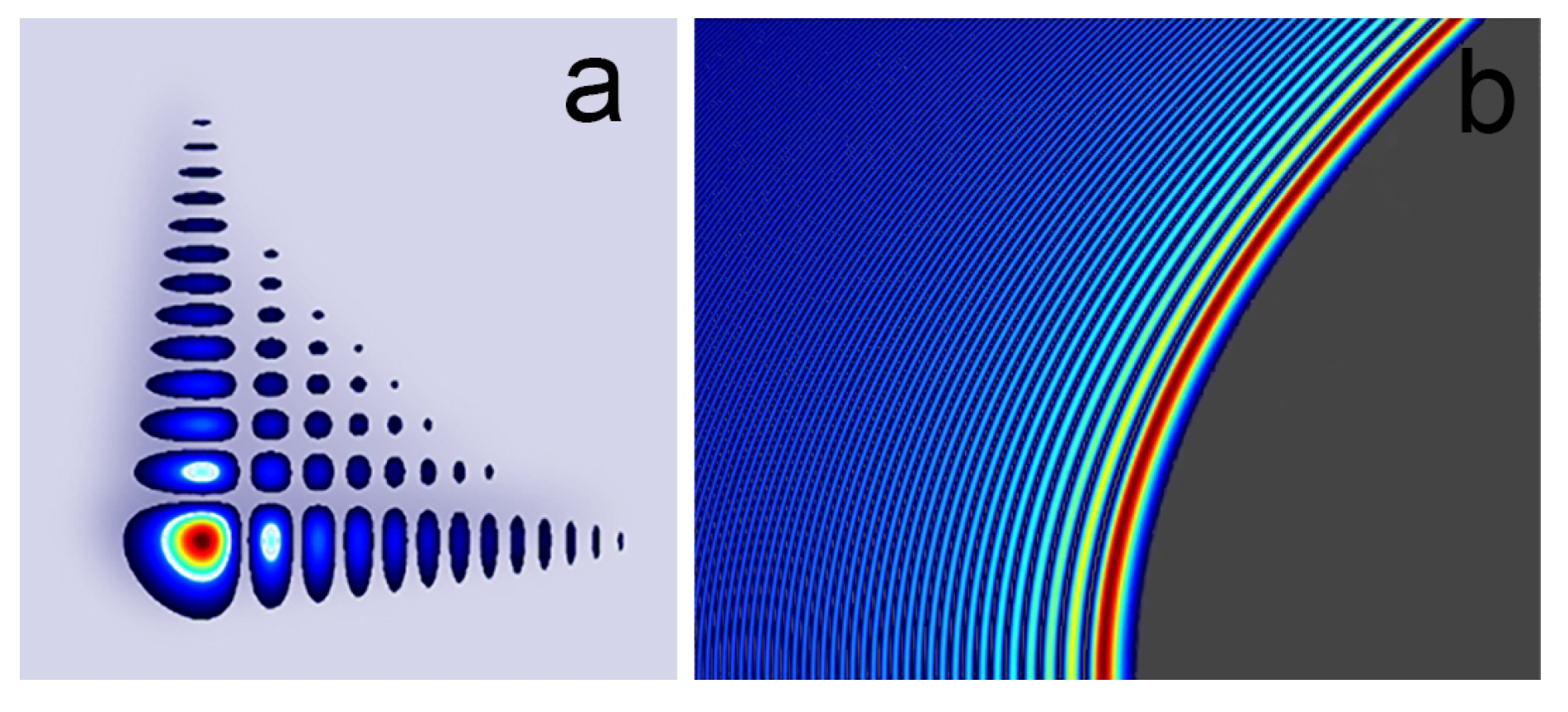
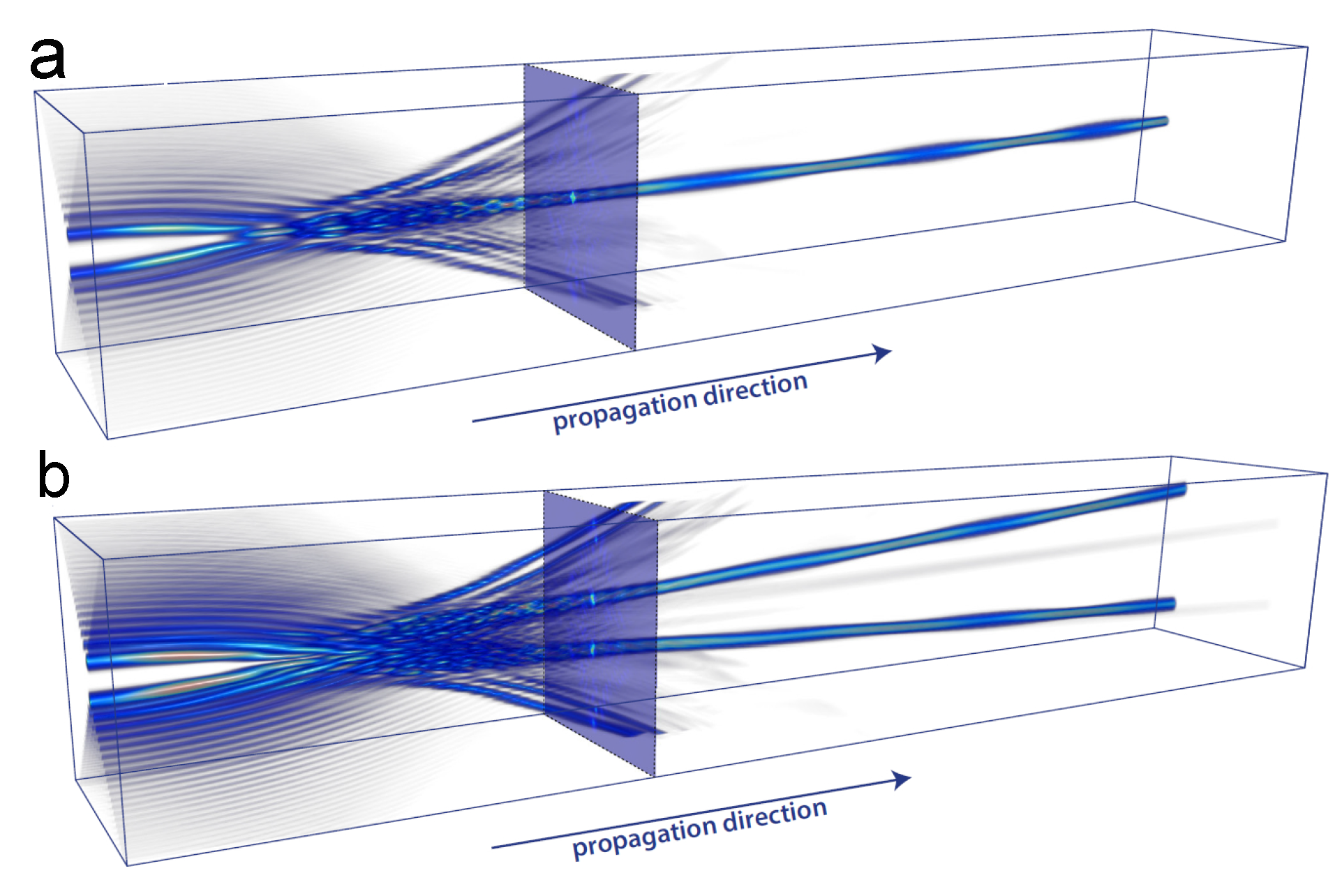
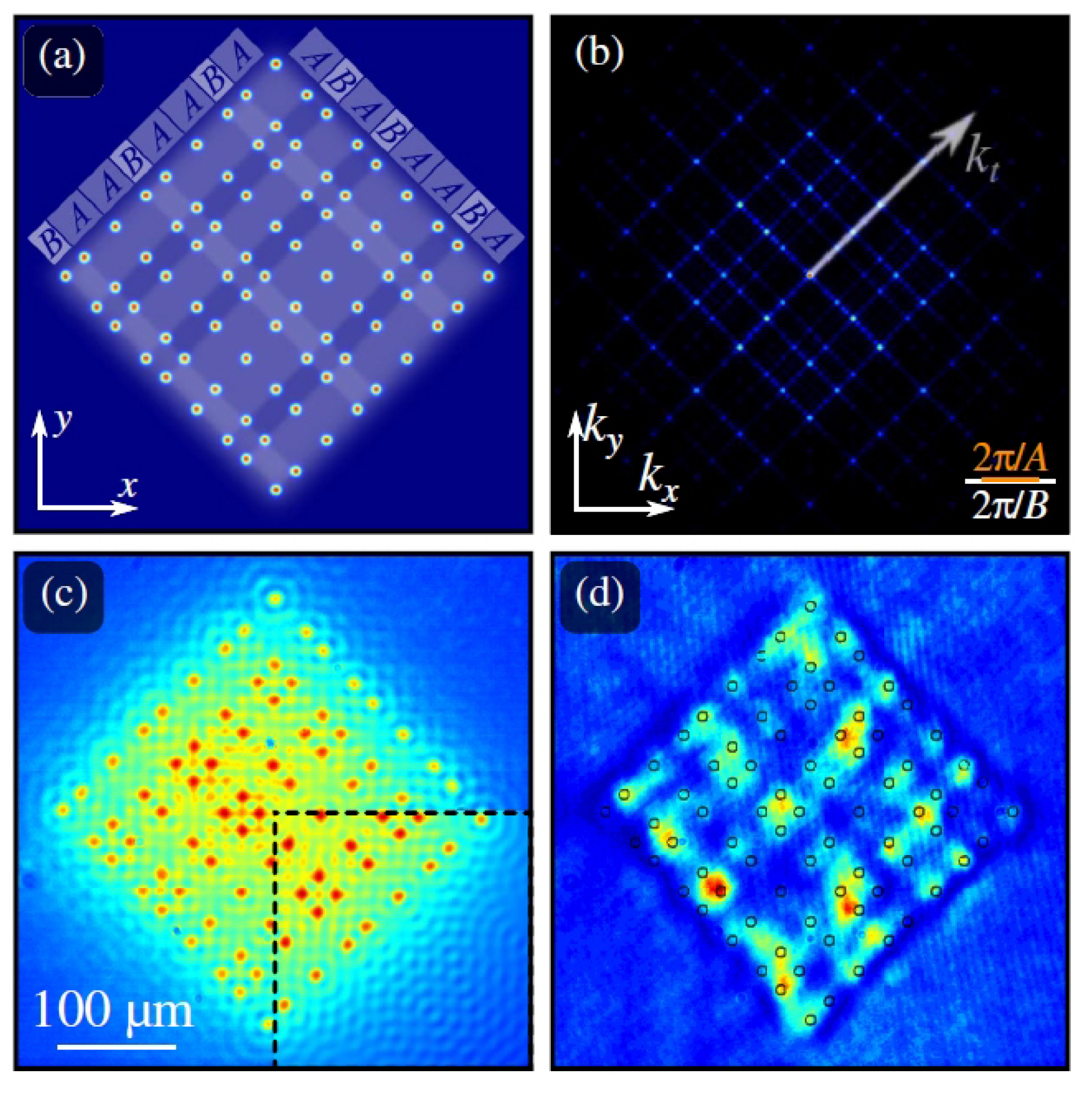
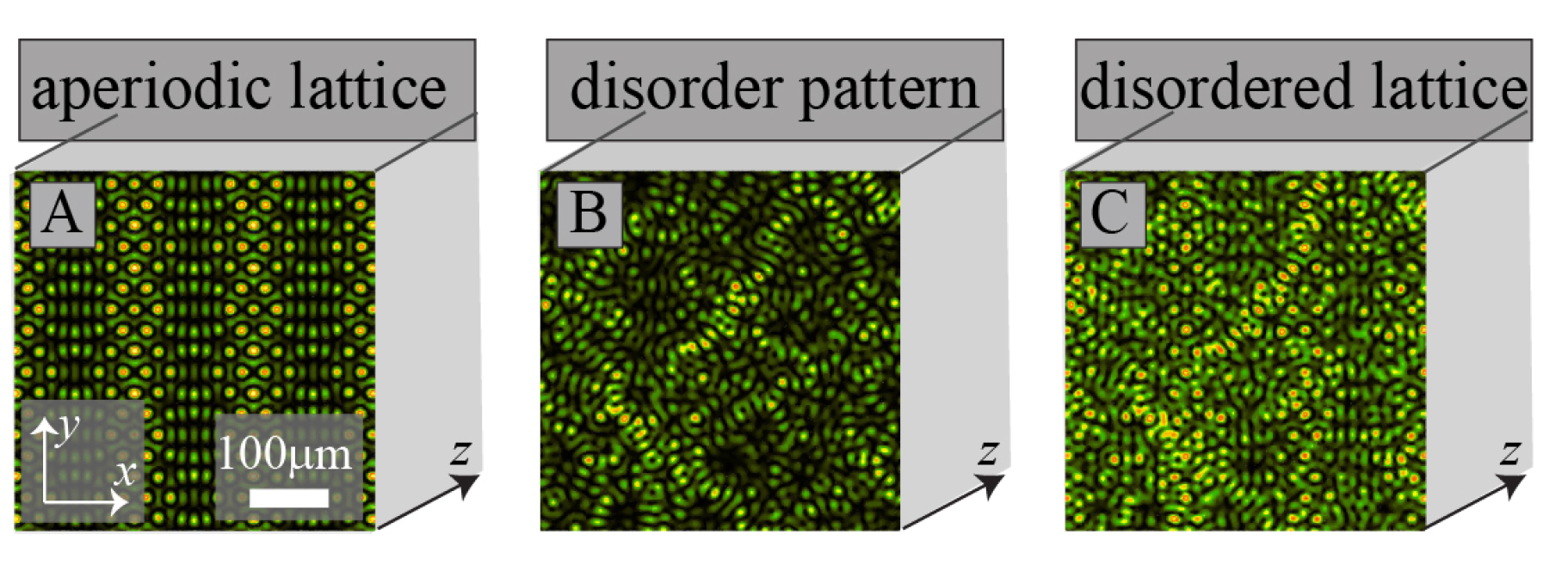
2. Structured Light: Nondiffracting and Accelerating Beams
2.1. Applications of Accelerating Beams
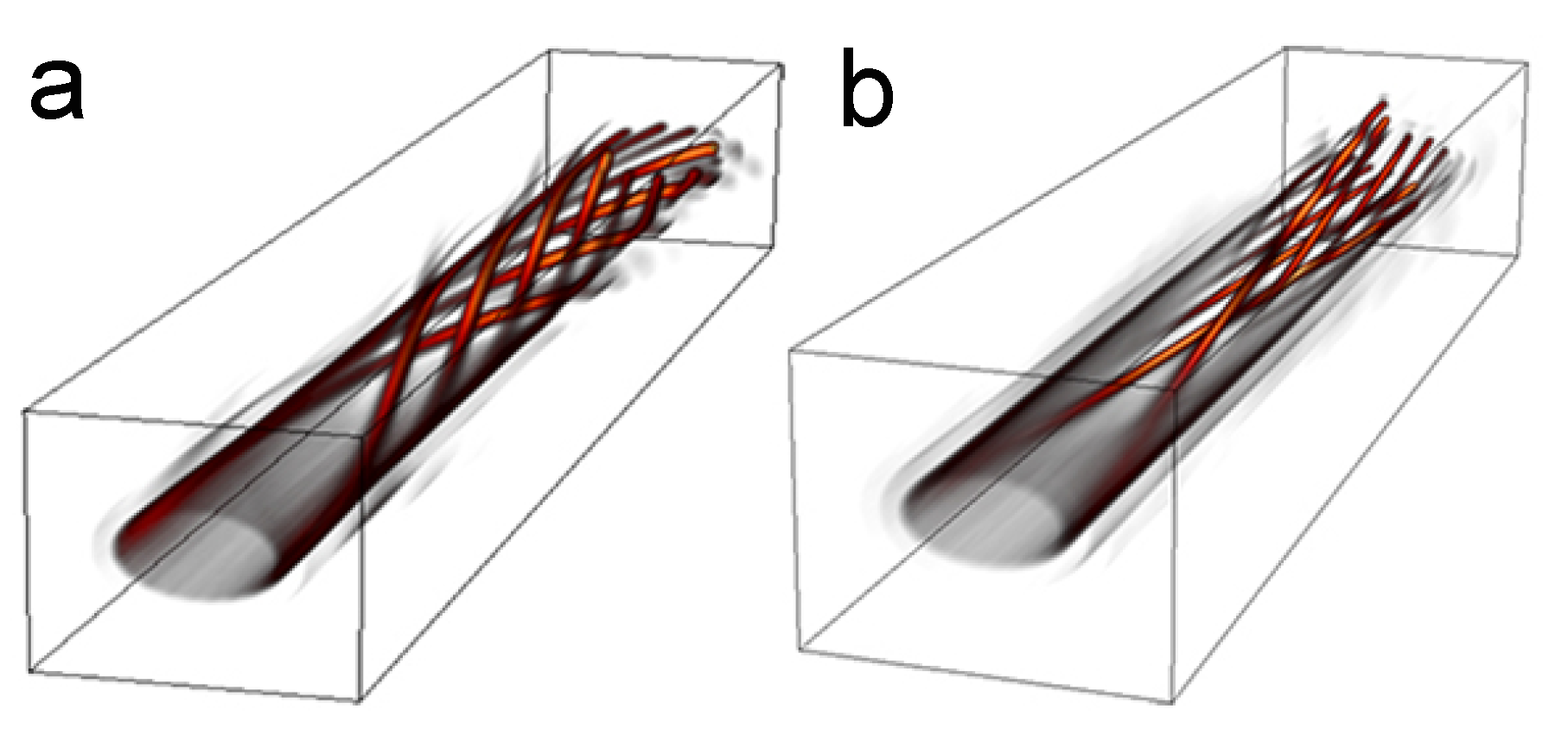
2.2. Applications of Nondiffracting Beams
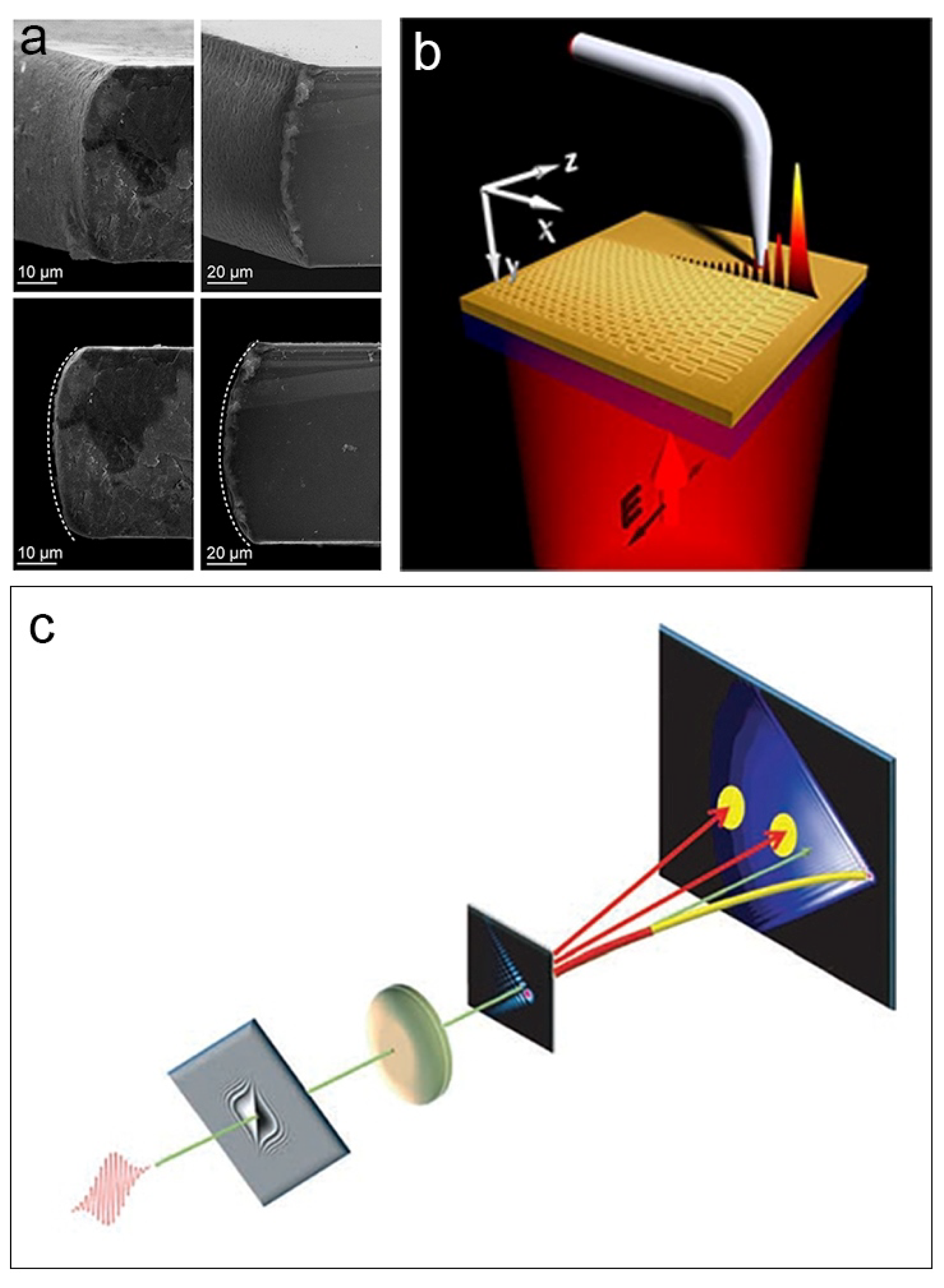
3. Structured Light: Probing Chirality in Molecular Systems Using Diffracting Laguerre-Gaussian Beams
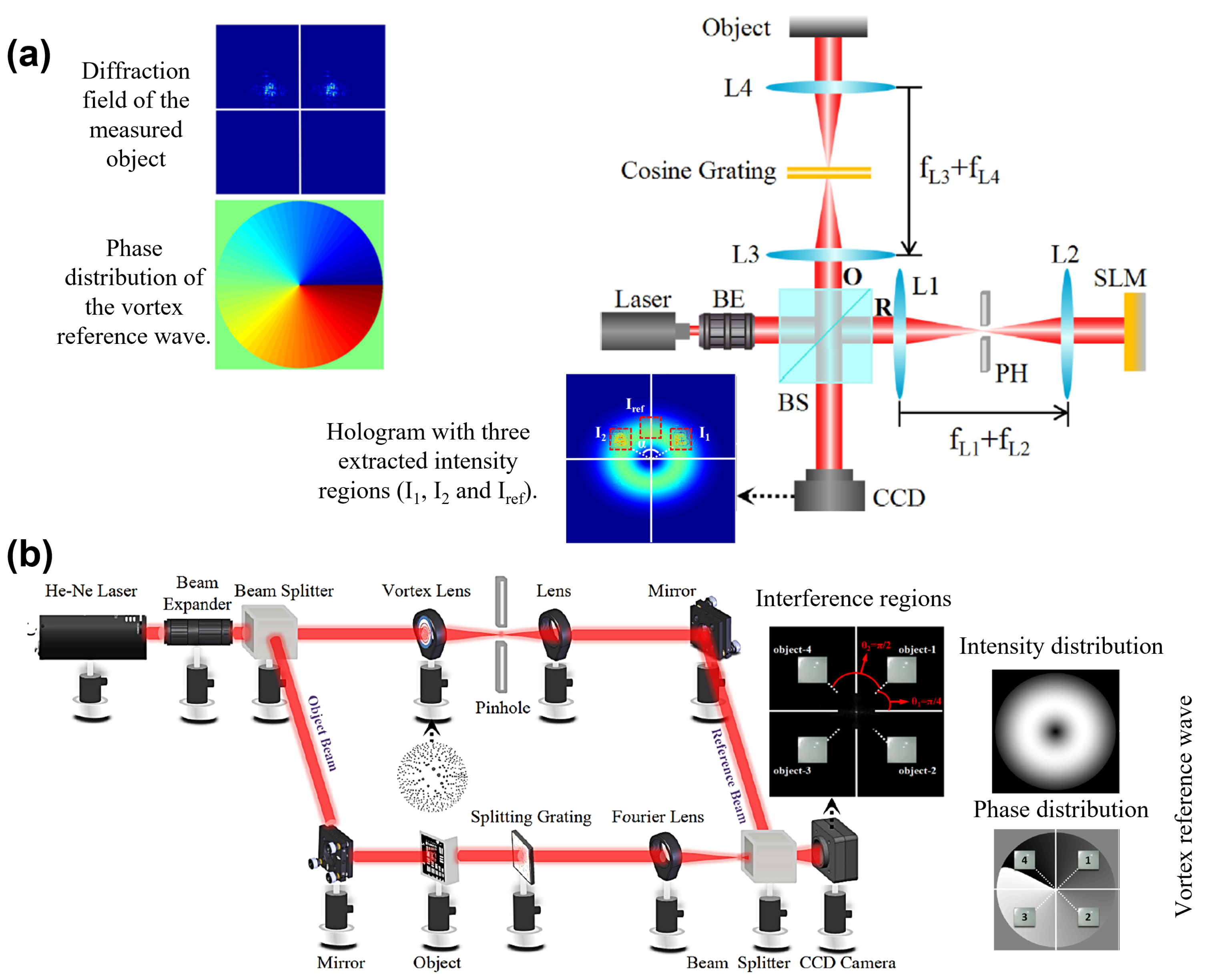
4. Structured Light: Holographic Applications
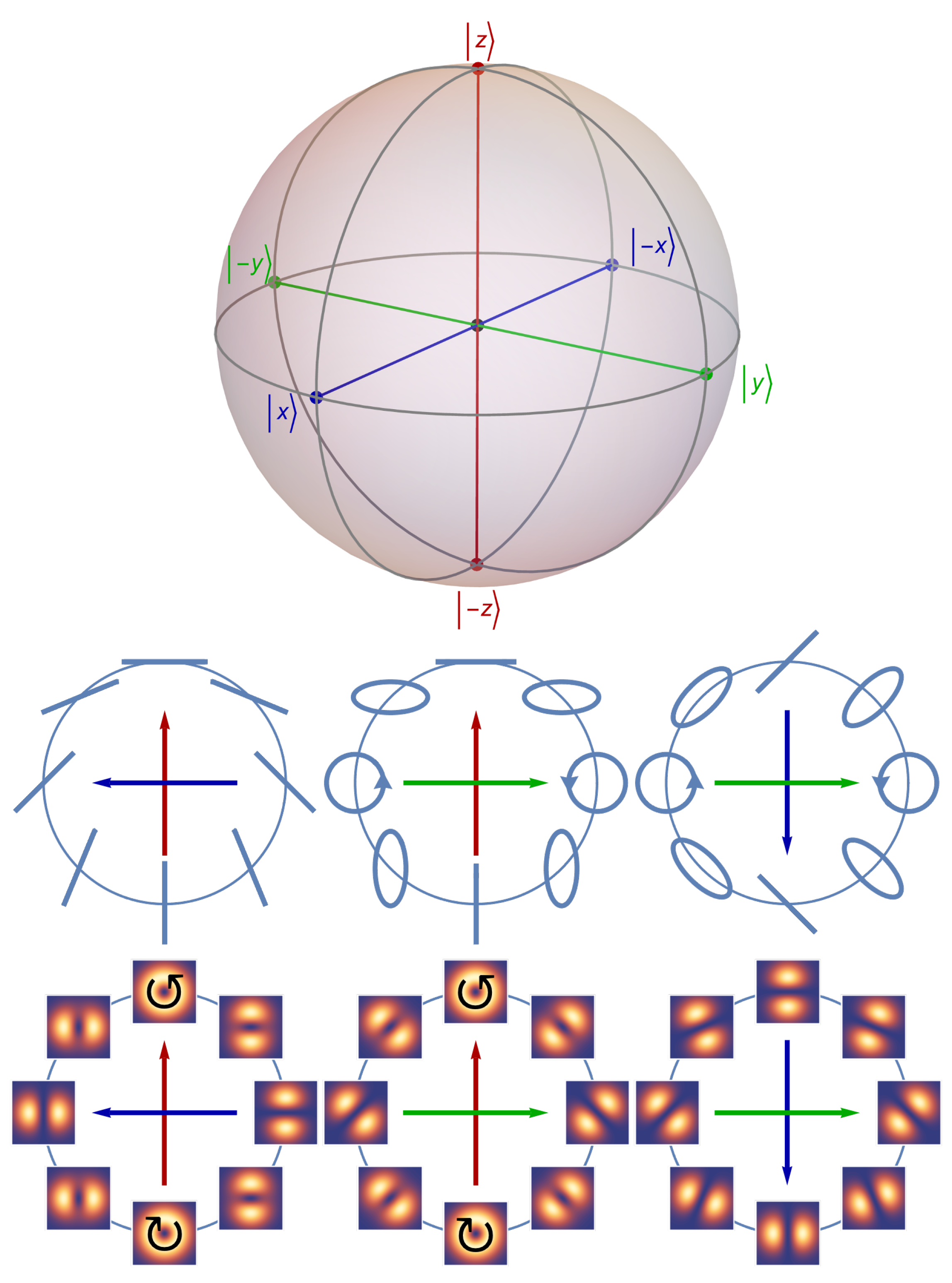
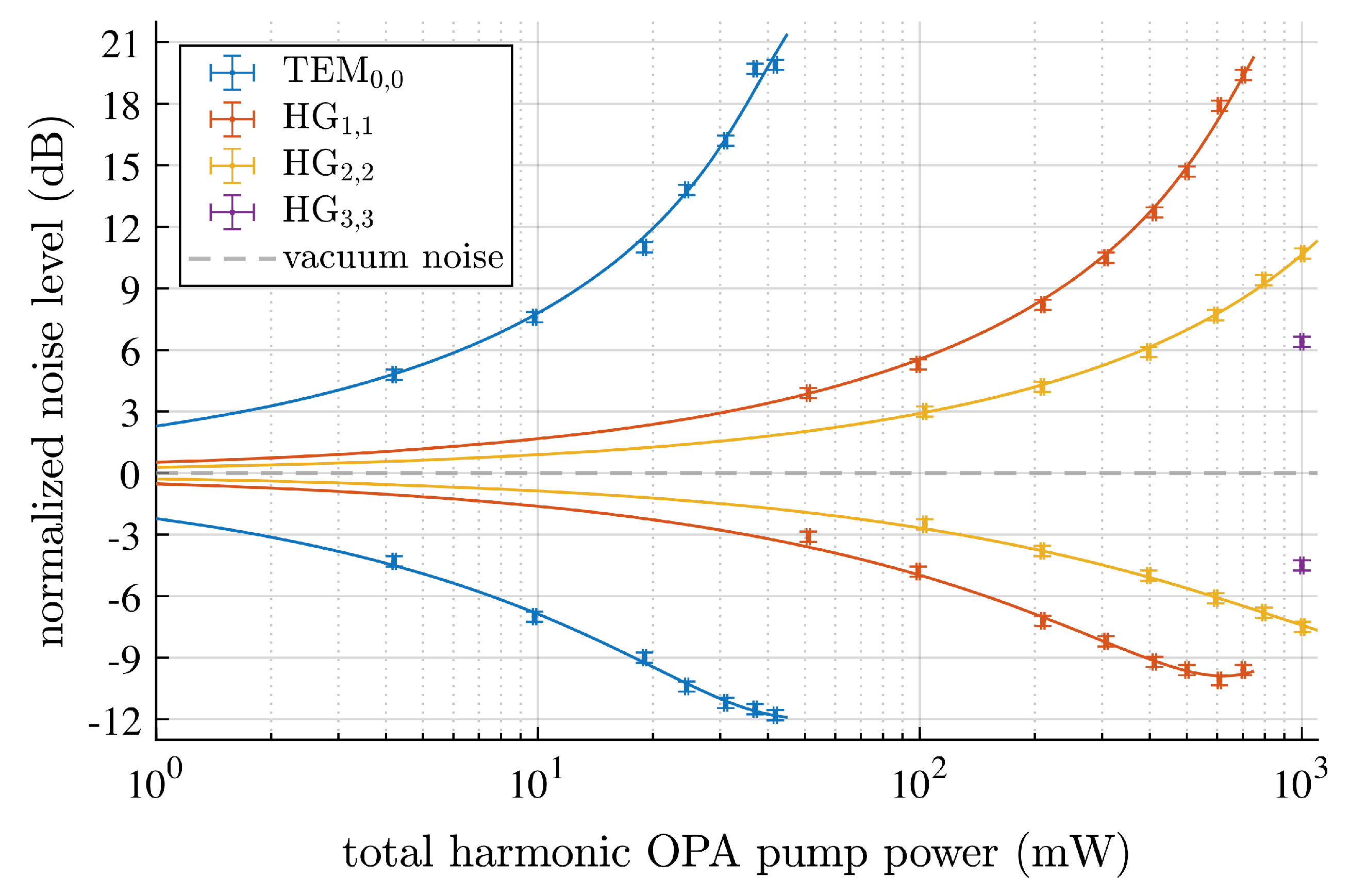
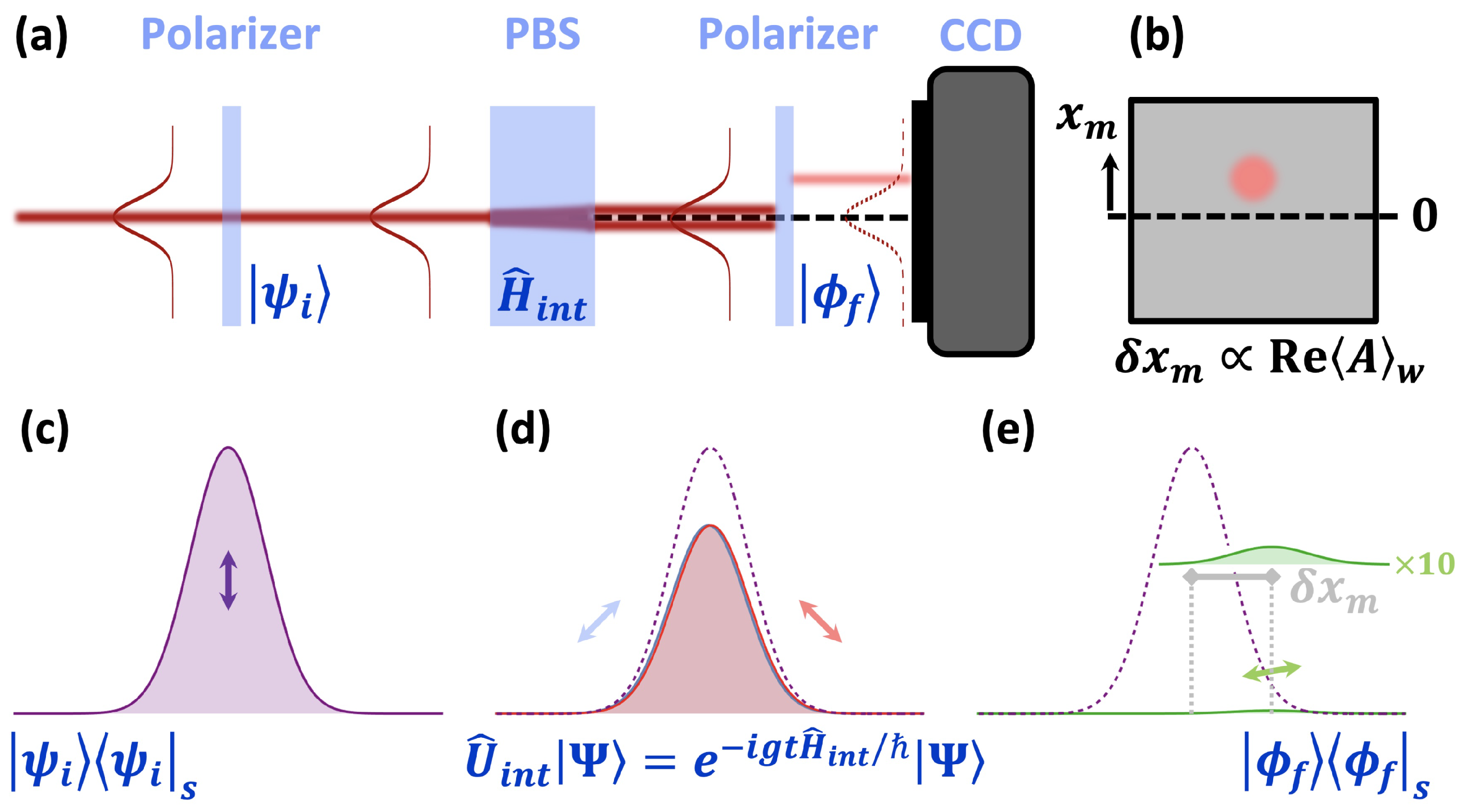
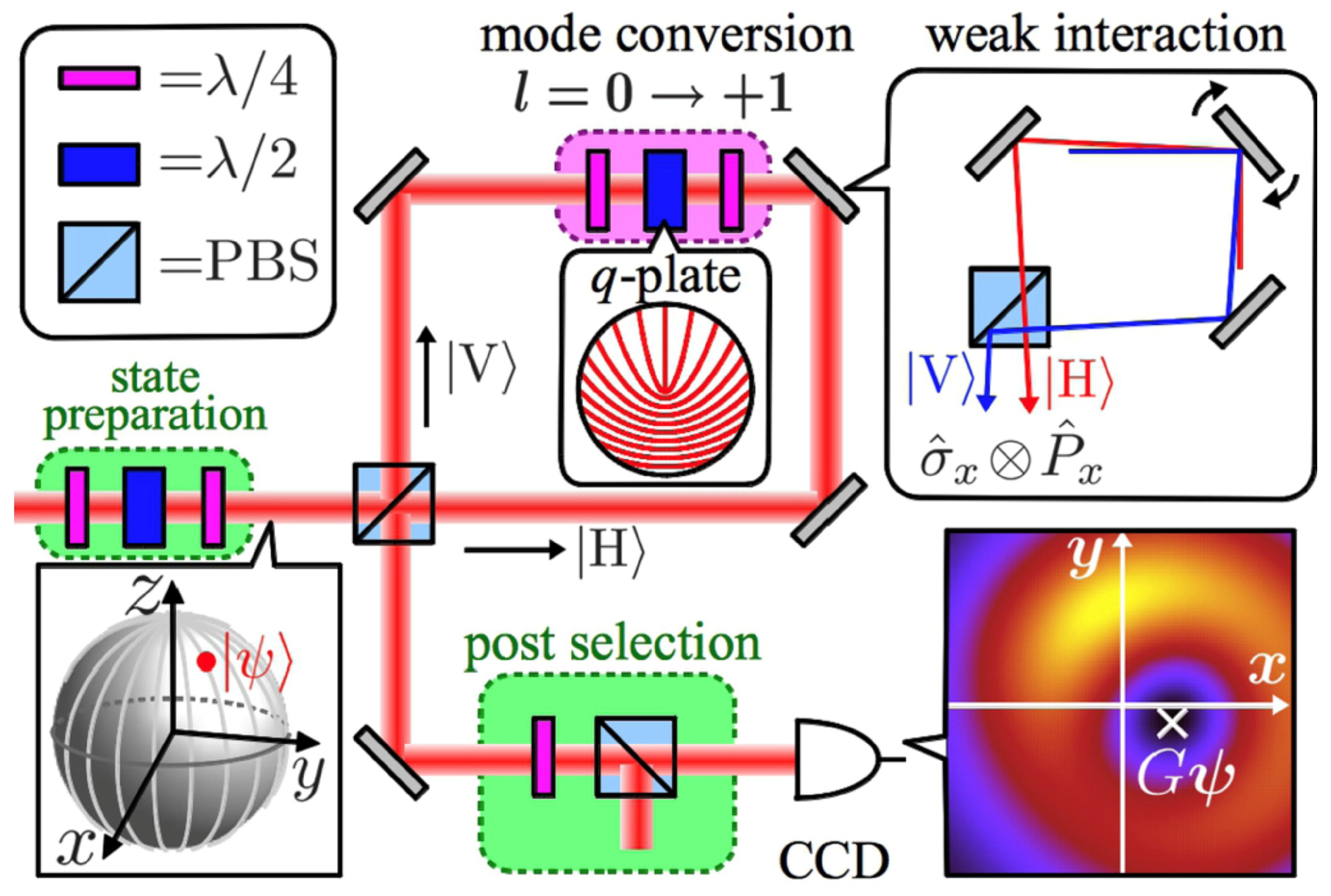
5. Structured Light: Quantum Viewpoint and Applications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haroche, S.; Raimond, J.-M. Exploring the Quantum: Atoms, Cavities and Photons; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Secor, J.; Alfano, R.; Ashrafi, S. Complex Light; IOP: Bristol, UK, 2017. [Google Scholar] [CrossRef]
- Zangwill, A. Modern Elecromagnetism; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2017, 19, 013001. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Karimi, E.; Padgett, M.J.; Alonso, M.A.; Dennis, M.R.; Dudley, A.; Forbes, A.; Zahedpour, S.; Hancock, S.W.; Milchberg, H.M.; et al. Roadmap on structured waves. J. Opt. 2023, 25, 103001. [Google Scholar] [CrossRef]
- Wang, J.; Castellucci, F.; Franke-Arnold, S. Vectorial light-matter interaction: Exploring spatially structured complex light fields. AVS Quantum Sci. 2020, 2, 031702. [Google Scholar] [CrossRef]
- Forbes, A.K.; Andrews, D.L. Orbital angular momentum of twisted light: Chirality and optical activity. J. Phys. Photonics 2021, 3, 022007. [Google Scholar] [CrossRef]
- Frankel, T. The Geometry of Physics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar] [CrossRef] [PubMed]
- Durnin, J. Exact solutions for nondiffracting beams. I. The scalar theory. J. Opt. Soc. Am. A 1987, 4, 651–654. [Google Scholar] [CrossRef]
- Boguslawski, M.; Rose, P.; Denz, C. Increasing the structural variety of discrete nondiffracting wave fields. Phys. Rev. A 2011, 84, 013832. [Google Scholar] [CrossRef]
- Rose, P.; Boguslawski, M.; Denz, C. Nonlinear lattice structures based on families of complex nondiffracting beams. New J. Phys. 2012, 14, 033018. [Google Scholar] [CrossRef]
- McQueen, C.; Arlt, J.; Dholakia, K. An experiment to study a “nondiffracting” light beam. Am. J. Phys. 1999, 67, 912–915. [Google Scholar] [CrossRef]
- Gutiérrez-Vega, J.C.; Iturbe-Castillo, M.D.; Chávez-Cerda, S. Alternative formulation for invariant optical fields: Mathieu beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef]
- Bandres, M.A.; Gutiérrez-Vega, J.C.; Chávez-Cerda, S. Parabolic nondiffracting optical wave fields. Opt. Lett. 2004, 29, 44–46. [Google Scholar] [CrossRef]
- Freedman, B.; Bartal, G.; Segev, M.; Lifshitz, R.; Christodoulides, D.N.; Fleischer, J.W. Wave and defect dynamics in nonlinear photonic quasicrystals. Nature 2006, 440, 04722. [Google Scholar] [CrossRef]
- Vicente, O.C.; Caloz, C. Bessel beams: A unified and extended perspective. Optica 2021, 8, 2334–2536. [Google Scholar] [CrossRef]
- Boguslawski, M.; Lučić, N.M.; Diebel, F.; Timotijević, D.V.; Denz, C.; Savić, D.M.J. Light localization in optically induced deterministic aperiodic Fibonacci lattices. Optica 2016, 3, 711–717. [Google Scholar] [CrossRef]
- Lóxpez-Mariscal, C.; Gutiérrez-Vega, J.C.; Milne, G.; Dholakia, K. Orbital angular momentum transfer in helical Mathieu beams. Opt. Express 2006, 14, 4182–4187. [Google Scholar] [CrossRef] [PubMed]
- Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically mediated particle clearing using Airy wavepackets. Nat. Photonics 2008, 2, 675–678. [Google Scholar] [CrossRef]
- Fleischer, J.; Segev, M.; Efremidis, N.; Christodoulides, D. Observation of two-dimensional discrete solitons in optically induced nonlinear photonic lattices. Nature 2003, 422, 147. [Google Scholar] [CrossRef]
- Sogomonian, S.; Klewitz, S.; Herminghaus, S. Self-reconstruction of a Bessel beam in a nonlinear medium. Opt. Commun. 1997, 139, 313–319. [Google Scholar] [CrossRef]
- Bouchal, Z.; Wagner, J.; Chlup, M. Self-reconstruction of a distorted nondiffracting beam. Opt. Commun. 1998, 151, 207–211. [Google Scholar] [CrossRef]
- Chávez-Cerda, S.; Meneses-Nava, M.A.; Hickmann, J.M. Interference of traveling nondiffracting beams. Opt. Lett. 1998, 23, 1871–1873. [Google Scholar] [CrossRef]
- Vasara, A.; Turunen, J.; Friberg, A.T. Realization of general nondiffracting beams with computer-generated holograms. J. Opt. Soc. Am. A 1989, 6, 1748–1754. [Google Scholar] [CrossRef] [PubMed]
- Scott, G.; McArdle, N. Efficient generation of nearly diffraction-free beams using an axicon. Opt. Eng. 1992, 31, 2640. [Google Scholar] [CrossRef]
- Chattrapiban, N.; Rogers, E.A.; Cofield, D.; Wendell, T.; Hill, I.; Roy, R. Generation of nondiffracting Bessel beams by use of a spatial light modulator. Opt. Lett. 2003, 28, 2183–2185. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V.; Balazs, N.L. Nonspreading wave packets. Am. J. Phys. 1979, 47, 264. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Ballistic dynamics of Airy beams. Opt. Lett. 2008, 33, 207–209. [Google Scholar] [CrossRef] [PubMed]
- Bandres, M.A.; Kaminer, I.; Mills, M.; Rodríguez-Lara, B.; Greenfield, E.; Segev, M.; Christodoulides, D.N. Accelerating Optical Beam. Opt. Photonics News 2013, 24, 30–37. [Google Scholar] [CrossRef]
- Besieris, I.M.; Shaarawi, A.M. A note on an accelerating finite energy Airy beam. Opt. Lett. 2007, 32, 2447–2449. [Google Scholar] [CrossRef]
- Novitsky, A.V.; Novitsky, D.V. Nonparaxial Airy beams: Role of evanescent waves. Opt. Lett. 2009, 34, 3430–3432. [Google Scholar] [CrossRef]
- Mathis, A.; Courvoisier, F.; Froehly, L.; Furfaro, L.; Jacquot, M.; Lacourt, P.A.; Dudley, J.M. Micromachining along a curve: Femtosecond laser micromachining of curved profiles in diamond and silicon using accelerating beams. Appl. Phys. Lett. 2012, 101, 071110. [Google Scholar] [CrossRef]
- Chong, A.; Renninger, W.H.; Christodoulides, D.N.; Wise, F.W. Airy-Bessel wave packets as versatile linear light bullets. Nat. Photonics 2010, 4, 103–106. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, S.; Liu, Y.; Yin, X.; Lu, C.; Chen, Z.; Zhang, X. Plasmonic Airy beams with dynamically controlled trajectories. Opt. Lett. 2011, 36, 3191–3193. [Google Scholar] [CrossRef] [PubMed]
- Minovich, A.; Klein, A.E.; Janunts, N.; Pertsch, T.; Neshev, D.N.; Kivshar, Y.S. Generation and Near-Field Imaging of Airy Surface Plasmons. Phys. Rev. Lett. 2011, 107, 116802. [Google Scholar] [CrossRef]
- Polynkin, P.; Kolesik, M.; Moloney, J.V.; Siviloglou, G.A.; Christodoulides, D.N. Curved Plasma Channel Generation Using Ultraintense Airy Beams. Science 2009, 324, 229–232. [Google Scholar] [CrossRef]
- Ellenbogen, T.; Voloch-Bloch, N.; Ganany-Padowicz, A.; Arie, A. Nonlinear generation and manipulation of Airy beams. Nat. Photon. 2009, 3, 395–398. [Google Scholar] [CrossRef]
- Broky, J.; Siviloglou, G.A.; Dogariu, A.; Christodoulides, D.N. Self-healing properties of optical Airy beams. Opt. Express 2008, 16, 12880–12891. [Google Scholar] [CrossRef]
- Efremidis, N.K. Airy trajectory engineering in dynamic linear index potentials. Opt. Lett. 2011, 36, 3006–3008. [Google Scholar] [CrossRef] [PubMed]
- Efremidis, N.K. Accelerating beam propagation in refractive-index potentials. Phys. Rev. A 2014, 89, 023841. [Google Scholar] [CrossRef]
- Makris, K.G.; Kaminer, I.; El-Ganainy, R.; Efremidis, N.K.; Chen, Z.; Segev, M.; Christodoulides, D.N. Accelerating diffraction-free beams in photonic lattices. Opt. Lett. 2014, 39, 2129–2132. [Google Scholar] [CrossRef]
- Chávez-Cerda, S.; Ruiz, U.; Arrizón, V.; Moya-Cessa, H.M. Generation of Airy solitary-like wave beams by acceleration control in inhomogeneous media. Opt. Express 2011, 19, 16448–16454. [Google Scholar] [CrossRef]
- Lučić, N.M.; Bokić, B.M.; Grujić, D.i.c.v.; Pantelić, D.V.; Jelenković, B.M.; Piper, A.; Jović, D.M.; Timotijević, D.V. Defect-guided Airy beams in optically induced waveguide arrays. Phys. Rev. A 2013, 88, 063815. [Google Scholar] [CrossRef]
- Diebel, F.; Bokić, B.M.; Boguslawski, M.; Piper, A.; Timotijević, D.V.; Jović, D.M.; Denz, C. Control of Airy-beam self-acceleration by photonic lattices. Phys. Rev. A 2014, 90, 033802. [Google Scholar] [CrossRef]
- Rose, P.; Diebel, F.; Boguslawski, M.; Denz, C. Airy beam induced optical routing. Appl. Phys. Lett. 2013, 102, 101101. [Google Scholar] [CrossRef]
- Bekenstein, R.; Segev, M. Self-accelerating optical beams in highly nonlocal nonlinear media. Opt. Express 2011, 19, 23706–23715. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, S.; Zhang, P.; Lou, C.; Xu, J.; Chen, Z. Persistence and breakdown of Airy beams driven by an initial nonlinearity. Opt. Lett. 2010, 35, 3952–3954. [Google Scholar] [CrossRef]
- Driben, R.; Konotop, V.V.; Meier, T. Coupled Airy breathers. Opt. Lett. 2014, 39, 5523–5526. [Google Scholar] [CrossRef] [PubMed]
- Diebel, F.; Bokić, B.M.; Timotijević, D.V.; Savić, D.M.J.; Denz, C. Soliton formation by decelerating interacting Airy beams. Opt. Express 2015, 23, 24351–24361. [Google Scholar] [CrossRef]
- Zannotti, A.; Vasiljević, J.M.; Timotijević, D.V.; Savić, D.M.J.; Denz, C. Morphing discrete diffraction in nonlinear Mathieu lattices. Opt. Lett. 2019, 44, 1592–1595. [Google Scholar] [CrossRef]
- Zannotti, A.; Vasiljević, J.M.; Timotijević, D.V.; Jović Savić, D.M.; Denz, C. Visualizing the Energy Flow of Tailored Light. Adv. Opt. Mater. 2018, 6, 1701355. [Google Scholar] [CrossRef]
- Vasiljević, J.M.; Zannotti, A.; Timotijević, D.V.; Denz, C.; Savić, D.M.J. Light transport and localization in disordered aperiodic Mathieu lattices. Opt. Lett. 2022, 47, 702–705. [Google Scholar] [CrossRef] [PubMed]
- Lakhtakia, A. (Ed.) Selected Papers on Natural Optical Activity; SPIE: Bellingham, WA, USA, 1990; Volume MS15. [Google Scholar]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; WoerdmanDurnin, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A. 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Rosales-Guzman, C.; Ndagano, B.; Forbes, A. A review of complex vector light fields and their applications. J. Opt. 2018, 20, 123001. [Google Scholar] [CrossRef]
- Dholakia, K.; Lee, W.M. Optical trapping takes shape: The use of structured light fields. Adv. At. Mol. Opt. Phys. 2008, 56, 261–337. [Google Scholar] [CrossRef]
- Piccirillo, B.; Toscano, C.; Vetrano, F.; Santamato, E. Orbital and Spin Photon Angular Momentum Transfer in Liquid Crystals. Phys. Rev. Lett. 2001, 86, 2285–2288. [Google Scholar] [CrossRef] [PubMed]
- Babiker, M.; Bennett, C.; Andrews, D.L.; Dávila Romero, L.C. Orbital Angular Momentum Exchange in the Interaction of Twisted Light with Molecules. Phys. Rev. Lett. 2002, 89, 143601. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.L.; Dávila Romero, L.C.; Babiker, M. On optical vortex interactions with chiral matter. Opt. Commun. 2004, 237, 133–139. [Google Scholar] [CrossRef]
- Coles, M.; Andrews, D.L. Chirality and angular momentum in optical radiation. Phys. Rev. A 2012, 85, 063810. [Google Scholar] [CrossRef]
- Araoka, F.; Verbiest, T.; Clays, K.; Persoons, A. Interactions of twisted light with chiral molecules: An experimental investigation. Phys. Rev. A 2005, 71, 055401. [Google Scholar] [CrossRef]
- Loeffler, W.; Broer, J.D.; Woerdman, P.J. Circular dichroism of cholesteric polymers and the orbital angular momentum of light. Phys. Rev. A 2011, 83, 065801. [Google Scholar] [CrossRef]
- Brullot, W.; Vanbel, K.M.; Swusten, T.; Verbiest, T. Resolving enantiomers using the optical angular momentum of twisted light. Sci. Adv. 2016, 2, e1501349. [Google Scholar] [CrossRef] [PubMed]
- Forbes, A.K.; Andrews, D.L. Optical orbital angular momentum: Twisted light and chirality. Opt. Lett. 2018, 43, 435–438. [Google Scholar] [CrossRef]
- Forbes, A.K.; Andrews, D.L. Spin-orbit interactions and chiroptical effects engaging orbital angular momentum of twisted light in chiral and achiral media. Phys. Rev. A 2019, 99, 023837. [Google Scholar] [CrossRef]
- Ni, J.; Liu, S.; Hu, G.; Hu, Y.; Lao, Z.; Li, J.; Zhang, Q.; Wu, D.; Dong, S.; Chu, J.; et al. Giant helical dichroism of single chiral nanostructures with photonic orbital angular momentum. ACS Nano 2021, 15, 2893–2900. [Google Scholar] [CrossRef]
- Ni, J.; Liu, S.; Lao, Z.; Wang, Z.; Huang, K.; Ji, S.; Li, J.; Huang, Z.; Xiong, Q.; Hu, Y.; et al. Gigantic vortical differential scattering as a monochromatic probe for multiscale chiral structures. Proc. Natl. Acad. Sci. USA 2021, 118, e2020055118. [Google Scholar] [CrossRef]
- Liu, S.; Ni, J.; Zhang, C.; Wang, X.; Cao, Y.; Wang, D.; Ji, S.; Pan, D.; Li, R.; Wu, H.; et al. Tailoring Optical Vortical Dichroism with Stereometamaterials. Laser Photonics Rev. 2022, 16, 2100518. [Google Scholar] [CrossRef]
- Begin, J.L.; Jain, A.; Parks, A.; Hufnagel, F.; Corkum, P.; Karimi, E.; Brabec, T.; Bhardwaj, R. Nonlinear helical dichroism in chiral and achiral molecules. Nat. Photonics 2023, 17, 82–88. [Google Scholar] [CrossRef]
- Gabor, D. A New Microscopic Principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef]
- Ruffato, G.; Rossi, R.; Massari, M.; Mafakheri, E.; Capaldo, P.; Romanato, F. Design, fabrication and characterization of Computer Generated Holograms for anti-counterfeiting applications using OAM beams as light decoders. Sci. Rep. 2017, 7, 18011. [Google Scholar] [CrossRef]
- Ashley, J.; Bernal, M.P.; Burr, G.W.; Coufal, H.; Guenther, H.; Hoffnagle, J.A.; Jefferson, C.M.; Marcus, B.; MacFarlane, R.M.; Shelby, R.M.; et al. Holographic Data Storage Technology. IBM J. Res. Dev. 2000, 44, 341–368. [Google Scholar] [CrossRef]
- Kosma, K.; Andrianakis, M.; Hatzigiannakis, K.; Tornari, V. Digital holographic interferometry for cultural heritage structural diagnostics: A coherent and a low-coherence optical set-up for the study of a marquetry sample. Strain 2018, 54, e12263. [Google Scholar] [CrossRef]
- Coppola, G.; Zito, G.; Luca, A.C.D.; Ferrara, M.A. Polarized Digital Holography as Valuable Analytical Tool in Biological and Medical Research. In Proceedings of the Digital Holography and Three-Dimensional Imaging 2019; Paper Th4A.5; Optica Publishing Group: Washington, DC, USA, 2019. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Y. Generation and Detection of Structured Light: A Review. Front. Phys. 2021, 9, 688284. [Google Scholar] [CrossRef]
- Hariharan, P. Basics of Holography; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Stoykova, E.; Kang, H.; Park, J. Twin-image problem in digital holography-a survey (Invited Paper). Chin. Opt. Lett. 2014, 12, 060013. [Google Scholar] [CrossRef]
- Tahara, T.; Lee, Y.; Ito, Y.; Xia, P.; Shimozato, Y.; Takahashi, Y.; Awatsuji, Y.; Nishio, K.; Ura, S.; Kubota, T.; et al. Superresolution of interference fringes in parallel four-step phase-shifting digital holography. Opt. Lett. 2014, 39, 1673–1676. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.S.; Cheng, X.; Ren, X.Y.; Ding, J.P.; Wang, H.T. Optical vortex phase-shifting digital holography. Opt. Express 2004, 12, 5166–5171. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Li, Y.; Zhou, S.; Liu, D.; Zhu, J. Phase-shifting digital holography with vortex beam in one single exposure. Optik 2019, 185, 1024–1029. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Zhou, S.; Liu, D.; Zhu, J. Single-shot phase-shifting digital holography with amplitude-only Fermat-spiral sieves. Laser Phys. Lett. 2019, 16, 025002. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E.; Bhatia, A.B.; Clemmow, P.C.; Gabor, D.; Stokes, A.R.; Taylor, A.M.; Wayman, P.A.; Wilcock, W.L. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Gustafsson, M.G.L. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J. Microsc. 2001, 198, 82–87. [Google Scholar] [CrossRef]
- Mudassar, A.A.; Hussain, A. Super-resolution of active spatial frequency heterodyning using holographic approach. Appl. Opt. 2010, 49, 3434–3441. [Google Scholar] [CrossRef]
- Gao, P.; Pedrini, G.; Osten, W. Structured illumination for resolution enhancement and autofocusing in digital holographic microscopy. Opt. Lett. 2013, 38, 1328–1330. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Kim, K.; Yoon, J.; Park, Y. Active illumination using a digital micromirror device for quantitative phase imaging. Opt. Lett. 2015, 40, 5407–5410. [Google Scholar] [CrossRef] [PubMed]
- Ganjkhani, Y.; Charsooghi, M.A.; Akhlaghi, E.A.; Moradi, A.R. Super-resolved Mirau digital holography by structured illumination. Opt. Commun. 2017, 404, 110–117. [Google Scholar] [CrossRef]
- Meng, Z.; Pedrini, G.; Lv, X.; Ma, J.; Nie, S.; Yuan, C. DL-SI-DHM: A deep network generating the high-resolution phase and amplitude images from wide-field images. Opt. Express 2021, 29, 19247–19261. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Briere, G.; Fang, X.; Ni, P.; Sawant, R.; Héron, S.; Chenot, S.; Vézian, S.; Damilano, B.; Brändli, V.; et al. Metasurface orbital angular momentum holography. Nat. Commun. 2019, 10, 2986. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Fang, X.; Jang, J.; Bürger, J.; Rho, J.; Maier, S.A. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat. Nanotechnol. 2020, 15, 948–955. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high-security encryption. Nat. Photonics 2020, 14, 101–108. [Google Scholar] [CrossRef]
- Zhou, H.; Sain, B.; Wang, Y.; Schlickriede, C.; Zhao, R.; Zhang, X.; Wei, Q.; Li, X.; Huang, L.; Zentgraf, T. Polarization-Encrypted Orbital Angular Momentum Multiplexed Metasurface Holography. ACS Nano 2020, 14, 5553–5559. [Google Scholar] [CrossRef] [PubMed]
- Trajtenberg-Mills, S.; Juwiler, I.; Arie, A. On-axis shaping of second-harmonic beams. Laser Photonics Rev. 2015, 9, L40–L44. [Google Scholar] [CrossRef]
- Fang, X.; Yang, H.; Yao, W.; Wang, T.; Zhang, Y.; Gu, M.; Xiao, M. High-dimensional orbital angular momentum multiplexing nonlinear holography. Adv. Photonics 2021, 3, 015001. [Google Scholar] [CrossRef]
- Töpfer, S.; Basset, M.G.; Fuenzalida, J.; Steinlechner, F.; Torres, J.P.; Gräfe, M. Quantum holography with undetected light. Sci. Adv. 2022, 8, eabl4301. [Google Scholar] [CrossRef]
- He, L.; Liu, K.; He, Z.; Cao, L. Three-dimensional holographic communication system for the metaverse. Opt. Commun. 2023, 526, 128894. [Google Scholar] [CrossRef]
- Aiello, A.; Töppel, F.; Marquardt, C.; Giacobino, E.; Leuchs, G. Quantum-like nonseparable structures in optical beams. New J. Phys. 2015, 17, 043024. [Google Scholar] [CrossRef]
- Forbes, A.; Aiello, A.; Ndagano, B. Classically entangled light. Prog. Opt. 2019, 64, 99–153. [Google Scholar] [CrossRef]
- Goldstein, D. Polarized Light, Revised and Expanded, 2nd ed.; Marcel Dekker Inc.: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Bengtsson, I.; Zyczkowski, K. Geometry of Quantum States; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Saito, S. Photonic quantum chromodynamics. Front. Phys. 2023, 11, 1225488. [Google Scholar] [CrossRef]
- Padgett, M.J.; Courtial, J. Poincaré-sphere equivalent for light beams containing orbital angular momentum. Opt. Lett. 1999, 24, 430–432. [Google Scholar] [CrossRef]
- Milione, G.; Sztul, H.I.; Nolan, D.A.; Alfano, R.R. Higher-order Poincaré sphere, Stokes parameters, and the angular momentum of light. Phys. Rev. Lett. 2011, 107, 053601. [Google Scholar] [CrossRef]
- Milione, G.; Evans, S.; Nolan, D.A.; Alfano, R.R. Higher order Pancharatnam-Berry phase and the angular momentum of light. Phys. Rev. Lett. 2012, 108, 190401. [Google Scholar] [CrossRef]
- Yang, L.P. Geometric phase for twisted light. Opt. Express 2023, 31, 10287–10296. [Google Scholar] [CrossRef]
- Gutiérrez-Cuevas, R.; Dennis, M.R.; Alonso, M.A. Generalized Gaussian beams in terms of Jones vectors. J. Opt. 2019, 21, 084001. [Google Scholar] [CrossRef]
- Dennis, M.R.; Alonso, M.A. Gaussian mode families from systems of rays. J. Phys. Photonics 2019, 1, 025003. [Google Scholar] [CrossRef]
- Gutiérrez-Cuevas, R.; Wadood, S.A.; Vamivakas, A.N.; Alonso, M.A. Modal Majorana sphere and hidden symmetries of structured-Gaussian beams. Phys. Rev. Lett. 2020, 125, 123903. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Wang, Z.; Fu, X.; Naidoo, D.; Forbes, A. SU(2) Poincaré sphere: A generalized representation for multidimensional structured light. Phys. Rev. A 2020, 102, 031501(R). [Google Scholar] [CrossRef]
- Shen, Y. Rays, waves, SU(2) symmetry and geometry: Toolkits for structured light. J. Opt. 2021, 23, 124004. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, J.; Lu, X.; Wang, Z.; Zhao, C.; Cai, Y. Review on fractional vortex beam. Nanophotonics 2022, 11, 241–273. [Google Scholar] [CrossRef]
- Götte, J.B.; Franke-Arnold, S.; Zambrini, R.; Barnett, S.M. Quantum formulation of fractional orbital angular momentum. J. Mod. Opt. 2007, 54, 1723–1738. [Google Scholar] [CrossRef]
- Oemrawsingh, S.S.R.; Ma, X.; Voigt, D.; Aiello, A.; Eliel, E.R.; ’t Hooft, G.W.; Woerdman, J.P. Experimental demonstration of fractional orbital angular momentum Entanglement of two photons. Phys. Rev. Lett. 2005, 95, 240501. [Google Scholar] [CrossRef] [PubMed]
- Sit, A.; Bouchard, F.; Fickler, R.; Gagnon-Bischoff, J.; Larocque, H.; Heshami, K.; Elser, D.; Peuntinger, C.; Günthner, K.; Heim, B.; et al. High-dimensional intracity quantum cryptography with structured photons. Optica 2017, 4, 1006–1010. [Google Scholar] [CrossRef]
- Bouchard, F.; Fickler, R.; Boyd, R.W.; Karimi, E. High-dimensional quantum cloning and applications to quantum hacking. Sci. Adv. 2017, 3, e1601915. [Google Scholar] [CrossRef]
- Ndagano, B.; Perez-Garcia, B.; Roux, F.S.; McLaren, M.; Rosales-Guzman, C.; Zhang, Y.; Mouane, O.; Hernandez-Aranda, R.I.; Konrad, T.; Forbes, A. Characterizing quantum channels with non-separable states of classical light. Nat. Phys. 2017, 13, 397–402. [Google Scholar] [CrossRef]
- Nape, I.; Singh, K.; Klug, A.; Buono, W.; Rosales-Guzman, C.; McWilliam, A.; Franke-Arnold, S.; Kritzinger, A.; Forbes, P.; Dudley, A.; et al. Revealing the invariance of vectorial structured light in complex media. Nat. Photonics 2022, 16, 538–546. [Google Scholar] [CrossRef]
- Sekga, C.; Mafu, M. Measurement device-independent quantum key distribution with vector vortex modes under diverse weather conditions. Sci. Rep. 2023, 13, 14931. [Google Scholar] [CrossRef] [PubMed]
- Klug, A.; Peters, C.; Forbes, A. Robust structured light in atmospheric turbulence. Adv. Photonics 2023, 5, 016006. [Google Scholar] [CrossRef]
- Bai, X.; Wang, Y.; Dai, K. Classification of 270 classes of vector vortex beams using Machine learning-based methods. Optik 2023, 291, 171362. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Science 2001, 412, 313–316. [Google Scholar] [CrossRef]
- Khoury, A.Z.; Souto Ribeiro, P.H.; Dechoum, K. Transfer of angular spectrum in parametric down-conversion with structured light. Phys. Rev. A 2020, 102, 033708. [Google Scholar] [CrossRef]
- Trajtenberg-Mills, S.; Karnieli, A.; Voloch-Bloch, N.; Megidish, E.; Eisenberg, H.S.; Arie, A. Simulating correlations of structured spontaneously down-converted photon pairs. Laser Photonics Rev. 2020, 14, 1900321. [Google Scholar] [CrossRef]
- Rodrigues, R.B.; Alves, G.B.; Barros, R.F.; Souza, C.E.R.; Khoury, A.Z. Generalized orbital angular momentum symmetry in parametric amplification. Phys. Rev. A 2022, 105, 013510. [Google Scholar] [CrossRef]
- Pinheiro da Silva, B.; Buono, W.T.; Pereira, L.J.; Tasca, D.S.; Dechoum, K.; Khoury, A.Z. Spin to orbital angular momentum transfer in frequency up-conversion. Nanophotonics 2022, 11, 771–778. [Google Scholar] [CrossRef]
- Buono, W.T.; Forbes, A. Nonlinear optics with structured light. Opto-Electron. Adv. 2022, 5, 210174. [Google Scholar] [CrossRef]
- Maruca, S.; Kumar, S.; Meng Sua, Y.; Chen, J.Y.; Shahverdi, A.; Huang, Y.P. Quantum Airy photons. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 175501. [Google Scholar] [CrossRef]
- Lib, O.; Bromberg, Y. Spatially entangled Airy photons. Opt. Lett. 2020, 45, 1399–1402. [Google Scholar] [CrossRef] [PubMed]
- Pimenta, R.C.S.; Santos, G.H.d.; Barreto, A.B.; Celeri, L.C.; Ribeiro, P.H.S. Photonic entanglement with accelerated light. Quantum 2024, 8, 1317. [Google Scholar] [CrossRef]
- Gréblacher, S.; Jennewein, T.; Vaziri, A.; Weihs, G.; Zeilinger, A. Experimental quantum cryptography with qutrits. New J. Phys. 2006, 8, 75. [Google Scholar] [CrossRef]
- Mirhosseini, M.; Magaña-Loaiza, O.S.; O’Sullivan, M.N.; Rodenburg, B.; Malik, M.; Lavery, M.P.J.; Padgett, M.J.; Gauthier, D.J.; Boyd, R.W. High-dimensional quantum cryptography with twisted light. New J. Phys. 2015, 17, 033033. [Google Scholar] [CrossRef]
- Mafu, M.; Dudley, A.; Goyal, S.; Giovannini, D.; McLaren, M.; Padgett, M.J.; Konrad, T.; Petruccione, F.; Lütkenhaus, N.; Forbes, A. Higher-dimensional orbital-angular-momentum-based quantum key distribution with mutually unbiased bases. Phys. Rev. A 2013, 88, 032305. [Google Scholar] [CrossRef]
- Fickler, R.; Lapkiewicz, R.; Plick, W.N.; Krenn, M.; Schaeff, C.; Ramelow, S.; Zeilinger, A. Quantum Entanglement of High Angular Momenta. Science 2012, 338, 640–643. [Google Scholar] [CrossRef] [PubMed]
- Fickler, R.; Campbell, G.; Buchlerd, B.; Lamd, P.K.; Zeilinger, A. Quantum entanglement of angular momentum states with quantum numbers up to 10,010. Proc. Natl. Acad. Sci. USA 2016, 113, 13642–13647. [Google Scholar] [CrossRef]
- Stav, T.; Faerman, A.; Maguid, E.; Oren, D.; Kleiner, V.; Hasman, E.; Segev, M. Quantum entanglement of the spin and orbital angular momentum of photons using metamaterials. Science 2018, 361, 1101–1104. [Google Scholar] [CrossRef]
- Nagali, E.; Sciarrino, F. Generation of hybrid polarization-orbital angular momentum entangled states. Opt. Express 2010, 18, 18243. [Google Scholar] [CrossRef]
- Shen, Y.; Rosales-Guzmán, C. Nonseparable states of light: From quantum to classical. Laser Photonics Rev. 2022, 16, 2100533. [Google Scholar] [CrossRef]
- Graffitti, F.; D’Ambrosio, V.; Proietti, M.; Ho, J.; Piccirillo, B.; de Lisio, C.; Marrucci, L.; Fedrizzi, A. Hyperentanglement in structured quantum light. Phys. Rev. Res. 2020, 2, 043350. [Google Scholar] [CrossRef]
- Chen, J.; Qi, G.z.; Wu, Y.; Shi, Y.; Zhao, C.l.; Jin, S.z. Partially coherent twisted vector vortex beam enabling manipulation of high-dimensional classical entanglement. Opt. Express 2023, 31, 38305. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Tie, X.; Tan, Z.; Wang, X.; Lei, S.; Wu, P. Recognizing OAM Modes of Electromagnetic Laguerre-Gaussian Schell-Model Vortex Beams in Atmospheric Turbulence from Polarization. Adv. Quantum Technol. 2023, 6, 2300233. [Google Scholar] [CrossRef]
- Hai, L.; Zhang, Z.; Liu, S.; Li, L.; Zhou, Z.; Wang, Q.; Gao, Y.; Gao, C.; Shen, Y.; Fu, S. Intra-Cavity Laser Manipulation of High-Dimensional Non-Separable States. Laser Photonics Rev. 2024, 18, 2300593. [Google Scholar] [CrossRef]
- Kopf, L.; Barros, R.; Fickler, R. Correlating Space, Wavelength, and Polarization of Light: Spatiospectral Vector Beams. ACS Photonics 2024, 11, 241–246. [Google Scholar] [CrossRef]
- Malik, M.; Erhard, M.; Huber, M.; Krenn, M.; Fickler, R.; Zeilinger, A. Multi-photon entanglement in high dimensions. Nat. Photon. 2016, 10, 248–252. [Google Scholar] [CrossRef]
- Wang, X.L.; Luo, Y.H.; Huang, H.L.; Chen, M.C.; Su, Z.E.; Liu, C.; Chen, C.; Li, W.; Fang, Y.Q.; Jiang, X.; et al. 18-Qubit entanglement with six photons’ three degrees of freedom. Phys. Rev. Lett. 2018, 120, 260502. [Google Scholar] [CrossRef] [PubMed]
- Krenn, M.; Huber, M.; Fickler, R.; Lapkiewicz, R.; Ramelowa, S.; Zeilinger, A. Generation and confirmation of a (100 × 100)-dimensional entangled quantum system. Proc. Natl. Acad. Sci. USA 2014, 111, 6243–6247. [Google Scholar] [CrossRef] [PubMed]
- Forbes, A.; Nape, I. Quantum mechanics with patterns of light: Progress in high dimensional and multidimensional entanglement with structured light. AVS Quantum Sci. 2019, 1, 011701. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, Y.; D’Errico, A.; Sit, A.; Heshami, K.; Karimi, E. Full Spatial Characterization of Entangled Structured Photons. Phys. Rev. Lett. 2024, 132, 063802. [Google Scholar] [CrossRef] [PubMed]
- Peters, C.; Ornelas, P.; Nape, I.; Forbes, A. Spatially resolving classical and quantum entanglement with structured photons. Phys. Rev. A 2023, 108, 053502. [Google Scholar] [CrossRef]
- Ye, Y.H.; Zeng, L.; Dong, M.X.; Zhang, W.H.; Li, E.Z.; Li, D.C.; Guo, G.C.; Ding, D.S.; Shi, B.S. Long-lived memory for orbital angular momentum quantum states. Phys. Rev. Lett. 2022, 129, 193601. [Google Scholar] [CrossRef]
- Zhou, Z.Q.; Hua, Y.L.; Liu, X.; Chen, G.; Xu, J.S.; Han, Y.J.; Li, C.F.; Guo, G.C. Quantum storage of three-dimensional orbital-angular-momentum entanglement in a crystal. Phys. Rev. Lett. 2015, 115, 070502. [Google Scholar] [CrossRef]
- Fickler, R.; Lapkiewicz, R.; Huber, M.; Lavery, M.P.J.; Padgett, M.J.; Zeilinger, A. Interface between path and orbital angular momentum entanglement for high-dimensional photonic quantum information. Nat. Commun. 2014, 5, 4502. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Y.; Qi, Z.; Feng, J.; Zheng, Y.; Chen, X. A two-way photonic quantum entanglement transfer interface. Npj Quantum Inf. 2022, 8, 8. [Google Scholar] [CrossRef]
- Cozzolino, D.; Bacco, D.; Da Lio, B.; Ingerslev, K.; Ding, Y.; Dalgaard, K.; Kristensen, P.; Galili, M.; Rottwitt, K.; Ramachandran, S.; et al. Orbital angular momentum states enabling fiber-based high-dimensional quantum communication. Phys. Rev. Appl. 2019, 11, 064058. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, D.; Zhang, W.; Chen, L. Structured-pump-enabled quantum pattern recognition. Phys. Rev. Lett. 2019, 122, 123901. [Google Scholar] [CrossRef]
- Uribe-Patarroyo, N.; Fraine, A.; Simon, D.S.; Minaeva, O.; Sergienko, A.V. Object identification using correlated orbital angular momentum states. Phys. Rev. Lett. 2013, 110, 043601. [Google Scholar] [CrossRef]
- Franke-Arnold, S. Optical angular momentum and atoms. Philos. Trans. R. Soc. A 2017, 375, 20150435. [Google Scholar] [CrossRef]
- Barnett, S.M.; Speirits, F.C.; Babiker, M. Optical angular momentum in atomic transitions: A paradox. J. Phys. A Math. Theor. 2022, 55, 234008. [Google Scholar] [CrossRef]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef]
- Picón, A.; Benseny, A.; Mompart, J.; Vázquez de Aldana, J.R.; Plaja, L.; Calvo, G.F.; Roso, L. Transferring orbital and spin angular momenta of light to atoms. New J. Phys. 2010, 12, 083053. [Google Scholar] [CrossRef]
- Barnett, S.M.; Berry, M.V. Superweak momentum transfer near optical vortices. J. Opt. 2013, 15, 125701. [Google Scholar] [CrossRef]
- Afanasev, A.; Carlson, C.E.; Mukherjee, A. Superkicks and the photon angular and linear momentum density. Phys. Rev. A 2022, 105, L061503. [Google Scholar] [CrossRef]
- Sola, I.R.; Malinovsky, V.S.; Ahn, J.; Shin, S.; Chang, B.Y. Two-qubit atomic gates: Spatio-temporal control of Rydberg interaction. Nanoscale 2023, 15, 4325. [Google Scholar] [CrossRef]
- Ishihara, J.; Mori, T.; Suzuki, T.; Sato, S.; Morita, K.; Kohda, M.; Ohno, Y.; Miyajima, K. Imprinting spatial helicity structure of vector vortex beam on spin texture in semiconductors. Phys. Rev. Lett. 2023, 130, 126701. [Google Scholar] [CrossRef]
- Andersen, M.F.; Ryu, C.; Cladé, P.; Natarajan, V.; Vaziri, A.; Helmerson, K.; Phillips, W.D. Quantized Rotation of Atoms from Photons with Orbital Angular Momentum. Phys. Rev. Lett. 2006, 97, 170406. [Google Scholar] [CrossRef]
- Wright, K.C.; Leslie, L.S.; Bigelow, N.P. Optical control of the internal and external angular momentum of a Bose-Einstein condensate. Phys. Rev. A 2008, 77, 041601. [Google Scholar] [CrossRef]
- Trawi, F.; Billard, F.; Faucher, O.; Béjot, P.; Hertz, E. Molecular Quantum Interface for Storing and Manipulating Ultrashort Optical Vortex. Laser Photonics Rev. 2023, 17, 2200525. [Google Scholar] [CrossRef]
- Verde, M.; Schmiegelow, C.T.; Poschinger, U.; Schmidt-Kaler, F. Trapped atoms in spatially-structured vector light fields. Sci. Rep. 2023, 13, 21283. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Y.; Li, M.; Liu, K.; Ciappina, M.F.; Lu, P. Atomic photoionization by spatiotemporal optical vortex pulses. Phys. Rev. A 2023, 107, 033112. [Google Scholar] [CrossRef]
- Berry, M.V.; Dennis, M.R. Quantum cores of optical phase singularities. J. Opt. A Pure Appl. Opt. 2004, 6, S178–S180. [Google Scholar] [CrossRef]
- Barnett, S.M. On the quantum core of an optical vortex. J. Mod. Opt. 2014, 55, 2279–2292. [Google Scholar] [CrossRef]
- Simpson, N.B.; Dholakia, K.; Allen, L.; Padgett, M.J. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt. Lett. 1997, 22, 52–54. [Google Scholar] [CrossRef] [PubMed]
- Friese, M.E.J.; Enger, J.; Rubinsztein-Dunlop, H.; Heckenberg, N.R. Optical angular-momentum transfer to trapped absorbing particles. Phys. Rev. A 1996, 54, 1593–1596. [Google Scholar] [CrossRef]
- O’Neil, A.T.; MacVicar, I.; Allen, L.; J, P.M. Intrinsic and Extrinsic Nature of the Orbital Angular Momentum of a Light Beam. Phys. Rev. Lett. 2002, 88, 053601. [Google Scholar] [CrossRef] [PubMed]
- Curtis, J.; Grier, D. Structure of optical vortices. Phys. Rev. Lett. 2003, 90, 133901. [Google Scholar] [CrossRef] [PubMed]
- Garcés-Chávez, V.; McGloin, D.; Padgett, M.J.; Dultz, W.; Schmitzer, H.; Dholakia, K. Observation of the Transfer of the Local Angular Momentum Density of a Multiringed Light Beam to an Optically Trapped Particle. Phys. Rev. Lett. 2003, 91, 103601. [Google Scholar] [CrossRef]
- Li, M.; Yan, S.; Yao, B.; Liang, Y.; Zhang, P. Spinning and orbiting motion of particles in vortex beams with circular or radial polarizations. Opt. Express 2016, 24, 20604–20612. [Google Scholar] [CrossRef]
- Babiker, M.; Andrews, D.L.; Lembessis, V.E. Atoms in complex twisted light. J. Opt. 2019, 21, 013001. [Google Scholar] [CrossRef]
- Ng, J.; Lin, Z.; Chan, C.T. Theory of Optical Trapping by an Optical Vortex Beam. Phys. Rev. Lett. 2010, 104, 103601. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ren, Y.X.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- Li, M.; Yan, S.; Zhang, Y.; Zhou, Y.; Yao, B. Orbital angular momentum in optical manipulations. J. Opt. 2022, 24, 114001. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 243–248. [Google Scholar] [CrossRef]
- Stickler, B.A.; Hornberger, K.; Kim, M.S. Quantum rotations of nanoparticles. Nat. Rev. 2021, 3, 589–597. [Google Scholar] [CrossRef]
- Stickler, B.A.; Papendell, B.; Kuhn, S.; Schrinski, B.; Millen, J.; Arndt, M.; Hornberger, K. Probing macroscopic quantum superpositions with nanorotors. New J. Phys. 2018, 20, 122001. [Google Scholar] [CrossRef]
- Zhao, R.; Manjavacas, A.; García de Abajo, F.J.; Pendry, J.B. Rotational Quantum Friction. Phys. Rev. Lett. 2012, 109, 123604. [Google Scholar] [CrossRef]
- Wood, A.A.; Hollenberg, L.C.L.; Scholten, R.E.; Martin, A.M. Observation of a Quantum Phase from Classical Rotation of a Single Spin. Phys. Rev. Lett. 2020, 124, 020401. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Kingsley-Smith, J.J.; Nikkhou1, M.; Sabin, J.A.; Rodríguez-Fortuño, F.J.; Xu, X.; Millen, J. Structured transverse orbital angular momentum probed by a levitated optomechanical sensor. Nat. Commun. 2023, 14, 2638. [Google Scholar] [CrossRef]
- Li, C.; Jang, J.; Badloe, T.; Yang, T.; Kim, J.; Kim, J.; Nguyen, M.; Maier, S.A.; Rho, J.; Ren, H.; et al. Arbitrarily structured quantum emission with a multifunctional metalens. eLight 2023, 3, 19. [Google Scholar] [CrossRef]
- Liang, H.; Ahmed, H.; Tam, W.Y.; Chen, X.; Li, J. Continuous heralding control of vortex beams using quantum metasurface. Commun. Phys. 2023, 6, 140. [Google Scholar] [CrossRef]
- Liu, X.; Kan, Y.; Kumar, S.; Kulikova, L.F.; Davydov, V.A.; Agafonov, V.N.; Zhao, C.; Bozhevolnyi, S.I. Ultracompact Single-Photon Sources of Linearly Polarized Vortex Beams. Adv. Mater. 2024, 36, 2304495. [Google Scholar] [CrossRef]
- Li, Z.; Guo, H.; Liu, H.; Li, J.; Sun, H.; Yang, R.; Liu, K.; Gao, J. Higher-order spatially squeezed beam for enhanced spatial measurements. Adv. Quantum Technol. 2022, 5, 2200055. [Google Scholar] [CrossRef]
- Heinze, J.; Willke, B.; Vahlbruch, H. Observation of squeezed states of light in higher-order Hermite-Gaussian modes with a quantum noise reduction of up to 10 dB. Phys. Rev. Lett. 2022, 128, 083606. [Google Scholar] [CrossRef]
- Goldberg, A.Z.; de la Hoz, P.; Björk, G.; Klimov, A.B.; Grassl, M.; Leuchs, G.; Sánchez-Soto, L.L. Quantum concepts in optical polarization. Adv. Opt. Photonics 2021, 13, 1–73. [Google Scholar] [CrossRef]
- Yang, L.P.; Jacob, Z. Non-classical photonic spin texture of quantum structured light. Commun. Phys. 2021, 4, 221. [Google Scholar] [CrossRef]
- Andrews, D.L. Symmetry and quantum features in optical vortices. Symmetry 2021, 13, 1368. [Google Scholar] [CrossRef]
- Williams, M.D.; Bradshaw, D.S.; Andrews, D.L. Quantum issues with structured light. Proc. SPIE 2016, 9764, 976407. [Google Scholar] [CrossRef]
- Smith, B.J.; Raymer, M.G. Photon wave functions, wave-packet quantization of light, and coherence theory. New J. Phys. 2007, 9, 414. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Bialynicka-Birula, Z. Quantum numbers and spectra of structured light. Phys. Scr. 2018, 93, 104005. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I. Helicity amplitudes, polarization of EM waves and Stokes parameters: Classical versus quantum theory. J. Opt. 2019, 21, 094002. [Google Scholar] [CrossRef]
- Nienhuis, G. Analogies between optical and quantum mechanical angular momentum. Philos. Trans. R. Soc. A 2017, 375, 20150443. [Google Scholar] [CrossRef]
- Sugic, D.; Droop, R.; Otte, E.; Ehrmanntraut, D.; Nori, F.; Ruostekoski, J.; Denz, C.; Dennis, M.R. Particle-like topologies in light. Nat. Commun. 2021, 12, 6785. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Zhang, Q.; Shi, P.; Du, L.; Yuan, X.; Zayats, A.V. Optical skyrmions and other topological quasiparticles of light. Nat. Photon. 2024, 18, 15–25. [Google Scholar] [CrossRef]
- Tamburini, F.; Thidé, B.; Licata, I.; Bouchard, F.; Karimi, E. Majorana bosonic quasiparticles from twisted photons in free space. Phys. Rev. A 2021, 103, 033505. [Google Scholar] [CrossRef]
- Li, Z.X.; Ruan, Y.P.; Tang, J.; Liu, Y.; Liu, J.J.; Tang, J.S.; Zhang, H.; Xia, K.Y.; Lu, Y.Q. Self-healing of a heralded single-photon Airy beam. Opt. Express 2021, 29, 40187. [Google Scholar] [CrossRef]
- Nape, I.; Otte, E.; Vallés, A.; Rosales-Guzmán, C.; Cardano, F.; Denz, C.; Forbes, A. Self-healing high-dimensional quantum key distribution using hybrid spin-orbit Bessel states. Opt. Express 2018, 26, 26946. [Google Scholar] [CrossRef]
- McLaren, M.; Mhlanga, T.; Padgett, M.J.; Roux, F.S.; Forbes, A. Self-healing of quantum entanglement after an obstruction. Nat. Commun. 2014, 5, 3248. [Google Scholar] [CrossRef]
- Yang, D.; Yu, Z.; Wang, W.; Hu, Z.D.; Zhu, Y. Underwater entanglement propagation of auto-focusing Airy beams. Opt. Express 2024, 32, 4887. [Google Scholar] [CrossRef]
- Giovannini, D.; Romero, J.; Potoček, V.; Ferenczi, G.; Speirits, F.; Barnett, S.M.; Faccio, D.; Padgett, M.J. Spatially structured photons that travel in free space slower than the speed of light. Science 2015, 347, 857–860. [Google Scholar] [CrossRef]
- Petrov, N.I. Speed of structured light pulses in free space. Sci. Rep. 2019, 9, 18332. [Google Scholar] [CrossRef]
- Silenko, A.J.; Zhang, P.; Zou, L. Relativistic quantum-mechanical description of twisted paraxial electron and photon beams. Phys. Rev. A 2019, 100, 030101(R). [Google Scholar] [CrossRef]
- Shen, Y.; Nape, I.; Yang, X.; Fu, X.; Gong, M.; Naidoo, D.; Forbes, A. Creation and control of high-dimensional multi-partite classically entangled light. Light Sci. Appl. 2021, 10, 50. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Wang, Z.; Yang, X.; Shen, Y.; Fu, X. Digitally tailoring arbitrary structured light of generalized ray-wave duality. Opt. Express 2020, 28, 31043. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Zdagkas, A.; Papasimakis, N.; Zheludev, N.I. Measures of space-time nonseparability of electromagnetic pulses. Phys. Rev. Res. 2021, 3, 013236. [Google Scholar] [CrossRef]
- Gomes, R.M.; Salles, A.; Toscano, F.; Souto Ribeiro, P.H.; Walborn, S.P. Observation of a nonlocal optical vortex. Phys. Rev. Lett. 2009, 103, 033602. [Google Scholar] [CrossRef]
- Qi, W.R.; Liu, R.; Kong, L.J.; Wang, Z.X.; Huang, S.Y.; Tu, C.; Li, Y.; Wang, H.T. Double-slit interference of single twisted photons. Chin. Opt. Lett. 2020, 18, 102601. [Google Scholar] [CrossRef]
- Aili, M.; Liu, P.; Chen, X.X.; Wu, Q.Y.; Meng, Z.; Yang, J.Z.; Li, J.; Zhang, A.N. Double-slit experiment with multiple vortex beams. Phys. Rev. A 2024, 109, 013521. [Google Scholar] [CrossRef]
- Franke-Arnold, S.; Barnett, S.M.; Yao, E.; Leach, J.; Courtial, J.; Padgett, M. Uncertainty principle for angular position and angular momentum. New J. Phys. 2004, 6, 103. [Google Scholar] [CrossRef]
- Gounden, N.; Epstein, J.; Ornelas, P.; Beck, G.; Nape, I.; Forbes, A. Popper’s conjecture with angular slits and twisted light. Sci. Rep. 2023, 13, 21701. [Google Scholar] [CrossRef]
- Nape, I.; Ndagano, B.; Forbes, A. Erasing the orbital angular momentum information of a photon. Phys. Rev. A 2017, 95, 053859. [Google Scholar] [CrossRef]
- Zhang, Y.; Agnew, M.; Roger, T.; Roux, F.S.; Konrad, T.; Faccio, D.; Leach, J.; Forbes, A. Simultaneous entanglement swapping of multiple orbital angular momentum states of light. Nat. Commun. 2017, 8, 632. [Google Scholar] [CrossRef]
- Liu, S.; Lou, Y.; Jing, J. Orbital angular momentum multiplexed deterministic all-optical quantum teleportation. Nat. Commun. 2020, 11, 3875. [Google Scholar] [CrossRef]
- Wang, X.L.; Cai, X.D.; Su, Z.E.; Chen, M.C.; Wu, D.; Li, L.; Liu, N.L.; Lu, C.Y.; Pan, J.W. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 2015, 518, 516–519. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Roux, F.S.; Konrad, T.; Agnew, M.; Leach, J.; Forbes, A. Engineering two-photon high-dimensional states through quantum interference. Sci. Adv. 2016, 2, e1501165. [Google Scholar] [CrossRef]
- Kevin, S.; Sahrai, M.; Asadpour, S.H. Controllable Hartman effect by vortex beam in a one dimensional photonic crystal doped by graphene quantum dots. Sci. Rep. 2023, 13, 2992. [Google Scholar] [CrossRef]
- Leach, J.; Jack, B.; Romero, J.; Ritsch-Marte, M.; Boyd, R.W.; Jha, A.K.; Barnett, S.M.; Franke-Arnold, S.; Padgett, M.J. Violation of a Bell inequality in two-dimensional orbital angular momentum state-spaces. Opt. Express 2009, 17, 8287–8293. [Google Scholar] [CrossRef]
- Romero, J.; Leach, J.; Jack, B.; Barnett, S.M.; Padgett, M.J.; Franke-Arnold, S. Violation of Leggett inequalities in orbital angular momentum subspaces. New J. Phys. 2010, 12, 123007. [Google Scholar] [CrossRef]
- Dada, A.; Leach, J.; Buller, G.S.; Padgett, M.J.; Andersson, E. Experimental high-dimensional two-photon entanglement and violations of generalized Bell inequalities. Nat. Phys. 2011, 7, 677–680. [Google Scholar] [CrossRef]
- Tang, Y.; Perrie, W.; Schille, J.; Loeschner, U.; Li, Q.; Liu, D.; Edwardson, S.P.; Forbes, A.; Dearden, G. High-quality vector vortex arrays by holographic and geometric phase control. J. Phys. D Appl. Phys. 2020, 53, 465101. [Google Scholar] [CrossRef]
- Qi, W.R.; Zhou, J.; Kong, L.J.; Xu, Z.P.; Meng, H.X.; Liu, R.; Wang, Z.X.; Tu, C.; Li, Y.L.; Cabello, A.; et al. Stronger Hardy-like proof of quantum contextuality. Photonics Res. 2022, 10, 1582–1593. [Google Scholar] [CrossRef]
- Karimi, E.; Leach, J.; Slussarenko, S.; Piccirillo, B.; Marrucci, L.; Chen, L.; She, W.; Franke-Arnold, S.; Padgett, M.J.; Santamato, E. Spin-orbit hybrid entanglement of photons and quantum contextuality. Phys. Rev. A 2010, 82, 022115. [Google Scholar] [CrossRef]
- Xu, J.M.; Zhen, Y.Z.; Yang, Y.X.; Cheng, Z.M.; Ren, Z.C.; Chen, K.; Wang, X.L.; Wang, H.T. Experimental Demonstration of Quantum Pseudotelepathy. Phys. Rev. Lett. 2022, 129, 050402. [Google Scholar] [CrossRef]
- Leach, J.; Jack, B.; Romero, J.; Jha, A.K.; Yao, A.M.; Franke-Arnold, S.; Ireland, D.G.; Boyd, R.W.; Barnett, S.M.; Padgett, M.J. Quantum correlations in optical angle-orbital angular momentum variables. Science 2010, 329, 662–665. [Google Scholar] [CrossRef] [PubMed]
- Slussarenko, S.; Joch, D.J.; Tischler, N.; Ghafari, F.; Shalm, L.K.; Verma, V.B.; Nam, S.W.; Pryde, G.J. Quantum steering with vector vortex photon states with the detection loophole closed. Npj Quantum Inf. 2022, 8, 20. [Google Scholar] [CrossRef]
- Stoklasa, B.; Motka, L.; Rehacek, J.; Hradil, Z.; Sánchez-Soto, L.L.; Agarwal, G.S. Experimental violation of a Bell-like inequality with optical vortex beams. New J. Phys. 2015, 17, 113046. [Google Scholar] [CrossRef]
- González-Domínguez, M.A.; Piceno-Martínez, A.E.; Rosales-Zárate, L.E.C. Nonlocality and quantum correlations in Ince-Gauss structured light modes. J. Opt. Soc. Am. B 2023, 40, 881. [Google Scholar] [CrossRef]
- Prevedel, R.; Cronenberg, G.; Tame, M.S.; Paternostro, M.; Walther, P.; Kim, M.S.; Zeilinger, A. Experimental realization of Dicke states of up to six qubits for multiparty quantum networking. Phys. Rev. Lett. 2009, 103, 020503. [Google Scholar] [CrossRef]
- Erhard, M.; Malik, M.; Krenn, M.; Zeilinger, A. Experimental Greenberger-Horne-Zeilinger entanglement beyond qubits. Nat. Photon 2018, 12, 759–764. [Google Scholar] [CrossRef]
- Wang, F.; Erhard, M.; Babazadeh, A.; Malik, M.; Krenn, M.; Zeilinger, A. Generation of the complete four-dimensional Bell basis. Optica 2017, 4, 1462. [Google Scholar] [CrossRef]
- Kong, L.J.; Li, Y.; Liu, R.; Qi, W.R.; Wang, Q.; Wang, Z.X.; Huang, S.Y.; Si, Y.; Tu, C.; Hu, W.; et al. Complete measurement and multiplexing of orbital angular momentum Bell states. Phys. Rev. A 2019, 100, 023822. [Google Scholar] [CrossRef]
- Wang, Y.; Ru, S.; Wang, F.; Zhang, P.; Li, F. Experimental demonstration of efficient high-dimensional quantum gates with orbital angular momentum. Quantum Sci. Technol. 2022, 7, 015016. [Google Scholar] [CrossRef]
- Babazadeh, A.; Erhard, M.; Wang, F.; Malik, M.; Nouroozi, R.; Krenn, M.; Zeilinger, A. High-dimensional single-photon quantum gates: Concepts and experiments. Phys. Rev. Lett. 2017, 119, 180510. [Google Scholar] [CrossRef] [PubMed]
- Vashukevich, E.A.; Bashmakova, E.N.; Golubeva, T.Y.; Golubev, Y.M. High-fidelity quantum gates for OAM single qudits on quantum memory. Laser Phys. Lett. 2022, 19, 025202. [Google Scholar] [CrossRef]
- Bashmakova, E.N.; Vashukevich, E.A.; Golubeva, T.Y. Parallel multi-two-qubit swap gate via quantum nondemolition interaction of orbital-angular-momentum light and an atomic ensemble. Phys. Rev. A 2024, 109, 012428. [Google Scholar] [CrossRef]
- Nape, I.; Sephton, B.; Ornelas, P.; Moodley, C.; Forbes, A. Quantum structured light in high dimensions. APL Photonics 2023, 8, 051101. [Google Scholar] [CrossRef]
- Eriksson, M.; Goldberg, A.; Hiekkamäki, M.; Bouchard, F.; Rehacek, J.; Hradil, Z.; Leuchs, G.; Fickler, R.; Sánchez-Soto, L. Sensing Rotations with Multiplane Light Conversion. Phys. Rev. Appl. 2023, 20, 024052. [Google Scholar] [CrossRef]
- Jayaseelan, M.; Murphree, J.D.; Schultz, J.T.; Ruostekoski, J.; Bigelow, N.P. Topological atom optics and beyond with knotted quantum wavefunctions. Commun Phys 2024, 7, 7. [Google Scholar] [CrossRef]
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef]
- Dressel, J.; Malik, M.; Miatto, F.M.; Jordan, A.N.; Boyd, R.W. Colloquium: Understanding quantum weak values: Basics and applications. Rev. Mod. Phys. 2013, 86, 307–316. [Google Scholar] [CrossRef]
- Forbes, A. Structured light from lasers. Laser Photonics Rev. 2019, 13, 1900140. [Google Scholar] [CrossRef]
- Resch, K.J.; Lundeen, J.S.; Steinberg, A.M. Experimental realization of the quantum box problem. Phys. Lett. 2004, 324, 125–131. [Google Scholar] [CrossRef]
- Ashby, J.M.; Schwarz, P.D.; Schlosshauer, M. Observation of the quantum paradox of separation of a single photon from one of its properties. Phys. Rev. A 2016, 94, 012102. [Google Scholar] [CrossRef]
- Kumar Pan, A. Disembodiment of arbitrary number of properties in quantum Cheshire cat experiment. Eur. Phys. J. D 2020, 74, 151. [Google Scholar] [CrossRef]
- Kocsis, S.; Braverman, B.; Ravets, S.; Stevens, M.J.; Mirin, R.P.; Shalm, L.K.; Steinberg, A.M. Observing the average trajectories of single photons in a two-slit interferometer. Science 2011, 332, 1170–1173. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Bekshaev, A.Y.; Kofman, A.G.; Nori, F. Photon trajectories, anomalous velocities and weak measurements: A classical interpretation. New J. Phys. 2013, 15, 073022. [Google Scholar] [CrossRef]
- Li, Y.; Ren, Z.C.; Kong, L.J.; Tu, C.; Wang, H.T. Trajectory-based unveiling of the angular momentum of photons. Phys. Rev. A 2017, 95, 043830. [Google Scholar] [CrossRef]
- Berry, M.V. Optical currents. J. Opt. A: Pure Appl. Opt. 2009, 11, 094001. [Google Scholar] [CrossRef]
- Berry, M.V. Quantum backflow, negative kinetic energy, and optical retro-propagation. J. Phys. A Math. Theor. 2010, 43, 415302. [Google Scholar] [CrossRef]
- Ghosh, B.; Daniel, A.; Gorzkowski, B.; Lapkiewicz, R. Azimuthal backflow in light carrying orbital angular momentum. Optica 2023, 10, 1217. [Google Scholar] [CrossRef]
- Lundeen, J.S.; Sutherland, B.; Patel, A.; Stewart, C.; Bamber, C. Direct measurement of the quantum wavefunction. Nature 2011, 474, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Malik, M.; Mirhosseini, M.; Lavery, M.P.J.; Leach, J.; Padgett, M.J.; Boyd, R.W. Direct measurement of a 27-dimensional orbital-angular-momentum state vector. Nat. Commun. 2014, 5, 3115. [Google Scholar] [CrossRef]
- Shi, Z.; Mirhosseini, M.; Margiewicz, J.; Malik, M.; Rivera, F.; Zhu, Z.; Boyd, R.W. Scan-free direct measurement of an extremely high-dimensional photonic state. Optica 2015, 2, 388–392. [Google Scholar] [CrossRef]
- Mirhosseini, M.; Lundeen, J.S.; Boyd, R.W. Direct measurement of the photon’s spatial wave function. In Quantum Photonics: Pioneering Advances and Emerging Applications; Springer Nature Switzerland AG: Cham, Switzerland, 2019; pp. 25–49. [Google Scholar] [CrossRef]
- Zhang, C.R.; Hu, M.J.; Hou, Z.B.; Tang, J.F.; Zhu, J.; Xiang, G.Y.; Li, C.F.; Guo, G.C.; Zhang, Y.S. Direct measurement of the two-dimensional spatial quantum wave function via strong measurements. Phys. Rev. A 2020, 101, 012119. [Google Scholar] [CrossRef]
- Zhang, C.R.; Hu, M.J.; Xiang, G.Y.; Zhang, Y.S.; Li, C.F.; Guo, G.C. Direct strong measurement of a high-dimensional quantum state. Chin. Phys. Lett. 2020, 37, 080301. [Google Scholar] [CrossRef]
- Yang, M.; Xiao, Y.; Liao, Y.W.; Liu, Z.H.; Xu, X.Y.; Xu, J.S.; Li, C.F.; Guo, G.C. Zonal reconstruction of photonic wavefunction via momentum weak measurement. Laser Photonics Rev. 2020, 14, 1900251. [Google Scholar] [CrossRef]
- de Lima Bernardo, B.; Azevedo, S.; Rosas, A. Simplified algebraic description of weak measurements with Hermite-Gaussian and Laguerre-Gaussian pointer states. Opt. Commun. 2014, 331, 194–197. [Google Scholar] [CrossRef]
- Turek, Y.; Kobayashi, H.; Akutsu, T.; Sun, C.P.; Shikano, Y. Post-selected von Neumann measurement with Hermite-Gaussian and Laguerre-Gaussian pointer states. New J. Phys. 2015, 17, 083029. [Google Scholar] [CrossRef]
- Kobayashi, H.; Nonaka, K.; Shikano, Y. Stereographical visualization of a polarization state using weak measurements with an optical-vortex beam. Phys. Rev. A 2014, 89, 053816. [Google Scholar] [CrossRef]
- Tukiainen, M.; Kobayashi, H.; Shikano, Y. Quantification of concurrence via weak measurement. Phys. Rev. A 2017, 95, 052301. [Google Scholar] [CrossRef]
- Xia, B.; Huang, J.; Li, H.; Liu, M.; Xiao, T.; Chen, F.; Zeng, G. Ultrasensitive measurement of angular rotations via a Hermite-Gaussian pointer. Photonics Res. 2022, 10, 2816–2827. [Google Scholar] [CrossRef]
- Xia, B.; Huang, J.; Fang, C.; Li, H.; Zeng, G. High-precision multiparameter weak measurement with Hermite-Gaussian pointer. Phys. Rev. Appl. 2020, 13, 034023. [Google Scholar] [CrossRef]
- Magaña-Loaiza, O.S.; Mirhosseini, M.; Rodenburg, B.; Boyd, R.W. Amplification of angular rotations using weak measurements. Phys. Rev. Lett. 2014, 112, 200401. [Google Scholar] [CrossRef]
- Resch, K.J.; Steinberg, A.M. Extracting joint weak values with local, single-particle measurements. Phys. Rev. Lett. 2004, 92, 130402. [Google Scholar] [CrossRef]
- Kobayashi, H.; Puentes, G.; Shikano, Y. Extracting joint weak values from two-dimensional spatial displacements. Phys. Rev. A 2012, 86, 053805. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, S.; Liang, X.; Zheng, H.; Zhong, Y.; Yu, J.; Chen, Z.; Zhang, L. Joint spatial weak measurement with higher-order Laguerre-Gaussian point states. Opt. Express 2022, 30, 17848–17857. [Google Scholar] [CrossRef]
- Puentes, G.; Hermosa, N.; Torres, J.P. Weak measurements with orbital-angular-momentum pointer states. Phys. Rev. Lett. 2012, 109, 040401. [Google Scholar] [CrossRef]
- Qiu, J.; Ren, C.; Zhang, Z. Precisely measuring the orbital angular momentum of beams via weak measurement. Phys. Rev. A 2016, 93, 063841. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, P.; Li, Q.; Wang, F.; Wang, C.; Zhou, Y.; Wang, J.; Gao, H.; Kwek, L.C.; Li, F. Measuring the topological charge of orbital angular momentum beams by utilizing weak measurement principle. Sci. Rep. 2019, 9, 7993. [Google Scholar] [CrossRef] [PubMed]
- Cormann, M.; Caudano, Y. Geometric description of modular and weak values in discrete quantum systems using the Majorana representation. J. Phys. A Math. Theor. 2017, 50, 305302. [Google Scholar] [CrossRef]
- Ballesteros Ferraz, L.; Lambert, D.L.; Caudano, Y. Geometrical interpretation of the argument of weak values of general observables in N-level quantum systems. Quantum Sci. Technol. 2022, 7, 045028. [Google Scholar] [CrossRef]
- Cormann, M.; Remy, M.; Kolaric, B.; Caudano, Y. Revealing geometric phases in modular and weak values with a quantum eraser. Phys. Rev. A 2016, 93, 042124. [Google Scholar] [CrossRef]
- Wang, B.; Li, P.; Chen, T.; Zhang, X. Accurately identifying mode indices of Laguerre-Gaussian beams via weak measurements. J. Opt. 2017, 19, 055603. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, P.; Wang, F.; Wang, Y.; Li, Q.; Liu, R.; Wang, J.; Gao, H.; Li, F. Experimentally measuring the mode indices of Laguerre-Gaussian beams by weak measurement. Opt. Express 2021, 29, 5419–5426. [Google Scholar] [CrossRef]
- Wang, A.; Zhu, J.; Luo, L.; Liu, X.; Ye, L.; Zhang, Z.; Du, J. Optical differentiation based on weak measurements. Opt. Lett. 2022, 47, 3880. [Google Scholar] [CrossRef]
- Fang, L.; Luo, L.; Zhao, R.; Liu, B. Measuring the Orbital Angular Momentum of Light Based on Optical Differentiation. IEEE Photonics J. 2023, 15, 1–7. [Google Scholar] [CrossRef]
- Bliokh, Y.K.; Aiello, A. Goos-Hänchen and Imbert-Fedorov beam shifts: An overview. J. Opt. 2013, 15, 014001. [Google Scholar] [CrossRef]
- Hosten, O.; Kwiat, P. Observation of the spin Hall effect of light via weak measurements. Science 2008, 319, 787–790. [Google Scholar] [CrossRef]
- Jayaswal, G.; Mistura, G.; Merano, M. Weak measurement of the Goos–Hänchen shift. Opt. Lett. 2013, 38, 1232–1234. [Google Scholar] [CrossRef]
- Jayaswal, G.; Mistura, G.; Merano, M. Observing angular deviations in light-beam reflection via weak measurements. Opt. Lett. 2014, 39, 6257–6260. [Google Scholar] [CrossRef]
- Goswami, S.; Pal, M.; Nandi, A.; Panigrahi, P.K.; Ghosh, N. Simultaneous weak value amplification of angular Goos-Hänchen and Imbert-Fedorov shifts in partial reflection. Opt. Lett. 2014, 39, 6229–6232. [Google Scholar] [CrossRef]
- Prajapati, C.; Viswanathan, N.K. Simultaneous weak measurement of angular and spatial Goos-Hänchen and Imbert-Fedorov shifts. J. Opt. 2017, 19, 105611. [Google Scholar] [CrossRef]
- Dennis, M.R.; Götte, J.B. The analogy between optical beam shifts and quantum weak measurements. New J. Phys. 2012, 14, 073013. [Google Scholar] [CrossRef]
- Dennis, M.R.; Götte, J.B. Beam shifts to reflected light beams and their axial structure. Proc. SPIE 2014, 9441, 94410M. [Google Scholar] [CrossRef]
- Merano, M.; Hermosa, N.; Woerdman, J.P.; Aiello, A. How orbital angular momentum affects beam shifts in optical reflection. Phys. Rev. A 2010, 82, 023817. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S.; Liu, J.; Wu, J.; Li, J. Spin-Hall Effect of Cylindrical Vector Vortex Beams. Photonics 2023, 10, 1356. [Google Scholar] [CrossRef]
- Long, W.; Pan, J.; Guo, X.; Liu, X.; Lin, H.; Zheng, H.; Yu, J.; Guan, H.; Lu, H.; Zhong, Y.; et al. Optimized weak measurement of orbital angular momentum-induced beam shifts in optical reflection. Photonics Res. 2019, 7, 1273–1278. [Google Scholar] [CrossRef]
- Mandal, S.; Das, A.; Pradhan, M. Weak measurement of the Goos-Hänchen shift for a Hermite-Gaussian laser beam. J. Opt. 2024, 26, 045403. [Google Scholar] [CrossRef]
- Prajapati, C.; Viswanathan, N.K. Enhancement of weak spin-Hall shift using higher-order helical-wavefront beams. OSA Contin. 2018, 1, 872–881. [Google Scholar] [CrossRef]
- Xie, S.; Zhu, J.; Wang, A.; Wang, Y.; Huang, Y.; Zhang, Z. Super amplification enabled by orbital angular momentum in weak measurement. Opt. Express 2024, 32, 11794. [Google Scholar] [CrossRef]
- Téppel, F.; Ornigotti, M.; Aiello, A. Goos-Hänchen and Imbert-Fedorov shifts from a quantum-mechanical perspective. New J. Phys. 2013, 15, 113059. [Google Scholar] [CrossRef]
- Shi, L.k.; Song, J.C.W. Shift vector as the geometric origin of beam shifts. Phys. Rev. B 2019, 100, 201405. [Google Scholar] [CrossRef]
- Xu, L.; Liu, Z.; Datta, A.; Knee, G.C.; Lundeen, J.S.; Lu, Y.Q.; Zhang, L. Approaching quantum-limited metrology with imperfect detectors by using weak-value amplification. Phys. Rev. Lett. 2020, 125, 080501. [Google Scholar] [CrossRef]
- Yin, X.; Hesselink, L. Goos-Hänchen shift surface plasmon resonance sensor. Appl. Phys. Lett. 2006, 89, 261108. [Google Scholar] [CrossRef]
- Wang, X.; Yin, C.; Sun, J.; Li, H.; Wang, Y.; Ran, M.; Cao, Z. High-sensitivity temperature sensor using the ultrahigh order mode-enhanced Goos-Hänchen effect. Opt. Express 2013, 11, 13380. [Google Scholar] [CrossRef]
- Xu, L.; Luo, L.; Wu, H.; Luo, Z.; Zhang, Z.; Shi, H.; Chang, T.; Wu, P.; Du, C.; Cui, H.L. Measurement of chiral molecular parameters based on a combination of surface plasmon resonance and weak value amplification. ACS Sens. 2020, 5, 2398–2407. [Google Scholar] [CrossRef] [PubMed]
- Tang, T.; Shen, K.; Li, J.; Liang, X.; Tang, Y.; Li, C.; He, Y. Optimal weak measurement scheme for chiral molecular detection based on photonic spin Hall effect. Opt. Express 2023, 31, 40308. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, S.; Zhang, Q.; Chen, Y.; Hu, X.; Zhang, H.; Zhang, Z. Complete chiroptical signal detection using weak measurement with intensity-contrast-ratio pointers. APL Photonics 2023, 8, 126102. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bokić, B.; de Coene, Y.; Ferrara, M.A.; Verbiest, T.; Caudano, Y.; Kolaric, B. Structured Light from Classical to Quantum Perspectives. Symmetry 2024, 16, 1053. https://doi.org/10.3390/sym16081053
Bokić B, de Coene Y, Ferrara MA, Verbiest T, Caudano Y, Kolaric B. Structured Light from Classical to Quantum Perspectives. Symmetry. 2024; 16(8):1053. https://doi.org/10.3390/sym16081053
Chicago/Turabian StyleBokić, Bojana, Yovan de Coene, Maria Antonietta Ferrara, Thierry Verbiest, Yves Caudano, and Branko Kolaric. 2024. "Structured Light from Classical to Quantum Perspectives" Symmetry 16, no. 8: 1053. https://doi.org/10.3390/sym16081053
APA StyleBokić, B., de Coene, Y., Ferrara, M. A., Verbiest, T., Caudano, Y., & Kolaric, B. (2024). Structured Light from Classical to Quantum Perspectives. Symmetry, 16(8), 1053. https://doi.org/10.3390/sym16081053







