Enhancing Symmetry and Memory in the Fractional Economic Growing Quantity (FEGQ) Model
Abstract
1. Introduction
- Memory augmentation of the EGQ model by introducing the fractional logistic function to the EGQ problem to describe item growth;
- Memory augmentation of the EGQ model by introducing the fractional IL to the EGQ problem;
- Memory augmentation of the EGQ model by introducing the fractional version of the total profit that implements previous fractional dynamic models;
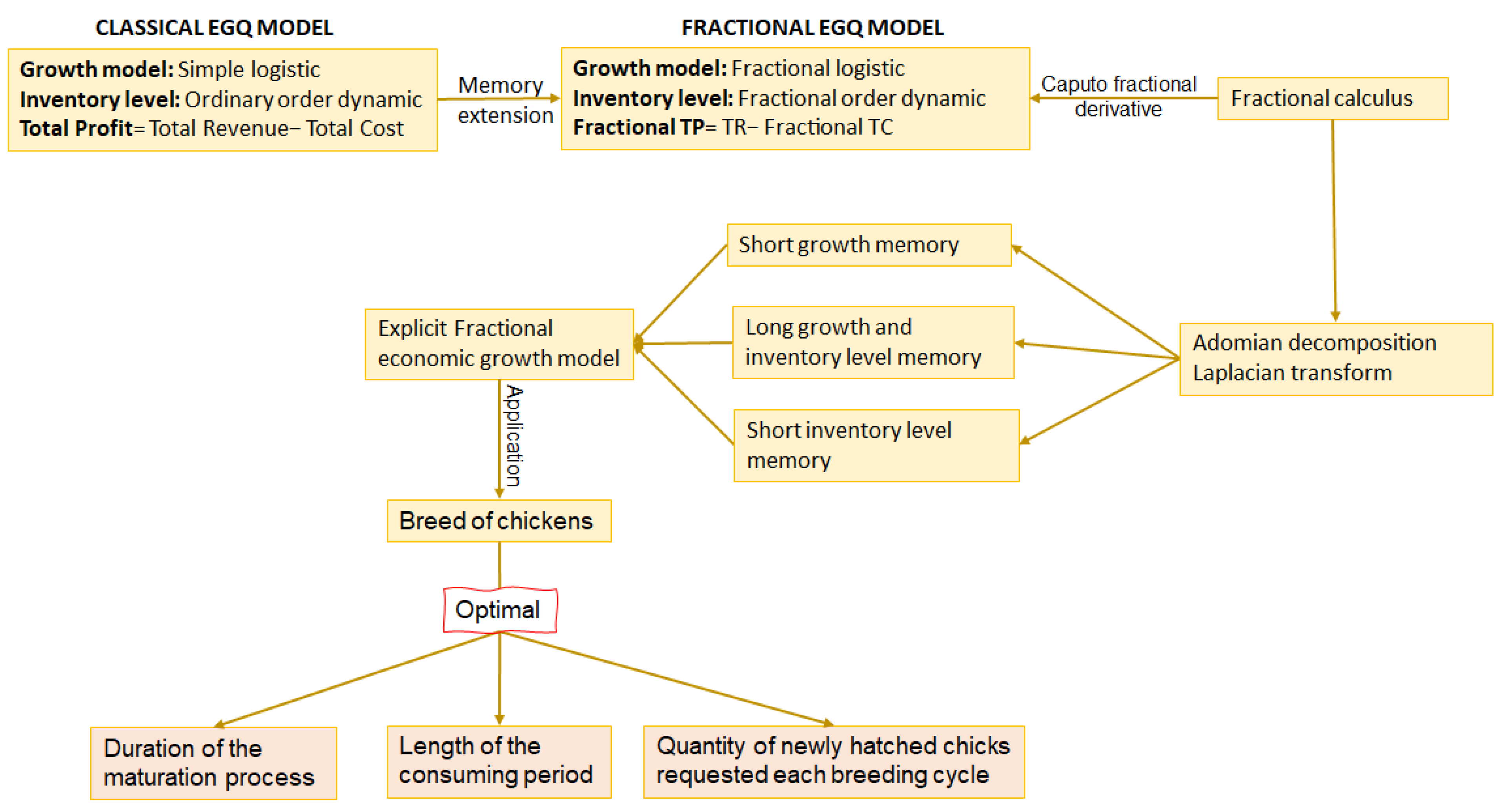
- Application of the resulting fractional economic growing quantity model, considering different fraction order, to estimate an optimal policy for a particular breed of chickens using the Adomian decomposition method.
2. Methodology
- A1
- The item’s annual demand remains consistent over time.
- A2
- The shortages are prohibited.
- A3
- The items ordered can grow before being slaughtered, and the cost of feeding them depends on the weight gained.
- A4
- The items with poorer quality and the items disposed of due to mortality are not considered.
3. Fractional Calculus Basics
3.1. Fractional Derivative of Riemann–Liouville and Caputo
3.2. Laplace Transformation of the Fractional Derivative and Integral
3.3. Principle of the Adomian Decomposition Method
3.4. Kernel-Dependent Derivative
4. Classic EGQ Model
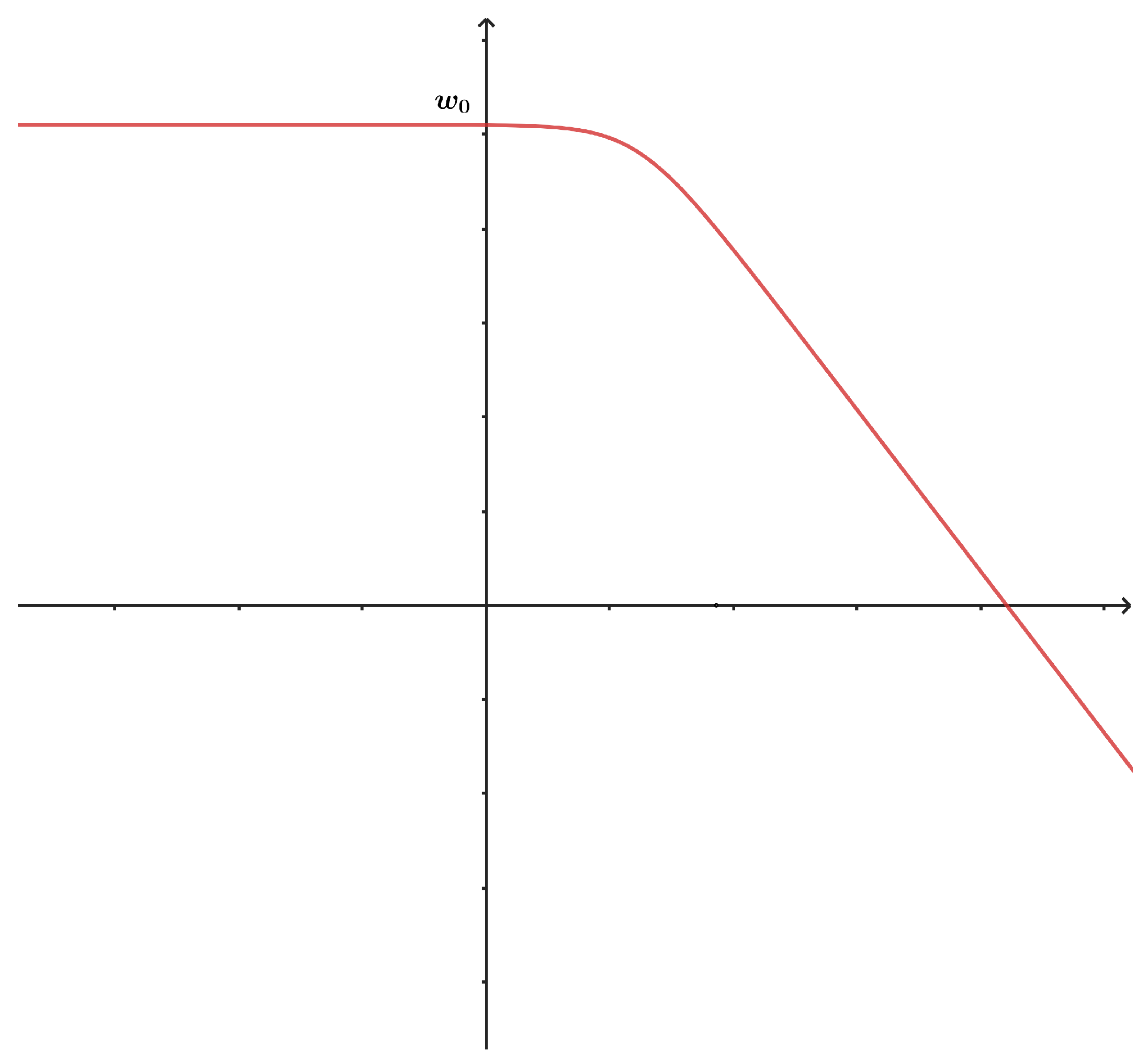
5. Proposed Fractional Economic Growing Quantity (FEGQ)
5.1. Fractional Logistic Function to EGQ Problem
5.2. Fractional IL to EGQ Problem
5.3. Fractional Economic Growth Quantity: Explicit Form
5.3.1. Classical Case: and
5.3.2. Short Holding Cost Memory: and
5.3.3. Short IL Memory: and
5.3.4. Long-Term Memory on IL and Carrying Costs
6. Experimentation
6.1. Classical EGQ Model vs. FEGQ ( and ) Model
6.2. Fractional Model with Short Holding Cost Memory: and
6.3. Fractional Model with Short IL Memory: and
6.4. Fractional Model with Long Memory IL and Holding Cost
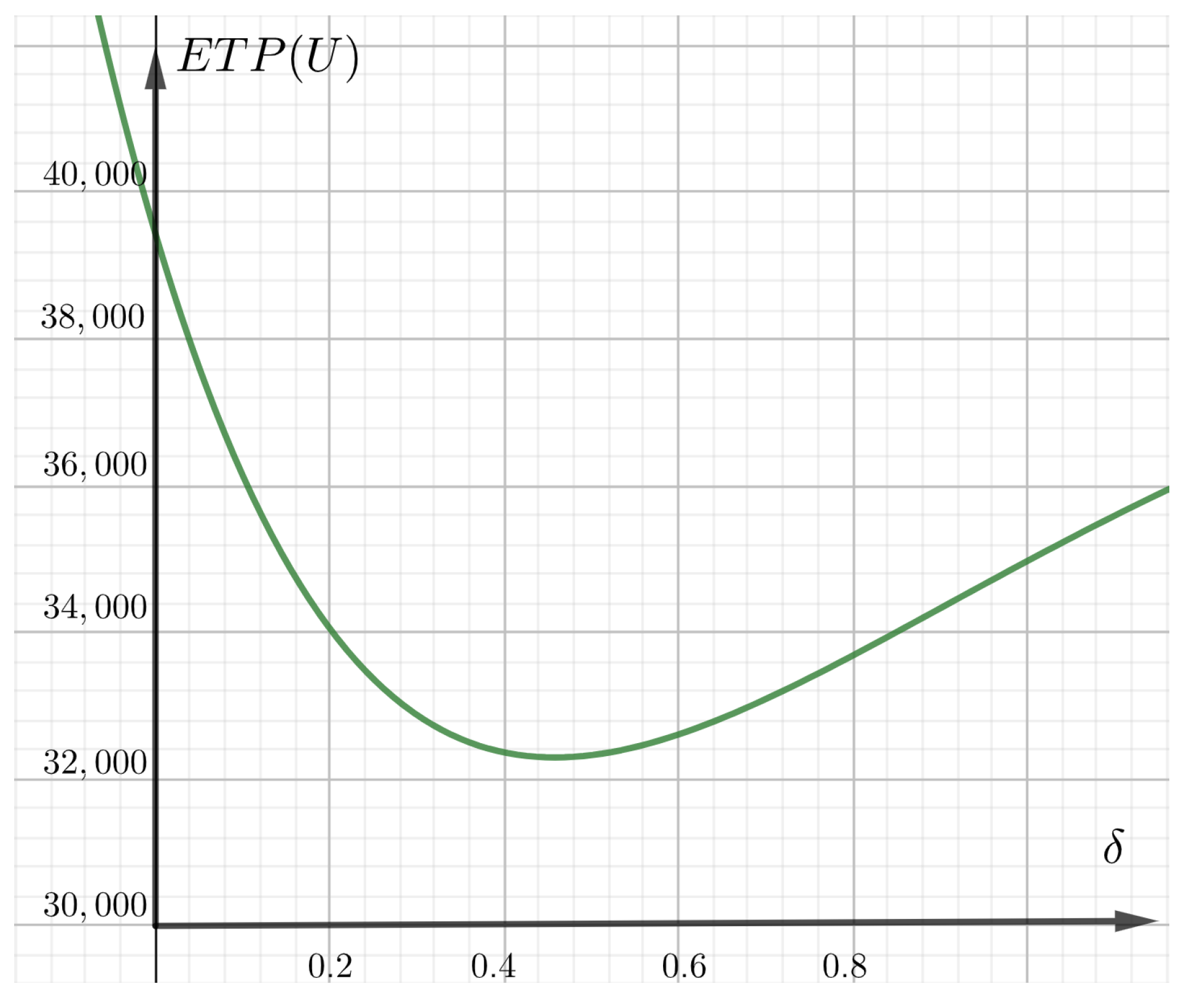
6.5. Sensitive Analysis
6.5.1. Case I:
6.5.2. Case II:
- Following Figure 7, if , the closer the chicken’s weight is to , the better is the overall total profit.
- If , in this case, the smaller the weight of the chicken, the better the overall total profit.
6.6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harris, F.W. How Many Parts to Make at Once. Factory Mag. Manag. 1913, 10, 135–136, 152. [Google Scholar] [CrossRef]
- Wilson, R.H. A Scientific Routine for Stock Control; Harvard University: Cambridge, MA, USA, 1934. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Tenreiro Machado, J.A. Fractional Derivatives and Their Applications. In Proceedings of the Sixth EUROMECH Nonlinear Dynamics Conference, Saint Petersburg, Russia, 30 June–4 July 2008; pp. 1–27. [Google Scholar]
- Baleanu, D.; Güvenç, Z.B.; Machado, J.T. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: New York, NY, USA, 2010; Volume 10, pp. 978–990. [Google Scholar]
- Machado, J.T.; Mata, M.E. Pseudo Phase Plane and Fractional Calculus Modeling of Western Global Economic Downturn. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 396–406. [Google Scholar] [CrossRef]
- Agila, A.; Baleanu, D.; Eid, R.; Irfanoglu, B. Applications of the Extended Fractional Euler-Lagrange Equations Model to Freely Oscillating Dynamical Systems. Rom. J. Phys. 2016, 61, 350–359. [Google Scholar]
- Das, A.K.; Roy, T.K. Fractional Order EGQ Model with Linear Trend of Time-Dependent Demand. Int. J. Intell. Syst. Appl. 2015, 3, 44–53. [Google Scholar]
- Das, A.K.; Roy, T.K. Fractional Order Generalized EPQ Model. Int. J. Comput. Appl. Math. 2017, 12, 525–536. [Google Scholar]
- Pakhira, R.; Ghosh, U.; Sarkar, S. Study of Memory Effects in an Inventory Model Using Fractional Calculus. Appl. Math. Sci. 2018, 12, 797–824. [Google Scholar] [CrossRef]
- Pakhira, R.; Ghosh, U.; Sarkar, S. Application of Memory Effects in an Inventory Model with Linear Demand and No Shortage. Int. J. Res. Advent Technol. 2018, 6, 8. [Google Scholar]
- Rahaman, M.; Mondal, S.P.; Shaikh, A.A.; Ahmadian, A.; Senu, N.; Salahshour, S. Arbitrary-Order Economic Production Quantity Model with and without Deterioration: Generalized Point of View. Adv. Differ. Equ. 2020, 2020, 16. [Google Scholar] [CrossRef]
- Das, A.K.; Roy, T.K.; Jana, D.K. Fractional order generalized EGQ model with demand-dependent unit purchasing cost under space constraints. In Recent Advances in Intelligent Information Systems and Applied Mathematics; Springer: New York, NY, USA, 2020; pp. 1–17. [Google Scholar]
- Rahaman, M.; Mondal, S.P.; Alam, S. An Estimation of Effects of Memory and Learning Experience on the EGQ Model with Price Dependent Demand. Rairo-Oper. Res. 2021, 55, 2991–3020. [Google Scholar] [CrossRef]
- Rahaman, M.; Mondal, S.P.; Chatterjee, B.; Alam, S.; Shaikh, A.A. Generalization of Classical Fuzzy Economic Order Quantity Model Based on Memory Dependency via Fuzzy Fractional Differential Equation Approach. J. Uncert. Sys. 2022, 15, 2250003. [Google Scholar] [CrossRef]
- Rezaei, J. Economic Order Quantity for Growing Items. Int. J. Prod. Econ. 2014, 155, 109–113. [Google Scholar] [CrossRef]
- Msomi, A.M.; Bansilal, S. Analysis of Students’ Errors and Misconceptions in Solving Linear Ordinary Differential Equations Using the Method of Laplace Transform. Int. Electron. J. Math. Educ. 2022, 17, em0670. [Google Scholar] [CrossRef]
- West, B.J. Exact Solution to Fractional Logistic Equation. Phys. A Stat. Mech. Its Appl. 2015, 429, 103–108. [Google Scholar] [CrossRef]
- Area, I.; Losada, J.; Nieto, J.J. A Note on the Fractional Logistic Equation. Phys. A Stat. Mech. Its Appl. 2016, 444, 182–187. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar-Gejji, V. Solving Fractional-Order Logistic Equation Using a New Iterative Method. Int. J. Differ. Equ. 2012, 2012, 1–12. [Google Scholar] [CrossRef][Green Version]
- Momani, S.; Qaralleh, R. Numerical Approximations and Padé Approximants for a Fractional Population Growth Model. Appl. Math. Model. 2007, 31, 1907–1914. [Google Scholar] [CrossRef]
- Sumiati, I.; Bon, S.A. Adomian Decomposition Method and the New Integral Transform. In Proceedings of the 2nd African International Conference on Industrial Engineering and Operations Management, Harare, Zimbabwe, 7–10 December 2020; pp. 1882–1887. [Google Scholar]
- Ouhmid, A.; Belhabib, F.; Elkari, B.; El Moutaouakil, K.; Ourabah, L.; Benslimane, M.; El Mekkaoui, J. Economic Growing Quantity: Broiler Chicken in Morocco. Stat. Optim. Inf. Comput. 2024, 12, 817–828. [Google Scholar] [CrossRef]
- El Moutaouakil, K.; Bouhanch, Z.; Ahourag, A.; Aberqi, A.; Karite, T. OPT-FRAC-CHN: Optimal Fractional Continuous Hopfield Network. Symmetry 2024, 16, 921. [Google Scholar] [CrossRef]
- El Moutaouakil, K.; El Ouissari, A.; Palade, V.; Charroud, A.; Olaru, A.; Baïzri, H.; Chellak, S.; Cheggour, M. Multi-Objective Optimization for Controlling the Dynamics of the Diabetic Population. Mathematics 2023, 11, 2957. [Google Scholar] [CrossRef]
- Sebatjane, M.; Adetunji, O. Economic Order Quantity Model for Growing Items with Imperfect Quality. Oper. Res. Perspect. 2019, 6, 100088. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W.; Lisowska, A. Newton’s Method with Fractional Derivatives and Various Iteration Processes via Visual Analysis. Numer. Algor. 2021, 86, 953–1010. [Google Scholar] [CrossRef]




| Parameters | |
| Weight of newly hatched chicks (g) | |
| Desired mass (g) | |
| N | Item’s yearly demand rate (g/year) |
| A | Carrying capacity (g) |
| n | Integration constant of the growth function |
| growth rate | |
| Decision Parameter | |
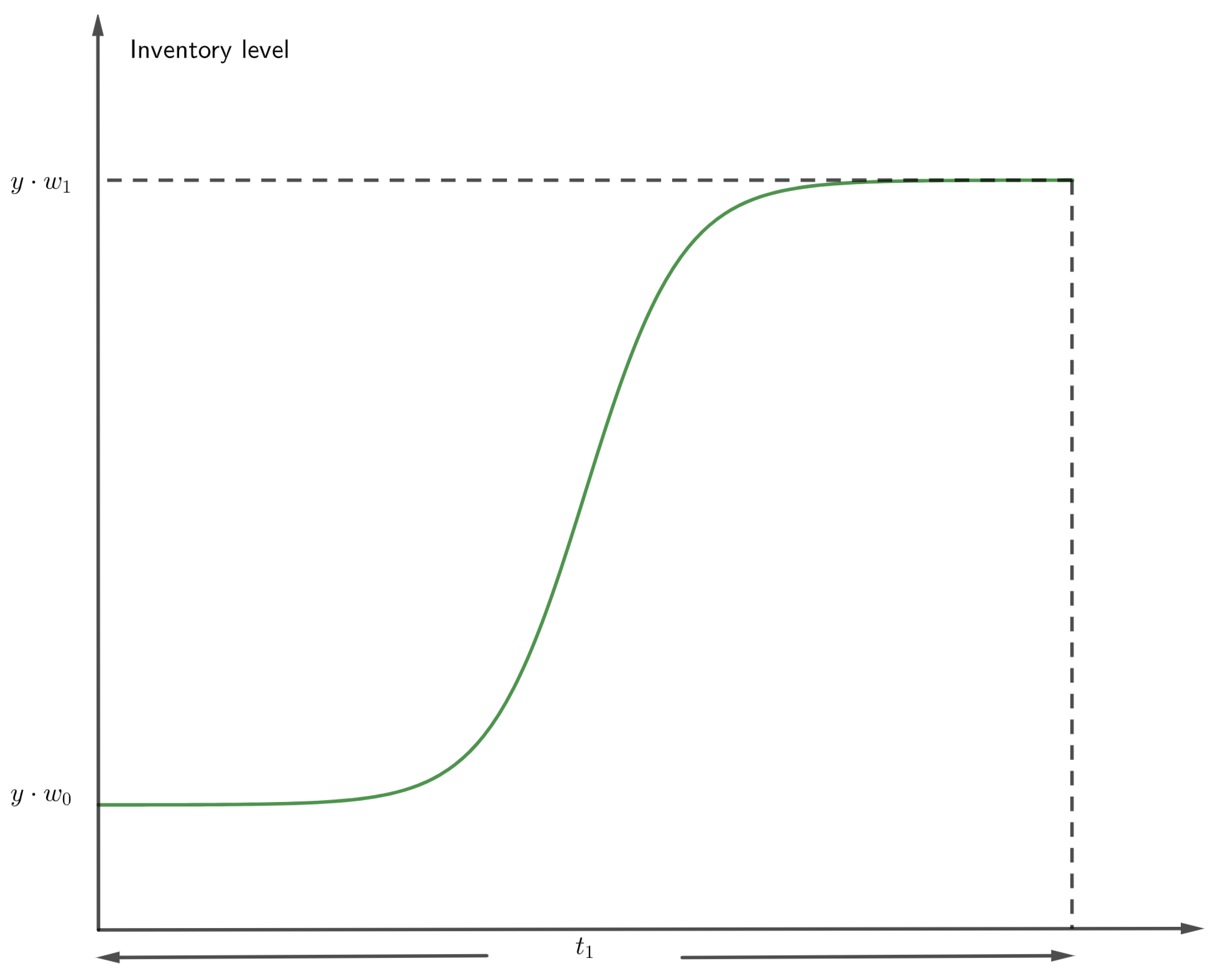
| y | Quantity of newly hatched chicks requested at each breeding cycle |
| T | Time span of the consumption phase (in years) |
| Cost components | |
| Price per unit (ZAR/g) | |
| s | Price of selling an individual item (ZAR/g) |
| The expense associated with storing a single unit of an item throughout the period of consumption (ZAR /g/year) | |
| Cost of maintaining a single unit item during the breeding period (ZAR /items) | |
| K | Capital of setting required for each growth cycle (ZAR) |
| q | Vaccination expenses |
| Feeding expenses (ZAR/g) | |
| Time period | |
| Duration of the maturation process (in years) | |
| T | Length of the consuming period (in years) |
| 1 | 0.95 | 0.9 | 0.85 | 0.80 | |||||||||||
| T | T | T | T | T | |||||||||||
| 1 | 34,973.46 | 0.223 | 0.0878 | 35,820.39 | 0.223 | 0.072 | 36,603.06 | 0.223 | 0.058 | 37,443.06 | 0.223 | 0.045 | 38,139.06 | 0.223 | 0.034 |
| 1 | 0.95 | 0.9 | 0.85 | 0.80 | |||||||||||
| T | T | T | T | T | |||||||||||
| 1 | 34,973.46 | 0.223 | 0.0878 | 35,820.39 | 0.223 | 0.072 | 36,603.06 | 0.223 | 0.058 | 37,443.06 | 0.223 | 0.045 | 38,139.06 | 0.223 | 0.034 |
| 0.9 | 34,597.22 | 0.221 | 0.0878 | 35,408.00 | 0.221 | 0.072 | 36,155.65 | 0.220 | 0.058 | 36,960.07 | 0.220 | 0.045 | 37,623.15 | 0.220 | 0.034 |
| 0.8 | 34,286.14 | 0.221 | 0.0878 | 35,054.91 | 0.221 | 0.072 | 35,761.41 | 0.220 | 0.058 | 36,523.28 | 0.220 | 0.045 | 37,146.26 | 0.219 | 0.034 |
| 0.7 | 34,076.66 | 0.225 | 0.0878 | 34,799.90 | 0.224 | 0.072 | 35,460.63 | 0.223 | 0.058 | 36,174.42 | 0.223 | 0.045 | 36,751.31 | 0.223 | 0.034 |
| 0.6 | 34,019.85 | 0.234 | 0.0878 | 34,696.63 | 0.233 | 0.072 | 35,310.27 | 0.232 | 0.058 | 35,973.87 | 0.231 | 0.045 | 36,501.98 | 0.231 | 0.034 |
| 0.5 | 34,184.18 | 0.251 | 0.0878 | 34,819.52 | 0.250 | 0.072 | 35,390.69 | 0.249 | 0.058 | 36,008.58 | 0.249 | 0.045 | 36,491.83 | 0.250 | 0.034 |
| 0.4 | 34,665.08 | 0.282 | 0.0878 | 35,273.15 | 0.282 | 0.072 | 35,816.35 | 0.282 | 0.058 | 36,404.17 | 0.284 | 0.045 | 36,858.04 | 0.286 | 0.034 |
| 0.3 | 35,600.19 | 0.347 | 0.0878 | 36,209.12 | 0.34 | 0.072 | 36,753.91 | 0.352 | 0.058 | 37,344.49 | 0.357 | 0.045 | 37,802.34 | 0.364 | 0.034 |
| 0.2 | 37,202.78 | 0.512 | 0.0878 | 37,859.94 | 0.52 | 0.072 | 38,456.91 | 0.537 | 0.058 | 39,104.44 | 0.556 | 0.045 | 39,621.40 | 0.578 | 0.034 |
| 0.1 | 39,842.33 | 1.31 | 0.0878 | 40,609.64 | 1.39 | 0.072 | 41,318.28 | 1.49 | 0.058 | 42,086.45 | 1.6 | 0.045 | 42,719.15 | 1.72 | 0.034 |
| 1 | 0.95 | 0.9 | 0.85 | 0.80 | |||||||||||
| T | T | T | T | T | |||||||||||
| 0.9 | 34,329.61 | 0.220 | 0.0878 | 35,188.55 | 0.220 | 0.072 | 35,959.21 | 0.220 | 0.058 | 36,799.21 | 0.220 | 0.045 | 37,495.21 | 0.220 | 0.034 |
| 0.8 | 33,687.84 | 0.219 | 0.0878 | 34,546.78 | 0.219 | 0.072 | 35,317.44 | 0.219 | 0.058 | 36,157.44 | 0.219 | 0.045 | 36,853.44 | 0.219 | 0.034 |
| 0.7 | 33,092.95 | 0.224 | 0.0878 | 33,951.88 | 0.224 | 0.072 | 34,722.55 | 0.224 | 0.058 | 35,562.55 | 0.224 | 0.045 | 36,258.55 | 0.224 | 0.034 |
| 0.6 | 32,621.55 | 0.236 | 0.0878 | 33,480.48 | 0.236 | 0.072 | 34,251.15 | 0.236 | 0.058 | 35,091.15 | 0.236 | 0.045 | 35,787.15 | 0.236 | 0.034 |
| 0.5 | 32,400.08 | 0.260 | 0.0878 | 33,259.01 | 0.260 | 0.072 | 34,029.68 | 0.260 | 0.058 | 34,869.68 | 0.260 | 0.045 | 35,565.68 | 0.260 | 0.034 |
| 0.4 | 32,629.16 | 0.310 | 0.0878 | 33,488.09 | 0.310 | 0.072 | 34,258.76 | 0.310 | 0.058 | 35,098.76 | 0.310 | 0.045 | 35,794.76 | 0.310 | 0.034 |
| 0.3 | 33,608.25 | 0.420 | 0.0878 | 34,467.19 | 0.420 | 0.072 | 35,237.85 | 0.420 | 0.058 | 36,077.85 | 0.420 | 0.045 | 36,773.85 | 0.420 | 0.034 |
| 0.2 | 35,729.97 | 0.732 | 0.0878 | 36,588.91 | 0.732 | 0.072 | 37,359.57 | 0.732 | 0.058 | 38,199.57 | 0.732 | 0.045 | 38,895.57 | 0.732 | 0.034 |
| 0.1 | 39,329.03 | 2.397 | 0.0878 | 40,187.96 | 2.397 | 0.072 | 40,958.63 | 2.397 | 0.058 | 41,798.63 | 2.397 | 0.045 | 42,494.63 | 2.397 | 0.034 |
| 1 | 0.95 | 0.9 | 0.85 | 0.80 | |||||||||||
| and | T | T | T | T | T | ||||||||||
| 32,985.33 | 5.03 | 0.0878 | 33,826.93 | 116.13 | 0.072 | 34,597.3 | 120.2 | 0.058 | 35,437.1 | 121.3 | 0.045 | 36,132.9 | 127.8 | 0.034 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouhmid, A.; El Moutaouakil, K.; Belhabib, F.; Patriciu, A.-M. Enhancing Symmetry and Memory in the Fractional Economic Growing Quantity (FEGQ) Model. Symmetry 2024, 16, 1057. https://doi.org/10.3390/sym16081057
Ouhmid A, El Moutaouakil K, Belhabib F, Patriciu A-M. Enhancing Symmetry and Memory in the Fractional Economic Growing Quantity (FEGQ) Model. Symmetry. 2024; 16(8):1057. https://doi.org/10.3390/sym16081057
Chicago/Turabian StyleOuhmid, Azedine, Karim El Moutaouakil, Fatima Belhabib, and Alina-Mihaela Patriciu. 2024. "Enhancing Symmetry and Memory in the Fractional Economic Growing Quantity (FEGQ) Model" Symmetry 16, no. 8: 1057. https://doi.org/10.3390/sym16081057
APA StyleOuhmid, A., El Moutaouakil, K., Belhabib, F., & Patriciu, A.-M. (2024). Enhancing Symmetry and Memory in the Fractional Economic Growing Quantity (FEGQ) Model. Symmetry, 16(8), 1057. https://doi.org/10.3390/sym16081057








