On the Spanning Cyclability of k-ary n-cube Networks ^†

Abstract

Embedding cycles into a network topology is crucial for a network simulation. In particular, embedding Hamiltonian cycles is a major requirement for designing good interconnection networks. A graph G is called r-spanning cyclable if, for any r distinct vertices $v_1,v_2,\dots ,v_r$ of G, there exist r cycles $C_1,C_2,\dots ,C_r$ in G such that $v_i$ is on $C_i$ for every i, and every vertex of G is on exactly one cycle $C_i$. If $r=1$, this is the classical Hamiltonian problem. In this paper, we focus on the problem of embedding spanning disjoint cycles in bipartite k-ary n-cubes. Let $k\ge 4$ be even and $n\ge 2$. It is shown that the n-dimensional bipartite k-ary n-cube $Q_n^k$ is m-spanning cyclable with $m\le 2n-1$. Considering the degree of $Q_n^k$, the result is optimal.

1. Introduction

An interconnection network’s design is typically represented by a graph G, with vertices representing processors and edges representing links between processors. Due to its appealing characteristics, including its symmetry, small diameter, regularity, high connectivity, relatively cheap link complexity, and recursive construction, the hypercube $Q_n$ is one of the most widely used network topologies [1,2]. Among various generalizations of the hypercube, the k-ary n-cube $Q_n^k$ may be the most important one that can be used to build networks on chips, data center networks, and parallel computing systems [3]. Also, it has many attractive properties, such as regularity, recursive structure, vertex symmetry and edge symmetry, reduced message latency, and ease of implementation [4].

Two basic network topologies that can be utilized to create straightforward algorithms with low communication costs are cycles (rings) and paths (linear arrays) [5]. For a network simulation, it is essential to incorporate cycles (paths) into the network architecture [5,6]. Numerous parallel methods based on cycles and paths have been developed to address a wide range of algebraic, graph, picture, and signal processing issues [1]. Embedding cycles or paths can also save a significant amount of transmission time. Numerous studies have been conducted on these issues; see, for instance, [6,7,8,9,10].

A path that contains all vertices of G is referred to as a Hamiltonian cycle. A graph G is Hamiltonian if it has such a cycle and Hamiltonian-connected if there is a Hamiltonian path between any two vertices $u,v\in G$. Hamiltonicity is a widely studied and essential subject. Problems involving the embedding of two or more paths in networks have appeared recently. Let S and T be two disjoint vertex subsets of size t in a graph G. A set of t vertex-disjoint paths between S and T whose unions cover every vertex of G forms a many-to-many t-disjoint path cover of G connecting S and T. If every vertex in S needs to be connected to a specific vertex in T, then it is paired; if not, it is unpaired. There are many papers on Hamiltonian paths or disjoint path covers in various networks. Let us now turn to k-ary n-cubes. Refs. [11,12,13,14,15,16] investigated Hamiltonian paths under various conditions of k-ary n-cubes. For disjoint path covers of k-ary n-cubes, we refer to [17,18,19,20] and the references therein.

There are several essential rules that we should follow when designing an interconnection network. Two fundamental principles are extendability and embeddability for various topologies [5]. This implies that building huge networks from small ones should be achievable. Thus, a large network can often be decomposed into a set of small sub-networks. It is well known that embedding Hamiltonian cycles is a major requirement in designing good interconnection networks [21]. Furthermore, embedding Hamiltonian cycles into these sub-networks is also important and essential. This feature can be used to identify failing parts in a multiprocessor system [22].

Considering the above research motivations, this paper will study the spanning cyclability of k-ary n-cubes. A graph G is called r-spanning cyclable if, for any r distinct vertices $v_1,v_2,\dots ,v_r$ of G, there exist r cycles $C_1,C_2,\dots ,C_r$ in G such that $v_i$ is on $C_i$ for every i, and every vertex of G is on exactly one cycle $C_i$. The spanning cyclability is closely related to another graph notation named a 2-factor. A 2-factor in a graph G is a spanning subgraph of G such that every vertex has degree two. Therefore, a graph G is r-spanning cyclable if, for any r distinct vertices $v_1,v_2,\dots ,v_r$ of G, it has a 2-factor with each cycle containing exactly one prescribed vertex.

Lin et al. [22] considered the spanning cyclability of hypercubes and showed that an n-dimensional hypercube $Q_n$ is r-spanning cyclable with $r\le n-1$. Yang et al. [23] considered the 2-spanning cyclability of the generalized Petersen graph $GP(n,k)$ with $k=1,2,3,4$. Qiao et al. [24] considered the spanning cyclability of enhanced hypercubes and showed that an n-dimensional enhanced hypercube $Q_{n,m}$ is r-spanning cyclable with $r\le n$. Also, they [25] considered the spanning cyclability of the Cayley graph ${\mathsf{\Gamma }}_n$ generated by a transposition tree and showed that ${\mathsf{\Gamma }}_n$ is r-spanning cyclable with $r\le n-2$. Wu et al. [26] considered the spanning cyclability of augmented cubes and showed that an n-dimensional augmented cube $A{Q}_n$ is r-spanning cyclable with $r\le 2n-4$. Also, Wu and Sabir [27] studied the spanning cyclability of hypercubes with prescribed edges in each cycle and showed that an n-dimensional hypercube $Q_n$ is spanning r-edge-cyclable with $r\le n-1$.

In this paper, we focus on the problem of embedding spanning disjoint cycles in k-ary n-cubes, with each cycle containing a prescribed vertex. Let $k\ge 4$ be even and $n\ge 2$; it is shown in this paper that the n-dimensional bipartite k-ary n-cube $Q_n^k$ is m-spanning cyclable with $m\le 2n-1$. The result is optimal in view of the degree of $Q_n^k$.

2. Preliminaries

We refer the reader to [28] for fundamental graph definitions that are not covered here. Let H and G be two graphs. If $V\left(H\right)=V\left(G\right)$ and $E\left(H\right)\subseteq E\left(G\right)$, then H is a spanning subgraph of G. Assume that a path in G is $P=⟨v_1,v_2,\dots ,v_m⟩$. The inverse path of P is represented by $P^{-}=⟨v_m,v_{m-1},\dots ,v_1⟩$. A similar cycle, $C^{-}$, can be defined from a cycle $C=⟨u_1,u_2,\dots ,u_m⟩$ of G.

The k-ary n-cube, denoted by $Q_n^k$, is a graph with the vertex set $V\left(Q_n^k\right)={\mathbb{Z}}_k^n$, where ${\mathbb{Z}}_k=\{0,1,2,\dots ,k-1\}$. Two vertices $u=u_{n-1}{u}_{n-2}\cdots u_0$ and $v=v_{n-1}{v}_{n-2}\cdots v_0$ are adjacent in $Q_n^k$ if and only if there exists an integer $i\in {\mathbb{Z}}_n$ such that $u_i=v_i\pm 1$$(modk)$ and $u_j=v_j$ for every $j\in {\mathbb{Z}}_n\setminus \left\{i\right\}$. Such an edge $(u,v)$ is referred to in this instance as an i-dimensional edge for $i\in {\mathbb{Z}}_n$. And, we use $E_i\left(Q_n^k\right)$, or $E_i$ for short, to represent the set of all i-dimensional edges of $Q_n^k$.

It is clear that $Q_n^k$ has $k^n$ vertices and is a bipartite graph when k is even. For any vertex $u=u_{n-1}{u}_{n-2}\cdots u_0\in V\left(Q_n^k\right)$, it has $2n$ neighbors. Moreover, the neighbor of u joining by an i-dimensional edge, denoted by $u\left(i^{+}\right)$ (resp. $u\left(i^{-}\right)$), is the vertex $u_{n-1}{u}_{n-2}\cdots u_{i+1}{v}_i{u}_{i-1}\cdots u_0$, where $v_i=u_i+1$ (resp. $v_i=u_i-1$ ). If ${\sum }_{i=0}^{n-1}{u}_i=0$ $(mod2)$ (resp. ${\sum }_{i=0}^{n-1}{u}_i=1$$(mod2)$), then we define u to be an even vertex (resp. odd vertex). If any two vertices $u,v\in V\left(Q_n^k\right)$ are both even or odd, then the parity indicator ${\tau }_{u,v}=0$; otherwise, ${\tau }_{u,v}=1$.

Let i be a specific dimension in ${\mathbb{Z}}_n$. Then, along its i-dimensional edges, $Q_n^k$ can be divided into k disjoint subgraphs: $Q_n^k\left[0\right],Q_n^k\left[1\right],\dots ,Q_n^k[k-1]$ (written $Q\left[j\right]$ for short for every $\left.j\in {\mathbb{Z}}_k\right)$. It is clear that each subgraph $Q\left[j\right]$ is isomorphic to $Q_{n-1}^k$, where $j\in {\mathbb{Z}}_k$. For $\ell ,h\in {\mathbb{Z}}_k$, define $Q_n^k[\ell ,h]$ (or $Q[\ell ,h])$ to be the subgraph induced by the vertex set ${\cup }_{j=\ell }^{h}V\left(Q\left[j\right]\right)$. In particular, we have $Q[\ell ,h]=Q[\ell ]$ if $\ell =h$. And, we have $Q[\ell ,h]=Q_n^k$ if $h=\ell -1$ by taking modulo k. Illustrations for $Q_n^4$ are shown in Figure 1, where $n=1,2,3$.

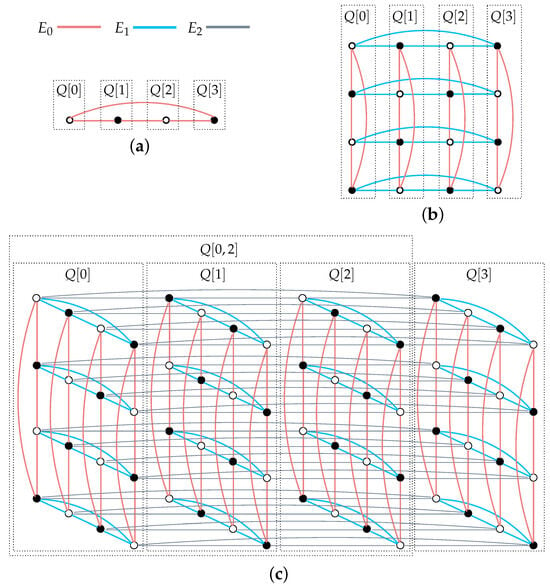
Figure 1. Illustrations for (a) $Q_1^4$; (b) $Q_2^4$; (c) $Q_3^4$.

Before proceeding to the main results, we first present two important lemmas on the existence of Hamiltonian paths or disjoint path covers of $Q_n^k$.

Lemma 1

([19]). Given $Q_n^k$ and its k subcubes $Q\left[i\right]$ for $0\le i\le k-1$, let j be an integer with $0\le i\le j\le k-1$. When k is odd, let u and v be any pair of vertices in $Q\left[i\right]$. There exists a path between u and v that covers all vertices of $Q[i,j]$. On the other hand, when k is even, let w be a white vertex and b be a black vertex in $Q\left[i\right]$. There exists a path between w and b that covers all vertices of $Q[i,j]$.

Lemma 2

([17]). Let $Q_n^k$ be a bipartite k-ary n-cube, where $k\ge 4$ is even and $n\ge 2$. Let F be a set of faulty edges with $\left|F\right|\le 2n-3$. Given any four vertices $s_1,t_1,s_2$, and $t_2$, such that each partite set contains two vertices, the graph $T-F$ has a paired 2-disjoint path cover consisting of an $\left(s_1,t_1\right)$-path and an $\left(s_2,t_2\right)$-path.

Bose et al. [3] show that $Q_n^k$ is Hamiltonian, so it is 1-spanning cyclable. In what follows, we will investigate the r-spanning cyclability of the bipartite k-ary n-cube for $r\ge 2$.

3. Spanning Cyclability of Bipartite $\mathbf{k}$-ary $\mathbf{n}$-cubes

Lemma 3.

The k-ary n-cube $Q_2^4$ is m-spanning cyclable with $m\le 3$.

Proof. 

It suffices to consider the cases in which $m=2,3$. Let $u=u_1{u}_0$ and $v=v_1{v}_0$ be two distinct vertices of $Q_2^4$, where $u_i,v_i\in {\mathbb{Z}}_4$ for $i=0,1$. Thus, $u_1\ne v_1$ or $u_0\ne v_0$. Without loss of generality, together with the fact that the k-ary n-cube is vertex-transitive, we may assume that $u=00$ and $v_1\ne 0$. Let $C_1=Q\left[0\right]$, $C_2=⟨10,20,30,31,21,11,12,22,32,33,23,13,10⟩$. Then, $\{C_1,C_2\}$ is a 2-factor such that $C_1$ contains u and $C_2$ contains v.

Now, suppose that $m=3$. Let $u=u_1{u}_0$, $v=v_1{v}_0$, and $w=w_1{w}_0$ be three distinct vertices of $Q_2^4$, where $u_i,v_i,w_i\in {\mathbb{Z}}_4$ for $i=0,1$. For the same reason, we may let $u=00$. If $v_1\ne w_1$ and both of them are not equal to 0, without loss of generality, let $v\in Q\left[i\right]$ and $w\in Q\left[j\right]$, where $i,j\in \{1,2,3\}$ and $i<j$. Then, it is easy to see that the subgraphs $Q[0,i-1]$, $Q[i,j-1]$, and $Q[j,3]$ form a desired 2-factor containing u, v, and w, respectively. The case in which $v_0\ne w_0$ and both of them are not equal to 0 can be solved similarly.

In what follows, suppose that both the sets $\{0,v_1,w_1\}$ and $\{0,v_0,w_0\}$ have a cardinality of two. Without loss of generality, suppose that $v_1=0$, $w_1\ne 0$, and $v_0=w_0\ne 0$. Let $C_1=⟨00,10,20,30,00⟩$. It is easy to find a 2-factor $\{C_2,C_3\}$ in the residual graph $P_3\square C_4$ such that $C_2$ contains v and $C_3$ contains w. Thus, $\{C_1,C_2,C_3\}$ forms a desired 2-factor of $Q_2^4$. The case in which $v_1=w_1\ne 0$, $v_0=0$, and $w_0\ne 0$ can be solved similarly. This completes the proof of Lemma 3. □

Theorem 1.

Let $k\ge 4$ be even, and let $n\ge 2$. Then, the bipartite k-ary n-cube $Q_n^k$ is m-spanning cyclable with $m\le 2n-1$.

Proof. 

It proceeds by induction on n. The result follows from Lemma 3 when $n=2$. Suppose that $Q_{n-1}^k$ is m-spanning cyclable with $m\le 2n-3$ and $n\ge 3$. Divide $Q_n^k$ into k disjoint subgraphs $Q\left[0\right]$, $Q\left[1\right]$, …, $Q[k-1]$ along its n-dimensional edges. Then, each $Q\left[j\right]$ with $j\in {\mathbb{Z}}_k$ is isomorphic to $Q_{n-1}^k$. Let S be any prescribed vertices of $Q_n^k$, and let $S_j=S\cap Q\left[j\right]$ with $j\in {\mathbb{Z}}_k$. Moreover, we use $s_j$ to denote the cardinality of $S_j$, and then $s_j\le 2n-1$. Since $Q_n^k$ is vertex-transitive, we may let $00\cdots 0\in S_0$. Thus, there exists at least one prescribed vertex belonging to $Q\left[0\right]$. According to the cardinality of the prescribed vertices in each $Q\left[j\right]$, we have the following cases.

Case 1. For every $j\in {\mathbb{Z}}_k$, we have $s_j\le 2n-3$. Let $Q\left[i_1\right]$, $Q\left[i_2\right]$, …, $Q\left[i_r\right]$ be subcubes so that each of them contains at least one prescribed vertex, where $0=i_1<i_2<\cdots <i_r$ and $r\le k$. By the induction hypothesis, $Q\left[i_p\right]$ is $s_{i_p}$-spanning cyclable for $1\le p\le r$. That is, there exist $s_{i_p}$ disjoint cycles in $Q\left[i_p\right]$ such that each cycle contains exactly one prescribed vertex and the union of all cycles spans $Q\left[i_p\right]$, and ${\sum }_{p=1}^r{s}_{i_p}=2n-1$. Therefore, we have obtained $2n-1$ disjoint cycles $C_1,C_2,\dots ,C_{2n-1}$ spanning $Q\left[R\right]$, where $R=\{i_1,i_2,\dots ,i_r\}$. If $r=k$, then $C_1,C_2,\dots ,C_{2n-1}$ form a desired 2-factor of $Q_n^k$. So, suppose that $r<k$; we shall add vertices of all other subcubes that contain no prescribed vertices to these $2n-1$ cycles.

Let $C_1^{\prime }\in \{C_1,C_2,\dots ,C_{2n-1}\}$ be a cycle in $Q\left[i_1\right]$; then, $C_1^{\prime }$ is an even cycle because $Q_n^k$ is bipartite for even k. Let $xy$ be an edge on $C_1^{\prime }$; then, we have ${\tau }_{x,y}=1$. Moreover, it is easy to see that ${\tau }_{x\left(n^{+}\right),y\left(n^{+}\right)}=1$. By Lemma 1, there is a Hamiltonian path P joining $x\left(n^{+}\right)$ and $y\left(n^{+}\right)$ in $Q[i_1+1,i_2-1]$. Removing the edge $xy$ and adding $xx\left(n^{+}\right)Py\left(n^{+}\right)y$ will result in a new cycle $C_1^{\prime \prime }$ that contains all vertices of $Q[i_1+1,i_2-1]$. With a similar method, the vertices of $Q[i_2+1,i_3-1]$ can be added to a cycle $C_2^{\prime }$ of $Q\left[i_2\right]$, which results in a new cycle $C_2^{\prime \prime }$. Continuing the above process recursively, the vertices of $Q[i_r+1,k-1]$ can be added to a cycle $C_r^{\prime }$ of $Q\left[i_r\right]$, which results in a new cycle $C_r^{\prime \prime }$. Thus, the new cycles, together with other cycles in $Q\left[R\right]$, form a desired 2-factor of $Q_n^k$.

Case 2. There exists some $j\in {\mathbb{Z}}_k$ such that $s_j=2n-2$. Without loss of generality, we may assume that $s_0=2n-2$. We distinguish several subcases as follows.

Case 2.1. For every $j^{\prime }\in {\mathbb{Z}}_k$ with $j^{\prime }\ne 0$, we have $s_{j^{\prime }}=0$. Let $u=0u_{n-2}{u}_{n-3}\cdots u_1{u}_0$ and $v=0v_{n-2}{v}_{n-3}\cdots v_1{v}_0$ be two distinct prescribed vertices in $Q\left[0\right]$. Then, there exists some $i\in {\mathbb{Z}}_{n-1}$ such that $u_i\ne v_i$. Divide $Q_n^k$ into k disjoint subgraphs $Q_{n-1}^i\left[0\right]$, $Q_{n-1}^i\left[1\right]$, …, $Q_{n-1}^i[k-1]$ along its i-dimensional edges. Thus, the prescribed vertices u and v belong to different subcubes of $Q_n^k$, and each subcube contains at most $2n-3$ prescribed vertices, which can be reduced to Case 1.

Case 2.2. For some $j^{\prime }\in {\mathbb{Z}}_k$ with $j^{\prime }\ne 0$, we have $s_{j^{\prime }}=1$. Let $S_0=\{v_1,v_2,\dots ,v_{2n-2}\}$ and $S_{j^{\prime }}=\left\{v_{2n-1}\right\}$. Since the subgraph $Q\left[j^{\prime }\right]$ is Hamiltonian, we obtain a cycle $C_{2n-1}$ containing the vertex $v_{2n-1}$ that spans $Q\left[j^{\prime }\right]$. By the induction hypothesis, there are $2n-3$ disjoint cycles $C_1,C_2,\dots ,C_{2n-3}$ of $Q\left[0\right]$ such that $v_x$ is in $C_x$ for $1\le x\le 2n-3$, and $C_1\cup C_2\cup \cdots \cup C_{2n-3}$ spans $Q\left[0\right]$. Thus, the prescribed vertex $v_{2n-2}$ must be on some cycle $C_x$, where $1\le x\le 2n-3$. Without loss of generality, suppose that $v_{2n-2}$ is on $C_{2n-3}$. We have the following subcases.

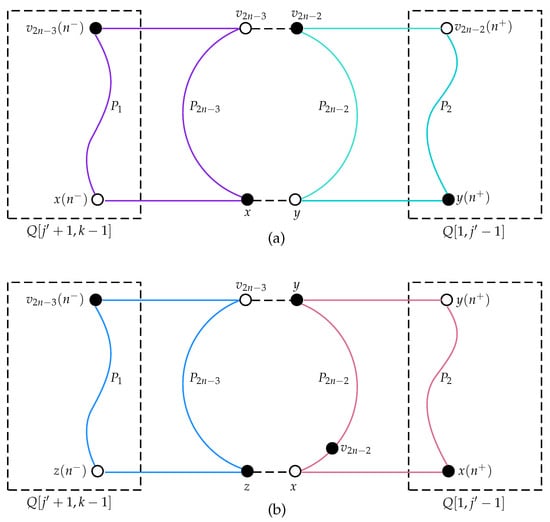
Case 2.2.1. Let $2\le j^{\prime }\le k-2$. Furthermore, if $v_{2n-2}$ is adjacent to $v_{2n-3}$ on $C_{2n-3}$, one may assume that $C_{2n-3}=⟨v_{2n-3},P_{2n-3},x,y,P_{2n-2},v_{2n-2},v_{2n-3}⟩$. Note that $Q_n^k$ is bipartite with even k, and we have ${\tau }_{v_{2n-3},v_{2n-2}}=1$. Since $|C_{2n-3}|\ge 4$, it follows that there exist such x and y satisfying $x\ne v_{2n-3}$, $y\ne v_{2n-2}$, and ${\tau }_{x,y}=1$. By Lemma 1, there is a Hamiltonian path $P_1$ joining $x\left(n^{-}\right)$ to $v_{2n-3}\left(n^{-}\right)$ passing through every vertex of $Q[j^{\prime }+1,k-1]$. Meanwhile, there is a Hamiltonian path $P_2$ joining $y\left(n^{+}\right)$ to $v_{2n-2}\left(n^{+}\right)$ that spans $Q[1,j^{\prime }-1]$. Let $C_{2n-3}^{\prime }=⟨v_{2n-3},P_{2n-3},x,x\left(n^{-}\right),P_1,v_{2n-3}\left(n^{-}\right),v_{2n-3}⟩$ and $C_{2n-2}=⟨v_{2n-2},P_{2n-2}^{-},y,y\left(n^{+}\right),P_2,v_{2n-2}\left(n^{+}\right),v_{2n-2}⟩$. Then, $\{C_1,C_2,\dots ,C_{2n-3}^{\prime },C_{2n-2},C_{2n-1}\}$ is a desired 2-factor of $Q_n^k$; see Figure 2a for an illustration.

Figure 2. Illustrations for Case 2.2.1 of Theorem 3.2.

If $v_{2n-3}$ is not adjacent to $v_{2n-2}$ on $C_{2n-3}$ and ${\tau }_{v_{2n-3},v_{2n-2}}=0$, we may assume that $C_{2n-3}=⟨v_{2n-3},P_{2n-3},x,v_{2n-2},P_{2n-2},y,v_{2n-3}⟩$. It is easy to see that ${\tau }_{v_{2n-3},x}=1$ and ${\tau }_{v_{2n-2},y}=1$. Thus, Lemma 1 results in a Hamiltonian path $P_1$ joining $x\left(n^{-}\right)$ to $v_{2n-3}\left(n^{-}\right)$ that spans $Q[j^{\prime }+1,k-1]$ and a Hamiltonian path $P_2$ joining $y\left(n^{+}\right)$ to $v_{2n-2}\left(n^{+}\right)$ that spans $Q[1,j^{\prime }-1]$. Let $C_{2n-3}^{\prime }=⟨v_{2n-3},P_{2n-3},x,x\left(n^{-}\right),P_1,v_{2n-3}\left(n^{-}\right),v_{2n-3}⟩$ and $C_{2n-2}=⟨v_{2n-2},P_{2n-2},y,y\left(n^{+}\right),P_2,v_{2n-2}\left(n^{+}\right),v_{2n-2}⟩$. Then, $\{C_1,C_2,\dots ,C_{2n-3}^{\prime },C_{2n-2},C_{2n-1}\}$ is a desired 2-factor of $Q_n^k$.

Now, assume that $v_{2n-3}$ is not adjacent to $v_{2n-2}$ on $C_{2n-3}$ and ${\tau }_{v_{2n-3},v_{2n-2}}=1$; then, $|C_{2n-3}|\le 6$. Let $C_{2n-3}=⟨v_{2n-3},P_{2n-3},z,x,v_{2n-2},P_{2n-2},y,v_{2n-3}⟩$. Such vertices z and x can be guaranteed because $v_{2n-3}$ is not adjacent to $v_{2n-2}$ on $C_{2n-3}$. Moreover, we have ${\tau }_{v_{2n-3},z}=1$ and ${\tau }_{x,y}=1$. Lemma 1 gives a Hamiltonian path $P_1$ joining $z\left(n^{-}\right)$ to $v_{2n-3}\left(n^{-}\right)$ that spans $Q[j^{\prime }+1,k-1]$ and a Hamiltonian path $P_2$ joining $y\left(n^{+}\right)$ to $x\left(n^{+}\right)$ that spans $Q[1,j^{\prime }-1]$. Let $C_{2n-3}^{\prime }=⟨v_{2n-3},P_{2n-3},z,z\left(n^{-}\right),P_1,v_{2n-3}\left(n^{-}\right),v_{2n-3}⟩$ and $C_{2n-2}=⟨v_{2n-2},P_{2n-2},y,y\left(n^{+}\right),P_2,x\left(n^{+}\right),x,v_{2n-2}⟩$. Then, $\{C_1,C_2,\dots ,C_{2n-3}^{\prime },C_{2n-2},C_{2n-1}\}$ is a desired 2-factor of $Q_n^k$; see Figure 2b for an illustration.

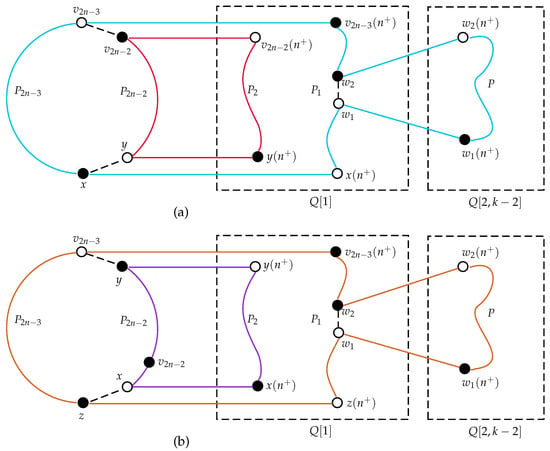
Case 2.2.2.$j^{\prime }=1$ or $j^{\prime }=k-1$. We may assume that $j^{\prime }=k-1$ because the case $j^{\prime }=1$ can be solved with a similar method. Also, we distinguish several situations according to the locations of $v_{2n-3}$ and $v_{2n-2}$ on $C_{2n-3}$. If $v_{2n-2}$ is adjacent to $v_{2n-3}$ on $C_{2n-3}$, assume that $C_{2n-3}=⟨v_{2n-3},P_{2n-3},x,y,P_{2n-2},v_{2n-2},v_{2n-3}⟩$. Note that $Q_n^k$ is bipartite with even k, and we have ${\tau }_{v_{2n-3},v_{2n-2}}=1$. Moreover, it follows that there exist such x and y satisfying $x\ne v_{2n-3}$, $y\ne v_{2n-2}$, and ${\tau }_{x,y}={\tau }_{x,v_{2n-3}}={\tau }_{y,v_{2n-2}}=1$. By Lemma 2, there is a paired 2-disjoint path cover $\{P_1,P_2\}$ in $Q\left[1\right]$ such that $P_1$ is a path joining $x\left(n^{-}\right)$ to $v_{2n-3}\left(n^{-}\right)$, and $P_2$ is a path joining $y\left(n^{-}\right)$ to $v_{2n-2}\left(n^{-}\right)$. Moreover, let $w_1{w}_2$ be an edge of the path cover. Without loss of generality, assume that $w_1{w}_2$ is on $P_1$, and $P_1=⟨x\left(n^{-}\right),L_1,w_1,w_2,L_2,v_{2n-3}\left(n^{-}\right)⟩$. By Lemma 1, there is a Hamiltonian path P joining $w_1\left(n^{-}\right)$ to $w_2\left(n^{-}\right)$ that spans $Q[2,k-2]$. Let $C_{2n-3}^{\prime }=⟨v_{2n-3},P_{2n-3},x,x\left(n^{-}\right),L_1,w_1,w_1\left(n^{-}\right),P,w_2\left(n^{-}\right),w_2,L_2,v_{2n-3}\left(n^{-}\right),v_{2n-3}⟩$ and $C_{2n-2}=⟨v_{2n-2},P_{2n-2}^{-},y,y\left(n^{-}\right),P_2,v_{2n-2}\left(n^{-}\right),v_{2n-2}⟩$. Then, $\{C_1,C_2,\dots ,C_{2n-3}^{\prime },C_{2n-2},$$C_{2n-1}\}$ is a desired 2-factor of $Q_n^k$; see Figure 3a for an illustration.

Figure 3. Illustrations for Case 2.2.2 of Theorem 3.2.

If $v_{2n-3}$ is not adjacent to $v_{2n-2}$ on $C_{2n-3}$ and ${\tau }_{v_{2n-3},v_{2n-2}}=0$, we may assume that $C_{2n-3}=⟨v_{2n-3},P_{2n-3},x,v_{2n-2},P_{2n-2},y,v_{2n-3}⟩$. It is easy to see that ${\tau }_{v_{2n-3},x}=1$ and ${\tau }_{v_{2n-2},y}=1$. By Lemma 2, there is a paired 2-disjoint path cover $\{P_1,P_2\}$ in $Q\left[1\right]$ such that $P_1$ is a path joining $x\left(n^{-}\right)$ to $v_{2n-3}\left(n^{-}\right)$, and $P_2$ is a path joining $y\left(n^{-}\right)$ to $v_{2n-2}\left(n^{-}\right)$. Moreover, let $w_1{w}_2$ be an edge of the path cover; that is, $w_1{w}_2$ is on $P_1$. Suppose that $P_1=⟨x\left(n^{-}\right),L_1,w_1,w_2,L_2,v_{2n-3}\left(n^{-}\right)⟩$. By Lemma 1, there is a Hamiltonian path P joining $w_1\left(n^{-}\right)$ to $w_2\left(n^{-}\right)$ that spans $Q[2,k-2]$. Let $C_{2n-3}^{\prime }=⟨v_{2n-3},P_{2n-3},x,x\left(n^{-}\right),L_1,w_1,w_1\left(n^{-}\right),$$P,w_2\left(n^{-}\right),w_2,L_2,v_{2n-3}\left(n^{-}\right),v_{2n-3}⟩$ and $C_{2n-2}=⟨v_{2n-2},P_{2n-2},y,y\left(n^{-}\right),P_2,v_{2n-2}\left(n^{-}\right),$$v_{2n-2}⟩$. Then, $\{C_1,C_2,\dots ,C_{2n-3}^{\prime },C_{2n-2},C_{2n-1}\}$ is a desired 2-factor of $Q_n^k$.

Now, assume that $v_{2n-3}$ is not adjacent to $v_{2n-2}$ on $C_{2n-3}$ and ${\tau }_{v_{2n-3},v_{2n-2}}=1$. It is easy to see that $|C_{2n-3}|\ge 6$. Let $C_{2n-3}=⟨v_{2n-3},P_{2n-3},z,x,v_{2n-2},P_{2n-2},y,v_{2n-3}⟩$. Thus, we have ${\tau }_{v_{2n-3},z}=1$ and ${\tau }_{x,y}=1$. Lemma 2 gives a paired 2-disjoint path cover $\{P_1,P_2\}$ in $Q\left[1\right]$ such that $P_1$ is a path joining $z\left(n^{-}\right)$ to $v_{2n-3}\left(n^{-}\right)$, and $P_2$ is a path joining $y\left(n^{-}\right)$ to $x\left(n^{-}\right)$. Moreover, let $w_1{w}_2$ be an edge of the path cover. Without loss of generality, assume that $w_1{w}_2$ is on $P_1$, and $P_1=⟨z\left(n^{-}\right),L_1,w_1,w_2,L_2,v_{2n-3}\left(n^{-}\right)⟩$. Lemma 1 gives a Hamiltonian path P joining $w_1\left(n^{-}\right)$ to $w_2\left(n^{-}\right)$ that spans $Q[2,k-2]$. Let $C_{2n-3}^{\prime }=⟨v_{2n-3},P_{2n-3},z,z\left(n^{-}\right),L_1,w_1,w_1\left(n^{-}\right),P,w_2\left(n^{-}\right),w_2,L_2,v_{2n-3}\left(n^{-}\right),v_{2n-3}⟩$ and $C_{2n-2}=⟨v_{2n-2},P_{2n-2},y,y\left(n^{-}\right),P_2,x\left(n^{-}\right),x,v_{2n-2}⟩$. Then, $\{C_1,C_2,\dots ,C_{2n-3}^{\prime },C_{2n-2},$$C_{2n-1}\}$ is a desired 2-factor of $Q_n^k$; see Figure 3b for an illustration.

Case 3. There exists some $j\in {\mathbb{Z}}_k$ such that $s_j=2n-1$. Without loss of generality, we may assume that $s_0=2n-1$. Let $u=0u_{n-2}{u}_{n-3}\cdots u_1{u}_0$ and $v=0v_{n-2}{v}_{n-3}\cdots v_1{v}_0$ be two distinct prescribed vertices in $Q\left[0\right]$. Then, there exists some $i\in {\mathbb{Z}}_{n-1}$ such that $u_i\ne v_i$. Divide $Q_n^k$ into k disjoint subgraphs $Q_n^k\left[0\right]$, $Q_n^k\left[1\right]$, …, $Q_n^k[k-1]$ along its i-dimensional edges. Thus, the prescribed vertices u and v belong to different subcubes of $Q_n^k$, and each subcube contains at most $2n-2$ prescribed vertices, which can be reduced to Case 2.

This completes the proof of Theorem 1. □

We provide an example to show that $Q_n^k$ is not $2n$-spanning cyclable. Let v be any vertex of $Q_n^k$, and let its neighbors be $v_1,v_2,\dots ,v_{2n}$. Then, $Q_n^k$ cannot be $2n$-spanning cyclable. Otherwise, we select the $2n$ prescribed vertices as $v_1,v_2,\dots ,v_{2n}$. Since v must be on some cycle, such a cycle must contain two of $v_1,v_2,\dots ,v_{2n}$, which is a contradiction.

4. Experimental Results and Analysis

In this section, we provide some experimental examples to demonstrate the performance of the main theorem. We focus on the 4-ary 3-cube $Q_3^4$, which contains 64 vertices. The spanning disjoint cycles of $Q_3^4$ are listed in Table 1. In order to make the experimental results easier to follow, we give some explanations. The left column of the table represents prescribed vertices of $Q_3^4$, while the right column of the table represents vertex-disjoint cycles of $Q_3^4$ such that every cycle contains a prescribed vertex and the union of all cycles spans $Q_3^4$. Let $S=\{001,003,010,030,100,300\}$; it is not difficult to see that $Q_3^4$ cannot be 6-spanning cyclable such that every cycle contains exactly one vertex of S. Therefore, the main theorem is optimal with respect to the degree of $Q_n^k$.

Table 1. Spanning disjoint cycles in $Q_3^4$.

Prescribed Vertices	Spanning Disjoint Cycles
{000, 111, 222, 333}	$⟨000,001,002,003,013,012,011,021,022,023,033,032,031,030,020,010,000⟩$
	$⟨100,101,102,103,113,112,111,121,122,123,133,132,131,130,120,110,100⟩$
	$⟨200,201,202,203,213,212,211,221,222,223,233,232,231,230,220,210,200⟩$
	$⟨300,301,302,303,313,312,311,321,322,323,333,332,331,330,320,310,300⟩$
{000, 010, 102, 212, 322}	$⟨000,001,002,003,033,032,031,030,000⟩$
	$⟨010,011,012,013,023,022,021,020,010⟩$
	$⟨100,101,102,103,113,112,111,121,122,123,133,132,131,130,120,110,100⟩$
	$⟨200,201,202,203,213,212,211,221,222,223,233,232,231,230,220,210,200⟩$
	$⟨300,301,302,303,313,312,311,321,322,323,333,332,331,330,320,310,300⟩$
{000, 001, 010, 113, 202}	$⟨000,300,301,302,303,333,332,331,330,030,033,003,000⟩$
	$⟨001,011,021,031,032,022,023,013,012,002,001⟩$
	$⟨010,310,311,312,313,323,322,321,320,020,010⟩$
	$⟨100,101,102,103,113,112,111,121,122,123,133,132,131,130,120,110,100⟩$
	$⟨200,201,202,203,213,212,211,221,222,223,233,232,231,230,220,210,200⟩$
{000, 020, 022, 100, 110}	$⟨000,300,301,302,303,333,332,331,330,030,033,003,000⟩$
	$⟨010,310,311,312,313,323,322,321,320,020,010⟩$
	$⟨001,011,021,031,032,022,023,013,012,002,001⟩$
	$⟨100,200,201,202,203,233,232,231,230,130,131,132,133,103,102,101,100⟩$
	$⟨110,210,211,212,213,223,222,221,220,120,121,122,123,113,112,111,110⟩$
{000, 010, 001, 011}	$⟨000,100,200,300,330,230,130,030,033,133,233,333,303,203,103,003,001⟩$
	$⟨010,110,210,310,320,220,120,020,023,123,223,323,313,213,113,013,010⟩$
	$⟨001,101,201,301,331,231,131,031,032,132,232,332,302,202,102,002,001⟩$
	$⟨011,111,211,311,321,221,121,021,022,122,222,322,312,212,112,012,011⟩$
{000, 003, 030, 033, 133}	$⟨000,300,200,201,211,210,310,311,301,001,011,010,000⟩$
	$⟨003,303,203,202,212,213,313,312,302,002,012,013,003⟩$
	$⟨030,330,230,220,221,231,331,321,320,020,021,031,030⟩$
	$⟨033,333,233,223,222,232,332,322,323,023,022,032,033⟩$
	$⟨100,101,102,103,113,112,111,121,122,123,133,132,131,130,120,110,100⟩$
{000, 010, 012, 022, 021}	$⟨000,300,200,201,211,210,310,311,301,001,000⟩$
	$⟨010,110,120,130,100,101,102,103,113,112,122,123,133,132,131,121,111⟩$
	$⟨003,303,203,202,212,213,313,312,302,002,012,013,003⟩$
	$⟨033,333,233,223,222,232,332,322,323,023,022,032,033⟩$
	$⟨030,330,230,220,221,231,331,321,320,020,021,031,030⟩$

5. Concluding Remarks

In a network simulation, it is essential to embed cycles into the network. In particular, having Hamiltonian cycles is a crucial requirement for developing high-quality interconnection networks. This paper studies the spanning cyclability of k-ary n-cubes and shows that an n-dimensional bipartite k-ary n-cube $Q_n^k$ is m-spanning cyclable with $m\le 2n-1$. Considering the degree of $Q_n^k$, the result is optimal. A natural question arises: Why do our results need to exclude the non-bipartite k-ary n-cube when $k\ge 3$ is odd? In fact, our original findings do not exclude the non-bipartite k-ary n-cube when k is odd. However, there are some difficulties we have not overcome. As shown in this paper, the proofs of several subcases in Case 2 of Theorem 1 depend on every cycle having a length of at least 4, and the methods are not appropriate for the case where $k=3$. Let $k\ge 3$ be odd. The spanning cyclability for the non-bipartite k-ary n-cube $Q_n^k$ will be addressed in future research.