Stable Majorana Zero-Energy Modes in Two-Dimensional Josephson Junctions
Abstract
:1. Introduction
2. Setup
3. Symmetry
4. Band Structures
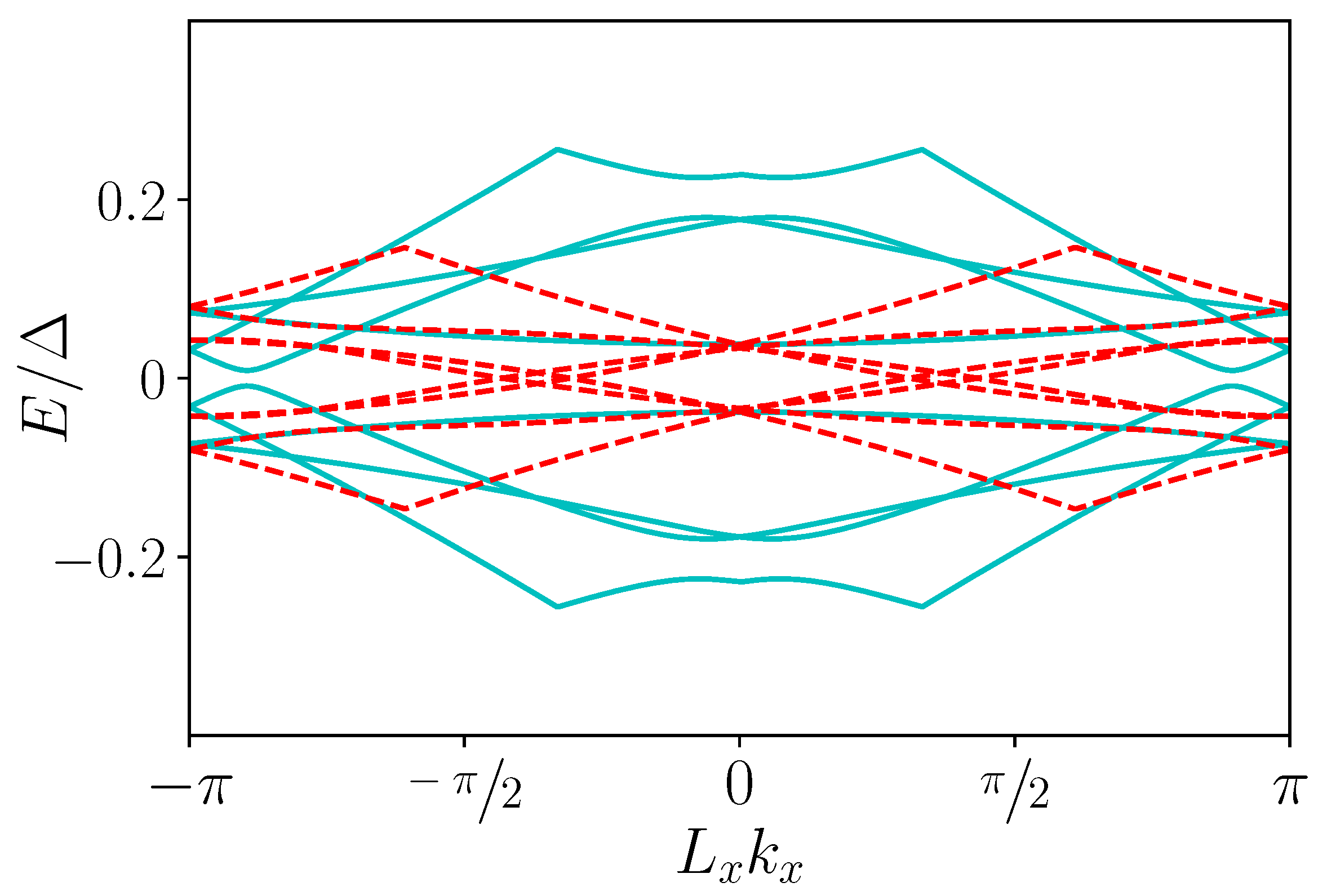
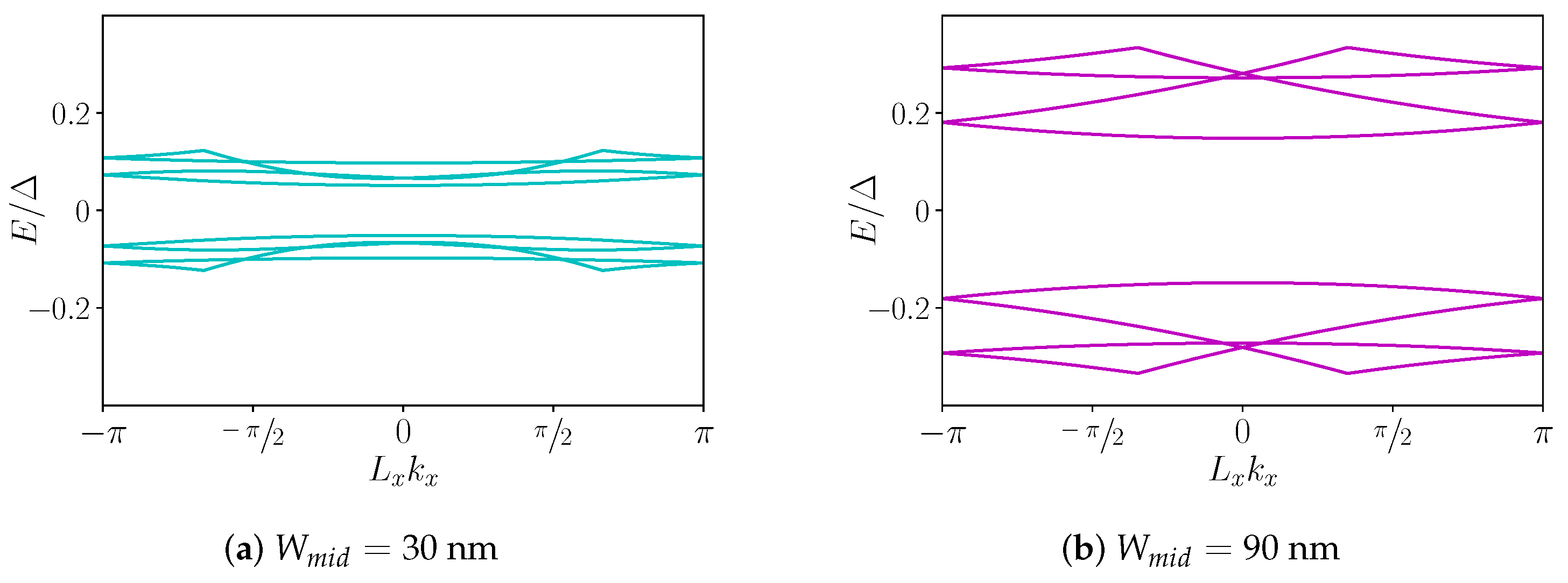
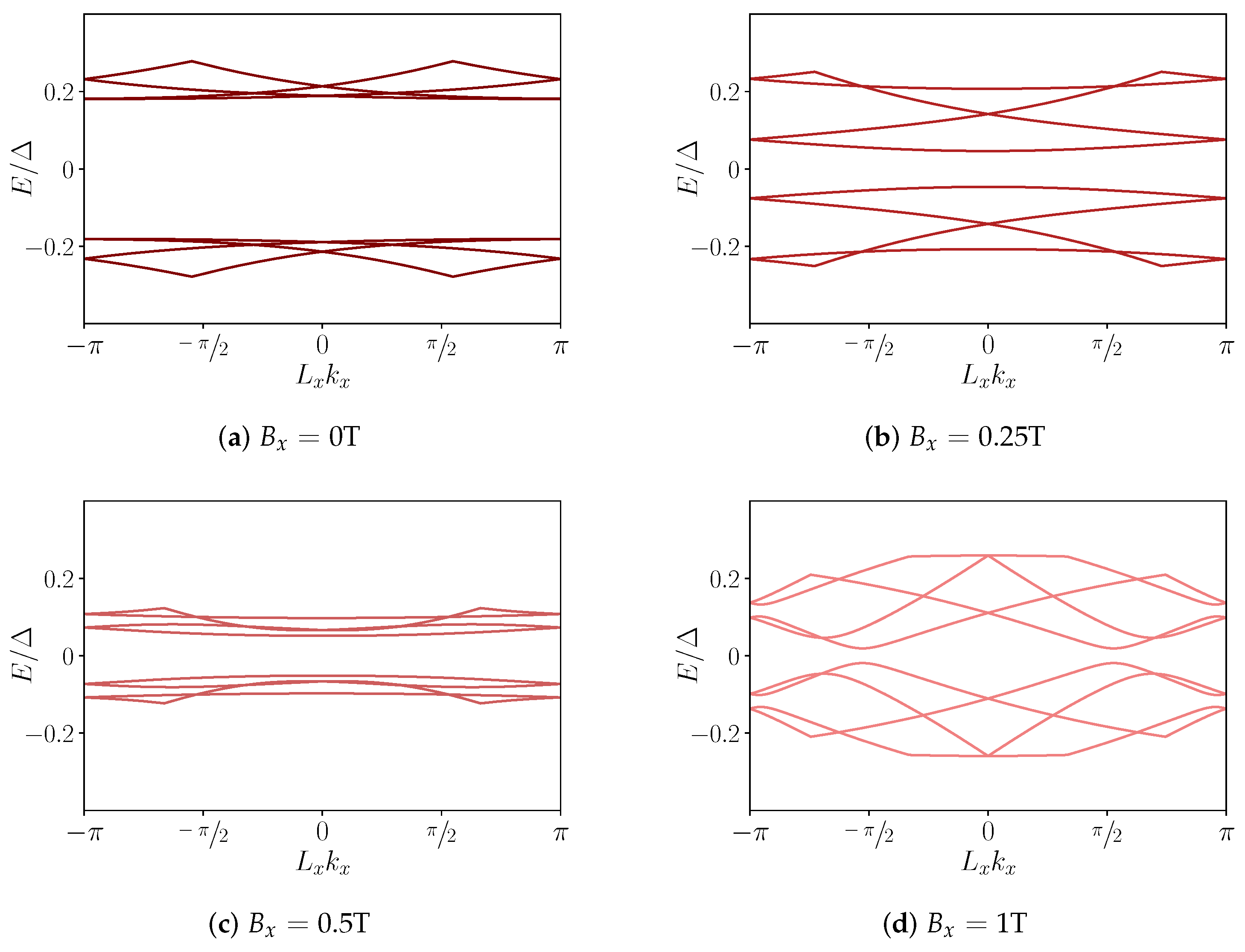
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Physics-Uspekhi 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 2012, 75, 076501. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yang, B.; Ma, G.; Li, J.; Zhang, S.; Chan, C.T. Non-Abelian physics in light and sound. Science 2024, 383, eadf9621. [Google Scholar] [CrossRef] [PubMed]
- Elliott, S.R.; Franz, M. Colloquium: Majorana fermions in nuclear, particle, and solid-state physics. Rev. Mod. Phys. 2015, 87, 137–163. [Google Scholar] [CrossRef]
- Lutchyn, R.M.; Bakkers, E.P.A.M.; Kouwenhoven, L.P.; Krogstrup, P.; Marcus, C.M.; Oreg, Y. Majorana zero modes in superconductor—Semiconductor heterostructures. Nat. Rev. Mater. 2018, 3, 52–68. [Google Scholar] [CrossRef]
- Jäck, B.; Xie, Y.; Yazdani, A. Detecting and distinguishing Majorana zero modes with the scanning tunnelling microscope. Nat. Rev. Phys. 2021, 3, 541–554. [Google Scholar] [CrossRef]
- Flensberg, K.; von Oppen, F.; Stern, A. Engineered platforms for topological superconductivity and Majorana zero modes. Nat. Rev. Mater. 2021, 6, 944–958. [Google Scholar] [CrossRef]
- Oreg, Y.; Refael, G.; von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 2010, 105, 177002. [Google Scholar] [CrossRef] [PubMed]
- Aasen, D.; Hell, M.; Mishmash, R.V.; Higginbotham, A.; Danon, J.; Leijnse, M.; Jespersen, T.S.; Folk, J.A.; Marcus, C.M.; Flensberg, K.; et al. Milestones Toward Majorana-Based Quantum Computing. Phys. Rev. X 2016, 6, 031016. [Google Scholar] [CrossRef]
- Yazdani, A.; von Oppen, F.; Halperin, B.I.; Yacoby, A. Hunting for Majoranas. Science 2023, 380, eade0850. [Google Scholar] [CrossRef]
- Leijnse, M.; Flensberg, K. Introduction to topological superconductivity and Majorana fermions. Semicond. Sci. Technol. 2012, 27, 124003. [Google Scholar] [CrossRef]
- Frolov, S.M.; Manfra, M.J.; Sau, J.D. Topological superconductivity in hybrid devices. Nat. Phys. 2020, 16, 718–724. [Google Scholar] [CrossRef]
- Aghaee, M.; Akkala, A.; Alam, Z.; Ali, R.; Alcaraz Ramirez, A.; Andrzejczuk, M.; Antipov, A.E.; Aseev, P.; Astafev, M.; Bauer, B.; et al. InAs-Al hybrid devices passing the topological gap protocol. Phys. Rev. B 2023, 107, 245423. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, S.; Zhang, G.; Liu, D.E. Recent progress on Majorana in semiconductor-superconductor heterostructures—Engineering and detection. Sci. China Phys. Mech. Astron. 2023, 66, 267003. [Google Scholar] [CrossRef]
- Marra, P. Majorana nanowires for topological quantum computation. J. Appl. Phys. 2022, 132, 231101. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [PubMed]
- Lutchyn, R.M.; Sau, J.D.; Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef]
- Sau, J.D.; Lutchyn, R.M.; Tewari, S.; Das Sarma, S. Generic New Platform for Topological Quantum Computation Using Semiconductor Heterostructures. Phys. Rev. Lett. 2010, 104, 040502. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chan, Y.h.; Hlevyack, J.A.; Bowers, J.W.; Chou, M.Y.; Chiang, T.C. Topological Quantum Well States in Pb/Sb Thin-Film Heterostructures. ACS Nano 2024, 18, 10243–10248. [Google Scholar] [CrossRef]
- Pientka, F.; Keselman, A.; Berg, E.; Yacoby, A.; Stern, A.; Halperin, B.I. Topological Superconductivity in a Planar Josephson Junction. Phys. Rev. X 2017, 7, 021032. [Google Scholar] [CrossRef]
- Hell, M.; Leijnse, M.; Flensberg, K. Two-Dimensional Platform for Networks of Majorana Bound States. Phys. Rev. Lett. 2017, 118, 107701. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.D. Circulator function in a Josephson junction circuit and braiding of Majorana zero modes. Sci. Rep. 2021, 11, 1826. [Google Scholar] [CrossRef] [PubMed]
- Yuan, T.; Zhou, F.; Chen, S.; Xiang, S.; Song, K.; Zhao, Y. Multipurpose Quantum Simulator Based on a Hybrid Solid-State Quantum Device. Symmetry 2019, 11, 467. [Google Scholar] [CrossRef]
- Ren, H.; Pientka, F.; Hart, S.; Pierce, A.T.; Kosowsky, M.; Lunczer, L.; Schlereth, R.; Scharf, B.; Hankiewicz, E.M.; Molenkamp, L.W.; et al. Topological superconductivity in a phase-controlled Josephson junction. Nature 2019, 569, 93–98. [Google Scholar] [CrossRef] [PubMed]
- Paudel, P.P.; Smith, N.O.; Stanescu, T.D. Disorder effects in planar semiconductor-superconductor structures: Majorana wires versus Josephson junctions. arXiv 2024, arXiv:2405.12192. [Google Scholar]
- Pan, X.H.; Chen, L.; Liu, D.E.; Zhang, F.C.; Liu, X. Majorana Zero Modes Induced by the Meissner Effect at Small Magnetic Field. Phys. Rev. Lett. 2024, 132, 036602. [Google Scholar] [CrossRef] [PubMed]
- Lesser, O.; Oreg, Y. Majorana zero modes induced by superconducting phase bias. J. Phys. D Appl. Phys. 2022, 55, 164001. [Google Scholar] [CrossRef]
- Fornieri, A.; Whiticar, A.M.; Setiawan, F.; Portolés, E.; Drachmann, A.C.C.; Keselman, A.; Gronin, S.; Thomas, C.; Wang, T.; Kallaher, R.; et al. Evidence of topological superconductivity in planar Josephson junctions. Nature 2019, 569, 89–92. [Google Scholar] [CrossRef] [PubMed]
- Flensberg, K. Tunneling characteristics of a chain of Majorana bound states. Phys. Rev. B 2010, 82, 180516. [Google Scholar] [CrossRef]
- Valentini, M.; Peñaranda, F.; Hofmann, A.; Brauns, M.; Hauschild, R.; Krogstrup, P.; San-Jose, P.; Prada, E.; Aguado, R.; Katsaros, G. Nontopological zero-bias peaks in full-shell nanowires induced by flux-tunable Andreev states. Science 2021, 373, 82–88. [Google Scholar] [CrossRef]
- Dartiailh, M.C.; Mayer, W.; Yuan, J.; Wickramasinghe, K.S.; Matos-Abiague, A.; Žutić, I.; Shabani, J. Phase Signature of Topological Transition in Josephson Junctions. Phys. Rev. Lett. 2021, 126, 036802. [Google Scholar] [CrossRef] [PubMed]
- Jeon, S.; Xie, Y.; Li, J.; Wang, Z.; Bernevig, B.A.; Yazdani, A. Distinguishing a Majorana zero mode using spin-resolved measurements. Science 2017, 358, 772–776. [Google Scholar] [CrossRef]
- Sun, L.; DiCarlo, L.; Reed, M.D.; Catelani, G.; Bishop, L.S.; Schuster, D.I.; Johnson, B.R.; Yang, G.A.; Frunzio, L.; Glazman, L.; et al. Measurements of Quasiparticle Tunneling Dynamics in a Band-Gap-Engineered Transmon Qubit. Phys. Rev. Lett. 2012, 108, 230509. [Google Scholar] [CrossRef]
- Laeven, T.; Nijholt, B.; Wimmer, M.; Akhmerov, A.R. Enhanced Proximity Effect in Zigzag-Shaped Majorana Josephson Junctions. Phys. Rev. Lett. 2020, 125, 086802. [Google Scholar] [CrossRef] [PubMed]
- Takei, S.; Fregoso, B.M.; Hui, H.Y.; Lobos, A.M.; Das Sarma, S. Soft Superconducting Gap in Semiconductor Majorana Nanowires. Phys. Rev. Lett. 2013, 110, 186803. [Google Scholar] [CrossRef]
- Heiss, W. Quantum Dots: A Doorway to Nanoscale Physics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Haim, A.; Stern, A. Benefits of Weak Disorder in One-Dimensional Topological Superconductors. Phys. Rev. Lett. 2019, 122, 126801. [Google Scholar] [CrossRef]
- Hassan, S.A.; Wu, B.H.; Xu, X.F.; Wang, C.R.; Cao, J.C. Bending effect on the Majorana bound states in planar Josephson junctions. J. Phys. Condens. Matter 2021, 33, 385001. [Google Scholar] [CrossRef]
- van Heck, B.; Mi, S.; Akhmerov, A.R. Single fermion manipulation via superconducting phase differences in multiterminal Josephson junctions. Phys. Rev. B 2014, 90, 155450. [Google Scholar] [CrossRef]
- Bardarson, J.H. A proof of the Kramers degeneracy of transmission eigenvalues from antisymmetry of the scattering matrix. J. Phys. A Math. Theor. 2008, 41, 405203. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Universal limit of critical-current fluctuations in mesoscopic Josephson junctions. Phys. Rev. Lett. 1991, 67, 3836–3839. [Google Scholar] [CrossRef]
- Oliinyk, A.; Yatsuta, I.; Malomed, B.; Yakimenko, A. Symmetry Breaking in Interacting Ring-Shaped Superflows of Bose—Einstein Condensates. Symmetry 2019, 11, 1312. [Google Scholar] [CrossRef]
- Akramov, M.; Askerzade, I.; Salati, M.; Karpova, O. Bogoliubov-de Gennes equation on graphs: A model for tree-branched Majorana wire network. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2023; Volume 2667, p. 012032. [Google Scholar]
- Pekerten, B.; Pakizer, J.D.; Hawn, B.; Matos-Abiague, A. Anisotropic topological superconductivity in Josephson junctions. Phys. Rev. B 2022, 105, 054504. [Google Scholar] [CrossRef]
- Sakurai, J.J.; Napolitano, J. Modern Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- Altland, A.; Zirnbauer, M. Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures. Phys. Rev. B 1997, 55, 1142–1161. [Google Scholar] [CrossRef]
- Ryu, S.; Schnyder, A.P.; Furusaki, A.; Ludwig, A.W.W. Topological insulators and superconductors: Tenfold way and dimensional hierarchy. New J. Phys. 2010, 12, 065010. [Google Scholar] [CrossRef]
- Melo, A.; Rubbert, S.; Akhmerov, A.R. Supercurrent-induced Majorana bound states in a planar geometry. SciPost Phys. 2019, 7, 039. [Google Scholar] [CrossRef]
- Groth, C.W.; Wimmer, M.; Akhmerov, A.R.; Waintal, X. Kwant: A software package for quantum transport. New J. Phys. 2014, 16, 063065. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Q.; Li, L.; Wen, Z. Stable Majorana zero-energy modes in two-dimensional Josephson Junctions. Zenodo 2024. [Google Scholar] [CrossRef]
- Kuiri, D.; Nowak, M.P. Non-local transport signatures of topological superconductivity in a phase-biased planar Josephson junction. Phys. Rev. B 2023, 108, 205405. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Wang, Q.; Li, L.; Wen, Z. Stable Majorana Zero-Energy Modes in Two-Dimensional Josephson Junctions. Symmetry 2024, 16, 1066. https://doi.org/10.3390/sym16081066
Huang Y, Wang Q, Li L, Wen Z. Stable Majorana Zero-Energy Modes in Two-Dimensional Josephson Junctions. Symmetry. 2024; 16(8):1066. https://doi.org/10.3390/sym16081066
Chicago/Turabian StyleHuang, Yuting, Qinyi Wang, Lei Li, and Zhenying Wen. 2024. "Stable Majorana Zero-Energy Modes in Two-Dimensional Josephson Junctions" Symmetry 16, no. 8: 1066. https://doi.org/10.3390/sym16081066




