The Properties of Structures with Two Planes of Symmetry
Abstract
:1. Introduction
2. Methods
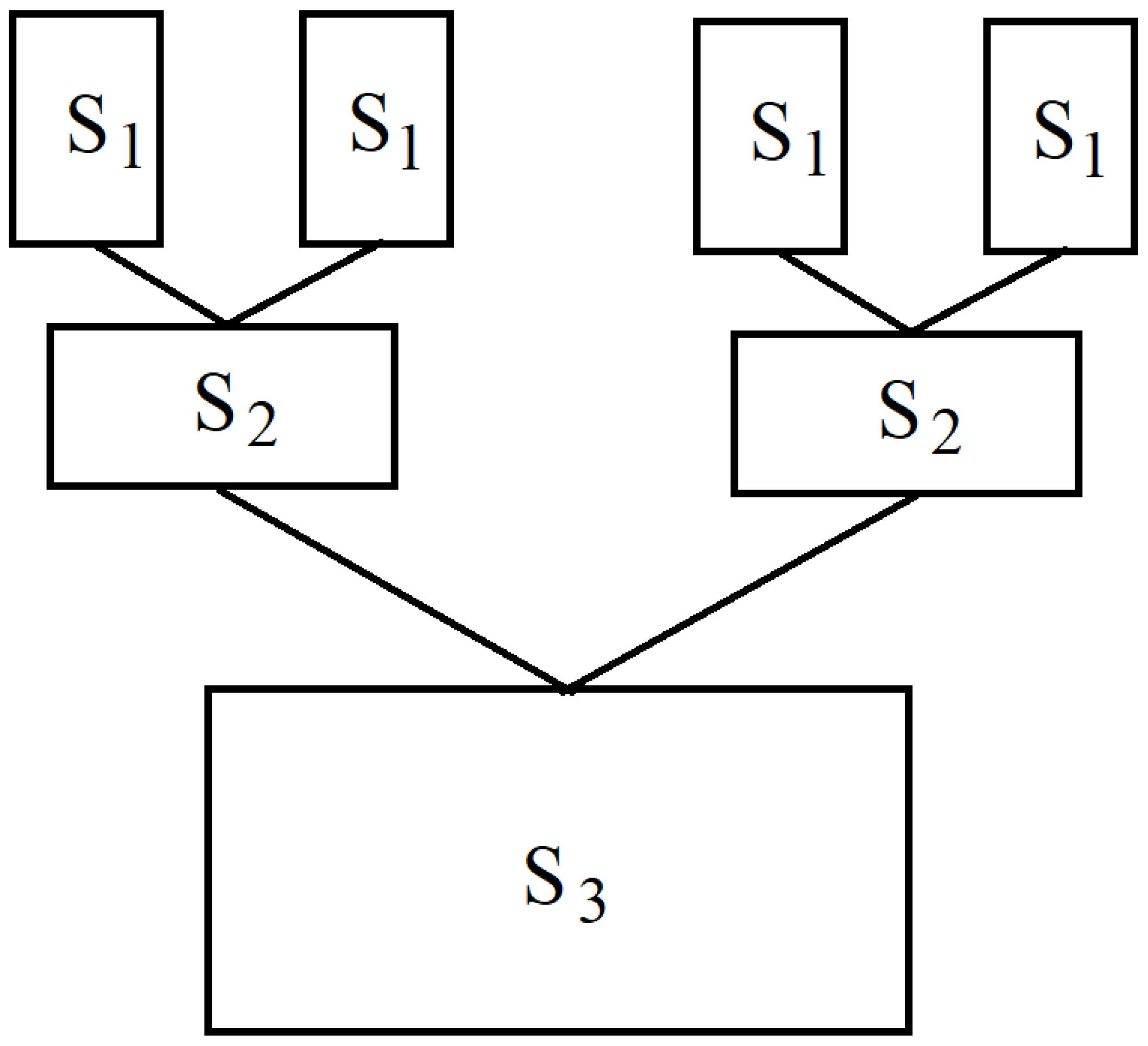
- —the inertial matrix for the subsystems ;
- —the inertial coupling matrix between the two identical parts and the system ;
- —the inertial matrix for the subsystem ;
- —the stiffness matrix for the subsystems ;
- —the stiffness coupling matrix between the two identical parts and the system ;
- —the stiffness matrix for the subsystem ;
- —the damping matrix for the subsystems ;
- —the damping coupling matrix between the two identical parts and the system ;
- —the damping matrix for the subsystem ;
- —the vector of independent coordinates for the subsystem on the left side;
- —the vector of independent coordinates for the subsystem on the right side;
- —the vector of independent coordinates for the subsystem .
3. Results
- -
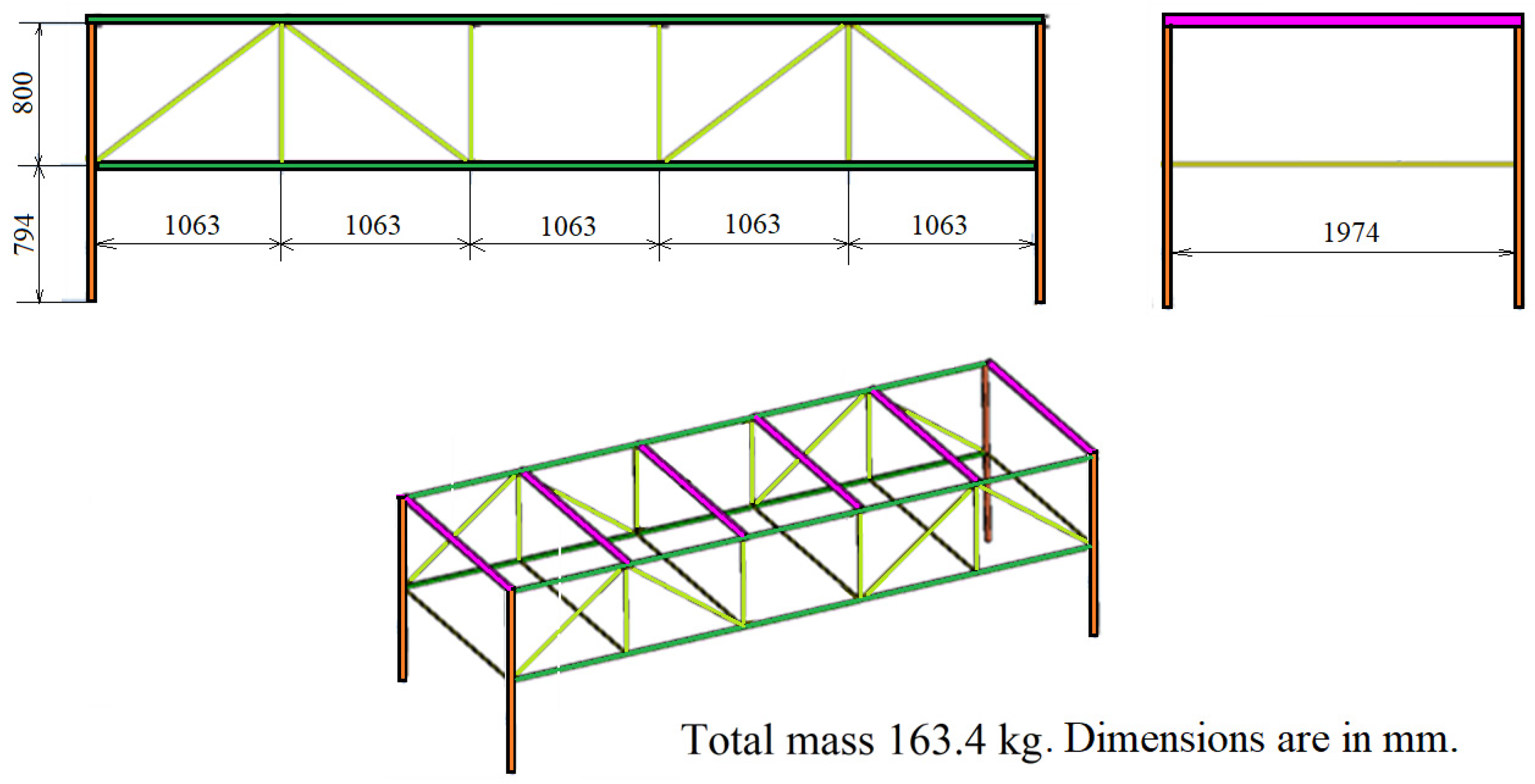
- The lower sole and the upper sole of the lattice beams are made of hot-rolled square pipe with a section of 30 × 2 mm;
- -
- The uprights—hot-rolled square pipe with a section of 20 × 2 mm;
- -
- The diagonals—hot-rolled square pipe with a section of 20 × 2 mm;
- -
- The uprights at the ends of the beams with lattices that also fulfill the role of pillars are made of hot-rolled square pipe with a section of 40 × 2.5 mm;
- -
- The other elements are made of laminated profiles with the U65 section.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meirovitch, L. Analytical Methods in Vibrations; McMillan: New York, NY, USA, 1967. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations; Dover Publications: Mineola, NY, USA, 1985. [Google Scholar]
- Douglas, T. Structural Dynamics and Vibrations in Practice: An Engineering Handbook; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Vlase, S.; Marin, M.; Öchsner, A. Considerations of the transverse vibration of a mechanical system with two identical bars. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 1318–1323. [Google Scholar] [CrossRef]
- Lin, J.; Jin, S.; Zheng, C.; Li, Z.M.; Liu, Y.H. Compliant assembly variation analysis of aeronautical panels using unified substructures with consideration of identical parts. Comput.-Aided Des. 2014, 57, 29–40. [Google Scholar] [CrossRef]
- Shi, C.Z.; Parker, R.G. Modal structure of centrifugal pendulum vibration absorber systems with multiple cyclically symmetric groups of absorbers. J. Sound Vib. 2013, 332, 4339–4353. [Google Scholar] [CrossRef]
- Celep, Z. On the axially symmetric vibration of thick circular plates. Arch. Appl. Mech. 1978, 47, 411–420. [Google Scholar] [CrossRef]
- Elkin, V.I. General-Solutions of Partial-Differential Equation Systems with Identical Principal Parts. Differ. Equ. 1985, 21, 952–959. [Google Scholar]
- Zingoni, A. On the symmetries and vibration modes of layered space grids. Eng. Struct. 2005, 7, 629–638. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Group-Theoretic Exploitations of Symmetry in Novel Prestressed Structures. Symmetry 2018, 10, 229. [Google Scholar] [CrossRef]
- Harth, P.; Beda, P.; Michelberger, P. Static analysis and reanalysis of quasi-symmetric structure with symmetry components of the symmetry groups C-3v and C-1v. Eng. Struct. 2017, 152, 397–412. [Google Scholar] [CrossRef]
- He, J.H.; Latifizadeh, H. A general numerical algorithm for nonlinear differential equations by the variational iteration method. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 4797–4810. [Google Scholar] [CrossRef]
- He, C.H.; Liu, C.; Gepreel, K.A. Low frequency property of a fractal vibration model for a concrete beam. Fractals 2021, 29, 2150117. [Google Scholar] [CrossRef]
- Bratu, P.; Nitu, M.C.; Tonciu, O. Effect of Vibration Transmission in the Case of the Vibratory Roller Compactor. Rom. J. Acoust. Vib. 2023, 20, 67–72. [Google Scholar]
- Rugina, C.; Sireteanu, T.; Chiroiu, V.; Munteanu, L.; Mitu, A.M. Experimental and Numerical Simulation of a Multilevel Structure Behaviour Subjected to Transient Loads. Rom. J. Acoust. Vib. 2023, 20, 147–156. [Google Scholar]
- Seeram, M.; Kumar, P. Free Vibration Analysis of Symmetric and Asymmetric RCC Structures. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1273, 012010. [Google Scholar] [CrossRef]
- Itu, C.; Bratu, P.; Borza, P.; Vlase, S.; Lixandroiu, D. Design and Analysis of Inertial Platform Insulation of the ELI-NP Project of Laser and Gamma Beam Systems. Symmetry 2020, 12, 1972. [Google Scholar] [CrossRef]
- Negrean, I.; Crisan, A.V.; Vlase, S. A New Approach in Analytical Dynamics of Mechanical Systems. Symmetry 2020, 12, 95. [Google Scholar] [CrossRef]
- Sharma, A.K.; Bensal, S. Free Vibration Analysis of Square Structure Plate with Different Boundary Conditions. Rom. J. Acoust. Vib. 2023, 20, 100–106. [Google Scholar] [CrossRef]
- Li, B.J.; Zheng, X.Z.; Zhao, J. Vibration analysis of structures with rotation and reflection symmetry. Shock. Vib. 1996, 3, 303–311. [Google Scholar] [CrossRef]
- Grolet, A.; Malbos, P.; Thouverez, F. Eigenvalue Method with Symmetry and Vibration Analysis of Cyclic Structures. In Proceedings of the 16th International Workshop on Computer Algebra in Scientific Computing (CASC 2014), Warsaw, Poland, 8–12 September 2014; Volume 8660, pp. 121–137. [Google Scholar]
- Whiston, G.S. Use of Screw Translational Symmetry for the Vibration Analysis of Structures. Int. J. Numer. Methods Eng. 1982, 18, 435–444. [Google Scholar] [CrossRef]
- Olson, B.J.; Shaw, S.W. Vibration absorbers for a rotating flexible structure with cyclic symmetry: Nonlinear path design. Nonlinear Dyn. 2010, 60, 149–182. [Google Scholar] [CrossRef]
- Fagert, J.; Mirshekari, M.; Noh, H.Y. Structure- and Sampling-Adaptive Gait Balance Symmetry Estimation Using Footstep-Induced Structural Floor Vibrations. J. Eng. Mech. 2021, 147, 04020151. [Google Scholar] [CrossRef]
- Wang, L.J.; Zhao, J.; Meng, J.A. Study on the 2-Stage Amplitude Amplification of Ultrasonic Vibration Turning System with Symmetry Structure. Chin. Sci. Bull. 1992, 37, 428–431. [Google Scholar]
- Whalen, T.M.; Healey, T.J. Free vibration analysis of rotating nonlinearly elastic structures with symmetry: An efficient group-equivariance approach. Nonlinear Dyn. 1997, 13, 1–37. [Google Scholar] [CrossRef]
- Quaegebeur, S.; Di Palma, N.; Thouverez, F. Exploiting internal resonances in nonlinear structures with cyclic symmetry as a mean of passive vibration control. Mech. Syst. Signal Process. 2022, 178, 04020151. [Google Scholar] [CrossRef]
- Wang, S.Y.; Meesap, C. Investigation on Mesh and Sideband Vibrations of Helical Planetary Ring Gear Using Structure, Excitation and Deformation Symmetries. Chin. J. Mech. Eng. 2018, 31, 104. [Google Scholar] [CrossRef]
- Modrea, A.; Munteanu, V.M.; Pruncu, C.I. Using the Symmetries in the Civil Engineering: An overview. Procedia Manuf. 2020, 46, 906–913. [Google Scholar] [CrossRef]
- Caughey, T.K.; O’Kelly, M.E.J. Classical normal modes in damped linear dynamic systems. ASME J. Appl. Mech. 1965, 32, 583–588. [Google Scholar] [CrossRef]
- Vlase, S.; Itu, C.; Vasile, O.; Nastac, C.; Stanciu, M.D.; Scutaru, M.L. Vibration Analysis of a Mechanical System Composed of Two Identical Parts. Rom. J. Acoust. Vib. 2018, 15, 58–63. [Google Scholar]
- Vlase, S.; Marin, M.; Scutaru, M.L.; Munteanu, R. Coupled transverse and torsional vibrations in a mechanical system with two identical beams. AIP Adv. 2017, 7, 6. [Google Scholar] [CrossRef]
- Codarcea-Munteanu, L.; Marin, M.; Vlase, S. The study of vibrations in the context of porous micropolar media thermoelasticity and the absence of energy dissipation. J. Comput. Appl. Mech. 2023, 54, 437–454. [Google Scholar]
- Vlase, S.; Paun, M. Vibration analysis of a mechanical system consisting of two identical parts. Rom. J. Tech. Sci. Appl. Mech. 2015, 60, 216–230. [Google Scholar]
- Vasile, O.; Vlase, S.; Năstac, C.; Scutaru, M.L. Experimental Analysis of a Mechanical System Composed by Two Identical Parts. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 2018, 61, 333–338. [Google Scholar]


| FULL | HALF_X | HALF_Z | QUARTER | ||||
|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | ||||
| Mode | Eigenfrequency [Hz] | Mode | Eigenfrequency [Hz] | Mode | Eigenfrequency [Hz] | Mode | Eigenfrequency [Hz] |
| 1 | 4.90 | 1 | 4.90 | ||||
| 2 | 9.29 | ||||||
| 3 | 10.74 | 1 | 10.74 | ||||
| 4 | 13.78 | 2 | 13.78 | ||||
| 5 | 16.37 | ||||||
| 6 | 16.87 | 3 | 16.87 | ||||
| 7 | 18.81 | 2 | 18.81 | ||||
| 8 | 19.70 | ||||||
| 9 | 22.60 | ||||||
| 10 | 23.50 | 4 | 23.50 | ||||
| 11 | 26.11 | ||||||
| 12 | 27.48 | 3 | 27.48 | 5 | 27.48 | 1 | 27.48 |
| 13 | 27.56 | ||||||
| 14 | 29.22 | 4 | 29.22 | ||||
| 15 | 29.89 | 5 | 29.89 | 6 | 29.89 | 2 | 29.89 |
| 16 | 31.00 | 6 | 31.00 | 7 | 31.00 | 3 | 31.00 |
| 17 | 31.00 | 7 | 31.00 | ||||
| 18 | 31.56 | 8 | 31.56 | ||||
| 19 | 32.17 | 9 | 32.17 | 8 | 32.17 | 4 | 32.17 |
| 20 | 32.54 | 9 | 32.54 | ||||
| 21 | 32.85 | 10 | 32.85 | ||||
| 22 | 33.01 | 11 | 33.01 | 10 | 33.01 | 5 | 33.01 |
| 23 | 33.96 | 12 | 33.96 | 11 | 33.96 | 6 | 33.96 |
| 24 | 34.17 | 13 | 34.17 | ||||
| 25 | 34.26 | 14 | 34.26 | 12 | 34.26 | 7 | 34.26 |
| 26 | 34.26 | 15 | 34.26 | ||||
| 27 | 34.54 | 16 | 34.54 | ||||
| 28 | 35.52 | 17 | 35.52 | 13 | 35.52 | 8 | 35.52 |
| 29 | 36.54 | 18 | 36.54 | 14 | 36.54 | ||
| 30 | 37.72 | 19 | 37.72 | 9 | 36.54 | ||
| 31 | 39.81 | 20 | 39.81 | 15 | 39.81 | 10 | 39.81 |
| 32 | 43.11 | ||||||
| 33 | 46.96 | 46.96 | 16 | 46.96 | 11 | 46.96 | |
| 34 | 47.21 | ||||||
| 35 | 52.38 | ||||||
| 36 | 52.56 | 52.56 | 17 | 52.56 | 12 | 52.56 | |
| 37 | 52.78 | ||||||
| 38 | 54.09 | 18 | 54.09 | ||||
| 39 | 61.29 | ||||||
| 40 | 65.36 | 65.36 | 19 | 65.36 | 13 | 65.36 | |
| 41 | 65.64 | 20 | 65.64 | ||||
| 42 | 67.96 | ||||||
| 43 | 68.32 | ||||||
| 44 | 70.33 | 70.33 | 70.33 | 14 | 70.33 | ||
| 45 | 70.42 | ||||||
| 46 | 71.00 | ||||||
| 47 | 71.74 | 71.74 | 71.74 | 15 | 71.74 | ||
| 48 | 72.23 | ||||||
| 49 | 72.88 | ||||||
| 50 | 73.72 | 73.72 | 73.72 | 16 | 73.72 | ||
| Type of Symmetry | |||
|---|---|---|---|
| Full System | Half System X | Half System Z | Quarter |
 Mode 1: 4.90 Hz | 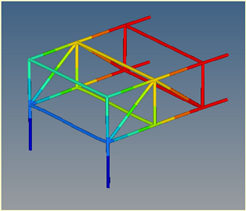 Mode 1: 4.90 Hz | ||
 Mode 3: 10.74 Hz |  Mode 1: 10.74 Hz | ||
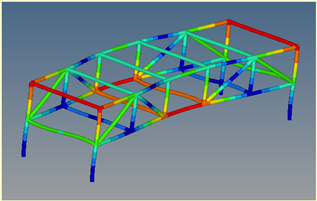 Mode 4: ν = 13.78 Hz | 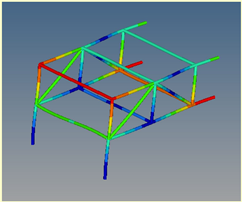 Mode 2: ν = 13.78 Hz | ||
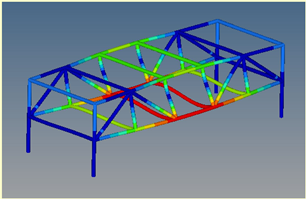 Mode 6: ν = 16.87 Hz |  Mode 3: ν = 16.87 Hz | ||
 Mode 7: ν = 18.81 Hz | 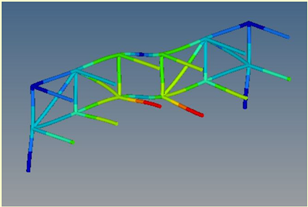 Mode 2: ν = 18.81 Hz | ||
 Mode 10: ν = 23.50 Hz | 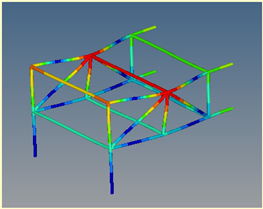 Mode 4: ν = 23.50 Hz | ||
 Mode 12: ν = 27.48 Hz | 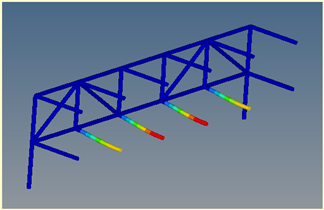 Mode 3: ν = 27.48 Hz | 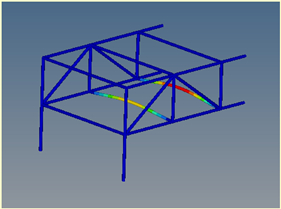 Mode 5: ν = 27.48 Hz |  Mode 1: ν = 27.48 Hz |
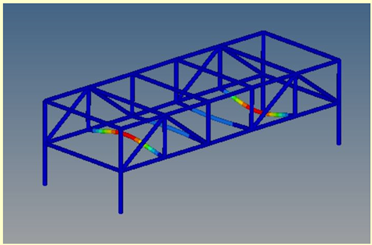 Mode 14: ν = 29.22 Hz | 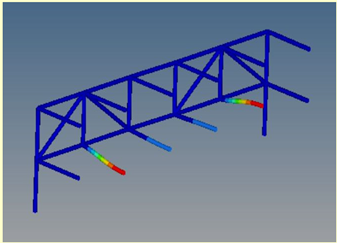 Mode 4: ν = 29.22 Hz | ||
 Mode 15: ν = 29.89 Hz | 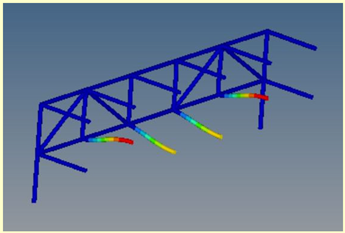 Mode 5: ν = 29.89 Hz | 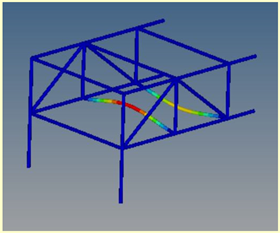 Mode 6: ν = 29.89 Hz | 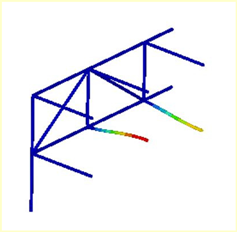 Mode 2: ν = 29.89 Hz |
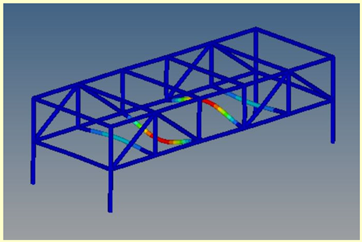 Mode 16: ν = 31.00 Hz | 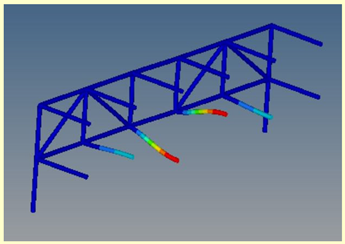 Mode 6: ν = 31.00 Hz |  Mode 7: ν = 31.00 Hz |  Mode 3: ν = 31.00 Hz |
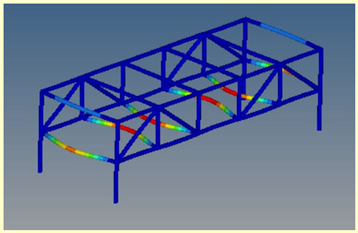 Mode 17: ν = 31.00 Hz | 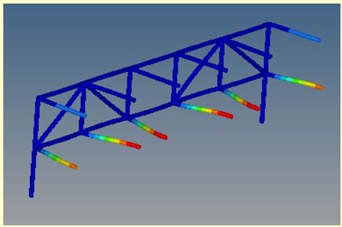 Mode 7: ν = 31.00 Hz | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlase, S.; Itu, C. The Properties of Structures with Two Planes of Symmetry. Symmetry 2024, 16, 1075. https://doi.org/10.3390/sym16081075
Vlase S, Itu C. The Properties of Structures with Two Planes of Symmetry. Symmetry. 2024; 16(8):1075. https://doi.org/10.3390/sym16081075
Chicago/Turabian StyleVlase, Sorin, and Calin Itu. 2024. "The Properties of Structures with Two Planes of Symmetry" Symmetry 16, no. 8: 1075. https://doi.org/10.3390/sym16081075
APA StyleVlase, S., & Itu, C. (2024). The Properties of Structures with Two Planes of Symmetry. Symmetry, 16(8), 1075. https://doi.org/10.3390/sym16081075







