Investigation of Analytical Soliton Solutions to the Non-Linear Klein–Gordon Model Using Efficient Techniques
Abstract
:1. Introduction
2. Description of Exact Approaches
2.1. Mapping Method
2.2. Generalized Riccati Equation Mapping Method
3. Implementation and Applications of the Exact Techniques
3.1. Applications of Mapping Method
- If , and , then the exact solution is
- If , and , then the exact solution is
- If , and , then the exact solution isor
- If , and , then the exact solution is
- If , and , then the exact solution is
- If , and , then the exact solution isorAs , then the above equation take the fromorAs , then the above equation also takes the form
- If , and , then the exact solution is
- If , and , then the exact solution is
- If , and , then the exact solution isor
- If , and , then the exact solution is
- If , and , then the exact solution is
- If , and , then the exact solution isorAs , then the above Equation take the formorAs , then the above Equation also take the form
3.2. Applications of Generalized Riccati Equation Mapping Method
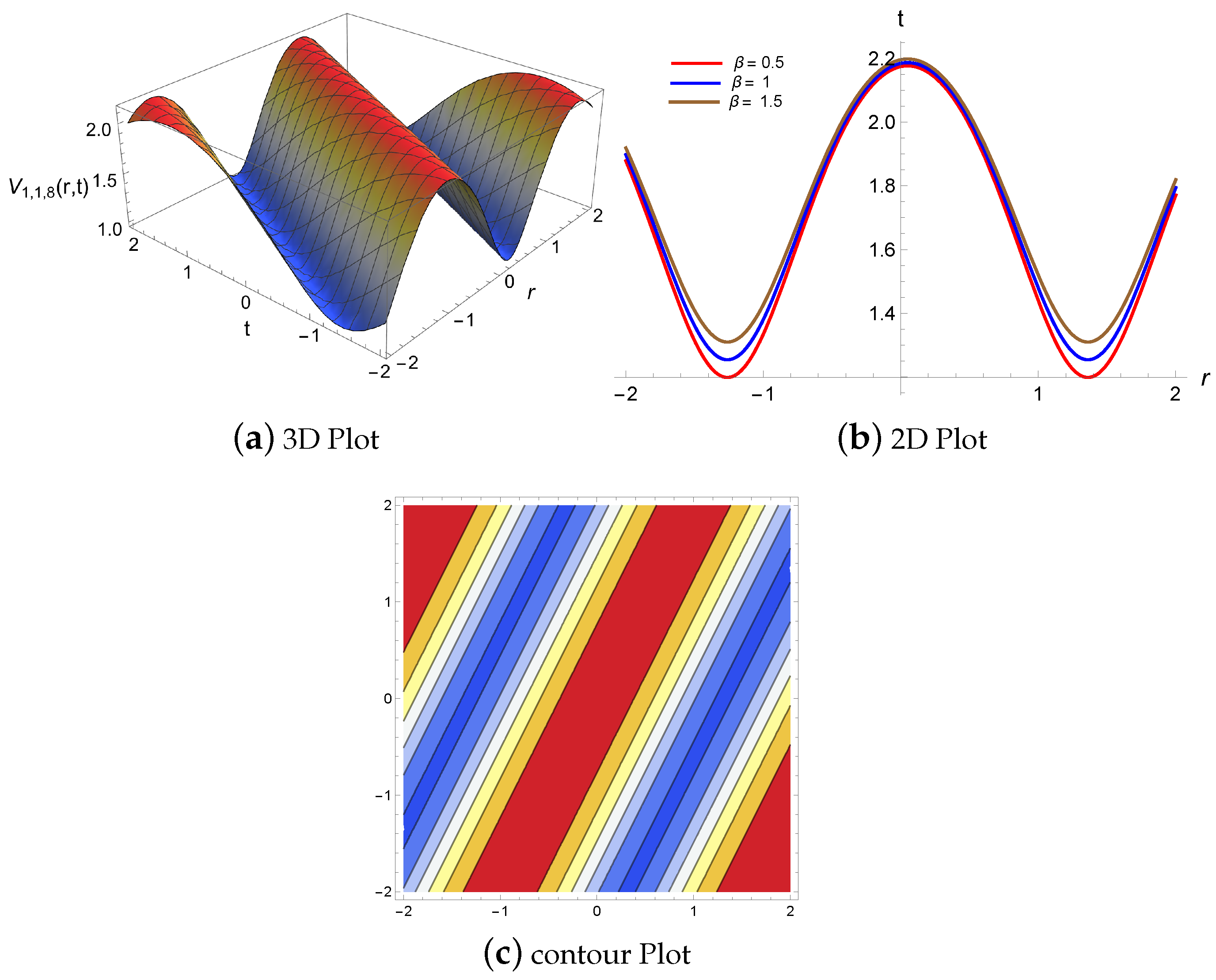
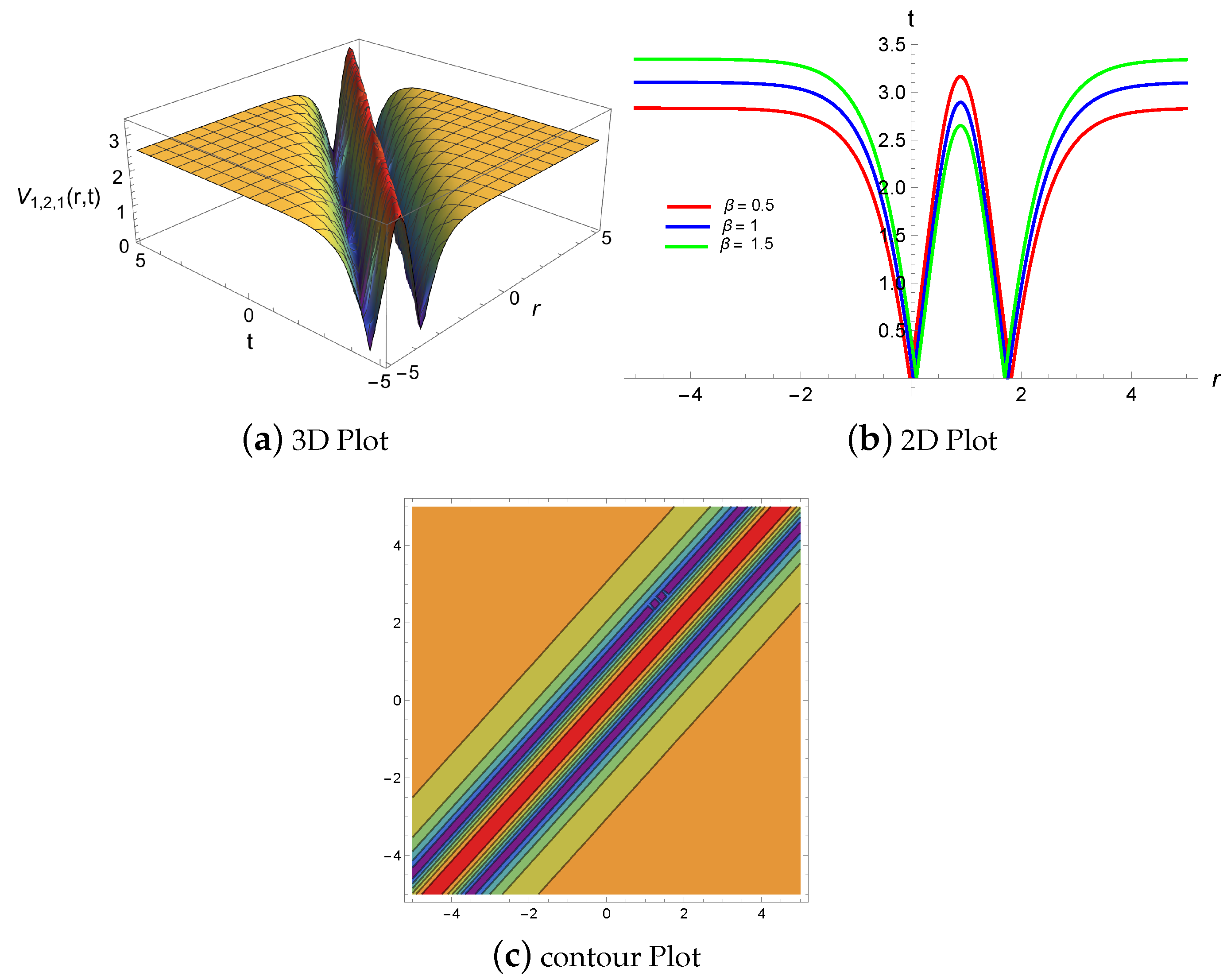
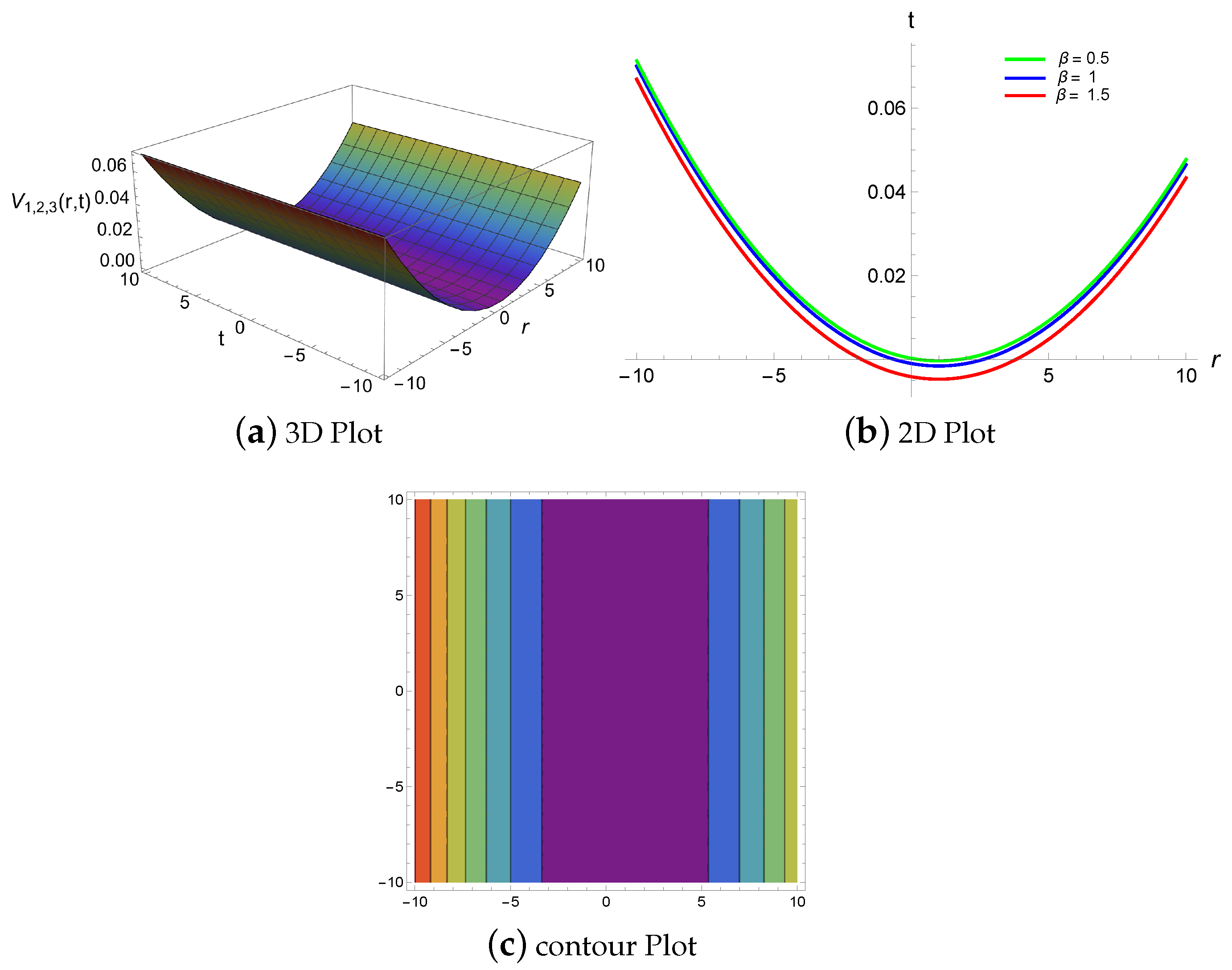
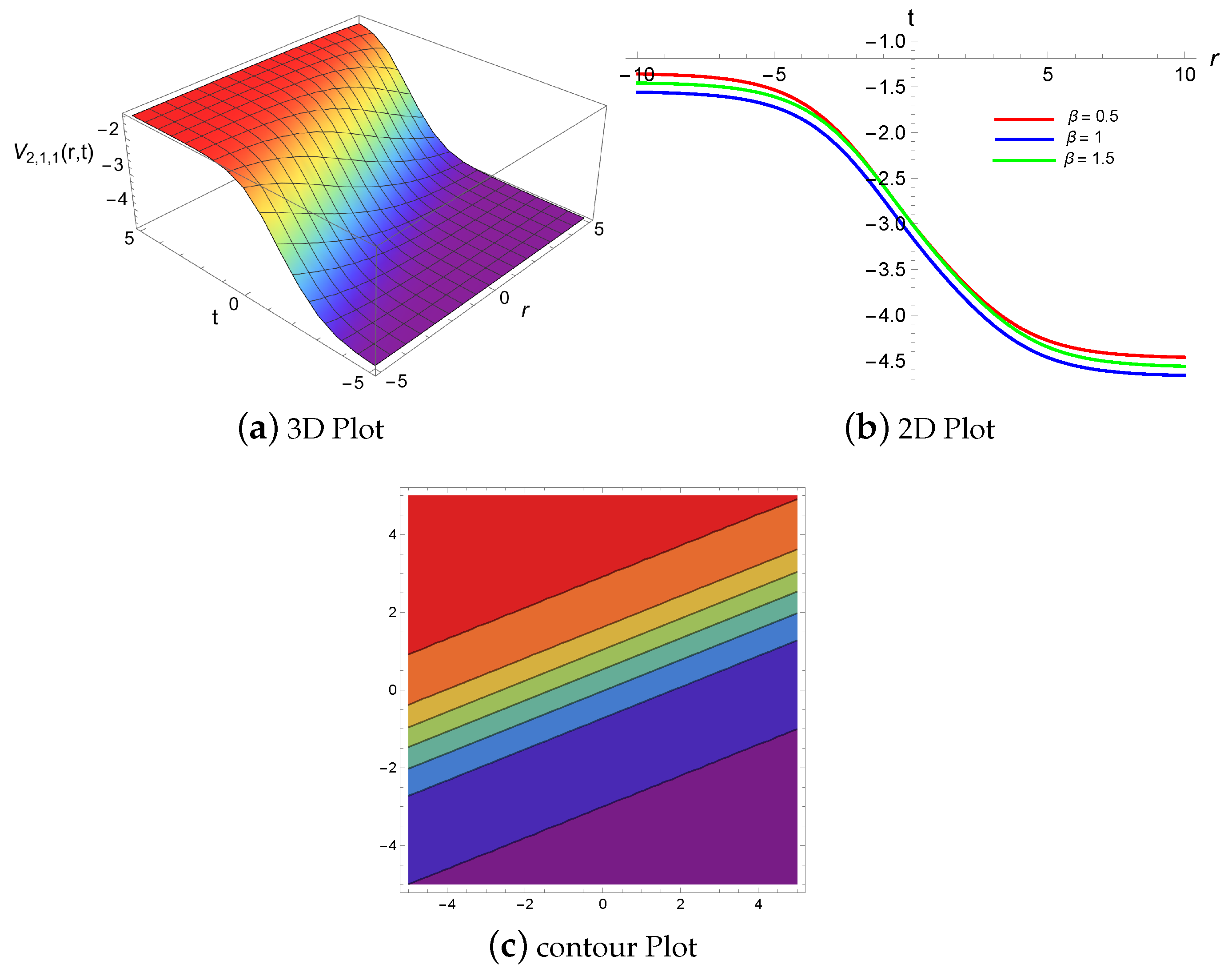
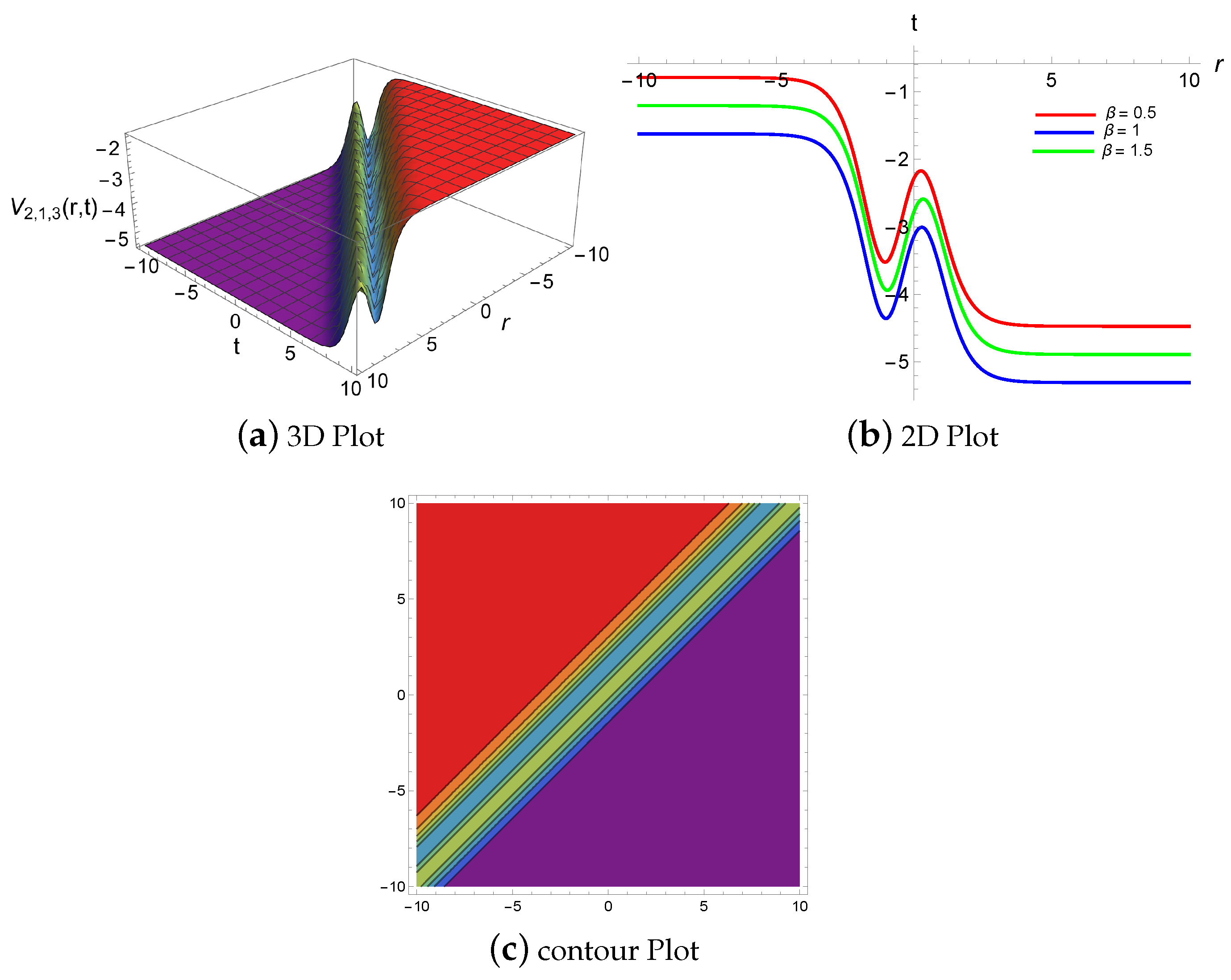
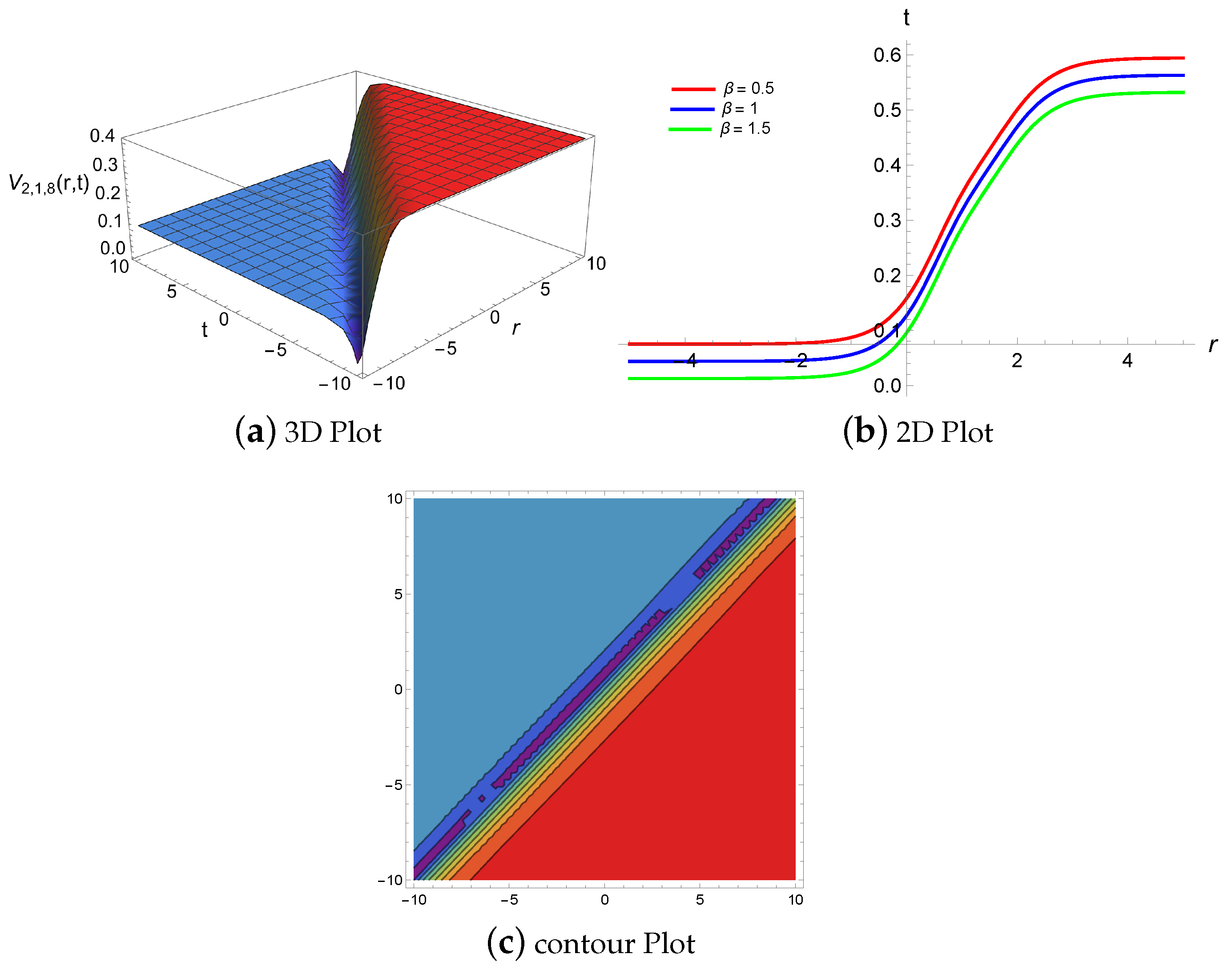
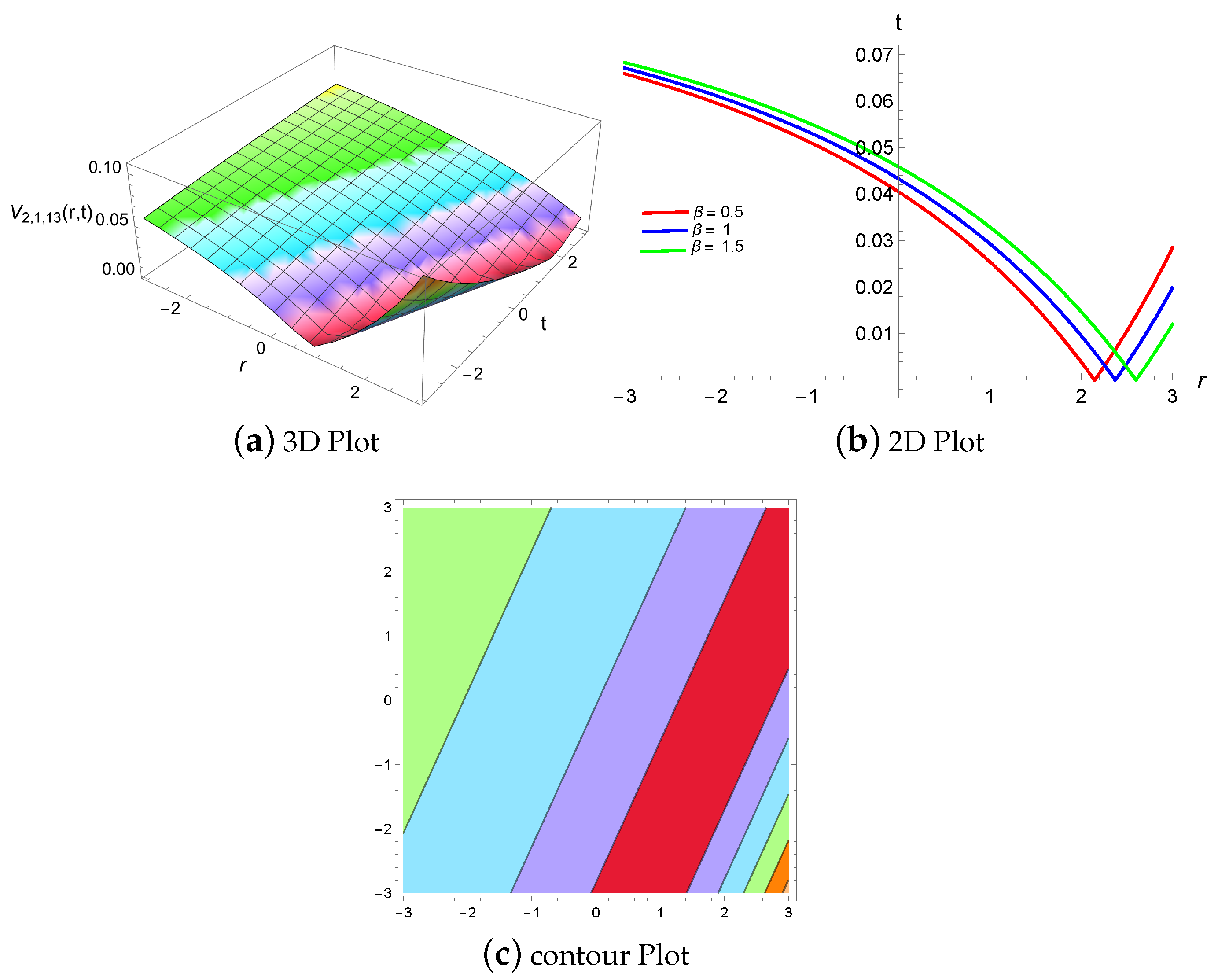
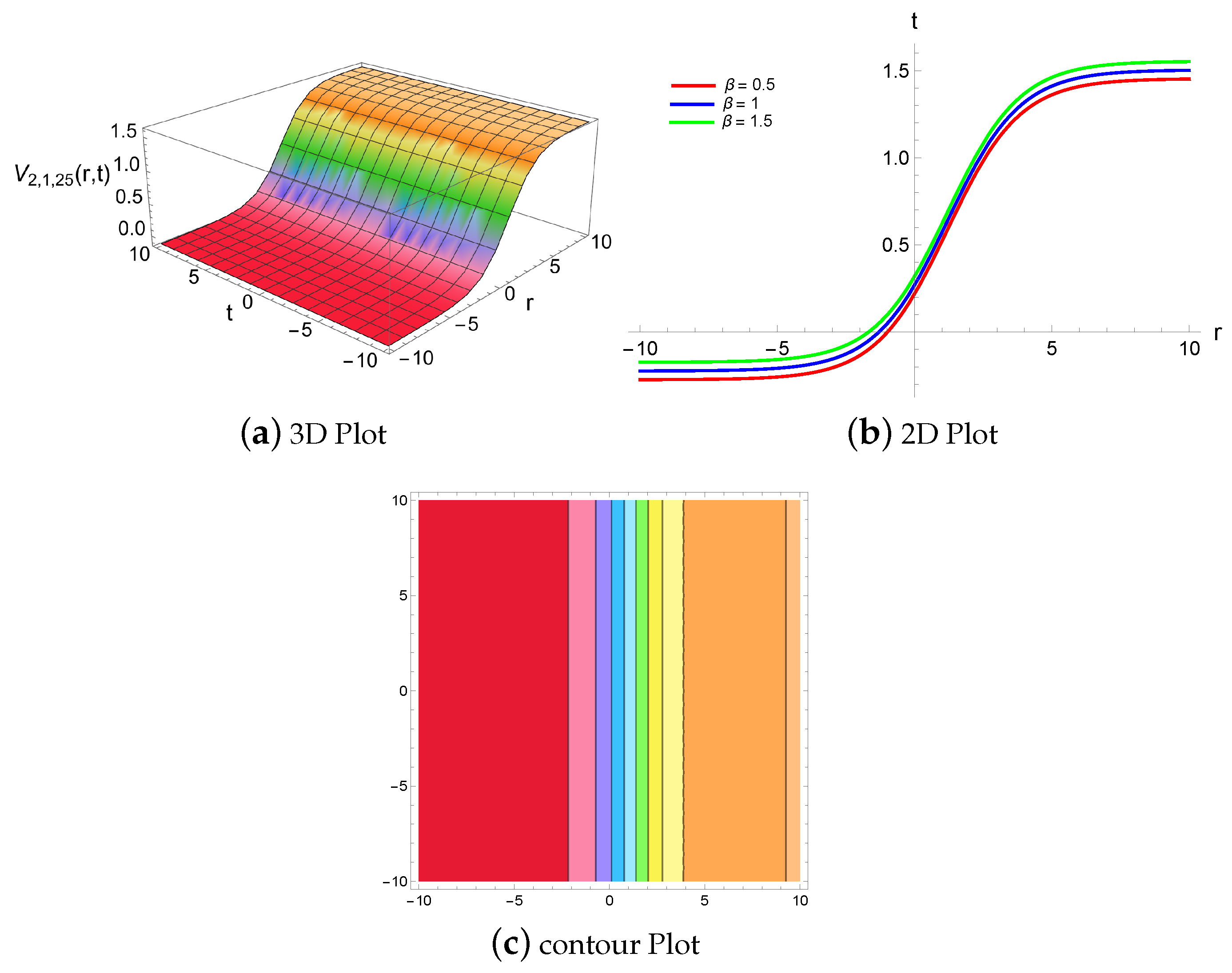
4. Results and Discussion
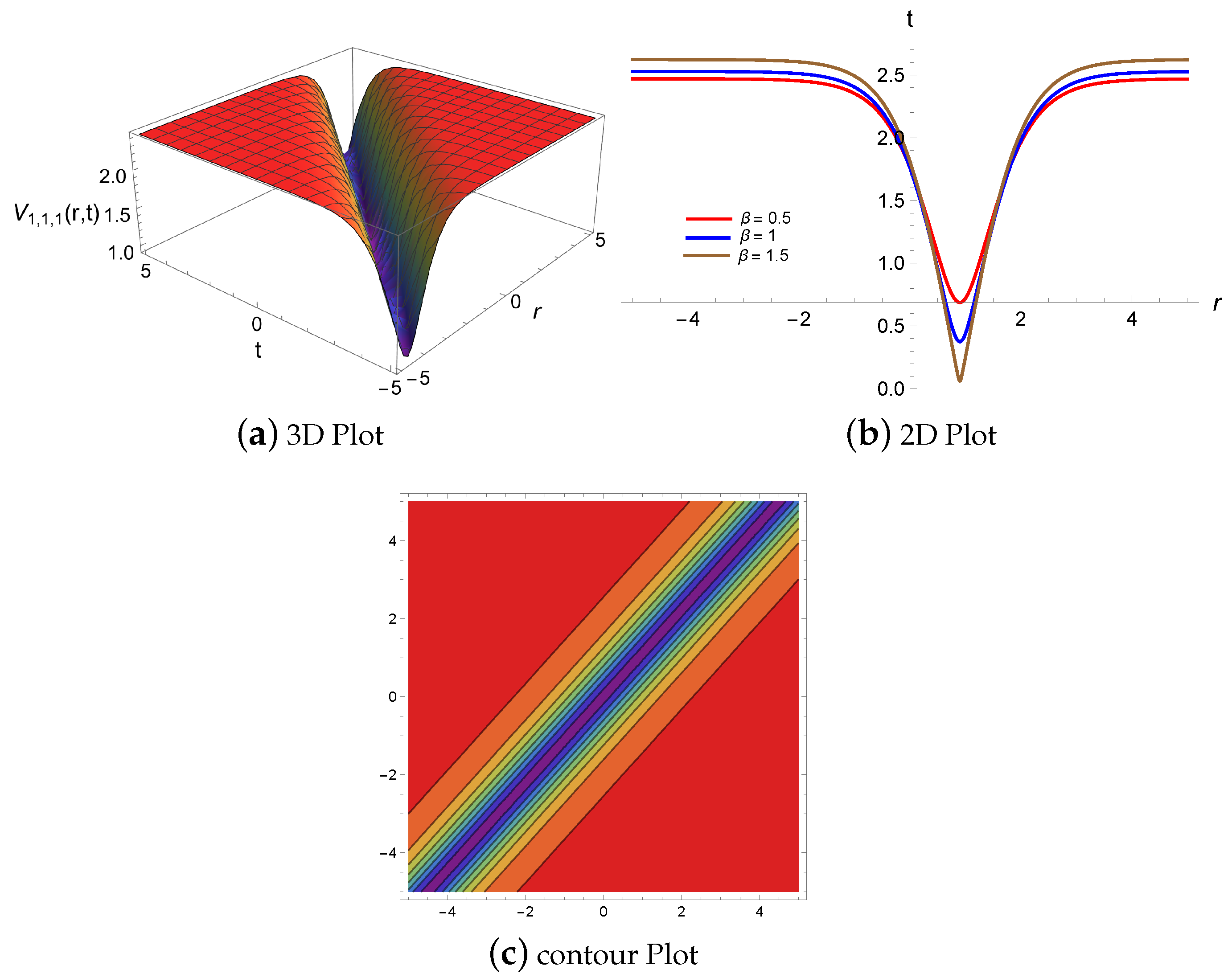
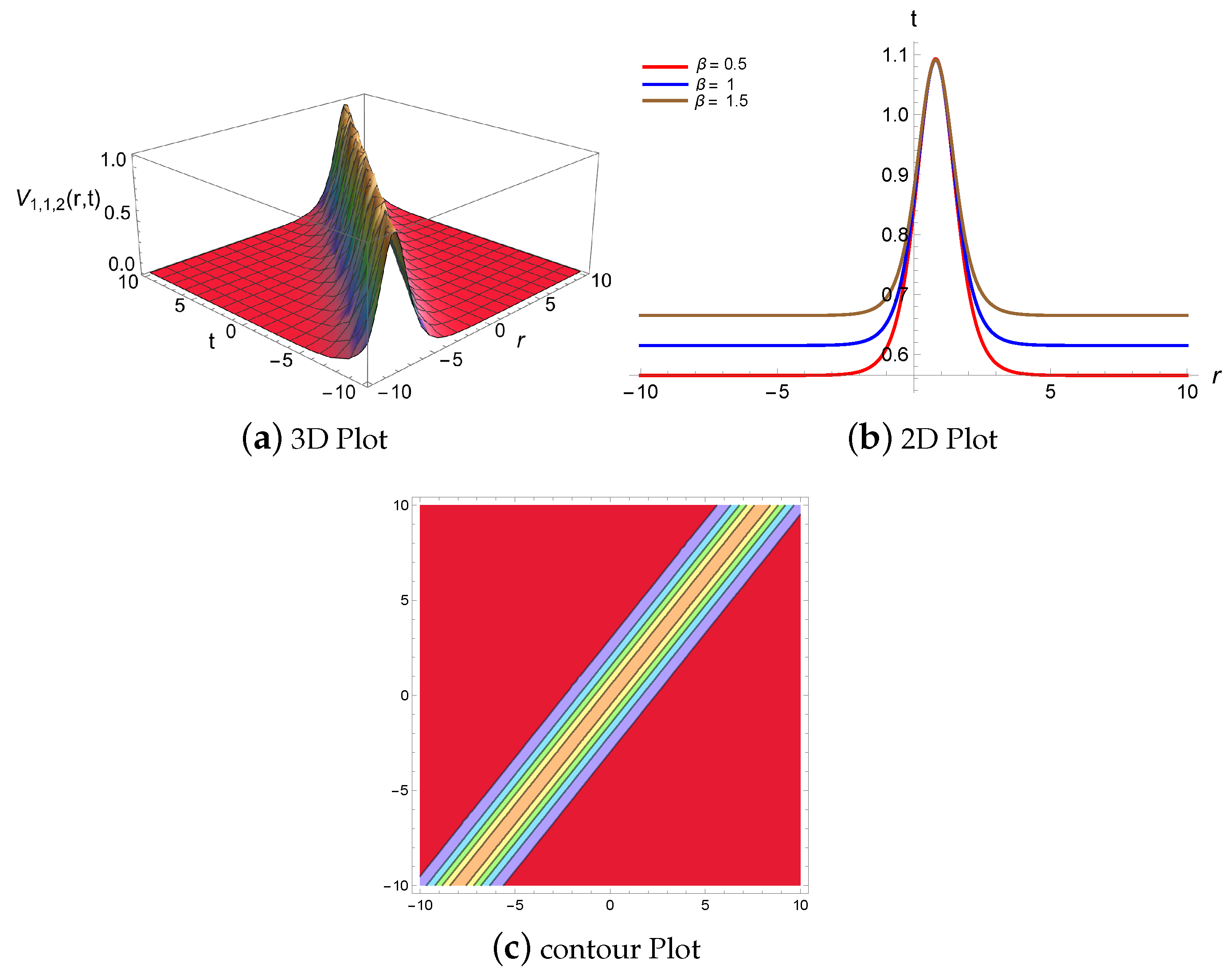
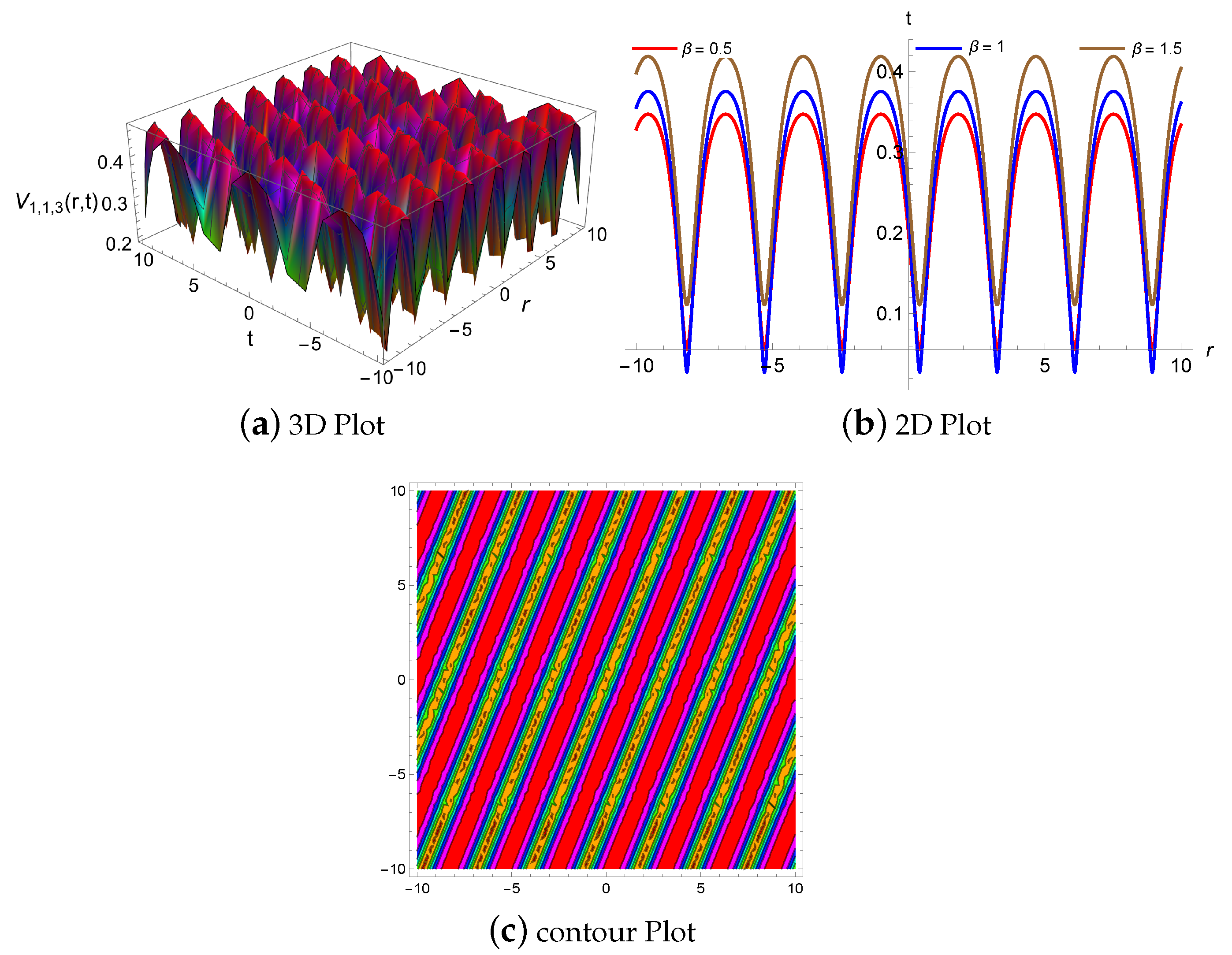
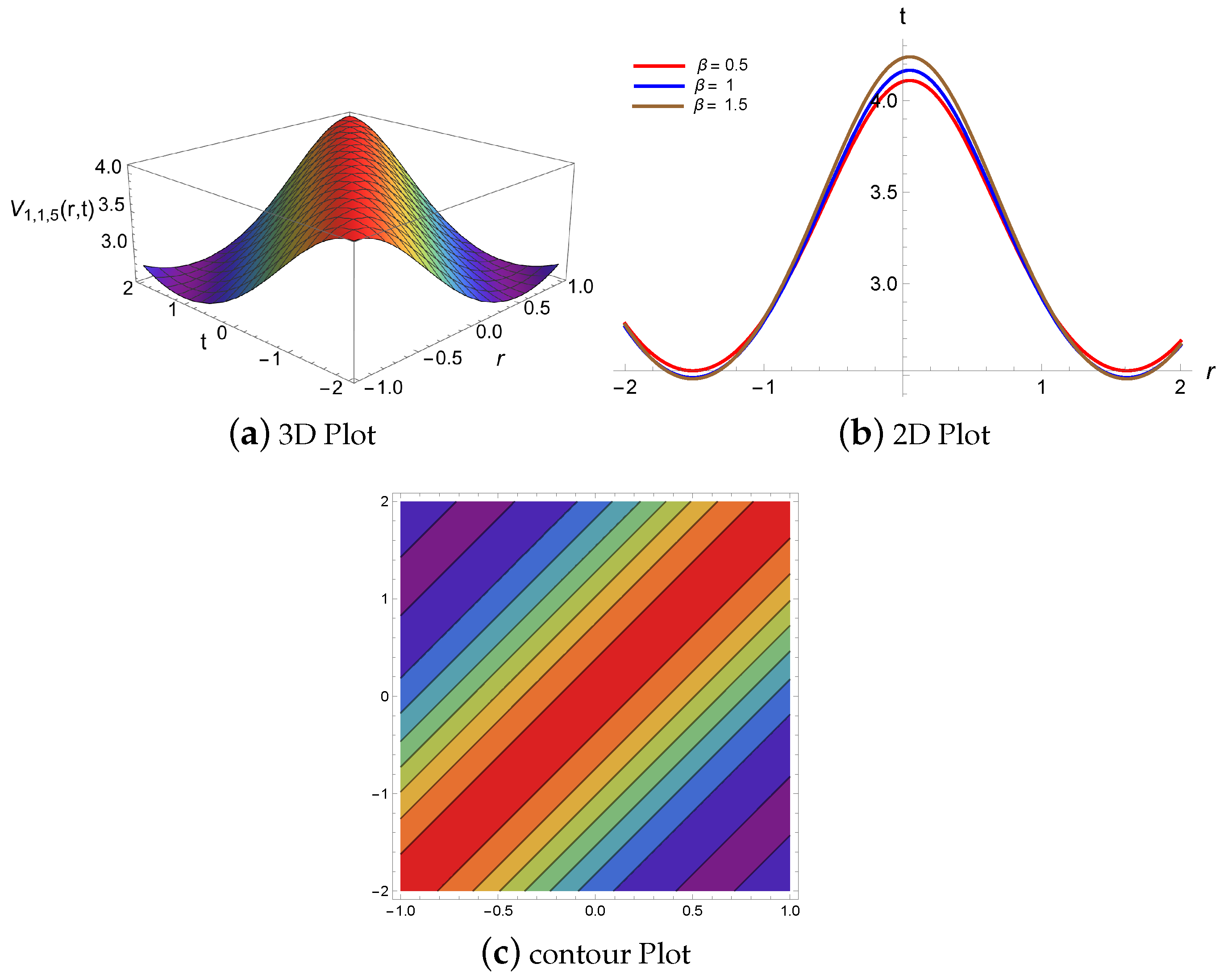
4.1. Physical Descriptions via Mapping Method
4.2. Physical Descriptions via Generalized Riccati Equation Mapping Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Das, A.; Ghosh, P.; Chandra, S.; Raj, V. Electron acoustic peregrine breathers in a quantum plasma with 1-D temperature anisotropy. IEEE Trans. Plasma Sci. 2021, 50, 1598–1609. [Google Scholar]
- Roshid, M.M.; Bairagi, T.; Rahman, M.M. Lump, interaction of lump and kink and solitonic solution of nonlinear evolution equation which describe incompressible viscoelastic Kelvin-Voigt fluid. Partial. Differ. Equations Appl. Math. 2022, 5, 100354. [Google Scholar]
- Aljahdaly, N.H.; El-Tantawy, S.A.; Wazwaz, A.M.; Ashi, H.A. Adomian decomposition method for modelling the dissipative higher-order rogue waves in a superthermal collisional plasma. J. Taibah Univ. Sci. 2021, 15, 971–983. [Google Scholar]
- Yao, S.W.; Zekavatm, S.M.; Rezazadeh, H.; Vahidi, J.; Ghaemi, M.B.; Inc, M. The solitary wave solutions to the Klein–Gordon-Zakharov equations by extended rational methods. Aip Adv. 2021, 11, 065218. [Google Scholar]
- Malik, S.; Almusawa, H.; Kumar, S.; Wazwaz, A.M.; Osman, M.S. A (2 + 1)-dimensional Kadomtsev-Petviashvili equation with competing dispersion effect: Painlevé analysis, dynamical behavior and invariant solutions. Results Phys. 2021, 23, 104043. [Google Scholar]
- Karjanto, N. Modeling Wave Packet Dynamics and Exploring Applications: A Comprehensive Guide to the Nonlinear Schrödinger Equation. Mathematics 2024, 12, 744. [Google Scholar] [CrossRef]
- Kurt, A.; Tozar, A.; Tasbozan, O. Applying the new extended direct algebraic method to solve the equation of obliquely interacting waves in shallow waters. J. Ocean. Univ. China 2020, 19, 772–780. [Google Scholar]
- Nadeem, M.; Iambor, L.F. The traveling wave solutions to a variant of the Boussinesq equation. Electron. J. Appl. Math. 2023, 1, 26–37. [Google Scholar]
- Liu, S.H.; Tian, B.; Wang, M. Painlevé analysis, bilinear form, Bäcklund transformation, solitons, periodic waves and asymptotic properties for a generalized Calogero–Bogoyavlenskii–Konopelchenko–Schiff system in a fluid or plasma. Eur. Phys. J. Plus 2021, 136, 917. [Google Scholar]
- Li, J.; Xu, C.; Lu, J. The exact solutions to the generalized (2 + 1)-dimensional nonlinear wave equation. Results Phys. 2024, 58, 107506. [Google Scholar]
- Zhou, Q.; Huang, Z.; Sun, Y.; Triki, H.; Liu, W.; Biswas, A. Collision dynamics of three-solitons in an optical communication system with third-order dispersion and nonlinearity. Nonlinear Dyn. 2023, 111, 5757–5765. [Google Scholar]
- Sun, Y.; Hu, Z.; Triki, H.; Mirzazadeh, M.; Liu, W.; Biswas, A.; Zhou, Q. Analytical study of three-soliton interactions with different phases in nonlinear optics. Nonlinear Dyn. 2023, 111, 18391–18400. [Google Scholar]
- Alquran, M.; Alhami, R. Convex-periodic, kink-periodic, peakon-soliton and kink bidirectional wave-solutions to new established two-mode generalization of Cahn-Allen equation. Results Phys. 2022, 34, 105257. [Google Scholar]
- Alquran, M.; Alhami, R. Analysis of lumps, single-stripe, breather-wave, and two-wave solutions to the generalized perturbed-KdV equation by means of Hirota’s bilinear method. Nonlinear Dyn. 2022, 109, 1985–1992. [Google Scholar]
- Sarwar, A.; Gang, T.; Arshad, M.; Ahmed, I.; Ahmad, M.O. Abundant solitary wave solutions for space-time fractional unstable nonlinear Schrödinger equations and their applications. Ain Shams Eng. J. 2023, 14, 101839. [Google Scholar]
- Abazari, R.; Jamshidzadeh, S. Exact solitary wave solutions of the complex Klein–Gordon equation. Opt. Int. J. Light Electron Opt. 2015, 126, 1970–1975. [Google Scholar]
- Yang, Y.; Yang, X.; Wang, J.; Liu, J. The numerical solution of the time-fractional non-linear Klein–Gordon equation via spectral collocation method. Therm. Sci. 2019, 23 Part A, 1529–1537. [Google Scholar]
- Alquran, M.; Dagher, A.; Al-Dolat, M. Exact Traveling Wave Solutions for the Celebrated Gardner Model and the Nonlinear Klein–Gordon System by Means of the Celebrated Unified Method. Int. J. Appl. Comput. Math. 2019, 5, 1–11. [Google Scholar]
- Ma, W.X. Riemann-Hilbert problems and inverse scattering of nonlocal real reverse-spacetime matrix AKNS hierarchies. Phys. D Nonlinear Phenom. 2022, 430, 133078. [Google Scholar]
- Alhojilan, Y.; Ahmed, H.M. Novel analytical solutions of stochastic Ginzburg-Landau equation driven by Wiener process via the improved modified extended tanh function method. Alex. Eng. J. 2023, 72, 269–274. [Google Scholar]
- Chu, Y.M.; Fahim, M.R.A.; Kundu, P.R.; Islam, M.E.; Akbar, M.A.; Inc, M. Extension of the sine-Gordon expansion scheme and parametric effect analysis for higher-dimensional nonlinear evolution equations. J. King Saud Univ.-Sci. 2021, 33, 101515. [Google Scholar]
- Rezazadeh, H.; Ullah, N.; Akinyemi, L.; Shah, A.; Mirhosseini-Alizamin, S.M.; Chu, Y.M.; Ahmad, H. Optical soliton solutions of the generalized non-autonomous nonlinear Schrödinger equations by the new Kudryashov’s method. Results Phys. 2021, 24, 104179. [Google Scholar]
- Malik, S.; Hashemi, M.S.; Kumar, S.; Rezazadeh, H.; Mahmoud, W.; Osman, M.S. Application of new Kudryashov method to various nonlinear partial differential equations. Opt. Quantum Electron. 2023, 55, 8. [Google Scholar]
- Raheel, M.; Zafar, A.; Nawaz, M.S.; Bekir, A.; Tariq, K.U. Exact soliton solutions to the time-fractional Kudryashov model via an efficient analytical approach. Pramana 2023, 97, 45. [Google Scholar]
- Ouahid, L.; Abdou, M.A.; Kumar, S.; Owyed, S.; Ray, S.S. A plentiful supply of soliton solutions for DNA Peyrard-Bishop equation by means of a new auxiliary equation strategy. Int. J. Mod. Phys. B 2021, 35, 2150265. [Google Scholar]
- Rehman, H.U.; Akber, R.; Wazwaz, A.M.; Alshehri, H.M.; Osman, M.S. Analysis of Brownian motion in stochastic Schrödinger wave equation using Sardar sub-equation method. Optik 2023, 289, 171305. [Google Scholar]
- Cakicioglu, H.; Ozisik, M.; Secer, A.; Bayram, M. Optical soliton solutions of Schrödinger-Hirota equation with parabolic law nonlinearity via generalized Kudryashov algorithm. Opt. Quantum Electron. 2023, 55, 407. [Google Scholar]
- Kabir, M.M.; Khajeh, A.; Abdi Aghdam, E.; Yousefi Koma, A. Modified Kudryashov method for finding exact solitary wave solutions of higher-order nonlinear equations. Math. Methods Appl. Sci. 2011, 34, 213–219. [Google Scholar]
- Ebaid, A. Exact solutions for the generalized Klein–Gordon equation via a transformation and Exp-function method and comparison with Adomian’s method. J. Comput. Appl. Math. 2009, 223, 278–290. [Google Scholar]
- Alaje, A.I.; Olayiwola, M.O.; Adedokun, K.A.; Adedeji, J.A.; Oladapo, A.O. Modified homotopy perturbation method and its application to analytical solitons of fractional-order Korteweg-de Vries equation. Beni-Suef Univ. J. Basic Appl. Sci. 2022, 11, 139. [Google Scholar]
- Rizvi, S.T.R.; Seadawy, A.R.; Younis, M.; Ali, I.; Althobaiti, S.; Mahmoud, S.F. Soliton solutions, Painleve analysis and conservation laws for a nonlinear evolution equation. Results Phys. 2021, 23, 103999. [Google Scholar]
- Hafez, M.G.; Alam, M.N.; Akbar, M.A. Exact traveling wave solutions to the Klein–Gordon equation using the novel (G’/G)-expansion method. Results Phys. 2014, 4, 177–184. [Google Scholar]
- Billig, Y. Principal vertex operator representations for toroidal Lie algebras. J. Math. Phys. 1998, 39, 3844–3864. [Google Scholar]
- Khalid, M.; Sultana, M.; Zaidi, F.; Arshad, U. Solving linear and nonlinear Klein–Gordon equations by new perturbation iteration transform method. Wms J. Appl. Eng. Math. 2016, 6, 115–125. [Google Scholar]
- Sadiya, U.; Inc, M.; Arefin, M.A.; Uddin, M.H. Consistent travelling waves solutions to the non-linear time fractional Klein–Gordon and Sine-Gordon equations through extended tanh-function approach. J. Taibah Univ. Sci. 2022, 16, 594–607. [Google Scholar]
- Alsisi, A. Analytical and numerical solutions to the Klein–Gordon model with cubic nonlinearity. Alex. Eng. J. 2024, 99, 31–37. [Google Scholar]
- Bildik, N.; Deniz, S. New approximate solutions to the nonlinear Klein–Gordon equations using perturbation iteration techniques. Discret. Contin. Dyn. Syst.-S 2020, 13, 503. [Google Scholar]
- Chowdhury, M.S.H.; Hashim, I. Application of homotopy-perturbation method to Klein–Gordon and sine-Gordon equations. Chaos Solitons Fractals 2009, 39, 1928–1935. [Google Scholar]
- Mat Zin, S.; Abbas, M.; Abd Majid, A.; Md Ismail, A.I. A new trigonometric spline approach to numerical solution of generalized nonlinear Klien-Gordon equation. PLoS ONE 2014, 9, e95774. [Google Scholar]
- Mat Zin, S.; Abd Majid, A.; Ismail, A.I.M.; Abbas, M. Application of Hybrid Cubic B-Spline Collocation Approach for Solving a Generalized Nonlinear Klien-Gordon Equation. Math. Probl. Eng. 2014, 2014, 108560. [Google Scholar]
- Dehghan, M.; Ghesmati, A. Application of the dual reciprocity boundary integral equation technique to solve the nonlinear Klein–Gordon equation. Comput. Phys. Commun. 2010, 181, 1410–1418. [Google Scholar]
- Zayed, E.M.; Alurrfi, K.A. Solitons and other solutions for two nonlinear Schrödinger equations using the new mapping method. Optik 2017, 144, 132–148. [Google Scholar]
- Rehman, H.U.; Saleem, M.S.; Zubair, M.; Jafar, S.; Latif, I. Optical solitons with Biswas–Arshed model using mapping method. Optik 2019, 194, 163091. [Google Scholar]
- Krishnan, E.V.; Al Gabshi, M.; Zhou, Q.; Khan, K.R.; Mahmood, M.F.; Xu, Y.; Biswas, A.; Belic, M. Solitons in optical metamaterials by mapping method. J. Optoelectron. Adv. Mater. 2015, 17, 511–516. [Google Scholar]
- Rabie, W.B.; Khalil, T.A.; Badra, N.; Ahmed, H.M.; Mirzazadeh, M.; Hashemi, M.S. Soliton Solutions and Other Solutions to the (4 + 1)-Dimensional Davey–Stewartson–Kadomtsev–Petviashvili Equation using Modified Extended Mapping Method. Qual. Theory Dyn. Syst. 2024, 23, 87. [Google Scholar]
- Rehman, H.U.; Seadawy, A.R.; Razzaq, S.; Rizvi, S.T. Optical fiber application of the Improved Generalized Riccati Equation Mapping method to the perturbed nonlinear Chen-Lee-Liu dynamical equation. Optik 2023, 290, 171309. [Google Scholar]
- Ahmed, N.; Baber, M.Z.; Iqbal, M.S.; Annum, A.; Ali, S.M.; Ali, M.; Akgül, A.; El Din, S.M. Analytical study of reaction diffusion Lengyel–Epstein system by generalized Riccati equation mapping method. Sci. Rep. 2023, 13, 20033. [Google Scholar]
- Hamad, I.S.; Ali, K.K. Investigation of Brownian motion in stochastic Schrödinger wave equation using the modified generalized Riccati equation mapping method. Opt. Quantum Electron. 2024, 56, 1–23. [Google Scholar]
- Al-Amry, M.S.; Al-Shaoosh, M.M. The Generalized Riccati Equation Mapping for Solving (cmZKB) and (pZK) Equations. Univ. Aden J. Nat. Appl. Sci. 2019, 23, 201–210. [Google Scholar]
- Hosseini, K.; Alizadeh, F.; Hinçal, E.; Kaymakamzade, B.; Dehingia, K.; Osman, M.S. A generalized nonlinear Schrödinger equation with logarithmic nonlinearity and its Gaussian solitary wave. Opt. Quantum Electron. 2024, 56, 929. [Google Scholar]
- Agom, E.U.; Ogunfiditimi, F.O. Exact solution of nonlinear Klein–Gordon equations with quadratic nonlinearity by modified Adomian decomposition method. J. Math. Comput. Sci. 2018, 8, 484–493. [Google Scholar]
- Roshid, M.M.; Karim, M.F.; Azad, A.K.; Rahman, M.M.; Sultana, T. New solitonic and rogue wave solutions of a Klein–Gordon equation with quadratic nonlinearity. Partial. Differ. Equations Appl. Math. 2021, 3, 100036. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vivas-Cortez, M.; Nageen, M.; Abbas, M.; Alosaimi, M. Investigation of Analytical Soliton Solutions to the Non-Linear Klein–Gordon Model Using Efficient Techniques. Symmetry 2024, 16, 1085. https://doi.org/10.3390/sym16081085
Vivas-Cortez M, Nageen M, Abbas M, Alosaimi M. Investigation of Analytical Soliton Solutions to the Non-Linear Klein–Gordon Model Using Efficient Techniques. Symmetry. 2024; 16(8):1085. https://doi.org/10.3390/sym16081085
Chicago/Turabian StyleVivas-Cortez, Miguel, Maham Nageen, Muhammad Abbas, and Moataz Alosaimi. 2024. "Investigation of Analytical Soliton Solutions to the Non-Linear Klein–Gordon Model Using Efficient Techniques" Symmetry 16, no. 8: 1085. https://doi.org/10.3390/sym16081085






