The Closed-Form Solutions of an SIS Epidemic Reaction–Diffusion Model with Advection in a One-Dimensional Space Domain
Abstract
:1. Introduction
2. Lie Symmetries for the Class (1)
2.1. Symmetry Infinitesimal Operator
2.2. Determing System
2.3. Lie Symmetries for the Standard Incidence
2.4. Lie Symmetries for the Mass Action Incidence
2.5. Lie Symmetries for Saturated Incidence
3. Reductions and Closed-Form Solutions of the SIS-RDA Epidemic Model for the Standard Incidence Function
3.1. Reductions of SIS-RDA Epidemic Model to a System of ODEs
3.2. Travelling Waves via and
3.3. Closed-Form Solutions by Using
3.3.1. Closed-Form Solution for
3.3.2. Closed-Form Solution for ,
4. The Transmission Dynamics of an Infectious Disease Utilizing the Closed-Form Solutions
4.1. A Cauchy Problem
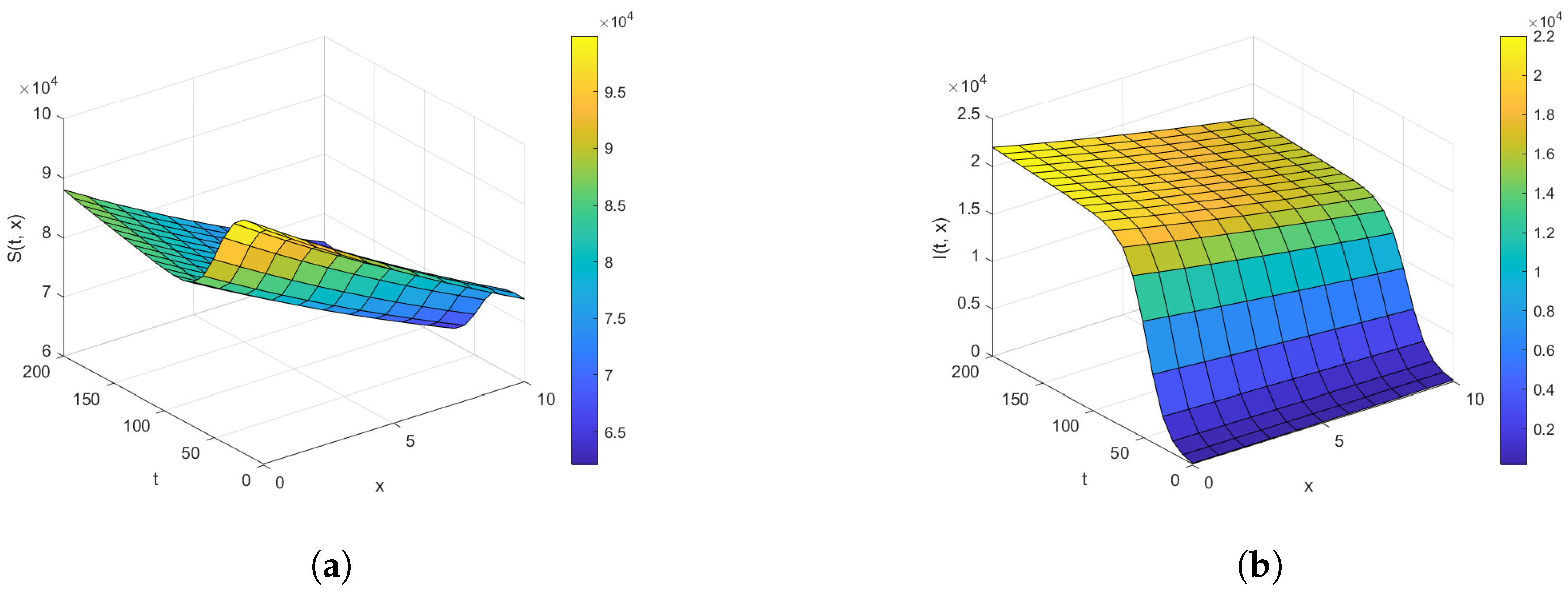
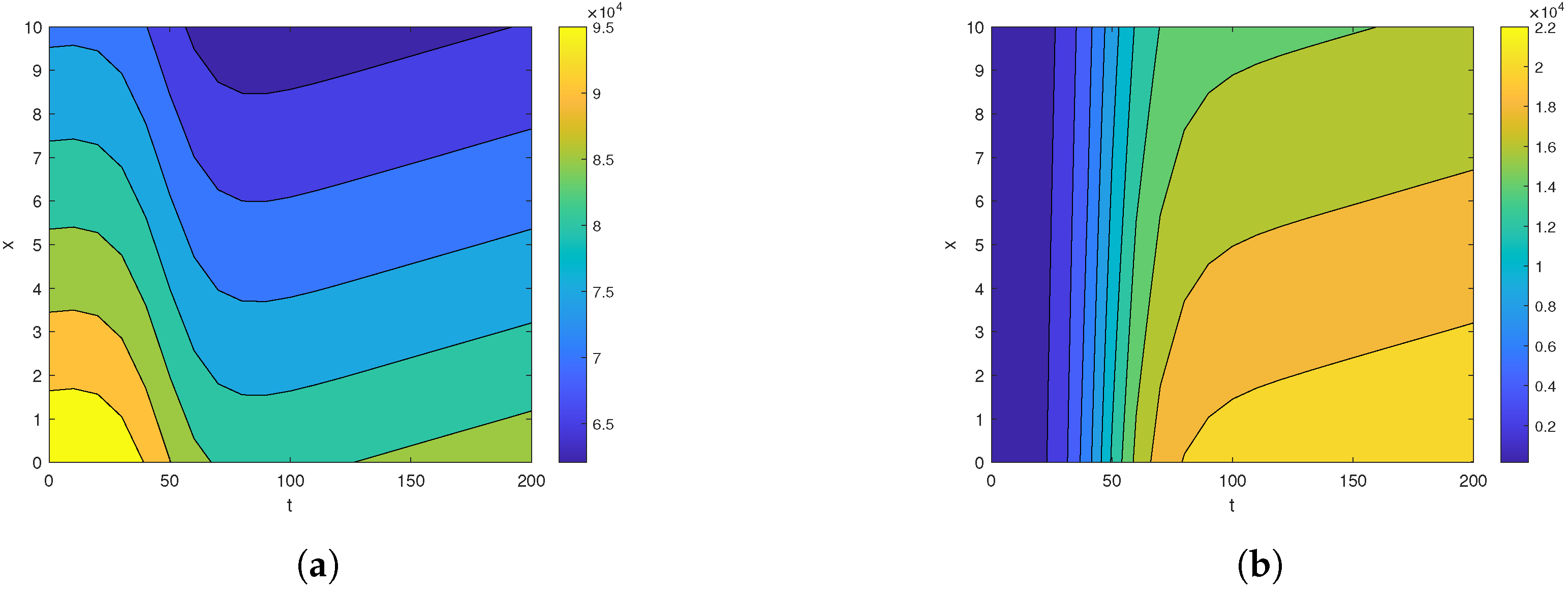
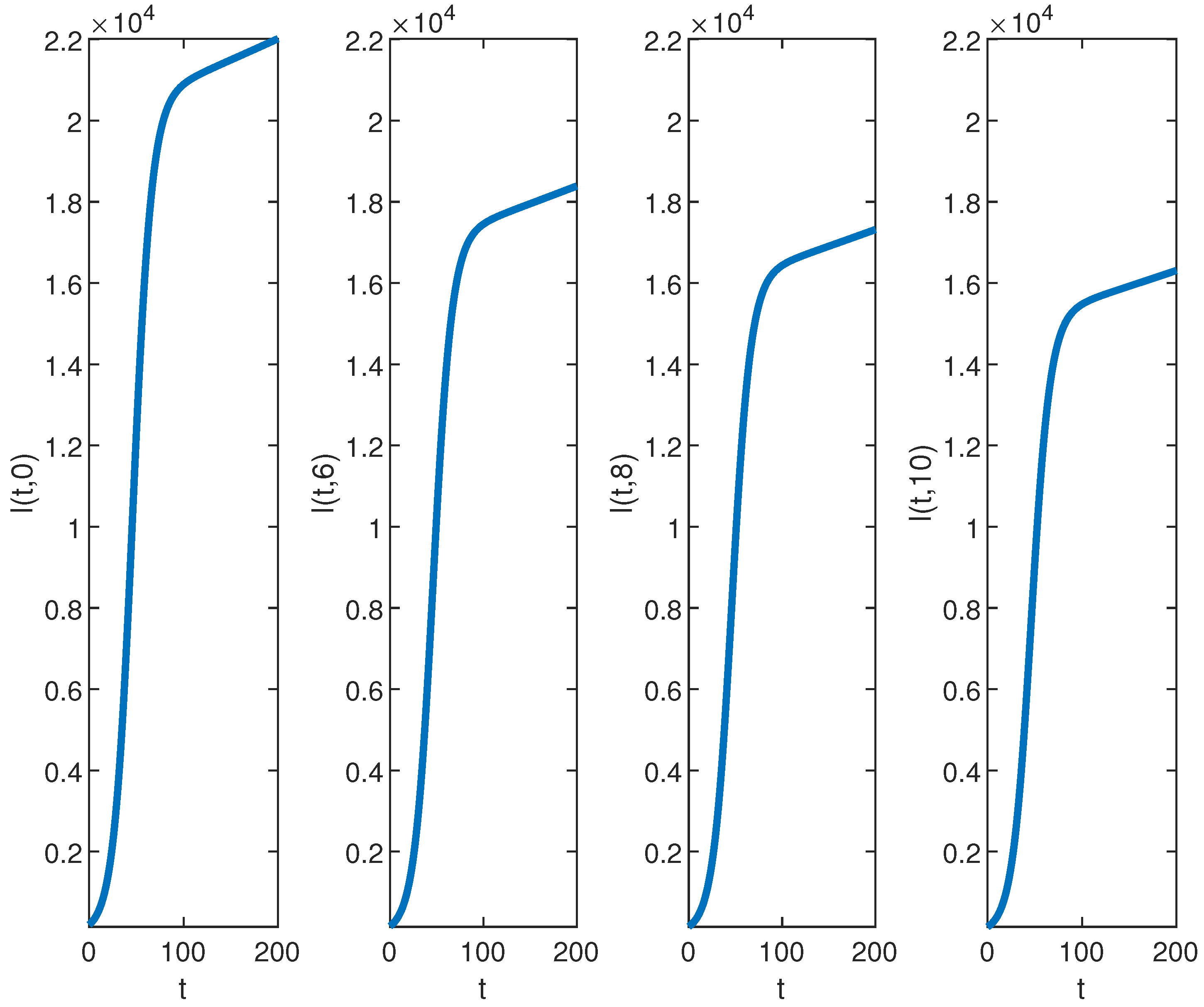
4.2. Visualization of Closed-Form Solutions
4.3. Effect of Varying the Diffusion Coefficient on Susceptible and Infected Populations
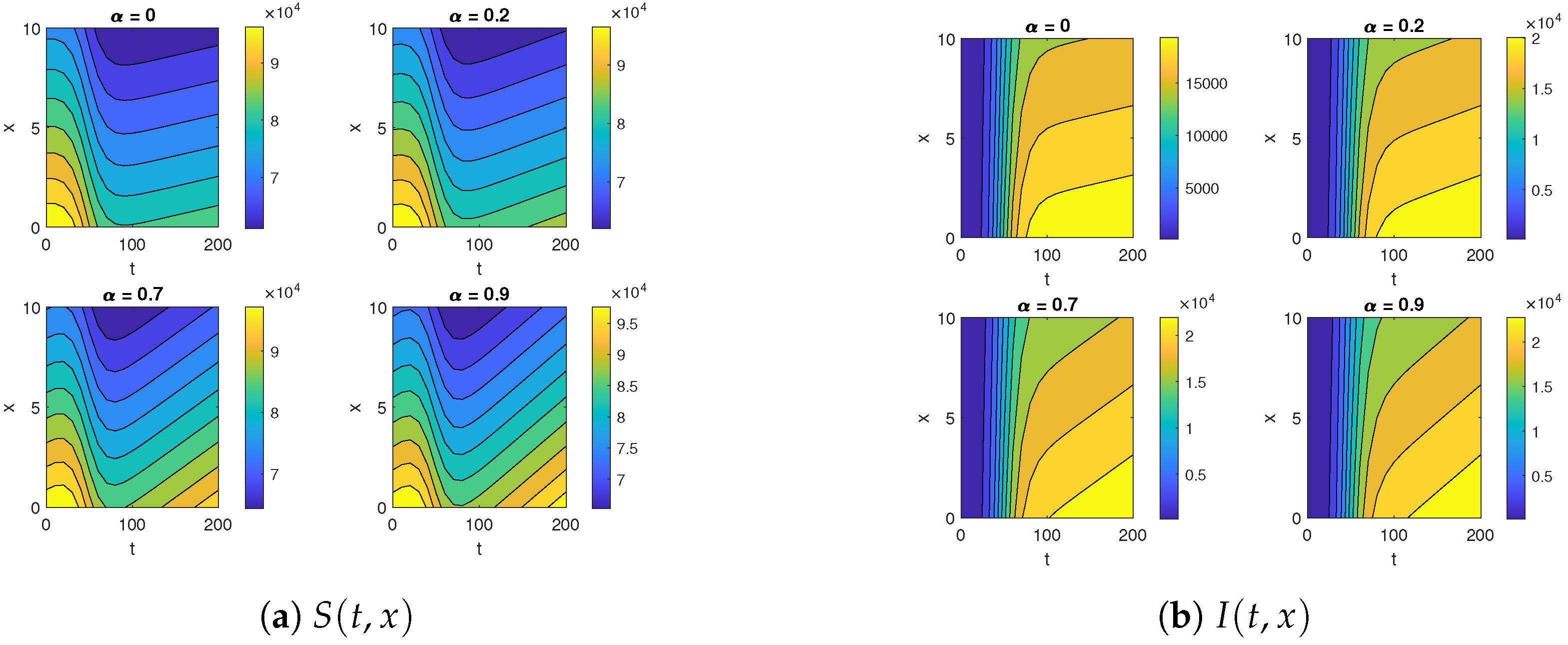
4.4. Effect of Varying the Advection Rate on Susceptible and Infected Populations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allen, L.J.S.; Bolker, B.M.; Lou, Y.; Nevai, A.L. Asymptotic profiles of the steady states for an SIS epidemic reaction-diffusion model. Discret. Contin. Dyn. Syst. 2008, 21, 1–20. [Google Scholar] [CrossRef]
- Fitzgibbon, W.E.; Langlais, M.; Morgan, J.J. A mathematical model of the spread of feline leukemia virus (FeLV) through a highly heterogeneous spatial domain. SIAM J. Math. Anal. 2001, 33, 570–588. [Google Scholar] [CrossRef]
- Fitzgibbon, W.E.; Langlais, M.; Morgan, J.J. A reaction-diffusion system modeling direct and indirect transmission of diseases. Discrete Contin. Dyn. Syst. Ser. B 2004, 4, 893–910. [Google Scholar] [CrossRef]
- Peng, R.; Liu, S. Global stability of the steady states of an SIS epidemic reaction-diffusion model. Nonlinear Anal. Theory Methods Appl. 2009, 71, 239–247. [Google Scholar] [CrossRef]
- Veliov, V.M. On the effect of population heterogeneity on dynamics of epidemic diseases. J. Math. Biol. 2005, 51, 123–143. [Google Scholar] [CrossRef]
- Gudelj, I.; White, K.A.J.; Britton, N.F. The effects of spatial movement and group interactions on disease dynamics of social animals. Bull. Math. Biol. 2004, 66, 91–108. [Google Scholar] [CrossRef] [PubMed]
- Lutscher, F.; Lewis, M.A.; McCauley, E. Effects of heterogeneity on spread and persistence in rivers. Bull. Math. Biol. 2006, 68, 2129–2160. [Google Scholar] [CrossRef]
- Desai, M.M.; Nelson, D.R. A quasispecies on a moving oasis. Theor. Popul. Biol. 2005, 67, 33–45. [Google Scholar] [CrossRef]
- Cui, R.; Lou, Y. A spatial SIS model in advective heterogeneous environments. J. Differ. Equ. 2016, 261, 3305–3343. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, Z.C.; Zhang, L. A reaction-diffusion-advection SIS epidemic model in a spatially-temporally heterogeneous environment. Discret. Contin. Dyn. Syst. Ser. B 2018, 23, 4557–4578. [Google Scholar] [CrossRef]
- Cui, R.; Li, H.; Peng, R.; Zhou, M. Concentration behavior of endemic equilibrium for a reaction-diffusion-advection SIS epidemic model with mass action infection mechanism. Calc. Var. Partial. Differ. Equ. 2021, 60, 184. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, R. Asymptotic behavior of an SIS model with saturation and spontaneous infection mechanism. Z. Angew. Math. Phys. 2020, 71, 1–21. [Google Scholar] [CrossRef]
- Ge, J.; Kim, K.I.; Lin, Z.; Zhu, H. A SIS-advection model in a low-risk and high-risk domain. J. Differ. Equ. 2015, 259, 5486–5509. [Google Scholar] [CrossRef]
- Rao, X.; Zhang, G.; Wang, X. A reaction-diffusion-advection SIS epidemic model with linear external source and open advective environments. Discret. Contin. Dyn. Syst. Ser. B 2022, 27, 6655–6677. [Google Scholar] [CrossRef]
- Bluman, G.W.; Cole, J.D. Similarity Methods for Differential Equations; Springer: New York, NY, USA, 1974. [Google Scholar]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Ibragimov, N.H. Transformation Groups Applied to Mathematical Physics; Reidel: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1986. [Google Scholar]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: Berlin, Germany, 1989. [Google Scholar]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Cantwell, B.J. Introduction to Symmetry Analysis; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ibragimov, N.H. A Practical Course in Differential Equations and Mathematical Modelling; World Scientific Publishing Co Pvt Ltd.: Singapore, 2009. [Google Scholar]
- Senthilvelan, M.; Torrisi, M. Potential symmetries and new solutions of a simplified model for reacting mixtures. J. Phys. A Math. Gen. 2000, 33, 405. [Google Scholar] [CrossRef]
- Torrisi, M.; Tracinà, R. An application of equivalence transformations to reaction diffusion equations. Symmetry 2015, 7, 1929–1944. [Google Scholar] [CrossRef]
- Wang, G. A new (3 + 1)-dimensional Schrödinger equation: Derivation, soliton solutions and conservation laws. Nonlinear Dyn. 2021, 104, 1595–1602. [Google Scholar] [CrossRef]
- Cherniha, R.M.; Davydovych, V.V. A reaction-diffusion system with cross-diffusion: Lie symmetry, exact solutions and their applications in the pandemic modelling. Eur. J. Appl. Math. 2022, 33, 785–802. [Google Scholar] [CrossRef]
- Freire, I.L.; Da Silva, P.L.; Torrisi, M. Lie and Noether symmetries for a class of fourth-order Emden-Fowler equations. J. Phys. A Math. Theor. 2013, 46, 245206. [Google Scholar] [CrossRef]
- Naz, R.; Johnpillai, A.; Mahomed, F.M.; Omame, A. Closed-form solutions for a reaction-diffusion SIR model with different diffusion coefficients. Discret. Contin. Dyn. Syst. Ser. S 2024. [Google Scholar] [CrossRef]
- Naz, R.; Johnpillai, A.; Mahomed, F.M. The exact solutions of a diffusive SIR model via symmetry groups. J. Math. 2024, 2024, 4598831. [Google Scholar] [CrossRef]
- Cheviakov, A.F.; Zhao, P. Analytical Properties of Nonlinear Partial Differential Equations: With Applications to Shallow Water Models; Springer Nature: Berlin/Heidelberg, Germany, 2024; Volume 10. [Google Scholar]
- Hereman, W. Symbolic software for Lie symmetry analysis. In CRC Handbook of Lie Group Analysis of Differential; CRC: Boca Raton, FL, USA, 1996; Volume 3, pp. 367–413. [Google Scholar]
- Hereman, W. Review of symbolic software for Lie symmetry analysis. Math. Comput. Model. 1997, 25, 115–132. [Google Scholar] [CrossRef]
- Cheviakov, A.F. GeM software package for computation of symmetries and conservation laws of differential equations. Comput. Phys. Commun. 2007, 176, 48–61. [Google Scholar] [CrossRef]
- Takahashi, L.T.; Maidana, N.A.; Ferreira, W.C.; Pulino, P.; Yang, H.M. Mathematical models for the Aedes aegypti dispersal dynamics: Travelling waves by wing and wind. Bull. Math. Biol. 2005, 67, 509–528. [Google Scholar] [CrossRef]
- Bacani, F.; Dimas, S.; Freire, I.L.; Maidana, N.A.; Torrisi, M. Mathematical modelling for the transmission of dengue: Symmetry and travelling wave analysis. Nonlinear Anal. Real World Appl. 2018, 41, 269–287. [Google Scholar] [CrossRef]

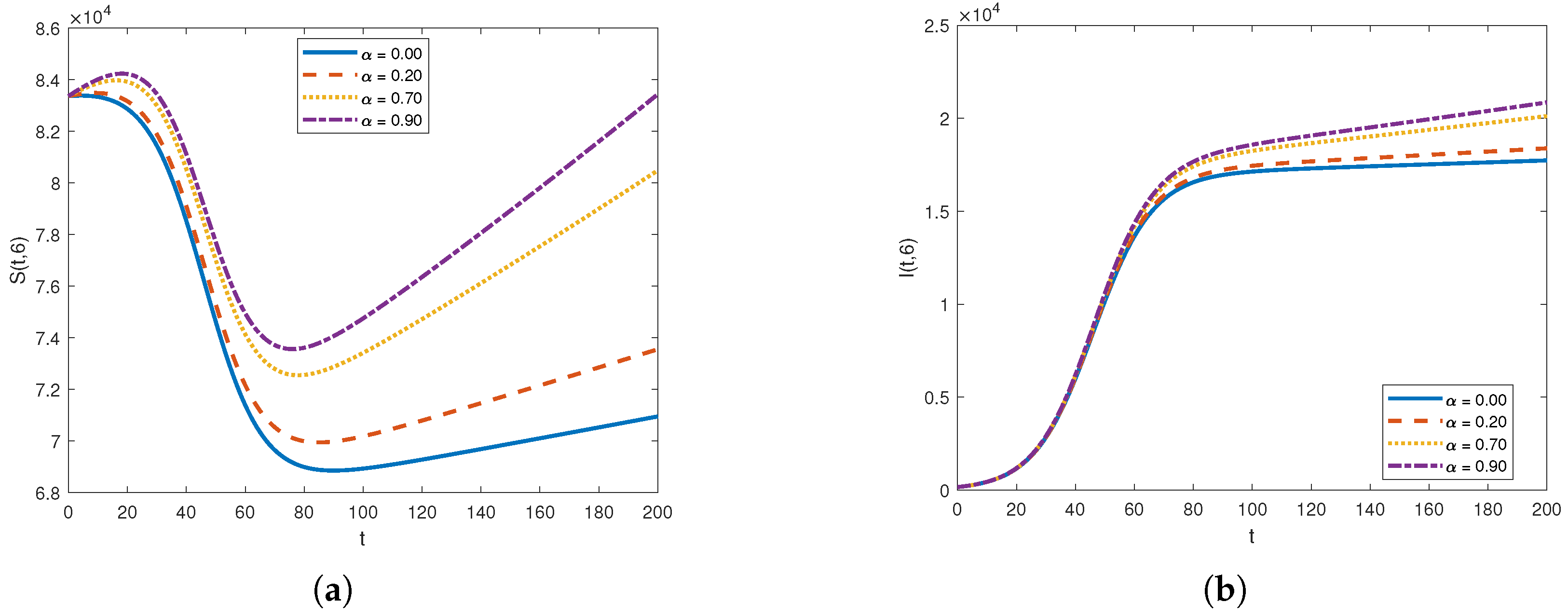

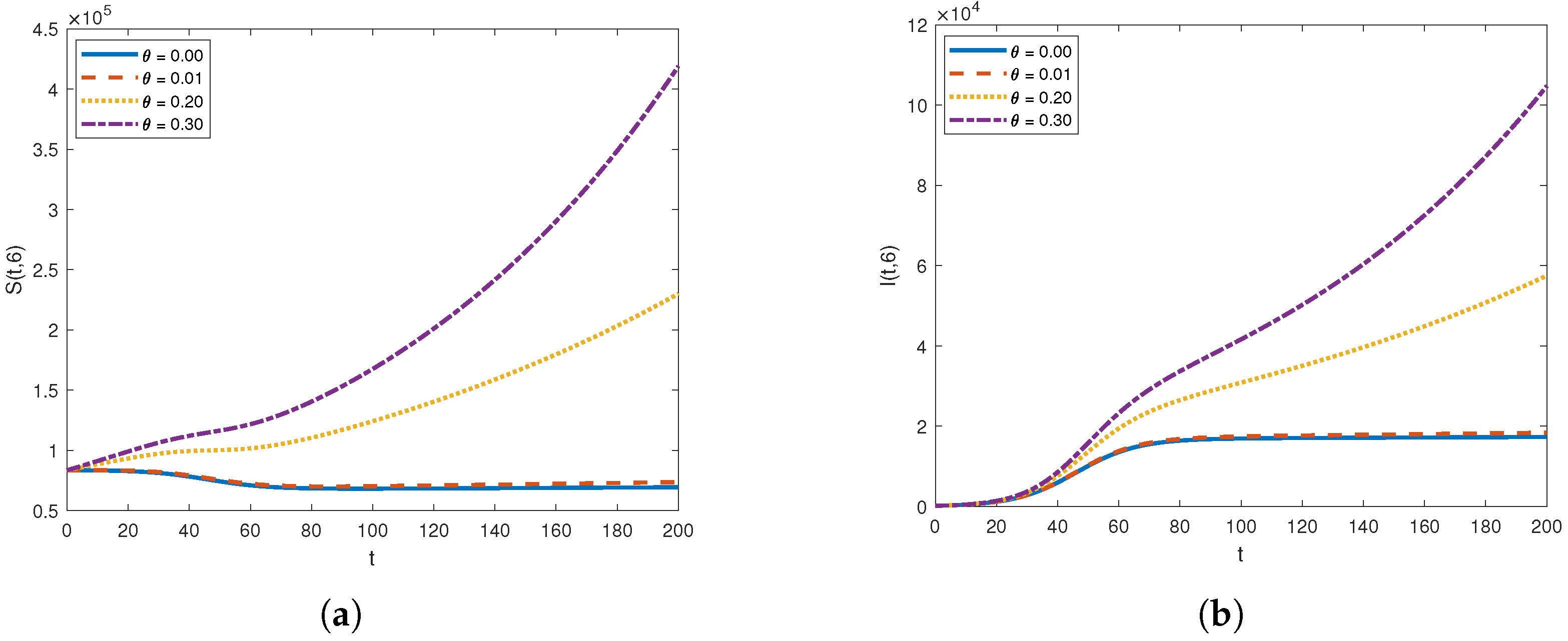
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naz, R.; Torrisi, M. The Closed-Form Solutions of an SIS Epidemic Reaction–Diffusion Model with Advection in a One-Dimensional Space Domain. Symmetry 2024, 16, 948. https://doi.org/10.3390/sym16080948
Naz R, Torrisi M. The Closed-Form Solutions of an SIS Epidemic Reaction–Diffusion Model with Advection in a One-Dimensional Space Domain. Symmetry. 2024; 16(8):948. https://doi.org/10.3390/sym16080948
Chicago/Turabian StyleNaz, Rehana, and Mariano Torrisi. 2024. "The Closed-Form Solutions of an SIS Epidemic Reaction–Diffusion Model with Advection in a One-Dimensional Space Domain" Symmetry 16, no. 8: 948. https://doi.org/10.3390/sym16080948




