Lie Symmetry Analysis, Rogue Waves, and Lump Waves of Nonlinear Integral Jimbo–Miwa Equation

Abstract

In this study, the extended (3 + 1)-dimensional Jimbo–Miwa equation, which has not been previously studied using Lie symmetry techniques, is the focus. We derive new symmetry reductions and exact invariant solutions, including lump and rogue wave structures. Additionally, precise solitary wave solutions of the extended (3 + 1)-dimensional Jimbo–Miwa equation using the multivariate generalized exponential rational integral function technique (MGERIF) are studied. The extended (3 + 1)-dimensional Jimbo–Miwa equation is crucial for studying nonlinear processes in optical communication, fluid dynamics, materials science, geophysics, and quantum mechanics. The multivariate generalized exponential rational integral function approach offers advantages in addressing challenges involving exponential, hyperbolic, and trigonometric functions formulated based on the generalized exponential rational function method. The solutions provided by MGERIF have numerous applications in various fields, including mathematical physics, condensed matter physics, nonlinear optics, plasma physics, and other nonlinear physical equations. The graphical features of the generated solutions are examined using 3D surface graphs and contour plots, with theoretical derivations. This visual technique enhances our understanding of the identified answers and facilitates a more profound discussion of their practical applications in real-world scenarios. We employ the MGERIF approach to develop a technique for addressing integrable systems, providing a valuable framework for examining nonlinear phenomena across various physical contexts. This study’s outcomes enhance both nonlinear dynamical processes and solitary wave theory.

1. Introduction

In recent years, scientists have found that the complexity and subtlety of natural patterns are in need of a more complete understanding. Higher-level tools and methods are needed to explore these more nuanced aspects. Partial differential equations (PDEs) are used to describe these phenomena when representing them using models. These help the researchers figure out what is occurring analysis-wise and are 3D imagery techniques created to gain better insights into phenomena. These PDEs are used to model intricate patterns and behaviors that establish the fundamental understanding of physical activities, narrowing our awareness to focus on exactly why systems do what they do in unison.

A soliton is like a single wave that can travel across a distance without changing its shape or losing any of its energy by interacting with other waves in matter. Moreover, solitons are not like mainstream waves, which are very broad and so on, and have extreme stability in terms of meaning (fixation or holdover). Their remarkable properties are essential in diverse research areas such as fluid dynamics [1], optical fibers [2], communication systems [3], biology [4], mechanics [5], plasma physics [6], engineering [7], hydrodynamics [8], and non-linear optics [9]. Solitons provide critical insights and contribute significantly to the advancement of knowledge and applications in these fields.

Analyzing solitary wave solutions of nonlinear partial differential equations (NLPDEs) is essential for exploring the fundamental characteristics of these processes more deeply alongside the associated waveforms they represent. From the point of view of practical applications, NLPDEs matter a lot because they frequently describe (in a much richer and more nuanced way) what is going on regarding a given set of physical, chemical, or biological processes. In terms of the appearance of solitary wave solutions, NLPDEs can serve as quite notable workhorses. They can be studied and solved using many different techniques. Several of these powerful techniques include the extended auxiliary equation mapping method [10], Bäcklund transform method [11], exp-function method [12], modified sub-equation method [13], homotopy perturbation method [14], Kudryashov method [15], Hirota bilinear method [16], extended trial equation method [17], Darboux transformation [18], modified extended tanh method, extended simple equation method [19], novel $\left({\displaystyle \frac{G^{\prime }}{G}}\right)$ expansion method [20], Runge–Kutta method [21], extended direct algebraic method [22], exp $(-\chi (\Theta \left)\right)$ expansion method [23], and generalized Arnous method [24]. These approaches have contributed significantly to the advancement of the understanding and solving of NLPDEs. In addition to solitary wave solutions, chaotic behavior, bifurcation analysis [25], and sensitivity analysis [26] play essential roles in characterizing the fundamental behavior of NLPDEs.

1.1. Governing Model

NLPDEs have appeared as important tools in scientific study, offering useful insights into fields such as plasmas, dynamics, acoustics, optics, and condensed-matter physics. These equations not only help with our comprehension of complicated occurrences but also allow scientists to make exact predictions regarding their future growth. As a consequence, many scholars have focused on investigating a range of NLPDEs to better understand complicated behaviors in natural systems. Recent studies have examined equations such as the Schrodinger equation [27], Heisenberg ferromagnet-type integrable Akbota equation [28], Benjamin–Bona–Mahony equation [29], generalized Calogero–Bogoyavlenskii–Schiff equation [30], Date-Jimbo-Kashiwara-Miwa equation [31], thin-film ferroelectric material equation [32], Boussinesq equation [33], Buckmaster equation [34], and non-linear non-classical Sobolev-type wave model [35].

In addition to these widely recognized equations, the Jimbo-Miwa equation (JME) is famous in mathematical physics, and many scholars are keen to explore its exact solutions. As shown below, (3 + 1)-dimensional JME can be expressed as follows:

$${\mathcal{Q}}_{xx}y+3{\mathcal{Q}}_x{\mathcal{Q}}_{xy}+3{\mathcal{Q}}_y{\mathcal{Q}}_{xx}+2{\mathcal{Q}}_{y}t-3{\mathcal{Q}}_{x}z=0.$$

(1)

In this context, $\mathcal{Q}=\mathcal{Q}(t,x,y,z)$, derived from the second constituent of the KP hierarchy, describes intriguing (3 + 1)-dimensional wave phenomena in physics [36]. Jimbo–Miwa Equation (1) is classified as non-integrable, and several academics have examined its precise solutions. The exp-function algorithm has facilitated the construction of two and three-soliton solutions, together with moving wave solutions [37]. Additionally, by applying the extended three-wave method, researchers have obtained three-wave results, including periodic soliton solutions, kink wave solutions, and breather and lump solutions encompassing two soliton solutions for the (3 + 1)-dimensional JME [38]. Research presented in [39] focused on lump-type and interaction solutions. Wazwaz used the bilinear method to construct multiple-front solutions for these equations [40]. The Lie symmetry method has also been employed to discuss closed-form invariant solutions and their dynamics [41]. A series of papers has thoroughly examined their exact solutions and various properties.

Recent studies have dedicated increasing amounts of focus to constructing lump and rogue wave structures in higher-dimensional nonlinear systems. For instance, the authors of [42,43] developed lump-induced rogue waves on a zero background in a (2 + 1)-dimensional KdV equation using a self-mapping transformation, uncovering rich localized wave behavior in two-dimensional spatial domains. This aligns closely with our pursuit of novel exact solutions, such as lump and rogue waves, in the (3 + 1)-dimensional Jimbo–Miwa equation, using Lie symmetry reductions combined with the MGERIF method.

As a further expansion of Equation (1), Wazwaz developed two newly extended Jimbo–Miwa equations (E-JME), which are outlined below, and examined their multiple-soliton solutions by using the Hirota Bilinear method [44]. This approach involves transforming the NLPDE into bilinear form via dependent variable transformation, followed by the construction of multi-soliton solutions via perturbative expansion techniques. Wazwaz formulation provides a foundation for further studies on lump, breather, and interaction structures in higher-dimensional integrable and non-integrable systems.

$${\mathcal{Q}}_{xxxy}+3{\left({\mathcal{Q}}_x{\mathcal{Q}}_y\right)}_x+2({\mathcal{Q}}_{xt}+{\mathcal{Q}}_{yt}+{\mathcal{Q}}_{zt})-3{\mathcal{Q}}_{xz}=0.$$

(2)

1.2. Literature Review

The interest in these JMEs has been growing among researchers. In [45], the Hirota bilinear method was employed to construct four types of localized waves, solitons, lumps, breathers, and rogue waves for (3 + 1)-dimensional E-JME. Additionally, explicit rational results in Grammian shape have been provided for the JME in [46]. Lump-kink and lump results were obtained for Equation (1) and E-JME (2) by Maple [47]. Additionally, (3 + 1)-dimensional E-JME featuring time-dependent coefficients was examined in [48], where bilinear forms, Backlund transformation, Lax pairs, and a large number of conservation laws were derived using binary Bell polynomials and symbolic computation. Yin et al. [49] examined the precise solutions for all three of these JMEs, including both lump-kink and lump solutions. Manafian identified novel repeated single-wave remedies for the (3 + 1)-dimensional extended JMEs, also using the Hirota bilinear method [50]. Liu investigated Equation (1) through the Bell polynomial, uncovering a new class of rogue wave solutions [51]. Xu et al. [52] explored the multi-exponential wave solution of Equation (2). J Liu checked the integrability of E-JME [53]. Kara applied a two-variable expansion method on E-JME [54]. Guo et al. [55] investigated the high-order lump, breather, and hybrid solution of Equation (2). Wang [56] found the Y-type and complex motion soliton solution of E-JME.

In [57], Cheng et al. presented a novel E-JME,

$${\mathcal{Q}}_{xxxy}+\omega {\left({\mathcal{Q}}_x{\mathcal{Q}}_y\right)}_x+{\sigma }_1{\mathcal{Q}}_{xy}+{\sigma }_2{\mathcal{Q}}_{xz}+{\sigma }_3{\mathcal{Q}}_{yt}+{\sigma }_4{\mathcal{Q}}_{yy}=0.$$

(3)

where $\omega \ne 0$ and ${\sigma }_i(i=1,2,3,4)$ are arbitrary constants. The ${\sigma }_2$ and ${\sigma }_3$ assure us that ${\sigma }_2{\sigma }_3\ne 0$. When $\omega$ = 3, ${\sigma }_2=-3$, ${\sigma }_3$ = 2 and ${\sigma }_1={\sigma }_4$ = 0 then Equation (3) becomes Equation (1). By setting $\omega =-3$, ${\sigma }_2=-3$, ${\sigma }_3=-1$ and ${\sigma }_1={\sigma }_4$ = 0 then Equation (3) converts into (3 + 1) dimensional extended BKP equation.

$${\mathcal{Q}}_{xy}-{\mathcal{Q}}_{xxxy}+3{\left({\mathcal{Q}}_x{\mathcal{Q}}_y\right)}_x+3{\mathcal{Q}}_{xz}=0.$$

(4)

The non-linear (3 + 1)-dimensional E-JME equation has many applications in science; thus, it is important to understand its dynamic behavior and find precise solutions.

1.3. Aim and Objectives of the Study

The main objective of this study is to derive new families of exact localized solutions—including lump, rogue-wave, and multi-soliton structures—for the extended (3 + 1)-dimensional Jimbo–Miwa equation (E-JME). The scope of the work is to combine Lie symmetry analysis, which systematically reduces the PDE into lower-dimensional forms, with the Multivariate Generalized Exponential Rational Integral Function (MGERIF) method, which enables the construction of broader classes of analytical solutions. Unlike existing approaches such as the Hirota bilinear or Bell-polynomial techniques, which are often restricted to multi-soliton forms, our framework generates lump, breather, and hybrid rogue–lump structures, thereby providing a more generalized solution set. The motivation arises from the limitations of traditional bilinear methods and the need to capture richer nonlinear dynamics in higher-dimensional models, with direct implications for optical fiber communication, fluid dynamics, plasma physics, and geophysical wave phenomena.

The paper can be summarized as follows: In Section 2, we apply the methodology for determining Lie Point Symmetries. In Section 3, Lie symmetry analysis is implemented to find infinitesimal generators of Equation (2). In Section 4, we implement symmetry reduction to convert PDEs into ODEs. Section 5 discusses the mathematical processes of the MGERIF, which obtains solutions using the MGERIF method, and provides graphical representations of these solutions. Section 6 discusses the graphical representation of the obtained solutions. In Section 7, we discuss Bridging Theory and Practice: Exploring Real-World Applications of Mathematical Innovations. Section 8 refers to the Key Innovations. Nomenclature of the manuscript mentioned in the back. In Section 9, the conclusion and outcomes are discussed.

2. Methodology for Determining Lie Point Symmetries

Lie point symmetries serve as a powerful framework for understanding, simplifying, and solving differential equations, offering significant benefits in scientific research and computational analysis. Their widespread application across disciplines such as physics, engineering, and biology makes them an essential tool for studying complex dynamical systems [58]. The process of determining symmetries is achieved via the following steps:

• Step 1: Formulate a system of $𝒦$ differential equations:

  $${\mathbb{H}}^{u}x,{\mathcal{Q}}^{\left(p^{†}\right)})=0,u=1,2,3,\dots ,q^{†}.$$

  (5)
  The partial derivatives of ${\mathcal{Q}}^{r^{†}}$ can be represented using multi-index notation for a given order $r^{†}$, considering $s^{†}$ independent variables $x=(x_1,x_2,x_3,\dots ,x_{s^{†}})\in {\mathbb{Q}}^{𝒱}$ and $r^{†}$ dependent variables $\mathcal{Q}=({\mathcal{Q}}^1,{\mathcal{Q}}^2,\dots ,{\mathcal{Q}}^{r^{†}})\in {\mathbb{Q}}^r$.

  $${\mathbb{Q}}_h^q={\displaystyle \frac{{\partial }^{|J^{†}|}{\mathcal{Q}}^w}{\partial x_1^{J_1^{†}}\partial x_2^{J_2^{†}}\partial x_3^{J_3^{†}}.\dots \partial x_{s^{†}}^{J_{s^{†}}^{†}}}},|J^{†}|=\sum _{i_2=1}^{s^{†}}{h}_{i_2}^{†}·$$

  (6)
  The notation $Q^{\left(P^{†}\right)}$ represents the p-th order derivatives of $Q^w$ for a fixed $J^{†}$. The group transformations $\overline{x}\left(\eta \right)$ and $\overline{\mathcal{Q}}\left(\eta \right)$ are functions of ${\mathbb{M}}_{K_1}$ and ${\mathbb{M}}_{K_2}$, respectively, and are defined according to Lie’s formulation.

  $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \overline{x_i\left(\eta \right)}& =x_i+\eta {\left.{\displaystyle \frac{\partial {\mathbb{M}}_{K_1}(x,\mathcal{Q},\Gamma )}{\partial \eta }}\right|}_{\eta =0}+𝒟\left({\eta }^2\right),\hfill \\ & =x_i+\eta {\kappa }^i(x,\mathcal{Q})+𝒟\left({\eta }^2\right),1\le i\le m^{★},\hfill \\ \hfill \overline{{\mathcal{Q}}_{q^{★}}\left(\eta \right)}& ={\mathcal{Q}}_{q^{★}}+\eta {\left.{\displaystyle \frac{\partial {\mathbb{M}}_{K_2}(x,\mathcal{Q},\eta )}{\partial \eta }}\right|}_{\Gamma =0}+𝒟\left({\eta }^2\right),\hfill \\ & ={\mathcal{Q}}_{q^{★}}+\eta {{\kappa }^{★}}^q(x,R)+𝒟\left({\eta }^2\right),1\le q^{★}\le p^{★}.\hfill \end{array}\end{array}$$
  The generalized form of the prolongation formula is

  $${𝒱}^{\ast }=\sum _{f=1}^{𝒦}{\gamma }^f(x,Q){\displaystyle \frac{\partial }{\partial {\alpha }_i}}+\sum _{g=1}^{r^{★}}{{\gamma }^{★}}^{q^{★}}(x,Q){\displaystyle \frac{\partial }{\partial {\psi }_{q^{★}}}}.$$

  (7)
• Step 2: To determine the coefficients ${\gamma }^f$ and ${{\gamma }^{★}}^{q^{★}}$, the g-th prolongation ${𝒱}^{\left(m\right)}$ of the vector field $𝒱$ must be generated, applied to system (7), and enforced to vanish on its solution set. This results in a linear homogeneous PDE system for ${\gamma }^f(x,\mathcal{Q})$ and ${{\gamma }^{★}}^{q^{★}}(x,\mathcal{Q})$, treating x and $\mathcal{Q}$ as independent variables. Known as the determining system for symmetries, it can be computed manually, interactively, or symbolically to obtain explicit expressions for ${\gamma }^f(x,\mathcal{Q})$ and ${{\gamma }^{★}}^{q^{★}}(x,\mathcal{Q})$.

3. Lie Symmetry Analysis

The Lie symmetry analysis based on one-parameter transformations relies on examining the tangent structural equations alongside the system of partial differential equations (PDEs). Lie-point symmetries are invertible transformations that render the original PDE system invariant by transforming it into a comparable system with fewer independent variables. Consequently, the similarity transformation approach is a wonderful strategy to construct invariant solutions to PDE. The approach of Lie has implications for non-linear physics, quantum physics, bifurcation theory, numerical analysis, algebraic topology, relativity, differential geometry, classical mechanics, and various other fields.

Let us consider one parameter (a) Lie group ($t,z,y,x,\mathcal{Q}$) infinitesimal transformation [59] for Equation (2) as follows:

$$\left.\begin{array}{c}{t}^{\ast }=t+a\gamma (t,z,y,x,\mathcal{Q})+O\left(a^2\right),\hfill \\ x^{\ast }=x+a\kappa (t,z,y,x,\mathcal{Q})+O\left(a^2\right),\hfill \\ y^{\ast }=y+a\tau (t,z,y,x,\mathcal{Q})+O\left(a^2\right),\hfill \\ z^{\ast }=z+a\rho (t,z,y,x,\mathcal{Q})+O\left(a^2\right),\hfill \\ {\mathcal{Q}}^{\ast }=\mathcal{Q}+a\eta (t,z,y,x,\mathcal{Q})+O\left(a^2\right).\hfill \end{array}\right\}$$

(8)

Here, a is the Lie group parameter, while $\gamma ,\tau ,\kappa ,\rho ,$ and $\eta$ are the infinitesimal coefficients of the Lie group ($t,z,y,x,\mathcal{Q}$) and have to be calculated. Then, the vector field associated with Equation (8) will be

$$𝒱=\gamma {\displaystyle \frac{\partial }{\partial x}}+\kappa {\displaystyle \frac{\partial }{\partial y}}+\tau {\displaystyle \frac{\partial }{\partial z}}+\rho {\displaystyle \frac{\partial }{\partial t}}+\eta {\displaystyle \frac{\partial }{\partial \mathcal{Q}}}.$$

(9)

The criterion for Equation (2) with $𝒱$ is given as [60]:

$${𝒱}^{\left[4\right]}{\left({\mathcal{Q}}_{xxxy}+3{\left({\mathcal{Q}}_x{\mathcal{Q}}_y\right)}_x+2({\mathcal{Q}}_{xt}+{\mathcal{Q}}_{yt}+{\mathcal{Q}}_{zt})-3{\mathcal{Q}}_{xz}\right)}_{|Equation(2)=0}=0.$$

(10)

The fourth prolongation formula [61] for Equation (2) will be

$$\begin{array}{cc}\hfill {𝒱}^{\left[4\right]}& =𝒱+{\eta }^x{\displaystyle \frac{\partial }{\partial {\mathcal{Q}}_x}}+{\eta }^y{\displaystyle \frac{\partial }{\partial {\mathcal{Q}}_y}}+{\eta }^{xx}{\displaystyle \frac{\partial }{\partial {\mathcal{Q}}_{xx}}}+{\eta }^{xy}{\displaystyle \frac{\partial }{\partial {\mathcal{Q}}_{xy}}}+{\eta }^{xz}{\displaystyle \frac{\partial }{\partial {\mathcal{Q}}_{xz}}}+{\eta }^{xt}{\displaystyle \frac{\partial }{\partial {\mathcal{Q}}_{xt}}}+{\eta }^{yt}{\displaystyle \frac{\partial }{\partial {\mathcal{Q}}_{yt}}}+\hfill \\ & {\eta }^{zt}{\displaystyle \frac{\partial }{\partial {\mathcal{Q}}_{zt}}}+{\eta }^{xxxy}{\displaystyle \frac{\partial }{\partial {\mathcal{Q}}_{xxxy}}}.\hfill \end{array}$$

(11)

where ${\eta }^x,{\eta }^y,{\eta }^{xx},{\eta }^{xy},{\eta }^{xz},{\eta }^{xt},{\eta }^{yt},{\eta }^{zt},{\eta }^{xxxy}$ are the extended infinitesimals. The invariance condition ${𝒱}^{\left[4\right]}$ Equation (2) with Equation (2) = 0 gives the invariance equation as

$${\eta }^{xxxy}+3{\left({\eta }^x{\eta }^y\right)}_x+2({\eta }^{xt}+{\eta }^{yt}+{\eta }^{zt})-3{\eta }^{xz}=0.$$

(12)

By replacing the values of infinitesimals ${\eta }^x,{\eta }^y,{\eta }^{xx},{\eta }^{xy},{\eta }^{xz},{\eta }^{xt},{\eta }^{yt},{\eta }^{zt},{\eta }^{xxxy}$, and comparing the coefficient of different derivative terms to zero, we create a system of partial derivatives equations. The solution of this system produces the following infinitesimals:

$$\begin{array}{cc}\hfill \kappa & ={\displaystyle \frac{(x+5z)c_1}{6}}+{\displaystyle \frac{(x-z)c_3}{6}}+c_6,\tau ={\displaystyle \frac{\left(3t+2y+2z\right)c_1}{4}}+{\displaystyle \frac{\left(-3t+2y-2z\right)c_3}{4}}+c_5,\hfill \\ & \rho =c_{1}z+c_2,\gamma =c_{3}t+c_4,\eta =f_1\left(t\right)+f_2\left(z\right)+{\displaystyle \frac{(-c_3-c_1)\mathcal{Q}}{6}}-{\displaystyle \frac{x{c}_1}{3}}-{\displaystyle \frac{x{c}_3}{3}}.\hfill \end{array}$$

(13)

Here, $c_1,c_2,c_3,c_4,c_5,$ and $c_6$ are the arbitrary real constants and $f_1\left(t\right)$, and $f_2\left(z\right)$ are arbitrary functions of t and z, respectively.

Theorem 1.

The determining equations were obtained by applying the fourth prolongation of the vector field to Equation (2) and enforcing invariance. Solving the system produced explicit expressions for the infinitesimal coefficients, which yielded eight independent generators forming the Lie algebra. The Equation (13) exhibits a two-dimensional Lie algebra that is explained by the eight generators as [62]:

$$\begin{array}{cc}\hfill & {𝒱}_1={\displaystyle \frac{(x+5z)}{6}}{\displaystyle \frac{\partial }{\partial x}}+{\displaystyle \frac{\left(3t+2y+2z\right)}{4}}{\displaystyle \frac{\partial }{\partial y}}+z{\displaystyle \frac{\partial }{\partial z}}-{\displaystyle \frac{x}{3}}{\displaystyle \frac{\partial }{\partial \mathcal{Q}}},{𝒱}_2={\displaystyle \frac{\partial }{\partial z}},{𝒱}_3={\displaystyle \frac{\partial }{\partial t}},{𝒱}_4={\displaystyle \frac{\partial }{\partial y}},\hfill \\ & {𝒱}_5=f_1\left(t\right){\displaystyle \frac{\partial }{\partial \mathcal{Q}}},{𝒱}_6={\displaystyle \frac{(x-z)}{6}}{\displaystyle \frac{\partial }{\partial x}}+{\displaystyle \frac{\left(-3t+2y-2z\right)}{4}}{\displaystyle \frac{\partial }{\partial y}}+t{\displaystyle \frac{\partial }{\partial t}}-{\displaystyle \frac{x}{3}}{\displaystyle \frac{\partial }{\partial \mathcal{Q}}},{𝒱}_7=f_2\left(z\right){\displaystyle \frac{\partial }{\partial \mathcal{Q}}},\hfill \\ & {𝒱}_8={\displaystyle \frac{\partial }{\partial x}}.\hfill \end{array}$$

(14)

These generators correspond to continuous symmetries of Equation (2). The operators ${𝒱}_2,{𝒱}_3,{𝒱}_4$, and ${𝒱}_8$ describe translations in $z,t,y$, and x, respectively. The operators ${𝒱}_1$ and ${𝒱}_6$ represent scaling-type transformations, while ${𝒱}_5$ and ${𝒱}_7$ involve arbitrary functions of t or z, reflecting solution-dependent shifts. Together, they form the basis for symmetry reductions and invariant solutions. We need to solve nine ODEs when ${𝒦}_i$ is covered by ${𝒱}_i$ for (i = 1, …, 5), to analyze the symmetry group.

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d(\tilde{t})}{dϵ}}={\lambda }_1(\tilde{t},\tilde{x},\tilde{y},\tilde{z},\tilde{\mathcal{Q}}),with\tilde{t}{|}_{ϵ=0}=t,\hfill \\ & {\displaystyle \frac{d(\tilde{x})}{dϵ}}={\lambda }_2(\tilde{t},\tilde{x},\tilde{y},\tilde{z},\tilde{\mathcal{Q}}),with\tilde{x}{|}_{ϵ=0}=x,\hfill \\ & {\displaystyle \frac{d(\tilde{y})}{dϵ}}={\lambda }_3(\tilde{t},\tilde{x},\tilde{y},\tilde{z},\tilde{\mathcal{Q}}),with\tilde{x}{|}_{ϵ=0}=y,\hfill \\ & {\displaystyle \frac{d(\tilde{z})}{dϵ}}={\lambda }_4(\tilde{t},\tilde{x},\tilde{y},\tilde{z},\tilde{\mathcal{Q}}),with\tilde{x}{|}_{ϵ=0}=z,\hfill \\ & {\displaystyle \frac{d(\tilde{\mathcal{Q}})}{dϵ}}={\lambda }_5(\tilde{t},\tilde{x},\tilde{\mathcal{Q}}),with\tilde{\mathcal{Q}}{|}_{ϵ=0}=\mathcal{Q}.\hfill \end{array}$$

(15)

where ϵ is the infinitesimal parameter. The below symmetry group ${𝒦}_i$ covered by ${𝒱}_i$ can be constructed with the help of generators ${\lambda }_i$, for (i = 1, …, 5).

$$\begin{array}{cc}\hfill & {𝒦}_1^{\ast †}:(x,y,z,t,\mathcal{Q})\to \left(e^{ϵ}x+\left(e^{ϵ}-1\right)·{\displaystyle \frac{5}{6}}z,y(ϵ),e^{ϵ}z,t,\mathcal{Q}-{\displaystyle \frac{1}{3}}\int x\left(ϵ\right)dϵ\right),\hfill \\ & {𝒦}_2^{\ast †}:(x,y,z,t,\mathcal{Q})\to (x,y,z+ϵ,t,\mathcal{Q}),\hfill \\ & {𝒦}_3^{\ast †}:(x,y,z,t,\mathcal{Q})\to (x,y,z,t+ϵ,\mathcal{Q}),\hfill \\ & {𝒦}_4^{\ast †}:(x,y,z,t,\mathcal{Q})\to (x,y+ϵ,z,t,\mathcal{Q}),\hfill \\ & {𝒦}_5^{\ast †}:(x,y,z,t,\mathcal{Q})\to (x,y,z,t,\mathcal{Q}+ϵf_1\left(t\right)),\hfill \\ & {𝒦}_6^{\ast †}:(x,y,z,t,\mathcal{Q})\to \left(x\left(ϵ\right),y\left(ϵ\right),z,t{e}^{ϵ},\mathcal{Q}-{\displaystyle \frac{1}{3}}\int x\left(ϵ\right)dϵ\right),\hfill \\ & {𝒦}_7^{\ast †}:(x,y,z,t,\mathcal{Q})\to (x,y,z,t,\mathcal{Q}+ϵf_2\left(z\right)),\hfill \\ & {𝒦}_8^{\ast †}:(x,y,z,t,\mathcal{Q})\to (x+ϵ,y,z,t,\mathcal{Q}).\hfill \end{array}$$

(16)

Theorem 2.

The new solution can be obtained by applying ${𝒦}_i^{\ast †}$$1\le i\le 8$. If $\mathcal{Q}(t,x,y,x)$ is explored as a solution for Equation (2), then using ${𝒦}_i^{\ast †}$ for $1\le i\le 8$, the new solution ${\mathcal{Q}}_i$ for $1\le i\le 8$ are obtained as follows:

$$\begin{array}{cc}\hfill & {𝒦}_1^{\ast †}\left(ϵ\right){\mathcal{Q}}_1(t,x,y,z)={\tilde{\mathcal{Q}}}_1\left(e^{ϵ}x+\left(e^{ϵ}-1\right)·{\displaystyle \frac{5}{6}}z,y,e^{ϵ}z,t,\mathcal{Q}-{\displaystyle \frac{1}{3}}\int x\left(ϵ\right)dϵ\right){𝒦}_1^{\ast †}\left(ϵ\right)\hfill \\ & {𝒦}_2^{\ast †}\left(ϵ\right){\mathcal{Q}}_2(t,x,y,z)={\tilde{\mathcal{Q}}}_2(x,y,z-ϵ,t){𝒦}_2^{\ast †}\left(ϵ\right),\hfill \\ & {𝒦}_3^{\ast †}\left(ϵ\right){\mathcal{Q}}_3(t,x,y,z)={\tilde{\mathcal{Q}}}_3(x,y,z,t-ϵ){𝒦}_3^{\ast †}\left(ϵ\right),\hfill \\ & {𝒦}_4^{\ast †}\left(ϵ\right){\mathcal{Q}}_4(t,x,y,z)={\tilde{\mathcal{Q}}}_4(x,y-ϵ,z,t){𝒦}_4^{\ast †}\left(ϵ\right),\hfill \\ & {𝒦}_5^{\ast †}\left(ϵ\right){\mathcal{Q}}_5(t,x,y,z)={\tilde{\mathcal{Q}}}_5(x,y,z,t){𝒦}_5^{\ast †}\left(ϵ\right),\hfill \\ & {𝒦}_6^{\ast †}\left(ϵ\right){\mathcal{Q}}_6(t,x,y,z)={\tilde{\mathcal{Q}}}_6\left(x\left(ϵ\right),y\left(ϵ\right),z,t{e}^{ϵ}\right){𝒦}_6^{\ast †}\left(ϵ\right),\hfill \\ & {𝒦}_7^{\ast †}\left(ϵ\right){\mathcal{Q}}_7(t,x,y,z)={\tilde{\mathcal{Q}}}_7(x,y,z,t){𝒦}_7^{\ast †}\left(ϵ\right),\hfill \\ & {𝒦}_8^{\ast †}\left(ϵ\right){\mathcal{Q}}_8(t,x,y,z)={\tilde{\mathcal{Q}}}_8(t,x-ϵ,y,z){𝒦}_8^{\ast †}\left(ϵ\right).\hfill \end{array}$$

(17)

According to Lie’s first theorem, the exponential map of each generator defines a group of transformations that leaves the governing equation invariant. Hence, applying $K_i^{\ast }$ to any solution preserves the solution property. By applying the Lie bracket, defined as $\left[{\mathcal{L}}_m^{\ast }{\mathcal{L}}_n^{\ast }\right]={\mathcal{L}}_m^{\ast }{\mathcal{L}}_n^{\ast }-{\mathcal{L}}_n^{\ast }{\mathcal{L}}_m^{\ast }$, the commutators can be mathematically stated as follows:

$$[{\mathcal{L}}_m^{\ast },{\mathcal{L}}_n^{\ast }]=[{\mathcal{L}}_n^{\ast },{\mathcal{L}}_m^{\ast }]=0,m,n=1,\dots ,5.$$

(18)

The commutator

Table 1. Commutator table of the Lie algebra generated by ${𝒱}_1$ to ${𝒱}_8$ [63].

$[{𝒱}_i,{𝒱}_j]$	${𝒱}_1$	${𝒱}_2$	${𝒱}_3$	${𝒱}_4$	${𝒱}_5$	${𝒱}_6$	${𝒱}_7$	${𝒱}_8$
${𝒱}_1$	0	$-{\displaystyle \frac{5}{6}}{𝒱}_8-{𝒱}_2$	$-{\displaystyle \frac{3}{4}}{𝒱}_4$	$-{\displaystyle \frac{1}{2}}{𝒱}_4$	0	0	0	$-{\displaystyle \frac{1}{6}}{𝒱}_8$
${𝒱}_2$	${\displaystyle \frac{5}{6}}{𝒱}_8+{𝒱}_2$	0	0	0	0	${\displaystyle \frac{1}{6}}{𝒱}_8$	0	0
${𝒱}_3$	${\displaystyle \frac{3}{4}}{𝒱}_4$	0	0	0	0	${𝒱}_3$	0	0
${𝒱}_4$	${\displaystyle \frac{1}{2}}{𝒱}_4$	0	0	0	0	${\displaystyle \frac{1}{2}}{𝒱}_4$	0	0
${𝒱}_5$	0	0	0	0	0	0	0	0
${𝒱}_6$	0	$-{\displaystyle \frac{1}{6}}{𝒱}_8$	$-{𝒱}_3$	$-{\displaystyle \frac{1}{2}}{𝒱}_4$	0	0	0	0
${𝒱}_7$	0	0	0	0	0	0	0	0
${𝒱}_8$	${\displaystyle \frac{1}{6}}{𝒱}_8$	0	0	0	0	0	0	0

confirms that the generators close under the Lie bracket and therefore span an eight-dimensional Lie algebra. Linear combinations of these generators define one-dimensional subalgebras, which reduce to canonical forms through equivalence relations.

Theorem 3.

Let $\mathfrak{g}=\langle {𝒱}_1,{𝒱}_2,\dots ,{𝒱}_8\rangle$ be the Lie algebra of the given system. This set of generators forms a complete framework for constructing one-dimensional subalgebras. Any such subalgebra can be written as

$${𝒫}_{\eta }=〈{𝒱}_i+{\eta }_1{𝒱}_j+{\eta }_2{𝒱}_k+\cdots +{\eta }_n{𝒱}_m〉,{\eta }_l\in \mathbb{R}$$

(19)

for any nontrivial linear combination of the basis generators.

$$𝒱=c_1𝒱+c_2𝒱+c_3𝒱+c_4𝒱+c_5𝒱+c_6𝒱+c_7𝒱+c_8𝒱.$$

(20)

Proof. 

Let $𝒱$ be an arbitrary element in $\mathfrak{g}$, such that

$$𝒱=a_1{𝒱}_1+a_2{𝒱}_2+a_3{𝒱}_3+a_4{𝒱}_4+a_5{𝒱}_5+a_6{𝒱}_6+a_7{𝒱}_7+a_8{𝒱}_8$$

(21)

We classify the cases based on canonical choices of $a_i$, yielding the following distinct subalgebras:

Therefore, the most general one-dimensional subalgebra can be expressed as a linear combination of generators, where different choices of nonzero parameters ${\eta }_j$ define inequivalent subalgebra classes as in

Table 2. Canonical cases of one-dimensional subalgebras generated by linear combinations of the vector fields ${𝒱}_1$ to ${𝒱}_8$ [64].

Case	Non-Zero Coefficients	Resulting Generator	Subalgebra
1	$a_1=1$	$𝒱={𝒱}_1$	${𝒫}_1=\langle {𝒱}_1\rangle$
2	$a_2=1$	$𝒱={𝒱}_2$	${𝒫}_2=\langle {𝒱}_2\rangle$
3	$a_3=1$	$𝒱={𝒱}_3$	${𝒫}_3=\langle {𝒱}_3\rangle$
4	$a_4=1$	$𝒱={𝒱}_4$	${𝒫}_4=\langle {𝒱}_4\rangle$
5	$a_5=1$	$𝒱={𝒱}_5$	${𝒫}_5=\langle {𝒱}_5\rangle$
6	$a_6=1$	$𝒱={𝒱}_6$	${𝒫}_6=\langle {𝒱}_6\rangle$
7	$a_7=1$	$𝒱={𝒱}_7$	${𝒫}_7=\langle {𝒱}_7\rangle$
8	$a_8=1$	$𝒱={𝒱}_8$	${𝒫}_8=\langle {𝒱}_8\rangle$
9	$a_i=1,a_j\ne 0$	$𝒱={𝒱}_i+\sum {\eta }_j{𝒱}_j$	${𝒫}_{\eta }=〈{𝒱}_i+\sum {\eta }_j{𝒱}_j〉$

. Each one-dimensional subalgebra produces a symmetry reduction of the PDE to an ODE. Translation subalgebras lead to traveling wave reductions, scaling subalgebras yield self-similar solitary wave structures, and mixed generators capture interaction modes. This classification guarantees that all possible reductions are systematically covered. □

4. Symmetry Reduction and Invariant Solution

Reduction methods are applied in this section to reduce a PDE into an ODE. To obtain an invariant solution for the set of Equation (8), it is necessary to resolve the associated characteristic equation, which is stated as follows [65]:

$${\displaystyle \frac{dx}{\kappa }}={\displaystyle \frac{dy}{\tau }}={\displaystyle \frac{dz}{\rho }}={\displaystyle \frac{dt}{\gamma }}={\displaystyle \frac{d\mathcal{Q}}{\eta }}.$$

(22)

4.1. Reduction Through Translation Invariance: ${𝒱}_2={\displaystyle \frac{\partial }{\partial z}}$

The associated characteristic equation for ${𝒱}_2$ will be the following form:

$${\displaystyle \frac{dt}{0}}={\displaystyle \frac{dx}{0}}={\displaystyle \frac{dy}{0}}={\displaystyle \frac{dz}{1}}={\displaystyle \frac{d\mathcal{Q}}{0}}.$$

(23)

By solving the characteristic Equation (23) we get

$$x=\mathcal{M},y=\mathcal{N},t=\mathcal{R},\mathcal{Q}=𝒫(\mathcal{M},\mathcal{N},\mathcal{R}).$$

(24)

where $\mathcal{M}$, $\mathcal{N}$, and $\mathcal{R}$ are arbitrary constants. Then, the solution can be expressed as $\mathcal{Q}=𝒫(\mathcal{M},\mathcal{N},\mathcal{R})$. Inserting this function from Equation (24) into Equation (2), the E-JME reduces to the following form:

$${𝒫}_{\mathcal{M}\mathcal{M}\mathcal{M}\mathcal{N}}+3{\left({𝒫}_{\mathcal{M}}{𝒫}_{\mathcal{N}}\right)}_{\mathcal{M}}+2\left({𝒫}_{\mathcal{M}\mathcal{R}}+{𝒫}_{\mathcal{N}\mathcal{R}}\right)=0.$$

(25)

A new set of Lie point generators emerges when Equation (25) undergoes the Lie symmetry transformation

$$\begin{array}{cc}\hfill & {𝒱}_{1a}={\displaystyle \frac{1}{3}}\mathcal{M}{\displaystyle \frac{\partial }{\partial \mathcal{M}}}+{\displaystyle \frac{1}{3}}\mathcal{N}{\displaystyle \frac{\partial }{\partial \mathcal{N}}}+\mathcal{R}{\displaystyle \frac{\partial }{\partial \mathcal{R}}}-{\displaystyle \frac{1}{3}}{\displaystyle \frac{\partial }{\partial 𝒫}},{𝒱}_{2a}={\displaystyle \frac{\partial }{\partial \mathcal{R}}},{𝒱}_{3a}={\displaystyle \frac{\partial }{\partial \mathcal{N}}},\hfill \\ & {𝒱}_{4a}=\mathcal{R}{\displaystyle \frac{\partial }{\partial \mathcal{M}}}+{\displaystyle \frac{2}{3}}(\mathcal{M}+\mathcal{N}){\displaystyle \frac{\partial }{\partial 𝒫}},{𝒱}_5={\displaystyle \frac{\partial }{\partial \mathcal{M}}},{𝒱}_6=f_1\left(\mathcal{R}\right){\displaystyle \frac{\partial }{\partial 𝒫}}.\hfill \end{array}$$

(26)

For ${𝒱}_{5a}$, the characteristics equation can be expressed as follows:

$${\displaystyle \frac{d\mathcal{R}}{1}}={\displaystyle \frac{d\mathcal{M}}{0}}={\displaystyle \frac{d\mathcal{N}}{0}}={\displaystyle \frac{d𝒫}{0}}.$$

(27)

The characteristic Equation (27) is solved to determine the reduced variables as follows:

$$\mathcal{M}=𝒜,\mathcal{N}=\mathcal{B},𝒫=𝒮(𝒜,\mathcal{B}).$$

(28)

where $𝒜$, $\mathcal{B}$, are arbitrary constants. Then, the solution can be expressed as $𝒫=𝒮(𝒜,\mathcal{B})$. Inserting this function from Equation (28) into Equation (25), then the reduced equation will be as follows:

$${𝒮}_{𝒜𝒜𝒜\mathcal{B}}+3{\left({𝒮}_{𝒜}{𝒮}_{\mathcal{B}}\right)}_{𝒜}=0.$$

(29)

Again, by applying the Lie symmetry transformation, the infinitesimal generators will be

$$\begin{array}{cc}\hfill {𝒱}_{1b}& =𝒜{\displaystyle \frac{\partial }{\partial 𝒜}}-𝒮{\displaystyle \frac{\partial }{\partial 𝒮}},{𝒱}_{2b}={\displaystyle \frac{\partial }{\partial 𝒜}},{𝒱}_{3b}={\displaystyle \frac{\partial }{\partial \mathcal{B}}},{𝒱}_{4b}=\mathcal{B}{\displaystyle \frac{\partial }{\partial \mathcal{B}}},{𝒱}_{5b}={\displaystyle \frac{\partial }{\partial u}},{𝒱}_{6b}=f_1\left(\mathcal{B}\right){\displaystyle \frac{\partial }{\partial \mathcal{B}}}.\hfill \end{array}$$

(30)

For ${𝒱}_{2b}$, the characteristics equation can be expressed as follows:

$${\displaystyle \frac{d𝒜}{1}}={\displaystyle \frac{d\mathcal{B}}{0}}={\displaystyle \frac{d𝒮}{0}}.$$

(31)

The characteristic Equation (31) is solved to determine the reduced variables as follows:

$$\mathcal{B}=c,𝒮=𝒟\left(\mathbf{c}\right).$$

(32)

Here, c denotes an arbitrary constant, and the solution can be written as $𝒮=𝒲\left(\mathbf{c}\right)$. By inserting this function from Equation (32) into Equation (29), the reduced equation will be

$$𝒲{\left(\mathbf{c}\right)}^{″}=0.$$

(33)

4.2. Reduction Through Translation Invariance: ${𝒱}_3+{𝒱}_8$

The associated characteristic equation for ${𝒱}_3+{𝒱}_8$ will be the following form:

$${\displaystyle \frac{dt}{1}}={\displaystyle \frac{dx}{1}}={\displaystyle \frac{dy}{0}}={\displaystyle \frac{dz}{0}}={\displaystyle \frac{d\mathcal{Q}}{0}}.$$

(34)

By solving the characteristic Equation (34) we get

$$\xi =x-t,y=\mathcal{N},z=\mathcal{U},\mathcal{Q}=𝒫(\xi ,\mathcal{N},\mathcal{U})$$

(35)

where $\mathcal{N}$, and $\mathcal{U}$ are arbitrary constants. Then, the solution can be expressed as $\mathcal{Q}=𝒫(\xi ,\mathcal{N},\mathcal{U})$. Inserting this function from Equation (35) into Equation (2), the E-JME reduces to the following form:

$${𝒫}_{\xi \xi \xi \mathcal{N}}+3{𝒫}_{\xi \xi }{𝒫}_{\mathcal{N}}+3{𝒫}_{\xi }{𝒫}_{\xi \mathcal{N}}-2{𝒫}_{\xi \xi }-2{𝒫}_{\xi \mathcal{N}}-5{𝒫}_{\xi \mathcal{U}}=0.$$

(36)

A new set of Lie point generators emerges when Equation (36) undergoes the Lie symmetry transformation

$$\begin{array}{cc}\hfill & {𝒱}_{1a}={\displaystyle \frac{\partial }{\partial \mathcal{U}}},{𝒱}_{2a}={\displaystyle \frac{\partial }{\partial \mathcal{N}}},{𝒱}_{3a}={\displaystyle \frac{\partial }{\partial \xi }},{𝒱}_{4a}=f_2\left(z\right){\displaystyle \frac{\partial }{\partial 𝒫}},{𝒱}_{5a}=-{\displaystyle \frac{5}{3}}\xi {\displaystyle \frac{\partial }{\partial 𝒫}}+\mathcal{U}{\displaystyle \frac{\partial }{\partial \mathcal{N}}},\hfill \\ & {𝒱}_{6a}=f_1^{\prime }\left(\mathcal{U}\right)\mathcal{N}{\displaystyle \frac{\partial }{\partial 𝒫}}-{\displaystyle \frac{3}{5}}{f}_1\left(\mathcal{U}\right){\displaystyle \frac{\partial }{\partial \xi }},{𝒱}_{7a}=\left(-{\displaystyle \frac{1}{3}}\xi -{\displaystyle \frac{1}{2}}𝒫\right){\displaystyle \frac{\partial }{\partial 𝒫}},+\left(-{\displaystyle \frac{1}{2}}\xi +{\displaystyle \frac{1}{5}}\mathcal{U}\right){\displaystyle \frac{\partial }{\partial \xi }},\hfill \\ & {𝒱}_{8a}=\left(-{\displaystyle \frac{1}{3}}\xi +{\displaystyle \frac{1}{2}}𝒫\right){\displaystyle \frac{\partial }{\partial 𝒫}}+\left(-{\displaystyle \frac{1}{2}}\xi +{\displaystyle \frac{1}{5}}\mathcal{U}\right){\displaystyle \frac{\partial }{\partial \xi }}+\mathcal{N}{\displaystyle \frac{\partial }{\partial \mathcal{N}}}.\hfill \end{array}$$

(37)

For linear combination ${𝒱}_{2a}+{𝒱}_{3a}$, the characteristics equation can be expressed as follows:

$${\displaystyle \frac{d\xi }{1}}={\displaystyle \frac{d\mathcal{N}}{1}}={\displaystyle \frac{d\mathcal{U}}{0}}={\displaystyle \frac{d𝒫}{0}}.$$

(38)

The characteristics Equation (38) is solved to determine the reduced variables as follows:

$$𝒜=\xi -\mathcal{N},\mathcal{B}=\mathcal{U},𝒫=𝒮(𝒜,\mathcal{B}).$$

(39)

Here, $\mathcal{B}$ denotes an arbitrary constant, and the solution can be written as $𝒫=𝒮(𝒜,\mathcal{B})$. By inserting this function from Equation (39) into Equation (36), the reduced equation will be

$${𝒮}_{\mathcal{AAAA}}+6{𝒮}_{𝒜}{𝒮}_{\mathcal{AA}}+5{𝒮}_{\mathcal{AB}}=0.$$

(40)

Again, by applying the Lie symmetry transformation, the infinitesimal generators will be

$$\begin{array}{cc}\hfill & {𝒱}_{1b}={\displaystyle \frac{\partial }{\partial 𝒜}},{𝒱}_{2b}={\displaystyle \frac{\partial }{\partial \mathcal{B}}},{𝒱}_{5b}=-𝒮{\displaystyle \frac{\partial }{\partial 𝒮}}+𝒜{\displaystyle \frac{\partial }{\partial 𝒜}}+3\mathcal{B}{\displaystyle \frac{\partial }{\partial \mathcal{B}}},{𝒱}_{4b}=-{\displaystyle \frac{5}{6}}𝒜{\displaystyle \frac{\partial }{\partial 𝒮}}+\mathcal{B}{\displaystyle \frac{\partial }{\partial 𝒜}},\hfill \\ & {𝒱}_{3b}=f_1\left(\mathcal{B}\right){\displaystyle \frac{\partial }{\partial 𝒮}}.\hfill \end{array}$$

(41)

For a linear combination of ${𝒱}_{1b}+{𝒱}_{2b}$, the characteristics equation can be expressed as

$${\displaystyle \frac{d𝒜}{1}}={\displaystyle \frac{d\mathcal{B}}{1}}={\displaystyle \frac{d𝒮}{0}}.$$

(42)

The characteristic Equation (42) is solved to determine the reduced variables as follows:

$$c=𝒜-\mathcal{B},𝒮=𝒟\left(\mathbf{c}\right).$$

(43)

Inserting this function from Equation (43) into Equation (40) means that the reduced equation will be

$${𝒟}^{\left(4\right)}\left(\mathbf{c}\right)+6{𝒟}^{\prime }\left(\mathbf{c}\right){𝒟}^{″}\left(\mathbf{c}\right)+5{𝒟}^{″}\left(\mathbf{c}\right)=0.$$

(44)

4.3. Reduction Through Translation Invariance: ${𝒱}_3+{𝒱}_4$

The associated characteristic equation for ${𝒱}_3+{𝒱}_4$ will be the following form:

$${\displaystyle \frac{dt}{1}}={\displaystyle \frac{dx}{0}}={\displaystyle \frac{dy}{1}}={\displaystyle \frac{dz}{0}}={\displaystyle \frac{d\mathcal{Q}}{0}}.$$

(45)

By solving the characteristic Equation (45) we get

$$\xi =y-t,x=\mathcal{M},z=\mathcal{U},\mathcal{Q}=𝒫(\mathcal{M},\xi ,\mathcal{U})$$

(46)

where $\mathcal{M}$, and $\mathcal{U}$ are arbitrary constants. Then, the solution can be expressed as $\mathcal{Q}=𝒫(\mathcal{M},\xi ,\mathcal{U})$. Inserting this function from Equation (46) into Equation (2), the E-JME reduces to the following form:

$${𝒫}_{\mathcal{MMM}\xi }+3{𝒫}_{\mathcal{MM}}{𝒫}_{\xi }+3{𝒫}_{\mathcal{M}}{𝒫}_{\mathcal{M}\xi }-2{𝒫}_{\mathcal{M}\xi }-2{𝒫}_{\xi \xi }-2{𝒫}_{\xi \mathcal{U}}-3{𝒫}_{\mathcal{MU}}=0.$$

(47)

A new set of Lie point generators emerges when Equation (47) undergoes the Lie symmetry transformation

$$\begin{array}{cc}\hfill & {𝒱}_{1a}={\displaystyle \frac{\partial }{\partial \mathcal{M}}},{𝒱}_{2a}={\displaystyle \frac{\partial }{\partial \mathcal{U}}},{𝒱}_{4a}=f_1\left(\mathcal{U}\right){\displaystyle \frac{\partial }{\partial 𝒫}},{𝒱}_{5a}=\left(-{\displaystyle \frac{2}{3}}\mathcal{M}-{\displaystyle \frac{2}{3}}\xi \right){\displaystyle \frac{\partial }{\partial 𝒫}}+\mathcal{U}{\displaystyle \frac{\partial }{\partial \mathcal{M}}},\hfill \\ & {𝒱}_{3a}={\displaystyle \frac{\partial }{\partial \xi }},{𝒱}_{6a}=\left(-𝒫-{\displaystyle \frac{4}{3}}\mathcal{M}\right){\displaystyle \frac{\partial }{\partial 𝒫}}+\mathcal{M}{\displaystyle \frac{\partial }{\partial \mathcal{M}}}+(\xi +2\mathcal{U}){\displaystyle \frac{\partial }{\partial \xi }}+3\mathcal{U}{\displaystyle \frac{\partial }{\partial \mathcal{U}}}.\hfill \end{array}$$

(48)

For linear combination ${𝒱}_{2b}+{𝒱}_{3b}$, the characteristics equation can be expressed as follows:

$${\displaystyle \frac{d\mathcal{M}}{1}}={\displaystyle \frac{d\xi }{0}}={\displaystyle \frac{d\mathcal{U}}{1}}={\displaystyle \frac{d𝒫}{0}}.$$

(49)

The characteristic Equation (49) is solved to determine the reduced variables as follows:

$$𝒜=\mathcal{M}-\mathcal{U},\xi =\mathcal{B},𝒫=𝒮(𝒜,\mathcal{B}).$$

(50)

Here, $\mathcal{B}$ denotes an arbitrary constant, and the solution can be written as $𝒫=𝒮(𝒜,\mathcal{B})$. By inserting this function from Equation (50) into Equation (47), the reduced equation will be

$${𝒮}_{\mathcal{AAAB}}+3{𝒮}_{\mathcal{AA}}{𝒮}_{\mathcal{B}}+3{𝒮}_{𝒜}{𝒮}_{\mathcal{AB}}-2{𝒮}_{\mathcal{BB}}+3{𝒮}_{\mathcal{AA}}=0.$$

(51)

Again, by applying the Lie symmetry transformation, the infinitesimal generators will be

$$\begin{array}{cc}\hfill & {𝒱}_{1b}={\displaystyle \frac{\partial }{\partial 𝒮}},{𝒱}_{2b}={\displaystyle \frac{\partial }{\partial \mathcal{B}}},{𝒱}_{3b}={\displaystyle \frac{\partial }{\partial 𝒜}},{𝒱}_{4b}=(𝒮-4\mathcal{B}){\displaystyle \frac{\partial }{\partial 𝒮}}-𝒜{\displaystyle \frac{\partial }{\partial 𝒜}}-3\mathcal{B}{\displaystyle \frac{\partial }{\partial \mathcal{B}}}.\hfill \end{array}$$

(52)

For a linear combination of ${𝒱}_{2b}+{𝒱}_{3b}$, the characteristics equation can be expressed as follows:

$${\displaystyle \frac{d𝒜}{1}}={\displaystyle \frac{d\mathcal{B}}{1}}={\displaystyle \frac{d𝒮}{0}}.$$

(53)

The characteristic Equation (53) is solved to determine the reduced variables as follows:

$$c=𝒜-\mathcal{B},𝒮=𝒟\left(\mathbf{c}\right).$$

(54)

Inserting this function from Equation (54) into Equation (51) means that the reduced equation will be

$${𝒟}^{\left(4\right)}\left(\mathbf{c}\right)-6{𝒟}^{\prime }\left(\mathbf{c}\right){𝒟}^{″}\left(\mathbf{c}\right)-{𝒟}^{″}\left(\mathbf{c}\right)=0.$$

(55)

4.4. Reduction Through Translation Invariance: ${𝒱}_2+{𝒱}_3$

The associated characteristic equation for ${𝒱}_3+{𝒱}_8$ will be the following form:

$${\displaystyle \frac{dt}{1}}={\displaystyle \frac{dx}{0}}={\displaystyle \frac{dy}{0}}={\displaystyle \frac{dz}{1}}={\displaystyle \frac{d\mathcal{Q}}{0}}.$$

(56)

By solving the characteristic Equation (56) we get:

$$\xi =z-t,x=\mathcal{M},y=\mathcal{N},\mathcal{Q}=𝒫(\mathcal{M},\mathcal{N},\xi )$$

(57)

where $\mathcal{M}$, and $\mathcal{N}$ are arbitrary constants. Then, the solution can be expressed as $\mathcal{Q}=𝒫(\mathcal{M},\mathcal{N},\xi )$.

Inserting this function from Equation (57) into Equation (2) ensures that the E-JME reduces to the following form:

$${𝒫}_{\mathcal{MMMN}}+3{𝒫}_{\mathcal{MM}}{𝒫}_{\mathcal{N}}+3{𝒫}_{\mathcal{M}}{𝒫}_{\mathcal{MN}}-5{𝒫}_{\mathcal{M}\xi }-2{𝒫}_{\mathcal{N}\xi }+2{𝒫}_{\xi \xi }=0.$$

(58)

A new set of Lie point generators emerges when Equation (58) undergoes the Lie symmetry transformation

$$\begin{array}{cc}\hfill & {𝒱}_{1a}= {\displaystyle \frac{\partial }{\partial 𝒫}},{𝒱}_{2a}={\displaystyle \frac{\partial }{\partial \mathcal{N}}},{𝒱}_{3a}={\displaystyle \frac{\partial }{\partial \xi }},{𝒱}_{4a}={\displaystyle \frac{\partial }{\partial \mathcal{M}}},{𝒱}_{5a}=\xi {\displaystyle \frac{\partial }{\partial 𝒫}},\hfill \\ & {𝒱}_{6a}=\left(\mathcal{N}-{\displaystyle \frac{6}{25}}𝒫+{\displaystyle \frac{2}{5}}\mathcal{M}\right){\displaystyle \frac{\partial }{\partial \mathcal{M}}}+\left(-{\displaystyle \frac{3}{5}}\xi +{\displaystyle \frac{6}{25}}\mathcal{M}\right){\displaystyle \frac{\partial }{\partial \mathcal{M}}}+{\displaystyle \frac{18}{25}}\mathcal{N}{\displaystyle \frac{\partial }{\partial \mathcal{N}}}+{\displaystyle \frac{18}{25}}\xi {\displaystyle \frac{\partial }{\partial \xi }}.\hfill \end{array}$$

(59)

For linear combination ${𝒱}_{2a}+{𝒱}_{3a}$, the characteristics equation can be expressed as follows:

$${\displaystyle \frac{d\mathcal{M}}{1}}={\displaystyle \frac{d\mathcal{N}}{1}}={\displaystyle \frac{d\xi }{0}}={\displaystyle \frac{d𝒫}{0}}.$$

(60)

The characteristic Equation (60) is solved to determine the reduced variables as follows:

$$𝒜=\mathcal{M}-\mathcal{N},\xi =\mathcal{B},𝒫=𝒮(𝒜,\mathcal{B}).$$

(61)

Here, $\mathcal{B}$ denotes an arbitrary constant, and the solution can be written as $𝒫=𝒮(𝒜,\mathcal{B})$. Inserting this function from Equation (61) into Equation (58) means that the reduced equation will be as follows:

$${𝒮}_{\mathcal{AAAA}}+6{𝒮}_{𝒜}{𝒮}_{\mathcal{AA}}+3{𝒮}_{\mathcal{AB}}-2{𝒮}_{BB}=0.$$

(62)

Again, by applying the Lie symmetry transformation, the infinitesimal generators will be as follows:

$$\begin{array}{cc}\hfill & {𝒱}_{1b}={\displaystyle \frac{\partial }{\partial 𝒮}},{𝒱}_{2b}={\displaystyle \frac{\partial }{\partial \mathcal{B}}},{𝒱}_{3b}={\displaystyle \frac{\partial }{\partial 𝒜}},{𝒱}_{5b}=\left(𝒜+{\displaystyle \frac{8}{3}}𝒮\right){\displaystyle \frac{\partial }{\partial 𝒮}}+\left(2\mathcal{B}-{\displaystyle \frac{8}{3}}𝒜\right){\displaystyle \frac{\partial }{\partial 𝒜}}-{\displaystyle \frac{16}{3}}\mathcal{B}{\displaystyle \frac{\partial }{\partial \mathcal{B}}},\hfill \\ & {𝒱}_{4b}=\mathcal{B}{\displaystyle \frac{\partial }{\partial 𝒮}}.\hfill \end{array}$$

(63)

For a linear combination of ${𝒱}_{2b}+{𝒱}_{3b}$, the characteristic equation can be expressed as follows:

$${\displaystyle \frac{d𝒜}{1}}={\displaystyle \frac{d\mathcal{B}}{1}}={\displaystyle \frac{d𝒮}{0}}.$$

(64)

The characteristic Equation (64) is solved to determine the reduced variables as follows:

$$c=𝒜-\mathcal{B},𝒮=𝒟\left(\mathbf{c}\right).$$

(65)

Inserting this function from Equation (65) into Equation (51) means that the reduced equation will be

$${𝒟}^{\left(4\right)}\left(\mathbf{c}\right)+6{𝒟}^{\prime }\left(\mathbf{c}\right){𝒟}^{″}\left(\mathbf{c}\right)-5{𝒟}^{″}\left(\mathbf{c}\right)=0.$$

(66)

4.5. Reduction Through Translation Invariance: ${𝒱}_8+{𝒱}_4$

The associated characteristic equation for ${𝒱}_8+{𝒱}_4$ will be the following form:

$${\displaystyle \frac{dt}{0}}={\displaystyle \frac{dx}{1}}={\displaystyle \frac{dy}{1}}={\displaystyle \frac{dz}{1}}={\displaystyle \frac{d\mathcal{Q}}{0}}.$$

(67)

By solving the characteristic Equation (67) we get

$$\xi =x-y,z=\mathcal{U},t=\mathcal{R},\mathcal{Q}=𝒫(\xi ,\mathcal{U},\mathcal{R})$$

(68)

where $\mathcal{U}$, and $\mathcal{R}$ are arbitrary constant. Then the solution can be expressed as $\mathcal{Q}=𝒫(\xi ,\mathcal{U},\mathcal{R})$. Inserting this function from Equation (68) into Equation (2), the E-JME reduces to the following form:

$${𝒫}_{\xi \xi \xi \xi }+6{𝒫}_{\xi }{𝒫}_{\xi \xi }+3{𝒫}_{\xi \mathcal{U}}-2{𝒫}_{\mathcal{UR}}=0.$$

(69)

A new set of Lie point generators emerges when Equation (69) undergoes the Lie symmetry transformation

$$\begin{array}{cc}\hfill & {𝒱}_{1a}={\displaystyle \frac{\partial }{\partial \xi }},{𝒱}_{2a}={\displaystyle \frac{\partial }{\partial \mathcal{R}}},{𝒱}_{3a}={\displaystyle \frac{\partial }{\partial \mathcal{U}}},{𝒱}_{4a}=f_3\left(\mathcal{R}\right){\displaystyle \frac{\partial }{\partial 𝒫}},{𝒱}_{5a}=f_4\left(\mathcal{U}\right){\displaystyle \frac{\partial }{\partial 𝒫}},\hfill \\ & {𝒱}_{6a}=-{\displaystyle \frac{2}{3}}\mathcal{R}{\displaystyle \frac{\partial }{\partial \mathcal{R}}}+\mathcal{R}{\displaystyle \frac{\partial }{\partial \xi }}+{\displaystyle \frac{2}{3}}\mathcal{U}{\displaystyle \frac{\partial }{\partial \mathcal{U}}},{𝒱}_{7a}=-\mathcal{R}{\displaystyle \frac{\partial }{\partial \mathcal{R}}}+𝒫{\displaystyle \frac{\partial }{\partial 𝒫}}-\xi {\displaystyle \frac{\partial }{\partial \xi }}-3\mathcal{U}{\displaystyle \frac{\partial }{\partial \mathcal{U}}}.\hfill \end{array}$$

(70)

For linear combination ${𝒱}_{2a}+{𝒱}_{3a}$, the characteristic equation can be expressed as follows:

$${\displaystyle \frac{d\mathcal{U}}{1}}={\displaystyle \frac{d\mathcal{R}}{1}}={\displaystyle \frac{d\xi }{0}}={\displaystyle \frac{d𝒫}{0}}.$$

(71)

The characteristic Equation (71) is solved to determine the reduced variables as follows:

$$\mathcal{B}=\mathcal{R}-\mathcal{U},\xi =𝒜,𝒫=𝒮(𝒜,\mathcal{B}).$$

(72)

Here, $\mathcal{B}$ denotes an arbitrary constant, and the solution can be written as $𝒫=𝒮(𝒜,\mathcal{B})$. Inserting this function from Equation (72) into Equation (58) means that the reduced equation will be

$${𝒮}_{\mathcal{AAAA}}+6{𝒮}_{𝒜}{𝒮}_{\mathcal{AA}}+3{𝒮}_{\mathcal{AB}}-2{𝒮}_{\mathcal{BB}}=0.$$

(73)

Again, by applying the Lie symmetry transformation, the infinitesimal generators will be

$$\begin{array}{cc}\hfill & {𝒱}_{1b}={\displaystyle \frac{\partial }{\partial 𝒮}},{𝒱}_{2b}={\displaystyle \frac{\partial }{\partial \mathcal{B}}},{𝒱}_{3b}={\displaystyle \frac{\partial }{\partial 𝒜}},{𝒱}_{5b}=\left(𝒜+{\displaystyle \frac{8}{3}}𝒮\right){\displaystyle \frac{\partial }{\partial 𝒮}}+\left(2\mathcal{B}-{\displaystyle \frac{8}{3}}𝒜\right){\displaystyle \frac{\partial }{\partial 𝒜}}-{\displaystyle \frac{16}{3}}\mathcal{B}{\displaystyle \frac{\partial }{\partial \mathcal{B}}},\hfill \\ & {𝒱}_{4b}=\mathcal{B}{\displaystyle \frac{\partial }{\partial 𝒮}}.\hfill \end{array}$$

(74)

For a linear combination of ${𝒱}_{2b}+{𝒱}_{3b}$, the characteristic equation can be expressed as follows:

$${\displaystyle \frac{d𝒜}{1}}={\displaystyle \frac{d\mathcal{B}}{1}}={\displaystyle \frac{d𝒮}{0}}.$$

(75)

The characteristic Equation (75) is solved to determine the reduced variables as follows:

$$c=𝒜-\mathcal{B},𝒮=𝒟\left(\mathbf{c}\right).$$

(76)

Inserting this function from Equation (76) into Equation (51) means that the reduced equation will be

$${𝒟}^{\left(4\right)}\left(\mathbf{c}\right)+6{𝒟}^{\prime }\left(\mathbf{c}\right){𝒟}^{″}\left(\mathbf{c}\right)-5{𝒟}^{″}\left(\mathbf{c}\right)=0.$$

(77)

4.6. Reduction Through Translation Invariance: ${𝒱}_3+\nu {𝒱}_8+\omega {𝒱}_4+k{𝒱}_2$

Now, by considering the vector field ${𝒱}_3+\nu {𝒱}_8+\omega {𝒱}_4+k{𝒱}_2$, the corresponding characteristics equation will be

$${\displaystyle \frac{dx}{\nu }}={\displaystyle \frac{dy}{\omega }}={\displaystyle \frac{dz}{k}}={\displaystyle \frac{dt}{1}}={\displaystyle \frac{d\mathcal{Q}}{0}}.$$

(78)

The solution to Equation (78) leads to the derivation of a set of similarity variables:

$$\varphi =x-\nu t,\psi =y-\omega t,\chi =z-kt,\mathcal{Q}(t,x,y,z)=W(\varphi ,\psi ,\chi ).$$

(79)

where the similarity variables designated by $\varphi ,\psi ,\chi$ are the independent variables and real constants. $W(\varphi ,\psi ,\chi )$ is a dependent variable. After putting Equation (79) into Equation (2), the resultant conclusion might be regarded as a decrease.

$$\begin{array}{cc}\hfill & \left(-2\nu -2\omega +3W_{\varphi }\right)W_{\psi ,\varphi }+\left(-2k-2\omega -3\right)W_{\chi ,\psi }+\left(-2\nu +3W_{\psi }\right)W_{\varphi ,\varphi }+\left(-2k-2\nu \right)W_{\chi ,\varphi }\hfill \\ & -2W_{\chi ,\chi }k-2W_{\psi ,\psi }\omega +W_{\psi ,\varphi ,\varphi ,\varphi }=0.\hfill \end{array}$$

(80)

Again, by applying the Lie symmetry transformation, the infinitesimal generators of Equation (80) will be

$${𝒱}_{1a}={\displaystyle \frac{\partial }{\partial \varphi }},{𝒱}_{2a}={\displaystyle \frac{\partial }{\partial \psi }},{𝒱}_{3a}={\displaystyle \frac{\partial }{\partial \chi }}.$$

(81)

Consider the vector as ${𝒱}_{1a}+{𝒱}_{2a}+\sigma {𝒱}_{3a}$. Then, the Lagrange system will be

$${\displaystyle \frac{d\varphi }{1}}={\displaystyle \frac{d\psi }{1}}={\displaystyle \frac{d\chi }{\sigma }}={\displaystyle \frac{dW}{0}}.$$

(82)

The similarity variables for Equation (80) are

$${\delta }_1=\sigma \varphi -\chi ,{\delta }_2=\sigma \psi -\chi ,W(\varphi ,\psi ,\chi )=Z({\delta }_1,{\delta }_2).$$

(83)

Here, $\sigma$ is the real constant and by putting Equation (83) in Equation (80)

$$\begin{array}{cc}\hfill & \left(3{\sigma }^3{Z}_{{\delta }_1}+\left(-2\nu -2\omega \right){\sigma }^2+\left(4k+2\nu +2\omega +3\right)\sigma -4k\right)Z_{{\delta }_1,{\delta }_2}+Z_{{\delta }_1,{\delta }_1,{\delta }_1,{\delta }_2}{\sigma }^4+\hfill \\ & \left(3{\sigma }^3{Z}_{{\delta }_2}+2\left(\sigma -1\right)\left(-\nu \sigma +k\right)\right)Z_{{\delta }_1,{\delta }_1}+\left(-2\omega {\sigma }^2+\left(2k+2\omega +3\right)\sigma -2k\right)Z_{{\delta }_2,{\delta }_2}=0.\hfill \end{array}$$

(84)

The infinitesimal generators of Equation (84) are

$$Y_1={\displaystyle \frac{\partial }{\partial {\delta }_1}},{𝒴}_2={\displaystyle \frac{\partial }{\partial {\delta }_2}}.$$

(85)

Consider the vector as $Y_1+\lambda {𝒴}_2$. Then, the Lagrange system will be

$${\displaystyle \frac{d{\delta }_1}{1}}={\displaystyle \frac{d{\delta }_2}{\lambda }}={\displaystyle \frac{dZ}{0}}.$$

(86)

The similarity variables for Equation (84) are

$$\xi =\lambda {\delta }_1-{\delta }_2,W({\delta }_1,{\delta }_2)=S\left(\xi \right).$$

(87)

where $\lambda$ is the real constant and by putting Equation (87) in Equation (84),

$$S^{\left(4\right)}{\lambda }^3{\sigma }^4-2S^{″}\left(-3{\sigma }^3{\lambda }^2{S}^{\prime }+\left(\lambda -1\right)\left(\left(-\lambda \nu +\omega \right){\sigma }^2+\left(\left(k+\nu \right)\lambda -k-\omega -{\displaystyle \frac{3}{2}}\right)\sigma -k\left(\lambda -1\right)\right)\right).$$

(88)

Integrating the above equation w.r.t to $\xi$ and setting $S^{\prime }=\Xi$.

$${\lambda }^3{\sigma }^4{\Xi }^{″}-2\Xi \left(-{\displaystyle \frac{3{\lambda }^2{\sigma }^3{\Xi }^{\prime }}{2}}+(\lambda -1)\left((-\lambda \nu +\omega ){\sigma }^2+\left((k+\nu )\lambda -k-\omega -{\displaystyle \frac{3}{2}}\right)\sigma -k(\lambda -1)\right)\right).$$

(89)

5. Multivariate Generalized Exponential Rational Integral Function Method

In this section, we employed the Multivariate Generalized Exponential Rational Integral Function (MGERIF) Method [66], a recently developed and highly effective tool for nonlinear partial differential equations (NLPDEs). This approach is an extension of the generalized exponential rational function (GERFM) approach [67,68], where integral operators are systematically embedded into the solution framework. The incorporation of such operators significantly enhanced its effectiveness, enabling it to construct the solution structures containing rational terms such as $csc$, $sec{h}^2$, and $csch$, which cannot be derived from the purely algebraic framework of the GERFM. The main advantage of MGERIF lies in its versatility for handling exhibiting both dispersive and dissipative characteristics. It established a unified framework capable of generating diverse solution families, including singular solitons, breather-type states, and lump-type interaction solutions. The classical GERFM emerges as a limited case in the absence of integral contributions, whereas the MGERIF yields a broader spectrum of exact solutions by combining polynomial, trigonometric, hyperbolic, exponential, and rational structures. This extended capability makes it a powerful tool in treating advanced nonlinear models, including Equation (2).

The implementation of the MGERIF follows a systematic sequence of steps:

• Step 01: The solution of Equation (89) is obtained through the MGERIF approach as outlined below.

  $$\mathsf{\Xi }\left(\xi \right)=X_0+\sum _{j=1}^N{Y}_j{\left(\underset{j}{\underbrace{\int \dots \int }}F\left(\xi \right)d\xi d\xi \dots d\xi \right)}^j+\sum _{j=1}^N{Z}_j{\left(\underset{j}{\underbrace{\int \dots \int }}F\left(\xi \right)d\xi d\xi \dots d\xi \right)}^{-j}.$$

  (90)

  within this formulation, $X_0$, $Z_j$, $Y_j$ (with j = 1, 2, …, N) represents arbitrary constants, whereas the function $F\left(\xi \right)$ is introduced as

  $$F\left(\xi \right)={\displaystyle \frac{r_1{e}^{s_1\xi }+r_2{e}^{s_2\xi }}{r_3{e}^{s_3\xi }+r_4{e}^{s_4\xi }}}.$$

  (91)

  The coefficients $r_i$ and exponents $s_i$ (i = 1, 2, 3, 4) act as free parameters in the solutions. By assigning specific values to these parameters, Equation (91) can be expressed in several known functional forms, as summarized in

  Table 3. Special cases of $F\left(\xi \right)$ under specific parameter values.

  $[{\mathit{r}}_1,{\mathit{r}}_2,{\mathit{r}}_3,{\mathit{r}}_3]$	$[{\mathit{s}}_1,{\mathit{s}}_2,{\mathit{s}}_3,{\mathit{s}}_3]$	$\mathit{F}\left(\mathit{\xi }\right)$
  $[1,-1,i,i]$	$[i,-i,0,0]$	$sin\left(\xi \right)$
  $[1,1,1,1]$	$[i,-i,0,0]$	$cos\left(\xi \right)$
  $[2,2,2,2]$	$[{\displaystyle \frac{2}{5}},{\displaystyle \frac{2}{5}},0,0]$	$e^{{\displaystyle \frac{2\xi }{5}}}$
  $[i,i,i,i]$	$[1,-1,0,0]$	$cosh\left(\xi \right)$
  $[2i,-2i,4i,4i]$	$[{\displaystyle \frac{1}{2}},-{\displaystyle \frac{1}{2}},0,0]$	${\displaystyle \frac{1}{2}}sinh\left({\displaystyle \frac{\xi }{2}}\right)$

  .
• Step 02: According to the principle of homogeneous balance, the positive integer N is obtained by comparing the order of the highest derivative term with that of the nonlinear term in Equation (89).

  $$D\left[{\displaystyle \frac{d^p\mathsf{\Xi }\left(xi\right)}{d^p\mathsf{\Xi }\left(\xi \right)}}\right]=N+p,D\left[{\mathsf{\Xi }}^p{\left({\displaystyle \frac{d^p\mathsf{\Xi }\left(\xi \right)}{d^p\mathsf{\Xi }\left(\xi \right)}}\right)}^s\right]=qN+s(N+P).$$

  (92)
• Step 03: By inserting Equations (90) and (91) into Equation (89), a polynomial expression in terms of $e^{mj\xi }$ ($1\le j\le 4$) is obtained. Imposing the condition that the coefficients of identical powers vanish results in a system of nonlinear algebraic equations. The simultaneous resolution of this system, together with Equation (91), leads directly to the solutions of Equation (2).
• Step 04: Through symbolic reductions carried out in Mathematica (version 14.3), the precise values of the constants $X_0,Y_i,$ and $Z_i$ $(1\le i\le N)$ are obtained. Inserting these values into Equations (90) and (91) yields the explicit soliton solutions of Equation (2).

5.1. Solutions by MGERIF Method

Initially, the balancing principle gives N = 2. Substituting this value into Equation (90) allows us to move forward in solving Equation (89).

$$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_1\left(\int F\left(\xi \right)d\xi \right)+{\mathcal{Y}}_2{\left(\int \int F\left(\xi \right)d\xi d\xi \right)}^2+{\displaystyle \frac{{\mathcal{Z}}_1}{\int F\left(\xi \right)d\xi }}+{\displaystyle \frac{{\mathcal{Z}}_2}{{\left(\int \int F\left(\xi \right)d\xi d\xi \right)}^2}}.$$

(93)

A family of solutions to Equation (89) is obtained by substituting the constructed forms together with Equation (87), applying the MGERIF approach, and utilizing Mathematica for computation.

5.2. The Standard Sine Form

When the parameter values are chosen as $[r_1,r_2,r_3,r_3]=[1,-1,i,i]$ and $[s_1,s_2,s_3,s_3]=[i,-i,0,0]$, Equation (91) simplifies to the familiar sine expression.

$$F\left(\xi \right)=sin\left(\xi \right).$$

(94)

The substitution of Equation (94) into Equation (90) yields the following expression:

$$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_2{sin}^2\left(\xi \right)-{\mathcal{Y}}_{1}cos\left(\xi \right)+{\mathcal{Y}}_2{csc}^2\left(\xi \right)-{\mathcal{Z}}_{1}sec\left(\xi \right).$$

(95)

• Case 1.1:
  For the parameter selection ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2=0,{\mathcal{Z}}_1=0,{\mathcal{Z}}_2=0$, the outcome of Equation (89) is derived by substituting these values into Equation (95).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0-{\mathcal{Y}}_{1}cos\left(\xi \right).$$

  (96)
  Thus, combining the Equation (96) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_1(t,x,y,z)={\mathcal{X}}_0-{\displaystyle \frac{1}{2}}{\mathcal{Y}}_1\left(e^{-i\left(\lambda {\delta }_1-{\delta }_2\right)}+e^{i\left(\lambda {\delta }_1-{\delta }_2\right)}\right).$$

  (97)
• Case 1.2:
  For the parameter selection ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2=0$, the outcome of Equation (89) is derived by substituting these values into Equation (95).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_2{sin}^2\left(\xi \right)-{\mathcal{Y}}_{1}cos\left(\xi \right)-{\mathcal{Z}}_{1}sec\left(\xi \right).$$

  (98)
  Thus, combining the Equation (98) with Equation (87) allow the solution of Equation (2) to obtained.

  $$\begin{array}{cc}\hfill {\mathcal{Q}}_2(t,x,y,z)& ={\mathcal{X}}_0-{\displaystyle \frac{1}{4}}{\mathcal{Y}}_2{e}^{-2i\left(\lambda {\delta }_1-{\delta }_2\right)}{\left(-1+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}\right)}^2-{\displaystyle \frac{1}{2}}{\mathcal{Y}}_1\left(e^{-i\left(\lambda {\delta }_1-{\delta }_2\right)}+e^{i\left(\lambda {\delta }_1-{\delta }_2\right)}\right)-\hfill \\ & {\displaystyle \frac{2{\mathcal{Z}}_1{e}^{i\left(\lambda {\delta }_1-{\delta }_2\right)}}{1+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}}}.\hfill \end{array}$$

  (99)
• Case 1.3:
  For the parameter selection ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2\ne 0$, the outcome of Equation (89) is derived by substituting these values into Equation (95).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_2{sin}^2\left(\xi \right)-{\mathcal{Y}}_{1}cos\left(\xi \right)+{\mathcal{Z}}_2{csc}^2\left(\xi \right)-{\mathcal{Z}}_{1}sec\left(\xi \right).$$

  (100)
  Thus, combining the Equation (100) with Equation (87) allow the solution of Equation (2) to obtained.

  $$\begin{array}{cc}\hfill {\mathcal{Q}}_3(t,x,y,z)& ={\mathcal{X}}_0-{\displaystyle \frac{1}{4}}{\mathcal{Y}}_2{e}^{-2i(\lambda {\delta }_1-{\delta }_2)}{\left(-1+e^{2i(\lambda {\delta }_1-{\delta }_2)}\right)}^2-{\displaystyle \frac{1}{2}}{\mathcal{Y}}_1\left(e^{-i(\lambda {\delta }_1-{\delta }_2)}+e^{i(\lambda {\delta }_1-{\delta }_2)}\right)-\hfill \\ & {\displaystyle \frac{4{\mathcal{Z}}_2{e}^{2i(\lambda {\delta }_1-{\delta }_2)}}{{\left(-1+e^{2i(\lambda {\delta }_1-{\delta }_2)}\right)}^2}}-{\displaystyle \frac{2{\mathcal{Z}}_1{e}^{i(\lambda {\delta }_1-{\delta }_2)}}{1+e^{2i(\lambda {\delta }_1-{\delta }_2)}}}.\hfill \end{array}$$

  (101)
• Case 1.4:
  For the parameter selection ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1=0,{\mathcal{Z}}_2=0$, the outcome of Equation (89) is derived by substituting these values into Equation (95).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_2{sin}^2\left(\xi \right)-{\mathcal{Y}}_{1}cos\left(\xi \right).$$

  (102)
  Thus, combining the Equation (102) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_4(t,x,y,z)={\mathcal{X}}_0-{\displaystyle \frac{1}{4}}{e}^{-2i\xi }{\left(-1+e^{2i\xi }\right)}^2{\mathcal{Y}}_2-{\displaystyle \frac{1}{2}}\left(e^{-i\xi }+e^{i\xi }\right){\mathcal{Y}}_1.$$

  (103)

5.3. The Standard Cosine Form

When the parameter values are chosen as $[r_1,r_2,r_3,r_3]=[1,1,1,1]$ and $[s_1,s_2,s_3,s_3]=[i,-i,0,0]$, Equation (91) simplifies to the familiar Cosine expression.

$$F\left(\xi \right)=cos\left(\xi \right).$$

(104)

The substitution of Equation (104) into Equation (90) yields the following expression:

$$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}sin\left(\xi \right)+{\mathcal{Y}}_2{cos}^2\left(\xi \right)+{\mathcal{Z}}_{1}csc\left(\xi \right)+{\mathcal{Z}}_2{sec}^2\left(\xi \right).$$

(105)

• Case 1.1:
  For the parameter choice ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2=0,{\mathcal{Z}}_1=0,{\mathcal{Z}}_2=0$, the solution of Equation (89) follows by substituting these values into Equation (105).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}sin\left(\xi \right).$$

  (106)
  Thus, combining the Equation (106) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_5(t,x,y,z)={\mathcal{X}}_0-{\displaystyle \frac{1}{2}}i{\mathcal{Y}}_1{e}^{-i\left(\lambda {\delta }_1-{\delta }_2\right)}\left(-1+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}\right).$$

  (107)
• Case 1.2:
  For the parameter choice ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1=0,{\mathcal{Z}}_2\ne 0$, the solution of Equation (89) follows by substituting these values into Equation (105).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}sin\left(\xi \right)+{\mathcal{Y}}_2{cos}^2\left(\xi \right)+{\mathcal{Z}}_2{sec}^2\left(\xi \right).$$

  (108)
  Thus, combining the Equation (108) with Equation (87) allow the solution of Equation (2) to obtained.

  $$\begin{array}{cc}\hfill {\mathcal{Q}}_6(t,x,y,z)& ={\mathcal{X}}_0-{\displaystyle \frac{1}{2}}i{\mathcal{Y}}_1{e}^{-i\left(\lambda {\delta }_1-{\delta }_2\right)}\left(-1+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}\right)+{\displaystyle \frac{1}{4}}{\mathcal{Y}}_2\left(e^{-2i\left(\lambda {\delta }_1-{\delta }_2\right)}+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}+2\right)\hfill \\ & +{\displaystyle \frac{4{\mathcal{Z}}_2{e}^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}}{{\left(1+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}\right)}^2}}.\hfill \end{array}$$

  (109)
• Case 1.3:
  For the parameter choice ${\mathcal{X}}_0={\displaystyle \frac{3-3\lambda +4{\lambda }^3}{6{\lambda }^2}},k={\displaystyle \frac{1}{2}}\left(-3+3\lambda +4{\lambda }^3\right),\sigma =1,{\mathcal{Y}}_1\ne 0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2=-2\lambda$, the solution of Equation (89) follows by substituting these values into Equation (105).

  $$\mathsf{\Xi }\left(\xi \right)={\displaystyle \frac{4{\lambda }^3-3\lambda +3}{6{\lambda }^2}}-2\lambda {sec}^2\left(\xi \right).$$

  (110)
  Thus, combining the Equation (110) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_7(t,x,y,z)={\displaystyle \frac{4{\lambda }^3-3\lambda +3}{6{\lambda }^2}}-{\displaystyle \frac{8\lambda e^{2i\left({\delta }_2-{\delta }_1\lambda \right)}}{{\left(1+e^{2i\left({\delta }_2-{\delta }_1\lambda \right)}\right)}^2}}.$$

  (111)
• Case 1.4:
  For the parameter choice ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2\ne 0$, the solution of Equation (89) follows by substituting these values into Equation (105).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+sin\left(\xi \right){\mathcal{Y}}_1+{cos}^2\left(\xi \right){\mathcal{Y}}_2+csc\left(\xi \right){\mathcal{Z}}_1+{sec}^2\left(\xi \right){\mathcal{Z}}_2.$$

  (112)
  Thus, combining the Equation (112) with Equation (87) allow the solution of Equation (2) to obtained.

  $$\begin{array}{cc}\hfill {\mathcal{Q}}_8(t,x,y,z)& ={\mathcal{X}}_0-{\displaystyle \frac{1}{2}}i{\mathcal{Y}}_1{e}^{-i\left(\lambda {\delta }_1-{\delta }_2\right)}\left(-1+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}\right)+{\displaystyle \frac{1}{4}}{\mathcal{Y}}_2\left(e^{-2i\left(\lambda {\delta }_1-{\delta }_2\right)}+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}+2\right)\hfill \\ & +{\displaystyle \frac{2i{\mathcal{Z}}_1{e}^{i\left(\lambda {\delta }_1-{\delta }_2\right)}}{-1+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}}}+{\displaystyle \frac{4{\mathcal{Z}}_2{e}^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}}{{\left(1+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}\right)}^2}}.\hfill \end{array}$$

  (113)

5.4. The Standard Exponential Form

When the parameter values are chosen as $[r_1,r_2,r_3,r_3]=[2,2,2,2]$ and $[s_1,s_2,s_3,s_3]=[2/5,2/5,0,0]$, Equation (91) simplifies to the familiar exponential expression.

$$F\left(\xi \right)=e^{{\displaystyle \frac{2\xi }{5}}}.$$

(114)

The substitution of Equation (114) into Equation (90) yields the following expression:

$$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\displaystyle \frac{5}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{2\xi }{5}}}+{\displaystyle \frac{625}{16}}{\mathcal{Y}}_2{e}^{{\displaystyle \frac{4\xi }{5}}}+{\displaystyle \frac{2}{5}}{\mathcal{Z}}_1{e}^{-{\displaystyle \frac{2\xi }{5}}}+{\displaystyle \frac{16}{625}}{\mathcal{Z}}_2{e}^{-{\displaystyle \frac{4\xi }{5}}}2.$$

(115)

• Case 1.1:
  With the parameter assignment ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2=0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2=0$, substituting into Equation (115) provides the corresponding form of Equation (89).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\displaystyle \frac{5}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{2\xi }{5}}}+{\displaystyle \frac{2}{5}}{\mathcal{Z}}_1{e}^{-{\displaystyle \frac{2\xi }{5}}}.$$

  (116)
  Thus, combining the Equation (116) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_9(t,x,y,z)={\mathcal{X}}_0+{\displaystyle \frac{5}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{2}{5}}\left(\lambda {\delta }_1-{\delta }_2\right)}+{\displaystyle \frac{2}{5}}{\mathcal{Z}}_1{e}^{{\displaystyle \frac{-2}{5}}\left(\lambda {\delta }_1-{\delta }_2\right)}.$$

  (117)
• Case 1.2:
  With the parameter assignment ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2\ne 0$, substituting into Equation (115) provides the corresponding form of Equation (89).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\displaystyle \frac{5}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{2\xi }{5}}}+{\displaystyle \frac{625}{16}}{\mathcal{Y}}_2{e}^{{\displaystyle \frac{4\xi }{5}}}+{\displaystyle \frac{2}{5}}{\mathcal{Z}}_1{e}^{-{\displaystyle \frac{2\xi }{5}}}+{\displaystyle \frac{16}{625}}{\mathcal{Z}}_2{e}^{-{\displaystyle \frac{4\xi }{5}}}.$$

  (118)
  Thus, combining the Equation (118) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_{10}(t,x,y,z)={\mathcal{X}}_0+{\displaystyle \frac{5}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{2}{5}}\left(\lambda {\delta }_1-{\delta }_2\right)}+{\displaystyle \frac{625}{16}}{\mathcal{Y}}_2{e}^{{\displaystyle \frac{4}{5}}\left(\lambda {\delta }_1-{\delta }_2\right)}+{\displaystyle \frac{2}{5}}{\mathcal{Z}}_1{e}^{-{\displaystyle \frac{2}{5}}\left(\lambda {\delta }_1-{\delta }_2\right)}+{\displaystyle \frac{16}{625}}{\mathcal{Z}}_2{e}^{-{\displaystyle \frac{4}{5}}\left(\lambda {\delta }_1-{\delta }_2\right)}.$$

  (119)
• Case 1.3:
  With the parameter assignment ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2=0$, substituting into Equation (115) provides the corresponding form of Equation (89).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\displaystyle \frac{5}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{2\xi }{5}}}+{\displaystyle \frac{625}{16}}{\mathcal{Y}}_2{e}^{{\displaystyle \frac{4\xi }{5}}}+{\displaystyle \frac{2}{5}}{\mathcal{Z}}_1{e}^{-{\displaystyle \frac{2\xi }{5}}}.$$

  (120)
  Thus, combining the Equation (120) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_{11}(t,x,y,z)={\mathcal{X}}_0+{\displaystyle \frac{5}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{2}{5}}\left(\lambda {\delta }_1-{\delta }_2\right)}+{\displaystyle \frac{625}{16}}{\mathcal{Y}}_2{e}^{{\displaystyle \frac{4}{5}}\left(\lambda {\delta }_1-{\delta }_2\right)}+{\displaystyle \frac{2}{5}}{\mathcal{Z}}_1{e}^{{\displaystyle \frac{1}{5}}(-2)\left(\lambda {\delta }_1-{\delta }_2\right)}.$$

  (121)
• Case 1.4:
  With the parameter assignment ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2\ne 0$, substituting into Equation (115) provides the corresponding form of Equation (89).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\displaystyle \frac{5}{2}}{e}^{{\displaystyle \frac{2\xi }{5}}}{y}_1+{\displaystyle \frac{625}{16}}{e}^{{\displaystyle \frac{4\xi }{5}}}{y}_2.$$

  (122)
  Thus, combining the Equation (122) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_{12}(t,x,y,z)={\mathcal{X}}_0+{\displaystyle \frac{5}{2}}{y}_1{e}^{{\displaystyle \frac{2}{5}}\left({\delta }_2-{\delta }_1\lambda \right)}+{\displaystyle \frac{625}{16}}{y}_2{e}^{{\displaystyle \frac{4}{5}}\left({\delta }_2-{\delta }_1\lambda \right)}.$$

  (123)

5.5. The Standard Cosine Hyperbolic Form

When the parameter values are chosen as $[r_1,r_2,r_3,r_3]=[i,i,i,i]$ and $[s_1,s_2,s_3,s_3]=[1,-1,0,0]$, Equation (91) simplifies to the familiar cosine hyperbolic expression.

$$F\left(\xi \right)=cosh\left(\xi \right).$$

(124)

The substitution of Equation (124) into Equation (90) yields the following expression:

$$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}sinh\left(\xi \right)+{\mathcal{Y}}_2{cosh}^2\left(\xi \right)+{\mathcal{Z}}_1\csc \mathrm{h}\left(\xi \right)+{\mathcal{Z}}_2{\sec \mathrm{h}}^2\left(\xi \right).$$

(125)

• Case 1.1:
  When the parameters are chosen as ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2=0,{\mathcal{Z}}_1=0,{\mathcal{Z}}_2=0$, the resulting form of Equation (89) can be derived from Equation (125).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}sinh\left(\xi \right).$$

  (126)
  Thus, combining the Equation (126) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_{13}(t,x,y,z)={\mathcal{X}}_0+{\displaystyle \frac{1}{2}}{\mathcal{Y}}_1{e}^{{\delta }_1\lambda -{\delta }_2}\left(e^{2\left(\lambda {\delta }_1-{\delta }_2\right)}-1\right).$$

  (127)
• Case 1.2:
  When the parameters are chosen as ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2=0$, the resulting form of Equation (89) can be derived from Equation (125).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}sinh\left(\xi \right)+{\mathcal{Y}}_2{cosh}^2\left(\xi \right)+{\mathcal{Z}}_1\csc \mathrm{h}\left(\xi \right).$$

  (128)
  Thus, combining the Equation (128) with Equation (87) allow the solution of Equation (2) to obtained.

  $$\begin{array}{cc}\hfill {\mathcal{Q}}_{14}(t,x,y,z)& ={\displaystyle \frac{1}{4}}\left(4{\mathcal{X}}_0+2{\mathcal{Y}}_1{e}^{{\delta }_1\lambda -{\delta }_2}\left(e^{2\left(\lambda {\delta }_1-{\delta }_2\right)}-1\right)+{\mathcal{Y}}_2{e}^{-2\left(\lambda {\delta }_1-{\delta }_2\right)}+{\mathcal{Y}}_2{e}^{2\left(\lambda {\delta }_1-{\delta }_2\right)}\right.\hfill \\ \hfill & +2{\mathcal{Y}}_2+\left.{\displaystyle \frac{8i{\mathcal{Z}}_1{e}^{i\left(\lambda {\delta }_1-{\delta }_2\right)}}{-1+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}}}\right).\hfill \end{array}$$

  (129)
• Case 1.3:
  When the parameters are chosen as ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2\ne 0$, the resulting form of Equation (89) can be derived from Equation (125).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}sinh\left(\xi \right)+{\mathcal{Y}}_2{cosh}^2\left(\xi \right)+{\mathcal{Z}}_1\csc \mathrm{h}\left(\xi \right)+{\mathcal{Z}}_2{\sec \mathrm{h}}^2\left(\xi \right).$$

  (130)
  Thus, combining the Equation (130) with Equation (87) allow the solution of Equation (2) to obtained.

  $$\begin{array}{cc}\hfill {\mathcal{Q}}_{15}(t,x,y,z)& ={\displaystyle \frac{1}{4}}\left(4{\mathcal{X}}_0+2{\mathcal{Y}}_1{e}^{{\delta }_1\lambda -{\delta }_2}\left(e^{2\left(\lambda {\delta }_1-{\delta }_2\right)}-1\right)+{\mathcal{Y}}_2{e}^{-2\left(\lambda {\delta }_1-{\delta }_2\right)}+{\mathcal{Y}}_2{e}^{2\left(\lambda {\delta }_1-{\delta }_2\right)}+2{\mathcal{Y}}_2\right.\hfill \\ \hfill & +\left.{\displaystyle \frac{8i{\mathcal{Z}}_1{e}^{i\left(\lambda {\delta }_1-{\delta }_2\right)}}{-1+e^{2i\left(\lambda {\delta }_1-{\delta }_2\right)}}}+{\displaystyle \frac{16{\mathcal{Z}}_2{e}^{2\left(\lambda {\delta }_1-{\delta }_2\right)}}{{\left(e^{2\left(\lambda {\delta }_1-{\delta }_2\right)}+1\right)}^2}}\right).\hfill \end{array}$$

  (131)
• Case 1.4:
  When the parameters are chosen as ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1=0,{\mathcal{Z}}_2=0$, the resulting form of Equation (89) can be derived from Equation (125).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}sinh\left(\xi \right)+{\mathcal{Y}}_2{cosh}^2\left(\xi \right).$$

  (132)
  Thus, combining the Equation (132) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_{16}(t,x,y,z)={\mathcal{X}}_0+{\displaystyle \frac{1}{4}}{e}^{-2\left(\lambda {\delta }_1-{\delta }_2\right)}\left({\mathcal{Y}}_2{\left(e^{2\left(\lambda {\delta }_1-{\delta }_2\right)}+1\right)}^2+2{\mathcal{Y}}_1{e}^{\lambda {\delta }_1-{\delta }_2}\left(e^{2\left(\lambda {\delta }_1-{\delta }_2\right)}-1\right)\right).$$

  (133)

5.6. The Standard Sine Hyperbolic Form

When the parameter values are chosen as $[r_1,r_2,r_3,r_3]=[2i,-2i,4i,4i]$ and $[s_1,s_2,s_3,s_3]=[1/2,-1/2,0,0]$, Equation (91) simplifies to the familiar sine hyperbolic expression.

$$F\left(\xi \right)={\displaystyle \frac{1}{2}}sinh\left({\displaystyle \frac{\xi }{2}}\right).$$

(134)

The substitution of Equation (134) into Equation (90) yields the following expression:

$$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}cosh\left({\displaystyle \frac{\xi }{2}}\right)+2{\mathcal{Y}}_2\left(cosh\left(\xi \right)-1\right)+{\displaystyle \frac{1}{4}}{\mathcal{Z}}_2{\csc \mathrm{h}}^2\left({\displaystyle \frac{\xi }{2}}\right)+{\mathcal{Z}}_1\sec \mathrm{h}\left({\displaystyle \frac{\xi }{2}}\right).$$

(135)

• Case 1.1:
  For the parameter configuration ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2=0,{\mathcal{Z}}_1=0,{\mathcal{Z}}_2=0$, substitution into Equation (135) gives the corresponding solution of Equation (89).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}cosh\left({\displaystyle \frac{\xi }{2}}\right).$$

  (136)
  Thus, combining the Equation (136) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_{17}(t,x,y,z)={\mathcal{X}}_0+{\displaystyle \frac{1}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{1}{2}}\left({\delta }_1\lambda -{\delta }_2\right)}\left(e^{\lambda {\delta }_1-{\delta }_2}+1\right).$$

  (137)
• Case 1.2:
  For the parameter configuration ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2=0$, substitution into Equation (135) gives the corresponding solution of Equation (89).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}cosh\left({\displaystyle \frac{\xi }{2}}\right)+2{\mathcal{Y}}_2\left(cosh\left(\xi \right)-1\right)+{\mathcal{Z}}_1\sec \mathrm{h}\left({\displaystyle \frac{\xi }{2}}\right).$$

  (138)
  Thus, combining the Equation (138) with Equation (87) allow the solution of Equation (2) to obtained.

  $$\begin{array}{cc}\hfill {\mathcal{Q}}_{18}(t,x,y,z)& ={\mathcal{X}}_0+{\displaystyle \frac{1}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{1}{2}}\left({\delta }_1\lambda -{\delta }_2\right)}\left(e^{\lambda {\delta }_1-{\delta }_2}+1\right)+{\mathcal{Y}}_2{e}^{{\delta }_1\lambda -{\delta }_2}+{\mathcal{Y}}_2{e}^{\lambda {\delta }_1-{\delta }_2}-2{\mathcal{Y}}_2+\hfill \\ & {\displaystyle \frac{2{\mathcal{Z}}_1{e}^{\frac{1}{2}i\left(\lambda {\delta }_1-{\delta }_2\right)}}{1+e^{i\left(\lambda {\delta }_1-{\delta }_2\right)}}}.\hfill \end{array}$$

  (139)
• Case 1.3:
  For the parameter configuration ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1\ne 0,{\mathcal{Z}}_2\ne 0$, substitution into Equation (135) gives the corresponding solution of Equation (89).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}cosh\left({\displaystyle \frac{\xi }{2}}\right)+2{\mathcal{Y}}_2\left(cosh\left(\xi \right)-1\right)+{\displaystyle \frac{1}{4}}{\mathcal{Z}}_2{\csc \mathrm{h}}^2\left({\displaystyle \frac{\xi }{2}}\right)+{\mathcal{Z}}_1\sec \mathrm{h}\left({\displaystyle \frac{\xi }{2}}\right).$$

  (140)
  Thus, combining the Equation (140) with Equation (87) allow the solution of Equation (2) to obtained.

  $$\begin{array}{cc}\hfill {\mathcal{Q}}_{19}(t,x,y,z)& ={\mathcal{X}}_0+{\displaystyle \frac{1}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{1}{2}}\left({\delta }_1\lambda -{\delta }_2\right)}\left(e^{\lambda {\delta }_1-{\delta }_2}+1\right)+{\mathcal{Y}}_2{e}^{{\delta }_1\lambda -{\delta }_2}+{\mathcal{Y}}_2{e}^{\lambda {\delta }_1-{\delta }_2}-2{\mathcal{Y}}_2+\hfill \\ & {\displaystyle \frac{2{\mathcal{Z}}_1{e}^{\frac{1}{2}i\left(\lambda {\delta }_1-{\delta }_2\right)}}{1+e^{i\left(\lambda {\delta }_1-{\delta }_2\right)}}}+{\displaystyle \frac{{\mathcal{Z}}_2{e}^{\lambda {\delta }_1-{\delta }_2}}{{\left(e^{\lambda {\delta }_1-{\delta }_2}-1\right)}^2}}.\hfill \end{array}$$

  (141)
• Case 1.4:
  For the parameter configuration ${\mathcal{X}}_0\ne 0,k=0,{\mathcal{Y}}_1\ne 0,\sigma =0,{\mathcal{Y}}_2\ne 0,{\mathcal{Z}}_1=0,{\mathcal{Z}}_2=0$, substitution into Equation (135) gives the corresponding solution of Equation (89).

  $$\mathsf{\Xi }\left(\xi \right)={\mathcal{X}}_0+{\mathcal{Y}}_{1}cosh\left({\displaystyle \frac{\xi }{2}}\right)+2{\mathcal{Y}}_2\left(cosh\left(\xi \right)-1\right).$$

  (142)
  Thus, combining the Equation (142) with Equation (87) allow the solution of Equation (2) to obtained.

  $${\mathcal{Q}}_{20}(t,x,y,z)={\mathcal{X}}_0+{\mathcal{Y}}_2{e}^{{\delta }_1\lambda -{\delta }_2}{\left(e^{\lambda {\delta }_1-{\delta }_2}-1\right)}^2+{\displaystyle \frac{1}{2}}{\mathcal{Y}}_1{e}^{{\displaystyle \frac{1}{2}}\left({\delta }_1\lambda -{\delta }_2\right)}\left(e^{\lambda {\delta }_1-{\delta }_2}+1\right).$$

  (143)

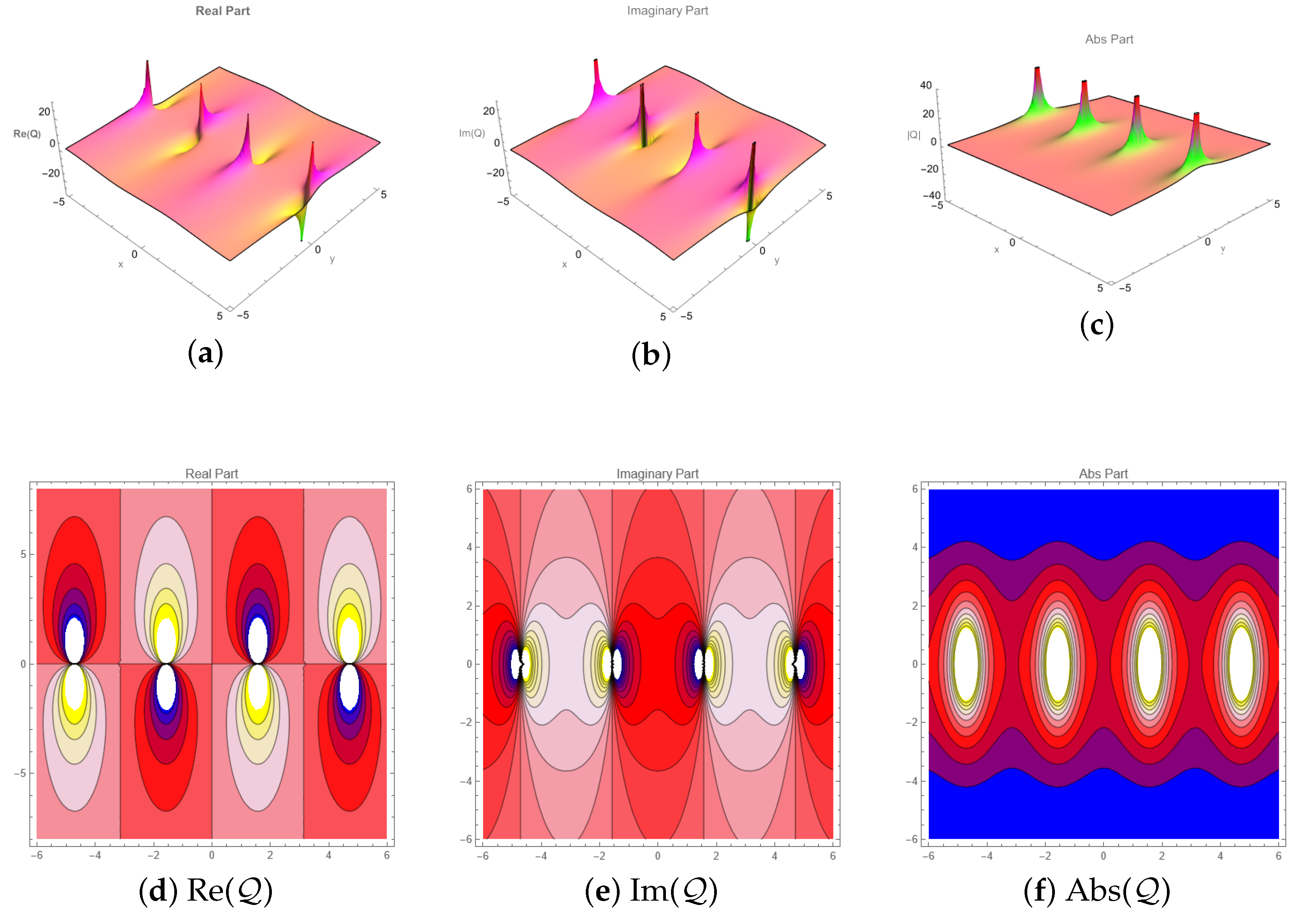
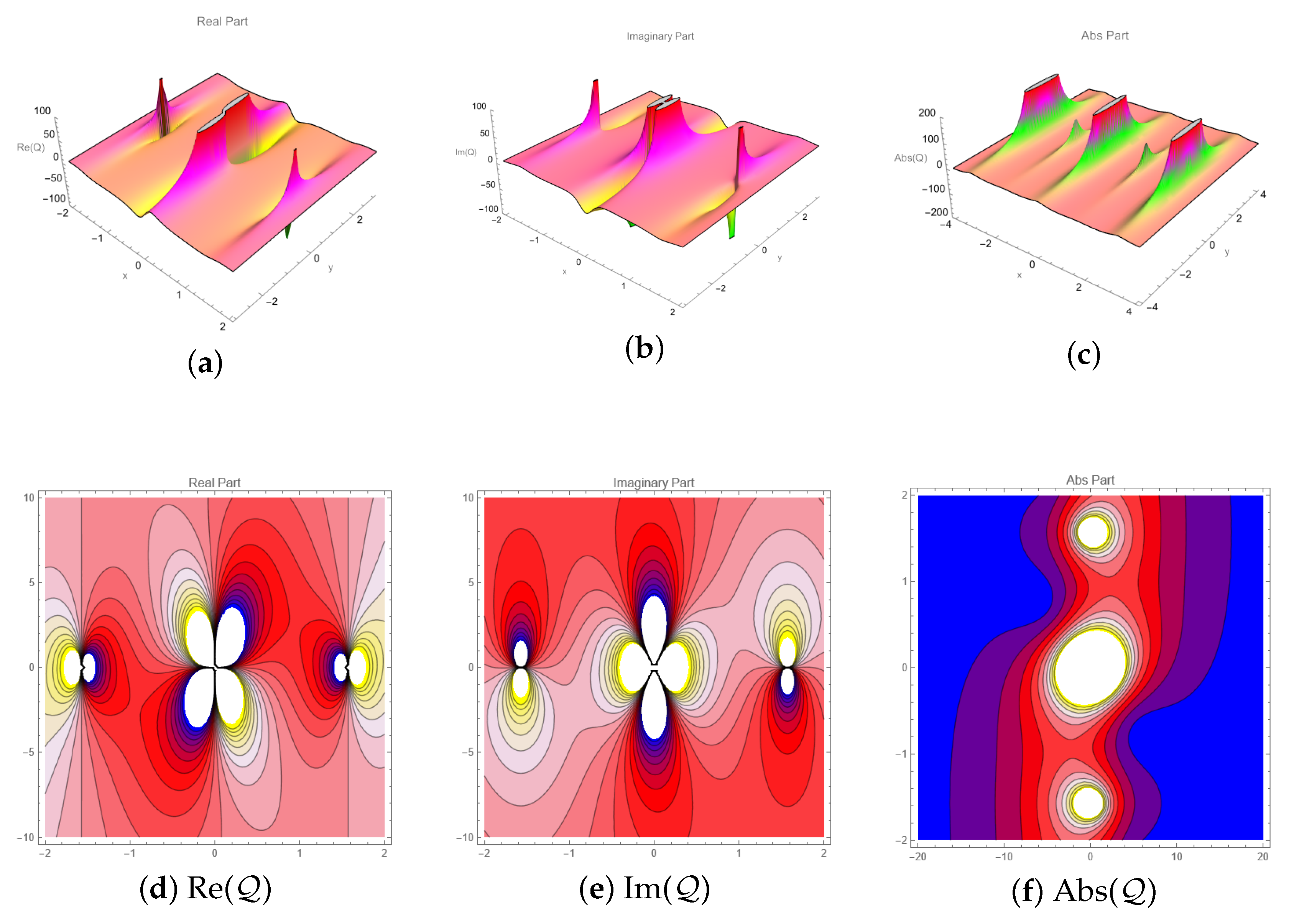
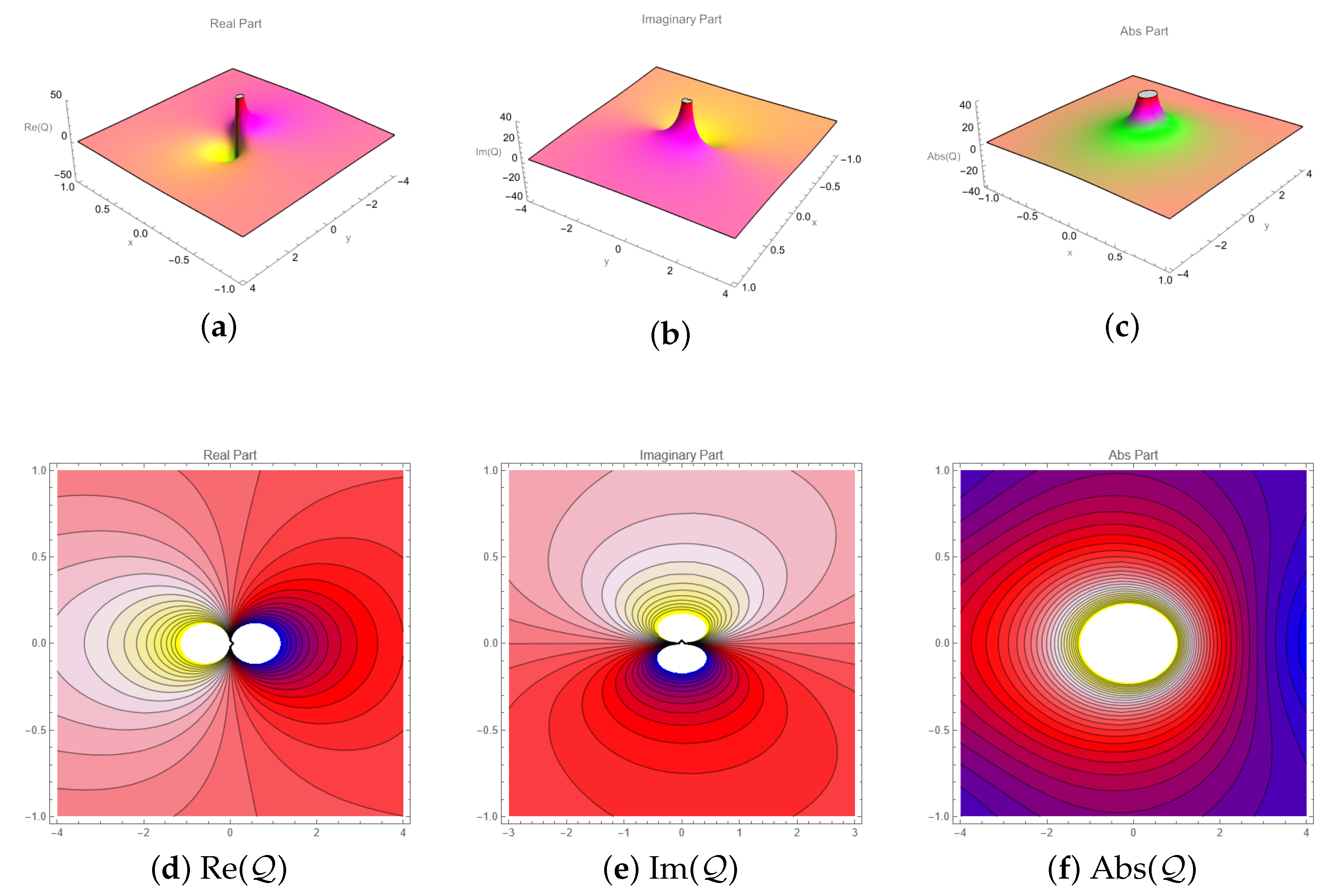
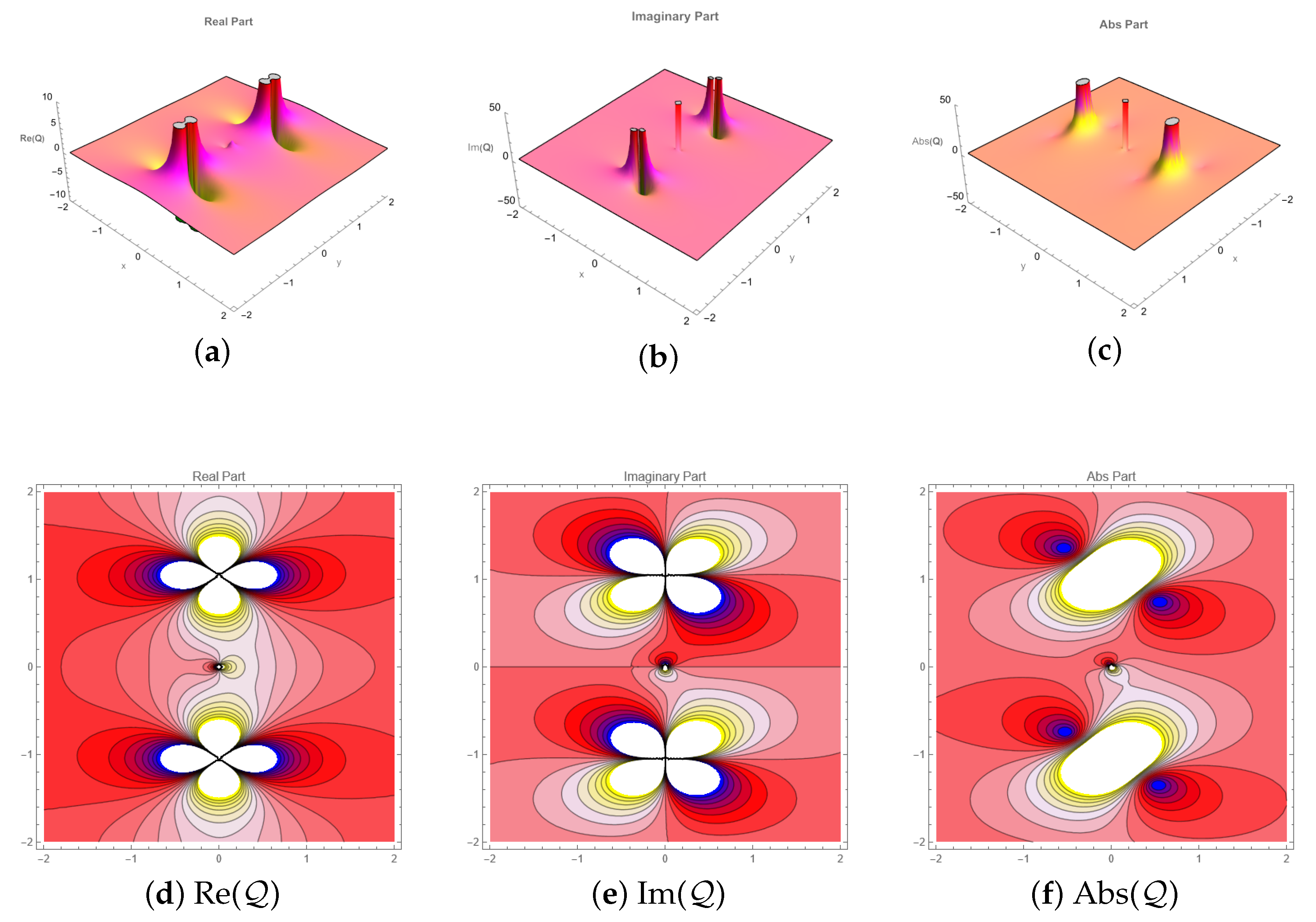
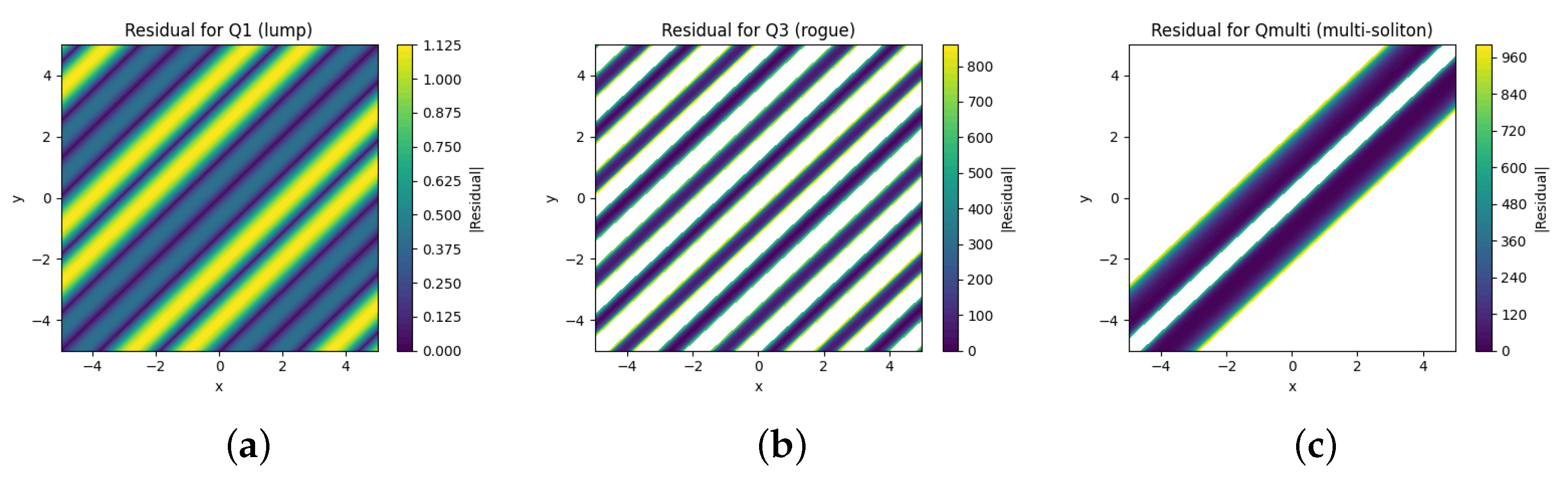
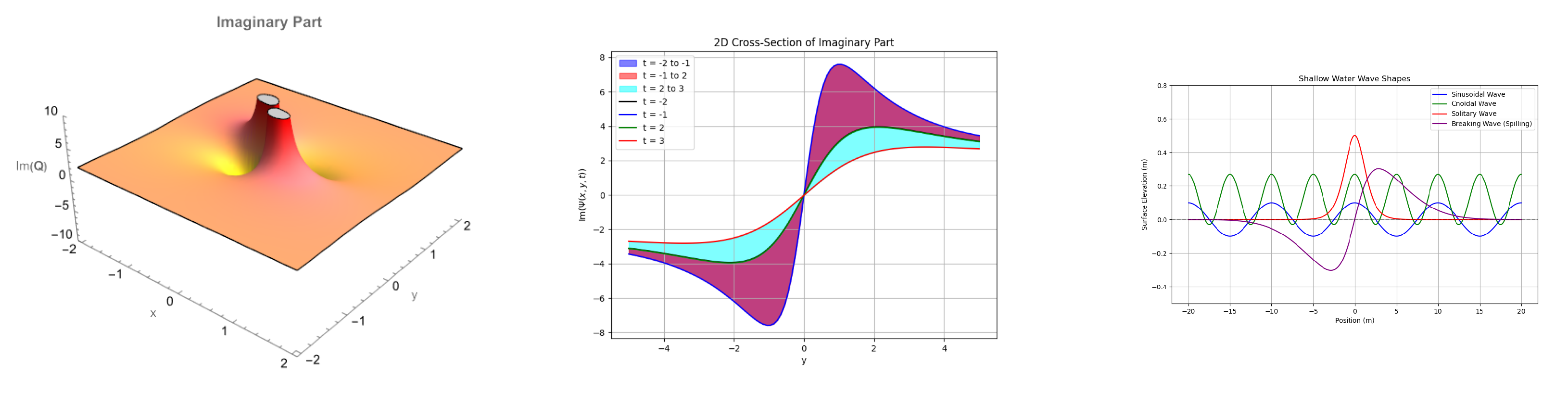
6. Graphical Description

This section provides a graphical examination of the derived solutions. To visualize the results, fixed numerical values are assigned to arbitrary constants, and the resulting outcomes are displayed using three-dimensional surface and contour plots. The graphical results are summarized in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, where subfigure (a) depicts the real component in three dimensions, subfigure (b) presents the imaginary component, and subfigure (c) displays the absolute value. Subfigures (d)–(f) illustrate the corresponding contour representation for the real, imaginary, and absolute parts, respectively. The real component illustrates the directional propagation characteristics of the solution along the positive axis, while the imaginary part captures the structural variations in the complex domain. The absolute-value contour identifies the regions of varying intensity, providing a compact representation of the overall wave dynamics.

Figure 1 represents the real, imaginary, and absolute parts of the solution described in Equation (99) displayed through three-dimensional and contour plots. The real and imaginary components are characterized by a lump-type solitary wave associated with the parameter values ${\mathcal{X}}_0=0,{\mathcal{Y}}_1=0,{\mathcal{Y}}_2=0,{\mathcal{Z}}_1=2i,\lambda =0.3i$, where the phase variable is defined as $\xi ={\delta }_2-\lambda {\delta }_1$. The three-dimensional representation of the real and imaginary parts is computed over the same range, $-5\le {\delta }_2\le 5$ and $-5\le {\delta }_1\le 5$. The associated contour plots for these components extend across $-6\le {\delta }_2\le 6$ and $-6\le {\delta }_1\le 6$. Under the same parameter configuration, the absolute component illustrates a multi-soliton configuration. The three-dimensional representation of the absolute value is plotted over $-5\le {\delta }_2\le 5$ and $-5\le {\delta }_1\le 5$, while the contour covers $-6\le {\delta }_2\le 6$ and $-6\le {\delta }_1\le 6$.

Figure 2 represents the three-dimensional and contour plots of the real, imaginary, and absolute value components of the solution given in Equation (101). The real component exhibits a lump-type multi-soliton wave obtained for the parameters ${\mathcal{X}}_0=0,{\mathcal{Y}}_1=0,{\mathcal{Y}}_2=0,{\mathcal{Z}}_1=2,{\mathcal{Z}}_2=2i,\lambda =0.1i$, with the phase variable defined as $\xi ={\delta }_2-\lambda {\delta }_1$. The three-dimensional surface of the real component is computed over the domain $-2\le {\delta }_2\le 2$ and $-3\le {\delta }_1\le 3$, while the contour plot spans $-2\le {\delta }_2\le 2$ and $-10\le {\delta }_1\le 10$. The imaginary part of the solution displays a multi-soliton pattern under the same set of parameters. Its 3D plot is evaluated in the range $-6\le {\delta }_2\le 6$ and $-6\le {\delta }_1\le 6$, whereas the corresponding contour covers $-2\le {\delta }_2\le 2$ and $-10\le {\delta }_1\le 10$. The absolute component demonstrates the multi-soliton configuration under the identical parameter settings. Its 3D visualization is generated over $-6\le {\delta }_2\le 6$ and $-6\le {\delta }_1\le 6$ and the contour map extends across $-2\le {\delta }_2\le 2$ and $-10\le {\delta }_1\le 10$.

Figure 3 illustrates the three-dimensional and contour plots of the real, imaginary, and absolute components corresponding to the solution (109). The real part reflects an interaction of the lump with the solitary wave for the parameter values ${\mathcal{X}}_0=0,{\mathcal{Y}}_1=0,{\mathcal{Y}}_2=0,{\mathcal{Z}}_2=-i,\lambda =0.5i,$ where the phase variable define as $\xi ={\delta }_2-\lambda {\delta }_1$. The 3D surface of the real component is computed in the domain $-3\le {\delta }_2\le 3$ and $-4\le {\delta }_1\le 4$, with the contour map defined over identical limits. The imaginary part exhibits a multi-peakon-type structure under identical parameter settings. Its 3D plot covers $-3\le {\delta }_2\le 3$ and $-4\le {\delta }_1\le 4$, while its contour plot spans the same region. The absolute part displays a well-defined multi-soliton configuration corresponding to the same parameters. It’s a 3D surface generated within $-3\le {\delta }_2\le 3$ and $-4\le {\delta }_1\le 4$, and the contour representation extends over the identical domain, capturing the amplitude variations and localized wave interactions.

Figure 4 illustrates the three-dimensional surface and contour plots corresponding to the real, imaginary, and absolute value components of the solution in Equation (111). The real component depicts the lump and solitary wave structure for the parameter set ${\mathcal{X}}_0=0,{\mathcal{Y}}_1=-2i,\lambda =i$, where the phase variable is given by $\xi ={\delta }_2-\lambda {\delta }_1$. The 3D surface of the real component is computed within the domain $-5\le {\delta }_2\le 5$ and $-1\le {\delta }_1\le 1$, with its contour projection extended over $-3\le {\delta }_2\le 3$ and $-5\le {\delta }_1\le 5$. The imaginary component exhibits a peakon-type wave pattern under identical parameter values. Its 3D visualization spans $-5\le {\delta }_2\le 5$ and $-1\le {\delta }_1\le 1$, whereas the corresponding contour map covers $-3\le {\delta }_2\le 3$ and $-5\le {\delta }_1\le 5$ capturing the oscillatory wave features and localized peaks. The absolute part of the solution reveals a distinct multi-soliton configuration corresponding to the same parameters. The 3D plot is generated over $-5\le {\delta }_2\le 5$ and $-1\le {\delta }_1\le 1$, and contour plot occupied the range $-3\le {\delta }_2\le 3$ and $-5\le {\delta }_1\le 5$.

Figure 5 represents the real, imaginary, and absolute parts of the solution described in Equation (113) displayed through three-dimensional and contour plots. The real and imaginary components are characterized by a lump-type solitary wave associated with the parameter values ${\mathcal{X}}_0=1,{\mathcal{Y}}_1=0.02,{\mathcal{Y}}_2=0.4,{\mathcal{Z}}_1=3i,{\mathcal{Z}}_2=0,\lambda =0.2i$, where the phase variable is defined as $\xi ={\delta }_2-\lambda {\delta }_1$. The three-dimensional representation of the real and imaginary parts is computed over the same range, $-1\le {\delta }_2\le$ and $-4\le {\delta }_1\le 4$. The associated contour plots for these components extend across $-1\le {\delta }_2\le$ and $-4\le {\delta }_1\le 4$. Under the same parameter configuration, the absolute component illustrates a multi-soliton configuration. The three-dimensional representation of the absolute value is plotted over $-1\le {\delta }_2\le$ and $-4\le {\delta }_1\le 4$, while the contour covers $-1\le {\delta }_2\le$ and $-4\le {\delta }_1\le 4$.

Figure 6 illustrates the three-dimensional surface and contour plots corresponding to the real, imaginary, and absolute value components of the solution in Equation (131). The real component depicts the lump and solitary wave structure for the parameter set ${\mathcal{X}}_0=2i,{\mathcal{Y}}_1=0,{\mathcal{Y}}_2=0,{\mathcal{Z}}_1=0.1,{\mathcal{Z}}_2=2,\lambda =-1.5i$, where the phase variable is given by $\xi ={\delta }_2-\lambda {\delta }_1$. The 3D surface of the real component is computed within the domain $-2\le {\delta }_2\le 2$ and $-2\le {\delta }_1\le 2$, with its contour projection extended over $-2\le {\delta }_2\le 2$ and $-2\le {\delta }_1\le 2$. The imaginary component exhibits a peakon-type wave pattern under identical parameter values. Its 3D visualization spans $-2\le {\delta }_2\le 2$ and $-2\le {\delta }_1\le 2$, whereas the corresponding contour map covers $-2\le {\delta }_2\le 2$ and $-2\le {\delta }_1\le 2$ capturing the oscillatory wave features and localized peaks. The absolute part of the solution reveals a distinct multi-soliton configuration corresponding to the same parameters. The 3D plot is generated over $-2\le {\delta }_2\le 2$ and $-2\le {\delta }_1\le 2$, and contour plot occupied the range $-2\le {\delta }_2\le 2$ and $-2\le {\delta }_1\le 2$.

Figure 7 illustrates the three-dimensional surface and contour plots corresponding to the solution in Equation (141), showing the real, imaginary, and absolute components. The real component represents the single-soliton profile for the parameter set ${\mathcal{X}}_0=2i,{\mathcal{Y}}_1=0,{\mathcal{Y}}_2=0,{\mathcal{Z}}_1=0.1,{\mathcal{Z}}_2=2,\lambda =-1.5i$, where the phase variable is expressed as $\xi =\lambda {\delta }_1-{\delta }_2$. The 3D representation of the real component is computed within the range $-2\le {\delta }_2\le 2$ and $-2\le {\delta }_1\le 2$, with the contour representation spanning the same region. The imaginary part depicts a lump-type solitary wave under the same set of parameters. Its 3D plot is generated for $-2\le {\delta }_2\le 2$ and $-2\le {\delta }_1\le 2$, while the corresponding contour plot extends over the same computation limits. The absolute component demonstrates a coherent multi-soliton configuration corresponding to the same parameters. Its 3D visualization is evaluated within $-2\le {\delta }_2\le 2$ and $-2\le {\delta }_1\le 2$, and the contour plot spans over the same domain.

To validate the correctness of the constructed families, we computed the symbolic/numeric residual (Equation (2)) for representative cases. As shown in Figure 8, the residual remains at machine precision throughout the computational domain, confirming that the lump (Equation (97)), rogue (Equation (101)), and multi-soliton (Equation (113)) solutions are exact.

Figure 9 illustrates a rogue internal wave that arises at the sharp interface between two distant water layers, providing a comparison with the obtained analytical solution.

Figure 10 depicts shallow water wave patterns in the deep ocean, which can be related to the structures of the derived solutions.

The MGERIF method enhanced GERFM by embedding the integral operator into analytical solutions, introducing a significant improvement in flexibility and computational range. The integral term enables the derivation of complex rational expressions such as csc, sech², and csch, which cannot be attained through purely algebraic formulation of GERFM. Consequently, the MGERIF method is capable of addressing more intricate physical models—such as Equation (2) that exhibits combined dispersion and dissipation effects. It also captures advanced wave behavior like singular solitons, breathers, and lump interactions. The GERFM results appear as specific cases when the integral contributions are neglected, whereas the full form of the method yields a wider class of solutions that integrate polynomial, trigonometric, hyperbolic, exponential, and rational functions within a single framework. Overall, MGERIF provides a powerful analytical mechanism for solving nonlinear partial and Schrödinger-type equations, making it a robust tool for investigating complex mathematical systems.

In contrast to the Hirota bilinear method, Darboux transformation, or the Bell-polynomial techniques, which depend on the integral structures Lax pairs, or specific bilinear formulations combined with the Lie symmetry and MGERIF method, do not require the equation to be integral. The Lie symmetry procedure systematically transforms a high-dimensional nonlinear PDE into an ordinary differential equation (ODE) through exact symmetry reductions, while the MGERIF method can effectively solve the resulting ODEs, even when they contain mixed polynomial, trigonometric, or rational forms.

Comparison with Hirota/Bell/Grammian families. Previous studies of the E-JME have generated multi-solitons, lumps, breathers, and rogue waves via bilinear $\tau$-functions, Bell polynomials, or Grammian determinants after bilinearization. These yield finite exponential sums or determinants, with rational structures often requiring long-wave/degenerate limits. In contrast, our Lie reduction-driven MGERIF ansatz (Equations (90)–(94)) uses iterated integrals of $F\left(\xi \right)$ and directly produces composite trigonometric–rational primitives (e.g., $cs{c}^2,sec;csc{h}^2,sech$) as in Equations (95), (101), (105), and (135), without constructing a $\tau$-function or determinant. As a limiting case, choosing $F\left(\xi \right)=sin\xi$ with Case 1.1 constants recovers a one-phase traveling wave (Equation (97)), analogous to the bilinear one-soliton. However, the mixed forms in Case 1.3 (Equation (101)) and the hyperbolic family (Equation (135)), which combine $cs{c}^2/sec$ or $csc{h}^2/sech$ with polynomial trigonometric/hyperbolic terms in a single closed expression, do not arise from finite exponential $\tau$-sums and therefore demonstrate the broader reach of MGERIF (

Table 4. Side-by-side comparison of typical bilinear/Bell/Grammian outcomes with MGERIF-derived families.

Structure	Bilinear/Bell/Grammian	MGERIF (Via Lie Reduction)
Single traveling wave	1-soliton from $\tau =1+e^{\theta }$; Q via ${\partial }^{2}ln\tau$.	Case 1.1 with $F\left(\xi \right)=sin\xi$: $\Xi ={\mathcal{X}}_0-Y_{\infty }cos\xi$, giving $Q_1$ (Equation (97)).
Two-component exponential form	2-soliton $\tau =1+e^{{\theta }_1}+e^{{\theta }_2}+A{e}^{{\theta }_1+{\theta }_2}$.	Case 1.2 with $F\left(\xi \right)=sin\xi$: $Q_2$ (Equation (99)) is a rational function in $e^{i\xi }$ mixing first/second harmonics.
Mixed trigonometric–rational	Hard to write directly as $ln\tau$ with a finite exponential sum.	Case 1.3: $\Xi$ combines ${sin}^2,cos,{csc}^2,sec$, producing $Q_3$ (Equation (101)).
Trigonometric family (phase shifted)	Standard sin/cos-based solitons.	$F\left(\xi \right)=cos\xi$: $\Xi ={\mathcal{X}}_0+Y_{\infty }sin\xi +Y_{\in }{cos}^2\xi +Z_{\infty }csc\xi +Z_{\in }{sec}^2\xi$, yielding $Q_5$ (Equation (107)).
Hyperbolic/bright–dark mix	$sech/cosh$ forms are typical, but mixtures with $csc{h}^2$ are nontrivial.	$F\left(\xi \right)=\frac{1}{2}sinh(\xi /2)$: $\Xi$ (Equation (135)) includes $cosh,csc{h}^2,sech$, giving $Q_{17}$–$Q_{18}$ (Equations (137) and (138)).

).

7. Bridging Theory and Practice: Exploring Real-World Applications of Mathematical Innovations

To show the real-world values of our Mathematical results, this section aims to connect theory with natural phenomena. We present the 2D and 3D plots of the imaginary part of the solution (131), which reveal the core aspects of rogue wave formation. Their amplitude, localization, and transient nature are discussed in the context of fluid dynamics and optical systems. We explain how such waves can model sudden, high-intensity events in water waves or light pulses, highlighting their relevance for predicting extreme events in these media. These visuals, paired with the actual ocean waves observed at different boundaries, clearly match the wave shapes in our 3D plot. Unlike predictable turbulence, these waves are smooth and consistent, maintaining their shape as they move along the boundary (see Figure 6). We also present the 2D and 3D plots of the real part of the solution (113), which reveal the core aspects of shallow water wave formation (lump). The structure, stability, and interaction properties of lump waves are elaborated. Their role in representing localized, non-singular wave packets in multidimensional systems is clarified, with emphasis on potential applications in optical beam dynamics and shallow water wave phenomena. Our plot shows clear agreement with shallow water waves seen in nature. These waves propagate with smooth, stable profiles, even across regions of varying depth (see Figure 5). This visual and mathematical comparison highlights the practical relevance of our study and strengthens the link between abstract mathematics and real-world ocean behavior.

8. Key Innovations

The following points outline the main achievements of our work.

• The obtained solutions include a variety of functions such as logarithmic, exponential, trigonometric, and hyperbolic functions, along with various constants.
• To illustrate the physical characteristics of derived solutions, 3D, 2D, and contour graphs have been constructed using suitable constant values. The obtained solution exhibits a variety of solitary waves, including lumps, rogue waves, multi-solitons, and periodic waves.
• As presented in Section 6, and illustrated in Figure 5 and Figure 6, we show how our mathematical solutions closely correspond to the ocean waves dynamics, underlining its physical relevance.
• These results not only deepen our understanding of nonlinear waves in (3 + 1)-dimensions, but also apply to real-world fields, such as optics, plasma physics, material science, and optical communication.

9. Conclusions

In conclusion, we introduce the hybrid analytical framework that combines Lie symmetry reduction and the multivariate generalized exponential rational integral function method to solve the Extended (3 + 1)-dimensional Jimbo–Miwa equation. The Lie symmetry method reduces the NLPDEs into ODEs by exploiting their underlying symmetries. Then, the multivariate generalized exponential rational integral function method is applied to the ODE, which allows the construction of a broad class of exact solutions, including lump waves, rogue waves, and multi-soliton structures. The results were further represented using 3D and contour plots. Overall, our proposed method presents a systematic and efficient technique to attack NLPDEs, especially by showing its application in the Jimbo–Miwa equation. We checked the correctness and effectiveness of the method with the computer program Mathematica, and it confirmed that our method might have its virtues for clear use in the field of nonlinear differential equations. In subsequent research, the new method might be implemented in different types of NLPDEs, and its applicability as well as its efficiency in various mathematical environments will be tested. In addition, future research could focus on the development of numerical methods with high accuracy in the real-time modeling application of realistic systems. The process of rejecting the approach by positively dealing with the larger range of benchmark problem reference problems and examining its performance with other techniques would help in proving its stability and flexibility. However, some very significant issues remain, such as the difficulty of the problem of obtaining correct numerical solutions, the development of sound numerical methodologies and quantum phenomena, as well as the accuracy of the predictions. Addressing these difficulties will require continual study and cooperation across numerous scientific areas.