Continuum Effect on Mirror Symmetry Breaking Within the Gamow Frameworks
Abstract
1. Introduction
2. Theoretical Framework
2.1. Berggren Basis
2.1.1. Woods–Saxon
2.1.2. Gamow Hartree–Fock
2.2. Gamow Shell Model with Many-Body Perturbation Theory
2.2.1. Model Space Effective Hamiltonian
2.2.2. Effective Operators
2.3. Gamow Coupled-Channel Approach
3. Results
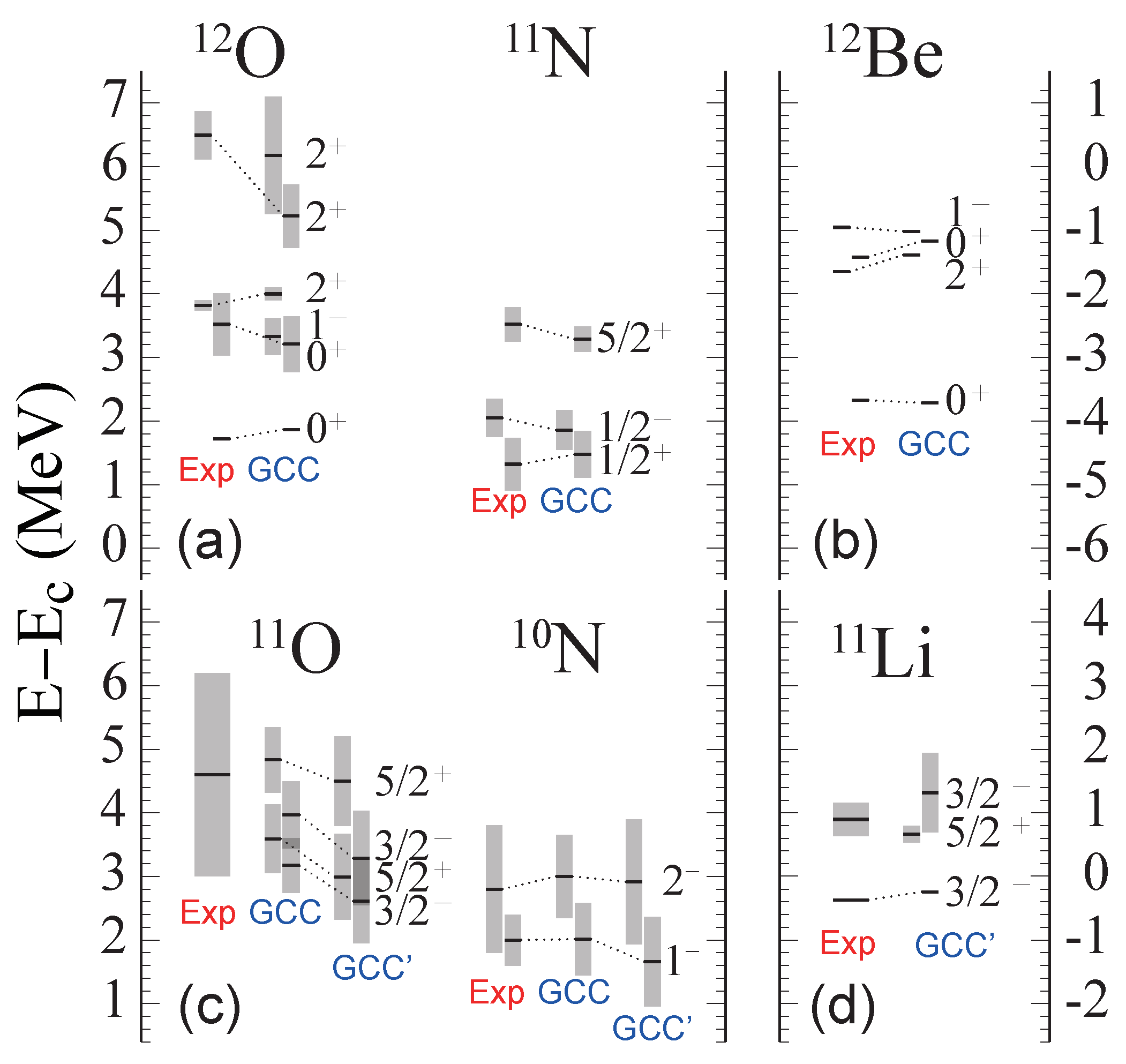
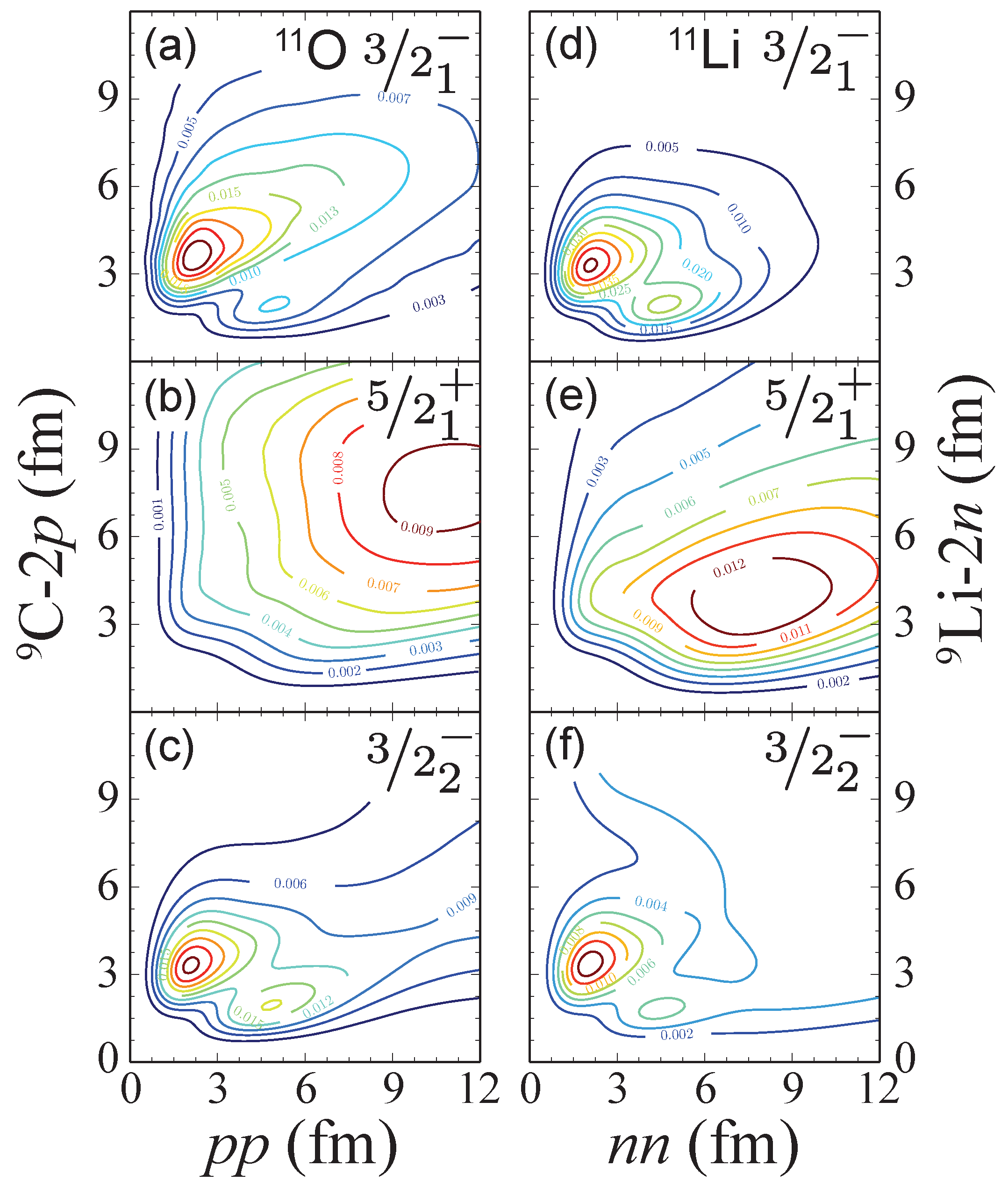
3.1. Mirror Symmetry Breaking in Nuclei at the Edge of the Nuclear Landscape
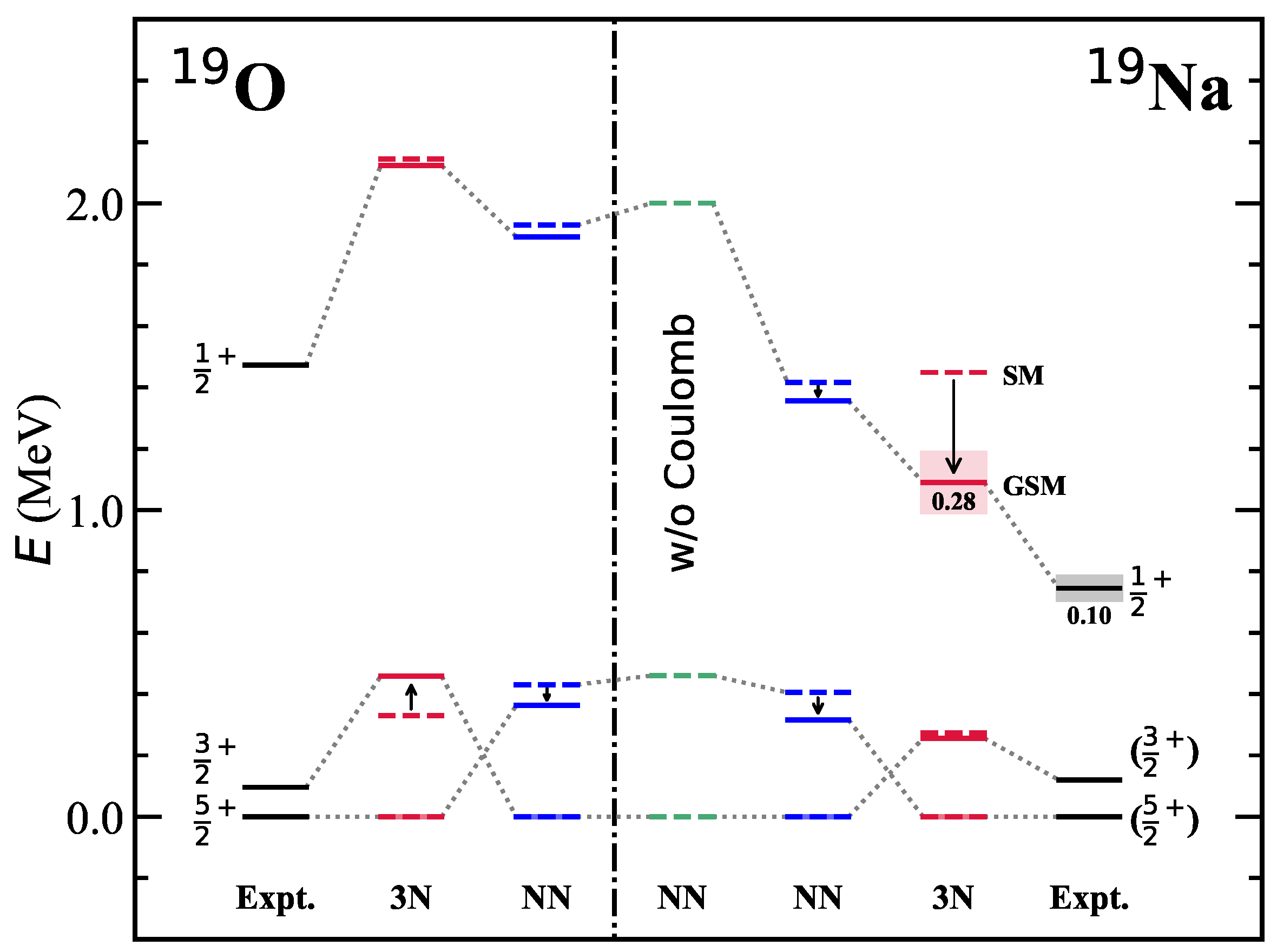
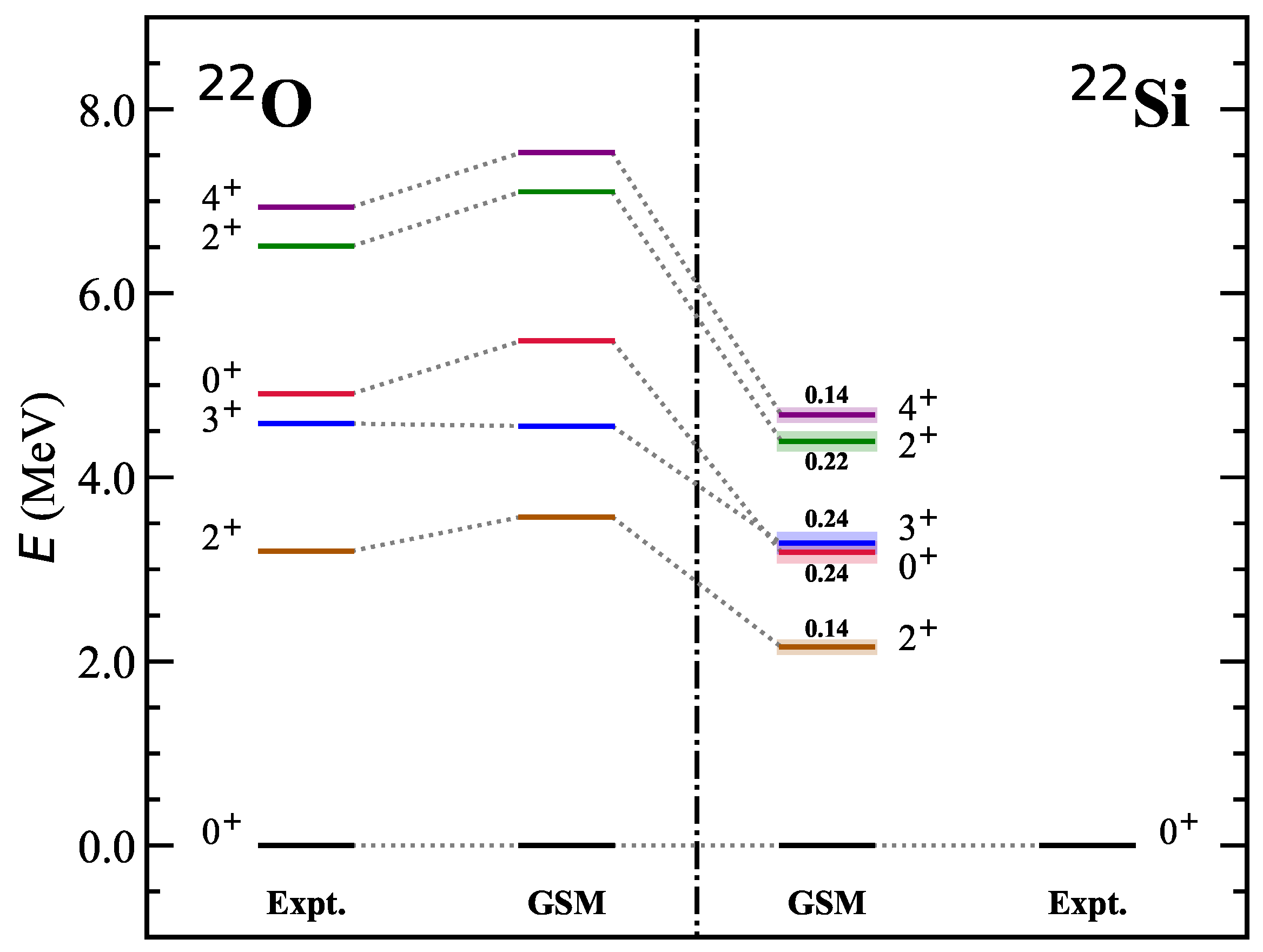
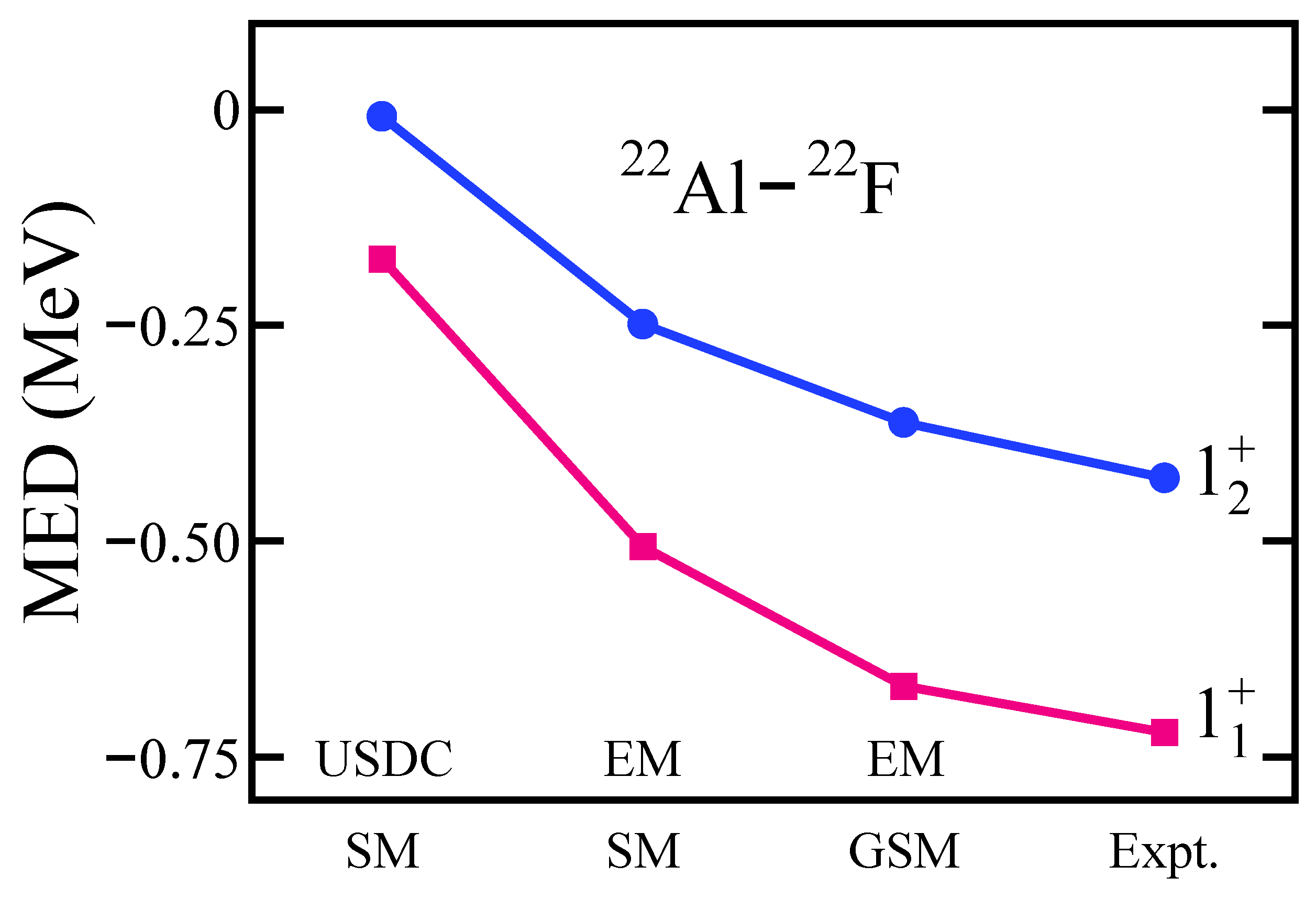
3.2. Mirror Symmetry Breaking in Excitation Spectra
3.3. Mirror Symmetry Breaking in -Decay Gamow–Teller Transitions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SM | shell model |
| GSM | Gamow shell model |
| GCC | Gamow coupled-channel |
| NCSM | no-core shell model |
| MBPT | many-body perturbation theory |
| MSB | mirror symmetry breaking |
| MED | mirror energy difference |
| TES | Thomas-Ehrman shift |
| GT | Gamow–Teller |
| INC | isospin-nonconserving |
| s.p. | single particle |
| GHF | Gamow Hartree–Fock |
| 2NF | nucleon–nucleon force |
| 3NF | three-nucleon force |
References
- Heisenberg, W. Über den Bau der Atomkerne. I. Z. Für Phys. 1932, 77, 1–11. [Google Scholar] [CrossRef]
- Gallant, A.T.; Brodeur, M.; Andreoiu, C.; Bader, A.; Chaudhuri, A.; Chowdhury, U.; Grossheim, A.; Klawitter, R.; Kwiatkowski, A.A.; Leach, K.G.; et al. Breakdown of the Isobaric Multiplet Mass Equation for the A=20 and 21 Multiplets. Phys. Rev. Lett. 2014, 113, 082501. [Google Scholar] [CrossRef] [PubMed]
- Stefan, I.; de Oliveira Santos, F.; Sorlin, O.; Davinson, T.; Lewitowicz, M.; Dumitru, G.; Angélique, J.C.; Angélique, M.; Berthoumieux, E.; Borcea, C.; et al. Probing Nuclear forces beyond the drip-line using the mirror nuclei 16N and 16F. Phys. Rev. C 2014, 90, 014307. [Google Scholar] [CrossRef]
- Hoff, D.E.M.; Rogers, A.M.; Wang, S.M.; Bender, P.C.; Brandenburg, K.; Childers, K.; Clark, J.A.; Dombos, A.C.; Doucet, E.R.; Jin, S.; et al. Mirror-symmetry violation in bound nuclear ground states. Nature 2020, 580, 52–55. [Google Scholar] [CrossRef]
- Webb, T.B.; Wang, S.M.; Brown, K.W.; Charity, R.J.; Elson, J.M.; Barney, J.; Cerizza, G.; Chajecki, Z.; Estee, J.; Hoff, D.E.M.; et al. First observation of unbound 11O, the mirror of the halo nucleus 11Li. Phys. Rev. Lett. 2019, 122, 122501. [Google Scholar] [CrossRef]
- Thomas, R.G. An Analysis of the Energy Levels of the Mirror Nuclei, C13 and N13. Phys. Rev. 1952, 88, 1109–1125. [Google Scholar] [CrossRef]
- Ehrman, J.B. On the Displacement of Corresponding Energy Levels of C13 and N13. Phys. Rev. 1951, 81, 412–416. [Google Scholar] [CrossRef]
- Auerbach, N.; Vinh Mau, N. About Coulomb energy shifts in halo nuclei. Phys. Rev. C 2000, 63, 017301. [Google Scholar] [CrossRef]
- Grigorenko, L.V.; Mukha, I.G.; Thompson, I.J.; Zhukov, M.V. Two-Proton Widths of O-12, N-16e, and Three-Body Mechanism of Thomas-Ehrman Shift. Phys. Rev. Lett. 2002, 88, 042502. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Niu, C.Y.; Brown, K.W.; Li, Z.H.; Hua, H.; Anthony, A.K.; Barney, J.; Charity, R.J.; Crosby, J.; Dell’Aquila, D.; et al. First Observation of the Four-Proton Unbound Nucleus Mg18. Phys. Rev. Lett. 2021, 127, 262502. [Google Scholar] [CrossRef] [PubMed]
- Lalanne, L.; Sorlin, O.; Poves, A.; Assié, M.; Hammache, F.; Koyama, S.; Suzuki, D.; Flavigny, F.; Girard-Alcindor, V.; Lemasson, A.; et al. Structure of Ca36 under the Coulomb Magnifying Glass. Phys. Rev. Lett. 2022, 129, 122501. [Google Scholar] [CrossRef] [PubMed]
- Trinder, W.; Adelberger, E.; Janas, Z.; Keller, H.; Krumbholz, K.; Kunze, V.; Magnus, P.; Meissner, F.; Piechaczek, A.; Pfützner, M.; et al. β-decay of37Ca. Phys. Lett. B 1995, 349, 267–271. [Google Scholar] [CrossRef]
- Tripathi, V.; Tabor, S.L.; Volya, A.; Liddick, S.N.; Bender, P.C.; Larson, N.; Prokop, C.; Suchyta, S.; Tai, P.L.; VonMoss, J.M. Split Isobaric Analog State in Ni55: Case of Strong Isospin Mixing. Phys. Rev. Lett. 2013, 111, 262501. [Google Scholar] [CrossRef] [PubMed]
- Orrigo, S.E.A.; Rubio, B.; Fujita, Y.; Blank, B.; Gelletly, W.; Agramunt, J.; Algora, A.; Ascher, P.; Bilgier, B.; Cáceres, L.; et al. Observation of the β-Delayed γ-Proton Decay of 56Zn and its Impact on the Gamow-Teller Strength Evaluation. Phys. Rev. Lett. 2014, 112, 222501. [Google Scholar] [CrossRef] [PubMed]
- Bennett, M.B.; Wrede, C.; Brown, B.A.; Liddick, S.N.; Pérez-Loureiro, D.; Bardayan, D.W.; Chen, A.A.; Chipps, K.A.; Fry, C.; Glassman, B.E.; et al. Isospin Mixing Reveals 30P(p,γ)31S Resonance Influencing Nova Nucleosynthesis. Phys. Rev. Lett. 2016, 116, 102502. [Google Scholar] [CrossRef]
- Liu, J.J.; Xu, X.X.; Sun, L.J.; Yuan, C.X.; Kaneko, K.; Sun, Y.; Liang, P.F.; Wu, H.Y.; Shi, G.Z.; Lin, C.J.; et al. Observation of a Strongly Isospin-Mixed Doublet in Si26 via β-Delayed Two-Proton Decay of P26. Phys. Rev. Lett. 2022, 129, 242502. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Xu, X.X.; Kaneko, K.; Sun, Y.; Lin, C.J.; Sun, L.J.; Liang, P.F.; Li, Z.H.; Li, J.; Wu, H.Y.; et al. Large Isospin Asymmetry in 22Si/22O Mirror Gamow-Teller Transitions Reveals the Halo Structure of 22Al. Phys. Rev. Lett. 2020, 125, 192503. [Google Scholar] [CrossRef]
- Charity, R.J.; Wylie, J.; Wang, S.M.; Webb, T.B.; Brown, K.W.; Cerizza, G.; Chajecki, Z.; Elson, J.M.; Estee, J.; Hoff, D.E.M.; et al. Strong Evidence for 9N and the Limits of Existence of Atomic Nuclei. Phys. Rev. Lett. 2023, 131, 172501. [Google Scholar] [CrossRef]
- Okołowicz, J.; Michel, N.; Nazarewicz, W.; Płoszajczak, M. Asymptotic normalization coefficients and continuum coupling in mirror nuclei. Phys. Rev. C 2012, 85, 064320. [Google Scholar] [CrossRef]
- Wang, S.M.; Nazarewicz, W. Fermion Pair Dynamics in Open Quantum Systems. Phys. Rev. Lett. 2021, 126, 142501. [Google Scholar] [CrossRef]
- Dobaczewski, J.; Michel, N.; Nazarewicz, W.; Płoszajczak, M.; Rotureau, J. Shell structure of exotic nuclei. Prog. Part. Nucl. Phys. 2007, 59, 432–445. [Google Scholar] [CrossRef]
- Michel, N.; Nazarewicz, W.; Ploszajczak, M.; Vertse, T. Shell Model in the Complex Energy Plane. J. Phys. G 2009, 36, 013101. [Google Scholar] [CrossRef]
- Forssén, C.; Hagen, G.; Hjorth-Jensen, M.; Nazarewicz, W.; Rotureau, J. Living on the edge of stability, the limits of the nuclear landscape. Phys. Scr. 2013, 2013, 014022. [Google Scholar] [CrossRef]
- Rotureau, J.; Okolowicz, J.; Ploszajczak, M. Microscopic theory of the two-proton radioactivity. Phys. Rev. Lett. 2005, 95, 042503. [Google Scholar] [CrossRef]
- Volya, A.; Zelevinsky, V. Discrete and continuum spectra in the unified shell model approach. Phys. Rev. Lett. 2005, 94, 052501. [Google Scholar] [CrossRef] [PubMed]
- Tsukiyama, K.; Otsuka, T.; Fujimoto, R. Low-lying continuum states of drip-line Oxygen isotopes. PTEP 2015, 2015, 093D01. [Google Scholar] [CrossRef]
- Id Betan, R.; Liotta, R.J.; Sandulescu, N.; Vertse, T. Two particle resonant states in a many body mean field. Phys. Rev. Lett. 2002, 89, 042501. [Google Scholar] [CrossRef]
- Michel, N.; Nazarewicz, W.; Ploszajczak, M.; Bennaceur, K. Gamow shell model description of neutron rich nuclei. Phys. Rev. Lett. 2002, 89, 042502. [Google Scholar] [CrossRef] [PubMed]
- Michel, N.; Płoszajczak, M. Gamow Shell Model: The Unified Theory of Nuclear Structure and Reactions; Springer: Cham, Switzerland, 2021; Volume 983. [Google Scholar] [CrossRef]
- Berggren, T. On the use of resonant states in eigenfunction expansions of scattering and reaction amplitudes. Nucl. Phys. A 1968, 109, 265–287. [Google Scholar] [CrossRef]
- Michel, N.; Nazarewicz, W.; Ploszajczak, M.; Okolowicz, J. Gamow shell model description of weakly bound nuclei and unbound nuclear states. Phys. Rev. C 2003, 67, 054311. [Google Scholar] [CrossRef]
- Michel, N.; Nazarewicz, W.; Ploszajczak, M.; Rotureau, J. Antibound states and halo formation in the Gamow Shell Model. Phys. Rev. C 2006, 74, 054305. [Google Scholar] [CrossRef]
- Fossez, K.; Rotureau, J.; Michel, N.; Nazarewicz, W. Continuum effects in neutron-drip-line oxygen isotopes. Phys. Rev. C 2017, 96, 024308. [Google Scholar] [CrossRef]
- Fossez, K.; Rotureau, J.; Nazarewicz, W. Energy Spectrum of Neutron-Rich Helium Isotopes: Complex Made Simple. Phys. Rev. C 2018, 98, 061302. [Google Scholar] [CrossRef]
- Mao, X.; Rotureau, J.; Nazarewicz, W.; Michel, N.; Id Betan, R.M.; Jaganathen, Y. Gamow Shell Model description of Li isotopes and their mirror partners. Phys. Rev. C 2020, 102, 024309. [Google Scholar] [CrossRef]
- Affranchino, S.; Id Betan, R.M. Neutron-pair structure in the continuum spectrum of 26O. Phys. Rev. C 2020, 102, 044330. [Google Scholar] [CrossRef]
- Michel, N.; Li, J.G.; Xu, F.R.; Zuo, W. Two-neutron halo structure of F31. Phys. Rev. C 2020, 101, 031301. [Google Scholar] [CrossRef]
- Wylie, J.; Okołowicz, J.; Nazarewicz, W.; Płoszajczak, M.; Wang, S.M.; Mao, X.; Michel, N. Spectroscopic factors in dripline nuclei. Phys. Rev. C 2021, 104, L061301. [Google Scholar] [CrossRef]
- Li, J.G.; Michel, N.; Zuo, W.; Xu, F.R. Unbound spectra of neutron-rich oxygen isotopes predicted by the Gamow shell model. Phys. Rev. C 2021, 103, 034305. [Google Scholar] [CrossRef]
- Li, H.H.; Li, J.G.; Michel, N.; Zuo, W. Investigation of unbound hydrogen isotopes with the Gamow shell model. Phys. Rev. C 2021, 104, L061306. [Google Scholar] [CrossRef]
- Linares Fernandez, J.P.; Michel, N.; Płoszajczak, M.; Mercenne, A. Description of Be7 and Li7 within the Gamow shell model. Phys. Rev. C 2023, 108, 044616. [Google Scholar] [CrossRef]
- Michel, N.; Nazarewicz, W.; Płoszajczak, M. Description of the Proton-Decaying 02+ Resonance of the α Particle. Phys. Rev. Lett. 2024, 131, 242502. [Google Scholar] [CrossRef]
- Xie, M.R.; Li, J.G.; Michel, N.; Li, H.H.; Wang, S.T.; Ong, H.J.; Zuo, W. Investigation of spectroscopic factors of deeply-bound nucleons in drip-line nuclei with the Gamow shell model. Phys. Lett. B 2023, 839, 137800. [Google Scholar] [CrossRef]
- Li, X.; Michel, N.; Li, J.G.; Zhou, X.R. Gamow shell model description of neutron-rich He hyper-isotopes. arXiv 2024, arXiv:2408.16223. [Google Scholar]
- Pfützner, M.; Mukha, I.; Wang, S. Two-proton emission and related phenomena. Prog. Part. Nucl. Phys. 2023, 132, 104050. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, S.M.; Fang, D.Q.; Ma, Y.G. Recent progress in two-proton radioactivity. Nucl. Sci. Tech. 2022, 33, 105. [Google Scholar] [CrossRef]
- Shi, G.Z.; Liu, J.J.; Lin, Z.Y.; Zhu, H.F.; Xu, X.X.; Sun, L.J.; Liang, P.F.; Lin, C.J.; Lee, J.; Yuan, C.X.; et al. β-delayed two-proton decay of 27S at the proton-dripline. Phys. Rev. C 2021, 103, L061301. [Google Scholar] [CrossRef]
- Wang, S.M.; Michel, N.; Nazarewicz, W.; Xu, F.R. Structure and decays of nuclear three-body systems: The Gamow coupled-channel method in Jacobi coordinates. Phys. Rev. C 2017, 96, 044307. [Google Scholar] [CrossRef]
- Binder, S.; Langhammer, J.; Calci, A.; Roth, R. Ab initio path to heavy nuclei. Phys. Lett. B 2014, 736, 119–123. [Google Scholar] [CrossRef]
- Hagen, G.; Ekström, A.; Forssén, C.; Jansen, G.R.; Nazarewicz, W.; Papenbrock, T.; Wendt, K.A.; Bacca, S.; Barnea, N.; Carlsson, B.; et al. Neutron and weak-charge distributions of the 48Ca nucleus. Nat. Phys. 2016, 12, 186–190. [Google Scholar] [CrossRef]
- Hagen, G.; Jansen, G.R.; Papenbrock, T. Structure of 78Ni from First-Principles Computations. Phys. Rev. Lett. 2016, 117, 172501. [Google Scholar] [CrossRef]
- Morris, T.D.; Simonis, J.; Stroberg, S.R.; Stumpf, C.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Papenbrock, T.; Roth, R.; Schwenk, A. Structure of the Lightest Tin Isotopes. Phys. Rev. Lett. 2018, 120, 152503. [Google Scholar] [CrossRef] [PubMed]
- Gysbers, P.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Morris, T.D.; Navrátil, P.; Papenbrock, T.; Quaglioni, S.; Schwenk, A.; Stroberg, S.R.; et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat. Phys. 2019, 15, 428–431. [Google Scholar] [CrossRef]
- Hu, B.S.; Jiang, W.G.; Miyagi, T.; Sun, Z.H.; Ekström, A.; Forssén, C.; Hagen, G.; Holt, J.D.; Papenbrock, T.; Stroberg, S.R.; et al. Ab initio predictions link the neutron skin of 208Pb to nuclear forces. Nat. Phys. 2022, 18, 1196–1200. [Google Scholar] [CrossRef] [PubMed]
- Lu, B.N.; Li, N.; Elhatisari, S.; Lee, D.; Epelbaum, E.; Meißner, U.G. Essential elements for nuclear binding. Phys. Lett. B 2019, 797, 134863. [Google Scholar] [CrossRef]
- Elhatisari, S.; Bovermann, L.; Ma, Y.Z.; Epelbaum, E.; Frame, D.; Hildenbr, F.; Kim, M.; Kim, Y.; Krebs, H.; Lähde, T.A.; et al. Wavefunction matching for solving quantum many-body problems. Nature 2024, 630, 59–63. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.W.; Meißner, U.G. Modern theory of nuclear forces. Rev. Mod. Phys. 2009, 81, 1773–1825. [Google Scholar] [CrossRef]
- Machleidt, R.; Entem, D. Chiral effective field theory and nuclear forces. Phys. Rep. 2011, 503, 1–75. [Google Scholar] [CrossRef]
- Bogner, S.K.; Furnstahl, R.J.; Perry, R.J. Similarity renormalization group for nucleon-nucleon interactions. Phys. Rev. C 2007, 75, 061001. [Google Scholar] [CrossRef]
- Bogner, S.; Furnstahl, R.; Schwenk, A. From low-momentum interactions to nuclear structure. Prog. Part. Nucl. Phys. 2010, 65, 94–147. [Google Scholar] [CrossRef]
- Hjorth-Jensen, M.; Kuo, T.T.; Osnes, E. Realistic effective interactions for nuclear systems. Phys. Rep. 1995, 261, 125–270. [Google Scholar] [CrossRef]
- Coraggio, L.; Covello, A.; Gargano, A.; Itaco, N.; Kuo, T. Shell-model calculations and realistic effective interactions. Prog. Part. Nucl. Phys. 2009, 62, 135–182. [Google Scholar] [CrossRef]
- Hagen, G.; Papenbrock, T.; Hjorth-Jensen, M.; Dean, D.J. Coupled-cluster computations of atomic nuclei. Rep. Prog. Phys. 2014, 77, 096302. [Google Scholar] [CrossRef] [PubMed]
- Hergert, H.; Bogner, S.; Morris, T.; Schwenk, A.; Tsukiyama, K. The In-Medium Similarity Renormalization Group: A novel ab initio method for nuclei. Phys. Rep. 2016, 621, 165–222. [Google Scholar] [CrossRef]
- Dickhoff, W.H.; Muther, H. Nucleon properties in the nuclear medium. Rep. Prog. Phys. 1992, 55, 1947. [Google Scholar] [CrossRef]
- Dickhoff, W.; Barbieri, C. Self-consistent Green’s function method for nuclei and nuclear matter. Prog. Part. Nucl. Phys. 2004, 52, 377–496. [Google Scholar] [CrossRef]
- Somà, V. Self-Consistent Green’s Function Theory for Atomic Nuclei. Front. Phys. 2020, 8, 340. [Google Scholar] [CrossRef]
- Lähde, T.A.; Meißner, U.G. Nuclear Lattice Effective Field Theory: An introduction; Springer: Cham, Switzerland, 2019; Volume 957. [Google Scholar] [CrossRef]
- Navrátil, P.; Gueorguiev, V.G.; Vary, J.P.; Ormand, W.E.; Nogga, A. Structure of A=10-13 Nuclei with Two- Plus Three-Nucleon Interactions from Chiral Effective Field Theory. Phys. Rev. Lett. 2007, 99, 042501. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, T.; Suzuki, T.; Holt, J.D.; Schwenk, A.; Akaishi, Y. Three-Body Forces and the Limit of Oxygen Isotopes. Phys. Rev. Lett. 2010, 105, 032501. [Google Scholar] [CrossRef] [PubMed]
- Roth, R.; Langhammer, J.; Calci, A.; Binder, S.; Navrátil, P. Similarity-Transformed Chiral NN+3N Interactions for the Ab Initio Description of 12C and 16O. Phys. Rev. Lett. 2011, 107, 072501. [Google Scholar] [CrossRef] [PubMed]
- Maris, P.; Vary, J.P.; Navrátil, P.; Ormand, W.E.; Nam, H.; Dean, D.J. Origin of the Anomalous Long Lifetime of 14C. Phys. Rev. Lett. 2011, 106, 202502. [Google Scholar] [CrossRef]
- Hagen, G.; Hjorth-Jensen, M.; Jansen, G.R.; Machleidt, R.; Papenbrock, T. Continuum Effects and Three-Nucleon Forces in Neutron-Rich Oxygen Isotopes. Phys. Rev. Lett. 2012, 108, 242501. [Google Scholar] [CrossRef]
- Hergert, H.; Binder, S.; Calci, A.; Langhammer, J.; Roth, R. Ab Initio Calculations of Even Oxygen Isotopes with Chiral Two-Plus-Three-Nucleon Interactions. Phys. Rev. Lett. 2013, 110, 242501. [Google Scholar] [CrossRef]
- Holt, J.D.; Menéndez, J.; Schwenk, A. Three-Body Forces and Proton-Rich Nuclei. Phys. Rev. Lett. 2013, 110, 022502. [Google Scholar] [CrossRef]
- Bogner, S.K.; Hergert, H.; Holt, J.D.; Schwenk, A.; Binder, S.; Calci, A.; Langhammer, J.; Roth, R. Nonperturbative Shell-Model Interactions from the In-Medium Similarity Renormalization Group. Phys. Rev. Lett. 2014, 113, 142501. [Google Scholar] [CrossRef] [PubMed]
- Fukui, T.; De Angelis, L.; Ma, Y.Z.; Coraggio, L.; Gargano, A.; Itaco, N.; Xu, F.R. Realistic shell-model calculations for p-shell nuclei including contributions of a chiral three-body force. Phys. Rev. C 2018, 98, 044305. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Xu, F.R.; Coraggio, L.; Hu, B.S.; Li, J.G.; Fukui, T.; De Angelis, L.; Itaco, N.; Gargano, A. Chiral three-nucleon force and continuum for dripline nuclei and beyond. Phys. Lett. B 2020, 802, 135257. [Google Scholar] [CrossRef]
- Hebeler, K.; Bogner, S.K.; Furnstahl, R.J.; Nogga, A.; Schwenk, A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys. Rev. C 2011, 83, 031301. [Google Scholar] [CrossRef]
- Simonis, J.; Stroberg, S.R.; Hebeler, K.; Holt, J.D.; Schwenk, A. Saturation with chiral interactions and consequences for finite nuclei. Phys. Rev. C 2017, 96, 014303. [Google Scholar] [CrossRef]
- Jiang, W.G.; Ekström, A.; Forssén, C.; Hagen, G.; Jansen, G.R.; Papenbrock, T. Accurate bulk properties of nuclei from A=2 to ∞ from potentials with Δ isobars. Phys. Rev. C 2020, 102, 054301. [Google Scholar] [CrossRef]
- Somà, V.; Navrátil, P.; Raimondi, F.; Barbieri, C.; Duguet, T. Novel chiral Hamiltonian and observables in light and medium-mass nuclei. Phys. Rev. C 2020, 101, 014318. [Google Scholar] [CrossRef]
- Stroberg, S.R.; Holt, J.D.; Schwenk, A.; Simonis, J. Ab Initio Limits of Atomic Nuclei. Phys. Rev. Lett. 2021, 126, 022501. [Google Scholar] [CrossRef]
- Hebeler, K. Three-nucleon forces: Implementation and applications to atomic nuclei and dense matter. Phys. Rep. 2021, 890, 1–116. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, Z.H.; Li, J.G.; Xu, Z.C.; Xu, F.R. Ab initio Gamow shell model with chiral three-nucleon force for 14O isotones. Chin. Sci. Bull. 2022, 67, 4101–4107. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, F.R.; Li, J.G.; Hu, B.S.; Cheng, Z.H.; Michel, N.; Ma, Y.Z.; Yuan, Q.; Zhang, Y.H. Ab initio descriptions of A=16 mirror nuclei with resonance and continuum coupling. Phys. Rev. C 2023, 108, 064316. [Google Scholar] [CrossRef]
- Coraggio, L.; De Gregorio, G.; Fukui, T.; Gargano, A.; Ma, Y.Z.; Cheng, Z.H.; Xu, F.R. The role of three-nucleon potentials within the shell model: Past and present. Prog. Part. Nucl. Phys. 2024, 134, 104079. [Google Scholar] [CrossRef]
- Shen, S.; Elhatisari, S.; Lee, D.; Meißner, U.G.; Ren, Z. Ab initio study of the beryllium isotopes 7Be to 12Be. arXiv 2024, arXiv:2411.14935. [Google Scholar]
- Zhang, S.; Elhatisari, S.; Meißner, U.G.; Shen, S. Lattice simulation of nucleon distribution and shell closure in the proton-rich nucleus 22Si. arXiv 2024, arXiv:2411.17462. [Google Scholar]
- Quaglioni, S.; Navrátil, P. Ab Initio Many-Body Calculations of n-3H, n-4He, p-3,4He, and n-10Be Scattering. Phys. Rev. Lett. 2008, 101, 092501. [Google Scholar] [CrossRef]
- Quaglioni, S.; Navrátil, P. Ab initio many-body calculations of nucleon-nucleus scattering. Phys. Rev. C 2009, 79, 044606. [Google Scholar] [CrossRef]
- Shirokov, A.M.; Mazur, A.I.; Mazur, I.A.; Vary, J.P. Shell model states in the continuum. Phys. Rev. C 2016, 94, 064320. [Google Scholar] [CrossRef]
- Mazur, I.A.; Shirokov, A.M.; Mazur, A.I.; Shin, I.J.; Kim, Y.; Maris, P.; Vary, J.P. Description of Continuum Spectrum States of Light Nuclei in the Shell Model. Phys. Part. Nucl. 2019, 50, 537–543. [Google Scholar] [CrossRef]
- Baroni, S.; Navrátil, P.; Quaglioni, S. Ab Initio Description of the Exotic Unbound 7He Nucleus. Phys. Rev. Lett. 2013, 110, 022505. [Google Scholar] [CrossRef]
- Baroni, S.; Navrátil, P.; Quaglioni, S. Unified ab initio approach to bound and unbound states: No-core shell model with continuum and its application to 7He. Phys. Rev. C 2013, 87, 034326. [Google Scholar] [CrossRef]
- Hagen, G.; Dean, D.J.; Hjorth-Jensen, M.; Papenbrock, T. Complex coupled-cluster approach to an ab-initio description of open quantum systems. Phys. Lett. B 2007, 656, 169–173. [Google Scholar] [CrossRef]
- Hu, B.S.; Wu, Q.; Sun, Z.H.; Xu, F.R. Ab initio Gamow in-medium similarity renormalization group with resonance and continuum. Phys. Rev. C 2019, 99, 061302. [Google Scholar] [CrossRef]
- Papadimitriou, G.; Rotureau, J.; Michel, N.; Płoszajczak, M.; Barrett, B.R. Ab initio no-core Gamow shell model calculations with realistic interactions. Phys. Rev. C 2013, 88, 044318. [Google Scholar] [CrossRef]
- Li, J.G.; Michel, N.; Hu, B.S.; Zuo, W.; Xu, F.R. Ab initio no-core Gamow shell-model calculations of multineutron systems. Phys. Rev. C 2019, 100, 054313. [Google Scholar] [CrossRef]
- Li, J.G.; Michel, N.; Zuo, W.; Xu, F.R. Resonances of A=4T=1 isospin triplet states within the ab initio no-core Gamow shell model. Phys. Rev. C 2021, 104, 024319. [Google Scholar] [CrossRef]
- Hagen, G.; Hjorth-Jensen, M.; Michel, N. Gamow shell model and realistic nucleon-nucleon interactions. Phys. Rev. C 2006, 73, 064307. [Google Scholar] [CrossRef]
- Tsukiyama, K.; Hjorth-Jensen, M.; Hagen, G. Gamow shell-model calculations of drip-line oxygen isotopes. Phys. Rev. C 2009, 80, 051301. [Google Scholar] [CrossRef]
- Sun, Z.H.; Wu, Q.; Zhao, Z.H.; Hu, B.S.; Dai, S.J.; Xu, F.R. Resonance and continuum Gamow shell model with realistic nuclear forces. Phys. Lett. B 2017, 769, 227–232. [Google Scholar] [CrossRef]
- Hu, B.S.; Wu, Q.; Li, J.G.; Ma, Y.Z.; Sun, Z.H.; Michel, N.; Xu, F.R. An ab-initio Gamow shell model approach with a core. Phys. Lett. B 2020, 802, 135206. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, Y.Z.; Li, J.G.; Hu, B.S.; Yuan, Q.; Cheng, Z.H.; Xu, F.R. The roles of three-nucleon force and continuum coupling in mirror symmetry breaking of oxygen mass region. Phys. Lett. B 2022, 827, 136958. [Google Scholar] [CrossRef]
- Xu, Z.C.; Zhang, S.; Li, J.G.; Jin, S.L.; Yuan, Q.; Cheng, Z.H.; Michel, N.; Xu, F.R. Complex valence-space effective operators for observables: The Gamow-Teller transition. Phys. Rev. C 2023, 108, L031301. [Google Scholar] [CrossRef]
- Ellis, P.J.; Osnes, E. An introductory guide to effective operators in nuclei. Rev. Mod. Phys. 1977, 49, 777–832. [Google Scholar] [CrossRef]
- Brandow, B.H. Linked-Cluster Expansions for the Nuclear Many-Body Problem. Rev. Mod. Phys. 1967, 39, 771–828. [Google Scholar] [CrossRef]
- Tichai, A.; Langhammer, J.; Binder, S.; Roth, R. Hartree–Fock many-body perturbation theory for nuclear ground-states. Phys. Lett. B 2016, 756, 283–288. [Google Scholar] [CrossRef]
- Roth, R.; Binder, S.; Vobig, K.; Calci, A.; Langhammer, J.; Navratil, P. Ab Initio Calculations of Medium-Mass Nuclei with Normal-Ordered Chiral NN+3N Interactions. Phys. Rev. Lett. 2012, 109, 052501. [Google Scholar] [CrossRef]
- Hu, B.S.; Xu, F.R.; Sun, Z.H.; Vary, J.P.; Li, T. Ab initio nuclear many-body perturbation calculations in the Hartree-Fock basis. Phys. Rev. C 2016, 94, 014303. [Google Scholar] [CrossRef]
- Tsunoda, N.; Takayanagi, K.; Hjorth-Jensen, M.; Otsuka, T. Multi-shell effective interactions. Phys. Rev. C 2014, 89, 024313. [Google Scholar] [CrossRef]
- Coraggio, L.; Itaco, N. Self-consistent nuclear shell-model calculation starting from a realistic NN potential. Phys. Lett. B 2005, 616, 43–47. [Google Scholar] [CrossRef][Green Version]
- Takayanagi, K. Effective interaction in non-degenerate model space. Nucl. Phys. A 2011, 852, 61–81. [Google Scholar] [CrossRef]
- Michel, N.; Aktulga, H.; Jaganathen, Y. Toward scalable many-body calculations for nuclear open quantum systems using the Gamow Shell Model. Comp. Phys. Comm. 2020, 247, 106978. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Xu, F.R.; Michel, N.; Zhang, S.; Li, J.G.; Hu, B.S.; Coraggio, L.; Itaco, N.; Gargano, A. Continuum and three-nucleon force in Borromean system: The 17Ne case. Phys. Lett. B 2020, 808, 135673. [Google Scholar] [CrossRef]
- Li, J.G.; Hu, B.S.; Wu, Q.; Gao, Y.; Dai, S.J.; Xu, F.R. Neutron-rich calcium isotopes within realistic Gamow shell model calculations with continuum coupling. Phys. Rev. C 2020, 102, 034302. [Google Scholar] [CrossRef]
- Geng, Y.F.; Li, J.G.; Ma, Y.Z.; Hu, B.S.; Wu, Q.; Sun, Z.H.; Zhang, S.; Xu, F.R. Excitation spectra of the heaviest carbon isotopes investigated within the CD-Bonn Gamow shell model. Phys. Rev. C 2022, 106, 024304. [Google Scholar] [CrossRef]
- Coraggio, L.; Itaco, N. Perturbative Approach to Effective Shell-Model Hamiltonians and Operators. Front. Phys. 2020, 8, 345. [Google Scholar] [CrossRef]
- Suzuki, K.; Okamoto, R. Effective Operators in Time-Independent Approach. Prog. Theor. Phys. 1995, 93, 905–917. [Google Scholar] [CrossRef]
- Michel, N.; Nazarewicz, W.; Płoszajczak, M. Proton-neutron coupling in the Gamow shell model: The lithium chain. Phys. Rev. C 2004, 70, 064313. [Google Scholar] [CrossRef]
- Xu, Z.C.; Hu, R.Z.; Jin, S.L.; Hou, J.H.; Zhang, S.; Xu, F.R. Collectivity of nuclei near the exotic doubly magic Ni78 by ab initio calculations. Phys. Rev. C 2024, 110, 024308. [Google Scholar] [CrossRef]
- Wang, S.M.; Nazarewicz, W.; Charity, R.J.; Sobotka, L.G. Nucleon–nucleon correlations in the extreme oxygen isotopes. J. Phys. G: Nucl. Part. Phys. 2022, 49, 10LT02. [Google Scholar] [CrossRef]
- Yang, Y.H.; Ma, Y.G.; Wang, S.M.; Zhou, B.; Fang, D.Q. Structure and decay mechanism of the low-lying states in 9Be and 9B. Phys. Rev. C 2023, 108, 044307. [Google Scholar] [CrossRef]
- Wang, Y.T.; Fang, D.Q.; Wang, K.; Xu, X.X.; Sun, L.J.; Bao, P.F.; Bai, Z.; Cao, X.G.; Dai, Z.T.; Ding, B.; et al. Observation of β-delayed 2He emission from the proton-rich nucleus 22Al. Phys. Lett. B 2018, 784, 12–15. [Google Scholar] [CrossRef]
- Wang, S.M.; Nazarewicz, W.; Charity, R.J.; Sobotka, L.G. Structure and decay of the extremely proton-rich nuclei 11,12O. Phys. Rev. C 2019, 99, 054302. [Google Scholar] [CrossRef]
- Zhang, S.; Geng, Y.F.; Xu, F.R. Ab Initio Gamow Shell-Model Calc. Dripline Nuclei. Nucl. Tech. 2023, 46, 080012. [Google Scholar] [CrossRef]
- Fortune, H.T. Energy and width of 11O(g.s.). Phys. Rev. C 2019, 99, 051302. [Google Scholar] [CrossRef]
- Garrido, E.; Jensen, A.S. Few-body structures in the mirror nuclei 11O and 11Li. Phys. Rev. C 2020, 101, 034003. [Google Scholar] [CrossRef]
- Webb, T.B.; Charity, R.J.; Elson, J.M.; Hoff, D.E.M.; Pruitt, C.D.; Sobotka, L.G.; Brown, K.W.; Barney, J.; Cerizza, G.; Estee, J.; et al. Invariant-mass spectrum of 11O. Phys. Rev. C 2020, 101, 044317. [Google Scholar] [CrossRef]
- Suzuki, D.; Iwasaki, H.; Beaumel, D.; Assié, M.; Baba, H.; Blumenfeld, Y.; de Oliveira Santos, F.; de Séréville, N.; Drouart, A.; Franchoo, S.; et al. Second 0+ state of unbound 12O: Scaling of mirror asymmetry. Phys. Rev. C 2016, 93, 024316. [Google Scholar] [CrossRef]
- Webb, T.B.; Charity, R.J.; Elson, J.M.; Hoff, D.E.M.; Pruitt, C.D.; Sobotka, L.G.; Brown, K.W.; Barney, J.; Cerizza, G.; Estee, J.; et al. Particle decays of levels in 11,12N and 12O investigated with the invariant-mass method. Phys. Rev. C 2019, 100, 024306. [Google Scholar] [CrossRef]
- Michel, N.; Li, J.G.; Xu, F.R.; Zuo, W. Proton decays in 16Ne and 18Mg and isospin-symmetry breaking in carbon isotopes and isotones. Phys. Rev. C 2021, 103, 044319. [Google Scholar] [CrossRef]
- Zhou, L.; Fang, D.Q.; Wang, S.M.; Hua, H. Structure and 2p decay mechanism of 18Mg. Nucl. Sci. Tech. 2024, 35, 107. [Google Scholar] [CrossRef]
- Brown, K.W.; Charity, R.J.; Sobotka, L.G.; Chajecki, Z.; Grigorenko, L.V.; Egorova, I.A.; Parfenova, Y.L.; Zhukov, M.V.; Bedoor, S.; Buhro, W.W.; et al. Observation of long-range three-body Coloumb effects in the decay of 16Ne. Phys. Rev. Lett. 2014, 113, 232501. [Google Scholar] [CrossRef]
- Evaluated Nuclear Structure Data File (ENSDF). Available online: https://www.nndc.bnl.gov/ensdf/ (accessed on 30 December 2024).
- Bardayan, D.W.; Blackmon, J.C.; Brune, C.R.; Champagne, A.E.; Chen, A.A.; Cox, J.M.; Davinson, T.; Hansper, V.Y.; Hofstee, M.A.; Johnson, B.A.; et al. Observation of the Astrophysically Important 3+ State in N-18e via Elastic Scattering of a Radioactive F-17 Beam from H-1. Phys. Rev. Lett. 1999, 83, 45–48. [Google Scholar] [CrossRef]
- Angulo, C.; Tabacaru, G.; Couder, M.; Gaelens, M.; Leleux, P.; Ninane, A.; Verbist, F.; Davinson, T.; Woods, P.J.; Schweitzer, J.S.; et al. Identification of a new low lying state in the proton dripline nucleus Na-19. Phys. Rev. C 2003, 67, 014308. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys. Rev. C 2003, 68, 041001. [Google Scholar] [CrossRef]
- Brown, B.A.; Richter, W.A. New “USD” Hamiltonians for the sd shell. Phys. Rev. C 2006, 74, 034315. [Google Scholar] [CrossRef]
- Kaneko, K.; Sun, Y.; Mizusaki, T.; Tazaki, S.; Ghorui, S. Isospin-symmetry breaking in superallowed Fermi β-decay due to isospin-nonconserving forces. Phys. Lett. B 2017, 773, 521–526. [Google Scholar] [CrossRef]
- Michel, N.; Nazarewicz, W.; Płoszajczak, M. Isospin mixing and the continuum coupling in weakly bound nuclei. Phys. Rev. C 2010, 82, 044315. [Google Scholar] [CrossRef]
- Magilligan, A.; Brown, B.A. New isospin-breaking “USD” Hamiltonians for the sd shell. Phys. Rev. C 2020, 101, 064312. [Google Scholar] [CrossRef]
- Brown, B.; Wildenthal, B. Experimental and theoretical Gamow-Teller beta-decay observables for the sd-shell nuclei. At. Data Nucl. Data Tables 1985, 33, 347–404. [Google Scholar] [CrossRef]
- Towner, I. Quenching of spin matrix elements in nuclei. Phys. Rep. 1987, 155, 263–377. [Google Scholar] [CrossRef]
- Hoferichter, M.; Menéndez, J.; Schwenk, A. Coherent elastic neutrino-nucleus scattering: EFT analysis and nuclear responses. Phys. Rev. D 2020, 102, 074018. [Google Scholar] [CrossRef]



| SM | GSM | Ref. [17] | ||||
|---|---|---|---|---|---|---|
| USDC | EM | EM | Expt. | Cal. | ||
| 22Si→22Al | 0.236 | 0.343 | 0.257 | 0.176 (16) | 0.242 | |
| 0.721 | 1.042 | 1.012 | 0.750 (41) | 0.863 | ||
| 22O→22F | 0.198 | 0.569 | 0.497 | 0.310 (32) | 0.428 | |
| 0.719 | 1.092 | 1.068 | 0.775 (77) | 0.848 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Xu, Z.; Wang, S. Continuum Effect on Mirror Symmetry Breaking Within the Gamow Frameworks. Symmetry 2025, 17, 169. https://doi.org/10.3390/sym17020169
Zhang S, Xu Z, Wang S. Continuum Effect on Mirror Symmetry Breaking Within the Gamow Frameworks. Symmetry. 2025; 17(2):169. https://doi.org/10.3390/sym17020169
Chicago/Turabian StyleZhang, Shuang, Zhicheng Xu, and Simin Wang. 2025. "Continuum Effect on Mirror Symmetry Breaking Within the Gamow Frameworks" Symmetry 17, no. 2: 169. https://doi.org/10.3390/sym17020169
APA StyleZhang, S., Xu, Z., & Wang, S. (2025). Continuum Effect on Mirror Symmetry Breaking Within the Gamow Frameworks. Symmetry, 17(2), 169. https://doi.org/10.3390/sym17020169






