Solvatochromic Analysis of Triton X-100 in Binary Mixtures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Spectral Measurements
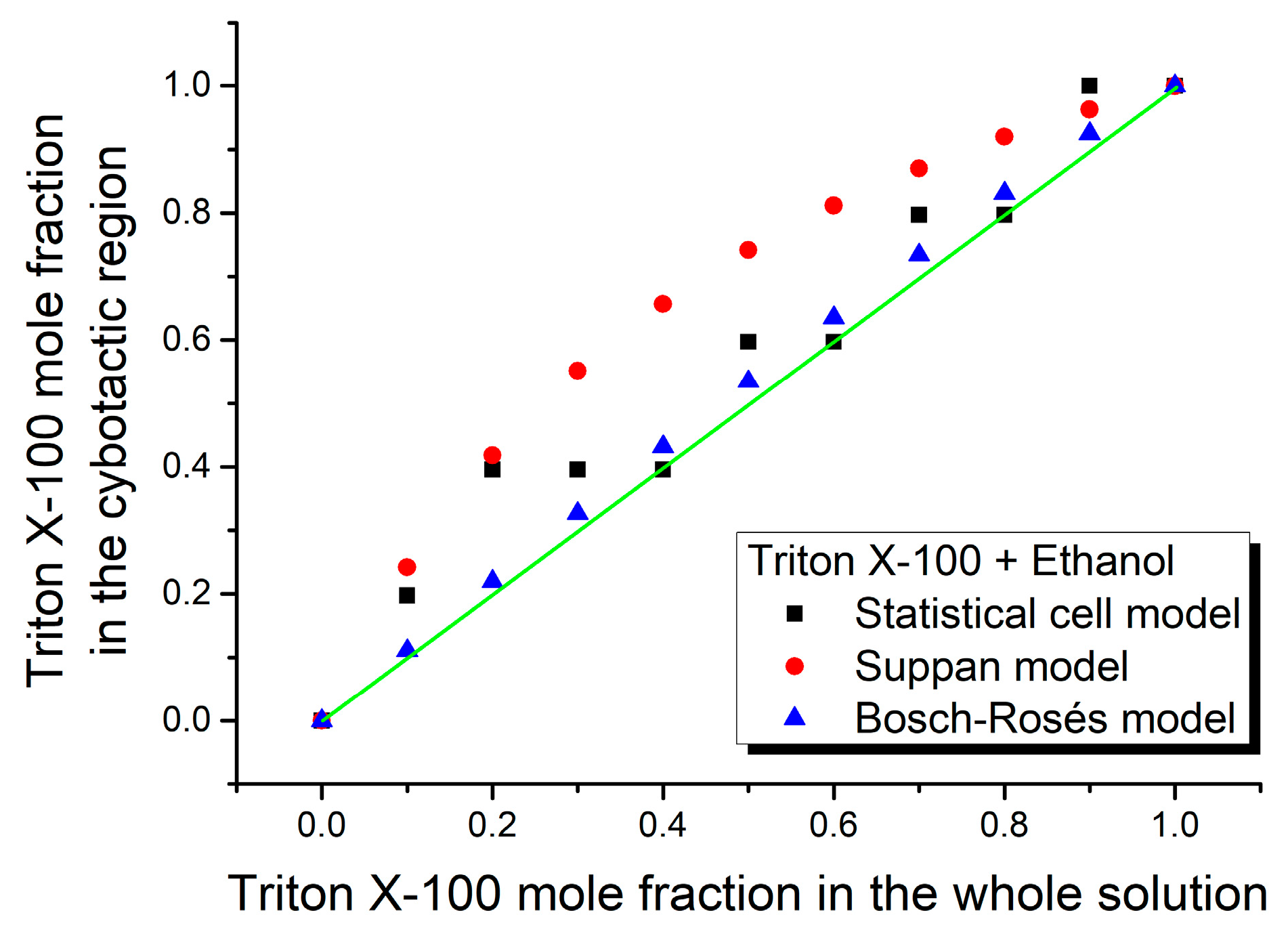
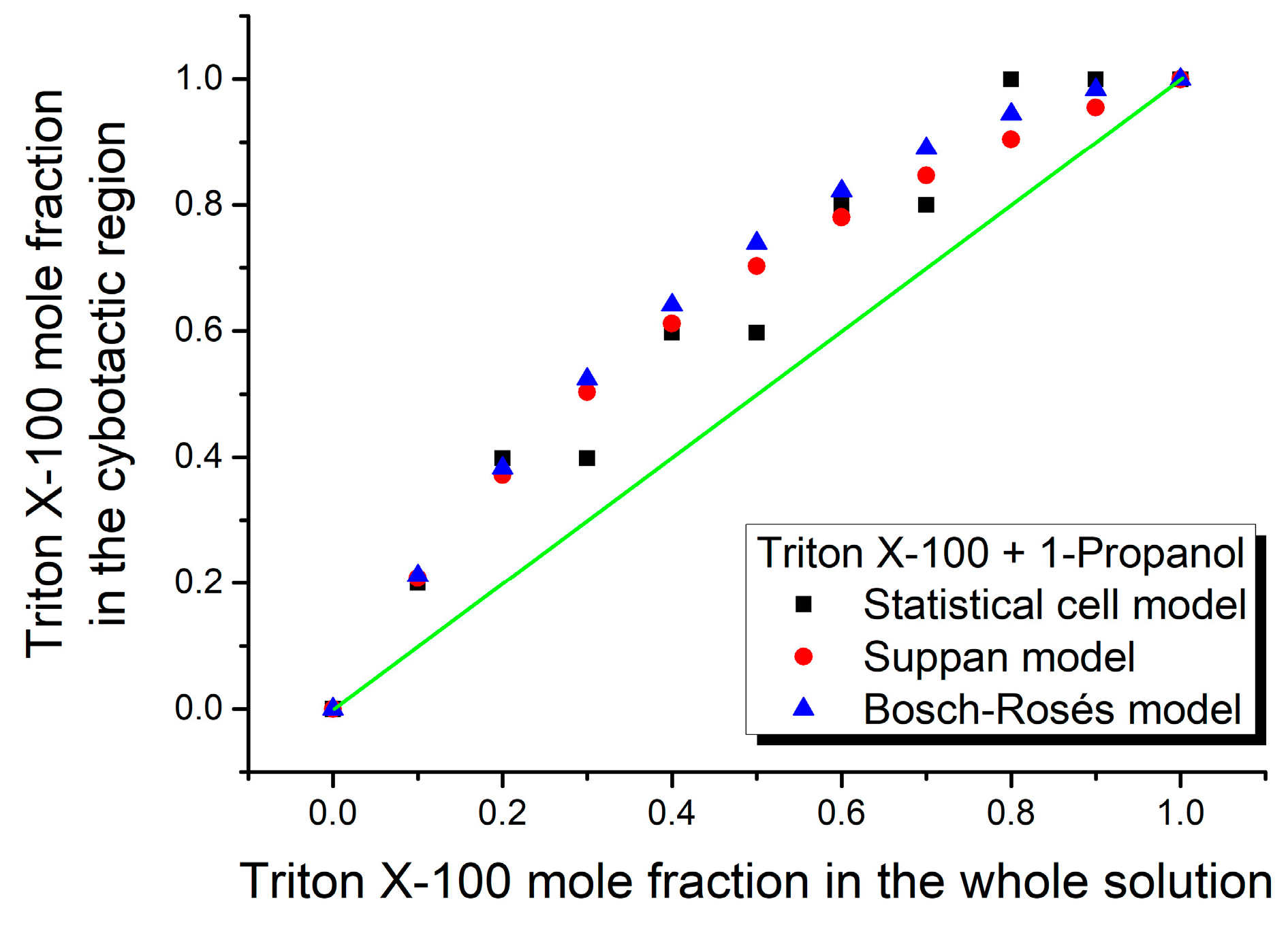
2.3. Theoretical Models
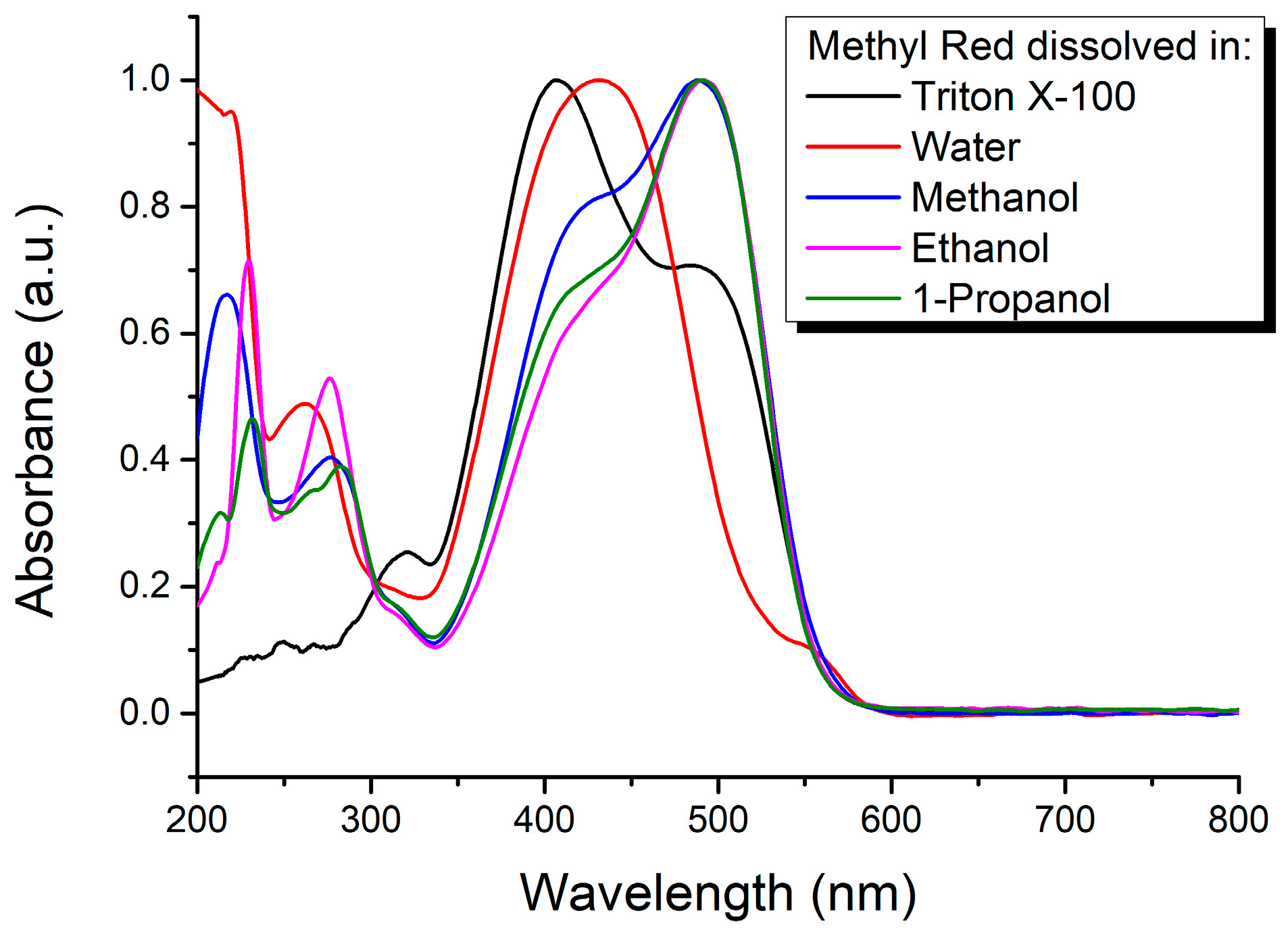
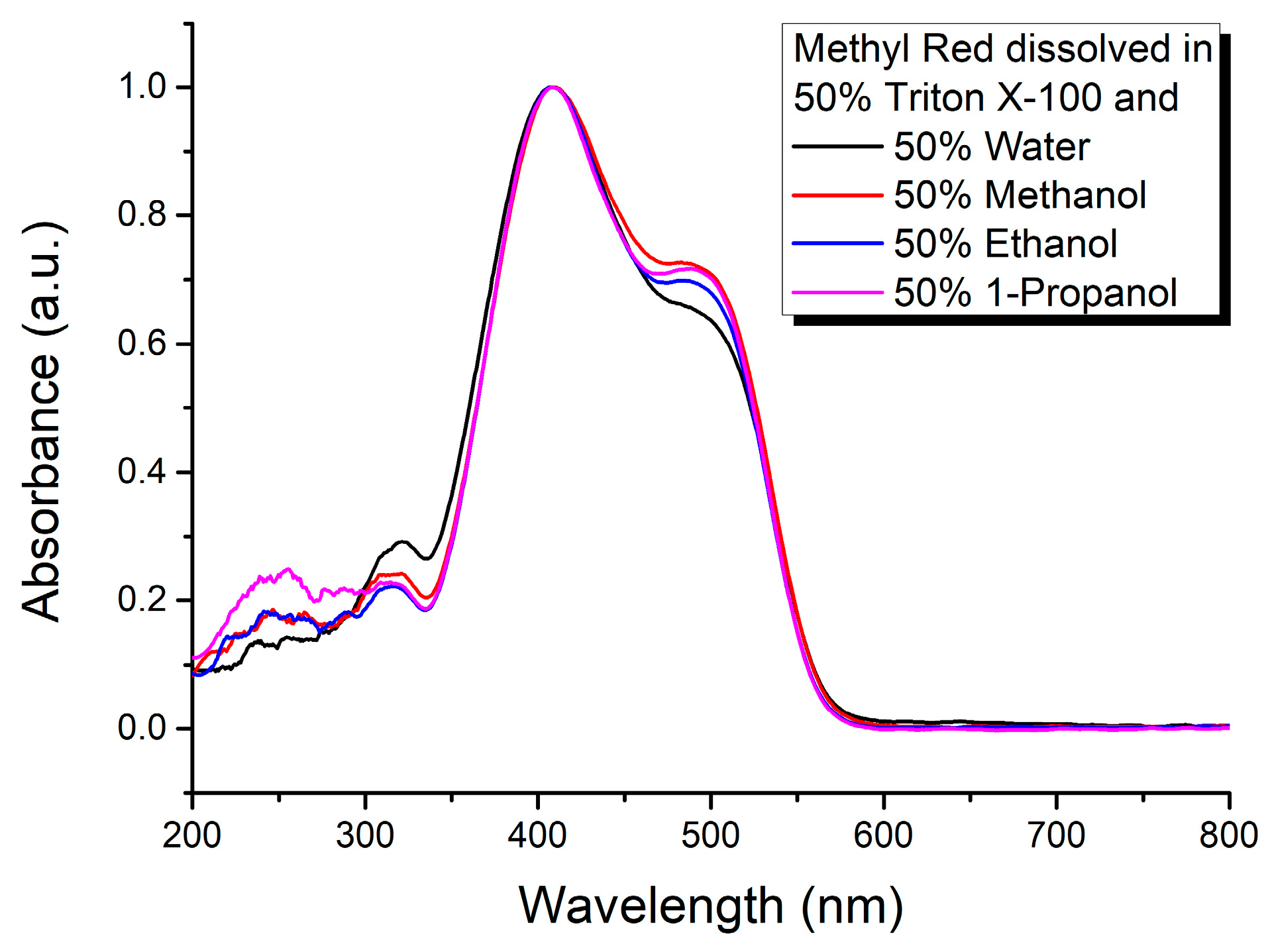
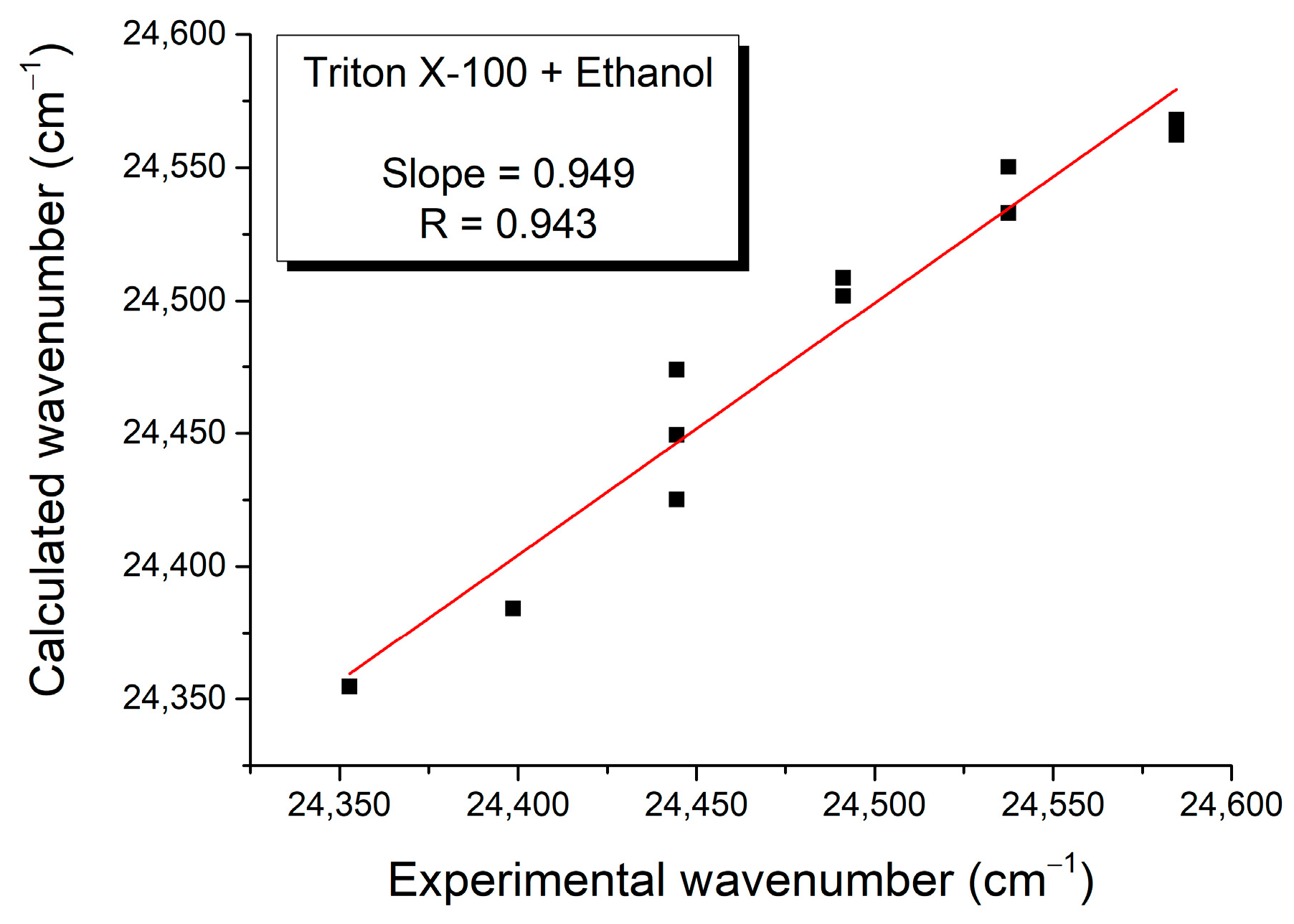
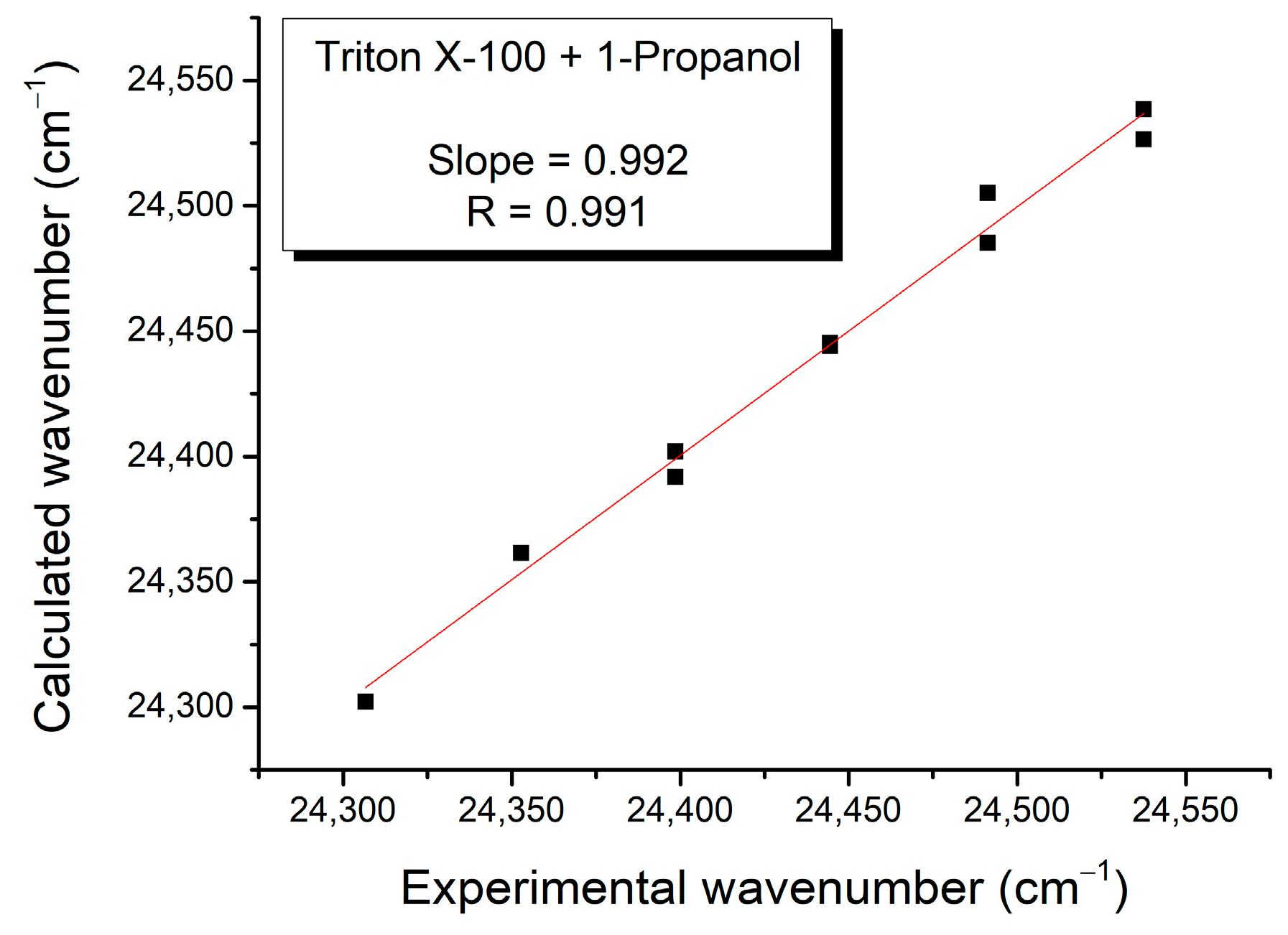
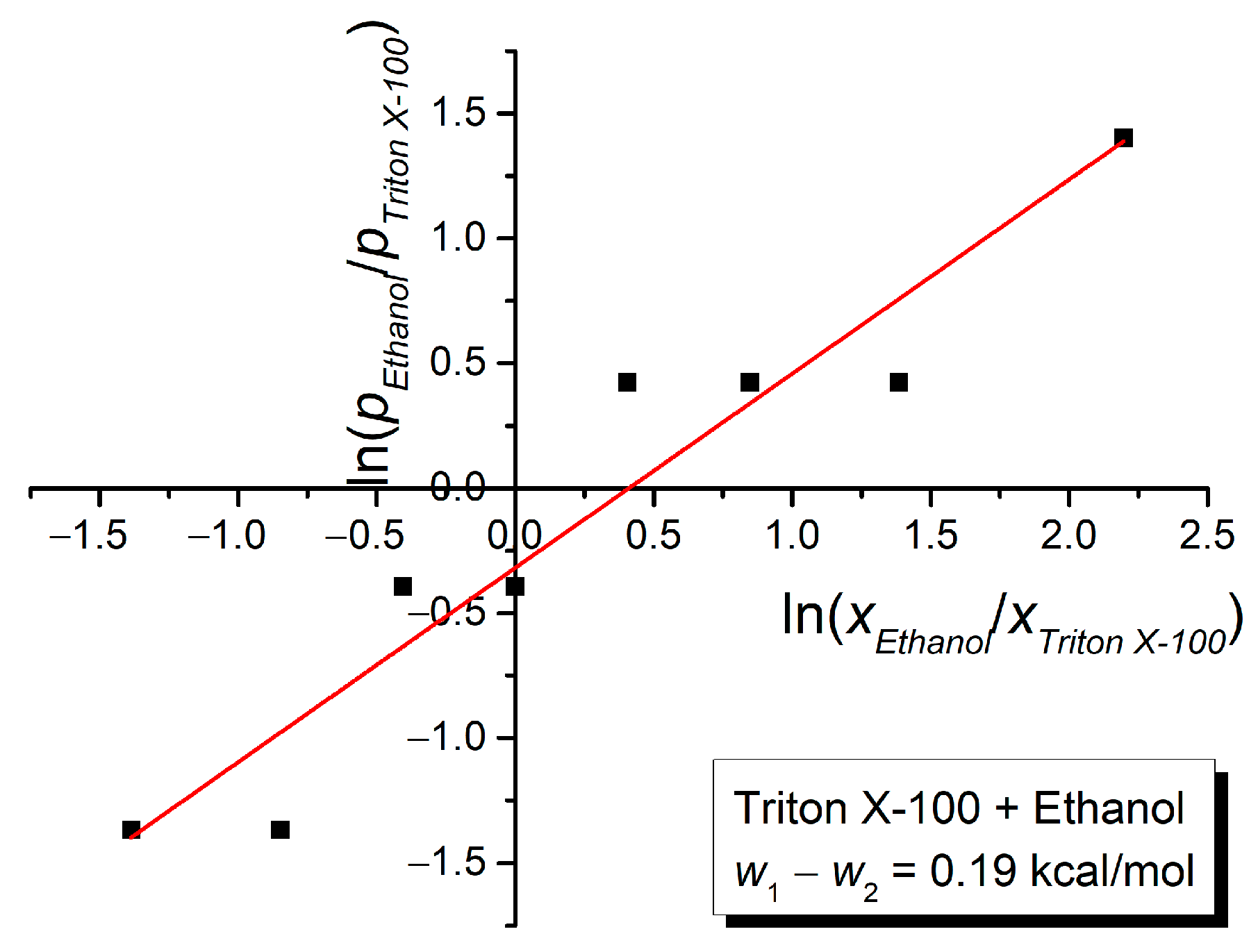
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zana, R. Aqueous surfactant-alcohol systems: A review. Adv. Colloid Interface Sci. 1995, 57, 1–64. [Google Scholar] [CrossRef]
- Zhong, X.; Chen, L.; Xu, J.; Cheng, K.; Wu, B. Two-photon and three photon fluorescence of Triton X-100 in the ultraviolet region. J. Fluoresc. 2021, 31, 1779–1785. [Google Scholar] [CrossRef] [PubMed]
- Fedyaeva, O.A.; Poshelyuzhnaya, E.G. Optical activity of Triton X-100 micelles in aqueous solutions. Russ. J. Phys. Chem A 2020, 94, 1957–1958. [Google Scholar] [CrossRef]
- Robson, R.J.; Dennis, E.A. The size, shape, and hydration of nonionic surfactant micelles. Triton X-100. J. Phys. Chem. 1977, 81, 1075–1078. [Google Scholar] [CrossRef]
- Qin, Y.; Zhou, Y.; Wang, K.; Gu, J.; Xiong, Z.; Zhang, W.; Chen, Y. In situ isolation of nuclei or nuclear proteins from adherent cells: A simple, effective method with less cytoplasmic contamination. Biol. Res. 2023, 56, 18. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Su, C.; Hu, S.; Chen, Y.; Shu, Y.; Yue, D.; Zhang, B.; Qi, Z.; Li, S.; Wang, X.; et al. The effect of residual Triton X-100 on structural stability and infection activity of adenovirus particles. Mol. Ther. Methods Clin. Dev. 2020, 19, 35–46. [Google Scholar] [CrossRef]
- Shahraki, S.; Bideskan, A.E.; Aslzare, M.; Tavakkoli, M.; Bahrami, A.R.; Hosseinian, S.; Matin, M.M.; Rad, A.K. Decellularization with Triton X-100 provides a suitable model for human kidney bioengineering using human mesenchymal stem cells. Life Sci. 2022, 295, 120167. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Zhao, X.; Su, W.; Tang, X. Triton X-100 modified ATP-responsive siRNA delivery agent for antitumor therapy. Mol. Pharm. 2021, 17, 3696–3708. [Google Scholar] [CrossRef]
- Mavani, A.; Ray, D.; Aswal, V.K.; Bhattacharyya, J. Application of drug aggregation to solubilize antimicrobial compound and enhancing its bioavailability. Appl. Biochem. Biotechnol. 2023, 195, 3206–3216. [Google Scholar] [CrossRef]
- Maya, S.A.; Shumon, M.A.H.; Islam, M.R.; Khan, J.M.; Khan, S.A.; Rana, S.; Hoque, M.A.; Rahman, M.M. Investigation of the impact of several diols on the phase behavior and physico-chemical quantities associated with the Triton X-100 and antidiabetic drug mixture. J. Indian Chem. Soc. 2024, 101, 101295. [Google Scholar] [CrossRef]
- Siposova, K.; Sedlak, E.; Kozar, T.; Nemergut, M.; Musatov, A. Dual effect of non-ionic detergent Triton X-100 on insulin amyloid formation. Colloids Surf. B Biointerfaces 2019, 173, 709–718. [Google Scholar] [CrossRef] [PubMed]
- Abdelfattah, A.; Samir, R.; Amin, H.M. Production of highly immunogenic and safe Triton X-100 produced bacterial ghost vaccine against Shigella flexneri 2b serotype. Gut Pathog. 2023, 15, 41. [Google Scholar] [CrossRef] [PubMed]
- Colavita, F.; Quartu, S.; Lalle, E.; Bordi, L.; Lapa, D.; Meschi, S.; Vulcano, A.; Toffoletti, A.; Bordi, E.; Paglia, M.G.; et al. Evaluation of inactivation effect of Triton X-100 on Ebola virus infectivity. J. Clin. Virol. 2017, 86, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Chong, R.; Rho, J.-E.R.; Yoon, H.-J.; Park, P.S.; Rho, T.-H.D.; Park, J.Y.; Park, L.; Kim, Y.-H.; Lee, J.H. Role of Triton X-100 in chemiluminescent enzyme immunoassays capable of diagnosing genetic disorders. Talanta 2013, 116, 403–408. [Google Scholar] [CrossRef] [PubMed]
- Unver, Y.; Yildiz, S.; Acar, M. Extracellular production of azurin from Pseudomonas aeruginosa in the presence of Triton X-100 or Tween 80. Bioprocess Biosyst. Eng. 2022, 45, 553–561. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, J.; Roy, S.; Pandey, P.; Mohanty, S.; Tandon, R.; Ghosh, S. Macrophage plasticity and differentiation on the decellularized human cornea. J. Mater. Res. 2023, 38, 4625–4640. [Google Scholar] [CrossRef]
- Asgari, F.; Asgari, H.R.; Najafi, M.; Eftekhari, B.S.; Vardiani, M.; Gholipourmalekabadi, M.; Koruji, M. Optimization of decellularized human placental macroporous scaffolds for spermatogonial stem cells homing. J. Mater. Sci. Mater. Med. 2021, 32, 47. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Jiang, D.; Zhang, J.; Lin, Q.; Huang, Z. Synthesis of organized hydroxyapatite (HA) using triton X-100. Ceram. Int. 2010, 36, 2441–2447. [Google Scholar] [CrossRef]
- Liu, P.; Luo, Y.; Liu, R.; Fan, W.; Fan, B. Triton X-100 enhanced antibacterial effect of photodynamic therapy against Enterococcus faecalis infection: An in vitro study. Colloids Surf. B Biointerfaces 2024, 240, 113978. [Google Scholar] [CrossRef]
- Muthusamy, P.; Antony, S.A.; Palani, G.; Saravanan, D.; Chithambaram, V. Synergistic in vitro antimicrobial activity of caffeine/AgNPs-triton X-100. Appl. Phys. A 2023, 129, 611. [Google Scholar] [CrossRef]
- Duan, M.; Sun, Q.; Fan, W.; Fan, B. Enhanced antibacterial effect against Enterococcus faecalis by silver ions plus Triton X-100 with low concentrations and cytotoxicity. Braz. J. Microbiol. 2022, 53, 161–169. [Google Scholar] [CrossRef] [PubMed]
- Rajabathar, J.R.; Arunachalam, P.; Al-Lohedan, H.A.; Thankappan, R.; Appaturi, J.N.; Pulingam, T.; Dahan, W.M. Polymer surfactant (Triton-100) assisted low cost method for preparing silver and graphene oxide modified Bi-MnOx nanocomposite for enhanced sensor and anti-microbial health care applications. J. Sol-Gel Sci. Technol. 2021, 97, 638–650. [Google Scholar] [CrossRef]
- Hristozova, A.D.; Simitchiev, K.K.; Kmetov, V.J.; Rosenberg, E. Compatibility of cloud point extraction with gas chromatography: Matrix effects of Triton X-100 on GC-MS and GC-MS/MS analysis of organochlorine and organophosphorus pesticides. Talanta 2024, 269, 125445. [Google Scholar] [CrossRef] [PubMed]
- Yurchenko, O.I.; Cherozhuk, T.V.; Kravchenko, O.A.; Baklanov, O.M. Determination of Zn, Mn, and Cd in strata water. J. Water Chem. Technol. 2022, 44, 26–30. [Google Scholar] [CrossRef]
- Yu, Q.; Mou, X.; Guo, L.; Chen, Z.; Lin, R.; Ding, Y. Triton X-100-directed synthesis of carbon nitride and nitrogen-doped carbon for ethylene dichloride dehydrochlorination. Carbon 2022, 196, 110–119. [Google Scholar] [CrossRef]
- Reddy, N.B.; Sundar, C.S.; Rani, C.R.; Rao, K.U.M.; Nayak, S.K.; Reddy, C.S. Triton X-100 catalyzed synthesis of α-aminophosphonates. Arab. J. Chem. 2016, 9, S685–S690. [Google Scholar] [CrossRef]
- Babbar, N.; Sharma, G.; Arya, S.K. Effective degradation of chicken feather waste by keratinase enzyme with Triton X-100 additive. Biocatal. Agric. Biotechnol. 2022, 44, 102447. [Google Scholar] [CrossRef]
- Wang, G.-L.; Din, A.U.; Qiu, Y.-S.; Wang, C.-L.; Wang, D.-H.; Wei, G.-Y. Triton X-100 improves co-production of β-1,3-D-glucan and pullulan by Aureobasidium pullulans. Appl. Microbiol. Biotechnol. 2020, 104, 10685–10696. [Google Scholar] [CrossRef] [PubMed]
- Trinh, T.H.T.; Kim, J.; Lee, C.-H.; Ryou, C. Non-ionic detergents Nonidet P-40 and Triton X-100 increase enzymatic activity of plasmin. Biochem. Biophys. Res. Commun. 2019, 512, 314–318. [Google Scholar] [CrossRef] [PubMed]
- Duan, X.; Zou, C.; Wu, J. Triton X-100 enhances the solubility and secretion ratio of aggregation-prone pullulanase produced in Escherichia coli. Bioresour. Technol. 2015, 194, 137–143. [Google Scholar] [CrossRef]
- Zheng, K.; Xia, W.; Wang, R.; Li, Y.; Zhang, W. Synergistic effect of Triton X-100 and kerosene on the flotation removal of unburned carbon from fly ash. Colloids Surf. A Physicochem. Eng. Asp. 2021, 622, 126668. [Google Scholar] [CrossRef]
- de Oliveira, A.E.; Ahuiar, M.L.; Guerra, V.G. Improved filter media with PVA/citric acid/Triton X-100 nanofibers for filtration of nanoparticles from air. Polym. Bull. 2021, 78, 6387–6408. [Google Scholar] [CrossRef]
- Feng, Y.; Tao, Y.; Qu, J.; Zhang, Y. Remediation of PAHs-contaminated soil by coupling Triton X-100 assisted washing and BiOBr/g-C3N4 photocatalytic process: Insights to the degradation mechanism and soil washing recycling. Chem. Eng. J. 2024, 497, 154285. [Google Scholar] [CrossRef]
- Shen, W.; Xu, J.; Zhu, L. Triton X-100 improves the reactivity and selectivity of sulfidized nanoscale zerovalent iron toward tetrabromobisphenol A: Implications for groundwater and soil remediation. J. Hazard. Mater. 2021, 416, 126119. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Huang, H.; Yi, F.; Wang, M.; Cheng, C.W. Inhibitory effect of calcium carbonate precipitation induced by Triton X-100 and microorganisms on coal dust. Constr. Build. Mater. 2024, 444, 137887. [Google Scholar] [CrossRef]
- Mahdi, W.A.; Hussain, A.; Bukhari, S.I.; Alshehri, S.; Singh, B.; Ali, N. Removal of clarithromycin from aqueous solution using water/Triton X-100/ethanol/olive oil green nanoemulsion method. J. Water Process Eng. 2021, 40, 101973. [Google Scholar] [CrossRef]
- Steevensz, A.; Madur, S.; Feng, W.; Taylor, K.E.; Bewtra, J.K.; Biswas, N. Crude soybean hull peroxidase treatment of phenol in synthetic and real wastewater: Enzyme economy enhanced by Triton X-100. Enzyme Microb. Technol. 2014, 55, 65–71. [Google Scholar] [CrossRef] [PubMed]
- Benderrag, A.; Haddou, B.; Daaou, M.; Benkhedja, H.; Bounaceur, B.; Kameche, M. Experimental and modeling studies on Cd (II) ions extraction by emulsion liquid membrane using Triton X-100 as biodegradable surfactant. J. Environ. Chem. Eng. 2019, 7, 103166. [Google Scholar] [CrossRef]
- Suwanchawalit, C.; Buddee, S.; Wongnawa, S. Triton X-100 induced cuboid-like BiVO4 microsphere with high photocatalytic performance. J. Environ. Sci. 2017, 55, 257–265. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Gao, X.; Ai, L.; Fan, H. Triton X-100-assisted synthesis of layered nanosheet-assembled flower-like BiOBr nanostructures with enhanced visible-light photocatalytic degradation of ciprofloxacin. J. Nanopart. Res. 2022, 24, 103. [Google Scholar] [CrossRef]
- Cong, R.P.; Guo, Y.H.; Zhou, J.Q.; Wang, J.W. Effect of Triton X-100 on Shiraia laccase production and its application in triclosan biodegradation. Sustain. Chem. Pharm. 2023, 35, 101209. [Google Scholar] [CrossRef]
- Dave, B.P.; Ghevariya, C.M.; Bhatt, J.K.; Dudhagara, D.R.; Rajpara, R.K. Enhanced biodegradation of total polycyclic aromatic hydrocarbons (TPAHs) by marine halotolerant Achromobacter xylosoxidans using Triton X-100 and β-cyclodextrin—A microcosm approach. Mar. Pollut. Bull. 2014, 79, 123–129. [Google Scholar] [CrossRef]
- Soares, M.E.; Araujo, A.J.; Silva, F.S.; Silva, M.R.A.; Barbosa, N.V. Regeneration of transformer oil using a microemulsion with Triton X-100. Braz. J. Chem. Eng. 2023, 40, 901–911. [Google Scholar] [CrossRef]
- Sardar, R.H.; Bera, A.; Chattopadhyay, S.; Mahato, J.C.; Sarraf, S.; Basu, A.K. Effect of dopants in the HTL layer on photovoltaic properties in hybrid perovskite solar cells. J. Mater. Sci. Mater. Electron. 2023, 34, 2138. [Google Scholar] [CrossRef]
- Rahman, M.F.; Hossain, J.; Kuddus, A.; Moon, M.M.A.; Ismail, A.B.M. Effect of Triton X-100 surfactant on thiol-amine cosolvents assisted facile synthesized CdS thin films on glass substrate by spin coating method. SN Appl. Sci. 2020, 2, 590. [Google Scholar] [CrossRef]
- Jung, Y.-S.; Yoo, B.; Lim, M.K.; Lee, S.Y.; Kim, K.-J. Effect of Triton X-100 in water-added electrolytes on the performance of dye-sensitized solar cells. Electrochim. Acta 2009, 54, 6286–6291. [Google Scholar] [CrossRef]
- Yeoh, C.H.; Chua, C.L.; Woon, K.L. Effects of nanoscale surface modification and triplet energy shielding of a single layer solution processed blue phosphorescent organic light emitting diode by using Triton X-100. Synth. Met. 2013, 172, 44–48. [Google Scholar] [CrossRef]
- Shinde, S.K.; Fulari, V.J.; Kim, D.-Y.; Maile, N.C.; Koli, R.R.; Dhaygude, H.D.; Ghodake, G.S. Chemical synthesis of flower-like hybrid Cu(OH)2/CuO electrode: Application of polyvinyl alcohol and Triton X-100 to enhance supercapacitor performance. Colloids Surf. B Biointerfaces 2017, 156, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Dissanayake, S.M.B.; Wimalasena, I.G.K.J.; Keppetipola, N.M.; Karunarathne, B.C.; Madagedara, A.D.T.; Cojocaru, L.; Uchida, S.; Rajapakse, R.M.G.; Tennakone, K.; Yoshimura, M.; et al. Effect of Triton X-100 surfactant concentration on the wettability of polyethylene-based separators used in supercapacitors. J. Sci. Adv. Mater. Devices 2024, 9, 100801. [Google Scholar] [CrossRef]
- Tevi, T.; Birch, S.W.S.; Thomas, S.W.; Takshi, A. Effect of Triton X-100 on the double layer capacitance and conductivity of poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS) films. Synth. Met. 2014, 191, 59–65. [Google Scholar] [CrossRef]
- Iyyappan, E.; Wilson, P. Synthesis of nanoscale hydroxyapatite particles using Triton X-100 as an organic modifier. Ceram. Int. 2013, 39, 771–777. [Google Scholar] [CrossRef]
- Kimura, K.; Gibo, M.; Nerome, C.; Kura, T.; Ooshiro, S.; Tamaki, Y. Nanoparticle formation by laser ablation of perylene microcrystals in an aqueous solution of Triton X-100. Chem. Phys. Lett. 2018, 691, 271–275. [Google Scholar] [CrossRef]
- Ramakanth, I.; Kolenčík, M.; Rao, M.S.; Sunil, B.R.; Vijayasree, U.; Durgababu, G.; Devi, S.A.; Šebesta, M.; Siva, T. Tuning the morphology and state of aggregation of fullerene C60 using non-ionic surfactants. Colloid J. 2021, 83, 474–482. [Google Scholar] [CrossRef]
- Daniele, V.; Taglieri, G. Synthesis of Ca(OH)2 nanoparticles with the addition of Triton X-100. Protective treatments on natural stones: Preliminary results. J. Cult. Herit. 2012, 13, 40–46. [Google Scholar] [CrossRef]
- Memon, A.F.; Ameen, S.; Qambrani, N.; Buledi, J.A.; Khand, N.H.; Solangi, A.R.; Taqvi, S.I.H.; Karaman, C.; Karimi, F.; Afsharmanesh, E. An improved electrochemical sensor based on Triton X-100 functionalized SnO2 nanoparticles for ultrasensitive determination of cadmium. Chemosphere 2022, 300, 134634. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhang, G.; Song, L.; Kuang, G.; Ding, Y.; Bu, S.; Chai, Y.; Fu, Y. Ultra-sensitive electrochemiluminescence monitoring of microRNA via Triton X-100 functionalized carbon dots-based nanocomposites. Sens. Actuators B Chem. 2024, 405, 135314. [Google Scholar] [CrossRef]
- Fonseca, L.P.; Pedrini, L.F.K.; Lima, J.V.M.; Escaliante, L.C.; Santos, S.B.O.; Scalvi, L.V.A. Enhancement of surface properties of sol gel tin dioxide thin films with addition of surfactant in the precursor solution. Appl. Phys. A 2021, 127, 503. [Google Scholar] [CrossRef]
- Li, F.; Li, H.; Jiang, H.; Zhang, K.; Chang, K.; Jia, S.; Jiang, W.; Shang, Y.; Lu, W.; Deng, S.; et al. Polypyrrole nanoparticles fabricated via Triton X-100 micelles template approach and their acetone gas sensing property. Appl. Surf. Sci. 2013, 280, 212–218. [Google Scholar] [CrossRef]
- Mukdasai, K.; Mukdasai, S. The fabrication of in situ Triton X-100 on multi-walled carbon nanotubes modified gold electrode for sensitive determination of caffeine. Int. J. Electrochem. Sci. 2018, 13, 58–70. [Google Scholar] [CrossRef]
- Pandey, P.; Somers, A.E.; Hait, S.K.; Forsyth, M.; Ramakumar, S.S.V. Short chain imidazolium ionic liquids: Synthesis and oil miscibility in various base oil by use of surfactant as high performance friction and antiwear lubricant additive. Tribol. Lett. 2021, 69, 95. [Google Scholar] [CrossRef]
- Attia, A.; Abdel-Fatah, H.T.M. Triton X-100 as a non-ionic surfactant for corrosion inhibition of mild steel during acid cleaning. Met. Mater. Int. 2020, 26, 1715–1724. [Google Scholar] [CrossRef]
- Abd-El-Nabey, B.A.; El-Housseiny, S.; Abd-El-Fatah, M.A. Improved corrosion resistance of permanganate-phosphate conversion coat on steel surface by surfactants. Sci. Rep. 2023, 13, 15781. [Google Scholar] [CrossRef] [PubMed]
- Rabaeh, K.A.; Basfar, A.A.; Moussa, A.A. Enhancement in sensitivity of nitro blue tetrazolium polyvinyl alcohol film dosimeters by sodium formate and Triton X-100. Radiat. Phys. Chem. 2012, 81, 479–483. [Google Scholar] [CrossRef]
- Maharaj, D.; Mohammed, T.; Mohammed, A.; Addison, L. Enhanced digestion of complex cosmetic matrices for analysis of As, Hg, Cd, Cr, Ni, and Pb using Triton X-100. MethodsX 2021, 8, 101241. [Google Scholar] [CrossRef]
- Robinson, J.E.; Sutton, C.M.; Reid, G.F. Dilute Triton X-100 in water as a reference liquid for hydrometer calibration using Cuckow’s method. Measurement 2014, 57, 132–137. [Google Scholar] [CrossRef]
- Nigam, S.; Rutan, S. Principles and applications of solvatochromism. Appl. Spectrosc. 2001, 55, 362A–370A. [Google Scholar] [CrossRef]
- Dorohoi, D.O.; Creanga, D.E.; Dimitriu, D.G.; Morosanu, A.C.; Gritco-Todirascu, A.; Mariciuc, G.G.; Puica Melniciuc, N.; Ardelean, E.; Cheptea, C. Computational and spectral means for characterizing the intermolecular interactions in solutions and for estimating excited state dipole moment of solute. Symmetry 2020, 12, 1299. [Google Scholar] [CrossRef]
- Dorohoi, D.O.; Gosav, S.; Morosanu, A.C.; Dimitriu, D.G.; Apreotesei, G.; Gosav, T. Molecular descriptors—Spectral properties relations for characterizing molecular interactions in binary and ternary solutions, excited state dipole moment estimation. Symmetry 2023, 15, 2075. [Google Scholar] [CrossRef]
- Babusca, D.; Benchea, A.C.; Dimitriu, D.G.; Dorohoi, D.O. Solvatochromic characterization of Sudan derivatives in binary and ternary solutions. Anal. Lett. 2016, 49, 2615–2626. [Google Scholar] [CrossRef]
- Dulcescu-Oprea, M.M.; Morosanu, A.C.; Dimitriu, D.G.; Gritco-Todirascu, A.; Dorohoi, D.O.; Cheptea, C. Solvatochromic study of pyridinium-acetyl-benzoyl methylid (PABM) in ternary protic solutions. J. Mol. Struct. 2021, 1227, 129539. [Google Scholar] [CrossRef]
- Dorohoi, D.O.; Dimitriu, D.G.; Morosanu, A.C.; Puica Melniciuc, N.; Hurjui, I.; Miron, M.; Mariciuc, G.G.; Closca, V.; Cheptea, C. Some aryl-1,2,4-triazol-1-ium phenacylids in binary hydroxyl solvent mixtures. Computational and spectral study. Symmetry 2021, 13, 1656. [Google Scholar] [CrossRef]
- Pavel, C.M.; Ambrosi, E.; Dimitriu, D.G.; Dorohoi, D.O. Complex formation and microheterogeneity in water-alcohol binary mixtures investigated by solvatochromic study. Eur. Phys. J. Spec. Top. 2023, 232, 415–425. [Google Scholar] [CrossRef]
- Cheptea, C.; Zara, A.; Ambrosi, E.; Morosanu, A.C.; Diaconu, M.; Miron, M.; Dorohoi, D.O.; Dimitriu, D.G. On the solvatochromism of fluorescein sodium. Symmetry 2024, 16, 673. [Google Scholar] [CrossRef]
- Pop, V.; Dorohoi, D.O.; Delibas, M. Considerations on the statistical model of intermolecular interactions in ternary solutions. An. St. Univ. Al. I. Cuza s. Ib 1986, 32, 79–84. [Google Scholar]
- Suppan, P. Local polarity of solvent mixtures in the field of electronically excited molecules and exciplexes. J. Chem. Soc. Faraday Trans 1 1987, 83, 495–509. [Google Scholar] [CrossRef]
- Bosch, E.; Rosés, M. Relationships between ET polarity and composition in binary solvent mixtures. J. Chem. Soc. Faraday Trans. 1992, 88, 3541–3546. [Google Scholar] [CrossRef]
- Rosés, M.; Ràfols, C.; Ortega, J.; Bosch, E. Solute-solvent and solvent-solvent interactions in binary solvent mixtures. Part 1. A comparison of several preferential solvation models for describing ET(30) polarity of dipolar hydrogen bond acceptor-cosolvent mixtures. J. Chem. Soc. Perkin Trans. 2 1995, 1995, 1607–1615. [Google Scholar] [CrossRef]
- Bosch, E.; Rosés, M.; Herodes, K.; Koppel, I.; Leito, I.; Koppel, I.; Taal, V. Solute-solvent and solvent-solvent interactions in binary solvent mixtures. Part 2. Effect of temperature on the ET(30) polarity parameter of dipolar hydrogen bond acceptor-hydrogen bond donor mixtures. J. Phys. Org. Chem. 1996, 9, 403–410. [Google Scholar] [CrossRef]
- Ortega, J.; Ràfols, C.; Bosch, E.; Rosés, M. Solute-solvent and solvent-solvent interactions in binary solvent mixtures. Part 3. The ET(30) polarity of binary mixtures of hydroxylic solvents. J. Chem. Soc. Perkin Trans. 2 1996, 1996, 1497–1503. [Google Scholar] [CrossRef]
- Kohantorabi, M.; Salari, H.; Fakhraee, M.; Gholami, M.R. Surfactant binary systems: Ab initio calculations, preferential solvation, and investigation of solvatochromic parameters. J. Chem. Eng. Data 2016, 61, 255–263. [Google Scholar] [CrossRef]
- Kohantorabi, M.; Fakhraee, M.; Salari, H.; Gholami, M.R. Probing solvent-solvent and solute-solvent interactions in surfactant binary mixtures: Solvatochromic parameters, preferential solvation, and quantum theory of atoms in molecules analysis. RSC Adv. 2016, 6, 18515. [Google Scholar] [CrossRef]
- Kamlet, M.J.; Abboud, J.L.M.; Taft, R.W. An examination of linear solvation energy relationships. In Progress in Physical Organic Chemistry; Taft, R.W., Ed.; Wiley Interscience: New York, NY, USA, 1981; Volume 13, pp. 485–630. [Google Scholar]
- Kamlet, M.J.; Abboud, J.L.; Taft, R.W. The solvatochromic comparison method. 6. The π* scale of solvent polarities. J. Am. Chem. Soc. 1977, 99, 6027–6038. [Google Scholar] [CrossRef]
- Taft, R.W.; Kamlet, M.J. The solvatochromic comparison method. 2. The α-scale of solvent hydrogen-bond donor (HBD) acidities. J. Am. Chem. Soc. 1976, 98, 2886–2894. [Google Scholar] [CrossRef]
- Kamlet, M.J.; Taft, R.W. The solvatochromic comparison method. I. The β-scale of solvent hydrogen-bond acceptor (HBA) basicities. J. Am. Chem. Soc. 1976, 98, 377–383. [Google Scholar] [CrossRef]
- Sator, N.; Pavloff, N.; Couëdel, L. Statistical Physics; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2024; pp. 138–147. [Google Scholar]
- Van, S.-P.; Hammond, G.S. Amine quenching of aromatic fluorescence and fluorescent exciplexes. J. Am. Chem. Soc. 1978, 100, 3895–3902. [Google Scholar] [CrossRef]
- Papadakis, R. Preferential solvation of a highly medium responsive pentacyanoferrate (II) complex in binary solvent mixtures: Understanding the role of dielectric enrichment and the specificity of solute-solvent interactions. J. Phys. Chem. B 2016, 120, 9422–9433. [Google Scholar] [CrossRef] [PubMed]
- Yadav, S.N.; Rai, S.; Bhattarai, A.; Sinha, B. Interaction between methyl red and cetyltrimethylammonium bromide under the influence of sodium polystyrene sulphonate in ethanol-water binary solvent systems: A spectrophotometric investigation. Heliyon 2024, 10, e33014. [Google Scholar] [CrossRef] [PubMed]
- Minisy, I.M.; Bober, P.; Šeděnková, I.; Stejskal, J. Methyl red dye in the tuning of polypyrrole conductivity. Polymer 2020, 207, 122854. [Google Scholar] [CrossRef]
- Khadka, B.; Bhattarai, A. UV-Vis studies on interaction between sodium dioctylsulfosuccinate (AOT) and methyl red. Rev. Roum. Chim. 2020, 65, 989–996. [Google Scholar] [CrossRef]
- Zhang, J.-H.; Liu, Q.; Chen, Y.-M.; Liu, Z.-Q.; Xu, C.-W. Determination of acid dissociation constant of methyl red by multi-peaks Gaussian fitting method based on UV-Visible absorption spectrum. Acta Phys. Chim. Sin. 2012, 28, 1030–1036. [Google Scholar] [CrossRef]
- Poblete, T.; Millán, D.; Rezende, M.C. Synergism in the solvation of solvatochromic probes in binary mixtures with ionic liquids. J. Mol. Liq. 2023, 391, 123227. [Google Scholar] [CrossRef]
- Fisher, R.A. On the interpretation of χ2 from contingency tables, and the calculation of P. J. R. Stat. Soc. 1922, 85, 87–94. [Google Scholar] [CrossRef]
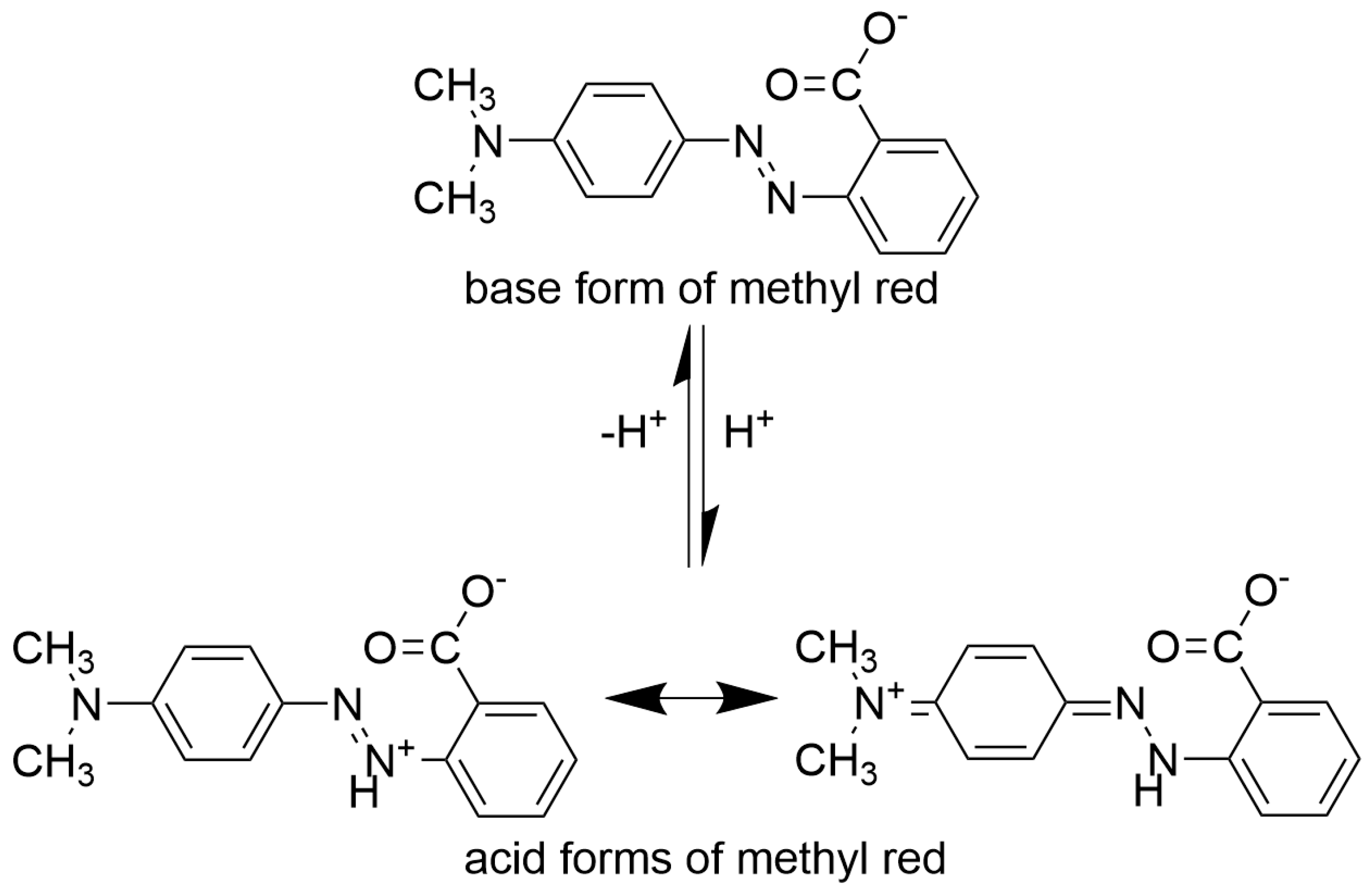
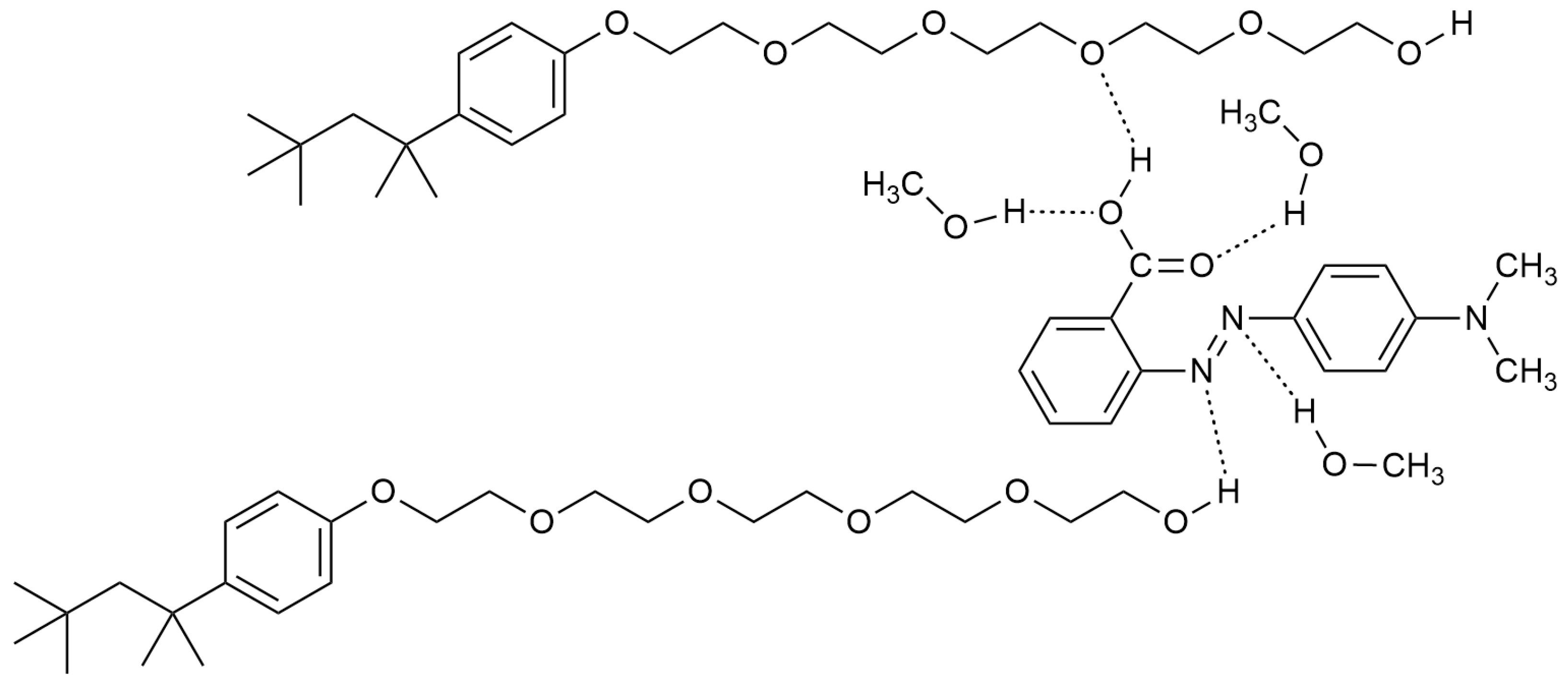
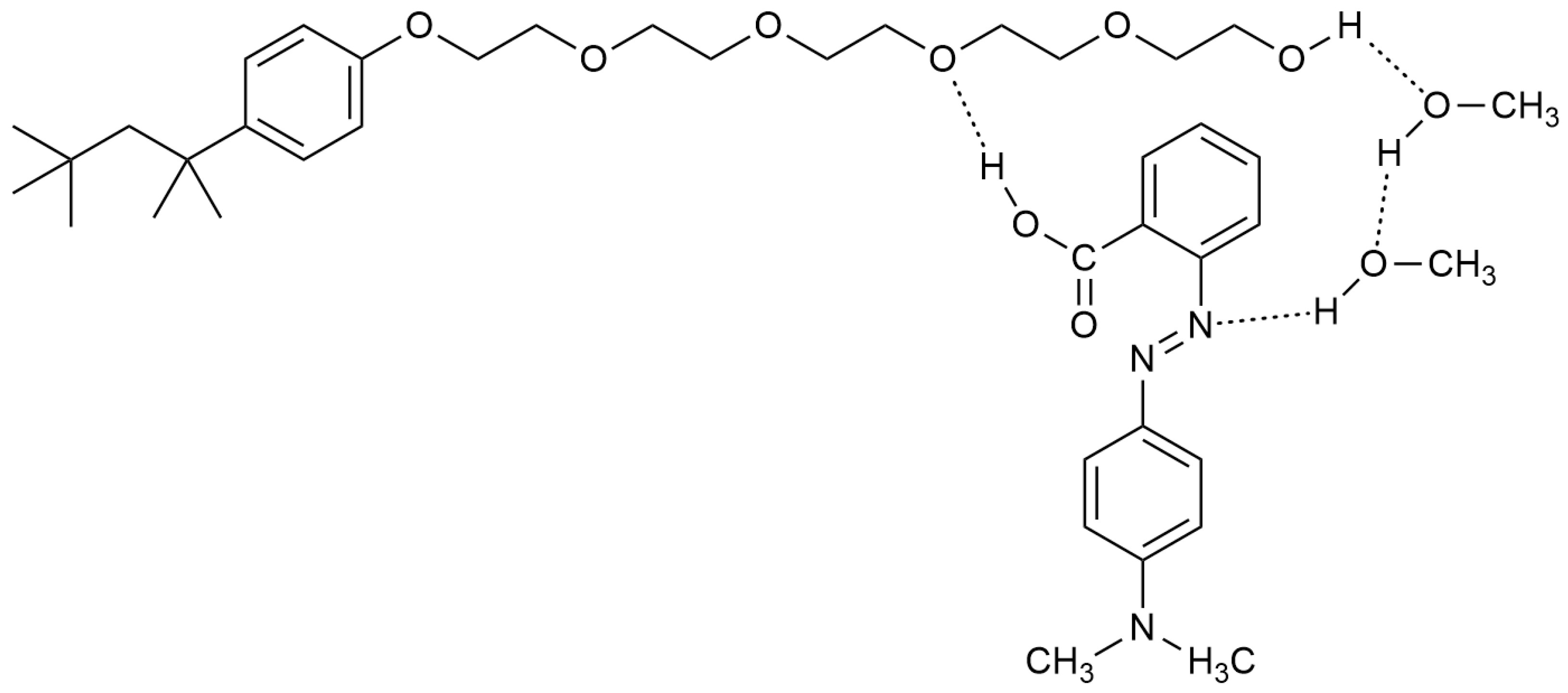
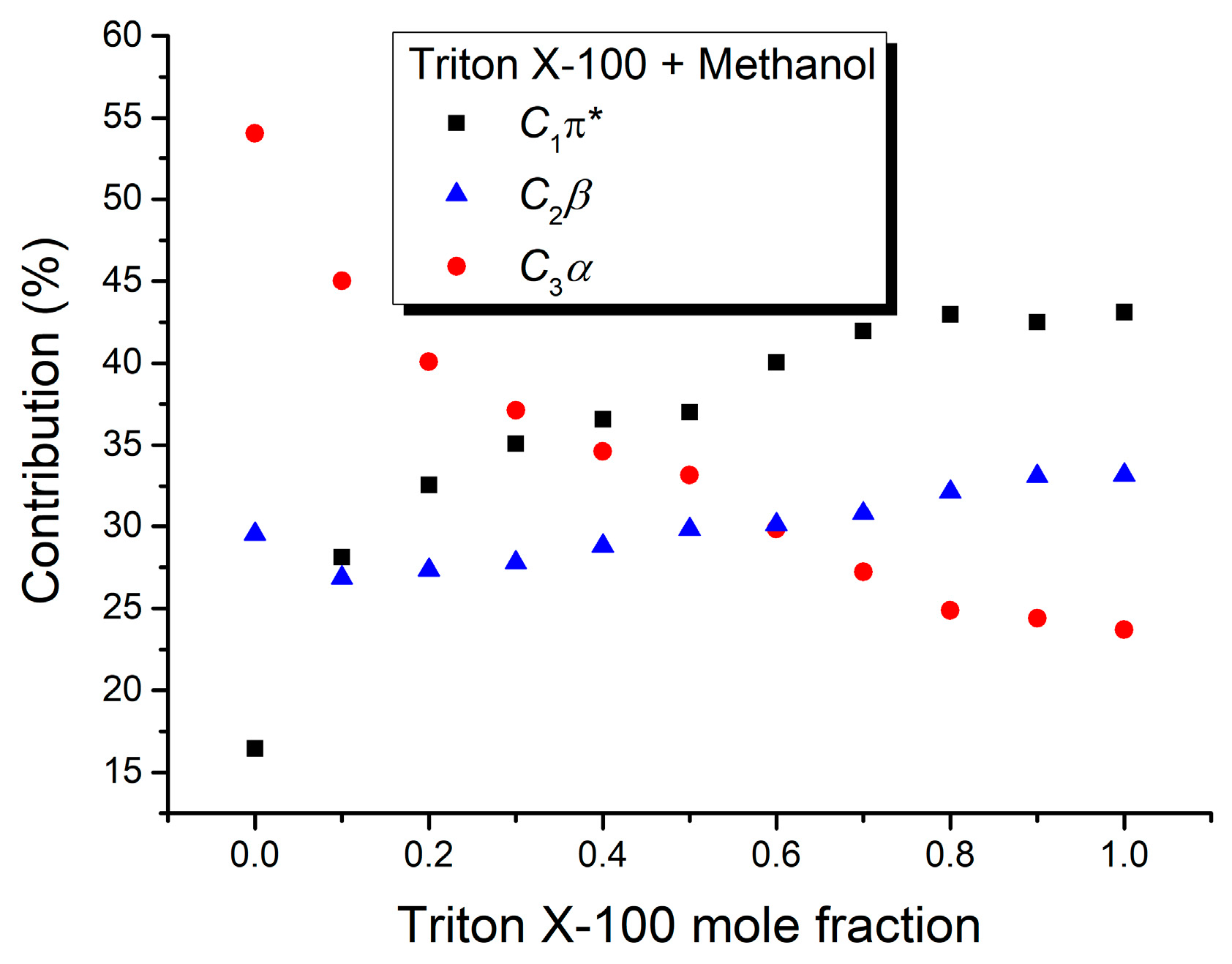
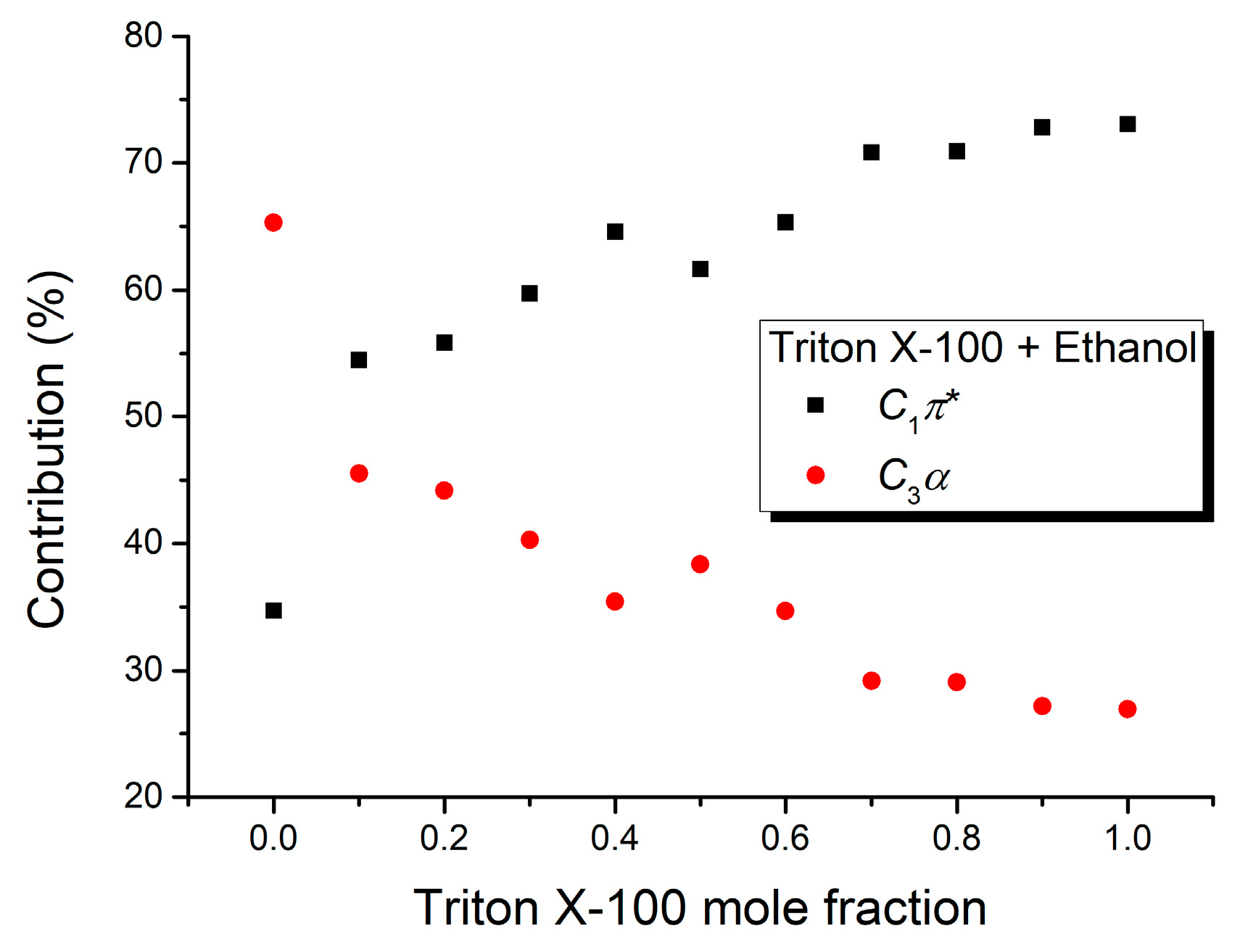

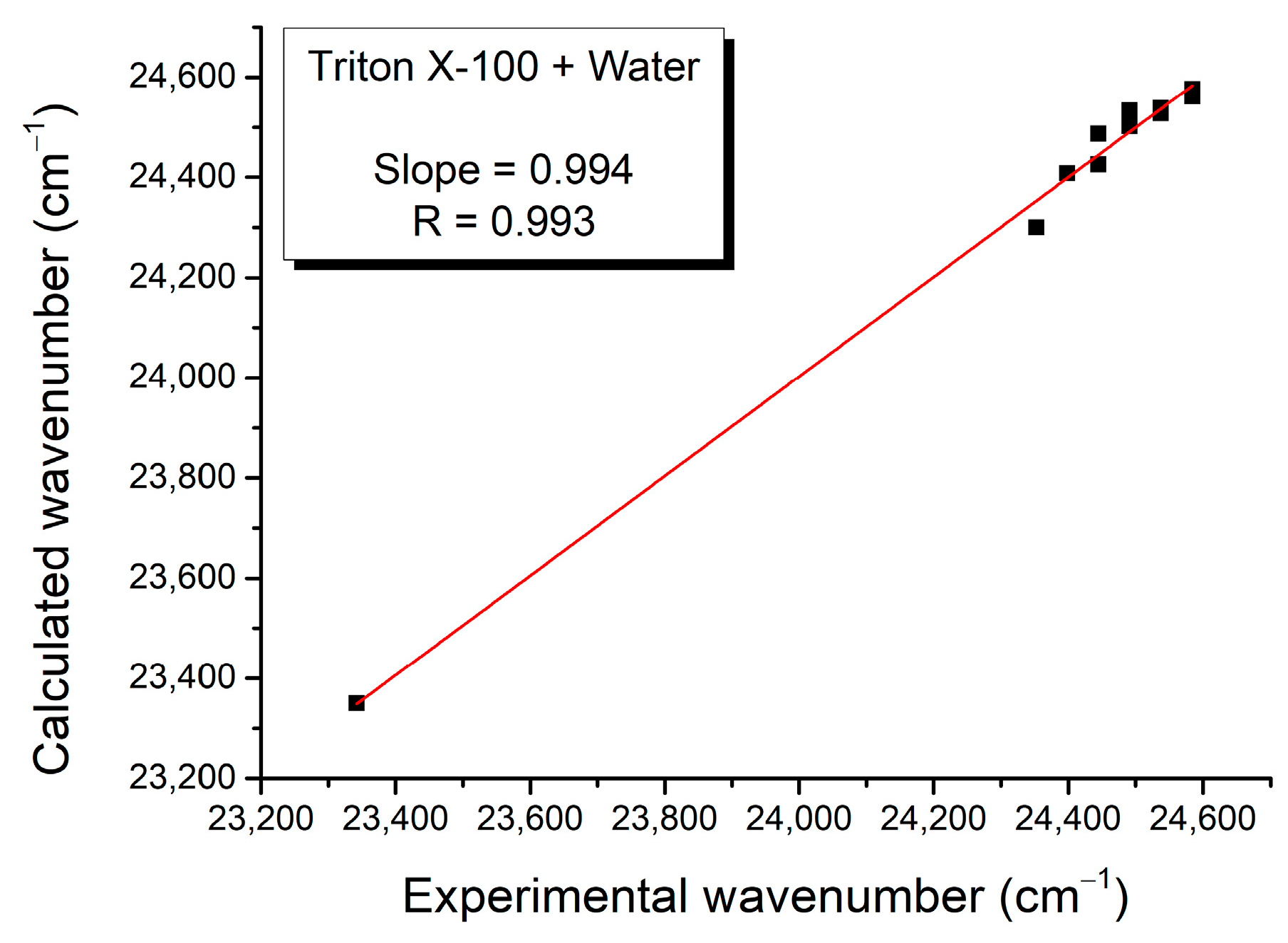
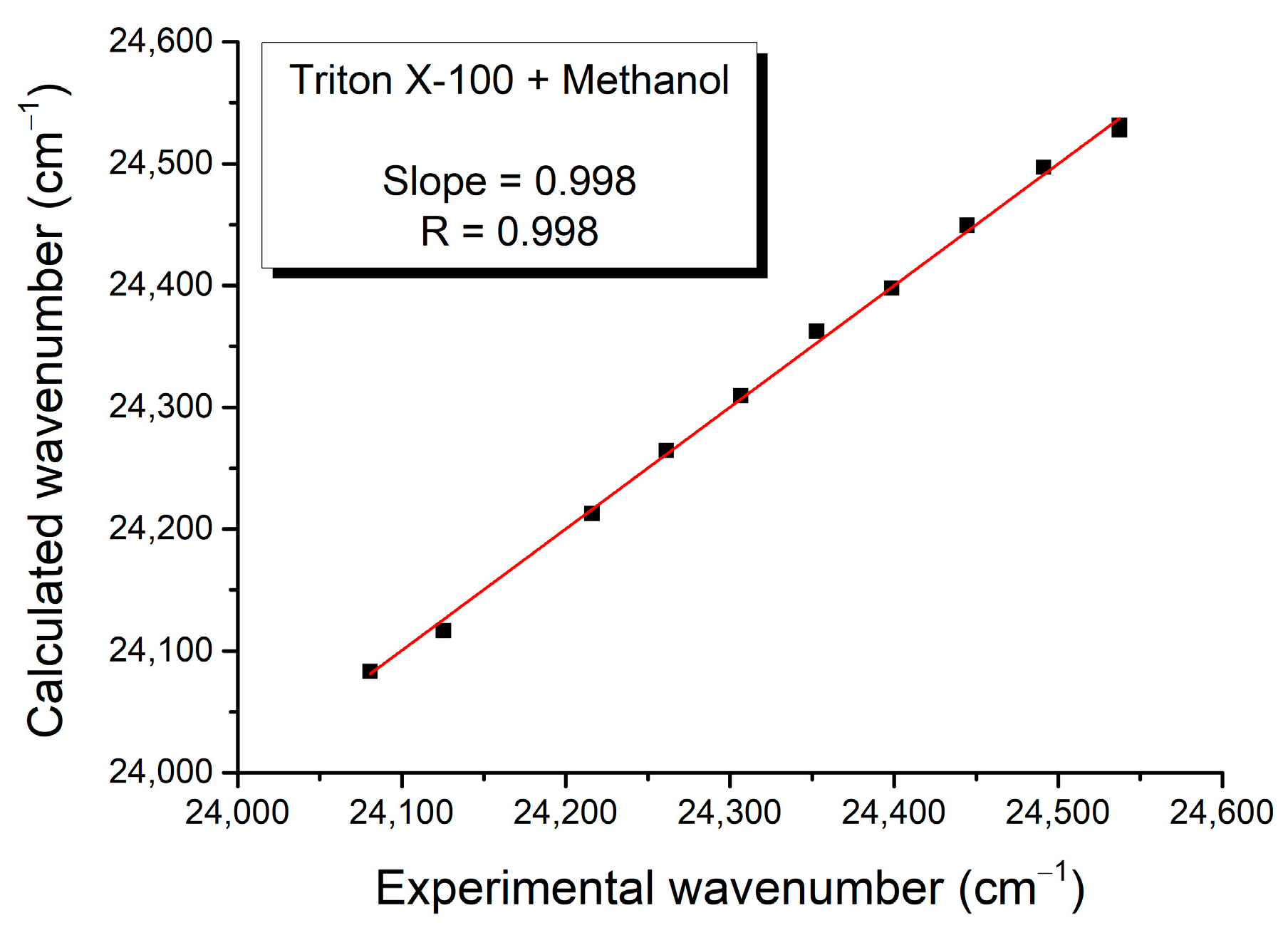


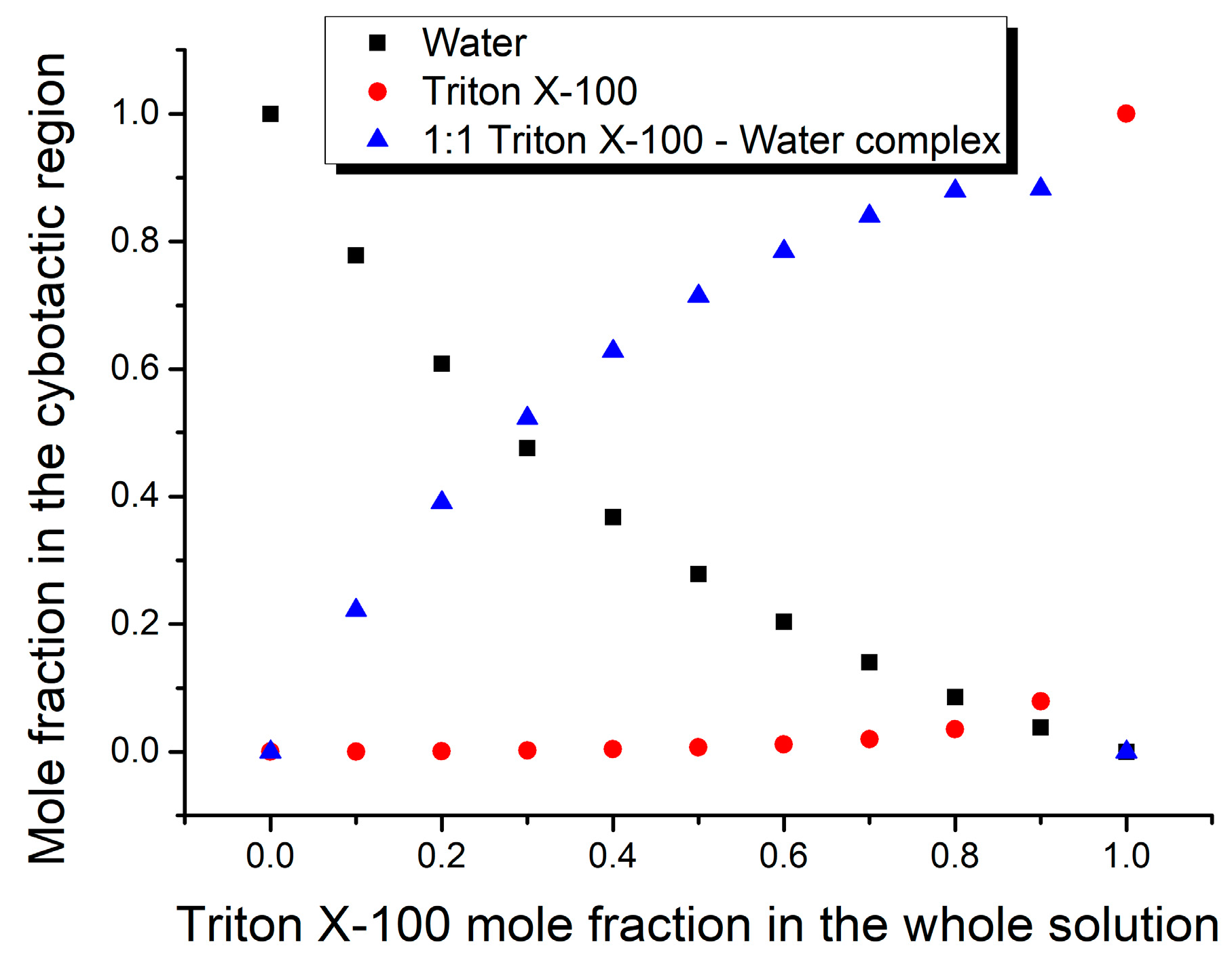

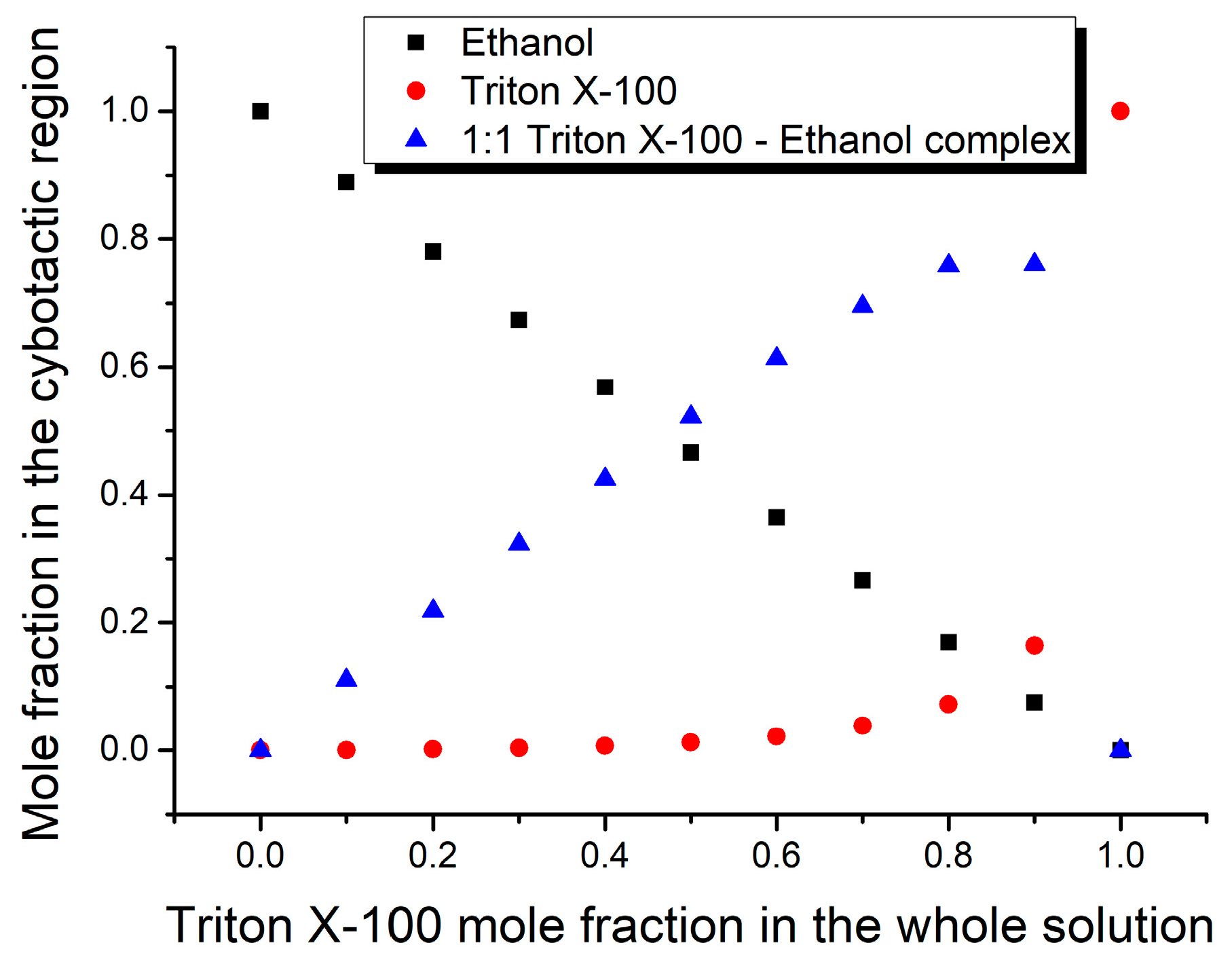

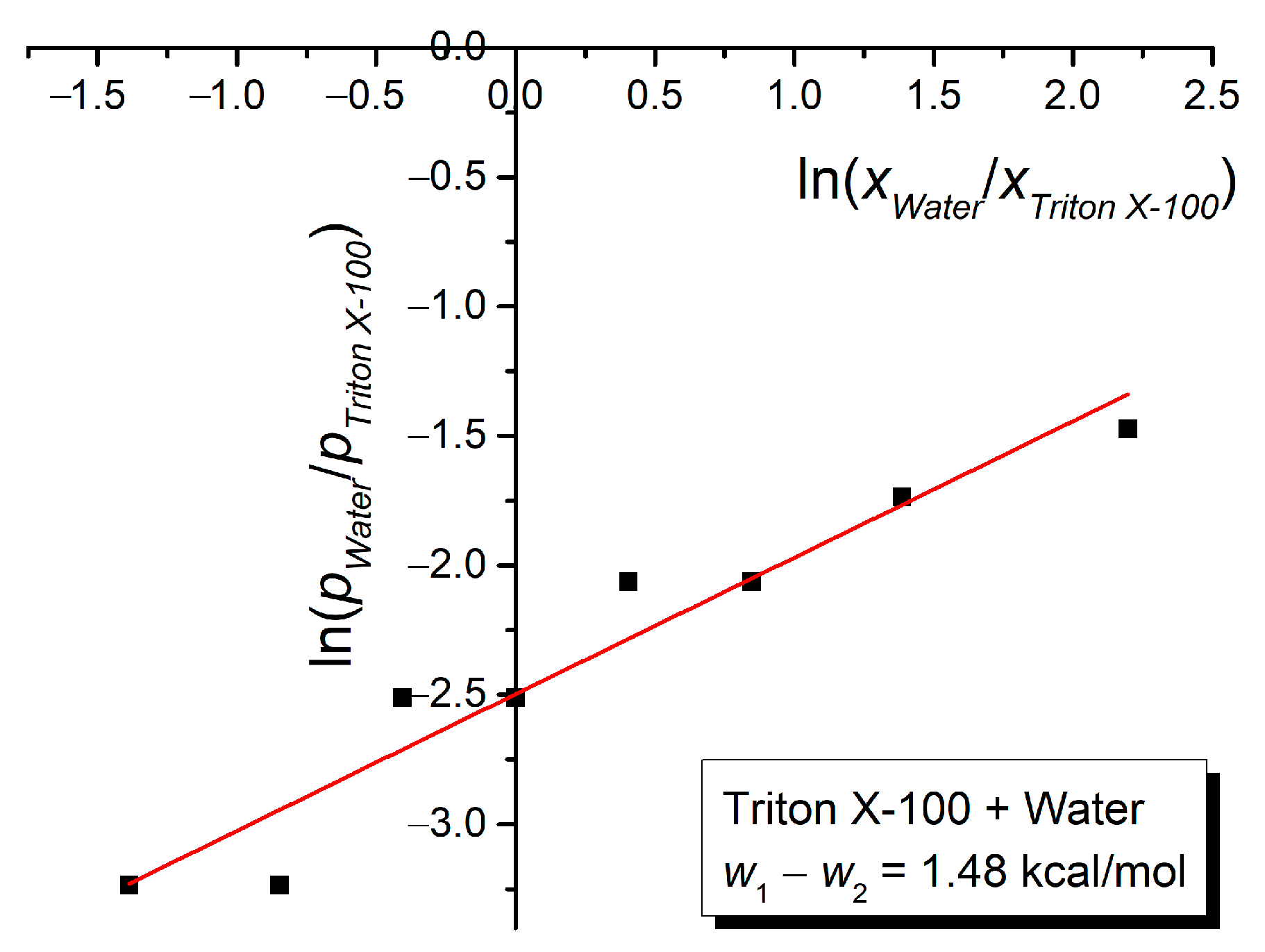
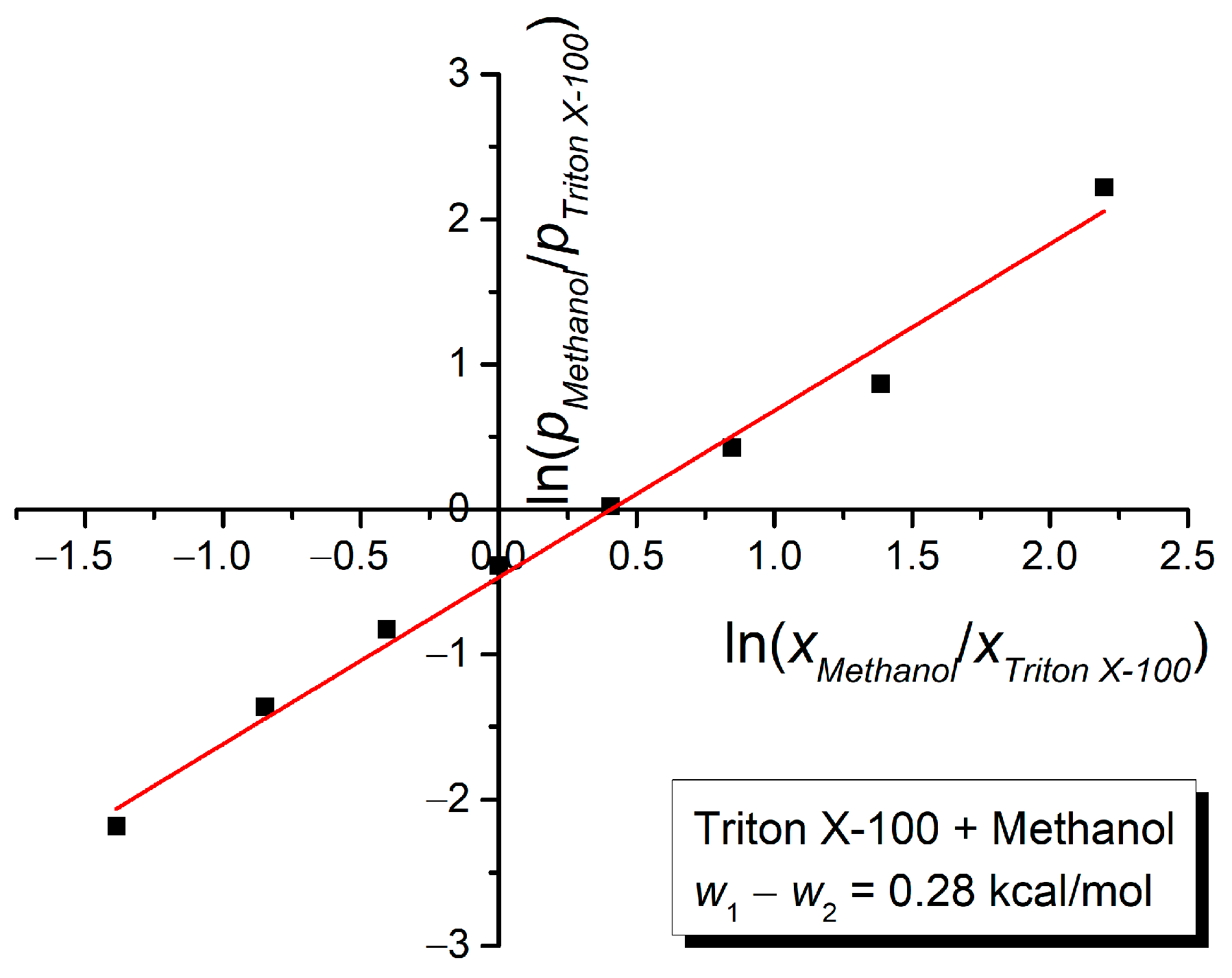

| Mole Fraction of Triton X-100 | π* | β | α | (cm−1) |
|---|---|---|---|---|
| 0.0 | 1.08 | 0.49 | 1.30 | 23,342 |
| 0.1 | 0.88 | 0.63 | 0.59 | 24,353 |
| 0.2 | 0.87 | 0.67 | 0.49 | 24,399 |
| 0.3 | 0.91 | 0.59 | 0.41 | 24,444 |
| 0.4 | 0.88 | 0.62 | 0.39 | 24,444 |
| 0.5 | 0.87 | 0.65 | 0.39 | 24,491 |
| 0.6 | 0.88 | 0.60 | 0.34 | 24,491 |
| 0.7 | 0.87 | 0.62 | 0.35 | 24,537 |
| 0.8 | 0.93 | 0.52 | 0.27 | 24,537 |
| 0.9 | 0.90 | 0.55 | 0.28 | 24,585 |
| 1.0 | 0.87 | 0.57 | 0.31 | 24,585 |
| Mole Fraction of Triton X-100 | π* | β | α | (cm−1) |
|---|---|---|---|---|
| 0.0 | 0.55 | 0.84 | 1.17 | 24,081 |
| 0.1 | 0.80 | 0.65 | 0.83 | 24,125 |
| 0.2 | 0.84 | 0.60 | 0.67 | 24,216 |
| 0.3 | 0.86 | 0.58 | 0.59 | 24,261 |
| 0.4 | 0.88 | 0.59 | 0.54 | 24,307 |
| 0.5 | 0.86 | 0.59 | 0.50 | 24,353 |
| 0.6 | 0.89 | 0.57 | 0.43 | 24,399 |
| 0.7 | 0.88 | 0.55 | 0.37 | 24,444 |
| 0.8 | 0.88 | 0.56 | 0.33 | 24,491 |
| 0.9 | 0.86 | 0.57 | 0.32 | 24,537 |
| 1.0 | 0.87 | 0.57 | 0.31 | 24,585 |
| Mole Fraction of Triton X-100 | π* | β | α | (cm−1) |
|---|---|---|---|---|
| 0.0 | 0.54 | 0.90 | 0.98 | 24,353 |
| 0.1 | 0.82 | 0.62 | 0.66 | 24,399 |
| 0.2 | 0.80 | 0.62 | 0.61 | 24,444 |
| 0.3 | 0.83 | 0.60 | 0.54 | 24,444 |
| 0.4 | 0.87 | 0.56 | 0.46 | 24,444 |
| 0.5 | 0.80 | 0.66 | 0.48 | 24,491 |
| 0.6 | 0.84 | 0.62 | 0.43 | 24,491 |
| 0.7 | 0.88 | 0.57 | 0.35 | 24,537 |
| 0.8 | 0.86 | 0.58 | 0.34 | 24,537 |
| 0.9 | 0.86 | 0.57 | 0.31 | 24,585 |
| 1.0 | 0.87 | 0.57 | 0.31 | 24,585 |
| Mole Fraction of Triton X-100 | π* | β | α | (cm−1) |
|---|---|---|---|---|
| 0.0 | 0.59 | 0.95 | 0.84 | 24,307 |
| 0.1 | 0.71 | 0.72 | 0.66 | 24,353 |
| 0.2 | 0.88 | 0.58 | 0.56 | 24,399 |
| 0.3 | 0.85 | 0.60 | 0.55 | 24,399 |
| 0.4 | 0.86 | 0.58 | 0.47 | 24,444 |
| 0.5 | 0.83 | 0.66 | 0.50 | 24,444 |
| 0.6 | 0.86 | 0.60 | 0.41 | 24,491 |
| 0.7 | 0.85 | 0.61 | 0.38 | 24,491 |
| 0.8 | 0.88 | 0.57 | 0.33 | 24,537 |
| 0.9 | 0.88 | 0.57 | 0.31 | 24,537 |
| 1.0 | 0.87 | 0.57 | 0.31 | 24,585 |
| (cm−1) | C1 | C2 | C3 | Adj. R-Square | F Value |
|---|---|---|---|---|---|
| 29,115 (694) 1 | −5237 (766) | 0.821 | 46.735 | ||
| 22,525 (1105) | 3138 (1860) | 0.156 | 2.846 | ||
| 24,938 (33) | −1194 (60) | 0.975 | 389.796 | ||
| 33,321 (986) | −7625 (668) | −3460 (747) | 0.945 | 87.149 | |
| 26,113 (257) | −1434 (313) | −934 (66) | 0.992 | 639.740 | |
| 24,471 (165) | 746 (260) | −1138 (49) | 0.986 | 355.108 | |
| 27,068 (958) | −2204 (807) | −518 (501) | −833 (118) | 0.992 | 430.510 |
| (cm−1) | C1 | C2 | C3 | Adj. R-Square | F Value |
|---|---|---|---|---|---|
| 23,423 (336) 1 | 1101 (400) | 0.396 | 7.566 | ||
| 25,210 (265) | −1434 (434) | 0.498 | 10.929 | ||
| 24,655 (41) | −569 (68) | 0.873 | 69.116 | ||
| 31,423 (3307) | −4019 (2134) | −6154 (2535) | 0.609 | 8.785 | |
| 25,829 (74) | −1158 (72) | −949 (27) | 0.996 | 1160.524 | |
| 23,910 (53) | 1663 (117) | −1048 (37) | 0.995 | 912.471 | |
| 24,972 (308) | −650 (187) | 764 (270) | −1002 (27) | 0.998 | 1454.548 |
| (cm−1) | C1 | C2 | C3 | Adj. R-Square | F Value |
|---|---|---|---|---|---|
| 24,041 (152) 1 | 542 (186) | 0.429 | 8.511 | ||
| 24,806 (120) | −517 (190) | 0.390 | 7.395 | ||
| 24,654 (26) | −344 (48) | 0.833 | 50.907 | ||
| 22,783 (2103) | 1416 (1469) | 873 (1456) | 0.385 | 4.132 | |
| 25,240 (150) | −569 (145) | −590 (69) | 0.936 | 73.950 | |
| 24,467 (65) | 453 (150) | −536 (73) | 0.912 | 52.958 | |
| 26,028 (780) | −1128 (780) | −511 (497) | −615 (73) | 0.936 | 50.010 |
| (cm−1) | C1 | C2 | C3 | Adj. R-Square | F Value |
|---|---|---|---|---|---|
| 23,890 (146) 1 | 679 (176) | 0.581 | 14.849 | ||
| 24,786 (96) | −529 (149) | 0.538 | 12.643 | ||
| 24,677 (15) | −471 (29) | 0.964 | 271.791 | ||
| 23,664 (1218) | 847 (916) | 138 (737) | 0.530 | 6.646 | |
| 24,905 (83) | −216 (78) | −575 (43) | 0.980 | 241.716 | |
| 24,604 (17) | 208 (43) | −595 (30) | 0.990 | 486.496 | |
| 24,365 (174) | 183 (132) | 339 (103) | −585 (29) | 0.991 | 361.996 |
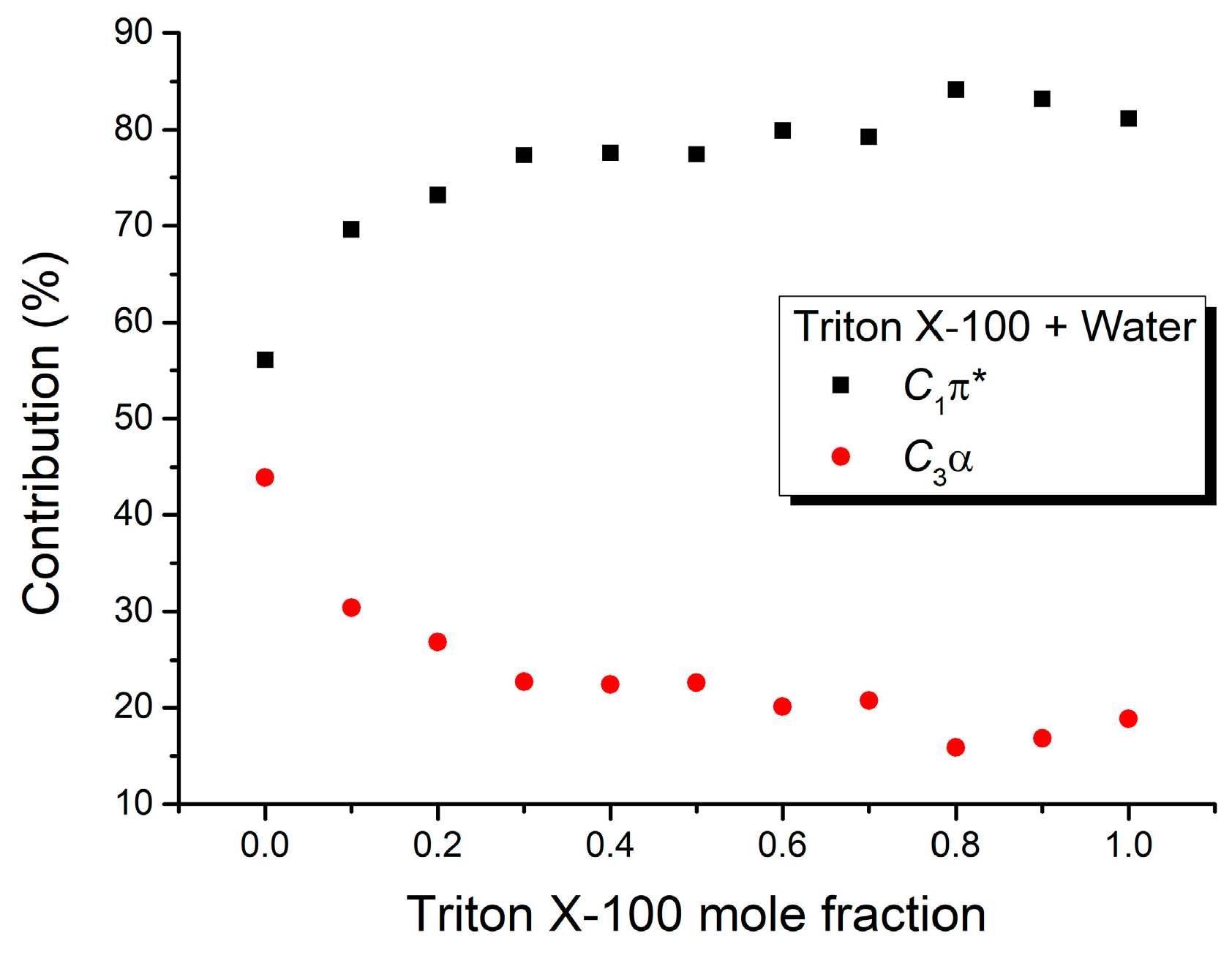
| Mole Fraction of Triton X-100 | C1π* (cm−1) | C1π* (%) | C3α (cm−1) | C3α (%) | (cm−1) |
|---|---|---|---|---|---|
| 0.0 | −1549.17 | 56.07 | −1213.67 | 43.93 | 23,351 |
| 0.1 | −1262.29 | 69.62 | −550.82 | 30.38 | 24,300 |
| 0.2 | −1247.95 | 73.18 | −457.46 | 26.82 | 24,408 |
| 0.3 | −1305.32 | 77.33 | −382.77 | 22.67 | 24,425 |
| 0.4 | −1262.29 | 77.61 | −364.10 | 22.39 | 24,487 |
| 0.5 | −1247.95 | 77.41 | −364.10 | 22.59 | 24,501 |
| 0.6 | −1262.29 | 79.91 | −317.42 | 20.09 | 24,534 |
| 0.7 | −1247.95 | 79.25 | −326.76 | 20.75 | 24,539 |
| 0.8 | −1334.01 | 84.11 | −252.07 | 15.89 | 24,527 |
| 0.9 | −1290.98 | 83.16 | −261.41 | 16.84 | 24,561 |
| 1.0 | −1247.95 | 81.17 | −289.41 | 18.83 | 24,576 |
| Mole Fraction of Triton X-100 | C1π* (cm−1) | C1π* (%) | C2β (cm−1) | C2β (%) | C3α (cm−1) | C3α (%) | (cm−1) |
|---|---|---|---|---|---|---|---|
| 0.0 | −357.47 | 16.46 | 641.44 | 29.54 | −1172.85 | 54.00 | 24,083 |
| 0.1 | −519.95 | 28.13 | 496.35 | 26.85 | −832.02 | 45.02 | 24,117 |
| 0.2 | −545.95 | 32.58 | 458.17 | 27.34 | −671.63 | 40.08 | 24,213 |
| 0.3 | −558.95 | 35.08 | 442.90 | 27.80 | −591.44 | 37.12 | 24,265 |
| 0.4 | −571.94 | 36.57 | 450.54 | 28.81 | −541.32 | 34.62 | 24,309 |
| 0.5 | −558.95 | 37.00 | 450.54 | 29.82 | −501.22 | 33.18 | 24,363 |
| 0.6 | −578.44 | 40.04 | 435.26 | 30.13 | −431.05 | 29.84 | 24,398 |
| 0.7 | −571.94 | 41.97 | 420.00 | 30.82 | −370.90 | 27.22 | 24,449 |
| 0.8 | −571.94 | 42.99 | 427.63 | 32.14 | −330.80 | 24.87 | 24,497 |
| 0.9 | −558.95 | 42.51 | 435.26 | 33.10 | −320.78 | 24.39 | 24,528 |
| 1.0 | −565.45 | 43.12 | 435.26 | 33.19 | −310.76 | 23.70 | 24,531 |
| Mole Fraction of Triton X-100 | C1π* (cm−1) | C1π* (%) | C3α (cm−1) | C3α (%) | (cm−1) |
|---|---|---|---|---|---|
| 0.0 | −307.30 | 34.69 | −578.44 | 65.31 | 24,355 |
| 0.1 | −466.64 | 54.50 | −389.56 | 45.50 | 24,384 |
| 0.2 | −455.25 | 55.84 | −360.05 | 44.16 | 24,425 |
| 0.3 | −472.33 | 59.71 | −318.73 | 40.29 | 24,449 |
| 0.4 | −495.09 | 64.58 | −271.51 | 35.42 | 24,474 |
| 0.5 | −455.25 | 61.64 | −283.32 | 38.36 | 24,502 |
| 0.6 | −478.02 | 65.32 | −253.81 | 34.68 | 24,509 |
| 0.7 | −500.78 | 70.80 | −206.59 | 29.20 | 24,533 |
| 0.8 | −489.40 | 70.92 | −200.68 | 29.08 | 24,550 |
| 0.9 | −489.40 | 72.79 | −182.98 | 27.21 | 24,568 |
| 1.0 | −495.09 | 73.01 | −182.98 | 26.99 | 24,562 |
| Mole Fraction of Triton X-100 | C2β (cm−1) | C2β (%) | C3α (cm−1) | C3α (%) | (cm−1) |
|---|---|---|---|---|---|
| 0.0 | 197.61 | 28.34 | −499.57 | 71.66 | 24,302 |
| 0.1 | 149.77 | 27.62 | −392.52 | 72.38 | 24,361 |
| 0.2 | 120.65 | 26.59 | −333.05 | 73.41 | 24,392 |
| 0.3 | 124.81 | 27.62 | −327.10 | 72.38 | 24,402 |
| 0.4 | 120.65 | 30.15 | −279.52 | 69.85 | 24,445 |
| 0.5 | 137.29 | 31.59 | −297.36 | 68.41 | 24,444 |
| 0.6 | 124.81 | 33.86 | −243.84 | 66.14 | 24,485 |
| 0.7 | 126.89 | 35.96 | −226.00 | 64.04 | 24,505 |
| 0.8 | 118.57 | 37.66 | −196.26 | 62.34 | 24,527 |
| 0.9 | 118.57 | 39.14 | −184.36 | 60.86 | 24,538 |
| 1.0 | 118.57 | 39.14 | −184.36 | 60.86 | 24,538 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ambrosi, E.; Zara, A.; Dorohoi, D.O.; Dimitriu, D.-G. Solvatochromic Analysis of Triton X-100 in Binary Mixtures. Symmetry 2025, 17, 199. https://doi.org/10.3390/sym17020199
Ambrosi E, Zara A, Dorohoi DO, Dimitriu D-G. Solvatochromic Analysis of Triton X-100 in Binary Mixtures. Symmetry. 2025; 17(2):199. https://doi.org/10.3390/sym17020199
Chicago/Turabian StyleAmbrosi, Ecaterina, Alexandru Zara, Dana Ortansa Dorohoi, and Dan-Gheorghe Dimitriu. 2025. "Solvatochromic Analysis of Triton X-100 in Binary Mixtures" Symmetry 17, no. 2: 199. https://doi.org/10.3390/sym17020199
APA StyleAmbrosi, E., Zara, A., Dorohoi, D. O., & Dimitriu, D.-G. (2025). Solvatochromic Analysis of Triton X-100 in Binary Mixtures. Symmetry, 17(2), 199. https://doi.org/10.3390/sym17020199






