Efficient Parallel Design for Self-Play in Two-Player Zero-Sum Games

Abstract

Self-play methods have achieved remarkable success in two-player zero-sum games, attaining superhuman performance in many complex game domains. Parallelizing learners is a feasible approach to handle complex games. However, parallelizing learners often leads to the suboptimal exploitation of computational resources, resulting in inefficiencies. This paper introduces the Mixed Hierarchical Oracle (MHO), which is designed to enhance training efficiency and performance in complex two-player zero-sum games. MHO efficiently leverages interaction data among parallelized solvers during the Parallelized Oracle (PO) process, while employing Model Soups (MS) to consolidate fragmented computational resources and Hierarchical Exploration (HE) to balance exploration and exploitation. These carefully designed enhancements for parallelized systems significantly improve the training performance of self-play. Additionally, MiniStar is introduced as an open source environment focused on small-scale combat scenarios, developed to facilitate research in self-play algorithms. The MHO is evaluated on both the AlphaStar888 matrix game and MiniStar environment, and ablation studies further demonstrates its effectiveness in improving the agent’s decision-making capabilities. This work highlight the potential of the MHO to optimize compute resource utilization and improve performance in self-play methods.

1. Introduction

Multi-agent reinforcement learning (MARL) [1] presents unique challenges due to the interdependence of agents’ actions, which causes the environment to appear non-stationary from the perspective of each agent [2,3]. Key difficulties in MARL include coordination and equilibrium selection, especially in competitive scenarios. These challenges often hinder convergence, destabilize learning processes, and complicate efficient policy space exploration.

Two-player zero-sum games are a prominent setting within MARL due to their analytical tractability and symmetry, making them a central focus of both theoretical and applied research. In this context, self-play has emerged as a promising approach to address the inherent complexities of MARL in competitive scenarios. By training an agent against copies or past versions of itself [4,5], self-play provides a stable and tractable learning framework. This approach has found widespread applications across various domains, demonstrating notable success in games such as Go [6,7,8,9], chess [8,9], poker [10,11], and video games [12,13], often exceeding human-level performance.

However, traditional self-play methods [14,15,16] face limitations in complex game environments characterized by vast strategy spaces [17]. The Policy Space Response Oracle (PSRO) [18] extends the Double Oracle (DO) [14] to large-scale games by integrating Reinforcement Learning (RL) [19] to approximate the best responses. The PSRO leverages Empirical Game-Theoretic Analysis (EGTA) [20,21] to study meta-strategies obtained through simulations, and it incorporates a meta-strategy solver to select adversarial strategies. This synthesis of the EGTA with RL enhances strategy selection in self-play while guaranteeing convergence toward the approximate Nash Equilibrium (NE).

Despite these advances, the PSRO continues to face significant computational challenges, with best response oracle calculations in complex scenarios remaining prohibitively expensive. Parallelizing the learning process offers a promising solution to address this challenge [18,22]. Deep Cognitive Hierarchy (DCH) [18] organizes training into a hierarchy, where each learner uses deep RL to train an oracle policy against the NE of a meta-game, improving training efficiency with oracle parallelism. Building upon DCH’s foundation, the P-PSRO [23] initializes a population of active policies with assigned hierarchical levels. The P-PSRO improves training efficiency via the parallelized warm-start training of higher-level active policies, employing the NE computed from lower-level policies. A key innovation of the P-PSRO is its optimization of the training hierarchy itself, alleviating the limitation of DCH, which needs to predetermine the number of PSRO iterations. The rectified PSRO (PSRO-rN) [24] is another PSRO of the parallel oracle, where each oracle is trained with the policies it currently beats, reducing redundant policies and improving training efficiency.

Nevertheless, resource utilization and training efficiency remain significant bottlenecks. Current methods for oracle parallelization typically distribute computational resources uniformly across all oracles, leading to suboptimal efficiency. Moreover, in the P-PSRO, the data generated from interactions between high-level active policies and low-level active policies are not utilized for training the low-level active policies, further reducing training efficiency. Additionally, there remain untapped opportunities to optimize parallelized RL oracles and fully realize their potential.

To address these challenges, this paper introduces the MHO framework, which advances parallel oracle methods through three synergistic innovations. First, the MHO employs the PO, which concurrently trains oracles across hierarchical levels, leveraging cross-level interaction data. This approach enhances training efficiency by using high-level vs. low-level policy trajectories to train both participating oracles. Second, the framework employs parameter fusion techniques, MS, to consolidate scattered training resources and initialize new oracles through strategic combinations of existing policy parameters. This approach mitigates cold-start inefficiencies while ensuring competitive viability against lower-level policies. Third, the MHO introduces a hierarchical mechanism, HE, which adjusts exploration–exploitation tradeoffs across hierarchy levels, with higher-level policies emphasizing exploration and lower-level policies focusing on exploitation.

This paper also introduces an open source environment for MiniStar, a variant of SMACv2 [25]. SMACv2 serves as a popular benchmark in MARL [26,27,28], but it only allows for controlling agents while relying on a built-in bot for the opposing side, thus preventing self-play between two learning agents. To overcome this limitation, MiniStar extends SMACv2 by permitting control over both sides, removing the need for a built-in bot and enabling self-play. By narrowing the scope to tactical engagements rather than full-length strategies, MiniStar decreases the complexity tied to long-horizon decision-making and highlights the core aspects of self-play algorithms without extensive RL optimization.

The principal contributions of this work can be summarized as follows:

• A formal analysis and empirical validation of the inefficiencies in current parallelized best response oracle systems.
• The MHO framework, improving training efficiency and strategic performance in complex games through optimized parallelization.
• MiniStar, a purpose-built benchmark environment for self-play research in tactical combat scenarios.

The remainder of this paper is structured as follows. Section 2 reviews the related work on self-play methods and simulation environments. Section 3 introduces the necessary theoretical preliminaries. Section 4 details the MHO framework, elaborating on its three key components—PO, MS, and HE. Section 5 provides extensive empirical evaluations, including benchmark experiments in AlphaStar888 and MiniStar, with comprehensive ablation studies to assess the impact of each MHO component. Finally, Section 6 concludes the paper with a summary of the findings and a discussion of future research directions.

2. Related Works

2.1. Self-Play Methods

In vanilla self-play [4], agents are trained by repeatedly playing against their latest versions. Fictitious Self-Play (FSP) [11] enables agents to play against their past selves to learn optimal strategies. Neural fictitious self-play [15] is a modern variant that combines FSP with deep learning techniques, using neural networks to approximate the best response. Prioritized fictitious self-play [13] utilizes a preference function to assign higher selection probabilities to higher-priority agents. The DO [14] method approximates the NE in zero-sum games by iteratively creating and solving a series of sub-games with a restricted set of pure strategies. The PSRO [18] is a generalization of the DO, using RL as an oracle to enable decision-making in complex gaming environments. It introduces the concept of a meta-strategy solver to assist in the selection of adversarial strategies, which guarantees convergence to an approximate NE.

To improve the efficiency of self-play training, distributed RL has been integrated into the oracle computation, significantly accelerating the learning process. Distributed RL utilizes parallelized environment sampling to enhance scalability, allowing agents to train in more complex settings. Techniques such as IMPALA [29] and Ape-X [30] have demonstrated efficient learning across various environments through distributed architectures. MALib [31] introduces a highly optimized computational framework that combines distributed RL with self-play, further improving training efficiency.

Unlike distributed RL, which parallelizes environment sampling, DCH [18] parallelizes the oracle computation in self-play and enhances training efficiency through training multiple oracles. The P-PSRO [23] builds upon DCH by refining its parallelization strategy and eliminating the requirement to predetermine the number of PSRO iterations, which is a limitation of DCH. The PSRO-rN [24] introduces an alternative form of parallelized best response oracle training, where each oracle is specifically trained against the policies it currently defeats, promoting greater strategic diversity.

2.2. Self-Play Simulation Environment

Compared to traditional board and card games, simulation environments are typically characterized by real-time operations, long periods, and higher complexity of environmental state transitions, such as StarCraft II [32], Google Research Football (GRF) [33], Dota 2 [12], and Honor of Kings [34,35,36]. These environments present agents with real-time, partially observable settings requiring continuous decision making over extended time horizons. Agents must handle large, continuous action spaces and deal with uncertainties introduced by dynamic opponents and environments. The complexity and high dimensionality of these environments necessitate extensive RL and engineering optimization before effective self-play can be conducted. For instance, AlphaStar [13] combines RL, self-play, and imitation learning [37] to achieve master-level performance using vast computational resources. OpenAI Five [12] demonstrates that self-play could be scaled to achieve superhuman performance in Dota 2 by training agents in a massively parallel framework. Similarly, Honor of Kings requires extensive feature processing and complex engineering optimizations to facilitate effective self-play training [34,35,36]. Even relatively small-scale GRF environments demand substantial pretraining, including imitation learning and curriculum learning, before self-play can be conducted successfully [38,39].

In contrast, lightweight multi-agent environments such as SMAC [40] and SMACv2 [25] provide a more accessible testing ground. However, these environments do not natively support self-play, as they are designed for training agents against built-in bots, rather than learning through direct competition between two learning agents. This limitation restricts their applicability in self-play research.

Motivated by this gap, MiniStar is introduced as a lightweight simulation environment designed to facilitate self-play training. MiniStar is a variant of SMACv2 that retains the core characteristics of SMACv2 while overcoming its limitation of training only against built-in bots. By enabling direct competition between learning agents, MiniStar provides a practical and efficient platform for studying self-play without the need for extensive RL engineering.

3. Preliminaries

3.1. Two-Player Normal-Form Games

A two-player normal-form game [41] is characterized by the tuple $(\mathcal{A},\mathbf{U})$, where $\mathcal{A}=({\mathcal{A}}_1,{\mathcal{A}}_2)$ represents the action sets for each player $i\in \{1,2\}$, and $\mathbf{U}=(u_1,u_2)$ denotes their respective utility functions. Formally, for each player i, the utility function $u_i:{\mathcal{A}}_1\times {\mathcal{A}}_2\to \mathbb{R}$ assigns a real-valued payoff to every possible action pair.

Players aim to maximize their expected utility by choosing a mixed strategy ${\pi }_i\in \Delta \left({\mathcal{A}}_i\right)$, where $\Delta \left({\mathcal{A}}_i\right)$ denotes the set of probability distributions over ${\mathcal{A}}_i$. For notational convenience, the opponent of player i is denoted as $-i$. The best response to an opponent’s mixed strategy ${\pi }_{-i}$ is the strategy $\mathcal{BR}\left({\pi }_{-i}\right)$ that maximizes player i’s utility as follows:

$$\mathcal{BR}\left({\pi }_{-i}\right)=arg\underset{{\pi }_i}{max}{G}_i({\pi }_i,{\pi }_{-i}),$$

(1)

where $G_i({\pi }_i,{\pi }_{-i})$ denotes the expected utility for player i when using policy ${\pi }_i$ against the opponent’s policy ${\pi }_{-i}$.

3.2. Meta-Strategy

The concept of a meta-game extends the game to a higher level of abstraction by considering a population of policies ${\Pi }_i={\pi }_i^1,{\pi }_i^2,\dots$ for each player i. In this context, choosing an action corresponds to selecting a specific policy from the set ${\Pi }_i$. The interactions within this expanded policy space are captured by the payoff matrix $M_{{\Pi }_i,{\Pi }_{-i}}$, where $M_{{\Pi }_i,{\Pi }_{-i}}[j,k]=G_i({\pi }_i^j,{\pi }_{-i}^k)$.

In the meta-game, a meta-strategy ${\sigma }_i$ represents a mixed strategy over the policy set ${\Pi }_i$, assigning probabilities to each policy in the set. Meta-games are often open-ended because an infinite number of mixed strategies can be constructed from the available policies.

In self-play methods, each player i maintains a set of strategies ${\Pi }_i$ for themselves and observes the opponent’s strategy set ${\Pi }_{-i}$. This framework allows for the construction of a meta-strategy ${\sigma }_i$ to elucidate the dynamics between players’ policies. The meta-strategy ${\sigma }_i$ for player i is derived from various solvers such as NE, fictitious play [42], or prioritized fictitious self-play.

When a new policy ${\pi }_i^{\prime }$ is introduced, the framework recalculates the best response, often referred to as the oracle. If the oracle is determined through RL, the best response is represented as follows:

$$\mathcal{BR}\left({\sigma }_{-i}\right)=\underset{{\pi }_i^{\prime }}{max}\sum _j{\sigma }_{-i}^j{E}_{{\pi }_i^{\prime },{\pi }_{-i}^j}\left[R\right],$$

(2)

where R denotes the RL reward, typically configured in a zero-sum setting, and $E_{{\pi }_i^{\prime },{\pi }_{-i}^j}\left[R\right]$ represents the expected reward when player i uses policy ${\pi }_i^{\prime }$ against the opponent’s policy ${\pi }_{-i}^j$.

To quantify how far the joint meta-strategy profile $\sigma =({\sigma }_1,{\sigma }_2)$ is from a NE, exploitability is measured using NashConv as follows [18]:

$$\mathrm{Expl}\left(\sigma \right)=\sum _{i=1}^2\left[G_i(\mathcal{BR}\left({\sigma }_{-i}\right),{\sigma }_{-i})-G_i({\sigma }_i,{\sigma }_{-i})\right],$$

(3)

where $\mathcal{BR}\left({\sigma }_{-i}\right)$ denotes the best response oracle to the opponent’s meta-strategy ${\sigma }_{-i}$. When the exploitability reaches zero, the joint meta-strategy profile $\sigma$ corresponds to a NE.

4. Methodology

This section introduces the MHO framework, which significantly enhance the training efficiency and performance of RL agents in self-play algorithms, particularly in complex environments. The MHO comprises the following three key components: PO, MS, and HE. These components aim to address the training efficiency of the policy learning process from different perspectives—sample utilization, cold-start issues, and exploration mechanisms—and are ultimately integrated to work synergistically. The detailed framework is illustrated in Figure 1, and the step-by-step procedure is provided in Algorithm 1.

Algorithm 1 Mixed Hierarchical Oracle (MHO)

1: Initialize the policy set ${\Pi }^f$.   2: /* Parallelized Oracle. */   3: Parallelize n active policies to initialize the active policy set ${\Pi }^a$.   4: Compute the meta-strategy ${\sigma }_i^j$ using fictitious self-play for the j-th active policy ${\pi }_i^j$.   5: for epoch in $\{1,2,...\}$ do   6:     for player $i\in \{1,2\}$ do   7:         for many episodes do   8:            /* Distributed, simultaneous. */   9:            for active policy ${\pi }_i^j\in {\Pi }^a$ do 10:                Sample ${\pi }_{-i}\sim {\sigma }_{-i}^j$. 11:                /* Hierarchical Exploration. */ 12:                Train ${\pi }_i^j$ using the objective in Equation (7). 13:            end for 14:         end for 15:         if ${\pi }_i^j$ converges (plateaus) and is the lowest-level active policy then 16:            Update the fixed policy set: ${\Pi }_i^f\leftarrow {\Pi }_i^f\cup \left\{{\pi }_i^j\right\}$. 17:            Remove the policy from the active set: ${\Pi }_i^a\leftarrow {\Pi }_i^a\backslash \left\{{\pi }_i^j\right\}$. 18:            /* Model Soups. */ 19:            Initialize new active policy ${\pi }_i^n$ at a higher level than all existing active policies. 20:            Update ${\pi }_i^n$ via MS (Equation (6)). 21:            Add the new policy to the active set: ${\Pi }_i^a\leftarrow {\Pi }_i^a\cup \left\{{\pi }_i^n\right\}$. 22:           Update the meta-strategy ${\sigma }_i$ for each active policy. 23:         end if 24:     end for 25: end for 26: Output the current lowest active policy as the final trained policy.

4.1. Parallelized Oracle

In P-PSRO training, two critical issues arise. First, when a high-level active policy samples experience against a lower-level active policy, only the high-level policy’s corresponding samples are retained for training; samples that belongs to the lower-level policy are discarded. For instance, as illustrated in Figure 1 (sample dispatch stage), when ${\pi }^4$ plays against ${\pi }^3$, the data generated for ${\pi }^3$ are not allocated to ${\pi }^3$ for learning. Second, each active policy during training is allocated an equal portion of the total computational resources, which reduces training efficiency.

To address the first issue identified in the P-PSRO, this study introduces a PO approach. The PO maintains a fixed policy set (${\Pi }^f$) and an active policy set (${\Pi }^a$). ${\Pi }^f$ retains the fixed model parameter, while ${\Pi }^a$ is trained by n parallel RL workers, each operating at the corresponding hierarchical level among n levels. Each active policy ${\pi }_i^j$ is trained against the meta-strategy derived from ${\Pi }^f$ and ${\Pi }^a$, which are obtained from lower levels of the hierarchy. When a high-level active policy interacts with a lower-level active policy, all resulting data samples are redistributed to the corresponding active policies. Once the lowest-level active policy ${\pi }_i^j$ converges, ${\pi }_i^j$ then transitions from ${\Pi }^a$ to ${\Pi }^f$, and ${\pi }_i^{j+1}$ becomes the new lowest-level active policy. A new active policy ${\pi }_i^n$ is initialized at a higher level than all existing active policies, marking the beginning of a new training cycle.

To more clearly illustrate the advantages of the PO over existing parallelized best response oracle systems, particularly the P-PSRO, a formal comparative analysis is conducted. In the PO approach, $w_{\mathrm{active},j}$ denotes the total sampling probability of the j-th policy interacting with all other active policies except itself. Let $m(m<j)$ be the number of active policies and n be the total number of sample environments. For the k-th active policy, the cumulative increase in the number of samples from other active policies $\Delta S_k$ is given by the following:

$$\Delta S_k={\displaystyle \frac{n}{m}}\times w_{\mathrm{active},j-m+k},$$

(4)

the total increase number of samples $\Delta S_{\mathrm{total}}$ is then adjusted as follows:

$$\Delta S_{\mathrm{total}}={\displaystyle \frac{n}{m}}\times \sum _{k=1}^m{w}_{\mathrm{active},j-m+k}.$$

(5)

During parallel training, each active policy further utilizes the data generated by the high-level policy while training with the fixed policy. Equation (5) demonstrates that the PO approach can leverage a larger volume of data, $\Delta S_{\mathrm{total}}$, than existing parallelized methods, without discarding any of them, thereby enhancing sample efficiency during training.

Although the PO approach alters how training data are gathered and redistributed, it does not significantly erode the approximate best response properties. In particular, when FSP is used as the meta-strategy solver, the method approximately retains the same convergence characteristics as standard FSP. This occurs because, as training progresses, the fixed policies dominate the overall strategy distribution.

4.2. Model Soups

To address the second issue in P-PSRO, where allocating equal computational resources leads to proportionally reduced training capacity for each oracle, the model fusion approach, MS, is incorporated to mitigate this limitation. This method effectively consolidates computational resources. Additionally, MS resolve the cold-start problem. When models are initialized from scratch in each new training round, agents may struggle to develop effective policies as opponents become increasingly strong. By employing MS, each oracle begins with a well-established policy foundation, thereby enhancing learning efficiency and overall performance.

Specifically, after each round of training, a new top-level active policy is obtained by the parameter fusion of the lower-level active policies and the fixed policies. This fusion shares the knowledge learned among different active policies, enhancing data utilization and accelerating learning in subsequent training rounds.

In the context of MS, the meta-strategy is employed as a weighted combination of the model parameters from the lower-level policies. Mathematically, for the set of policies ${\Pi }_i=\{{\pi }_i^1,{\pi }_i^2,\cdots ,{\pi }_i^j\}$, and ${\theta }_{{\pi }_i^j}$ denotes the parameters of the j-th policy; under the meta-strategy ${\sigma }_i$, the new policy ${\theta }_{{\pi }_i^{j+1}}$ is computed as follows:

$${\theta }_{{\pi }_i^{j+1}}=\sum _{k=1}^j{\sigma }_i^{j+1,k}·{\theta }_{{\pi }_i^k}.$$

(6)

MS mitigate computational fragmentation caused by the PO through the fusion of model parameters across different learners, effectively recombining the split computational resources. This fusion enhances data utilization by sharing knowledge within the policy pool, overcoming the inefficiency of independent learning in parallelized settings.

4.3. Hierarchical Exploration

In self-play algorithms, it is often necessary to truncate the approximate best response operator at each iteration, which can lead to suboptimal training outcomes. To migrate this issue, the exploration mechanism HE is introduced within the PO approach, assigning different exploration factors to various levels of the active policy pool.

Specifically, the highest-level active policies are more inclined to explore during training after initialization, and they gradually shift towards exploitation as training progresses. To achieve this, an entropy regularization term is incorporated into the computation of the best respone oracle. The entropy term encourages exploration by penalizing deterministic behavior in the policy, thus promoting stochasticity during training.

Let $H\left(\pi \right)$ represent the entropy of a policy $\pi$. The objective function for Equation (2) is modified as follows:

$$\mathcal{BR}\left({\sigma }_{-i}\right)=\underset{{\pi }_i^{\prime }}{max}\sum _j{\sigma }_{-i}^j{E}_{{\pi }_i^{\prime },{\pi }_{-i}^j}\left[R\right]-{\lambda }_{k}H\left({\pi }_i^{\prime }\right),$$

(7)

here, ${\lambda }_k$ is a hyperparameter that controls the strength of the entropy regularization. As training progresses, ${\lambda }_k$ decreases in tandem with the shift of policies from high-active to low-active levels, with the highest-level policy having the largest ${\lambda }_k$ value and the lowest-level policy having the smallest. This synchronized reduction of ${\lambda }_k$ ensures that exploration is encouraged early in the training, while policies progressively focus more on exploitation as they transition towards lower activity levels. This mechanism effectively maintains a balance between exploration and exploitation across different policy tiers, ensuring that agents explore sufficiently in the early stages, while refining and exploiting learned strategies in the later stages.

5. Experiments

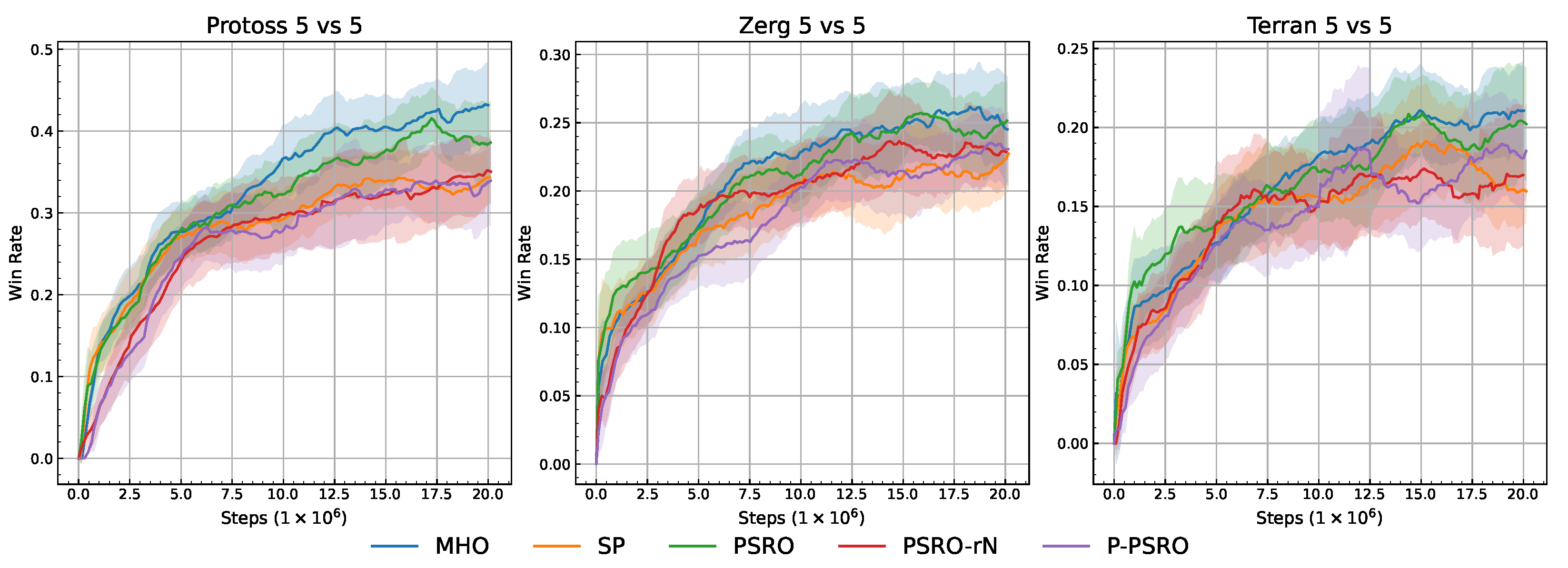
5.1. Experimental Setup

To evaluate the effectiveness of the MHO in complex two-player zero-sum games, this study compares the MHO with representative self-play algorithms, including the PSRO [18], P-PSRO [23], PSRO-rN [24], and Self-Play (SP) [16]. The experiments span both matrix games and the MiniStar environment. The hyperparameter settings for the experiments are provided in Appendix A.

All experiments were implemented in Python (version 3.8.0), utilizing PyTorch (version 1.10.0) for neural network training and optimization, NumPy and Pandas for data processing, and Matplotlib for result visualization. The MiniStar environment was managed using Python to facilitate efficient simulation and interaction. Experiments were conducted on a server equipped with an Intel(R) Xeon(R) CPU E5-2690 v4 processor, 220 GB of RAM, and a NVIDIA RTX 3090 GPU with 24 GB of dedicated memory. This computational setup ensured efficient model training, simulation, and evaluation, accommodating for the intensive requirements of RL and extensive self-play iterations.

5.2. Experimental Environment

5.2.1. Martix Game

AlphaStar888 [43] is an empirical game derived from the solution process of StarCraft II [13], featuring a payoff table involving 888 RL policies. It can be viewed as a zero-sum symmetric two-player game with only one state. In this state, there are 888 legal actions, and any mixed strategy corresponds to a discrete probability distribution over these actions.

5.2.2. Simulation Scenario

The MiniStar environment is a simplified version of StarCraft II [32], designed specifically for skirmish scenarios and self-play research. By focusing on localized battle control rather than the full spectrum of StarCraft II gameplay, which includes resource management, mission planning, and large-scale battle control, MiniStar allows agents to concentrate on the microlevel manipulation of decision-making actions. This targeted approach reduces the complexity of the environment, enabling the more efficient development of zero-sum game algorithms in focused combat situations. In SMAC [40] and SMACv2 [25], agents control one faction while the opposing faction is managed by a built-in bot, and there is no support for agents to control both factions. By contrast, MiniStar extends SMACv2 by allowing agents to control both factions simultaneously in a self-play setting, eliminating the need for built-in bots.The MiniStar environment is an open source environment and available at https://github.com/QrowBranwen/MiniStar (accessed on 7 January 2025).

In the experiment, each of the three races is tested under the 5v5 matchmaking mode. For Zerg, they are zergling, hydralisk, and baneling; for Terran, they are marine, marauder, and medivac; and for Protoss, they are stalkers, zealots, and colossi. The three racial unit weights relative to a fixed unit order are [0.45, 0.45, 0.1], and birth locations are randomized for the Surround and Reflect scheme. Every algorithm employs the Multi-Agent Proximal Policy Optimization (MAPPO) algorithm [44] as the oracle, relying exclusively on self-play for 20 million steps and without using data from matches against the built-in AI.

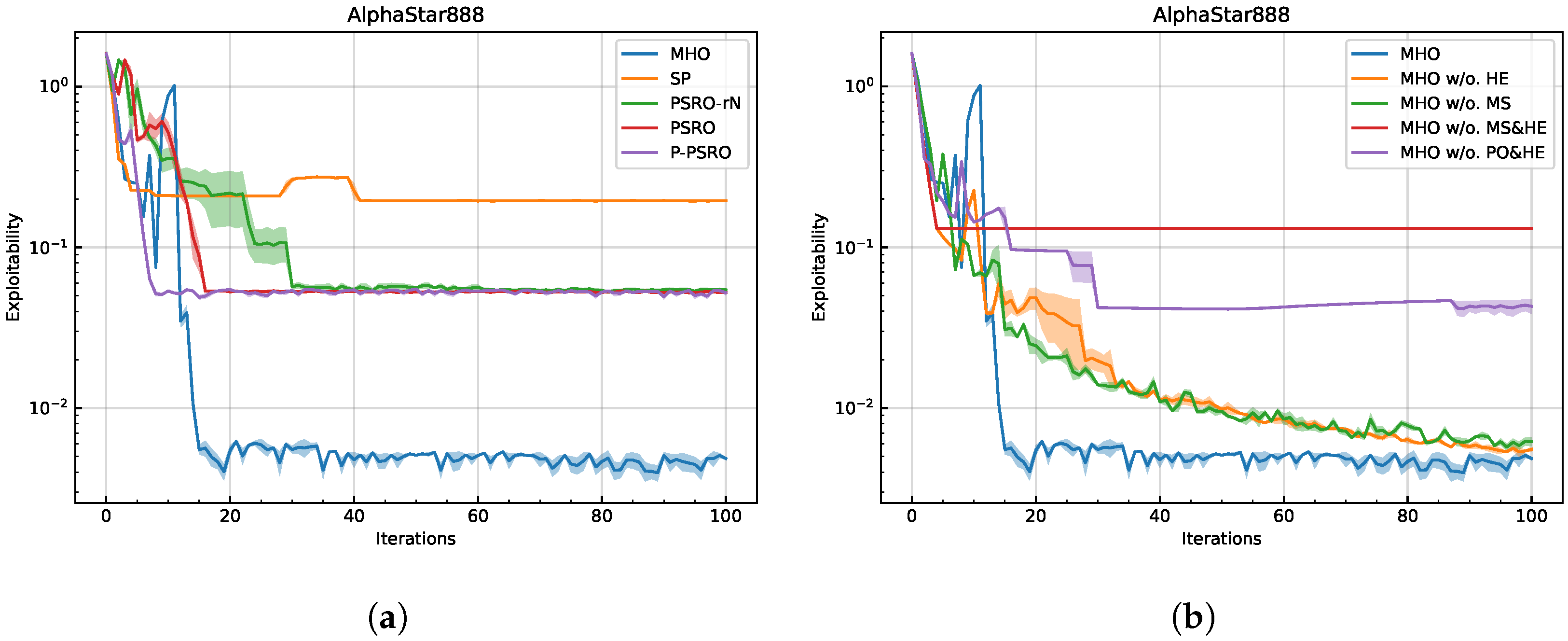
5.3. Results and Analysis

For AlphaStar888, the experimental results are shown in Figure 2. The experiments recorded the exploitability [18] of each algorithm’s current policy set, which was then plotted against iterations, with iterations on the horizontal axis and exploitability on the vertical axis. The results demonstrate that the MHO algorithm achieves the best performance.

In MiniStar, to benchmark performance, pairwise matches are conducted among the models produced by each algorithm, and the resulting win rate matrix is reported. This direct comparison allows us to quantitatively assess the relative strengths of the different methods. The experimental results are presented in Figure 3. The MHO consistently outperforms the baseline methods (PSRO, PSRO-rN, P-PSRO, and SP) in all three races (Protoss, Zerg, and Terran) in 5v5 settings, achieving the highest expected win rate. In addition, throughout the training process, each algorithm’s policy is periodically evaluated against built-in AI. The win rate curves from these evaluations serve as an indirect measure of the training progress, providing further insights into how each algorithm evolves over time. The experimental results are presented in Figure 4. Compared to other parallelized methods (P-PSRO, PSRO-rN), the MHO exhibits faster convergence and superior final performance, demonstrating improved training efficiency and strategic effectiveness. Overall, the MHO maintains a higher win rate.

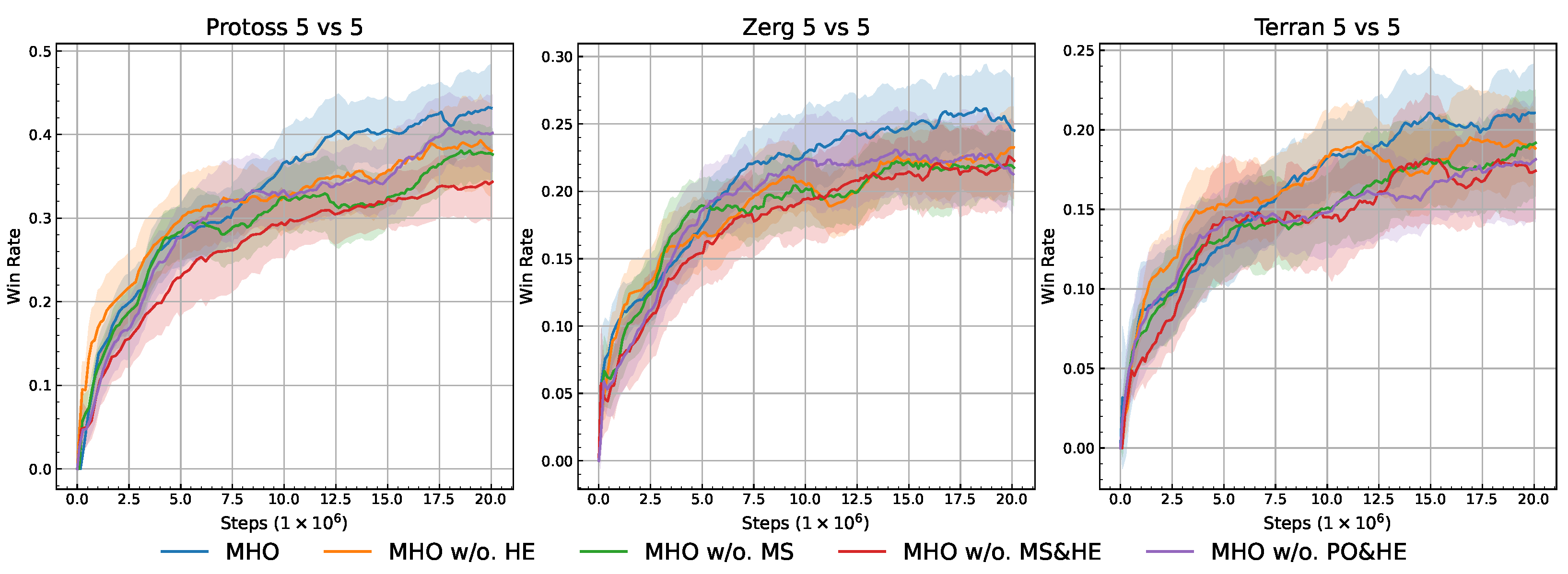
5.4. Ablation Studies

The contribution of each component of the MHO, including the PO, MS, and HE, is rigorously evaluated through a series of ablation experiments conducted on both the AlphaStar888 benchmark and the MiniStar environment. This study follows a subtractive methodology as follows: starting from the full MHO configuration (PO + MS + HE), we then remove individual components or their combinations. This strategy helps us precisely isolate the impact of each module and ensure that performance differences can be clearly attributed to the presence or absence of specific elements.

The study considers the following variants:

• MHO (Full):PO + MS + HE.
• MHO w/o. HE: Remove HE.
• MHO w/o. MS: Remove MS.
• MHO w/o. MS&HE: Remove both MS and HE.
• MHO w/o. PO&HE: Remove both PO and HE.

These subsets allow us to examine the effect of eliminating key components individually and in combination, thereby testing each module’s unique and synergistic contributions.

5.4.1. Parallelized Oracle

Considering AlphaStar888 is a single-step matrix game, the discussion of sample utilization is focused on the MiniStar environment. In Figure 5, MHO w/o. MS&HE exhibits slower convergence in the early stages. A similar phenomenon appears when comparing the PSRO and the P-PSRO in Figure 4, where the P-PSRO exhibits slower convergence as well. These findings confirm that dividing total computational resources among multiple oracles can reduce early-phase training efficiency.

To further examine this effect more closely, the PO is introduced into the PSRO (denoted as PO-PSRO) for a more granular comparison, as shown in Figure 6. The results indicate that the PO-PSRO attains faster convergence in the early training stages. This improvement arises because the PO approach leverages more samples, enhancing the efficiency of the training process.

From the perspective of the final results, the ablation experiments in AlphaStar888 and MiniStar, Figure 2b and Figure 7, show that the MHO w/o. HE outperforms the MHO w/o. PO&HE, and the MHO w/o. HE achieves better results than the MHO w/o. PO&HE.

5.4.2. Model Soups

In Figure 5, when the PO is paired with the MS component (MHO w/o. HE), it achieves faster early-stage convergence than the MHO w/o. PO&HE. This observation indicates that MS indirectly consolidate computational resources otherwise fragmented by PO, thus retaining parallelization benefits while mitigating the PO’s inherent drawbacks.

As shown in Figure 2b, Figure 5, and Figure 7, comparisons between the MHO and the MHO w/o.MS, as well as between the MHO w/o. HE and the MHO w/o. MS&HE, consistently demonstrate the effectiveness of the MS component. By integrating knowledge acquired through parallelized learning, MS indirectly boost data utilization and enhance overall training efficiency and performance.

5.4.3. Hierarchical Exploration

As shown in Figure 2b, Figure 5, and Figure 7, comparisons between the MHO and the MHO w/o. HE, as well as between the MHO w/o. MS and the MHO w/o. MS&HE, demonstrate that incorporating HE achieves superior performance. HE promotes broader strategy exploration during the early stages of training and, in the later phases, shifts toward exploitation to improve final decision-making performance.

5.4.4. Ablation Studies Summary

When all three components are present, their benefits combine synergistically. The MHO achieves superior results, faster improvements, lower exploitability, and stronger final performance than any configuration missing one or more modules.

6. Conclusions

This paper introduces the MHO to address suboptimal resource utilization in parallelized RL oracles. The MHO integrates three key techniques, the PO, MS, and HE, to significantly improve training efficiency and model performance. Specifically, the PO increases the amount of interaction data available, thus enhancing learning speed. MS effectively amalgamate knowledge from multiple hierarchical policies, mitigating the inefficiencies caused by uniform resource allocation while simultaneously alleviating the cold-start problem. HE further refines the training process by promoting broader strategy exploration during the initial phases, followed by more fine-grained exploitative learning in later stages, culminating in a better performance.In the AlphaStar888 matrix game and MiniStar environment, the MHO demonstrates superior performance over multiple baseline self-play algorithms. Ablation studies confirm the mutually complementary nature of the three core components, showing that they collectively drive efficient learning in complex adversarial scenarios. Overall, the MHO provides a scalable, high-efficiency solution for two-player zero-sum games in large-scale, high-dimensional settings, offering effective perspectives for future research in RL and self-play research.

Furthermore, to address the shortage of suitable simulation scenarios for game research in this domain, this paper presents the MiniStar environment. By focusing on simplified battle engagements rather than the full complexity of real-time strategy games, MiniStar substantially reduces the engineering overhead typically required in zero-sum research, thus serving as a lightweight and flexible platform for the broader community.

Future work will focus on the following areas: The efficient integration of parallel training in self-play and distributed RL parallel sampling, rather than treating them as independent components, to further enhance training efficiency and enable the application of the framework to larger-scale training scenarios. Further optimization of the parallelized framework while ensuring strict theoretical guarantees for convergence. Enhancement of the MiniStar environment, as the current scenarios do not fully emphasize environmental factors such as terrain, which may limit the exploration of strategy diversity. Future improvements will introduce more diverse training scenarios, providing a richer simulation environment for two-player zero-sum game research.