On the Existence of Perfect (1, 2)-Dominating Sets in Graphs

Abstract

In this paper, we investigate the existence of perfect $(1,2)$-dominating sets ($(1,2)$-PDS) in graphs with three vertices of maximum degree equal to $n-2$. A perfect $(1,2)$-dominating set is a special case of a $(1,2)$-dominating set. Graphs with such dominating sets may exhibit a symmetric structure. If a graph has at least one vertex of degree one, then it has a $(1,2)$-PDS. Hence, we consider only graphs with a minimum degree greater than or equal to 2. Therefore, a symmetric or asymmetric structure of graphs can be useful in determining whether a graph has a $(1,2)$-PDS. On the other hand, the symmetric or asymmetric structure may be even more helpful when studying the existence of $(1,2)$-PDS in relation to the maximum degree of a graph. Moreover, we analyze the structural conditions under which $(1,2)$-PDS exist, considering cases where the three vertices are adjacent or nonadjacent, and whether their neighborhoods are identical or distinct. Our study provides necessary and sufficient conditions for the existence of $(1,2)$-PDS in the given cases, extending the understanding of $(1,2)$-domination and its applications.

1. Introduction

In general, we use the standard terminology and notation of graph theory; see [1]. Let $G=\left(V\right(G),E(G\left)\right)$ be an undirected, simple graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. Two vertices $x,y$ of G are adjacent, or neighbors, if $xy$ is an edge in G. The degree of a vertex $x\in V\left(G\right)$ is denoted by $d_G\left(x\right)$ and the maximum degree of G is denoted by $\Delta \left(G\right)$. The set of all vertices of maximum degree is denoted by $S_{\Delta \left(G\right)}$. The number $\delta \left(G\right)$ is the minimum degree of G. A vertex of degree 1 is a leaf and $L\left(G\right)=\{x\in V\left(G\right):d_G\left(x\right)=1\}$. The set $N_G\left(v\right)=\{u\in V\left(G\right):uv\in E\left(G\right)\}$ is an open neighborhood of a vertex v and the set $N_G\left[v\right]=N_G\left(v\right)\cup \left\{v\right\}$ is a closed neighborhood. The distance between vertices $x,y$ in G is denoted by $d_G(x,y)$. Let $V_0\subset V$, then for $x\in V\setminus V_0$ the distance is defined as $d_G(x,V_0)=min\{d_G(x,y):y\in V_0\}$. A maximal, with respect to a set inclusion, connected subgraph of G is called a component of G. A cutvertex in a graph G is a vertex whose removal increases the number of connected components of G.

Graph theory has been an essential area of mathematical research due to its wide range of applications and theoretical richness. This paper explores the concept of domination in graphs, a topic that has gained significant attention since its introduction in the 19th century by de Jaenish [2] in chessboard problems and formalized by Berge [3] and Ore [4] in the 1960s. A dominating set (DS) of a graph G is a subset $D\subseteq V\left(G\right)$ such that every vertex $x\in V\left(G\right)\setminus D$ is adjacent to at least one vertex $y\in D$. In particular, $V\left(G\right)$ is also dominating.

Over the decades, various generalizations and modifications of dominating sets have been proposed, including the concept of secondary domination, introduced by Hedetniemi et al. in 2008 [5]. Let $k\in \mathbb{N}$. A subset $D\subseteq V\left(G\right)$ is called a $(1,k)$-dominating set (or $(1,k)$-DS) if each vertex $v\in V\setminus D$ has a neighbor in D and another vertex in D at a distance of at most k from v. In particular, $V\left(G\right)$ is also a $(1,k)$-DS for every $k\ge 1$. In [5], it was proved that the study of a $(1,k)$-DS is meaningful only for $k\in \{1,2,3,4\}$.

Among the special cases, $(1,1)$-dominating sets, also known as 2-dominating or double dominating sets, have been extensively studied; see [6,7,8,9]. However, the study of $(1,2)$-dominating sets has appeared as a natural extension, with interesting properties and computational challenges. The concept of $(1,2)$-dominating sets has inspired significant research in recent years. Michalski et al. [10], Kayathri and Vallirani [11], and Raczek [12,13] have explored its structural properties and computational complexity. Additionally, independent dominating sets in graphs and their products were studied in [5,14,15]. Furthermore, the notion of proper $(1,2)$-dominating sets was introduced by Michalski in [16], which improved the study of these subsets by excluding cases that are $(1,1)$-dominating sets. A subset $D\subset V\left(G\right)$ is a proper $(1,2)$-DS if D is a $(1,2)$-DS and not a $(1,1)$-DS, i.e., D is $(1,2)$-dominating, and there exists a vertex $x\in V\left(G\right)\setminus D$ such that x has exactly one neighbor in D, and there is a vertex $u\in D$ such that $d_G(x,u)=2$. Since the set $V\left(G\right)$ is a $(1,1)$-DS, it is not the proper $(1,2)$-DS. The properties of proper $(1,2)$-DS and the problem of its existence were considered in the papers [10,17,18].

Motivated by the above, Bednarz and Pirga studied $(1,2)$-dominating sets and introduced the concept of a perfect $(1,2)$-dominating set, a special case of a proper $(1,2)$-DS (see [19]). A subset $D\subset V\left(G\right)$ is a perfect $(1,2)$-dominating set of G (or $(1,2)$-PDS) if every vertex $x\in V\left(G\right)\setminus D$ has exactly one neighbor in D, and there exists a vertex $u\in D$ such that $d_G(x,u)=2$. In this case, we say that x is perfect $(1,2)$-dominated by D (abbreviated as x is $(1,2)$-PD).

A proper $(1,2)$-DS only requires the existence of at least one vertex outside D that satisfies the domination condition, meaning that there exists a vertex $u\in D$ such that $d_G(x,u)=2$. A perfect $(1,2)$-DS imposes this condition on all vertices outside D. Thus, every perfect $(1,2)$-dominating set is a proper $(1,2)$-dominating set, but not every proper $(1,2)$-dominating set is perfect, as it may fail to enforce this condition for all vertices outside D.

It is evident that if D is a perfect $(1,2)$-dominating set, then it is also a proper $(1,2)$-DS, and $V\left(G\right)$ cannot be a perfect $(1,2)$-dominating set. In [19], the problem of the existence of $(1,2)$-PDS in graphs was considered. Specifically, the focus was on the class of graphs with at most two vertices of maximum degree, analyzing the structural conditions under which such sets exist. First, the case where the maximum degree of a vertex was $n-1$ was considered.

Theorem 1

([19]). Let G be a connected n-vertex graph of the maximum degree $\Delta \left(G\right)=n-1$, $n\ge 3$. If G has a $(1,2)$-PDS, then G has the unique vertex of maximum degree $\Delta \left(G\right)$.

A complete characterization of graphs with $\Delta \left(G\right)=n-1$ which admit a $(1,2)$-PDS was also presented.

Theorem 2

([19]). Let G be a connected n-vertex graph, $n\ge 3$ with the unique vertex of maximum degree $\Delta \left(G\right)=n-1$. G has a $(1,2)$-PDS if and only if the vertex of maximum degree is a cutvertex.

Next, the existence of a $(1,2)$-PDS in graphs where the maximum degree of a vertex was $n-2$ was examined. Complete solutions, along with necessary and sufficient conditions, were provided for graphs with one or two such vertices.

This paper is a continuation of the research presented in [19]. Necessary and sufficient conditions for the existence of $(1,2)$-PDS will be proven in the case where there are three vertices with a maximum degree of $n-2$. We will consider cases where these vertices are adjacent or nonadjacent and whether their neighborhoods are identical or distinct.

It is worth emphasizing that dominating sets have a wide range of applications. In [13], Raczek described numerous applications of dominating sets, including $(1,2)$-dominating sets. Dominating sets in networks represent a subset of special nodes (e.g., servers or service providers) that ensure direct resource availability. The domination number is the smallest possible size of such a subset. Applications of domination parameters include environmental sensors, vehicular communication, road safety, healthcare, peer-to-peer messaging, disaster rescue, and defense systems. Another application is the relationship between the minimum dominating set problem and other NP-hard problems, such as the vertex k-center problem, which plays a crucial role in optimization and facility location theory (see [20]).

In some networks, higher reliability is required, where a backup node can take over if a primary node fails. In such cases, $(1,2)$-domination can be useful, as backup nodes can be located at a distance of 1 or 2. While backup nodes at a distance of 2 may operate with reduced performance, they ensure that critical tasks are covered in emergencies, similar to how emergency numbers function during poor signal coverage.

An example application of $(1,2)$-dominating sets is in pandemic scenarios, such as ensuring optimal placement of medical care facilities. Towns are represented as vertices, and edges connect towns within a specified distance. The minimum $(1,2)$-dominating set identifies the best locations for medical facilities, ensuring every town has access to a primary facility within a certain distance and a backup facility within twice that distance.

A similar application can be identified in the case of perfect $(1,2)$-domination. Another example of such an application is related to wars or natural disasters. In such situations, perfect $(1,2)$-dominating sets can ensure that each point (e.g., a town or a strategic location) has access to a primary shelter or resource hub, with an additional backup shelter located at a greater distance. This ensures that in emergencies, all points have a safe and reliable refuge, even if one shelter becomes inaccessible due to unforeseen circumstances.

2. Perfect $\mathbf{(}\mathbf{1}\mathbf{,}\mathbf{2}\mathbf{)}$-Dominating Sets in Graphs with Maximum Degree $\mathbf{\Delta }\mathbf{\left(}\mathit{G}\mathbf{\right)}\mathbf{=}\mathit{n}\mathbf{-}\mathbf{2}$

We will consider cases where $|S_{\Delta \left(G\right)}|=3$. Let $\Delta \left(G\right)=n-2$ and $S_{\Delta \left(G\right)}=\{x,y,z\}$. In this paper, we will consider the following cases:

(i)

x and y are not adjacent, and z is adjacent to both x and y, and $N\left(x\right)=N\left(y\right)$, $N\left(x\right)\ne N\left(z\right)$, $N\left(y\right)\ne N\left(z\right)$;

(ii)

$x,y$ and z are adjacent, and $N\left[x\right]=N\left[y\right]=N\left[z\right]$;

(iii)

$x,y$ and z are adjacent, and $N\left[x\right]=N\left[y\right]$, $N\left[x\right]\ne N\left[z\right]$, $N\left[y\right]\ne N\left[z\right]$;

(iv)

$x,y$ and z are adjacent, and $N\left[x\right]\ne N\left[y\right]$, $N\left[x\right]\ne N\left[z\right]$, $N\left[y\right]\ne N\left[z\right]$.

It was proved in [19] that if graph G satisfies $L\left(G\right)\ne \varnothing$, then G has a $(1,2)$-PDS. Therefore, in our subsequent considerations, we assume that $\delta \left(G\right)\ge 2$.

Theorem 3.

Let G be an n-vertex connected graph, $n\ge 6$ and $\delta \left(G\right)\ge 2$, $\Delta \left(G\right)=n-2$, such that $S_{\Delta \left(G\right)}=\{x,y,z\}$ and $x,y$ are not adjacent and $N\left(x\right)=N\left(y\right)$. A vertex z is adjacent to x and to y and $N\left(x\right)\ne N\left(z\right)$ and $N\left(y\right)\ne N\left(z\right)$. A graph G has a $(1,2)$-PDS if and only if there exists a unique vertex $u\in V\left(G\right)$ of degree 2 adjacent to vertices x and y.

Proof. 

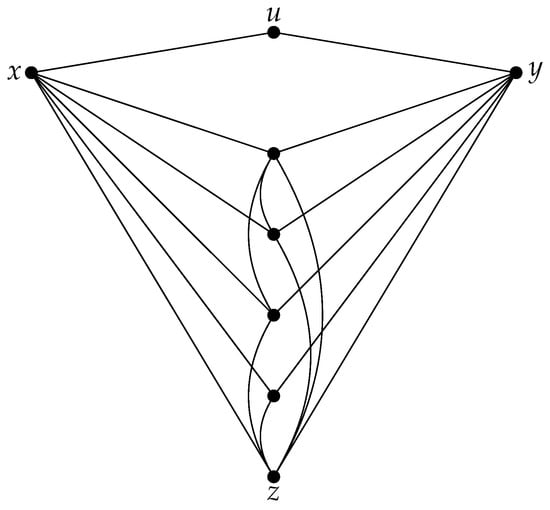
Let us assume that the assumptions of Theorem 3 are satisfied. Let R be a set defined as $R=N\left(z\right)\setminus \{x,y\}$. Then, there is no vertex in R that is adjacent to all other vertices in this set. Otherwise, if at least one vertex in R is adjacent to all other vertices in this set, then it has a degree $n-2$, which contradicts the assumption that $|S_{\Delta \left(G\right)}| =3$.

If $n<6$, then no graph G satisfies the above assumptions. Let $n\ge 6$ and $\delta \left(G\right)\ge 2$, $\Delta \left(G\right)=n-2$, such that $S_{\Delta \left(G\right)}=\{x,y,z\}$ and $x,y$ are not adjacent, and $N\left(x\right)=N\left(y\right)$. Suppose that there exists a unique vertex $u\in V\left(G\right)$ such that $d_G\left(u\right)=2$ and it is adjacent to x and y. Because $N\left(x\right)=N\left(y\right)$ and a vertex $z\in S_{\Delta \left(G\right)}$ is adjacent to x and y, it implies that u is the only vertex of a graph G that is not adjacent to a vertex z; otherwise, $d_G\left(z\right)<n-2$. Hence, $u\notin R$ and $u\notin S_{\Delta \left(G\right)}$. Then, sets $D_1=\{x,u\}$ or $D_2=\{y,u\}$ are $(1,2)$-PDS of a graph G. An example of such a graph for $n=8$, where $S_{\Delta \left(G\right)}=\{x,y,z\}$ and $\Delta \left(G\right)=6$, is shown in Figure 1.

Now, suppose that a graph G has a $(1,2)$-PDS and let us denote it by D. It is clear that $\left|D\right|\ge 2$ and also only one of the vertices from the set $S_{\Delta \left(G\right)}$ is in D; otherwise, D is a $(1,1)$-dominating set. Assume that $x\in D$. Hence all vertices from a set R and a vertex z are dominated by x. Moreover, $\left|\right(V\left(G\right)\setminus \{x,y,z\})\cap D|\le 1$, otherwise vertices $y,z$ are $(1,1)$-dominated by D, which is a contradiction. From the fact that $x,y,z\in S_{\Delta \left(G\right)}$ and $N\left(x\right)=N\left(y\right)$ and $N\left(x\right)\ne N\left(z\right)$ and $N\left(y\right)\ne N\left(z\right)$, it follows that there exists a unique vertex u in a graph G that is not adjacent to z; otherwise, $z\notin S_{\Delta \left(G\right)}$. A vertex u is adjacent to x and to y; otherwise, $x,y\notin S_{\Delta \left(G\right)}$. Hence, $u\notin R$ and $u\in V\left(G\right)\setminus \{x,y,z\}$. Therefore, $u\in D$. Because u is adjacent to x and to y, it follows that $d_G\left(u\right)=2$. If $d_G\left(u\right)\ge 3$, then there exists a vertex $v\in R$ adjacent to u. Therefore, v is $(1,1)$-dominated by D, a contradiction. Thus, the theorem is proved. ☐

Theorem 4.

Let G be an n-vertex connected graph, $n\ge 7$ and $\delta \left(G\right)\ge 2$, $\Delta \left(G\right)=n-2$, such that $S_{\Delta \left(G\right)}=\{x,y,z\}$ and $x,y,z$ are adjacent, $N\left[x\right]=N\left[y\right]=N\left[z\right]$. We denote a set of vertices by $B=N\left(x\right)\setminus \{y,z\}$. Let u be a unique vertex that is not adjacent to vertices $x,y,z$. A graph G has a $(1,2)$-PDS if and only if there is a vertex $v\in B$ such that every $v^{\prime }\in B\setminus \left\{v\right\}$ is adjacent to either u or v, and $N\left(u\right)\cap N\left(v\right)=\varnothing$, and every vertex from $N\left(u\right)$ is not adjacent to at least one vertex from $B\setminus \left\{v\right\}$ and

(i)

$uv\in E\left(G\right)$ and $\left|N\right(u\left)\right|\ge 3$;

(ii)

$uv\notin E\left(G\right)$ and every vertex from $N\left(v\right)\setminus \{x,y\}$ is adjacent to a vertex from $N\left(u\right)$.

Proof. 

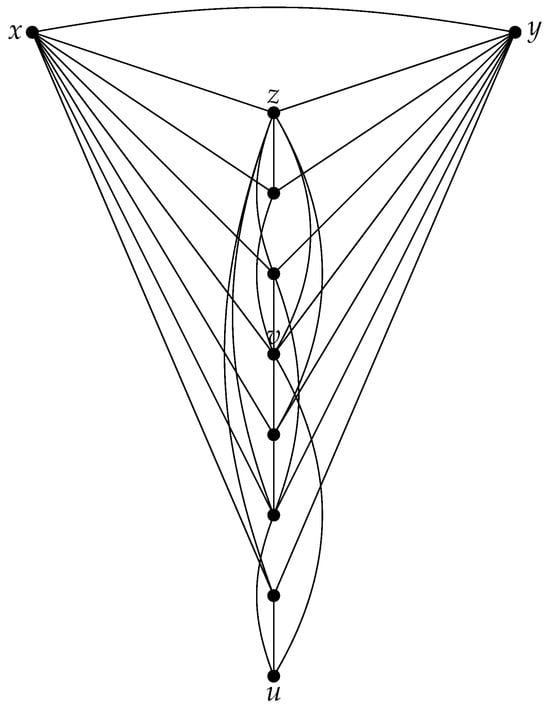
Let us assume that the assumptions of Theorem 4 are satisfied. Let G be an n-vertex connected graph, $n\ge 7$, $\delta \left(G\right)\ge 2$, $\Delta \left(G\right)=n-2$, such that $S_{\Delta \left(G\right)}=\{x,y,z\}$. If $n<7$, then there is no graph satisfying the above assumptions. Let u be a unique vertex that is neither adjacent to x, y, nor z. Let $B=N\left(x\right)\setminus \{y,z\}$. Then, there is no vertex adjacent to all other vertices in B; otherwise, there is a vertex $v^{\prime }\in B$ such that $d_G\left(v^{\prime }\right)=n-2$, which contradicts the cardinality of a set $S_{\Delta \left(G\right)}$. Since $N\left[x\right]=N\left[y\right]=N\left[z\right]$, it follows that a vertex $z\in S_{\Delta \left(G\right)}$ is adjacent to all vertices from set B. Assume that there is a vertex $v\in B$ such that every $v^{\prime }\in B\setminus \left\{v\right\}$ is adjacent to either u or v, and $N\left(u\right)\cap N\left(v\right)=\varnothing$, and every vertex from $N\left(u\right)$ is not adjacent to at least one vertex from $B\setminus \left\{v\right\}$, and conditions (i) or (ii) are valid. We will prove that a set $D=\{u,v\}$ is a $(1,2)$-PDS of a graph G. Vertices $x,y,z$ are dominated by $v\in B$. Because u is neither adjacent to x, y, nor z, it follows that $d_G(x,u)=d_G(y,u)=d_G(z,u)=2$. Hence $x,y,z$ are $(1,2)$-PD by D. If a vertex $u^{\prime }\in N\left(u\right)$, then $u^{\prime }$ is dominated by u. By the connectivity of G, there is a path $u^{\prime }-x-v$; hence, $u^{\prime }$ is $(1,2)$-PD by D. If $u^{\prime }\in N\left(v\right)$, then $u^{\prime }$ is dominated by v. If a condition (i) is valid, then there is a path $u^{\prime }-v-u$ in graph G and $u^{\prime }$ is $(1,2)$-PD by D. Since $\left|N\right(u\left)\right|\ge 3$, then $d_G\left(v\right)\le n-3$. If condition (ii) is valid, then there exists a vertex $v^{\prime }\in N\left(u\right)$ such that $u^{\prime }{v}^{\prime }\in E\left(G\right)$. Hence, there exists a path $u^{\prime }-v^{\prime }-u$ in graph G, and $u^{\prime }$ is $(1,2)$-PD by D. From the fact that $N\left(u\right)\cap N\left(v\right)=\varnothing$, all vertices in B are not $(1,1)$-dominated by D. Because there is no vertex adjacent to all other vertices in B, and every vertex in $N\left(u\right)$ is not adjacent to at least one vertex in $B\setminus \left\{v\right\}$, it follows that $d_G\left(u^{″}\right)\le n-3$ for all $u^{″}\in B$. An example graph for $n=10$, where $S_{\Delta \left(G\right)}=\{x,y,z\}$, and $\Delta \left(G\right)=8$ for case (i) is presented in Figure 2.

Conversely, assume that G has a $(1,2)$-PDS, which we denote by D. Firstly, we prove some claims.

• (1) $D\ne \{x,y\}$, and $D\ne \{x,z\}$, and $D\ne \{y,z\}$.
• If $D=\{x,y\}$, then vertices from set B are $(1,1)$-dominated, a contradiction. Analogously we can prove that $D\ne \{x,z\}$ and $D\ne \{y,z\}$.
• (2) $u\in D$
• It is obvious because a vertex u is the only vertex in a graph G such that $d_G(x,u)=d_G(y,u)=d_G(z,u)=2$; otherwise, $x,y,z$ are not $(1,2)$-PD by D.
• (3) $x\notin D$, $y\notin D$, and $z\notin D$.
• Assume that $x\in D$. Then, there exists a vertex $u^{\prime }\in B$ that is adjacent to a vertex u and to x. Hence, $u^{\prime }$ is $(1,1)$-dominated by D because $u\in D$ by (2). Analogously, we can prove that $y\notin D$ and $z\notin D$.
• (4) $|D\cap B|=1$.
• If $|D\cap B|=\varnothing$, then $x\in D$, $y\in D$ or $z\in D$, which contradicts (3). Assume that $|D\cap B|\ge 2$. Vertices $x,y,z$ are adjacent to every vertex in set B; hence, $x,y,z$ are $(1,1)$-dominated by D, a contradiction.

From claims (1)–(4), it follows that there exists a vertex $v\in B$ such that $v\in D$. Hence, $D=\{u,v\}$. Vertices $x,y,z$ are $(1,2)$-PD by D. Since $u,v\in D$, it implies that every vertex $v^{\prime }\in B\setminus \left\{v\right\}$ is adjacent to either u or v, and $N\left(u\right)\cap N\left(v\right)=\varnothing$; otherwise, there exists a vertex $w\in B$ such that either w is not dominated or w is $(1,1)$-dominated by D. Moreover, every vertex $u^{\prime }\in N\left(u\right)$ is not adjacent to at least one vertex in $B\setminus \left\{v\right\}$; otherwise, $d_G\left(u^{\prime }\right)=n-2$, which contradicts $|S_{\Delta \left(G\right)}|=3$. Since $\delta \left(G\right)\ge 2$, a vertex u is adjacent to at least two vertices in set B. If u is adjacent to a vertex $v\in B$, then a vertex u must be adjacent to two other vertices in set B; otherwise, $d_G\left(v\right)=n-2$, which contradicts $v\notin S_{\Delta \left(G\right)}$. Hence, $\left|N\right(u\left)\right|\ge 3$, and condition (i) is valid. If u is not adjacent to v, then every vertex in $N\left(v\right)\setminus \{x,y\}$ is adjacent to a vertex in $N\left(u\right)$; otherwise, there exists a vertex $v^{\prime }\in N\left(v\right)$ that is dominated by v but is not $(1,2)$-PD by D. Hence, condition (ii) is valid. Thus, the theorem is proved. ☐

Theorem 5.

Let G be an n-vertex connected graph, $n\ge 6$, and $\delta \left(G\right)\ge 2$, $\Delta \left(G\right)=n-2$, such that $S_{\Delta \left(G\right)}=\{x,y,z\}$, where $x,y,z$ are adjacent and $N\left[x\right]=N\left[y\right]$ and $N\left[x\right]\ne N\left[z\right]$, $N\left[y\right]\ne N\left[z\right]$. Let us denote by H a set of vertices of graph G such that $H=N\left(x\right)\setminus \left\{y\right\}$. Let u be a unique vertex not adjacent to x or y but adjacent to z. A graph G has a $(1,2)$-PDS if and only if there exists a vertex $v\in H$ such that every $v^{\prime }\in H\setminus \left\{v\right\}$ is adjacent to u or v, and $N\left(u\right)\cap N\left(v\right)=\varnothing$, and every vertex in $N\left(u\right)$ is not adjacent to at least one vertex in $H\setminus \left\{v\right\}$.

Proof. 

Let G be an n-vertex connected graph. Let $x,y,z\in S_{\Delta \left(G\right)}$, where $x,y,z$ are adjacent and $N\left[x\right]=N\left[y\right]$ and $N\left[x\right]\ne N\left[z\right]$, $N\left[y\right]\ne N\left[z\right]$. If $n<6$, then no graph satisfies the assumptions of this theorem. Let $n\ge 6$ and u be a unique vertex adjacent to a vertex z. Let $H=N\left(x\right)\setminus \left\{y\right\}$. Then, there is no vertex adjacent to all other vertices in H. Otherwise, there exists a vertex $p\ne z$ in H with degree $n-2$, which contradicts the cardinality of the set $S_{\Delta \left(G\right)}$.

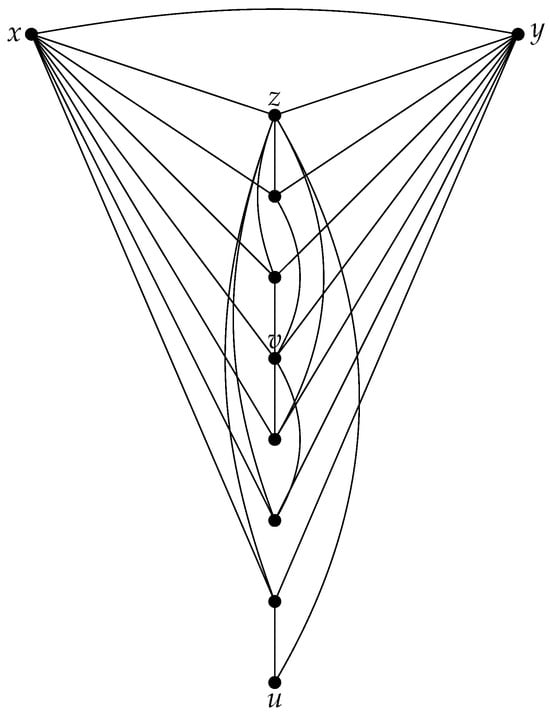
Suppose there exists a vertex $v\in H$ such that every vertex $v^{\prime }\in H\setminus \left\{v\right\}$ is adjacent to u or v, and $N\left(u\right)\cap N\left(v\right)=\varnothing$, and every vertex in $N\left(u\right)$ is not adjacent to at least one vertex in $H\setminus \left\{v\right\}$. We will prove that a set $D=\{u,v\}$ is a $(1,2)$-PDS of a graph G. Vertices x and y are dominated by $v\in H$ and $d_G(x,u)=d_G(y,u)=2$. Hence, $x,y$ are $(1,2)$-PD by D. Since $z\in S_{\Delta \left(G\right)}$ and $N\left[x\right]\ne N\left[z\right]$ and $N\left[y\right]\ne N\left[z\right]$, a vertex z is not adjacent to exactly one vertex in a set H. If $z\ne v$, then z is not adjacent to a vertex v. Hence, z is dominated by u, and there exists a path $z-x-v$, then z is $(1,2)$-PD by D. If $z=v$, then z is not adjacent to one vertex $u^{\prime }\in N\left(u\right)\subset H$. Every vertex $v^{\prime }\in H\setminus \left\{v\right\}$ is dominated by u or v and is not $(1,1)$-dominated because $N\left(u\right)\cap N\left(v\right)=\varnothing$. If $v^{\prime }\in N\left(v\right)$, then there exists a path $v^{\prime }-z-u$; hence, $v^{\prime }$ is $(1,2)$-PD by D. If $v^{\prime }\in N\left(u\right)$, then there exists a path $v^{\prime }-x-v$; hence, $v^{\prime }$ is $(1,2)$-PD by D. Since every vertex in $N\left(u\right)$ is not adjacent to at least one vertex in $H\setminus \left\{v\right\}$, its degree is less than or equal to $n-3$. An example graph for $n=10$, where $S_{\Delta \left(G\right)}=\{x,y,z\}$, and $\Delta \left(G\right)=8$, and $zv\notin E\left(G\right)$ is presented in Figure 3.

Conversely, assume that a set D is $(1,2)$-PDS of a graph G. We will prove the following claims.

• (1) $D\ne \{x,y\}$.
• If $D=\{x,y\}$, then vertices in a set H are $(1,1)$-dominated, a contradiction.
• (2) $u\in D$.
• Because $N\left[x\right]=N\left[y\right]$ and $x,y\in S_{\Delta \left(G\right)}$, a vertex u is the only vertex in G not adjacent to vertices x and y. Hence, $d_G(x,u)=d_G(y,u)=2$; otherwise, $x,y$ are not $(1,2)$-PD by D.
• (3) $x\notin D$ and $y\notin D$.
• This can be proved analogously to case (3) in Theorem 4.
• (4) $|D\cap H|=1$.
• If $|D\cap H|=\varnothing$, then x or y is in D, contradicting (3). If $|D\cap H|\ge 2$, then vertices x and y are $(1,1)$-dominated by D, because they are adjacent to every vertex in a set H, a contradiction.

From the above cases, it follows that there exists a vertex $v\in H$ such that $v\in D$. Hence, $D=\{u,v\}$. It is obvious that every vertex $v^{\prime }\in H\setminus \left\{v\right\}$ is adjacent to either u or v, and $N\left(u\right)\cap N\left(v\right)=\varnothing$; otherwise, $v^{\prime }$ would be either $(1,1)$- dominated by D or not dominated at all. Since H contains no vertex adjacent to all other vertices in H, every vertex $v^{\prime }\in N\left(v\right)$ satisfies the condition $d_G\left(v^{\prime }\right)\le n-3$. Furthermore, because $\delta \left(G\right)\ge 2$ and a vertex z is adjacent to a vertex u, there must exist at least one vertex $u^{\prime }\in H$ such that $u^{\prime }\ne z$ is adjacent to u. Consequently, every vertex $u^{\prime }\in N\left(u\right)$ is not adjacent to at least one vertex in a set $H\setminus \left\{v\right\}$. Otherwise, there would exist a vertex $u^{″}\in N\left(u\right)$ such that $d_G\left(u^{″}\right)=n-2$, which would contradict the assumption that $|S_{\Delta \left(G\right)}|=3$. Vertices x and y are $(1,2)$-PD by D because x and y are adjacent to a vertex v. By (2), it follows that $d_G(x,u)=d_G(y,u)=2$. Thus, the theorem is proved. ☐

Theorem 6.

Let G be an n-vertex connected graph with $n\ge 6$, $\delta \left(G\right)\ge 2$ and $\Delta \left(G\right)=n-2$, such that $S_{\Delta \left(G\right)}=\{x,y,z\}$, where $x,y,z$ are adjacent. If $N\left[x\right]\ne N\left[y\right]$, $N\left[x\right]\ne N\left[z\right]$, and $N\left[y\right]\ne N\left[z\right]$, then there is no $(1,2)$-PDS in G.

Proof. 

Assume that G is an n-vertex connected graph with $n\ge 6$, $\delta \left(G\right)\ge 2$ and $\Delta \left(G\right)=n-2$, such that $S_{\Delta \left(G\right)}=\{x,y,z\}$, where $x,y,z$ are adjacent. Since $N\left[x\right]\ne N\left[y\right]$, $N\left[x\right]\ne N\left[z\right]$, $N\left[y\right]\ne N\left[z\right]$ and $x,y,z\in S_{\Delta \left(G\right)}$, it follows that there exist vertices $x^{\prime },y^{\prime },u$ such that $x^{\prime }$ is adjacent to both x and z but not to y, and $y^{\prime }$ is adjacent to both y and z but not to x, and u is adjacent to both x and y but not to z.

By contradiction, assume that G has a $(1,2)$-PDS, denoted by D. Hence, every vertex $v\notin D$ must have exactly one neighbor in D and another vertex in D at a distance of exactly 2. If $x\in D$, then all vertices in G are dominated by x, except for $y^{\prime }$, which is not adjacent to x. The vertex $y^{\prime }$ cannot belong to D because, in that case, y would be $(1,1)$-dominated. Hence, $y^{\prime }$ is not in the set D and is not dominated, leading to a contradiction. In the same way, we can prove that $y,z\notin D$. If $x^{\prime }\in D$, then the vertices x and z are dominated. The only vertex at a distance of 2 from x is $y^{\prime }$, which cannot be in D because, in that case, vertex z would be $(1,1)$-dominated. Thus, there is no vertex that belongs to D without $(1,1)$-dominating other vertices. Therefore, $x^{\prime },y^{\prime },u\notin D$.

Finally, consider any vertex $v\in N\left(x\right)\cap N\left(y\right)\cap N\left(z\right)$ which belongs to D. Then, there is no vertex in D at a distance of 2 from $x,y$ or z such that the remaining vertices are not $(1,1)$-dominated.

Taking all the considered cases into account, we conclude that a $(1,2)$-PDS cannot exist in G. ☐

3. Conclusions

In this paper, we examined the existence of perfect $(1,2)$-dominating sets in graphs with exactly three vertices of maximum degree equal to $n-2$. By analyzing cases where the vertices are adjacent or nonadjacent and whether their neighborhoods are identical or distinct, we derived necessary and sufficient conditions for the existence of $(1,2)$-PDS in such graphs.

Our results provide a deeper understanding of the structural properties of graphs supporting perfect $(1,2)$-domination. Notably, we demonstrated how the arrangement of high-degree vertices and their neighborhoods influences the existence of $(1,2)$-PDS. Additionally, we discussed cases involving graphs with $n-1$ or $n-2$ vertices of degree $n-2$, further extending the applicability of our findings.

The results presented here contribute to the growing body of knowledge on domination in graphs, offering insights that could be applied in various domains, such as network reliability, resource allocation, and disaster management. Future studies could investigate similar domination problems in other classes of graphs with distinct structural constraints.