Symmetric and Asymmetric Failure Mechanism of Deep Tunnel Excavation Under Complex Environmental Conditions
Abstract
:1. Introduction
2. Numerical Modeling of Strain Softening and Spatial Variability
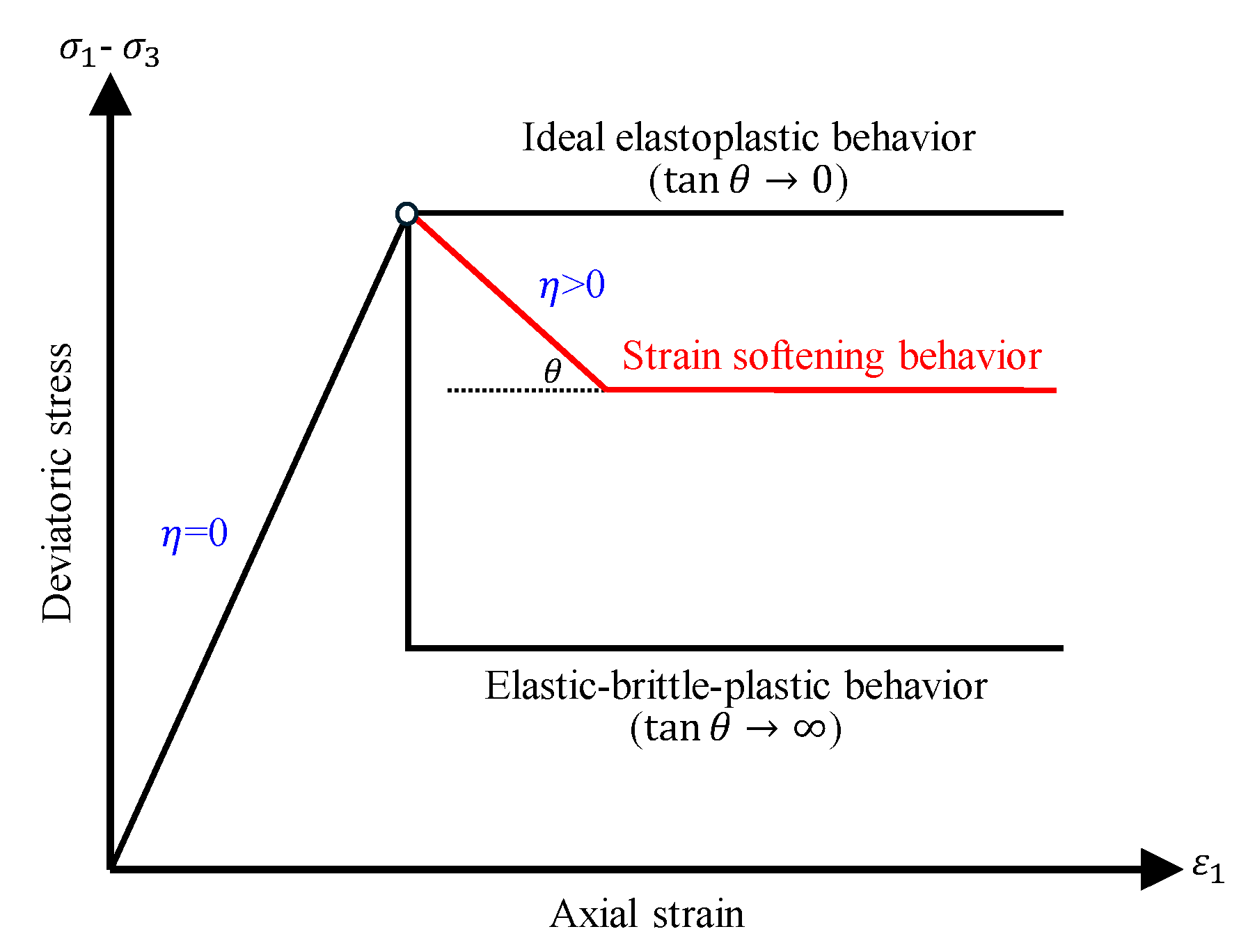
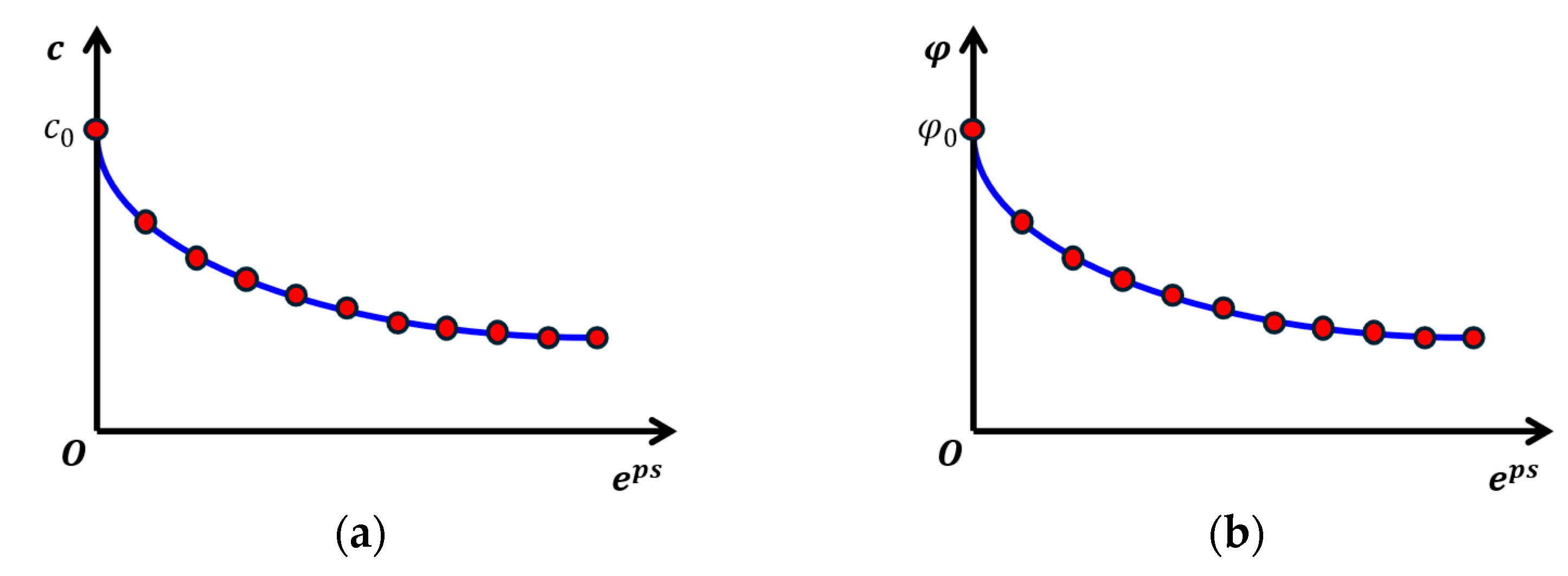
2.1. Strain—Softening Model
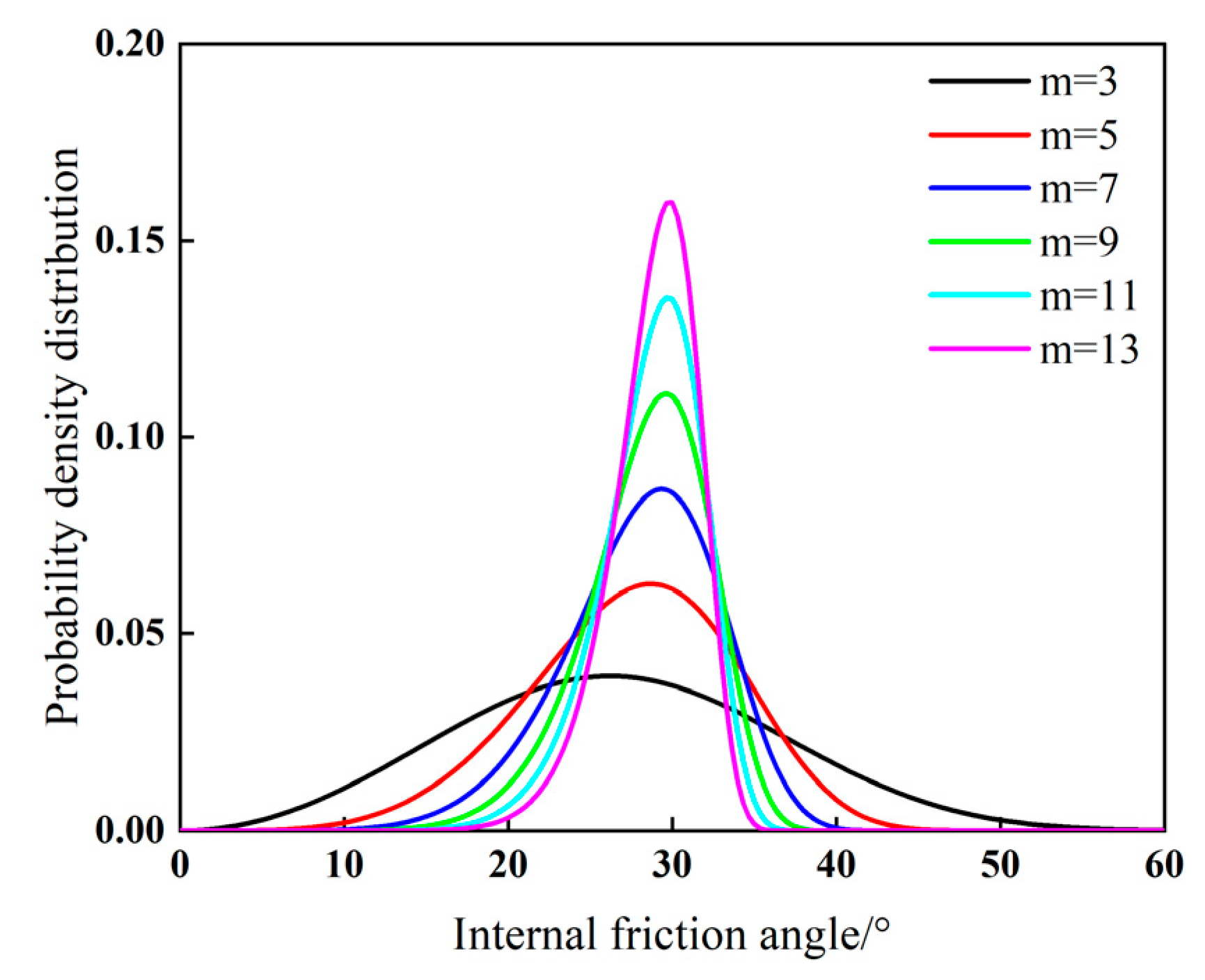
2.2. Numerical Realization of Spatial Variability
3. Numerical Analysis During Deep Tunnel Excavation
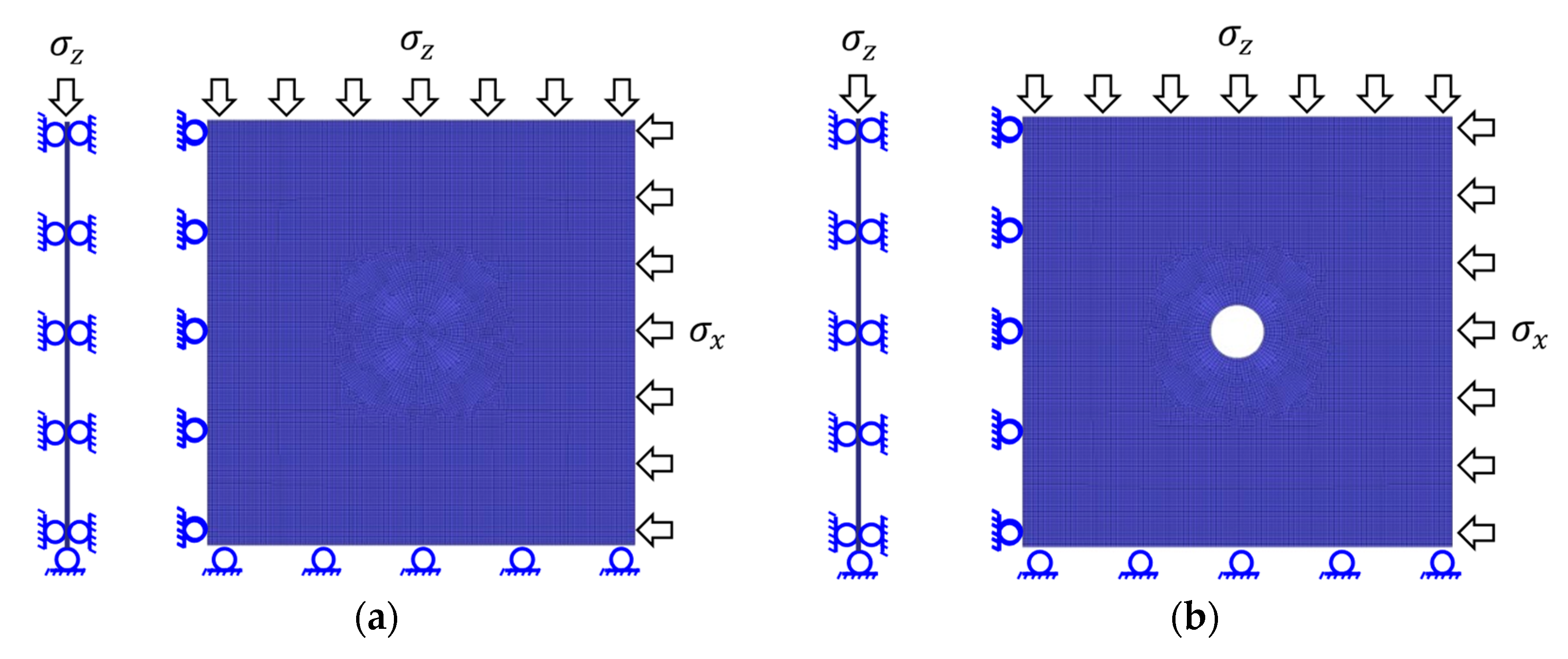
3.1. Numerical Model Establishment
3.2. Analysis of Numerical Simulation Results
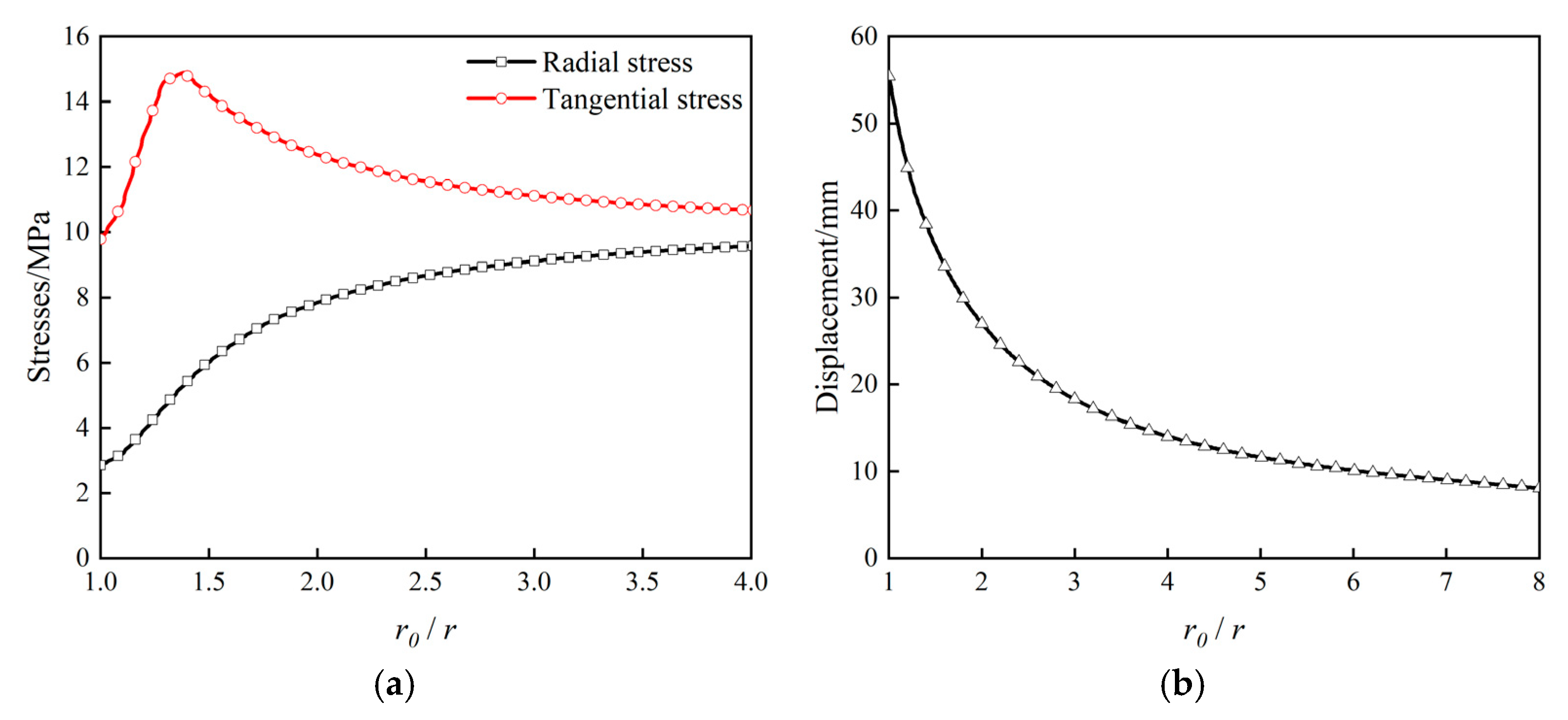
3.2.1. Simulation Results Based on Ideal Elastic–Plastic Model
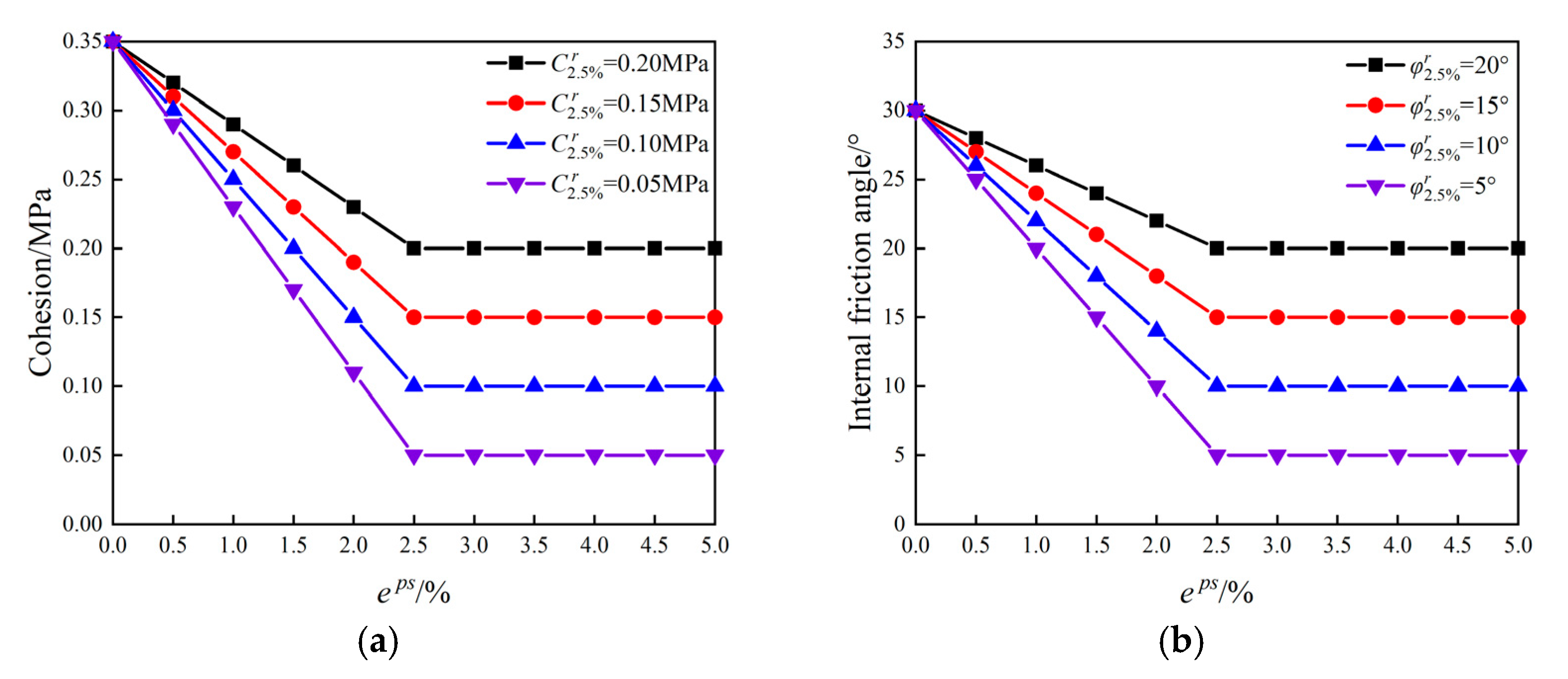
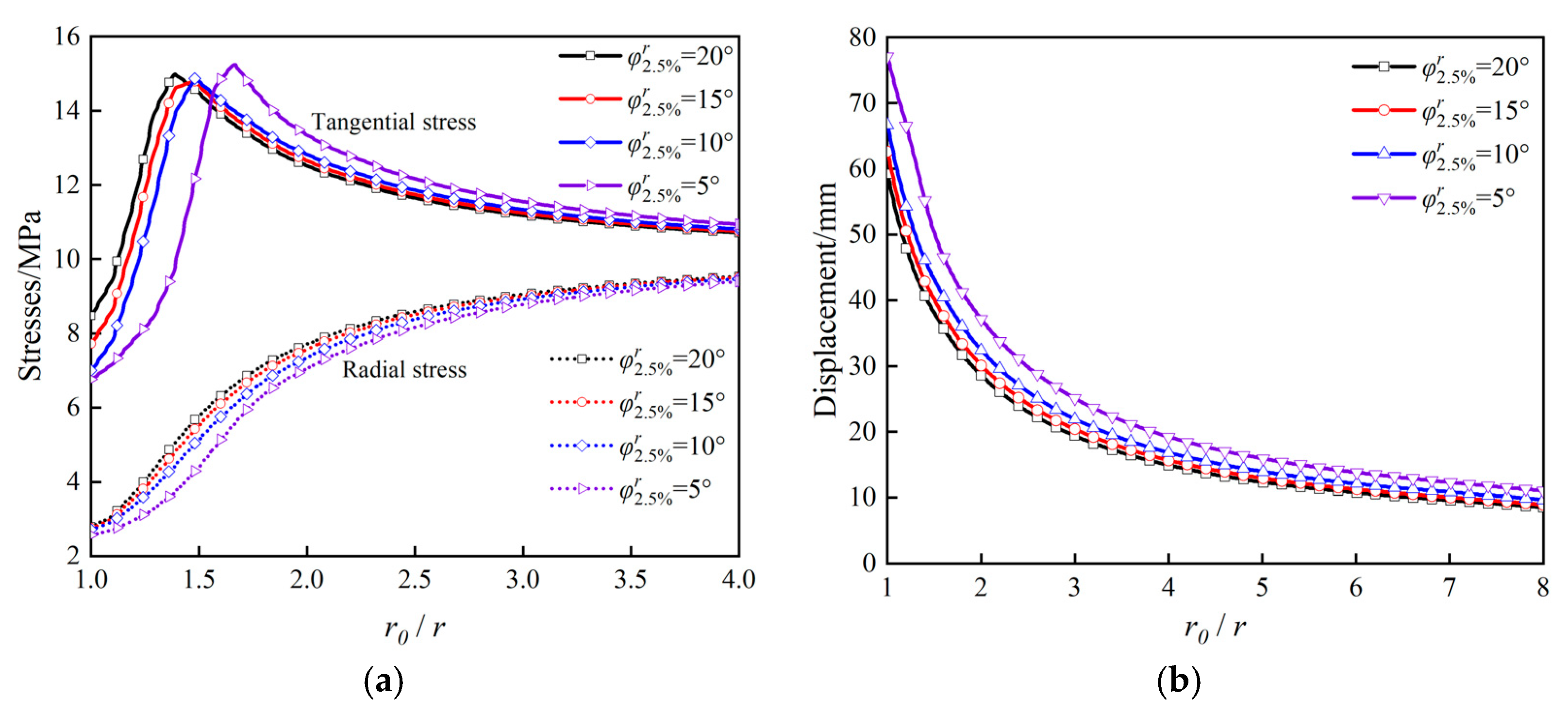
3.2.2. Simulation Results Based on Strain Softening Model
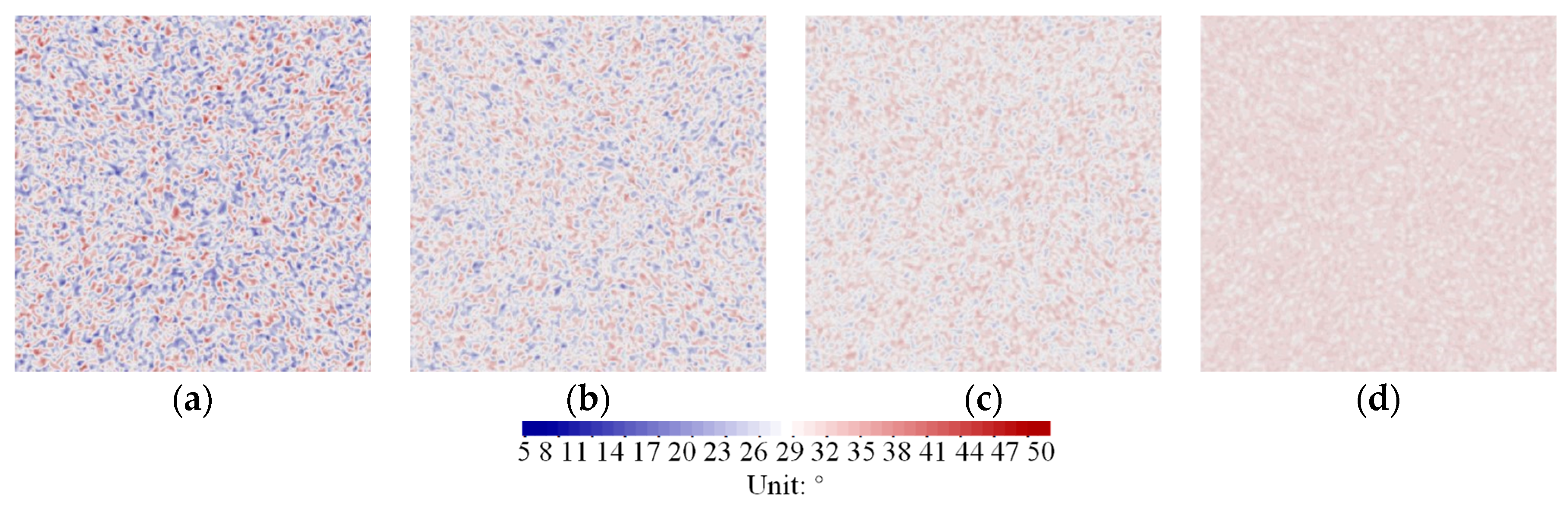
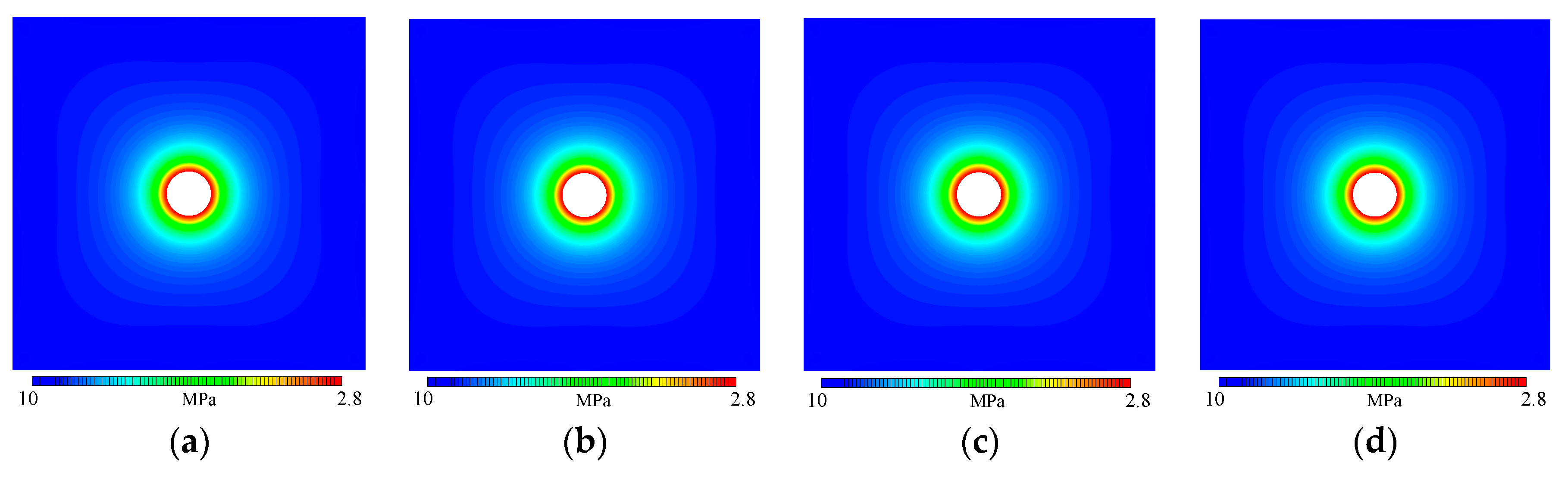
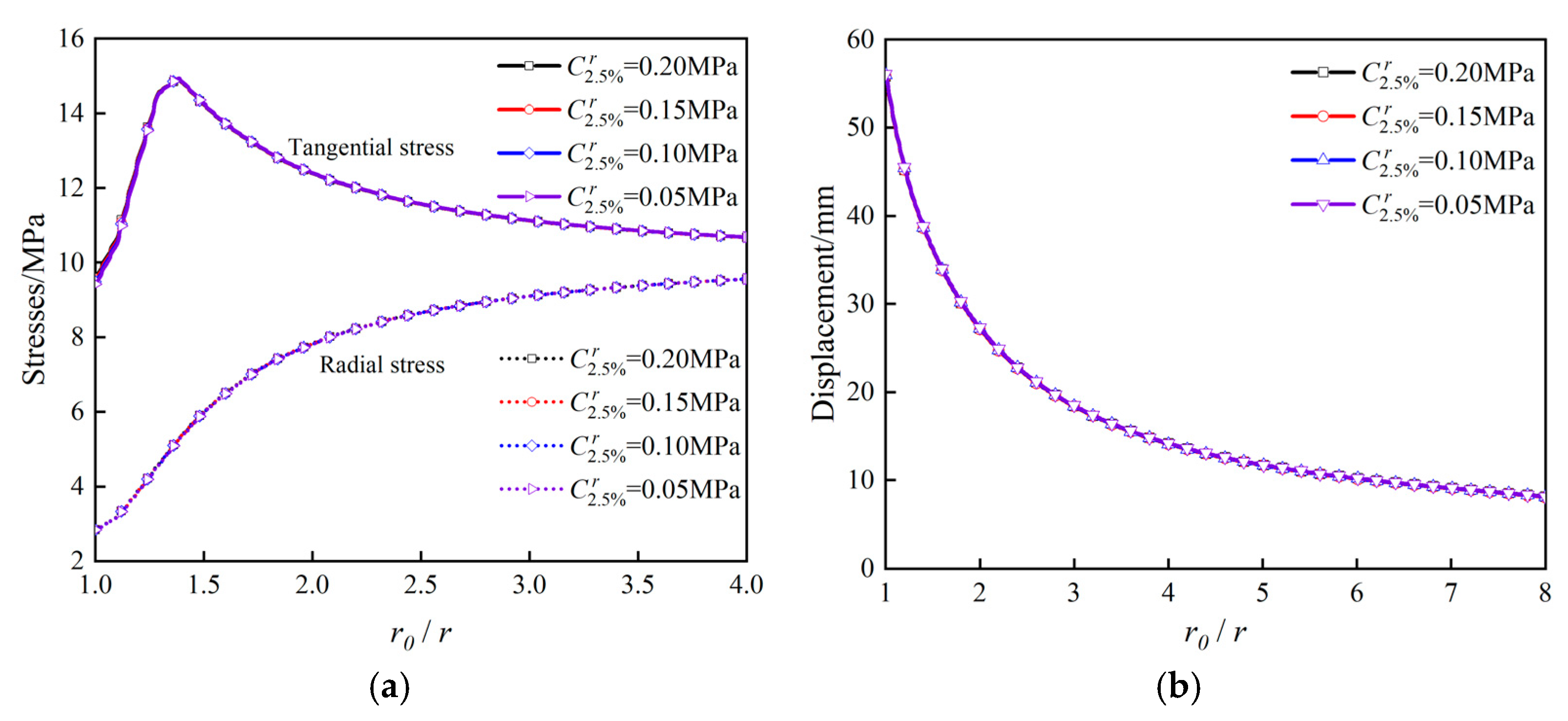
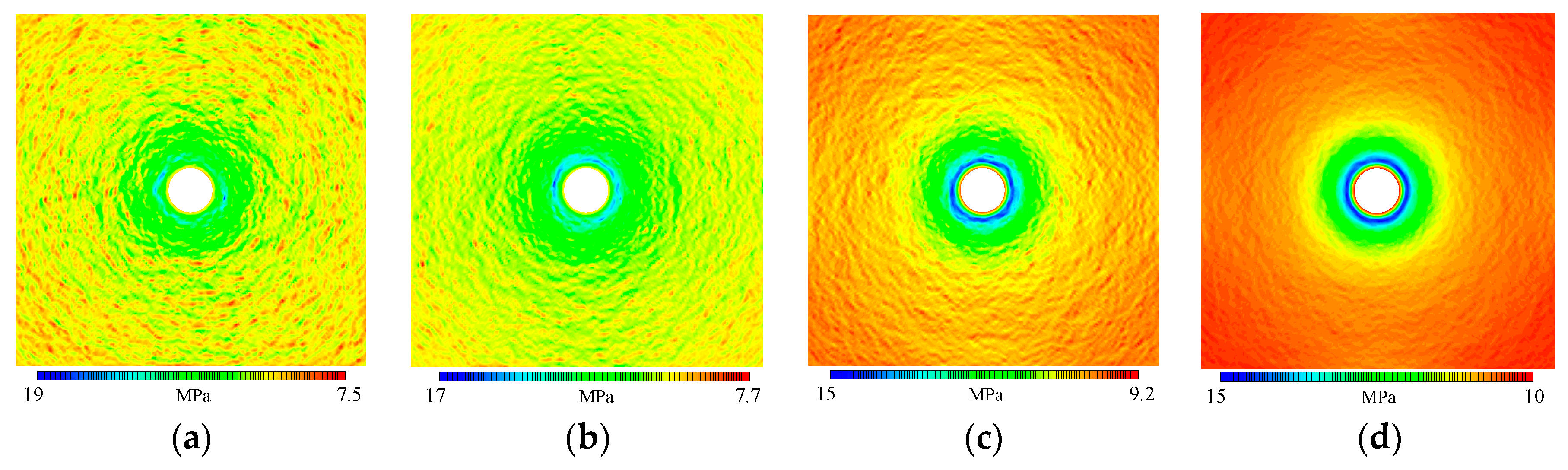
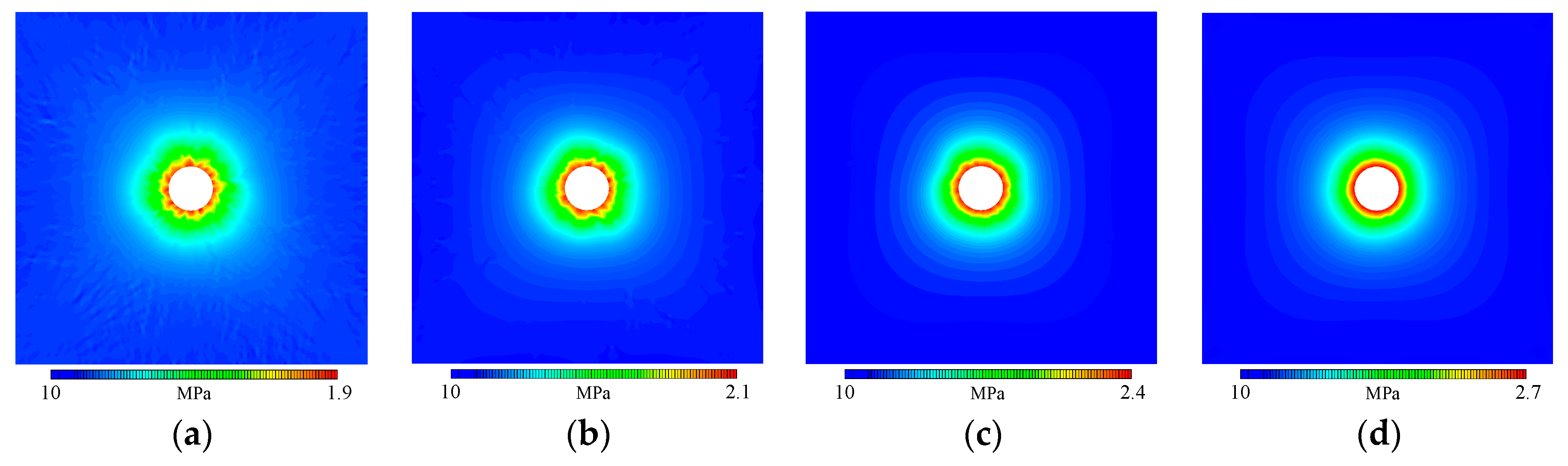
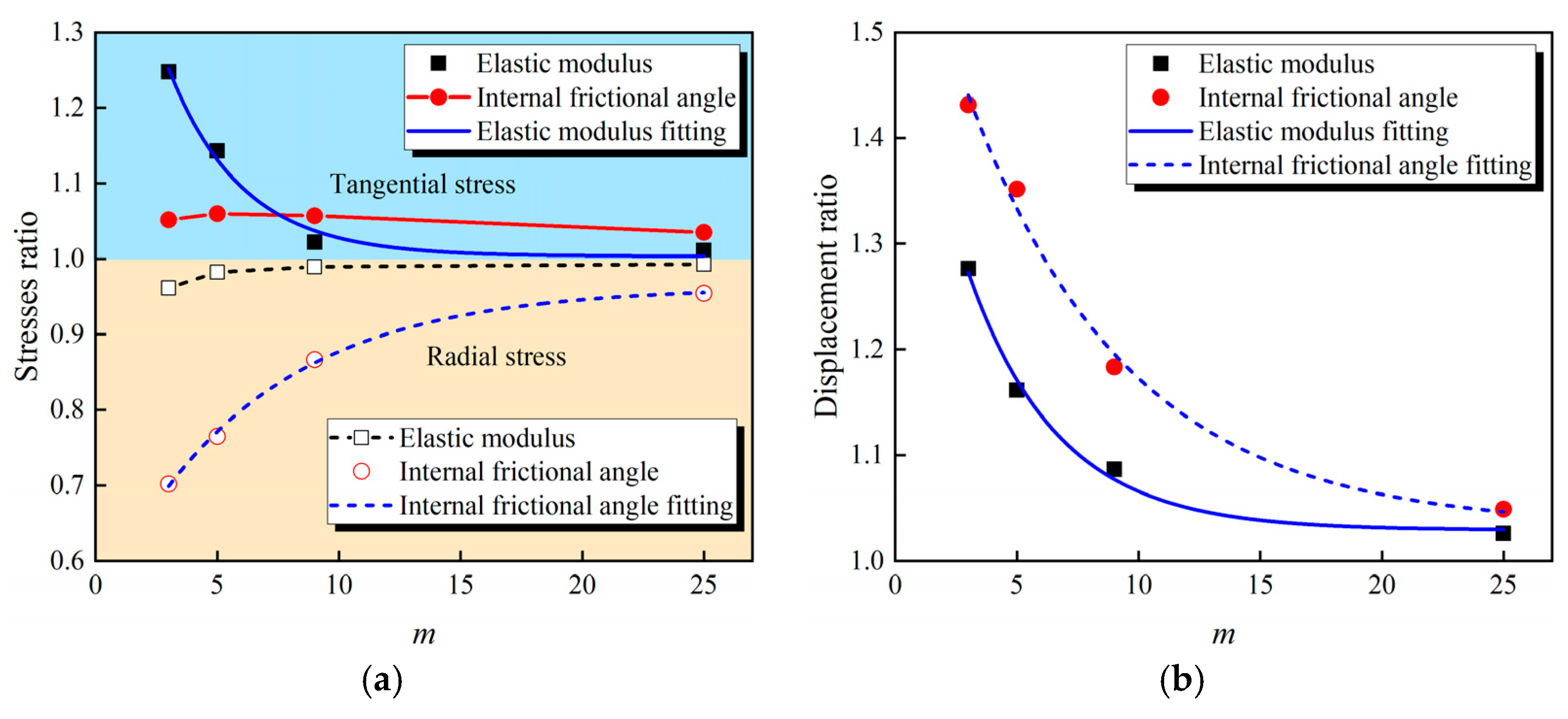
3.2.3. Simulation Results Considering the Spatial Variability Effect
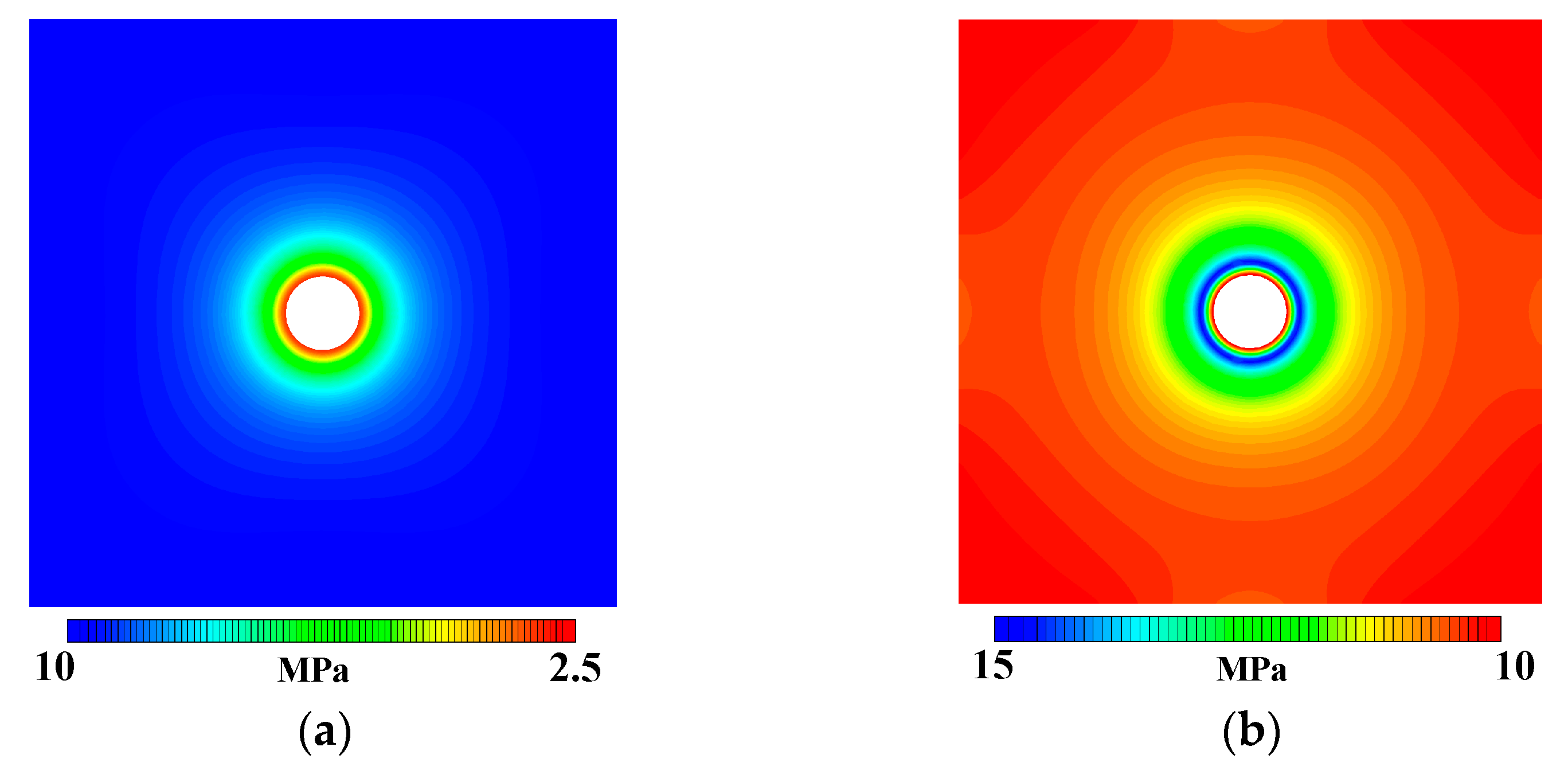
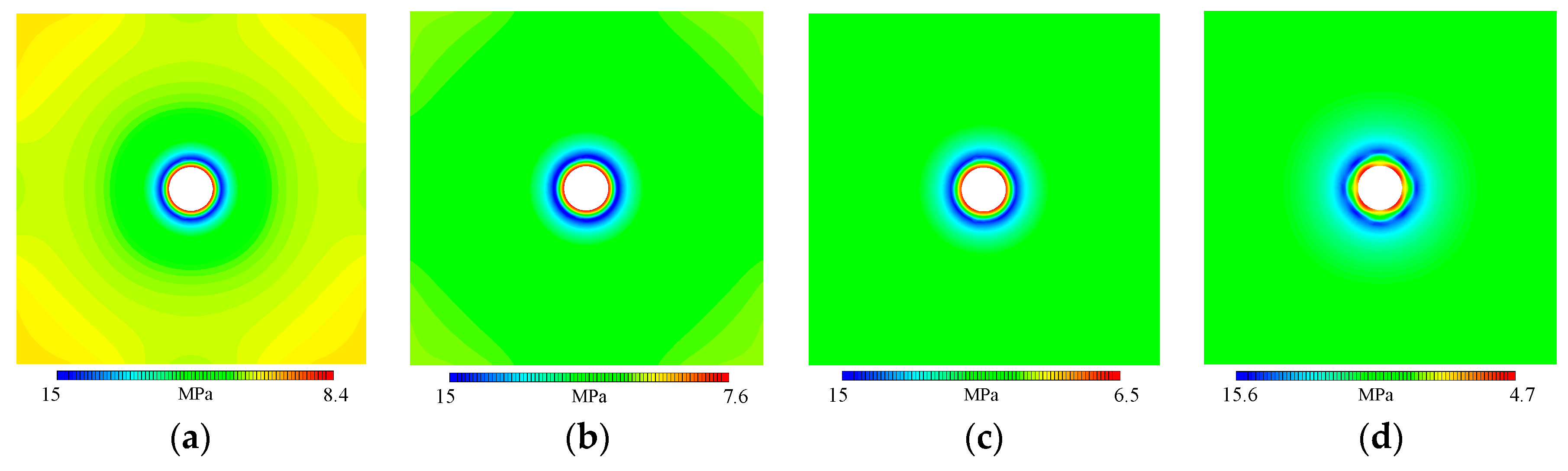
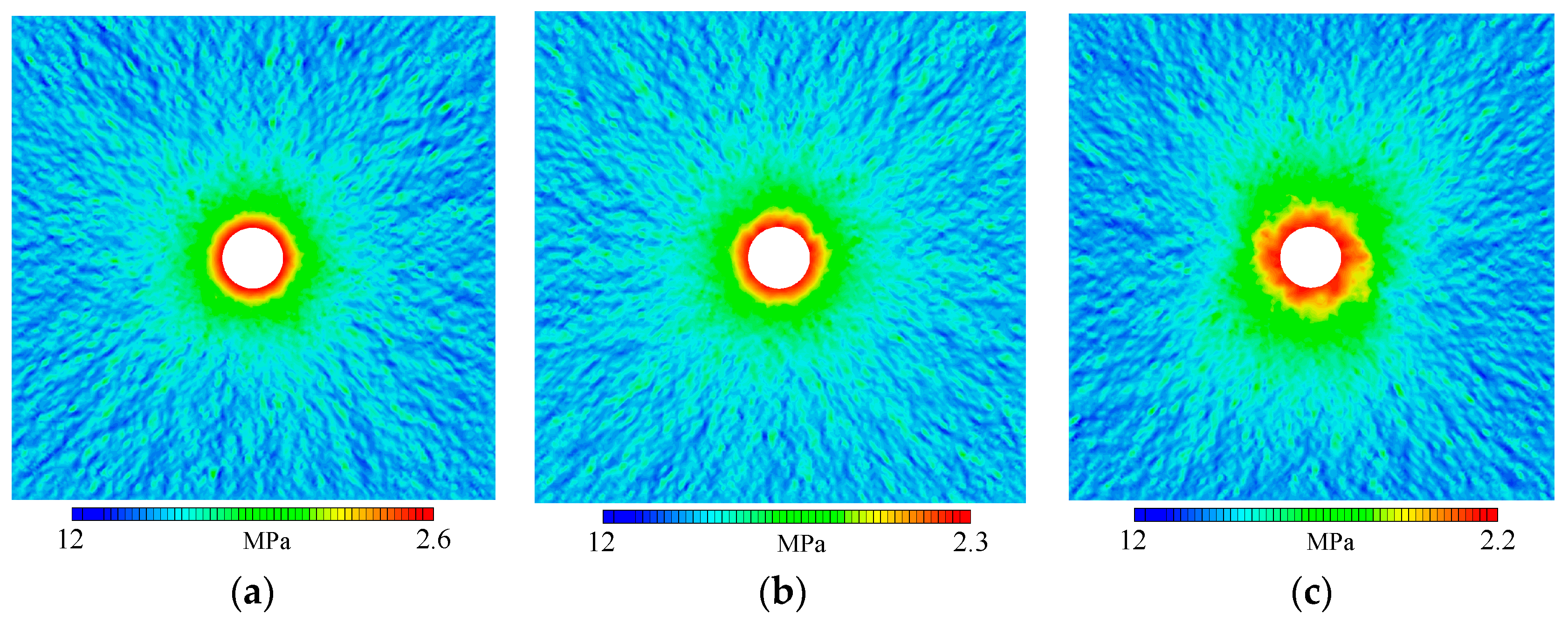
3.2.4. Coupling Effect of Strain Softening and Spatial Variability
4. Conclusions
- (a)
- The strain softening behavior of the internal friction angle significantly affects the plastic zone radius and tunnel displacement. In contrast, for weak surrounding rock with low initial cohesion, its influence on the mechanical response is relatively negligible.
- (b)
- Spatial variability of elastic modulus primarily influences tangential stress distribution, and the internal friction angle exerts a greater influence on radial stress and displacement. Near the tunnel wall, the internal friction angle’s variability leads to pronounced localized stress concentrations, surpassing those caused by the elastic modulus and increasing the risk of localized collapse or instability. Furthermore, analysis reveals that the peak value ratio of stress and displacement between spatial variability and homogeneous models exhibits a strong exponential correlation with the homogeneity parameter. This underscores the importance of incorporating spatial variability of geotechnical parameters in tunnel stability evaluations to accurately predict mechanical behavior and maintain structural safety.
- (c)
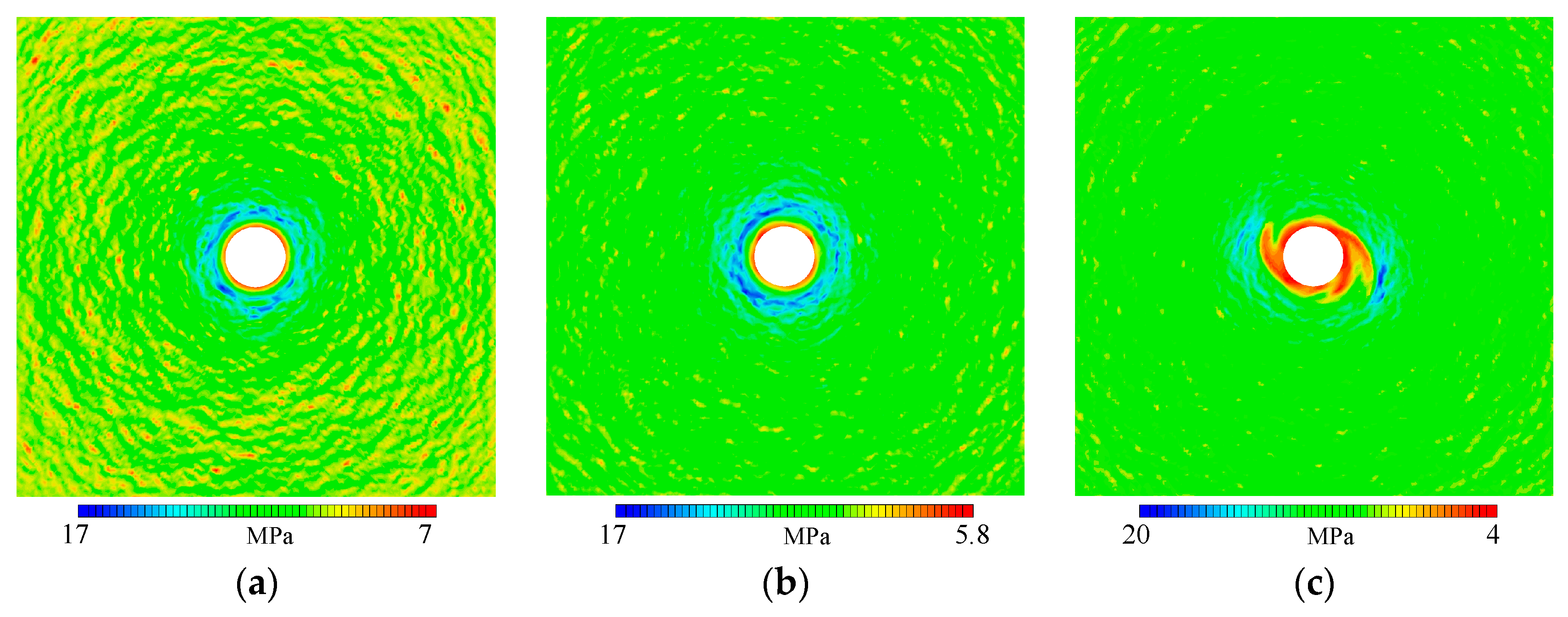
- The coupling effect of strain softening and spatial variability exerts a more significant impact on the mechanical response compared to individual effects. Under extreme coupling conditions, the tunnel’s failure mode shifts from a general asymmetric failure to localized asymmetric failure. The peak value of tangential stress and displacement reaches 1.4 times and 4 times that of the ideal model, respectively. These findings highlight the significant amplification impact of strain softening and spatial variability on tunnel excavation, underscoring that it cannot be disregarded.
- (d)
- Based on the numerical simulation results, a construction management approach is proposed, focusing on regulating plastic shear strain and improving the homogeneity of the surrounding rock. Disaster prevention measures include optimizing excavation methods and sequences, reinforcing the support system, and applying pre-reinforcement strategies. The results provide a scientific basis and practical recommendations for disaster prevention and mitigation in tunnel construction within complex geological settings.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Tu, W.; Shi, S.; Chen, J.; Zhang, Y. Mechanism of water inrush in tunnel construction in karst area. Geomatics. Nat. Hazards Risk 2016, 7, 35–46. [Google Scholar] [CrossRef]
- Kaufmann, G.; Romanov, D. Modelling long-term and short-term evolution of karst in the vicinity of tunnels. J. Hydrol. 2020, 581, 124282. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, Y.; Li, C.; Li, C.; Lan, T.; Ping, S.; Cao, Y. An experimental study on the corrosion characteristics of the karst tunnel engineering area in Southwest China. Bull. Eng. Geol. Environ. 2019, 78, 4047–4061. [Google Scholar] [CrossRef]
- Xu, C.; Zhou, X.; Wang, H.; Gao, X.; Li, X. A case study of thaumasite sulfate attack in tunnel engineering. Adv. Civ. Eng. 2021, 2021, 8787757. [Google Scholar] [CrossRef]
- Yau, K.; Paraskevopoulou, C.; Konstantis, S. Spatial variability of karst and effect on tunnel lining and water inflow: A probabilistic approach. Tunn. Undergr. Space Technol. 2020, 97, 103248. [Google Scholar] [CrossRef]
- Zhang, L.W.; Fu, H.; Wu, J.; Zhang, X.Y.; Zhao, D.K. Effects of karst cave shape on the stability and minimum safety thickness of tunnel surrounding rock. Int. J. Geomech. 2021, 21, 04021150. [Google Scholar] [CrossRef]
- Alija, S.; Torrijo, F.J.; Quinta-Ferreira, M. Geological engineering problems associated with tunnel construction in karst rock masses: The case of Gavarres Tunnel (Spain). Eng. Geol. 2013, 157, 103–111. [Google Scholar] [CrossRef]
- Read, H.E.; Hegemier, G.A. Strain-softening of rock, soil and concrete: A review article. Mech. Mater. 1984, 3, 271–294. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. Three-dimensional static and seismic stability analysis of a tunnel face driven in weak rock masses. Int. J. Geomech. 2018, 18, 04018055. [Google Scholar] [CrossRef]
- Lu, W.; Zhu, Z.; He, Y.; Que, X. Strength characteristics and failure mechanism of a columnar jointed rock mass under uniaxial, triaxial, and true triaxial confinement. Rock Mech. Rock Eng. 2021, 54, 2425–2439. [Google Scholar] [CrossRef]
- Wang, Y.N.; Wang, L.C.; Zhou, H.Z. An experimental investigation and mechanical modeling of the combined action of confining stress and plastic strain in a rock mass. Bull. Eng. Geol. Environ. 2022, 81, 204. [Google Scholar] [CrossRef]
- Rong, P.; Zuo, Y.; Lin, J.; Chen, Q.; Zheng, L.; Jin, K. Study of mechanical properties and failure characteristics of combined rock mass with weak interlayer. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 89. [Google Scholar] [CrossRef]
- Renani, R.H.; Martin, D.C. Cohesion degradation and friction mobilization in brittle failure of rocks. Int. J. Rock Mech. Min. Sci. 2018, 106, 1–13. [Google Scholar] [CrossRef]
- Xiong, L.; Wu, S.; Zhang, S. Mechanical behavior of a granite from Wuyi Mountain: Insights from strain-based approaches. Rock Mech. Rock Eng. 2019, 52, 719–736. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Gu, Q.; Wu, P.; Jiang, B. An improved strain-softening constitutive model of granite considering the effect of crack deformation. J. Rock Mech. Geotech. Eng. 2024, 16, 1202–1215. [Google Scholar] [CrossRef]
- Zhang, F.; Yashima, A.; Ye, G.L.; Adachi, T.; Oka, F. An elastoplastic strain-hardening and strain-softening constitutive model for soft rock considering the influence of intermediate stress. Soils Found. 2003, 43, 107–117. [Google Scholar] [CrossRef]
- Shen, P.; Tang, H.; Ning, Y.; Xia, D. A damage mechanics based on the constitutive model for strain-softening rocks. Eng. Fract. Mech. 2019, 216, 106521. [Google Scholar] [CrossRef]
- Xiao, Y.; Qiao, Y.; He, M.; Li, H.; Cheng, T.; Tang, J. A unified strain-hardening and strain-softening elastoplastic constitutive model for intact rocks. Comput. Geotech. 2022, 148, 104772. [Google Scholar] [CrossRef]
- Wang, T.; Ma, Z. Research on strain-softening constitutive model of coal-rock combined body with damage threshold. Int. J. Damage Mech. 2022, 31, 22–42. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, X.F.; Jiang, B.S.; Liu, R.C.; Li, G.M. A finite strain solution for strain-softening rock mass around circular roadways. Tunn. Undergr. Space Technol. 2021, 111, 103873. [Google Scholar] [CrossRef]
- Chu, Z.; Wu, Z.; Liu, Q.; Weng, L.; Xu, X.; Wu, K.; Sun, Z. Visco-elastic-plastic solution for deep buried tunnels considering tunnel face effect and sequential installation of double linings. Comput. Geotech. 2024, 165, 105930. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.-Y.; Jiang, Y.-J.; Lu, M.-M.; Jiang, B.-S. A numerical large strain solution for circular tunnels excavated in strain-softening rock masses. Comput. Geotech. 2019, 114, 103142. [Google Scholar] [CrossRef]
- Zhang, Q.; Quan, X.-W.; Wang, H.-Y.; Jiang, B.-S.; Liu, R.-C. A numerical solution of a circular tunnel in a confining pressure-dependent strain-softening rock mass. Comput. Geotech. 2020, 121, 103473. [Google Scholar] [CrossRef]
- Wu, P.; Zhang, Q.; Li, S.; Liu, R.; Wang, H.; Han, G. A numerical strain-softening solution of a circular opening in nonlinear yield rock masses. Tunn. Undergr. Space Technol. 2024, 153, 106035. [Google Scholar] [CrossRef]
- Fei, S.; Alfonso, R. Numerical solutions for tunnels excavated in strain-softening rock masses considering a combined support system. Appl. Math. Modell. 2021, 92, 905–930. [Google Scholar] [CrossRef]
- Guan, K.; Zhu, W.; Wei, J.; Liu, X.; Niu, L.; Wang, X. A finite strain numerical procedure for a circular tunnel in strain-softening rock mass with large deformation. Int. J. Rock Mech. Min. Sci. 2018, 112, 266–280. [Google Scholar] [CrossRef]
- Guo, X.; Du, D.; Dias, D. Reliability analysis of tunnel lining stability based on strain-softening characteristics. Eng. Struct. 2019, 192, 305–321. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Gao, Q.; Ma, X.; Zhou, H.; Wang, Z. Probabilistic analysis of ground settlement induced by tunnel excavation in multilayered soil considering spatial variability. Comput. Geotech. 2024, 165, 105951. [Google Scholar] [CrossRef]
- Zhang, Z.; Ji, J.; Guo, X.; Goh, S.H. Inverse reliability analysis and design for tunnel face stability considering soil spatial variability. J. Rock Mech. Geotech. Eng. 2024, 16, 1552–1564. [Google Scholar] [CrossRef]
- Miranda, T.; Viana, A.; Martins, F.F.; Guo, X.; Cristelo, N.; Dias, D. Numerical analysis of a tunnel behaviour considering the spatial variability of the geotechnical parameters. Proc. Inst. Civ. Eng.-Geotech. Eng. 2024, 177, 392–404. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Yuan, S.; Zhang, T.; Song, J.; Chen, W. Probabilistic stability analysis of qanat tunnels in c-φ soil considering soil spatial variability. Eur. J. Environ. Civ. Eng. 2022, 27, 3763–3783. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Hu, M. Three-dimensional large deformation modeling of landslides in spatially variable and strain-softening soils subjected to seismic loads. Can. Geotech. J. 2023, 60, 426–437. [Google Scholar] [CrossRef]
- Cai, W.; Dou, L.; Ju, Y.; Cao, W.; Yuan, S.; Si, G. A plastic strain-based damage model for heterogeneous coal using cohesion and dilation angle. Int. J. Rock Mech. Min. Sci. 2018, 110, 151–160. [Google Scholar] [CrossRef]
- Zhou, X. Analysis of the localization of deformation and the complete stress-strain relation for mesoscopic heterogeneous brittle rock under dynamic uniaxial tensile loading. Int. J. Solids Struct. 2003, 41, 1725–1738. [Google Scholar] [CrossRef]
- Alonso, E.; Alejano, L.R.; Varas, F.; Fdez-Manin, G.; Carranza-Torres, C. Ground response curves for rock masses exhibiting strain-softening behaviour. Int. J. Numer. Anal. Methods Geomech. 2003, 27, 1153–1185. [Google Scholar] [CrossRef]
- Sun, M.; Yan, Q.; Zhang, J.; Wang, E.; Yao, C.; Wang, X. A practical method for considering soil strain softening effect in the tunnel face stability analysis by numerical modeling. B Eng. Geol. Environ. 2022, 8, 486. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, J.; Chen, R.; Huang, J.; Li, J. Three-dimensional analysis of tunnel face stability in spatially variable soils. Comput. Geotech. 2019, 111, 76–88. [Google Scholar] [CrossRef]
- Cheng, H.-Z.; Chen, J.; Chen, R.-P.; Chen, G.-L. Reliability study on shield tunnel face using a random limit analysis method in multilayered soils. Tunn. Undergr. Space Technol. 2019, 84, 353–363. [Google Scholar] [CrossRef]







| Elastic Modulus (GPa) | Poisson Ratio / | Density (N/m3) | Internal Friction Angle (°) | Cohesion (MPa) | Tension Strength (MPa) |
|---|---|---|---|---|---|
| 1.2 | 0.4 | 2000 | 30 | 0.35 | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zeng, Y. Symmetric and Asymmetric Failure Mechanism of Deep Tunnel Excavation Under Complex Environmental Conditions. Symmetry 2025, 17, 416. https://doi.org/10.3390/sym17030416
Zhang Y, Zeng Y. Symmetric and Asymmetric Failure Mechanism of Deep Tunnel Excavation Under Complex Environmental Conditions. Symmetry. 2025; 17(3):416. https://doi.org/10.3390/sym17030416
Chicago/Turabian StyleZhang, Yao, and Yu Zeng. 2025. "Symmetric and Asymmetric Failure Mechanism of Deep Tunnel Excavation Under Complex Environmental Conditions" Symmetry 17, no. 3: 416. https://doi.org/10.3390/sym17030416
APA StyleZhang, Y., & Zeng, Y. (2025). Symmetric and Asymmetric Failure Mechanism of Deep Tunnel Excavation Under Complex Environmental Conditions. Symmetry, 17(3), 416. https://doi.org/10.3390/sym17030416






