Quantitative Optimization of the Heating Element for Enhanced Temperature Uniformity in an Embryo Chamber
Abstract
1. Introduction
2. Materials and Methods
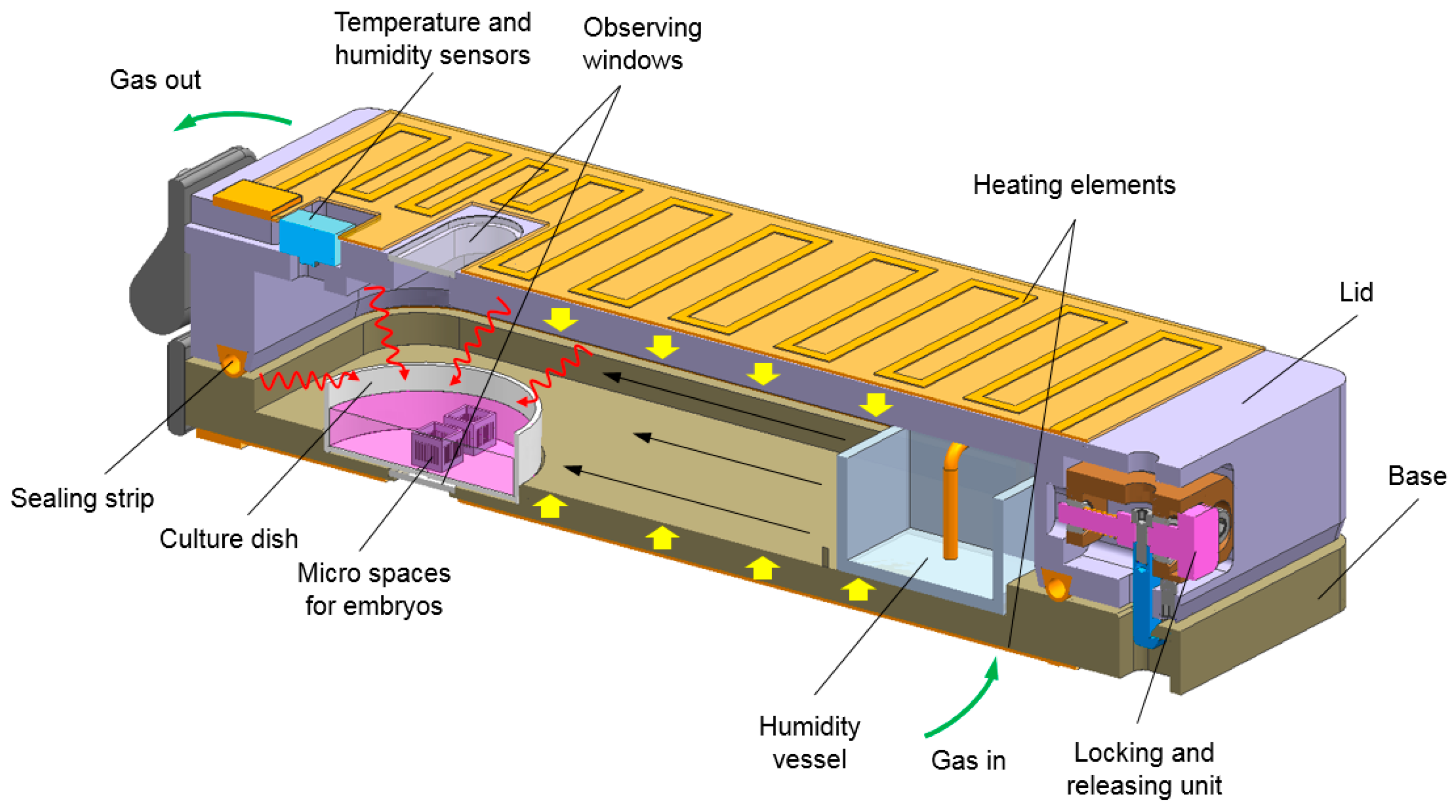
2.1. Heat Transfer System for Embryo Chamber
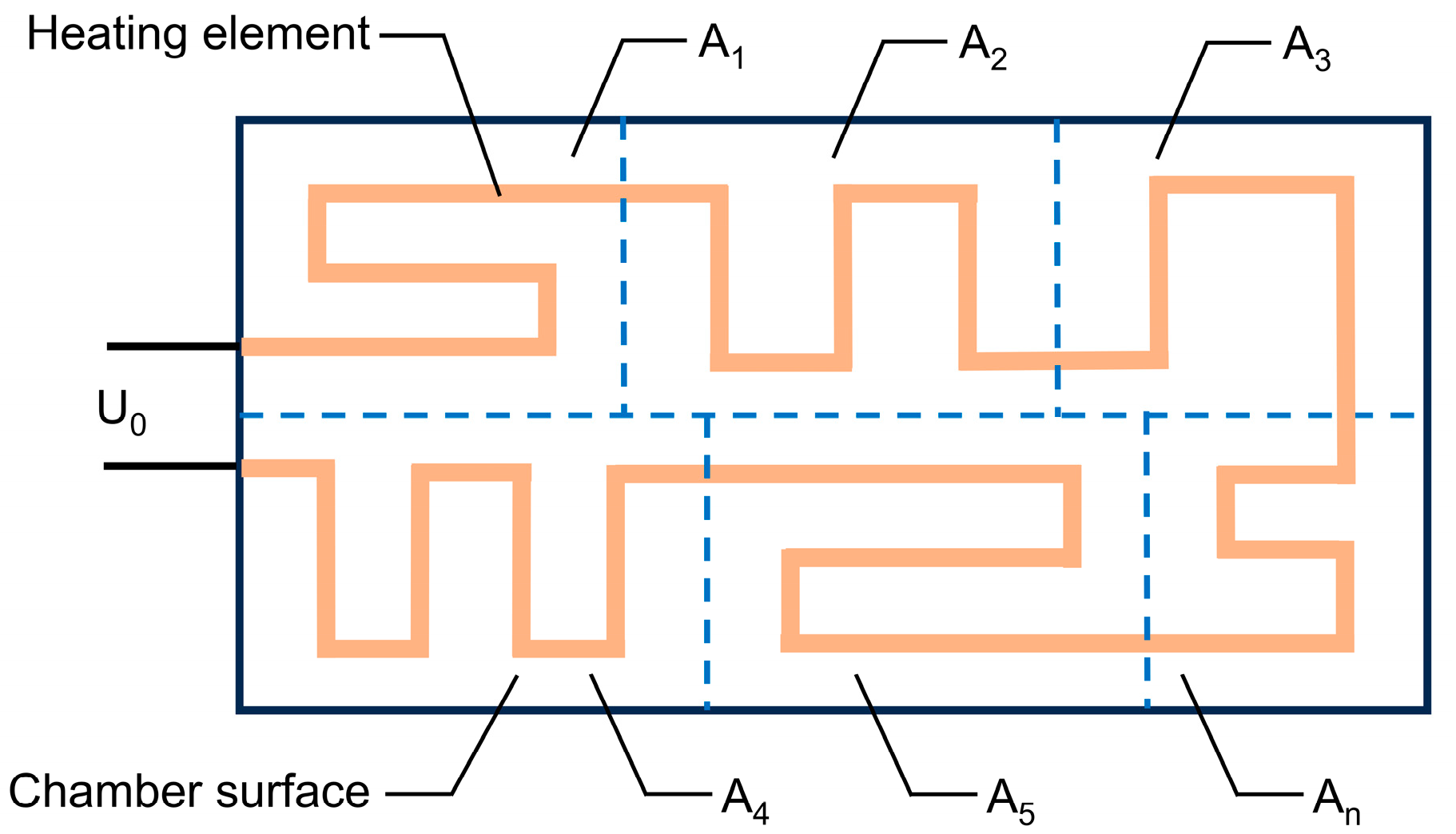
2.2. Quantitative Optimization of Heating Element
2.3. Temperature Simulation of Chamber Surface
2.4. Temperature Simulation of Assembled Chamber
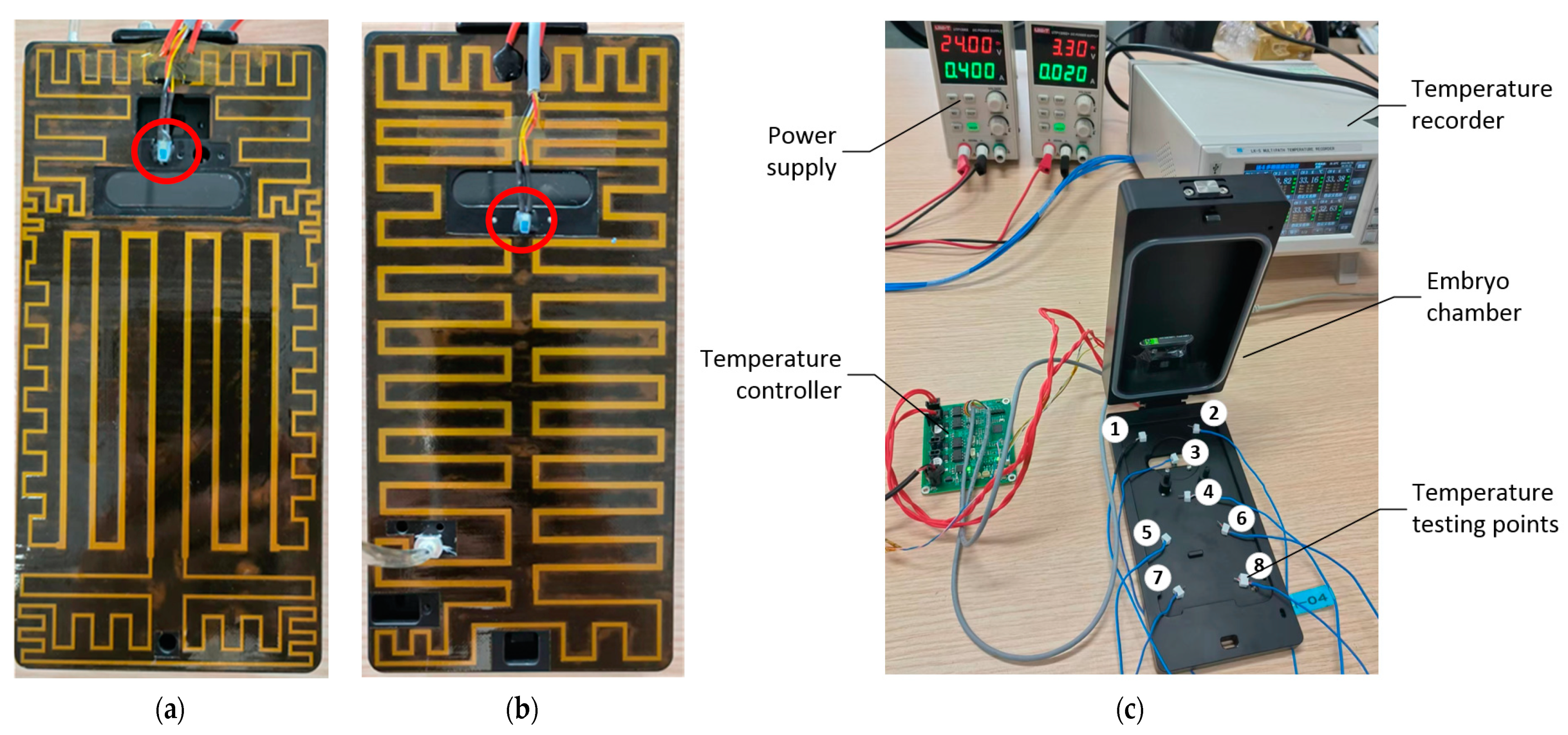
2.5. Temperature Experiment on the Fabricated Chamber
3. Results
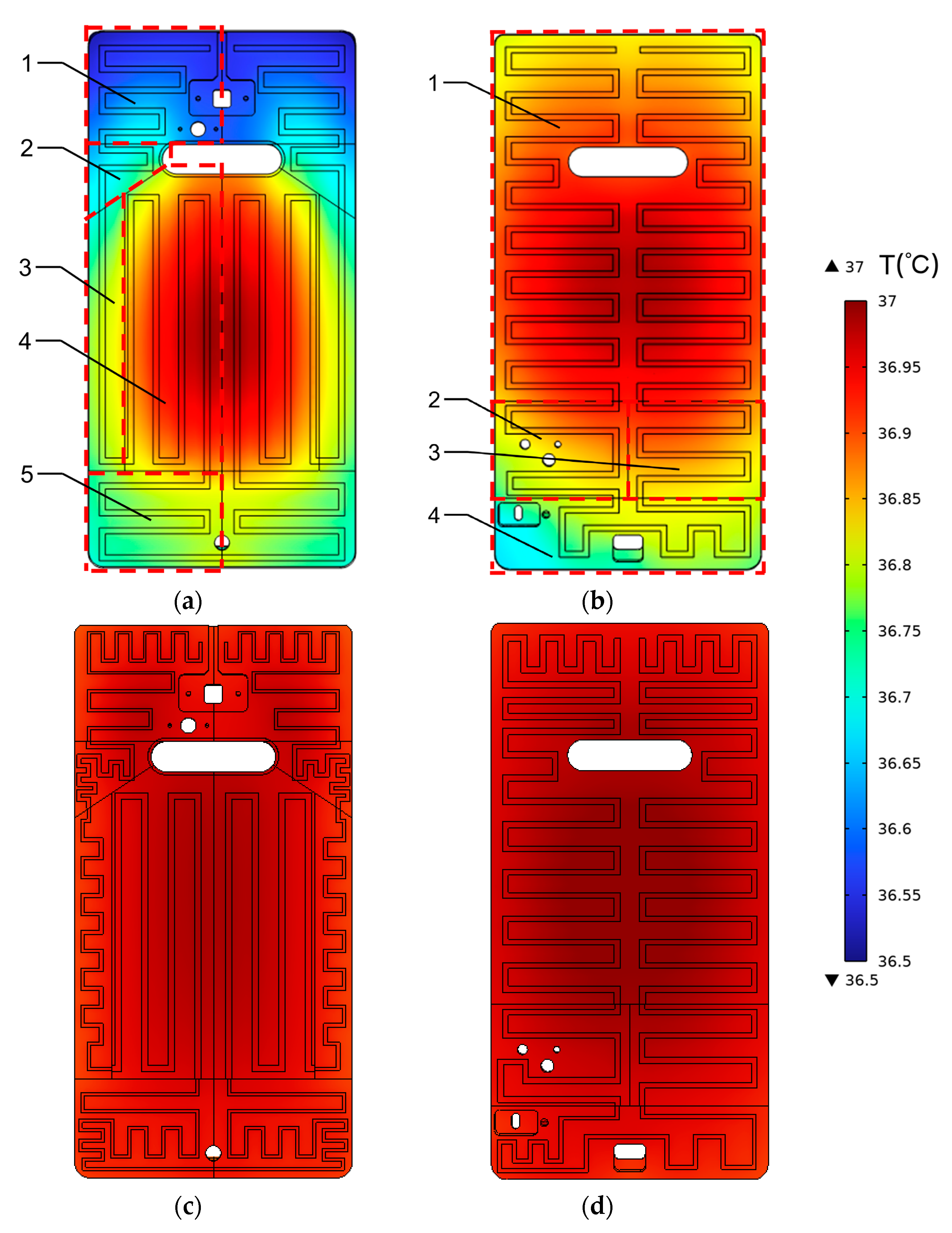
3.1. Optimization of Temperature Uniformity on the Chamber Surface
3.2. Temperature Field of Assembled Chamber
3.3. Temperature Distribution Within the Fabricated Chamber
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ART | Assisted reproductive technology |
References
- Brown, J.D.; Dillon, H.E.; Kaweesa, D.V.; Harada, A.M. The impact of transient heat transfer on tissue culture cell distribution. Biosyst. Eng. 2017, 163, 28–36. [Google Scholar] [CrossRef]
- Phelan, K.; May, K.M. Basic techniques in mammalian cell tissue culture. Curr. Protoc. Cell Biol. 2015, 66, 1.1.1–1.1.22. [Google Scholar]
- Walters, E.A.; Brown, J.L.; Krisher, R.; Voelkel, S.; Swain, J.E. Impact of a controlled culture temperature gradient on mouse embryo development and morphokinetics. Reprod. BioMed. Online 2020, 40, 494–499. [Google Scholar]
- Almeida, P.A.; Bolton, V.N. The effect of temperature fluctuations on the cytoskeletal organisation and chromosomal constitution of the human oocyte. Zygote 1995, 3, 357–365. [Google Scholar]
- Sugiyama, S.; Mcgowan, M.; Kafi, M.; Phillips, N.; Young, M. Effects of increased ambient temperature on the development of in vitro derived bovine zygotes. Theriogenology 2003, 60, 1039–1047. [Google Scholar]
- Nguyen, Q.; Sommer, S.; Greene, B.; Wrenzycki, C.; Wagner, U.; Ziller, V. Effects of opening the incubator on morphokinetics in mouse embryos. Eur. J. Obstet. Gynecol. Reprod. Biol. 2018, 229, 64–69. [Google Scholar] [PubMed]
- Swain, J.E. Optimal human embryo culture. Semin. Reprod. Med. 2015, 33, 103–117. [Google Scholar]
- Anifandis, G. Temperature variations inside commercial IVF incubators. J. Assist. Reprod. Genet. 2013, 30, 1587–1588. [Google Scholar] [CrossRef][Green Version]
- Braga, P.C. A variable-thickness, multipurpose culture chamber for high-magnification observation. J. Microsc. 1990, 159, 285–288. [Google Scholar]
- Imashiro, C.; Jin, Y.; Hayama, M.; Yamada, T.G.; Funahashi, A.; Sakaguchi, K.; Umezu, S.; Komotori, J. Titanium Culture Vessel Presenting Temperature Gradation for the Thermotolerance Estimation of Cells. Cyborg Bionic Syst. 2023, 4, 0049. [Google Scholar] [CrossRef]
- Soreide, E.; Denbeigh, J.M.; Lewallen, E.A.; Thaler, R.; Samsonraj, R.M.; Jones, D.L.; Xu, W.; Larson, D.; Nordsletten, L.; Kakar, S.; et al. A multi-chamber tissue culture device for load-dependent parallel evaluation of tendon explants. BMC Musculoskelet. Disord. 2019, 20, 549. [Google Scholar] [CrossRef] [PubMed]
- Saalfrank, D.; Konduri, A.K.; Latifi, S.; Habibey, R.; Golabchi, A.; Martiniuc, A.V.; Knoll, A.; Ingebrandt, S.; Blau, A. Incubator-independent cell-culture perfusion platform for continuous long-term microelectrode array electrophysiology and time-lapse imaging. R. Soc. Open Sci. 2015, 2, 150031. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.M.; Jin, J.S.; Yan, Z.T. Fluid-solid coupling numerical simulation of charge process in variable-mass thermodynamic system. J. Cent. South Univ. 2012, 19, 1063–1072. [Google Scholar] [CrossRef]
- Morville, S.; Carin, M.; Peyre, P.; Gharbi, M.; Carron, D.; Le Masson, P.; Fabbro, R. 2D longitudinal modeling of heat transfer and fluid flow during multilayered direct laser metal deposition process. J. Laser Appl. 2012, 24, 032008. [Google Scholar] [CrossRef]
- Mäki, A.J.; Verho, J.; Kreutzer, J.; Ryynänen, T.; Rajan, D.; Pekkanen-Mattila, M.; Ahola, A.; Hyttinen, J.; Aalto-Setälä, K.; Lekkala, J.; et al. A portable microscale cell culture system with indirect temperature control. SLAS Technol. Transl. Life Sci. Innov. 2018, 23, 566–579. [Google Scholar] [CrossRef]
- Imashiro, C.; Takeshita, H.; Morikura, T.; Miyata, S.; Takemura, K.; Komotori, J. Development of accurate temperature regulation culture system with metallic culture vessel demonstrates different thermal cytotoxicity in cancer and normal cells. Sci. Rep. 2021, 11, 21466. [Google Scholar] [CrossRef] [PubMed]
- Ho, K.H.; Hu, C.K.; Li, T.T. Numerical analysis for thermal field of susceptor in MOCVD reactor. In Proceedings of the 2015 China Semiconductor Technology International Conference, Shanghai, China, 15–16 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–3. [Google Scholar]
- Ling, W.; Zhou, W.; Cui, J.; Shen, Z.; Wei, Q.; Chu, X. Experimental study on the heating/cooling and temperature uniformity performance of the microchannel temperature control device for nucleic acid PCR amplification reaction of COVID-19. Appl. Therm. Eng. 2023, 226, 120342. [Google Scholar] [CrossRef]
- Mu, Y.T.; Chen, L.; He, Y.L.; Tao, W.Q. Numerical study on temperature uniformity in a novel mini-channel heat sink with different flow field configurations. Int. J. Heat Mass Transf. 2015, 85, 147–157. [Google Scholar] [CrossRef]
- Bergheau, J.M.; Fortunier, R. Finite Element Simulation of Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Blomfield, S.; Redding, G.P.; Bronlund, J.E.; Stewart, B.; Peek, J. A Model for Characterisation of the Thermal Environment of Embryos in a Petri Dish During In Vitro Culture. Cell. Mol. Bioeng. 2016, 9, 546–555. [Google Scholar] [CrossRef]
- Benyahia, N.; Aksouh, M.; Mataoui, A.; Oztop, H.F. Coupling turbulent natural convection-radiation-conduction in differentially heated cavity with high aspect ratio. Int. J. Therm. Sci. 2020, 158, 106518. [Google Scholar] [CrossRef]
- Incropera, F.P. Fundamentals of Heat and Mass Transfer; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Allué Hoyos, C. Applicability of COMSOL Multiphysics to Combined Heat, Air and Moisture Transfer Modelling in Building Envelopes. Master’s Thesis, Tampere University of Technology, Tampere, Finland, 2014. [Google Scholar]
- Salvi, D.; Boldor, D.; Aita, G.M.; Sabliov, C.M. COMSOL Multiphysics model for continuous flow microwave heating of liquids. J. Food Eng. 2011, 104, 422–429. [Google Scholar] [CrossRef]
- Li, P.; Hebibul, R.; Zhao, L.; Li, Z.; Zhao, Y.; Jiang, Z. Vibration and large deformation simulation analysis of graphene membrane for nanomechanical applications. In Proceedings of the 2016 IEEE 11th Annual International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Sendai, Japan, 17–20 April 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 209–212. [Google Scholar]
- Wang, C.; Pei, Y.; Mu, Z.; Fan, L.; Kong, J.; Tian, G.; Miao, S.; Meng, X.; Qiu, H. Simulation Analysis of 3-D Airflow and Temperature Uniformity of Paddy in a Laboratory Drying Oven. Foods 2024, 13, 3466. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Yi, Y.; Zhou, Y.; Cai, H. Highly stretchable and flexible graphene/ito hybrid transparent electrode. Nanoscale Res. Lett. 2016, 11, 108. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.M.; Jung, J.W.; Kim, Y.J. Design and evaluation of thermally conductive sheet structure to enhance the thermal stability of transparent oled displays. J. Opt. Soc. Am. B Opt. Phys. 2022, 39, 3216–3222. [Google Scholar]
- Lee, M.; Grazi, R.; Seifer, D. Incorporation of the Cook K-Minc incubator and media system into the IVF lab: The future of IVF. J. Clin. Embryol. 2010, 13, 21–32. [Google Scholar]
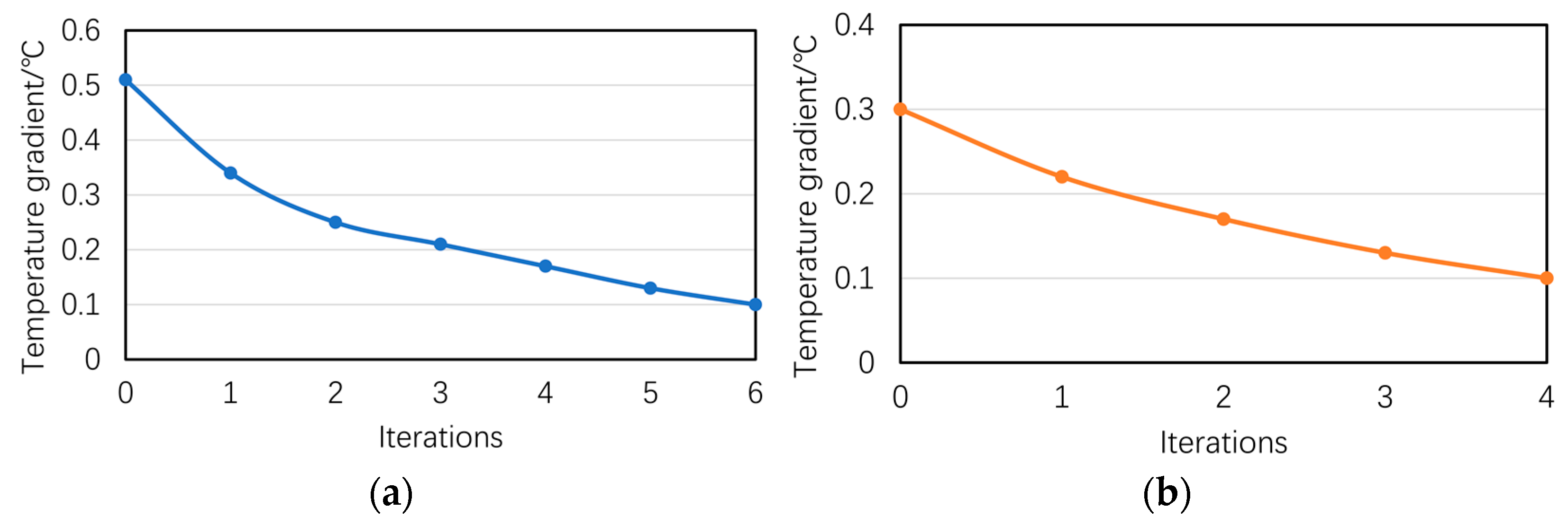

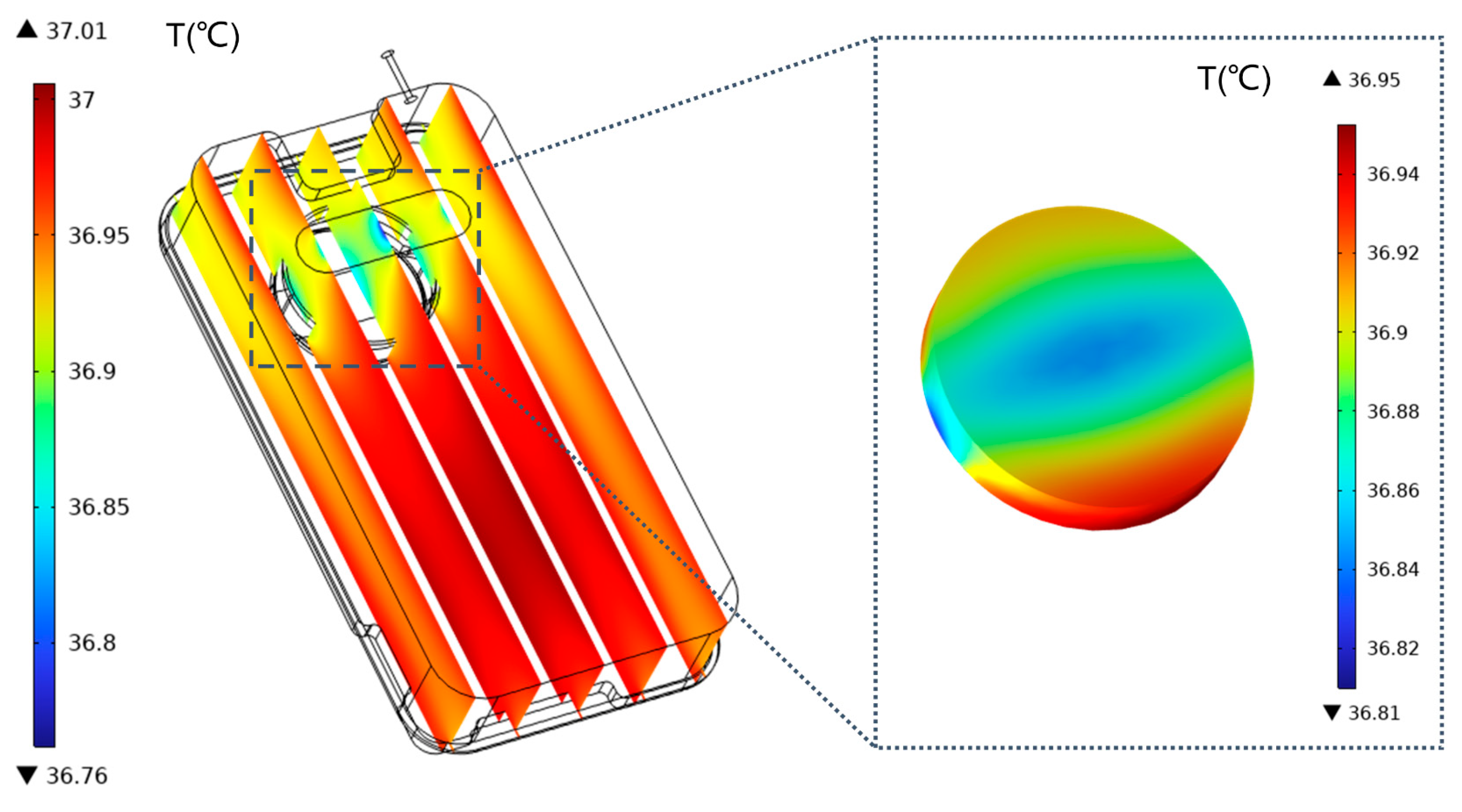

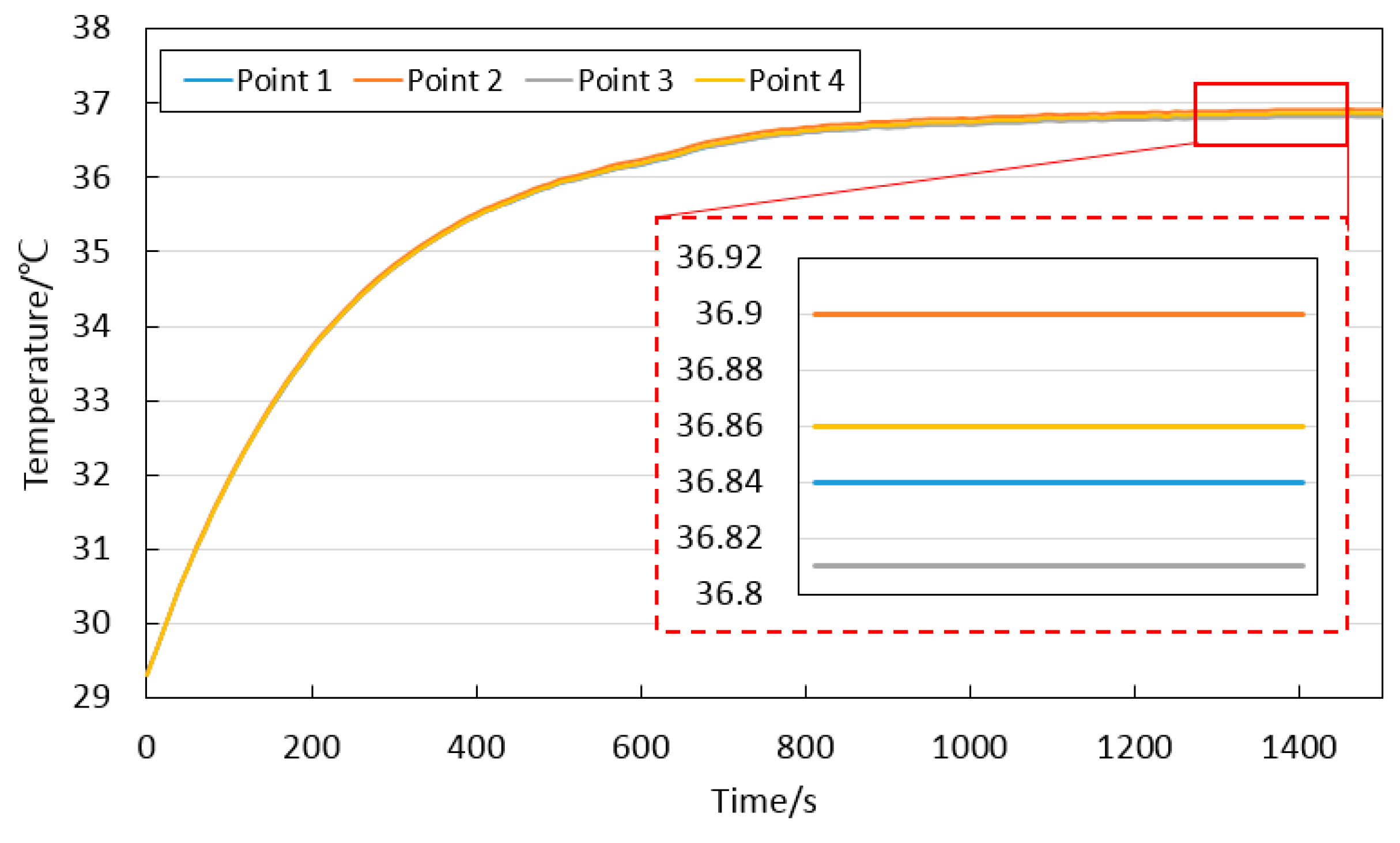
| Project | Parameters |
|---|---|
| Lid and base material | 6061 alloy |
| Sealing strip material | nylon |
| Glass material | SiO2 |
| Metal foil resistivity | 1.4 × 10−6 Ω·m |
| Ambient temperature | 293.15 K |
| Upper surface convective heat transfer coefficient of the lid | 4.1 W/(m2·K) |
| Bottom surface convective heat transfer coefficient of the base | 2.1 W/(m2·K) |
| Side surface convective heat transfer coefficient | 5.9 W/(m2·K) |
| Lid surface emissivity | 0.2 |
| Insulation cotton surface emissivity | 0.8 |
| Glass surface emissivity | 0.9 |
| Thickness of the metal foil | 0.05 mm |
| Initial width of the metal foil | 2 mm |
| Gas flow rate | 30 mL/min |
| Parameter | Region No. | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 5 | |
| k | 5 | |||
| Ai | 0.0026 m2 | 0.00073 m2 | 0.00236 m2 | 0.003 m2 |
| hi | 5.1 W/(m2·K) | 5.2 W/(m2·K) | 5.3 W/(m2·K) | 5.1 W/(m2·K) |
| ΔTi | 0.331 °C | 0.251 °C | 0.187 °C | 0.182 °C |
| l0i | 162 mm | 54 mm | 91.5 mm | 174 mm |
| w0i | 2 mm | 2 mm | 2 mm | 2 mm |
| Ra | 24.2 Ω | |||
| U0 | 7.46 V | |||
| Iteration | Modified Parameter | Acceleration Factor | Region No. | |||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 5 | |||
| 1 | w′ | 5 | 0.4 mm | 0.25 mm | 0.35 mm | 0.25 mm |
| The rate of change of w′ | 20% | 12.5% | 17.5% | 12.5% | ||
| 2 | w′ | 10 | 0.4 mm | 0.3 mm | 0.5 mm | 0.3 mm |
| The rate of change of w′ | 25% | 17% | 30% | 17% | ||
| 3 | l′ | 10 | 30 mm | 10 mm | 26 mm | 35 mm |
| The rate of change of l′ | 18.5% | 18.5% | 28.4% | 20% | ||
| 4 | w′ | 10 | 0.1 mm | 0.1 mm | 0.2 mm | 0.1 mm |
| The rate of change of w′ | 8.3% | 6.9% | 19% | 6.9% | ||
| 5 | w′ | 10 | 0.15 mm | 0 | 0 | 0.2 mm |
| The rate of change of w′ | 13.6% | 0 | 0 | 14.8% | ||
| 6 | l′ | 10 | 20 mm | 10 mm | 20 mm | 25 mm |
| The rate of change of l′ | 10.4% | 15.4% | 17% | 12% | ||
| Iteration | Modified Parameter | Acceleration Factor | Region No. | |||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 | w′ | 10 | 0 | 0.15 mm | 0.15 mm | 0.8 mm |
| The rate of change of w′ | 0 | 7.5% | 7.5% | 40% | ||
| 2 | l′ | 10 | 0 | 7 mm | 0 | 17 mm |
| The rate of change of l′ | 0 | 4% | 0 | 13.5% | ||
| 3 | l′ | 10 | 0 | 5 mm | 0 | 13 mm |
| The rate of change of l′ | 0 | 2.7% | 0 | 9.1% | ||
| 4 | l′ | 10 | 80 mm | 0 | 0 | 20 mm |
| The rate of change of l′ | 6.1% | 0 | 0 | 12.9% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Zeng, W.; Xiao, D.; Zhao, Z.; Sun, H. Quantitative Optimization of the Heating Element for Enhanced Temperature Uniformity in an Embryo Chamber. Symmetry 2025, 17, 478. https://doi.org/10.3390/sym17040478
Song Y, Zeng W, Xiao D, Zhao Z, Sun H. Quantitative Optimization of the Heating Element for Enhanced Temperature Uniformity in an Embryo Chamber. Symmetry. 2025; 17(4):478. https://doi.org/10.3390/sym17040478
Chicago/Turabian StyleSong, Yu, Weijun Zeng, Donggen Xiao, Zhenying Zhao, and Haixuan Sun. 2025. "Quantitative Optimization of the Heating Element for Enhanced Temperature Uniformity in an Embryo Chamber" Symmetry 17, no. 4: 478. https://doi.org/10.3390/sym17040478
APA StyleSong, Y., Zeng, W., Xiao, D., Zhao, Z., & Sun, H. (2025). Quantitative Optimization of the Heating Element for Enhanced Temperature Uniformity in an Embryo Chamber. Symmetry, 17(4), 478. https://doi.org/10.3390/sym17040478






