One-Cycle Control with Composite Function Embedded for Boost Converters

Abstract

It has been confirmed that a larger stability domain has more advantages for system operation. In this paper, a novel one-cycle control (OCC) embedded with a composite function is proposed. Its control principle is based on maintaining the symmetry of the volt-second value for the inductor in each cycle. Then, selecting the reference voltage as the study variable, the stability boundaries and identify stable parameter domains are studied by establishing a state-space average model. The results demonstrate that, compared with the conventional OCC, the proposed OCC with composite function $\sqrt{\mathrm{u}}$ embedded achieves an expanded stable parameter domain, effectively delaying the occurrence of instability phenomena from ${\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}=2{\mathrm{u}}_{\mathrm{i}\mathrm{n}}$ to ${\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}=3{\mathrm{u}}_{\mathrm{i}\mathrm{n}}$. Both the simulation and experimental results conclusively validate the theoretical analysis, confirming the effectiveness and superiority of the proposed control strategy.

1. Introduction

As a power electronic converter, boost converters have been widely used in many fields, such as new energy generation, computer power supply, and automotive electronic system [1,2,3]. Power electronic converters are highly nonlinear systems, so they are prone to exhibit bifurcation, oscillation, chaos, and many other nonlinear behaviors, which cause the system to be unstable. Various existing linear or non-linear control methods, such as current-mode control, adaptive feedback control, bang-bang control, sliding Mode Control, model predictive control (MPC), and one-cycle control (OCC), present different non-linear characteristics and stable parameter domains [4,5,6,7,8,9,10].

However, the stability of the system is essential for normal operation. In fact, the stability of the system is closely related to the control strategy adopted by the system. Thus, many existing control methods have been improved and various non-linear control strategies have been proposed for improving stability. For controlling chaos, the Ott-Grebogi−Yorke (OGY) method has been proposed, but it is difficult to implement [11]. Time-delay feedback control (TDF) has been proposed for improving non-linear characteristics in power electronic converters, which is an effective and popular method, but its delay signal is difficult to produce [12,13]. To avoid these problems, filters have been added to the control strategy for improving the stability of the system; however, the addition of filters often increases the control parameters that need to be determined [14,15]. This leads to greater computational complexity. Further, the resonant parametric perturbation involving non-feedback control confirms that it is able to control the non-linear phenomena in DC−DC converters. The challenge when using this method is that some parameters must be perturbed at appropriate frequencies and amplitudes [16].

Recently, the energy balance control (EBC) strategy has been proposed, which has proven to effectively extend the stable parameter domain of the systems, while avoiding unstable behaviors such as Hopf bifurcation, oscillation, and even chaos [17,18]. By building the sample-data model, the CFOCC method has been verified to have the ability to eliminate the bifurcation of the OCC buck-boost converter [19].

In summary, the majority of stable domain expansion methods used at present have issues such as difficulty determining feedback signals and control parameters as well as increasing the system order. Thus, this paper presents a novel one-cycle control with a composite function embedded. The contributions of this article are as follows: (1) By embedding the composite function, the distribution of the system eigenvalues in the complex plane is changed, then the non-linear stability performance of the OCC boost converter is improved by delaying the appearance of the bifurcation point. (2) The change in distribution of the system eigenvalues enlarges the stable region. (3) The embedding of the function does not increase the order of the system, and thus does not increase the computational complexity. Based on the symmetry concept, the control of the converters is implemented by keeping the balance of absorbing and releasing electrical energy in each cycle. 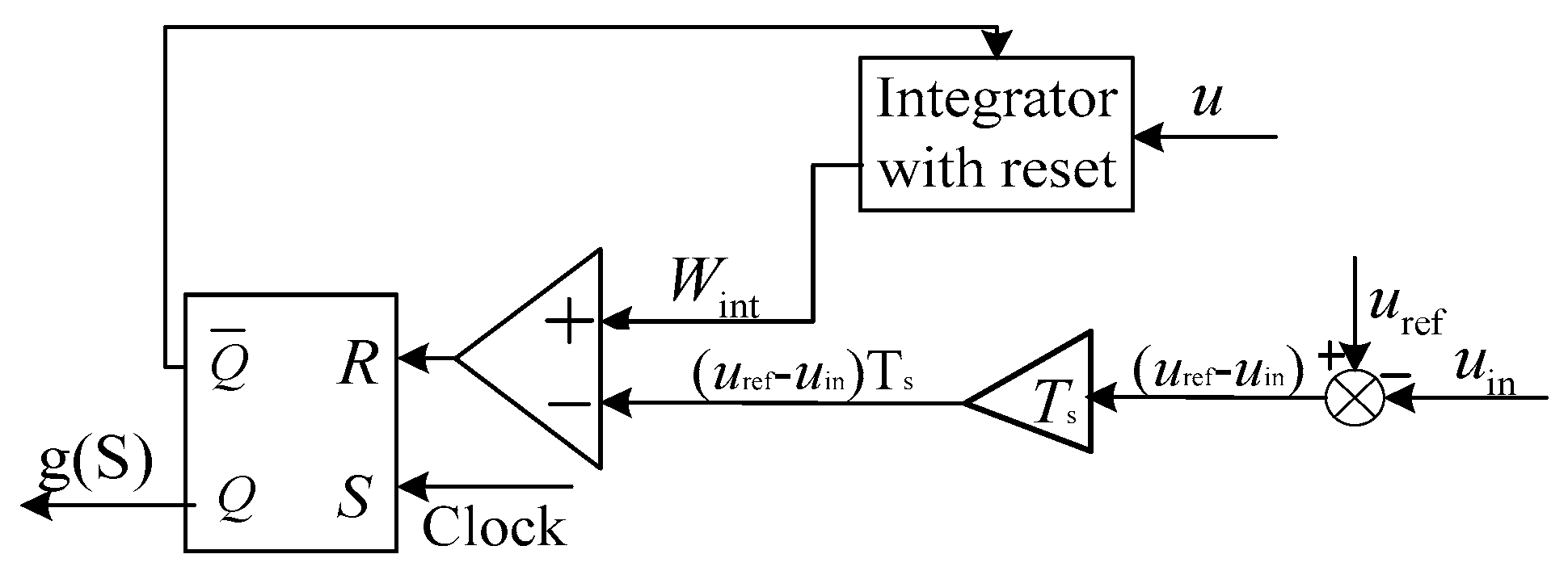The paper is organized as follows: in Section 2, the average model of a boost converter and stability analysis of the conventional OCC boost converter are discussed. In Section 3, the converter with the proposed OCC with the composite function embedded is introduced and its stability is analyzed using an average model. The proposed method and the non-linear stability theoretical analysis are confirmed through calculations, simulations, and experiments in Section 4 and Section 5. Section 6 concludes this article.

2. The Average Model of a Boost Converter and Stability Analysis of the Conventional OCC Boost Converter

This section presents a comparative stability analysis stability of the boost converter using the average modes of both the conventional OCC and the proposed OCC with the embedded composite function. First, the average model of a boost converter is built, then the working principle and average model of a conventional OCC boost converter are derived.

2.1. The Average Model of a Boost Converter

The structure of a boost converter is shown in Figure 1, where i represents the current of the inductor, i_c represents the current across the capacitor, i_o represents the current of the load, u represents the output voltage, and T_s is the switching cycle.

Under the CCM operation mode, the boost converter operates in two states: state 1 where S is in the on-state, state 2 where S is in the off-state. Thus, according to [20], this boost converter is described as follows:

$$\begin{array}{c}{\displaystyle \frac{\mathrm{d}\mathrm{i}}{\mathrm{d}\mathrm{t}}}={\displaystyle \frac{u_{\mathrm{i}\mathrm{n}}}{\mathrm{L}}}-{\displaystyle \frac{1-\mathrm{s}}{\mathrm{L}}}u\\ {\displaystyle \frac{\mathrm{d}\mathrm{u}}{\mathrm{d}\mathrm{t}}}=-{\displaystyle \frac{\mathrm{u}}{\mathrm{R}\mathrm{C}}}+i{\displaystyle \frac{1-\mathrm{s}}{\mathrm{C}}}\end{array}$$

(1)

where s = 1 denotes that S is in the on-state and s = 0 denotes that S is in the off-state [20].

2.2. The Stability Analysis of the OCC Boost Converter

To analyze the stability of a conventional OCC boost converter, its average model is derived according to [20]. As shown in Figure 2, the control equation of the OCC boost converter is obtained as follows:

$${\int }_{(n-1)T_s}^{(n-1)T_s+t_{on}\left(n\right)}udt=(u_{ref}-u_{in})T_s$$

(2)

Then, the average model of (2) can be obtained as follows:

$$ud=u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}}$$

(3)

where d, which can be expressed as ${\displaystyle \frac{T_{on}\left(n\right)}{T_s}}$, represents the duty ratio of the boost converter.

From (3), d can be derived as follows:

$$d={\displaystyle \frac{u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}}}{u}}$$

(4)

Replacing s in (1) with d derived in (4), the average state space model of the conventional OCC boost converter is deduced as

$$\begin{array}{c}{\displaystyle \frac{di}{dt}}={\displaystyle \frac{u_{\mathrm{i}\mathrm{n}}}{L}}-{\displaystyle \frac{u}{L}}[1-{\displaystyle \frac{u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}}}{u}}],\\ {\displaystyle \frac{du}{dt}}=-{\displaystyle \frac{u}{RC}}+{\displaystyle \frac{i}{C}}[1-{\displaystyle \frac{u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}}}{u}}]\end{array}$$

(5)

Setting ${\displaystyle \frac{di}{dt}}$ and ${\displaystyle \frac{du}{dt}}$ in (5) to be 0, the value of u and i can be derived from (5); here, $u=\mathrm{V}+\tilde{u}$, $i=\mathrm{I}+\widetilde{𝚤}$. The equilibrium point needs to be derived; during the calculation, $\tilde{u}$ and $\widetilde{𝚤}$ are ignored when ${\displaystyle \frac{di}{dt}}$ and ${\displaystyle \frac{du}{dt}}$ in (5) are set to be 0, thus the equilibrium point can be expressed using only $\mathrm{V}$ and $\mathrm{I}$, as follows:

$$\begin{array}{c}\mathrm{V}=u_{\mathrm{r}\mathrm{e}\mathrm{f}}\\ \mathrm{I}={\displaystyle \frac{u_{\mathrm{r}\mathrm{e}\mathrm{f}}^2}{u_{in}R}}\end{array}$$

(6)

At this equilibrium point, the Jacobian matrix can be obtained as follows.

$$J=\left(\begin{array}{cc}0& -{\displaystyle \frac{1}{\mathrm{L}}}\\ {\displaystyle \frac{\mathrm{V}-{\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}+{\mathrm{u}}_{\mathrm{i}\mathrm{n}}}{\mathrm{C}\mathrm{V}}}& -{\displaystyle \frac{1}{\mathrm{R}\mathrm{C}}}+{\displaystyle \frac{\mathrm{I}({\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}-{\mathrm{u}}_{\mathrm{i}\mathrm{n}})}{\mathrm{C}{\mathrm{V}}^2}}\end{array}\right)$$

(7)

Substituting (6) into the Jacobian matrix (7) obtains

$$J=\left(\begin{array}{cc}0& -{\displaystyle \frac{1}{\mathrm{L}}}\\ {\displaystyle \frac{{\mathrm{u}}_{\mathrm{i}\mathrm{n}}}{\mathrm{C}{\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}& {\displaystyle \frac{({\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}-2{\mathrm{u}}_{\mathrm{i}\mathrm{n}})}{\mathrm{C}\mathrm{R}{\mathrm{u}}_{\mathrm{i}\mathrm{n}}}}\end{array}\right)$$

(8)

According to det[λI − J] = 0,where I is a 2 × 2 unity matrix, the characteristic equation is derived as follows:

$$\mathrm{f}(\lambda )={\lambda }^2+[-{\displaystyle \frac{(u_{\mathrm{r}\mathrm{e}\mathrm{f}}-2u_{\mathrm{i}\mathrm{n}})}{CR{u}_{\mathrm{i}\mathrm{n}}}}]\lambda +{\displaystyle \frac{u_{\mathrm{i}\mathrm{n}}}{LC{u}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}$$

(9)

To obtain the closed-form expression of the stability of the converter, (9) is rewritten according to the second-order Padé approximation as follows:

$$a_2{\lambda }^2+a_1\lambda +a_0$$

(10)

where $a_2=1$, $a_1=-{\displaystyle \frac{(u_{\mathrm{r}\mathrm{e}\mathrm{f}}-2u_{\mathrm{i}\mathrm{n}})}{CR{u}_{\mathrm{i}\mathrm{n}}}}$ and $a_0={\displaystyle \frac{u_{\mathrm{i}\mathrm{n}}}{LC{u}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}$.

According to the Routh criterion, the stable condition of the system is when all roots are on the left side of the complex plane, which means that all $a_i$ are positive for a second-degree polynomial. Here, it can be seen that if $u_{\mathrm{r}\mathrm{e}\mathrm{f}}<2u_{\mathrm{i}\mathrm{n}}$, then $a_0>$ 0, $a_1>$ 0, and $a_2>$ 0 are obtained. Thus, the sufficient and necessary condition for the stability of the OCC boost converter is $u_{\mathrm{r}\mathrm{e}\mathrm{f}}<2u_{\mathrm{i}\mathrm{n}}$.

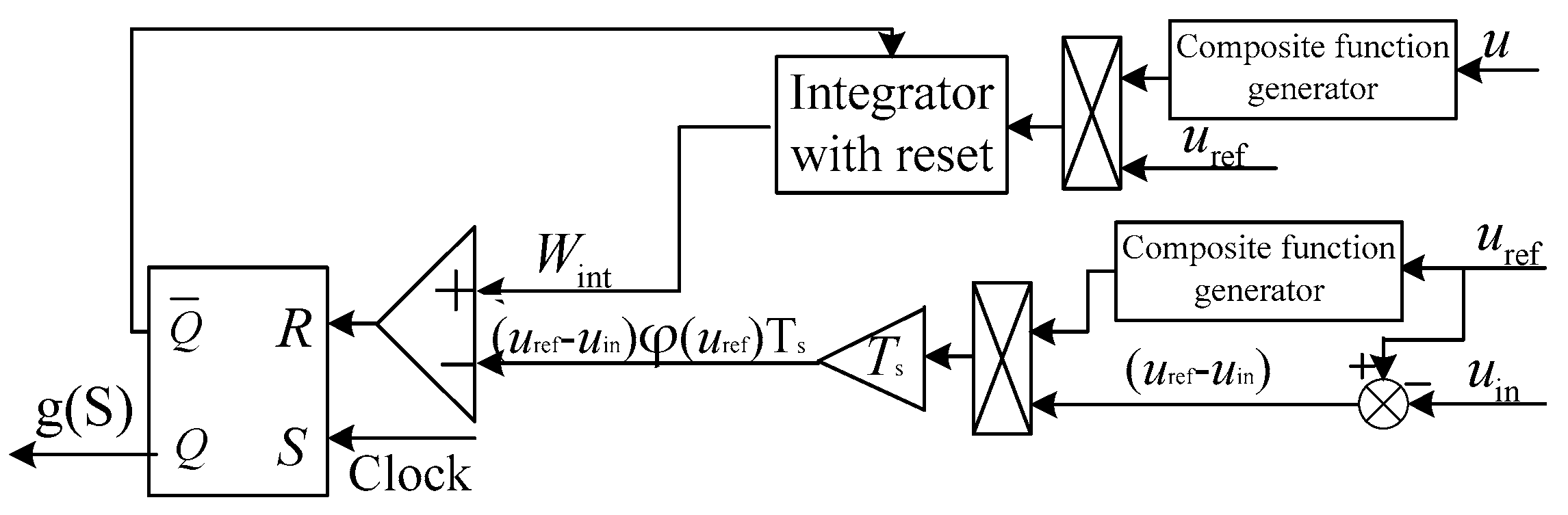
3. Stability Analysis of the Boost Converter Using the Proposed OCC with Composite Function Embedded

3.1. The Working Principle and Average Model of the Boost Converter Using the Proposed OCC with the Composite Function Embedded

It is known that under fixed circuit parameters, the control principle affects the stability. Thus, based on the conventional OCC, we aimed to embed a composite function in order to change the eigenvalues of the system. The structure of the proposed OCC with the composite function embedded is shown in Figure 3. The structure shows that it is also constituted by a reset integrator, a comparator, and an RS flip-flop but with a composite function.

With the composite function, the control equation of the proposed OCC is written as follows:

$${\int }_{(n-1)T_s}^{(n-1)T_s+t_{on}\left(n\right)}{u}_{ref}\phi \left(u\right)dt=(u_{ref}-u_{in})\phi \left(u_{ref}\right)T_s$$

(11)

where $\phi (u)={\displaystyle \frac{u}{u_{\mathrm{r}\mathrm{e}\mathrm{f}}}}$.

From (10), it can be found that, when φ(u) is a positive strictly increasing function, the system can converge at the equilibrium point in the same way as (2). Here, φ(u) is chosen as $\phi \left(u\right)=\sqrt{u}$. Then, (10) is rewritten as (11):

$${\int }_{(n-1)T_s}^{(n-1)T_s+t_{on}\left(n\right)}{u}_{\mathrm{r}\mathrm{e}\mathrm{f}}\sqrt{u}dt=(u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{in})\sqrt{u_{\mathrm{r}\mathrm{e}\mathrm{f}}}{T}_s$$

(12)

Then, the average model of (11) is obtained as follows:

$$u_{\mathrm{r}\mathrm{e}\mathrm{f}}\sqrt{u}d=(u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{in})\sqrt{u_{\mathrm{r}\mathrm{e}\mathrm{f}}}$$

(13)

And d is derived as follows:

$$d={\displaystyle \frac{(u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{in})\sqrt{u_{\mathrm{r}\mathrm{e}\mathrm{f}}}}{u_{\mathrm{r}\mathrm{e}\mathrm{f}}\sqrt{u}}}$$

(14)

Replacing s in (1) with d derived in (13), the average state space model of the boost converter for the OCC with the composite function embedded is derived as

$$\begin{array}{c}{\displaystyle \frac{di}{dt}}={\displaystyle \frac{u_{\mathrm{i}\mathrm{n}}}{L}}-{\displaystyle \frac{u}{L}}[1-{\displaystyle \frac{{(u}_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}})\sqrt{u_{\mathrm{r}\mathrm{e}\mathrm{f}}}}{u_{\mathrm{r}\mathrm{e}\mathrm{f}}\sqrt{u}}}]\\ {\displaystyle \frac{du}{dt}}=-{\displaystyle \frac{u}{RC}}+{\displaystyle \frac{i}{C}}[1-{\displaystyle \frac{{(u}_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}})\sqrt{u_{\mathrm{r}\mathrm{e}\mathrm{f}}}}{u_{\mathrm{r}\mathrm{e}\mathrm{f}}\sqrt{u}}}]\end{array}$$

(15)

3.2. The Stability Analysis of the Proposed OCC Boost Converter

Setting ${\displaystyle \frac{di}{dt}}$ and ${\displaystyle \frac{du}{dt}}$ in (14) to be 0, the equilibrium point can be obtained as follows:

$$\begin{array}{c}V=u_{ref}\\ I={\displaystyle \frac{u_{ref}^2}{u_{in}R}}\end{array}$$

(16)

Then, the Jacobian matrix evaluated at the equilibrium point is obtained as follows:

$$J=\left(\begin{array}{cc}0& -{\displaystyle \frac{1}{\mathrm{L}}}-{\displaystyle \frac{u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}}}{2\mathrm{L}\sqrt{\mathrm{u}{\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}}\\ {\displaystyle \frac{1}{\mathrm{C}}}\left[1-{\displaystyle \frac{u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}}}{u_{\mathrm{r}\mathrm{e}\mathrm{f}}\sqrt{u}}}\right]& -{\displaystyle \frac{1}{\mathrm{R}\mathrm{C}}}+{\displaystyle \frac{\mathrm{I}(u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}})}{2\mathrm{C}u\sqrt{u_{\mathrm{r}\mathrm{e}\mathrm{f}}}\sqrt{\mathrm{u}}}}\end{array}\right)$$

(17)

Substituting (15) into the Jacobian matrix obtains

$$\mathrm{J}=\left(\begin{array}{cc}0& -{\displaystyle \frac{1}{\mathrm{L}}}-{\displaystyle \frac{u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}}}{{2Lu}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}\\ {\displaystyle \frac{u_{\mathrm{i}\mathrm{n}}}{{Cu}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}& -{\displaystyle \frac{1}{\mathrm{R}\mathrm{C}}}+{\displaystyle \frac{u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{\mathrm{i}\mathrm{n}}}{2\mathrm{R}\mathrm{C}{u}_{\mathrm{i}\mathrm{n}}}}\end{array}\right)$$

(18)

According to det[λI − J] = 0 and the second-order Padé approximation, the characteristic quasi-polynomial equation can be written as follows:

$$a_2{\lambda }^2+a_1\lambda +a_0$$

(19)

where ${\mathrm{a}}_2=1$, $a_1={\displaystyle \frac{3u_{in}-u_{ref}}{2RC{u}_{in}}}$ and $a_0=[{\displaystyle \frac{1}{L}}+{\displaystyle \frac{(u_{\mathrm{r}\mathrm{e}\mathrm{f}}-u_{in})}{2L{u}_{ref}}}]{\displaystyle \frac{{\mathrm{u}}_{\mathrm{i}\mathrm{n}}}{C{u}_{\mathrm{r}\mathrm{e}\mathrm{f}}}}$.

From (18), it is obvious that ${\mathrm{a}}_2>0$ and ${\mathrm{a}}_0>0$. Here, it can be seen that if ${\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}<3{\mathrm{u}}_{\mathrm{i}\mathrm{n}}$ is satisfied, then ${\mathrm{a}}_1>0$ is obtained. Compared with the stability condition of the conventional OCC, it can be seen that the unstable behavior is delayed; thus, the stable parameter domain is extended by embedding function $\phi \left(\mathrm{u}\right)$, which is chosen as $\sqrt{\mathrm{u}}$ here.

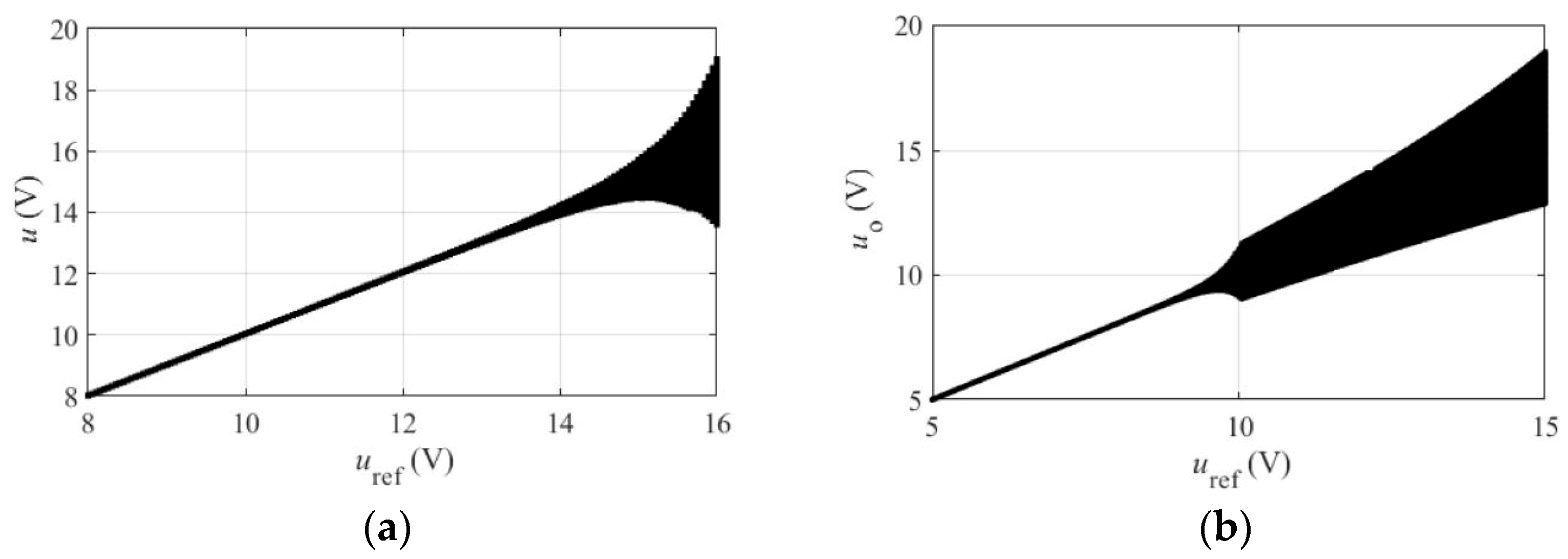
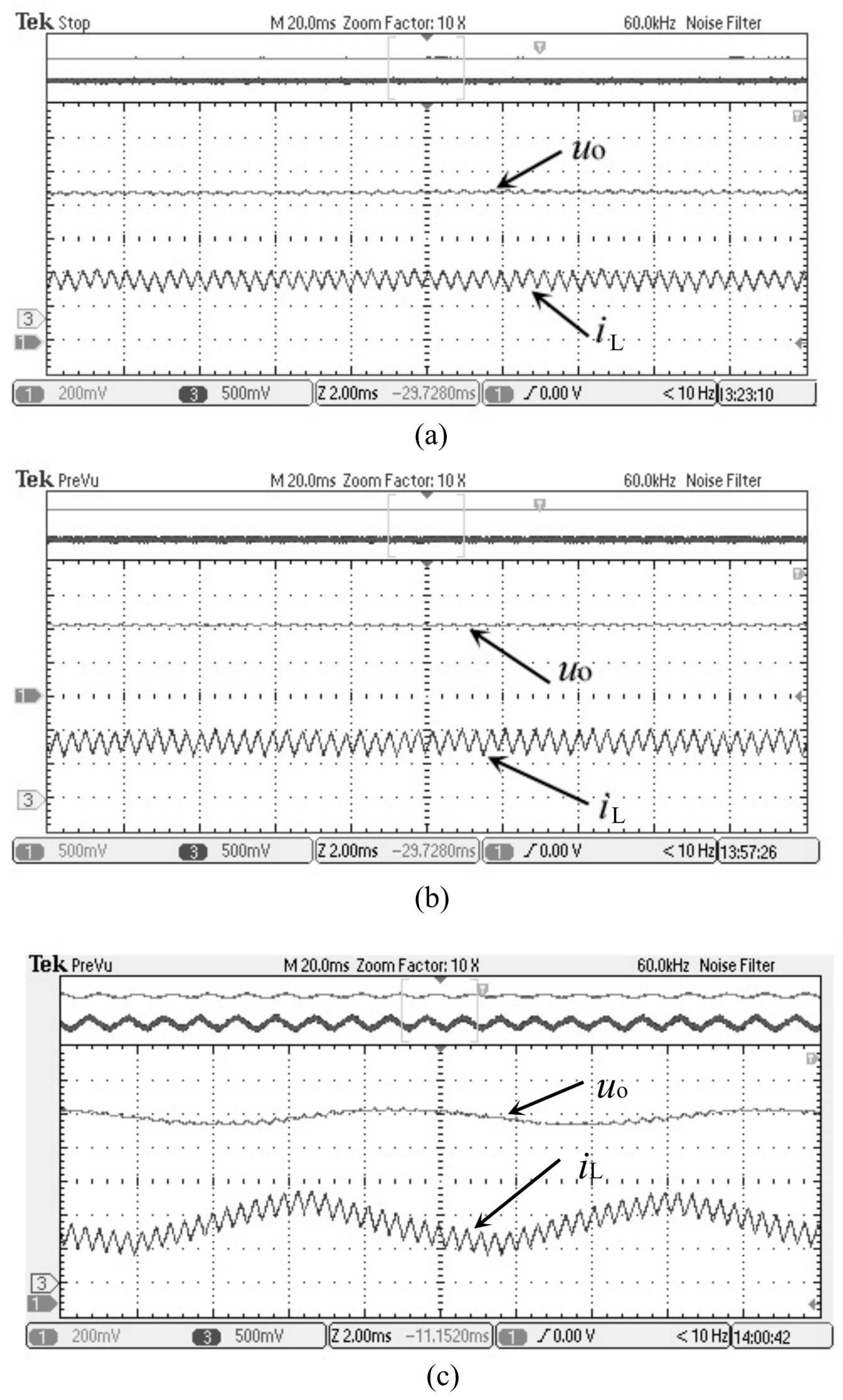
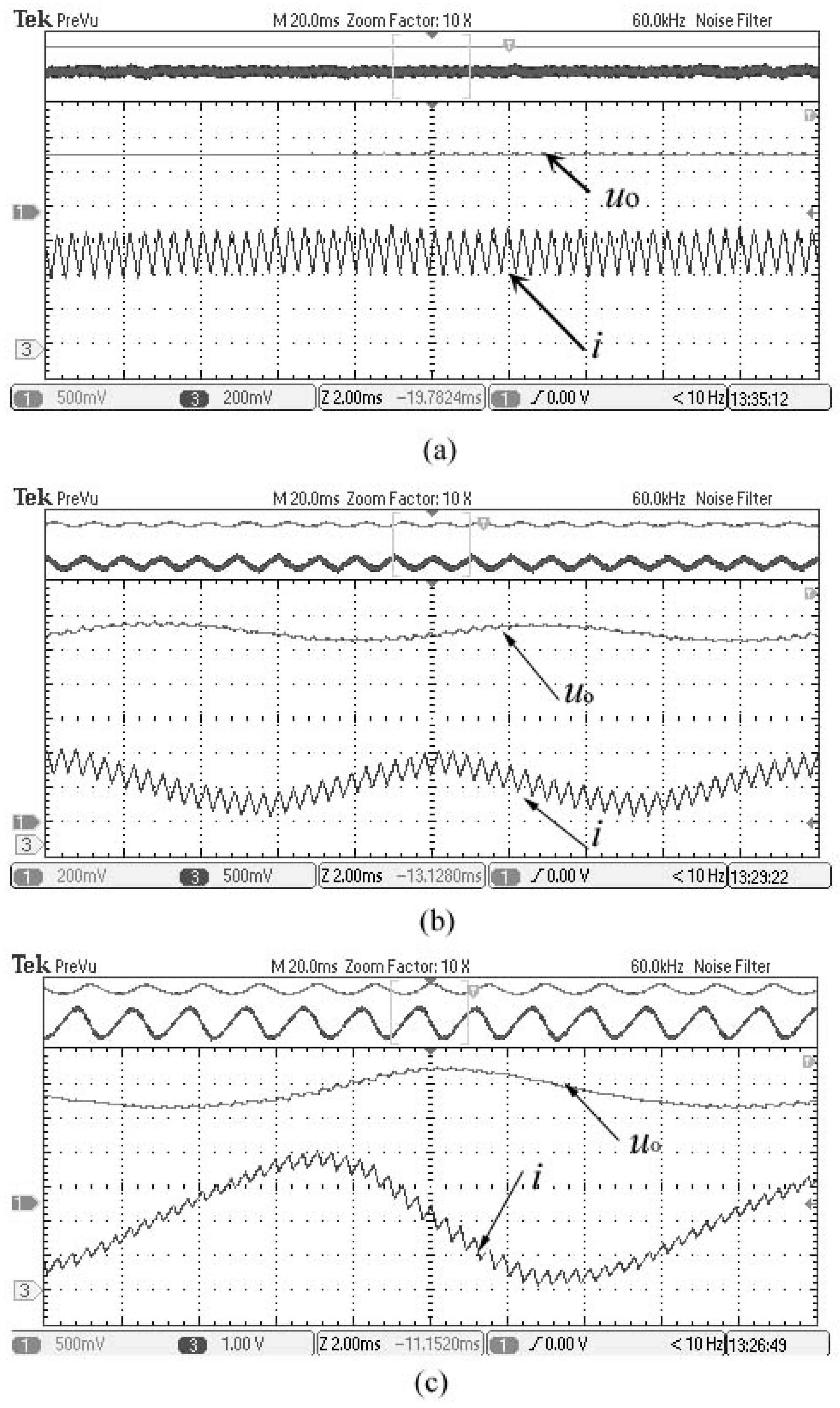
4. Calculation Verification

The previous sections present the theoretical analysis of the stability of the boost converter using both the proposed OCC with a composite function embedded and the conventional OCC described in the previous section. To verify the results of the above theoretical analysis, take ${\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ as the variable parameter, and its characteristic roots can be calculated using the circuit parameters listed in

Table 1. The circuit parameters of the boost converter.

${\mathit{u}}_{\mathit{i}\mathit{n}}$ (V)	L (µH)	C (µF)	R (Ω)	${\mathit{f}}_{\mathit{s}}$ (Hz)
5	3000	460	30	5000

. These circuit parameters are set based on the laboratory verification. Figure 4 shows the bifurcation diagram of the proposed OCC with the composite function $\sqrt{\mathrm{u}}$ embedded and the conventional OCC. Figure 4a shows the bifurcation diagram of the proposed OCC with composite function $\sqrt{\mathrm{u}}$ embedded, as the reference voltage ${\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ varies from 8 V to 16 V. From the results, it can be seen that the boost converter with the proposed OCC with the composite function embedded loses its stability when ${\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ increases to approximately 15 V. In contrast, Figure 4b shows that when varying ${\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ from 5 V to 15 V for the conventional OCC, the boost converter with the conventional OCC losses its stability when ${\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ is greater than approximately 10 V. This comparison shows that, compared with the conventional OCC, the proposed OCC with composite function $\sqrt{\mathrm{u}}$ embedded has a wider stability domain parameter.

5. Simulation and Experimental Verification

To verify the theoretical analysis and the calculation results for the stability of the boost converter in the previous section, according the circuit parameters listed in Table 1, the dynamic stability of the boost converter is tested in simulations and experiments under varying ${\mathrm{u}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$. Figure 5 and Figure 6 display the simulation results. Figure 7 displays the experimental setup and Figure 8 and Figure 9 display the experimental results.

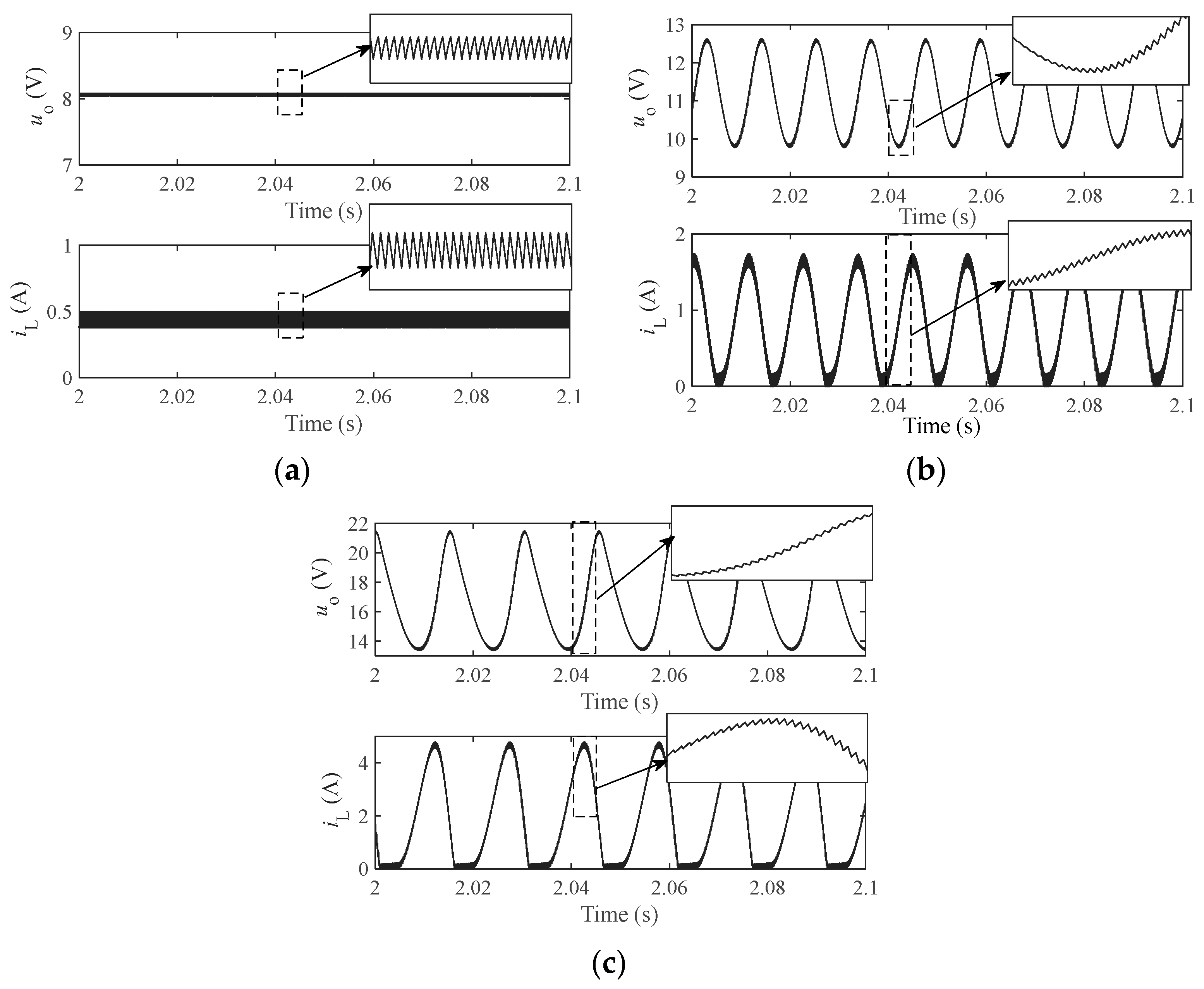
5.1. The Simulation Results

Based on the parameters listed in Table 1, a boost converter is built using Matlab Simulink. Figure 5 and Figure 6 display the results of the boost converter with the proposed OCC, with $\sqrt{\mathrm{u}}$ embedded and the conventional OCC, respectively. From Figure 5a,b, it can be seen that, under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 8 V and $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 11 V, the boost converter can operate in a stable manner, and no bifurcation or other non-linear phenomena occur. Figure 5c shows that bifurcation occurs in the boost converter under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 16 V, which means that the boost converter system using the proposed OCC with $\sqrt{\mathrm{u}}$ embedded loses its stability.

Figure 6 displays the simulation results of the boost converter with the conventional OCC. The results show that, under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 8 V, the boost converter can maintain stable operation without any bifurcation or other nonlinear phenomena, as shown in Figure 6a. But, Figure 6b shows that bifurcation occurs in the boost converter under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 11 V, and with the increase in $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$, bifurcation becomes increasingly severe, and if $u_{\mathrm{r}\mathrm{e}\mathrm{f}}$ continues to grow, other nonlinear phenomena will even cause chaos. The results show that the simulation results are consistent with the calculation results.

5.2. The Experimental Results

Based on the parameters listed in Table 1 a boost converter is built. The experimental prototype and control platform are shown in Figure 7. A MOSFET switch IRF640N and fast recovery diode BYW29-200 are used for the boost converter experimental prototype. The control is implemented with a Micro controller STM32H7.

The experimental results are shown in Figure 8 and Figure 9. From the results, it can be seen that the experimental results are consistent with the simulation results. Using the proposed OCC with composite function $\sqrt{\mathrm{u}}$ embedded, the boost converter can maintain stable operation under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 8 V and $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 11 V, and no bifurcation or other non-linear phenomena occur, as shown in Figure 8a,b. When ${ u}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ increases to 15 V, bifurcation occurs in the boost converter, just like under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 16 V, as shown in Figure 8c. As shown in Figure 9, using the conventional OCC, the boost converter works in a stable manner under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 8 V; however, when ${ u}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ increases into about 10 V, bifurcation occurs in the boost converter, just like under $u_{\mathrm{r}\mathrm{e}\mathrm{f}}=$ 11 V, as shown in Figure 9b. Obviously, the converter is no longer stable. Further, bifurcation becomes more severe when ${ u}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ continues to increase, as shown in Figure 9c. From Figure 9c, it can be seen that output voltage oscillates.

Table 2. The comparison results.

${\mathbf{u}}_{\mathbf{r}\mathbf{e}\mathbf{f}}$ (V)	Theoretical		Simulation		Experiment
	OCC	$\mathbf{OCC} \mathbf{with} \sqrt{\mathbf{u}}$ Embedded	OCC	$\mathbf{OCC} \mathbf{with} \sqrt{\mathbf{u}}$ Embedded	OCC	$\mathbf{OCC} \mathbf{with} \sqrt{\mathbf{u}}$ Embedded
8	stable	stable	stable	stable	stable	stable
11	unstable	stable	unstable	stable	unstable	stable
16	unstable	unstable	unstable	unstable	unstable	unstable

shows the comparison results of the boost converter with the conventional OCC and the proposed OCC with $\sqrt{\mathrm{u}}$ embedded. From these results, it can be seen the simulation and experiment results are mostly in agreement with the theories, whereby the boost converter using the proposed OCC with $\sqrt{\mathrm{u}}$ embedded has wider stable parameter domains.

6. Conclusions

In this study, a novel OCC is proposed by embedding a composite function into the conventional OCC, thus effectively expanding the stable operating region of the boost converters. First, the state-space averaged models are built and the stability boundary is found. Then, stable parameter domains are obtained by analyzing the Jacobian matrix. Then, simulation and experimental models are developed to validate the theoretical predictions. The comparison of these results to the conventional OCC demonstrate that the incorporation of a square function $\sqrt{\mathrm{u}}$ as the composite function significantly extends the stable operating range from 2u_in to 3u_in, which effectively delays the occurrence of instability phenomena, including Hopf bifurcation, double frequency bifurcation, and chaotic behavior.

While the current study specifically employs a square function as the composite element, the proposed control method is not limited to this particular function. In fact, various commonly used functions, such as the logarithmic function and arc-tangent function, can be used as the embedded composite functions. Future research will explore these alternatives in order to select the optimal function. Future research will also explore the comparison with other advanced control strategies, i.e., adaptive OCC, to further verify its advantages.