A Design Approach for Asymmetric Coupled Line In-Phase Power Dividers with Arbitrary Terminal Real Impedances and Arbitrary Power Division Ratio
Abstract
:1. Introduction
- Firstly, ACL provides an additional line width variable, allowing for more design freedom.
- Secondly, the terminal real impedances of ACL devices can simultaneously take on different values, endowing them with the capability of impedance transformation and expanding the application space of devices.
2. Theoretical Analysis and Design Methodology
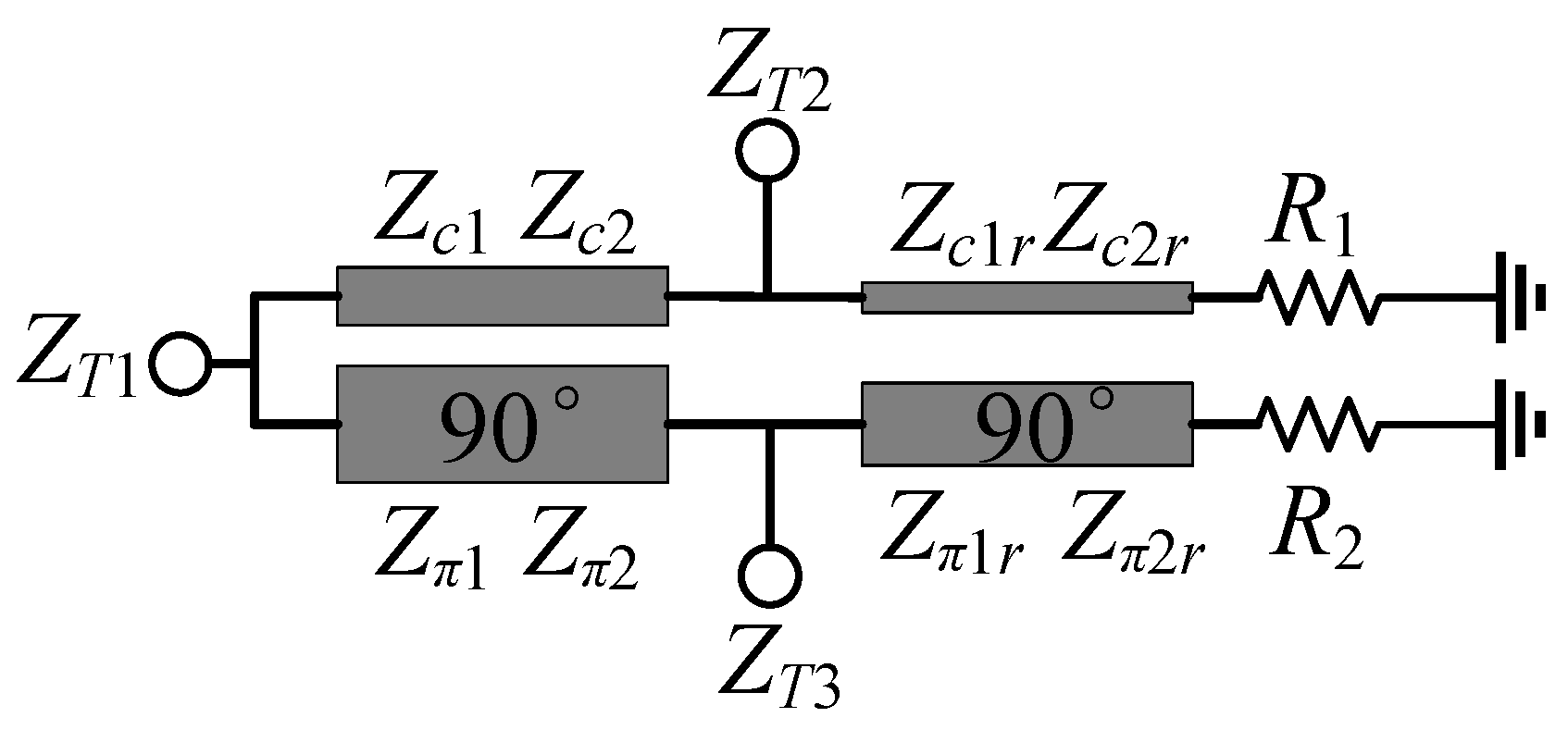
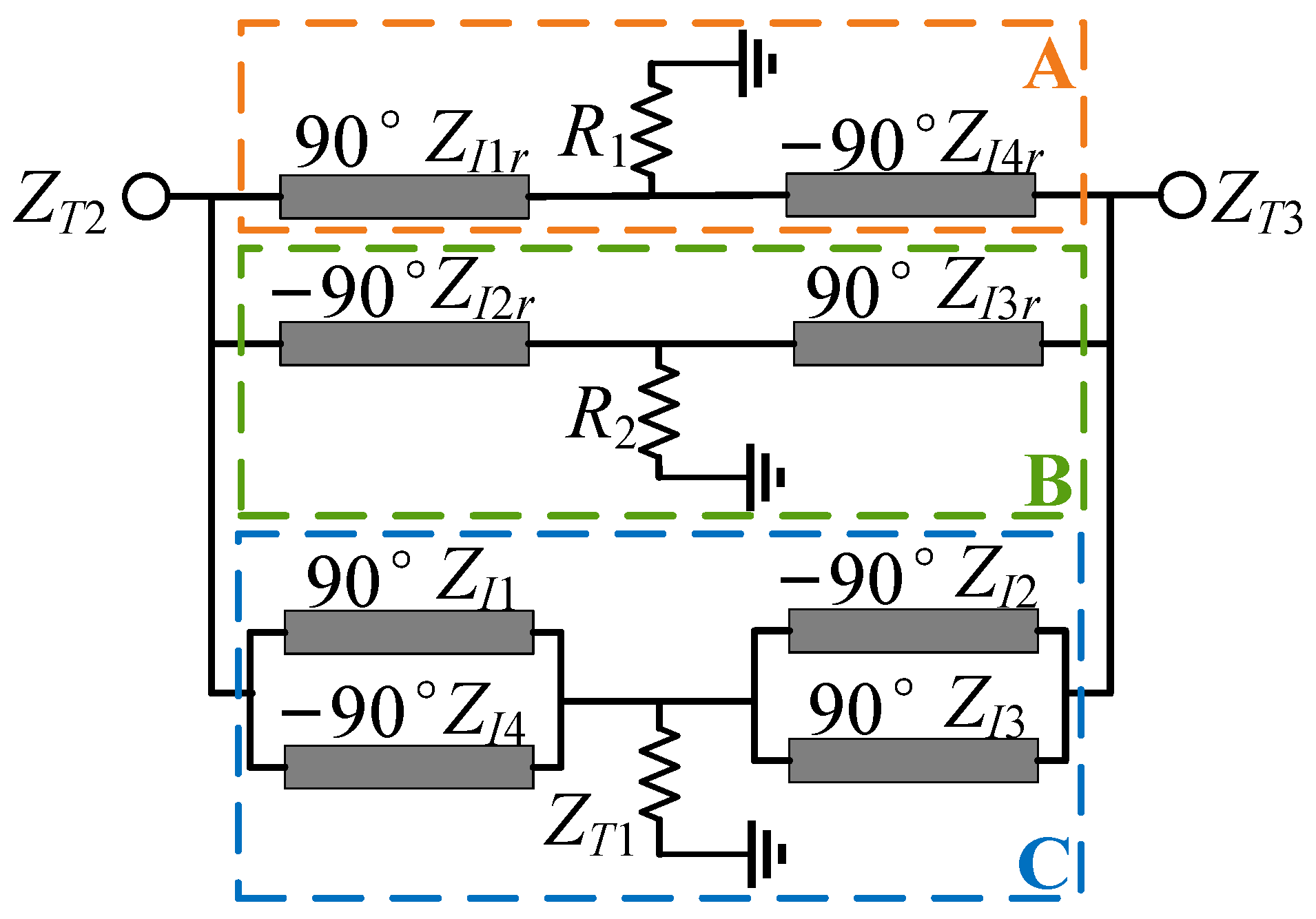
2.1. Two-Resistor APCD Structure
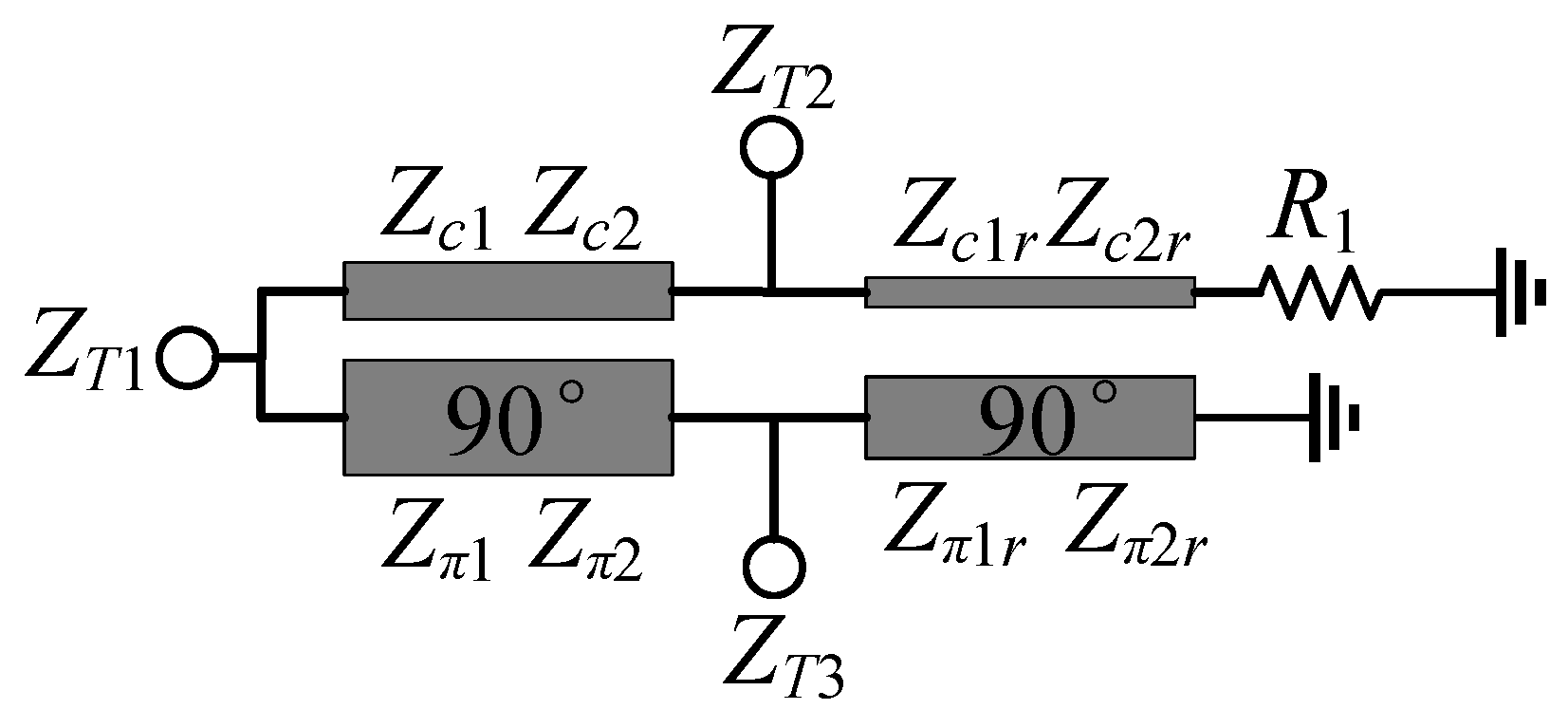
2.2. Single-Resistor APCD Structure
- Determine the targeted power division ratio Rp, terminal real impedance values ZT1, ZT2, and ZT3, self-specified values of K2, K6, R1 (for the single-resistor structure), and self-specified values K2, R1, and R2 (for the two-resistor structure).
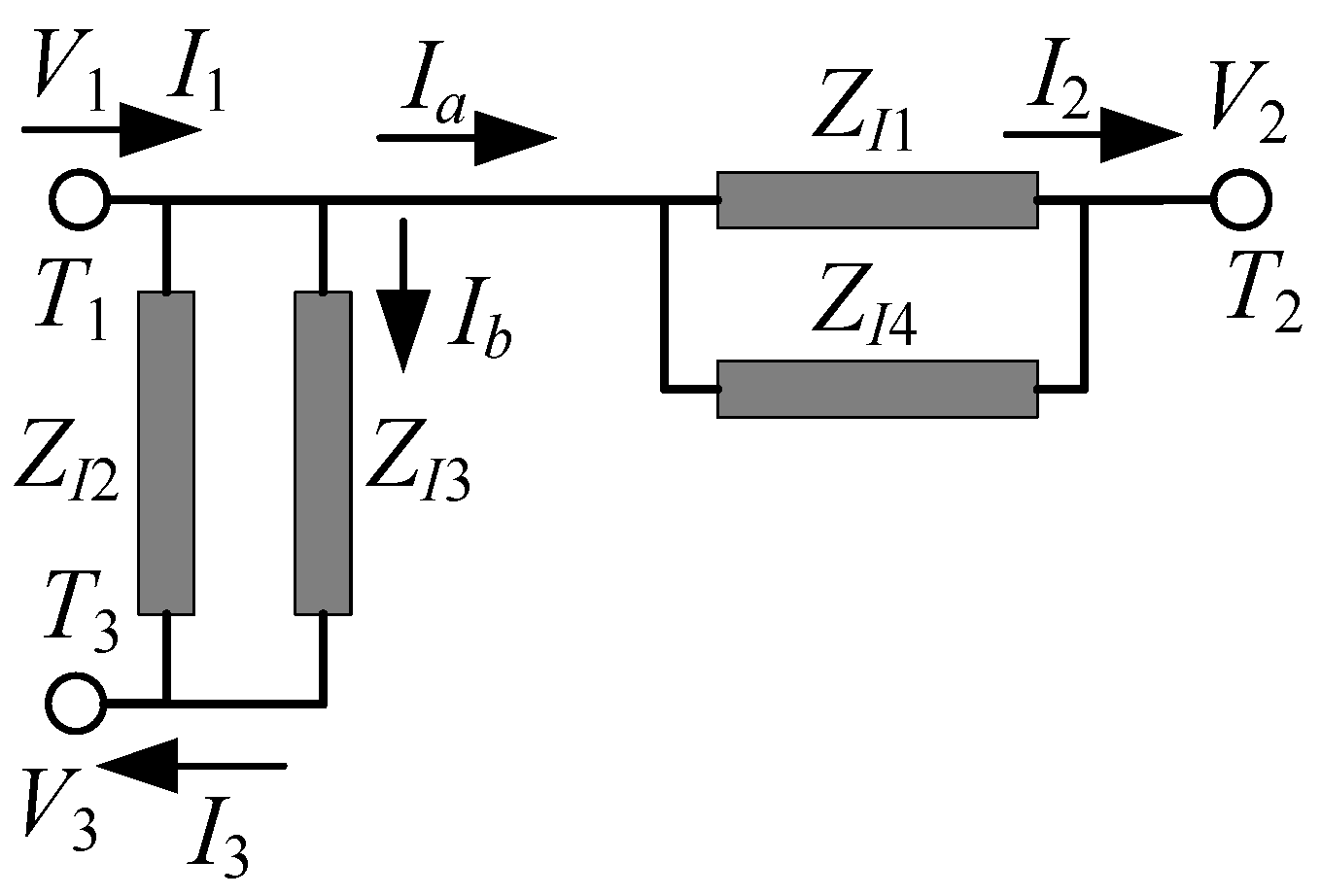
- Calculate values of the eight image impedances ZIi (i = 1, 2, 3, 4) and ZIjr (j = 1, 2, 3, 4) by the formula (12) or (15).
- Obtain the initial geometric parameter values of the two ACL sections by the solving software introduced in Section 3, from ZIi (i = 1, 2, 3, 4) and ZIjr (j = 1, 2, 3, 4).
- Fine-turn the ACPD model to realize better performance.
3. Automatic Solution Software for ACLs
- Firstly, the theoretical foundation of CLS lies in the analytical solution of telegraph equations, which provides an accurate description of coupled line behavior without relying on approximate simplifications. This ensures that the physical characteristics of coupled lines are faithfully represented in CLS.
- Secondly, CLS employs a stable and accurate mapping relationship constructed by an MLP neural network. This network effectively correlates the desired characteristic impedances with the geometric parameters of coupled microstrip lines. By training on ample sample data, the MLP neural network learns to predict these parameters reliably, thereby enhancing the overall precision and reliability of CLS in determining the geometric parameters of coupled lines.
4. Experimental Implementation of ACPDs
4.1. Design Processes and Circuit Fabrication
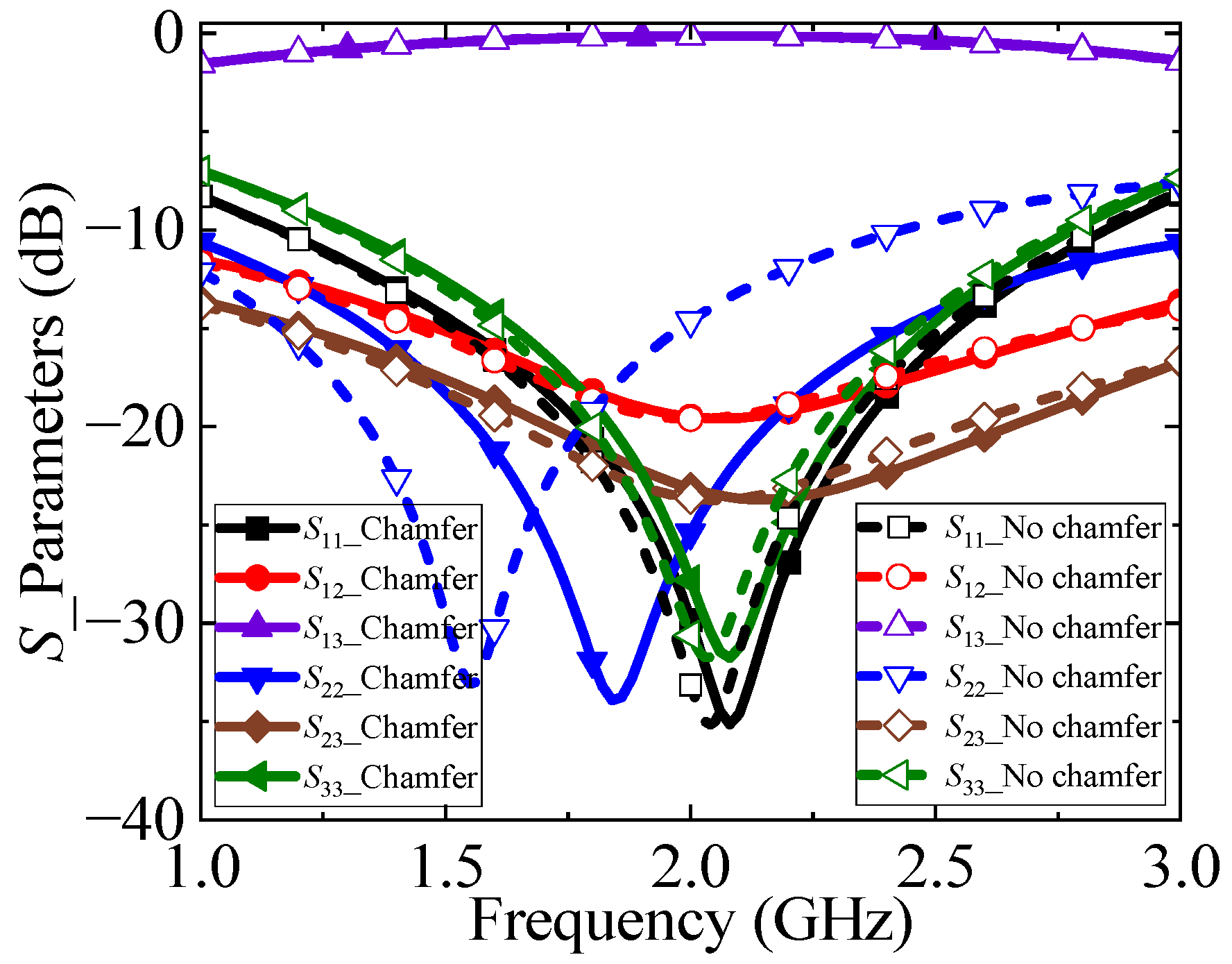
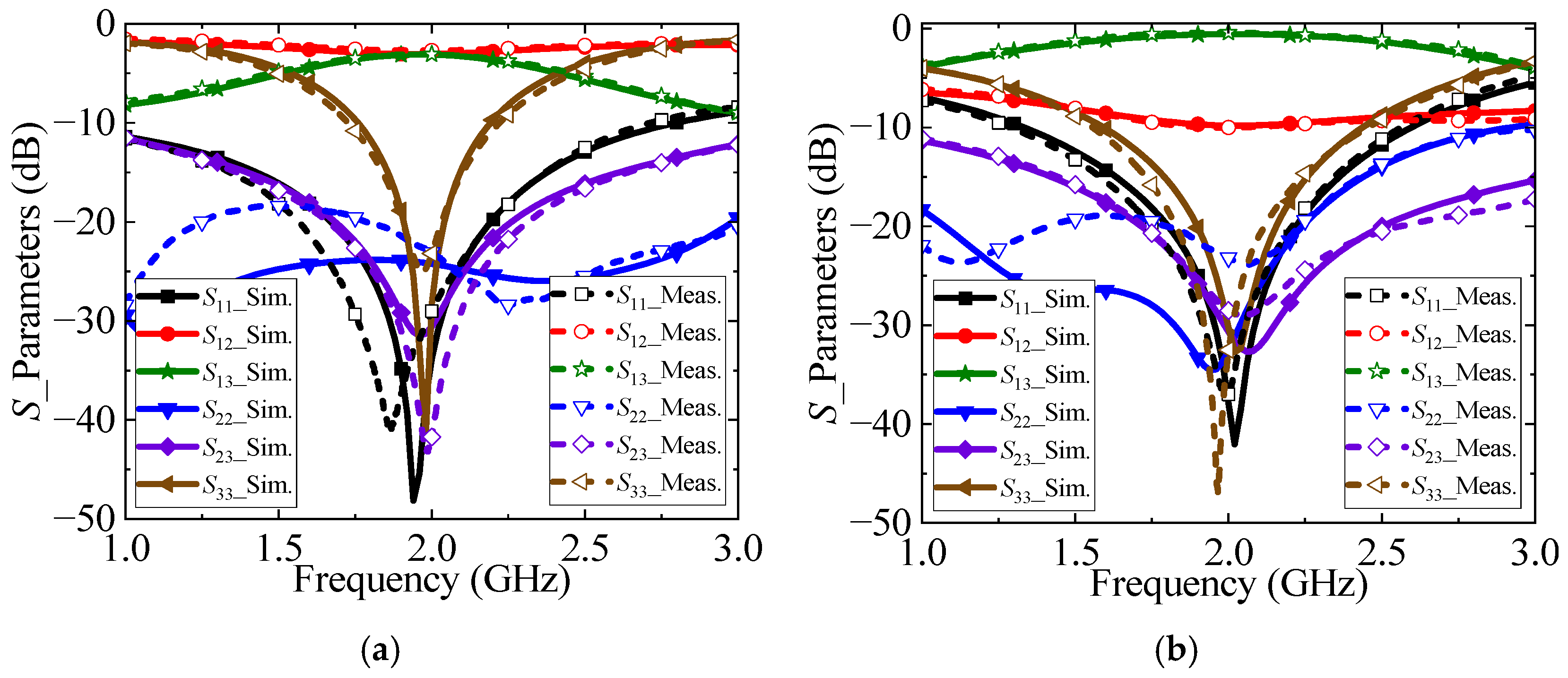
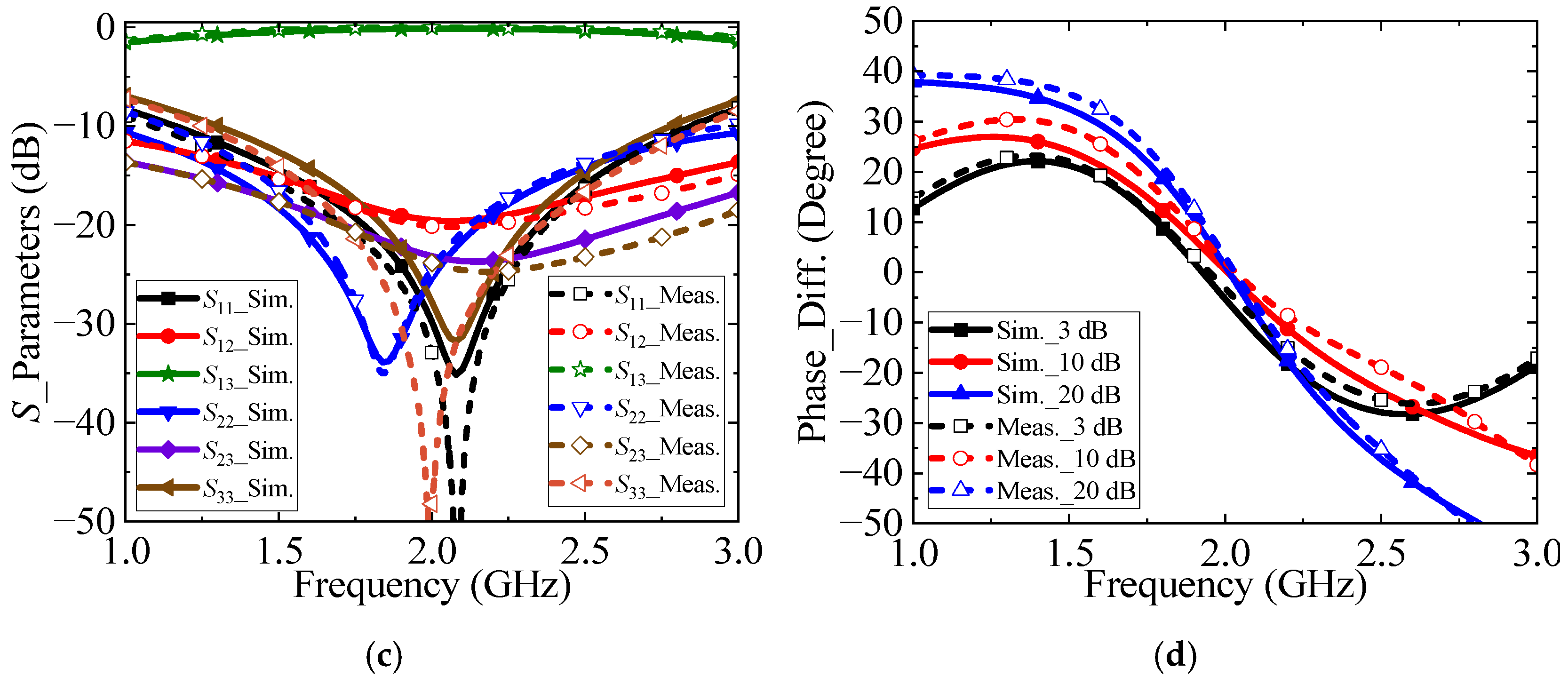
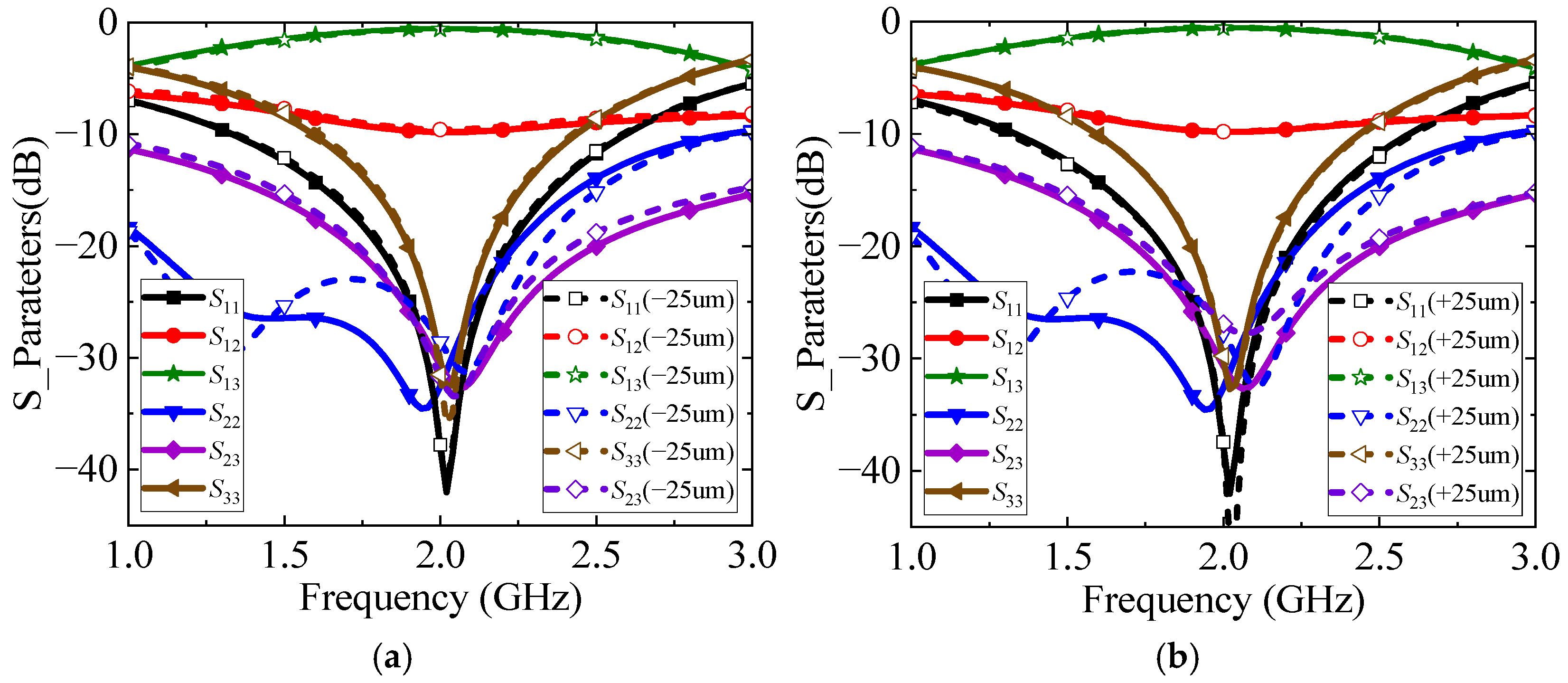
4.2. S-Parameter Performance Analysis
4.3. Performance Comparison
5. Application of Devices with Arbitrary Terminal Real Impedances and Arbitrary Power Division Ratio
6. Conclusions
- ACPD possesses the capability of flexible impedance transformation.
- ACPD requires only one isolation resistor for both equal and unequal power division cases, and resistor values can be flexibly determined.
- ACPD can easily achieve a large in-phase PDR. ACPD realized the large in-phase PDR of 100:1 (20 dB) and offers a broad in-phase PDR range from 1:1 (3 dB) to 100:1 (10 dB).
- ACPD is compact and the positions of the two output ports can be arranged as needed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wincza, K.; Gruszczynski, S. Reduced-length tandem directional couplers composed of coupled-line sections with fixed coupling coefficient. IEEE Trans. Microw. Theory Tech. 2021, 69, 1625–1634. [Google Scholar] [CrossRef]
- Luo, Z.H.; Zhang, G.; Wang, H.W.; Li, N.; Tam, K.W.; Tang, L.M. Dual-band and triple-band filtering power dividers using coupled lines. IEEE Trans. Circuits Syst. II Express Briefs. 2023, 70, 1440–1444. [Google Scholar] [CrossRef]
- Li, D.; Xu, K.D. Multifunctional switchable filter using coupled-line structure. IEEE Microw. Compon. Lett. 2021, 31, 457–460. [Google Scholar] [CrossRef]
- Zhou, Z.; Ge, Y.; Yuan, J.; Xu, Z.; Chen, Z.D. Wideband MIMO antennas with enhanced isolation using coupled CPW transmission lines. IEEE Trans. Antennas Propag. 2023, 71, 1414–1423. [Google Scholar] [CrossRef]
- Zhou, R.; Chen, J.; Li, Z.; Yu, J.; Tang, D.; Hong, W. A 260-GHz power amplifier with 12.5-dBm Psat and 21.4-dB peak gain utilizing a modified coupled-line-balun network. IEEE Trans. Microw. Theory Tech. 2024, 72, 3031–3045. [Google Scholar]
- Tripathi, V.K. Asymmetric coupled transmission lines in an inhomogeneous medium. IEEE Trans. Microwave Theory Tech. 1975, 23, 734–739. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, B.; Mao, J.F. A design approach for asymmetric coupled line tandem couplers with arbitrary terminal real impedances and arbitrary power dividing ratio. IEEE Trans. Microw. Theory Tech. 2024, 72, 3542–3553. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, Y.; Zhang, T.; Che, W.; Xue, Q. N-way Gysel power divider with arbitrary power-dividing ratio. IEEE Trans. Microw. Theory Tech. 2019, 67, 659–669. [Google Scholar] [CrossRef]
- Nemati, R.; Karimian, S.; Shahi, H.; Masoumi, N.; Safavi-Naeini, S. Multisection combined Gysel–Wilkinson power divider with arbitrary power division ratios. IEEE Trans. Microw. Theory Tech. 2021, 69, 1567–1578. [Google Scholar] [CrossRef]
- Chen, S.; Yu, Y.; Tang, M. Dual-band Gysel power divider with different power dividing ratios. IEEE Microw. Compon. Lett. 2019, 29, 462–464. [Google Scholar] [CrossRef]
- Lin, F.; Chu, Q.X.; Gong, Z.; Lin, Z. Compact broadband Gysel power divider with arbitrary power-dividing ratio using microstrip/ slotline phase inverter. IEEE Trans. Microwave Theory Tech. 2012, 60, 1226–1234. [Google Scholar]
- Ooi, B.L. Compact EBG in-phase hybrid-ring equal power divider. IEEE Trans. Microw. Theory Tech. 2005, 53, 2329–2334. [Google Scholar]
- Wang, X.; Wu, K.L.; Yin, W.Y. A compact Gysel power divider with unequal power-dividing ratio using one resistor. IEEE Trans. Microw. Theory Tech. 2014, 62, 1480–1486. [Google Scholar] [CrossRef]
- Wang, K.X.; Zhang, X.Y.; Hu, B.J. Gysel power divider with arbitrary power ratios and filtering responses using coupling structure. IEEE Trans. Microw. Theory Tech. 2014, 62, 431–440. [Google Scholar]
- Luo, M.; Xu, X.; Tang, X.H.; Zhang, Y.H. A compact balanced-to-balanced filtering Gysel power divider using λg/2 resonators and short-stub-loaded resonator. IEEE Microw. Compon. Lett. 2017, 27, 645–647. [Google Scholar]
- Gharehaghaji, H.S.; Shamsi, H. Design of unequal dual band Gysel power divider with isolation bandwidth improvement. IEEE Microw. Compon. Lett. 2017, 27, 138–140. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, P.C.; Xia, B.; Wei, G.R.; Xiong, C.; Mao, J.F. A new wideband RLGC extraction method for multiconductor transmission lines using improved mode tracking algorithm. IEEE Trans. Electromagn. Compat. 2024, 66, 293–301. [Google Scholar]
- Zhang, N.; Wang, X.; Zhu, L.; Lu, G. A novel unequal power divider with general isolation topology: Design and verification. IEEE Microw. Compon. Lett. 2023, 33, 19–22. [Google Scholar]
- Wu, Y.; Liu, Y.; Li, S. A modified Gysel power divider of arbitrary power ratio and real terminated impedances. IEEE Microw. Compon. Lett. 2011, 21, 601–603. [Google Scholar]
- Xia, B.; Cheng, J.D.; Xiong, C.; Xiao, H.; Wu, L.S.; Mao, J.F. A new Gysel out-of-phase power divider with arbitrary power dividing ratio based on analysis method of equivalence of N-port networks. IEEE Trans. Microw. Theory Tech. 2021, 69, 1343–1355. [Google Scholar] [CrossRef]
- Chiu, L.; Xue, Q. A parallel-strip ring power divider with high isolation and arbitrary power-dividing ratio. IEEE Trans. Microw. Theory Techn. 2007, 55, 2419–2426. [Google Scholar] [CrossRef]


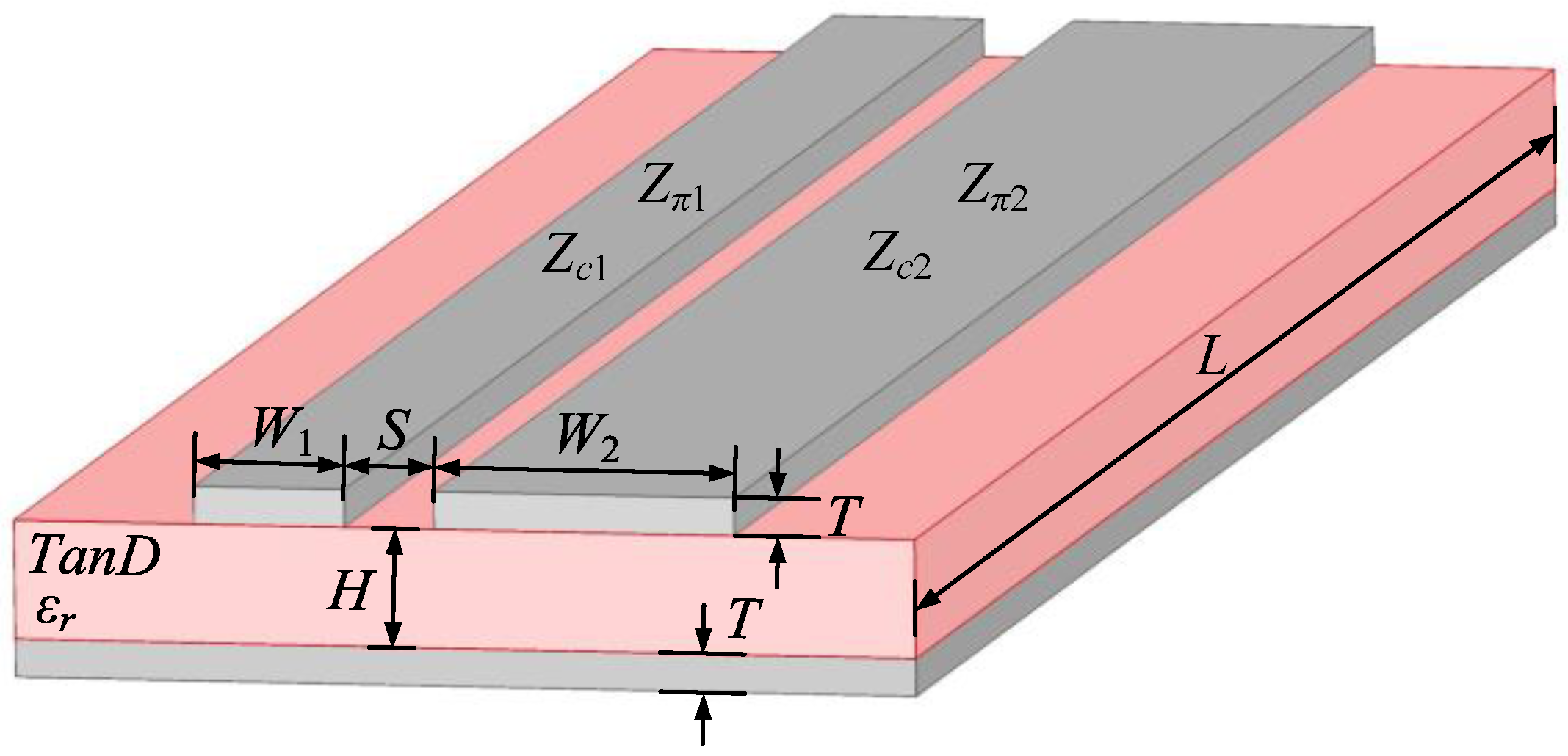
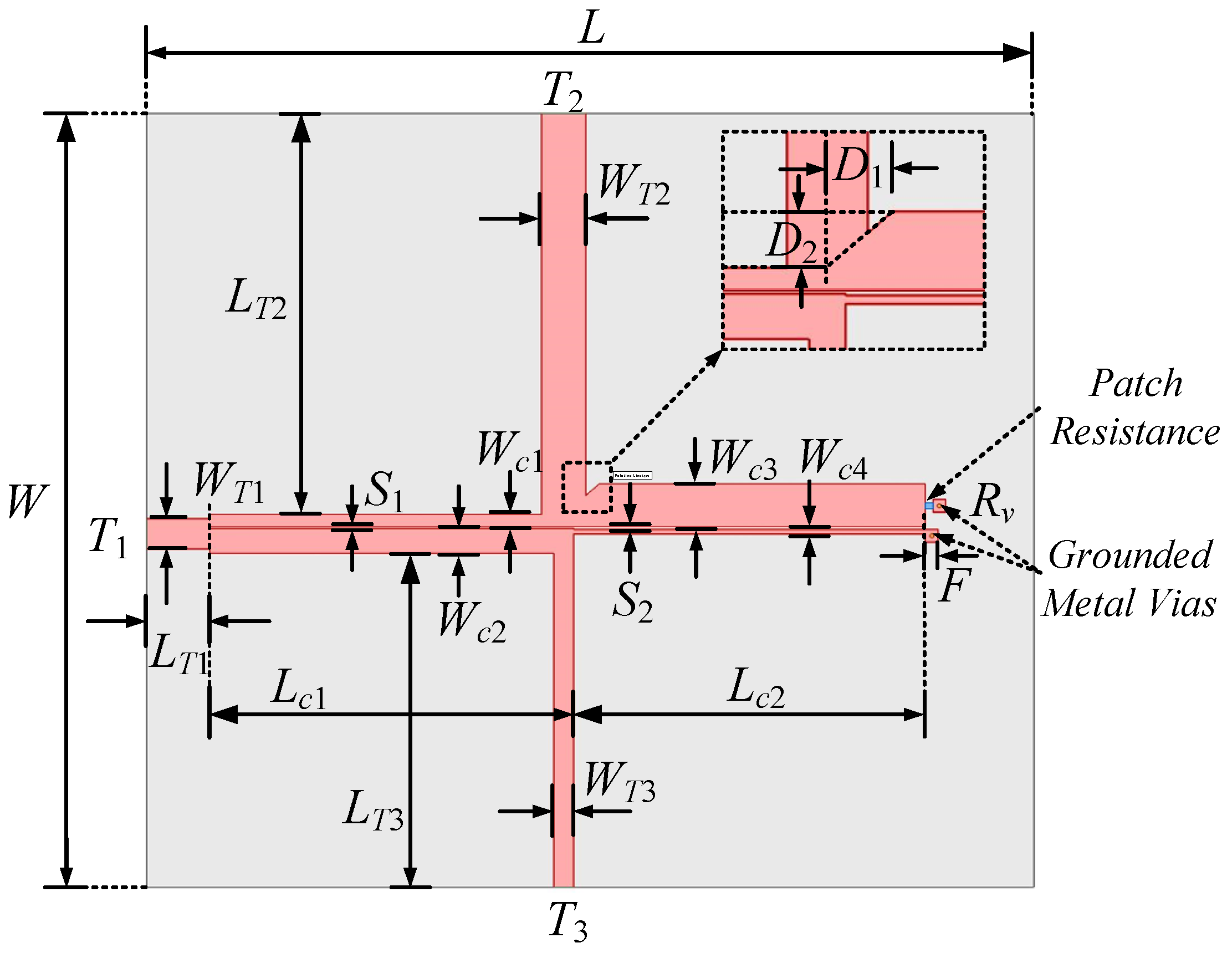


| Parameters | x | y | Rp | t | K2 | K6 | K1 | K3 | K4 | K5 |
| 3 dB | 0.8 | 2.8 | 1 | 3 | 3 | 1 | 0.8898 | 1.3229 | 2.1909 | 4.0988 |
| 10 dB | 0.6 | 1.7 | 0.1 | 0.72 | 3.6 | 1.5 | 1.4992 | 0.9910 | 0.6893 | 3.6693 |
| 20 dB | 0.86 | 1.26 | 0.01 | 0.6 | 3 | 3.445 | 2.2695 | 0.8198 | 0.7219 | 8.7382 |
| Parameters | ZT1 (Ω) | ZT2 (Ω) | ZT3 (Ω) | R (Ω) | ZI1 (Ω) | ZI2 (Ω) | ZI3 (Ω) | ZI1r (Ω) | ZI2r (Ω) | ZI3r (Ω) |
| 3 dB | 50 | 40 | 140 | 150 | 44.49 | 150 | 66.145 | 109.545 | 204.94 | 50 |
| 10 dB | 50 | 30 | 85 | 36 | 74.96 | 180 | 49.55 | 34.465 | 183.465 | 75 |
| 20 dB | 50 | 43 | 63 | 30 | 113.475 | 150 | 40.99 | 36.095 | 436.91 | 172.25 |
| Parameters | L (mm) | H (mm) | T (mm) | TanD | εr |
|---|---|---|---|---|---|
| Values | 28 | 0.787 | 0.017 | 0.0009 | 2.2 |
| Parameters (mm) | Wc1 | Wc2 | S1 | Wc3 | Wc4 | S2 |
|---|---|---|---|---|---|---|
| 3 dB | 2.14 | 0.89 | 0.15 | 0.16 | 0.87 | 0.15 |
| 10 dB | 1.04 | 1.88 | 0.15 | 3.35 | 0.37 | 0.21 |
| 20 dB | 0.16 | 2.41 | 0.14 | 3.79 | 0.24 | 1.98 |
| Parameters (mm) | Wc1 | Wc2 | Wc3 | Wc4 | S1 | S2 | Lc1 | Lc2 | WT1 | LT1 |
| 3 dB | 2.1 | 0.93 | 0.15 | 0.94 | 0.15 | 0.15 | 29.49 | 28.51 | 2.4 | 5 |
| 10 dB | 0.97 | 1.95 | 3.4 | 0.36 | 0.15 | 0.21 | 28.69 | 27.77 | 2.4 | 5 |
| 20 dB | 0.15 | 2.38 | 3.8 | 0.24 | 0.15 | 2 | 29.62 | 25.59 | 2.4 | 5 |
| Parameters (mm) | WT2 | LT2 | WT3 | LT3 | W | L | D1 | D2 | F | Rv |
| 3 dB | 2.83 | 25.1 | 2.4 | 27.07 | 55.35 | 70 | 0 | 0 | 1 | 0.15 |
| 10 dB | 3.46 | 31.73 | 2.4 | 26.45 | 61.25 | 70 | 2.8 | 2.43 | 1 | 0.15 |
| 20 dB | 2.52 | 26.75 | 2.4 | 25.28 | 54.71 | 70 | 4.72 | 3.65 | 1 | 0.15 |
| S-Parameters | S11/S22/S23/S33 (dB) | S12 (dB) | S13 (dB) |
|---|---|---|---|
| 3 dB | <−15 | −3 ± 0.2 | −3 ± 0.2 |
| 10 dB | <−15 | −10 ± 0.5 | −0.4 ± 0.2 |
| 20 dB | <−20 | −20 ± 1.5 | −0.03 ± 0.1 |
| Refs. | TRI | MPDR | RN | Phase Relationship | FBW (%) | Circuit Element Type | Occupied Area (λg2) |
|---|---|---|---|---|---|---|---|
| [11] | Fixed | 2:1 | 2 | In-phase | 137.5 | Branch lines with one slotline phase inverter as the isolation path | 0.072 |
| [13] | Fixed | 4:1 | 2/1 * | In-phase | 57.69 | Branch lines with one SCL section as the isolation path | 0.114 1 |
| [18] | Fixed | 8:1 | 2 | In-phase | 66.67 | Branch lines with one coupled line section as the isolation path | 0.045 |
| [19] | Arbitrary | 2:1 | 2 | In-phase | 20.96 | Five sections of branch lines | - |
| This work | Arbitrary | 100:1 | 1 | In-phase | 34/42/60 2 | Two sections of ACLs | 0.033 |
| [20] | Arbitrary | 1000:1 | 1 | Out-of-phase | 100 | Branch lines with one SCL section as the transition path | 0.046 |
| [21] | Arbitrary | 12:1 | 2 | Out-of-phase | 120 | Parallel-strip ring with one swap as the isolation path | - |
| Contribution | Impedance transformation, miniaturization, high in-phase power division ratio | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xia, B.; Mao, J. A Design Approach for Asymmetric Coupled Line In-Phase Power Dividers with Arbitrary Terminal Real Impedances and Arbitrary Power Division Ratio. Symmetry 2025, 17, 562. https://doi.org/10.3390/sym17040562
Zhang Y, Xia B, Mao J. A Design Approach for Asymmetric Coupled Line In-Phase Power Dividers with Arbitrary Terminal Real Impedances and Arbitrary Power Division Ratio. Symmetry. 2025; 17(4):562. https://doi.org/10.3390/sym17040562
Chicago/Turabian StyleZhang, Yan, Bin Xia, and Junfa Mao. 2025. "A Design Approach for Asymmetric Coupled Line In-Phase Power Dividers with Arbitrary Terminal Real Impedances and Arbitrary Power Division Ratio" Symmetry 17, no. 4: 562. https://doi.org/10.3390/sym17040562
APA StyleZhang, Y., Xia, B., & Mao, J. (2025). A Design Approach for Asymmetric Coupled Line In-Phase Power Dividers with Arbitrary Terminal Real Impedances and Arbitrary Power Division Ratio. Symmetry, 17(4), 562. https://doi.org/10.3390/sym17040562






