Research on the Damage Mechanism and Shear Strength Weakening Law of Rock Discontinuities Under Dynamic Load Disturbance
Abstract
1. Introduction
2. Numerical Simulation Protocol for Dynamic Load Disturbance in Rock Discontinuity
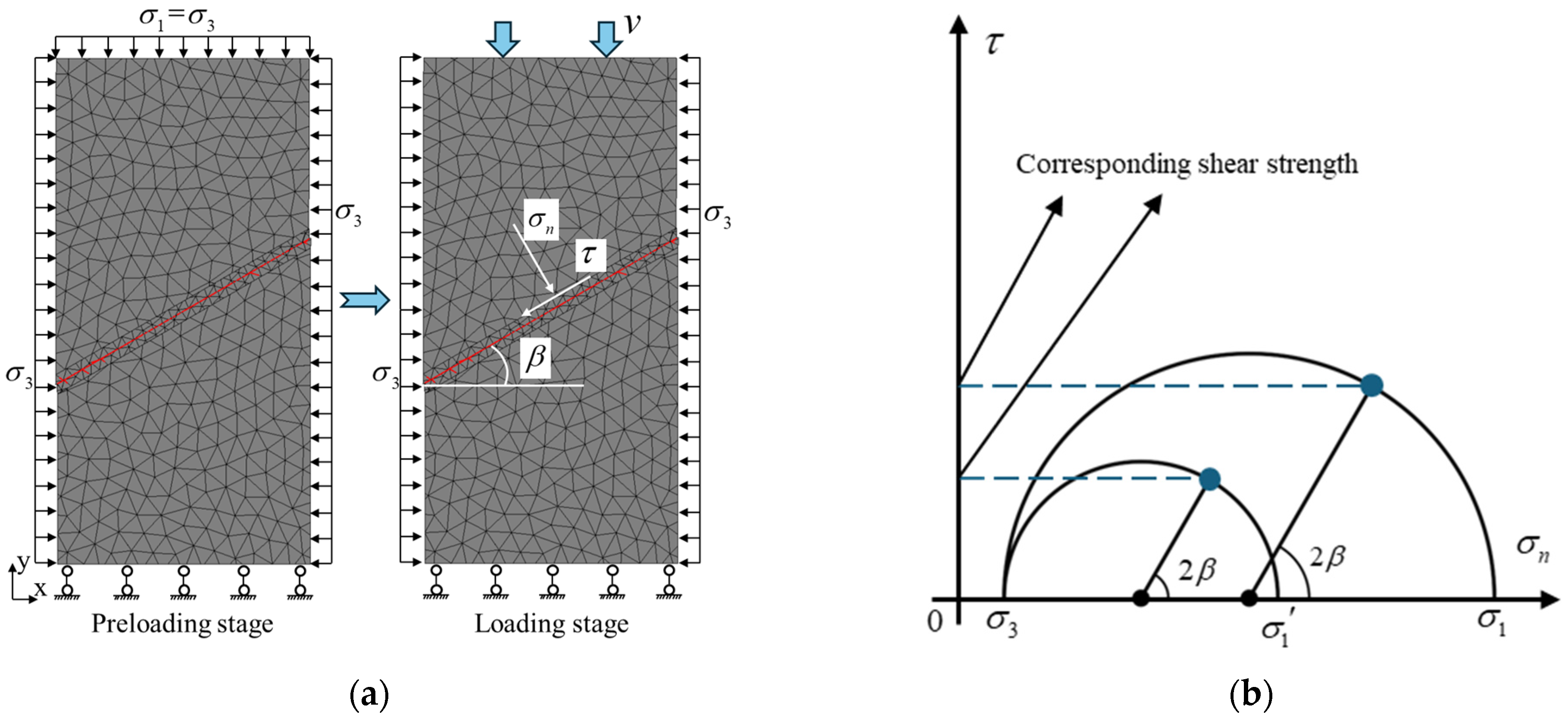
2.1. Model Construction and Parameter Calibration
2.2. Orthogonal Experimental Design for Dynamic Load Disturbance
3. Dominant Controlling Factors and Formation Mechanisms of Discontinuity Damage Under Dynamic Load Disturbance
3.1. Characterization Indices for Discontinuity Damage
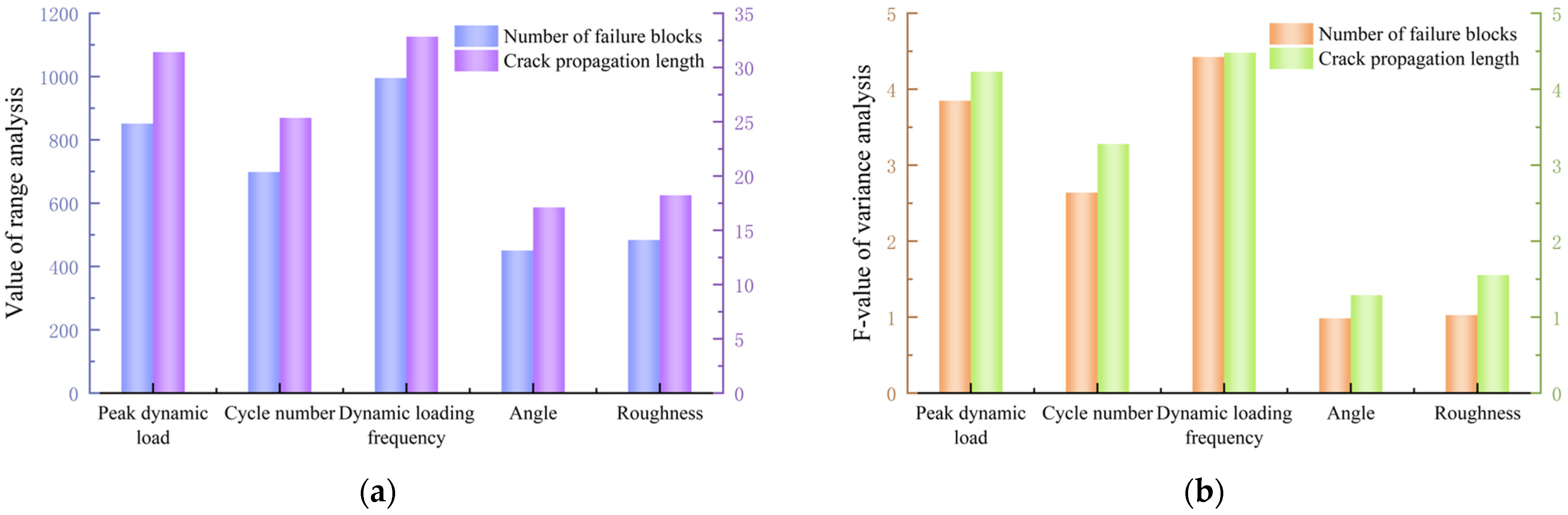
3.2. Sensitivity Analysis for Different Influencing Factors
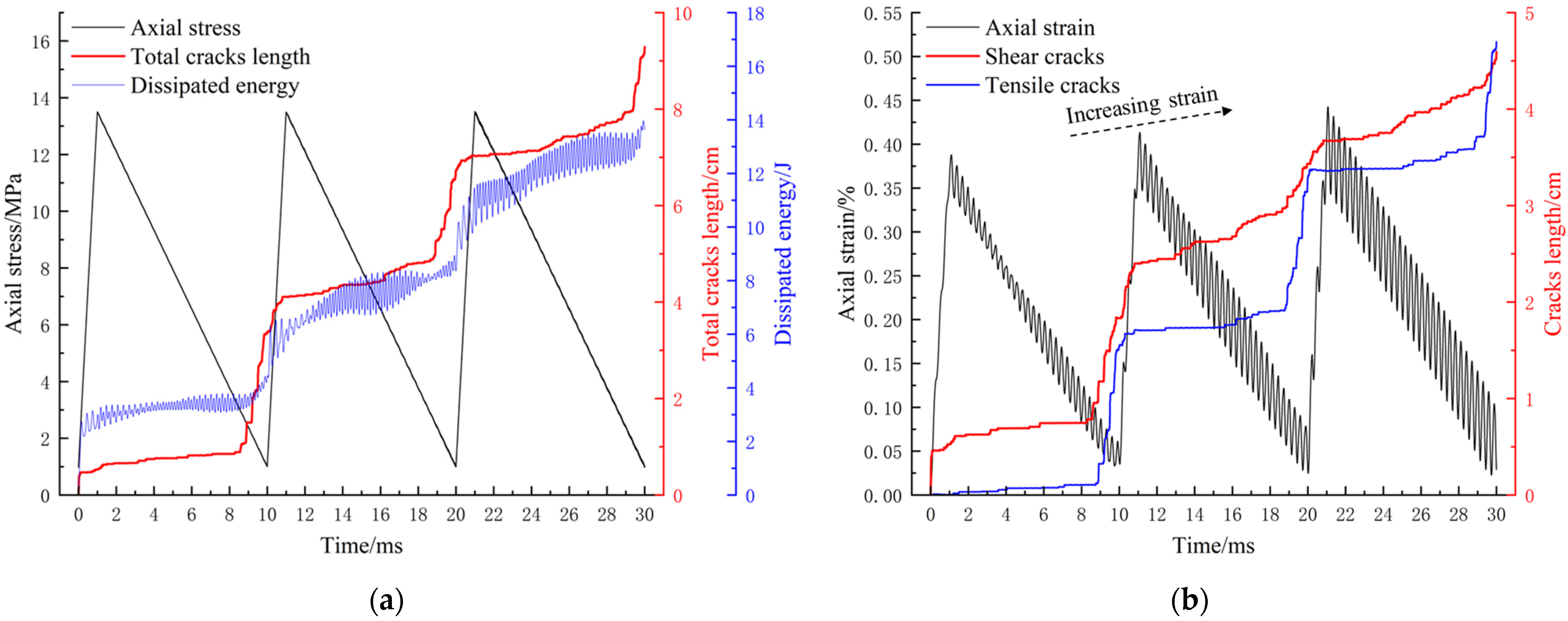
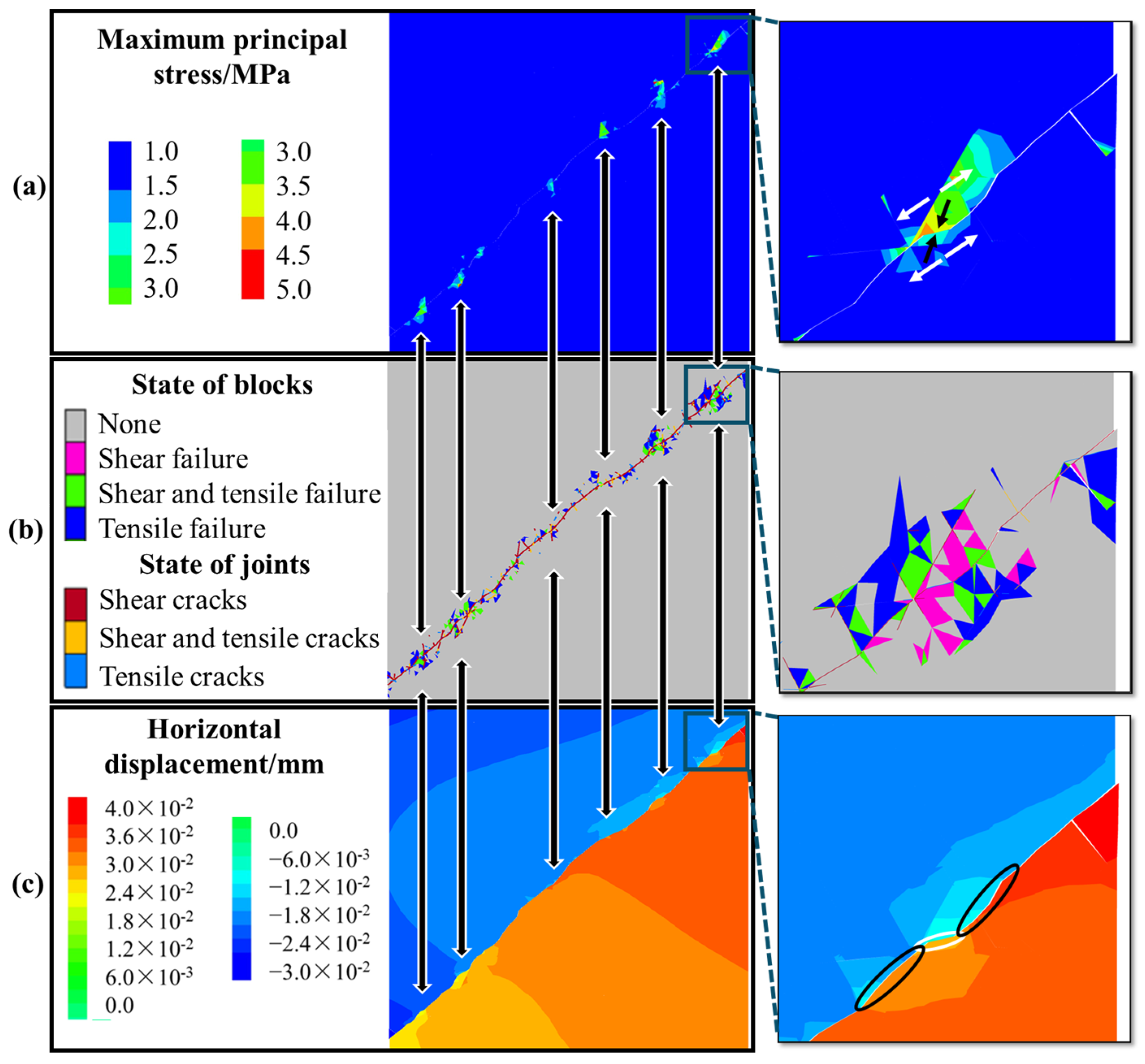
3.3. Characteristics and Formation Mechanism of Discontinuity Damage
4. Law of Shear Strength Weakening of Discontinuity After Dynamic Load Disturbance
4.1. Calculation Method for the Shear Strength of Discontinuities After Dynamic Load Disturbance
4.2. The Weakening Law of the Shear Strength of the Discontinuity Under the Dominant Controlling Factors
5. Laboratory Test Verification of the Damage Mechanism and the Law of Strength Weakening
5.1. Laboratory Test Verification Plan
5.2. Verification of Damage Mechanism and Law of Strength Weakening
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UDEC | Universal Distinct Element Code |
| JRC | Joint Roughness Coefficient |
References
- Liu, C.Z. Genetic Types of Landslide and Debris Flow Disasters in China. Geol. Rev. 2014, 60, 858–868. [Google Scholar] [CrossRef]
- Hong, Z.-J.; Si, K.; Li, Z.-H.; Zhu, C.; Du, F.; Cao, Z. Study on the Strength Characteristics of Sandstone Subjected to Coupled Static and Dynamic Loads from the Perspective of Microscopic Crack Propagation. Geomech. Geophys. Geo-Energy Geo-Resour. 2025, 11, 21. [Google Scholar] [CrossRef]
- Liu, J.; Cong, Y.; Zhang, L.M.; Wang, Z.Q. Mesoscopic Damage Mechanism of Granite under True Triaxial Loading and Unloading. J. Cent. South Univ. (Sci. Technol.) 2021, 52, 2677–2688. [Google Scholar] [CrossRef]
- Shi, Z.; Wu, C.; Li, X.; Xu, Y.; Li, K.; Sun, J. Dynamic Response and Energy Characterisation of High-Strength Sandstone under Progressive Cyclic Loading Based on Sustainable Mining. Appl. Sci. 2024, 14, 1101. [Google Scholar] [CrossRef]
- Geranmayeh Vaneghi, R.; Ferdosi, B.; Okoth, A.D.; Kuek, B. Strength Degradation of Sandstone and Granodiorite under Uniaxial Cyclic Loading. J. Rock Mech. Geotech. Eng. 2018, 10, 117–126. [Google Scholar] [CrossRef]
- Kim, J.-S.; Lee, C.; Kim, G.-Y. Estimation of Damage Evolution within an in Situ Rock Mass Using the Acoustic Emissions Technique under Incremental Cyclic Loading. Geotech. Test. J. 2021, 44, 1358–1378. [Google Scholar] [CrossRef]
- Niktabar, S.M.M.; Rao, K.S.; Shrivastava, A.K.; Ščučka, J. Effect of Load Frequency and Amplitude of Displacement on Soft Synthetic Rock Joints under Cyclic Shear Loads. Bull. Eng. Geol. Environ. 2024, 83, 389. [Google Scholar] [CrossRef]
- Soomro, M.H.A.A.; Indraratna, B.; Karekal, S. Critical Shear Strain and Sliding Potential of Rock Joint under Cyclic Loading. Transp. Geotech. 2022, 32, 100708. [Google Scholar] [CrossRef]
- Peellage, W.H.; Fatahi, B.; Rasekh, H. Assessment of Cyclic Deformation and Critical Stress Amplitude of Jointed Rocks Via Cyclic Triaxial Testing. J. Rock Mech. Geotech. Eng. 2023, 15, 1370–1390. [Google Scholar] [CrossRef]
- Peellage, W.H.; Fatahi, B.; Rasekh, H. Experimental Investigation for Vibration Characteristics of Jointed Rocks Using Cyclic Triaxial Tests. Soil Dyn. Earthq. Eng. 2022, 160, 107377. [Google Scholar] [CrossRef]
- Siamaki, A.; Esmaieli, K.; Mohanty, B. Degradation of a Discrete Infilled Joint Shear Strength Subjected to Repeated Blast-Induced Vibrations. Int. J. Min. Sci. Technol. 2018, 28, 561–571. [Google Scholar] [CrossRef]
- Gao, B.L.; Zhang, J.H.; Zhang, L.Q. Deterioration Characteristics of Structural Plane and Dynamic Instability Mechanism of High Dangerous Rock Mass under Earthquake. Earth Sci. 2022, 47, 4417–4427. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, R.; Pan, P.; Qi, J.; Su, G.; Zheng, H. Shear Failure Behaviors and Degradation Mechanical Model of Rockmass under True Triaxial Multi-Level Loading and Unloading Shear Tests. Int. J. Min. Sci. Technol. 2024, 34, 1385–1408. [Google Scholar] [CrossRef]
- Li, J.; Guo, P.; Cui, H.; Song, S.; Zhao, W.; Chu, J.; Xie, W. Dynamic Response Mechanism of Impact Instability Induced by Dynamic Load Disturbance to Surrounding Rock in High Static Loading Roadway. Minerals 2021, 11, 971. [Google Scholar] [CrossRef]
- Yousif, O.S.Q.; Karakouzian, M. Distinct Element Modeling of Uniaxial Compression Tests of Tuff-Like Lithophysal Material; Using Voronoi Tessellation System. Geotech. Geol. Eng. 2023, 41, 319–335. [Google Scholar] [CrossRef]
- Akasheva, Z.K.; Bolysbek, D.; Assilbekov, B.; Yergesh, A.; Zhanseit, A.Y. Pore-Network Modeling and Determination of Rock and Two-Phase Fluid Flow Properties. Eng. J. Satbayev Univ. 2021, 143, 106–114. [Google Scholar] [CrossRef]
- Du, J.; Huang, X.; Yang, G.; Xue, L.; Wu, B.; Zang, M.; Zhang, X. UDEC Modelling on Dynamic Response of Rock Masses with Joint Stiffness Weakening Attributed to Particle Crushing of Granular Fillings. Rock Mech. Rock Eng. 2023, 56, 1823–1841. [Google Scholar] [CrossRef]
- Miao, C.; Liu, J.; Gao, M.; Li, J.; Pang, D.; Yuan, K. Insight into the Overload Failure Mechanism of Anchored Slope with Weak Structural Planes. Bull. Eng. Geol. Environ. 2024, 83, 390. [Google Scholar] [CrossRef]
- Xu, W.; Hu, X.L.; Huang, L.; Zou, Z.X.; Ni, W.D.; Liu, X. Research on RQD of Rock Mass Calculated by Three-Dimensional Discontinuity Network Simulation Method and Its Accuracy Comparison. Chin. J. Rock Mech. Eng. 2012, 31, 822–833. [Google Scholar]
- Shan, R.; Liu, N.; Sun, P.; Zhao, Z.; Dong, R.; Dou, H.; Meng, H.; Bai, Y. Experimental and Numerical Simulation Study of Rough Jointed Rock Samples under Triaxial Compression Conditions. Eng. Fract. Mech. 2025, 314, 110707. [Google Scholar] [CrossRef]
- Li, K.; Yu, W.J.; Liao, Z.; Guo, H.X.; Pan, B.; Khamphouvanh, V.; Yang, J. A Laboratory-Testing-Tased Study on Mechanical Properties and Dilatancy Characteristics of Deeply Buried Mudstone under Different Stress Loading Rates. J. Coal Sci. Eng. China 2023, 48, 3360–3371. [Google Scholar] [CrossRef]
- Wang, Y.; He, M. Numerical Investigation on Effect of Inclination and Position of Structural Planes on Rockbursts Triggered by Blasting Disturbance in Deep-Buried Tunnels. Rock Mech. Rock Eng. 2025, 58, 2739–2761. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, Q.; Li, S.; Wang, H.; Han, G. A Shear Strength Criterion of Rock Joints under Dynamic Normal Load. Int. J. Rock Mech. Min. Sci. 2025, 186, 106002. [Google Scholar] [CrossRef]
- Zhu, Q.; Yin, Q.; Tao, Z.; Yin, Z.; Jing, H.; Meng, B.; He, M.; Wu, S.; Wu, J. Shearing Characteristics and Instability Mechanisms of Rough Rock Joints under Cyclic Normal Loading Conditions. J. Rock Mech. Geotech. Eng. 2024, in press. [Google Scholar] [CrossRef]
- Wang, K.X.; Xu, W.G.; Pan, Y.S.; Xue, J.Q.; Oparin, V.N.; Kiryaeva, T.A. Study on Tensile-Compression Damage and Fracture of Weak Interlayers in Block Rock Masses Induced by Quasi-Resonance. Chin. J. Rock Mech. Eng. 2025, 44, 114–127. [Google Scholar] [CrossRef]
- Mashinskii, E.I. Elastic–Microplastic Nature of Wave Propagation in the Weakly Consolidated Rock. J. Appl. Geophys. 2014, 101, 11–19. [Google Scholar] [CrossRef]
- Wang, W.; Wang, H.; Zhang, B.; Wu, Y.; Zhang, J.; Sun, D. Experimental Technique of Rock Multi-Strain Rates Dynamic and Static Load Superposition and Its Application. Rock Mech. Rock Eng. 2025, 58, 3159–3174. [Google Scholar] [CrossRef]
- Barton, N. A Relationship between Joint Roughness and Joint Shear Strength. Proc. Int. Symp. Rock Mech. 1971, 1–8. Available online: https://www.researchgate.net/publication/296798762_A_relationship_between_joint_roughness_and_joint_shear_strength (accessed on 29 March 2025).
- Barton, N.; Choubey, V. The Shear Strength of Rock Joints in Theory and Practice. Rock Mech. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, L. The Affecting Factors of Slope Stability Based on Orthogonal Design. Adv. Mater. Res. 2013, 690–693, 756–759. [Google Scholar] [CrossRef]
- Ni, Y.; Wang, R.; Leng, X.; Xia, F.; Wang, F. Modelling of Particle Flow Code Geotechnical Material Parameter Relationships Based on Orthogonal Design and Back Propagation Neural Network. Comput. Part. Mech. 2025, 12, 371–398. [Google Scholar] [CrossRef]
- Sun, Z.; Han, Y.; Liu, F.; Min, R. Sensitivity Analysis of Influencing Factors of Vertical Bearing Capacity of Rock-Socketed Piles Based on Orthogonal Test. In Frontier Research on High Performance Concrete and Mechanical Properties; Xiang, P., Yang, H., Yan, J., Eds.; Springer Nature: Singapore, 2025; pp. 93–106. [Google Scholar]
- Abdellah, R.; Bader, S.; Kim, J.-G.; Mohamed Ali, M. Numerical Simulation of Mechanical Behavior of Rock Samples under Uniaxial and Triaxial Compression Testsy. Min. Miner. Depos. 2023, 17, 1–11. [Google Scholar] [CrossRef]
- West, I.; Walton, G. Quantitative Evaluation of the Effects of Input Parameter Heterogeneity on Model Behavior for Bonded Block Models of Laboratory Rock Specimens. Rock Mech. Rock Eng. 2023, 56, 7129–7146. [Google Scholar] [CrossRef]
- Kim, J.; Kumpulainen, S.; Ferrari, A.; Pintado, X.; Laloui, L.; Heino, V. Salinity-Dependent Ultimate Shear Strength of Compacted Wyoming-Type Bentonite Investigated by Triaxial Tests. Appl. Clay Sci. 2024, 261, 107576. [Google Scholar] [CrossRef]
- Jang, H.-S.; Zhang, Q.-Z.; Kang, S.-S.; Jang, B.-A. Determination of the Basic Friction Angle of Rock Surfaces by Tilt Tests. Rock Mech. Rock Eng. 2018, 51, 989–1004. [Google Scholar] [CrossRef]
- Yang, S.Q.; Dai, Y.H.; Han, L.J.; Jin, Z.Q. Experimental Study on Mechanical Behavior of Brittle Marble Samples Containing Different Flaws under Uniaxial Compression. Eng. Fract. Mech. 2009, 76, 1833–1845. [Google Scholar] [CrossRef]
- Vasyliev, L.; Malich, M.; Vasyliev, D.; Katan, V.; Rizo, Z. Improving a Technique to Calculate Strength of Cylindrical Rock Samples in Terms of Uniaxial Compression. Min. Miner. Depos. 2023, 17, 43–50. [Google Scholar] [CrossRef]
- Yong, R.; Zhong, Z.; Du, S.G.; Zheng, S.; Zhang, Y.Y. Review on Research Advance of Basic Friction Angle of Rock Joints. Chin. J. Rock Mech. Eng. 2022, 41, 254–270. [Google Scholar] [CrossRef]
- Li, W.; Ji, Z.S.; Dong, Z.Y.; Li, Z.L.; Li, Y. Vibration Analysis of Rock under Impact Loads Based on the Renormalization Method. J. Vib. Shock. 2016, 35, 49–54. [Google Scholar] [CrossRef]
- Gao, X.; Jia, J.; Zhang, L.; Zhao, Y.; Tu, B. Mechanical Properties and Reasonable Proportions of Granite Similar Materials with Varying Degrees of Weathering. Environ. Earth Sci. 2025, 84, 140. [Google Scholar] [CrossRef]


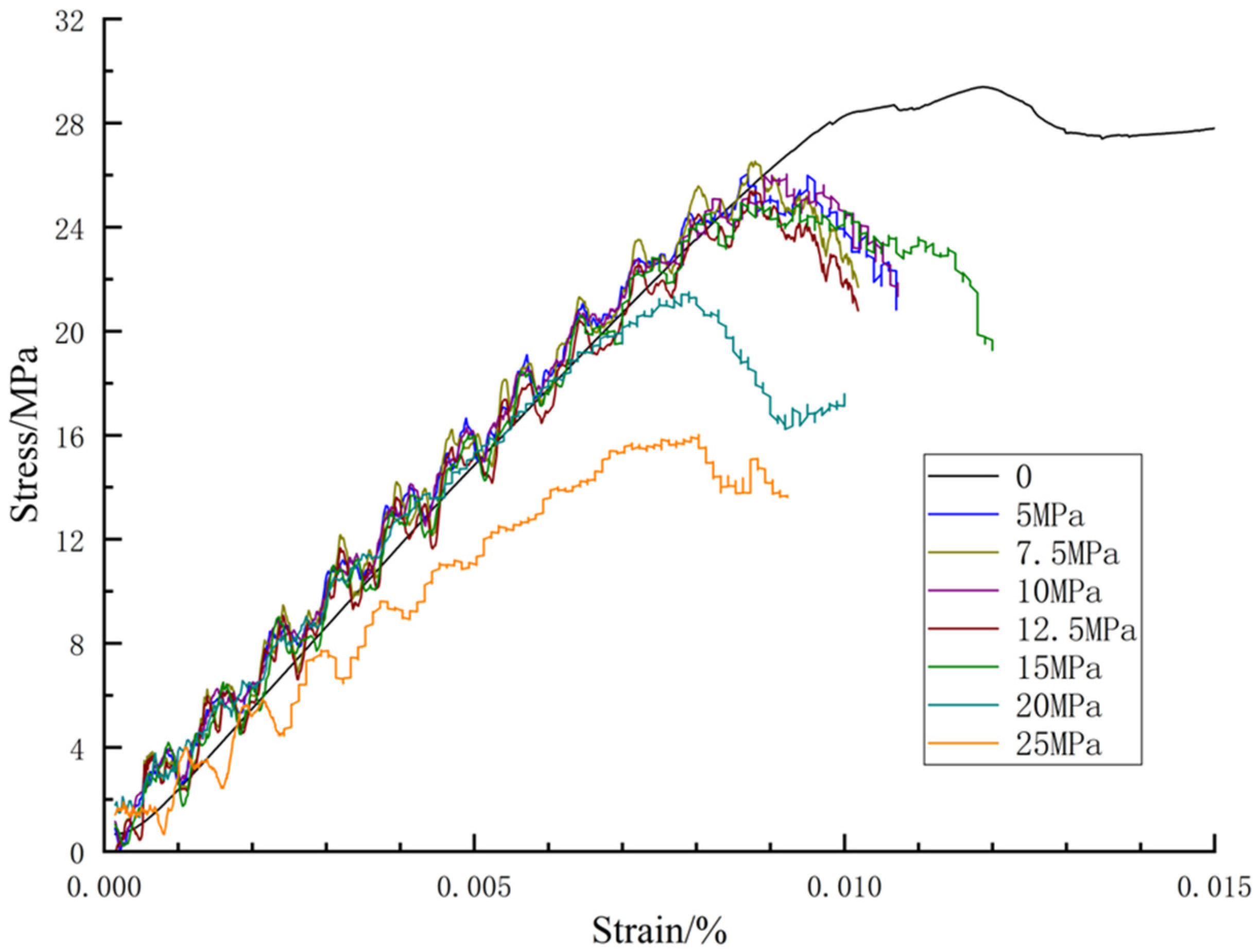
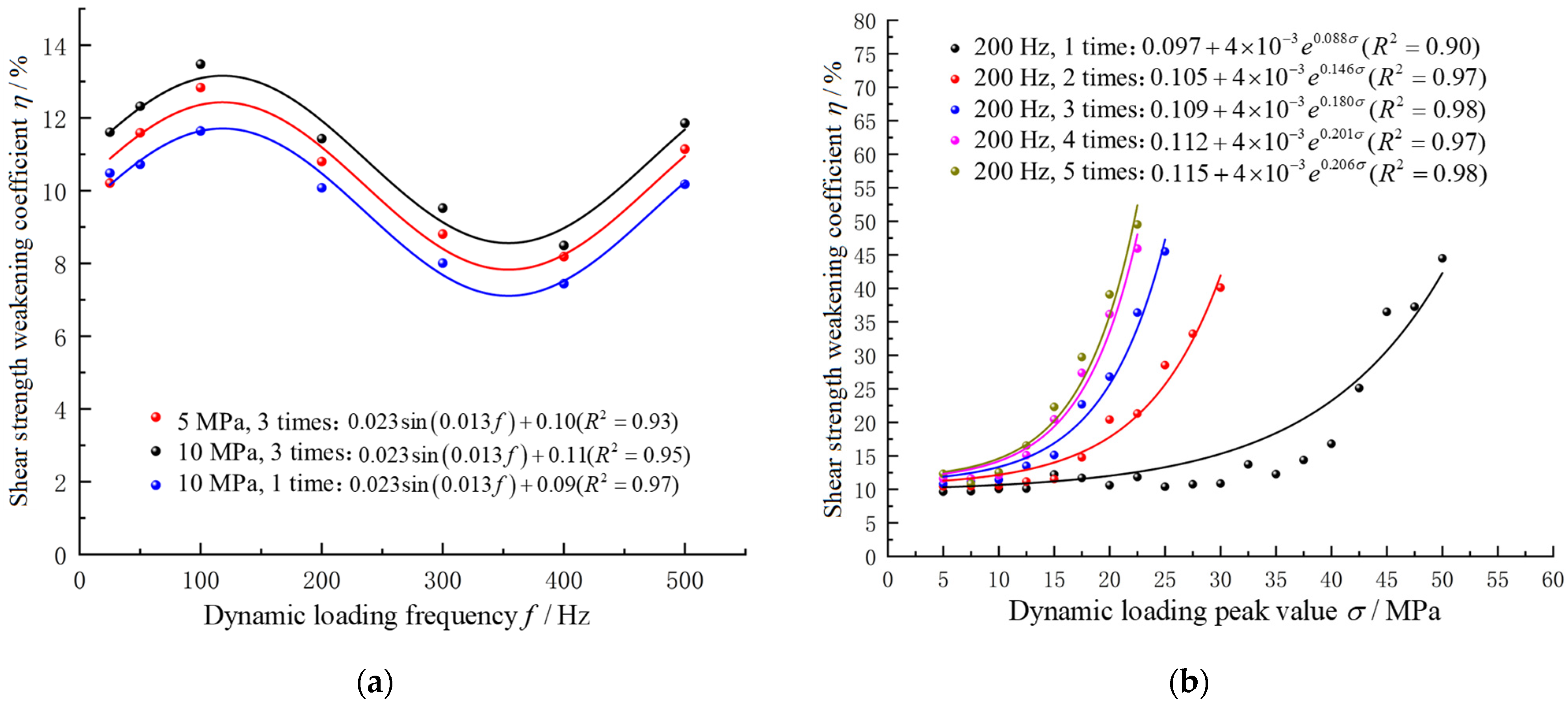
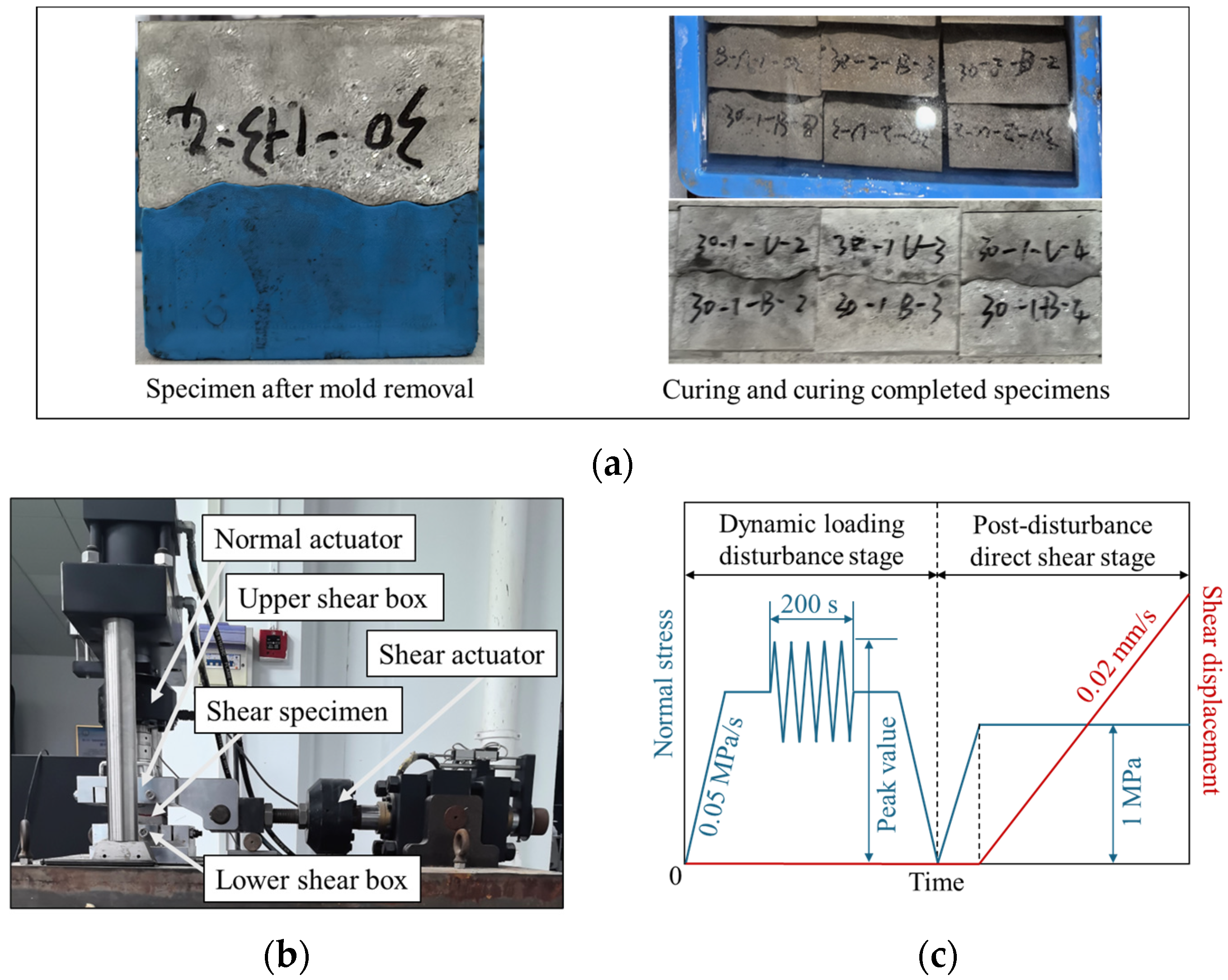
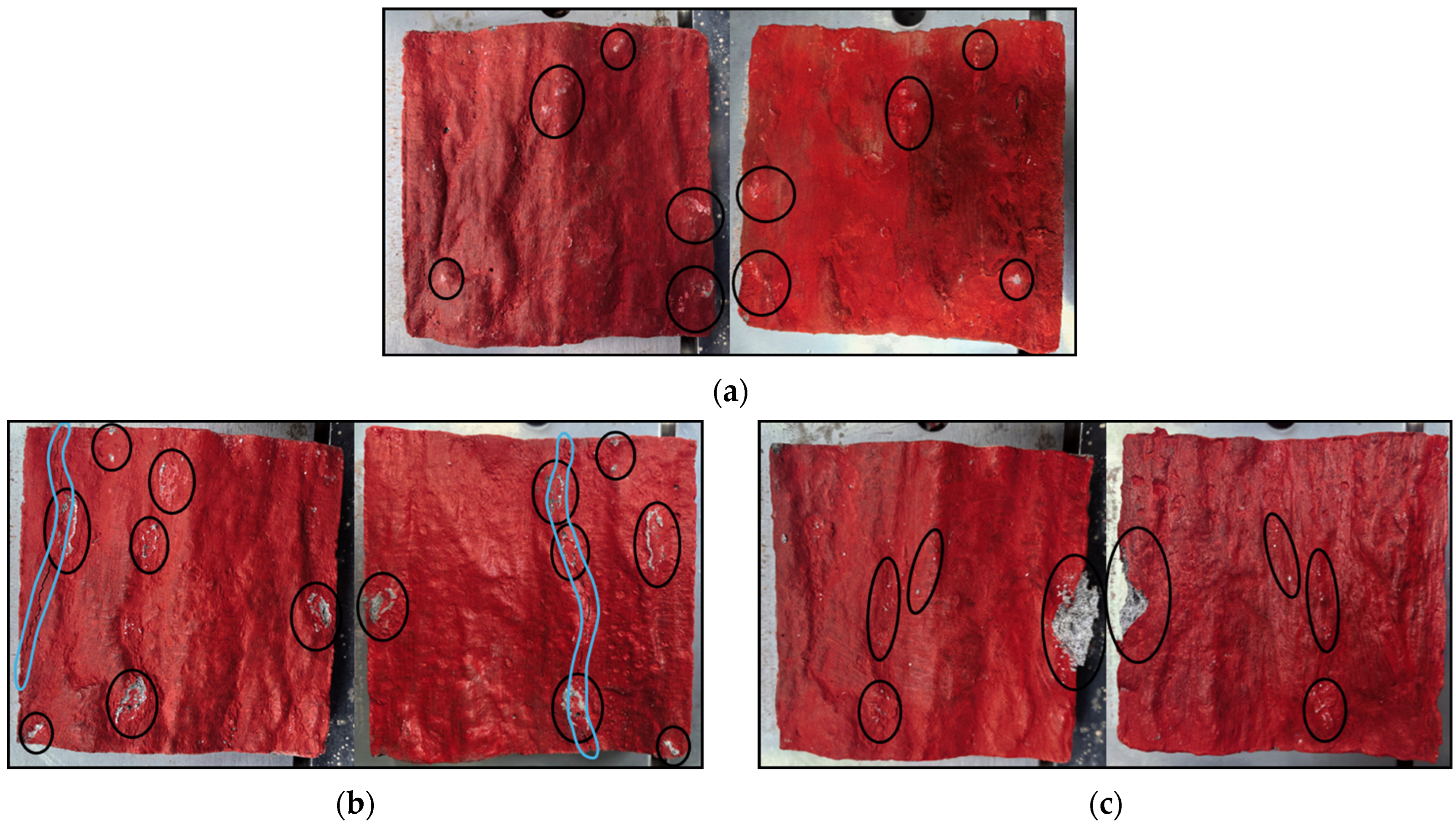
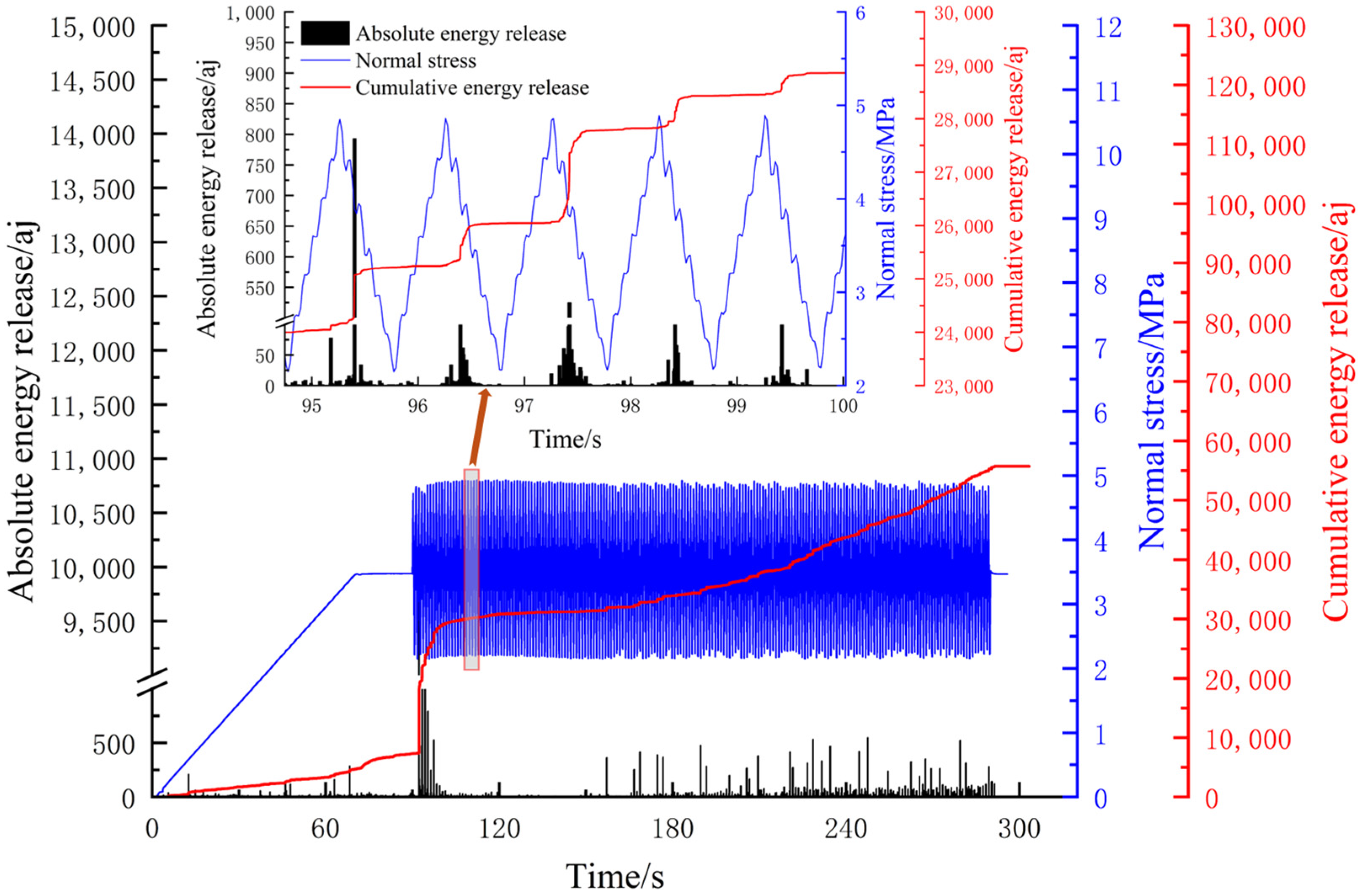
| Density (kg/m3) | Bulk Modulus K (Pa) | Shear Modulus G (Pa) | Friction Angle (°) | Cohesion C (Pa) | Tensile Strength T (Pa) | |
|---|---|---|---|---|---|---|
| Blocks at both ends | 2160 | 2.38 × 109 | 1.32 × 109 | 43 | 6.72 × 106 | 3.83 × 106 |
| Blocks near discontinuity | 2160 | 7.80 × 108 | 4.50 × 108 | 43 | 2.06 × 106 | 1.12 × 106 |
| Normal Stiffness Kn (Pa/m) | Shear Stiffness Ks (Pa/m) | Friction Angle (°) | Cohesion c (Pa) | Tensile Strength t (Pa) | |
|---|---|---|---|---|---|
| Joints at both ends | 4.16 × 1013 | 1.66 × 1013 | 39 | 6.72 × 106 | 3.83 × 106 |
| Joints near discontinuity | 4.16 × 1013 | 1.66 × 1013 | 39 | 2.06 × 106 | 1.12 × 106 |
| Discontinuity | 4.16 × 1013 | 1.66 × 1013 | 39 | 0.0 | 0.0 |
| Levels | Factors | ||||
|---|---|---|---|---|---|
| Peak Dynamic Load (MPa) | Cycle Number (times) | Dynamic Loading Frequency (Hz) | Inclination Angle (°) | Roughness | |
| 1 | 5 | 1 | 100 | 0 | 0 |
| 2 | 7.5 | 2 | 200 | 10 | 5 |
| 3 | 10 | 3 | 300 | 20 | 9 |
| 4 | 12.5 | 4 | 400 | 30 | 15 |
| 5 | 15 | 5 | 500 | 40 | 19 |
| Group Number | Peak Dynamic Load (MPa) | Cycle Number (times) | Dynamic Loading Frequency (Hz) | Inclination Angle (°) | Roughness | Group Number | Peak Dynamic Load (MPa) | Cycle Number (times) | Dynamic Loading Frequency (Hz) | Inclination Angle (°) | Roughness |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 15.0 | 2 | 100 | 20 | 5 | 14 | 15.0 | 1 | 400 | 30 | 9 |
| 2 | 5.0 | 4 | 200 | 20 | 9 | 15 | 7.5 | 2 | 500 | 10 | 9 |
| 3 | 10.0 | 5 | 300 | 0 | 9 | 16 | 5.0 | 1 | 100 | 0 | 0 |
| 4 | 5.0 | 3 | 500 | 30 | 15 | 17 | 10.0 | 2 | 200 | 30 | 0 |
| 5 | 12.5 | 4 | 300 | 30 | 5 | 18 | 15.0 | 3 | 300 | 10 | 0 |
| 6 | 7.5 | 4 | 400 | 40 | 0 | 19 | 10.0 | 4 | 100 | 10 | 15 |
| 7 | 7.5 | 1 | 300 | 20 | 15 | 20 | 12.5 | 5 | 500 | 20 | 0 |
| 8 | 10.0 | 3 | 400 | 20 | 19 | 21 | 12.5 | 1 | 200 | 10 | 19 |
| 9 | 15.0 | 4 | 500 | 0 | 19 | 22 | 10.0 | 1 | 500 | 40 | 5 |
| 10 | 7.5 | 5 | 100 | 30 | 19 | 23 | 5.0 | 2 | 300 | 40 | 19 |
| 11 | 12.5 | 2 | 400 | 0 | 15 | 24 | 12.5 | 3 | 100 | 40 | 9 |
| 12 | 5.0 | 5 | 400 | 10 | 5 | 25 | 15.0 | 5 | 200 | 40 | 15 |
| 13 | 7.5 | 3 | 200 | 0 | 5 |
| Group Number | Number of Failure Blocks (Number) | Crack Propagation Length (cm) | Group Number | Number of Failure Blocks (Number) | Crack Propagation Length (cm) |
|---|---|---|---|---|---|
| 1 | 58 | 3.74 | 14 | 373 | 3.03 |
| 2 | 72 | 2.96 | 15 | 162 | 5.13 |
| 3 | 119 | 7.40 | 16 | 2 | 0.49 |
| 4 | 416 | 8.37 | 17 | 70 | 9.30 |
| 5 | 179 | 7.03 | 18 | 97 | 11.03 |
| 6 | 218 | 12.14 | 19 | 93 | 4.13 |
| 7 | 1 | 0.17 | 20 | 1941 | 69.51 |
| 8 | 18 | 1.12 | 21 | 137 | 3.62 |
| 9 | 2508 | 93.06 | 22 | 260 | 7.61 |
| 10 | 130 | 4.61 | 23 | 32 | 0.91 |
| 11 | 113 | 8.89 | 24 | 341 | 9.29 |
| 12 | 4 | 0.63 | 25 | 1733 | 59.58 |
| 13 | 2 | 0.24 |
| Levels | Factors | ||||
|---|---|---|---|---|---|
| Peak Dynamic Load (MPa) | Cycle Number (Times) | Dynamic Loading Frequency (Hz) | Inclination Angle (°) | Roughness | |
| 1 | 105 | 155 | 125 | 549 | 466 |
| 2 | 103 | 87 | 403 | 99 | 81 |
| 3 | 112 | 175 | 62 | 418 | 213 |
| 4 | 633 | 723 | 145 | 247 | 471 |
| 5 | 954 | 785 | 1057 | 517 | 565 |
| Range | 851 | 698 | 995 | 450 | 484 |
| Levels | Factors | ||||
|---|---|---|---|---|---|
| Peak Dynamic Load (MPa) | Cycle Number (Times) | Dynamic Loading Frequency (Hz) | Inclination Angle (°) | Roughness | |
| 1 | 2.67 | 2.98 | 4.45 | 22.02 | 20.49 |
| 2 | 4.46 | 5.60 | 15.14 | 4.91 | 2.44 |
| 3 | 5.91 | 6.01 | 3.90 | 15.50 | 5.56 |
| 4 | 18.26 | 22.46 | 5.16 | 5.06 | 16.23 |
| 5 | 34.09 | 28.35 | 36.74 | 17.90 | 20.66 |
| Range | 31.42 | 25.36 | 32.83 | 17.11 | 18.22 |
| Source | Type III Sum of Squares | Degrees of Freedom | Mean Square | F-Value | Significance | Ranking |
|---|---|---|---|---|---|---|
| Corrected model | 9,709,510.800 | 20 | 485,475.54 | 2.584 | 0.185 | |
| Intercept | 3,297,129.64 | 1 | 3,297,129.6 | 17.549 | 0.014 | |
| Peak dynamic load | 2,892,135.76 | 4 | 723,033.94 | 3.848 | 0.110 | 2 |
| Cycle number | 1,982,242.16 | 4 | 495,560.54 | 2.638 | 0.185 | 3 |
| Dynamic loading frequency | 3,324,510.56 | 4 | 831,127.64 | 4.424 | 0.089 | 1 |
| Inclination angle | 739,263.36 | 4 | 184,815.84 | 0.984 | 0.506 | 5 |
| Roughness | 771,358.96 | 4 | 192,839.74 | 1.026 | 0.490 | 4 |
| Error | 751,546.56 | 4 | 187,886.64 | |||
| Total | 137,58187 | 25 | ||||
| Corrected total | 10,461,057.36 | 24 |
| Source | Type III Sum of Squares | Degrees of Freedom | Mean Square | F-Value | Significance | Ranking |
|---|---|---|---|---|---|---|
| Corrected model | 12,595.178 | 20 | 629.759 | 2.966 | 0.150 | |
| Intercept | 4461.52 | 1 | 4461.52 | 21.011 | 0.010 | |
| Peak dynamic load | 3591.85 | 4 | 897.963 | 4.229 | 0.096 | 2 |
| Cycle number | 2784.24 | 4 | 696.06 | 3.278 | 0.138 | 3 |
| Dynamic loading frequency | 3805.01 | 4 | 951.253 | 4.48 | 0.088 | 1 |
| Inclination angle | 1095.43 | 4 | 273.858 | 1.29 | 0.406 | 5 |
| Roughness | 1318.65 | 4 | 329.661 | 1.553 | 0.340 | 4 |
| Error | 849.353 | 4 | 212.338 | |||
| Total | 17906.1 | 25 | ||||
| Corrected total | 13444.5 | 24 |
| Group Number | Peak Dynamic Load (MPa) | Dynamic Loading Frequency (Hz) | Action Time (s) |
|---|---|---|---|
| A1 | 2 | 1 | 200 |
| A2 | 3.5 | 1 | 200 |
| A3 | 5 | 1 | 200 |
| Degree of Dynamic Load Disturbance | The Shear Strength in Laboratory Test (MPa) | Shear Strength Weakening Coefficient (%) |
|---|---|---|
| Undisturbed | 1.060 | |
| The peak dynamic load is 2 MPa | 1.014 | 4.34 |
| The peak dynamic load is 3.5 MPa | 0.974 | 8.11 |
| The peak dynamic load is 5 MPa | 0.884 | 16.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Gao, Z.; Liu, G.; Du, C.; Liu, W.; Wang, Z. Research on the Damage Mechanism and Shear Strength Weakening Law of Rock Discontinuities Under Dynamic Load Disturbance. Symmetry 2025, 17, 569. https://doi.org/10.3390/sym17040569
Luo Z, Gao Z, Liu G, Du C, Liu W, Wang Z. Research on the Damage Mechanism and Shear Strength Weakening Law of Rock Discontinuities Under Dynamic Load Disturbance. Symmetry. 2025; 17(4):569. https://doi.org/10.3390/sym17040569
Chicago/Turabian StyleLuo, Zhanyou, Zhifeng Gao, Guangjian Liu, Cheng Du, Weiming Liu, and Zhiyong Wang. 2025. "Research on the Damage Mechanism and Shear Strength Weakening Law of Rock Discontinuities Under Dynamic Load Disturbance" Symmetry 17, no. 4: 569. https://doi.org/10.3390/sym17040569
APA StyleLuo, Z., Gao, Z., Liu, G., Du, C., Liu, W., & Wang, Z. (2025). Research on the Damage Mechanism and Shear Strength Weakening Law of Rock Discontinuities Under Dynamic Load Disturbance. Symmetry, 17(4), 569. https://doi.org/10.3390/sym17040569




