Exploring Chaos in Fractional Order Systems: A Study of Constant and Variable-Order Dynamics
Abstract
1. Introduction
2. Definitions
3. Algorithms for Fractional Systems with Constant vs. Variable Order
3.1. Constant Order
3.2. Variable Order
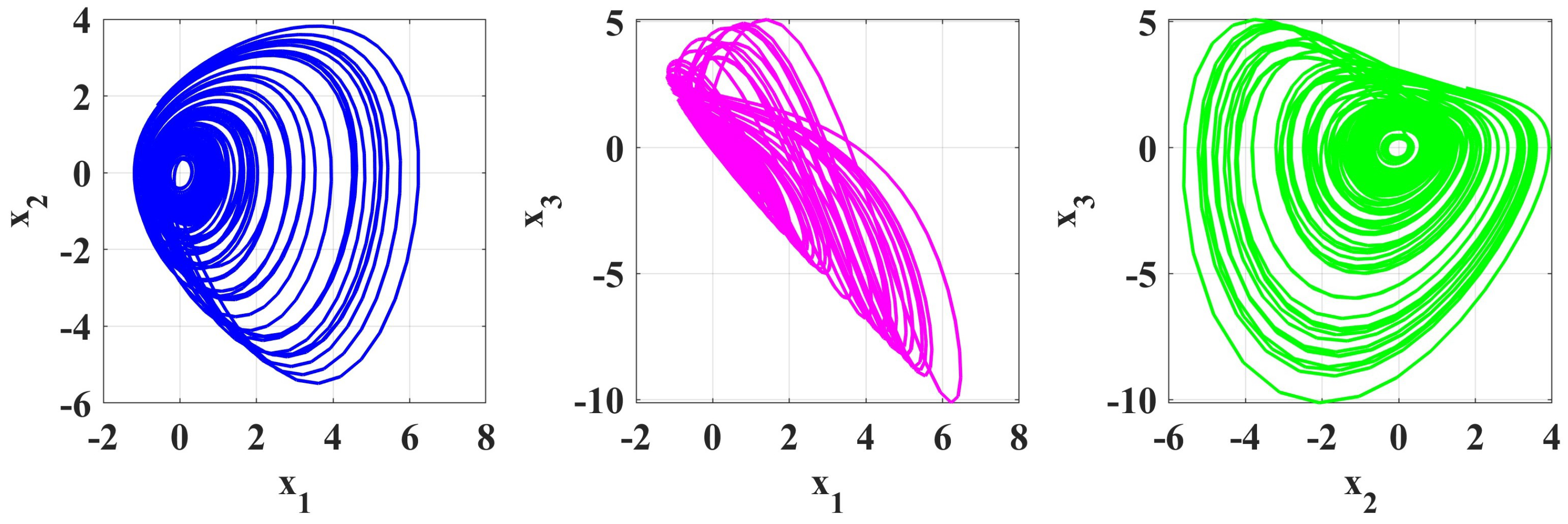
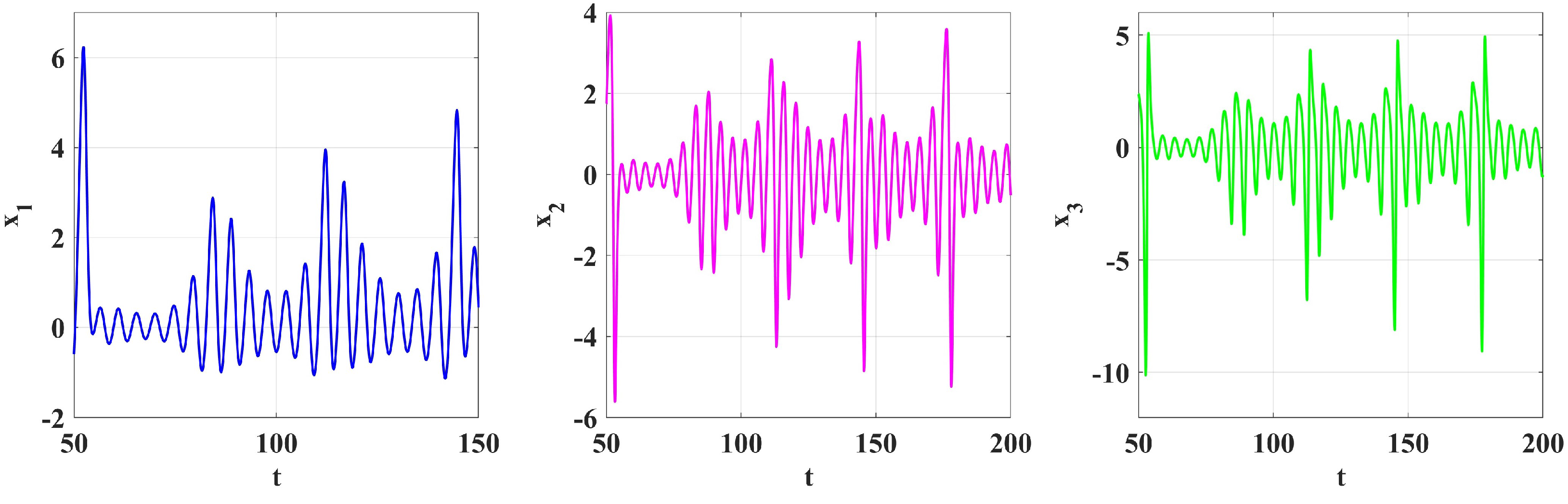
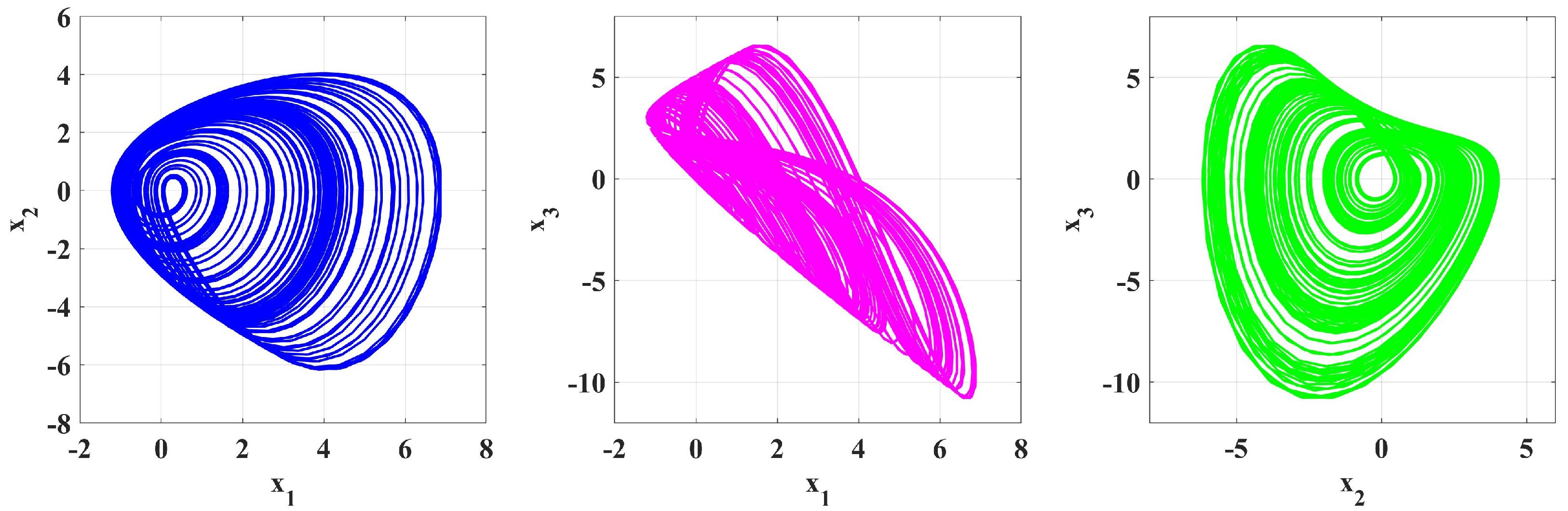
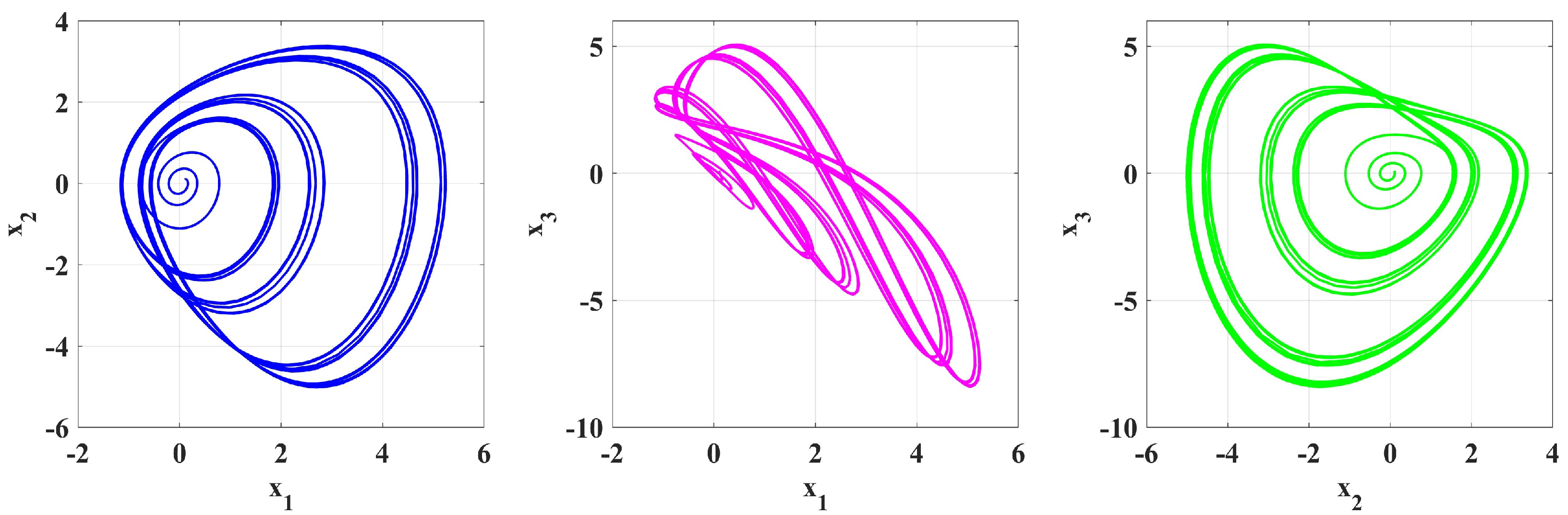
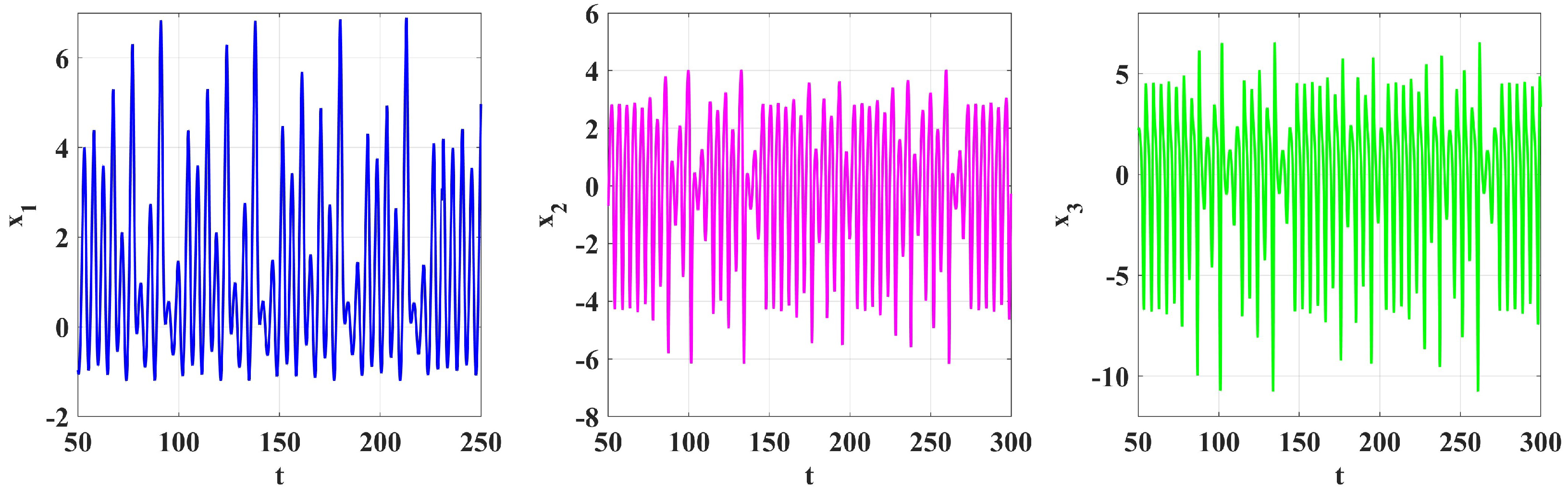
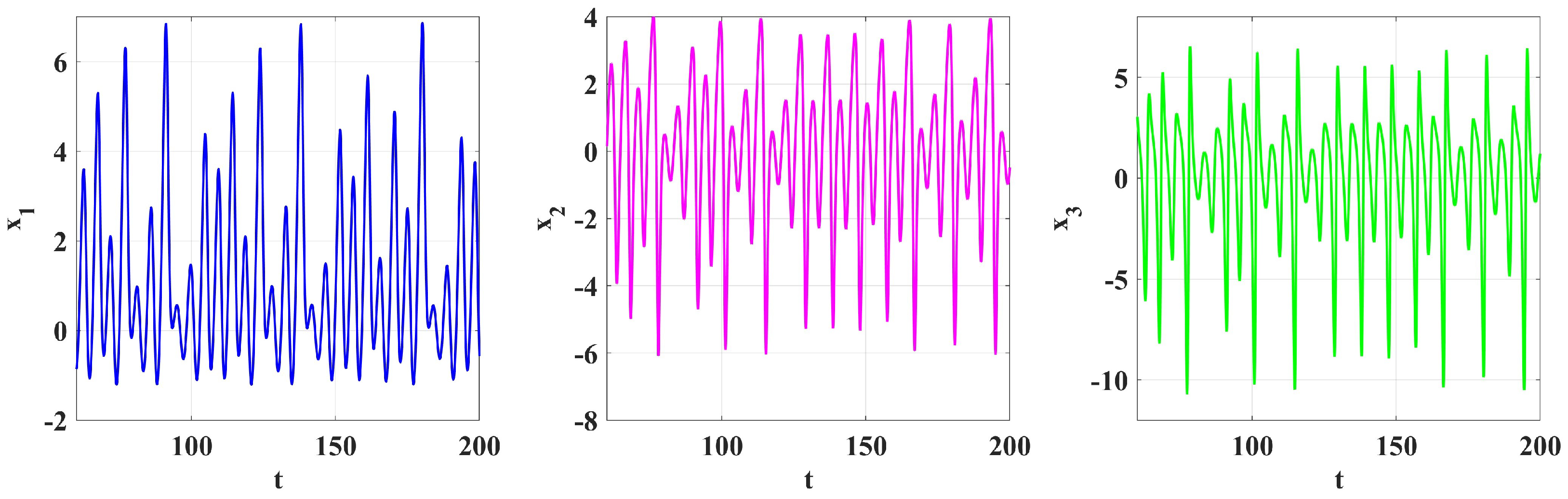
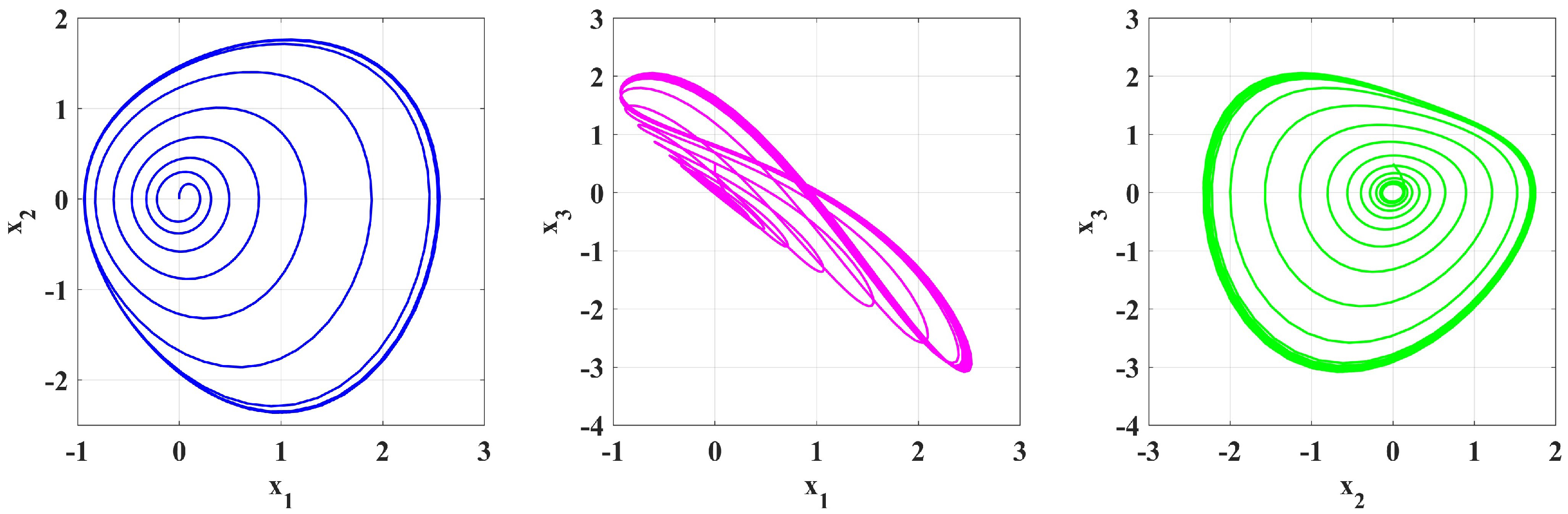
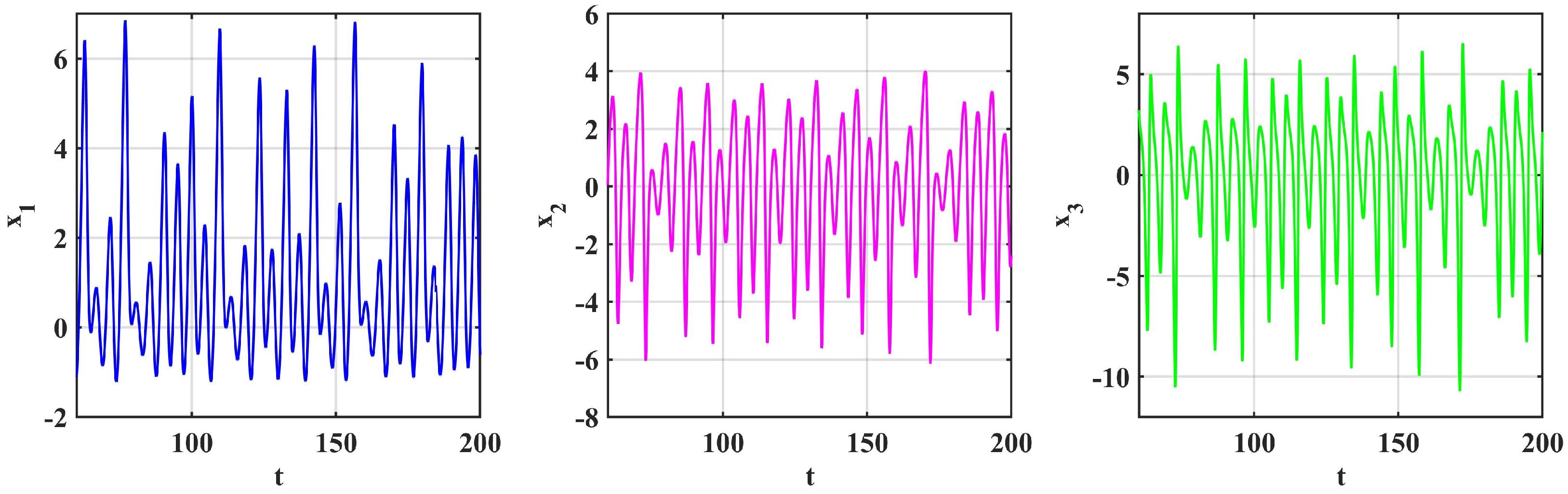
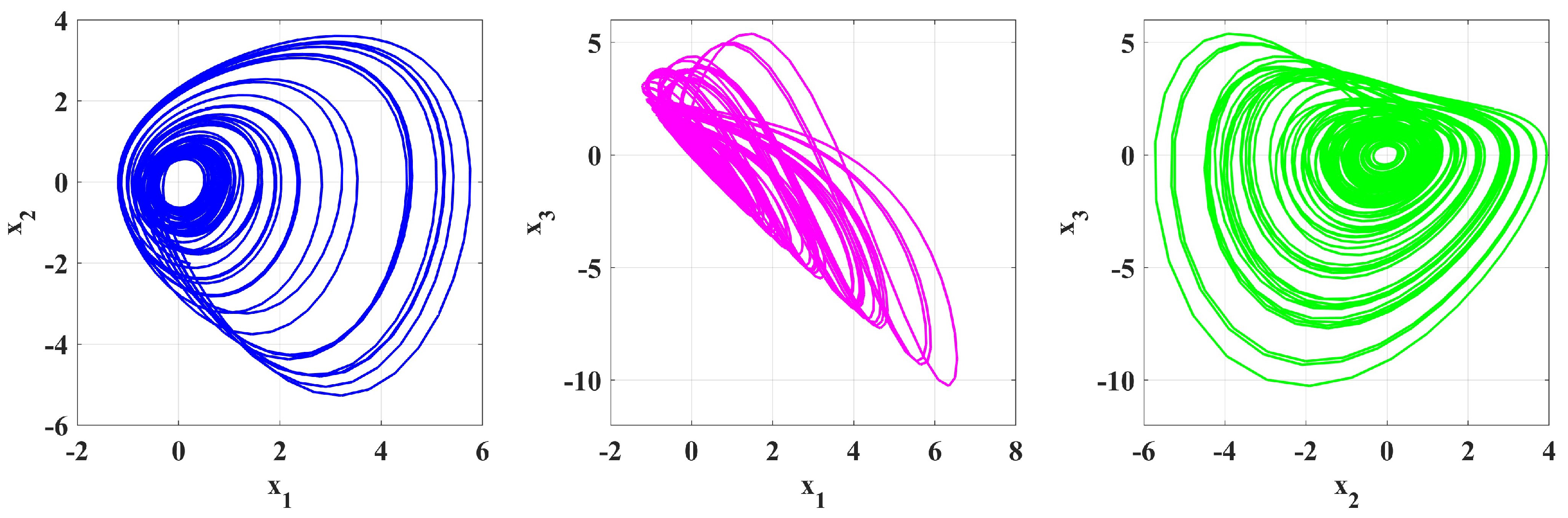
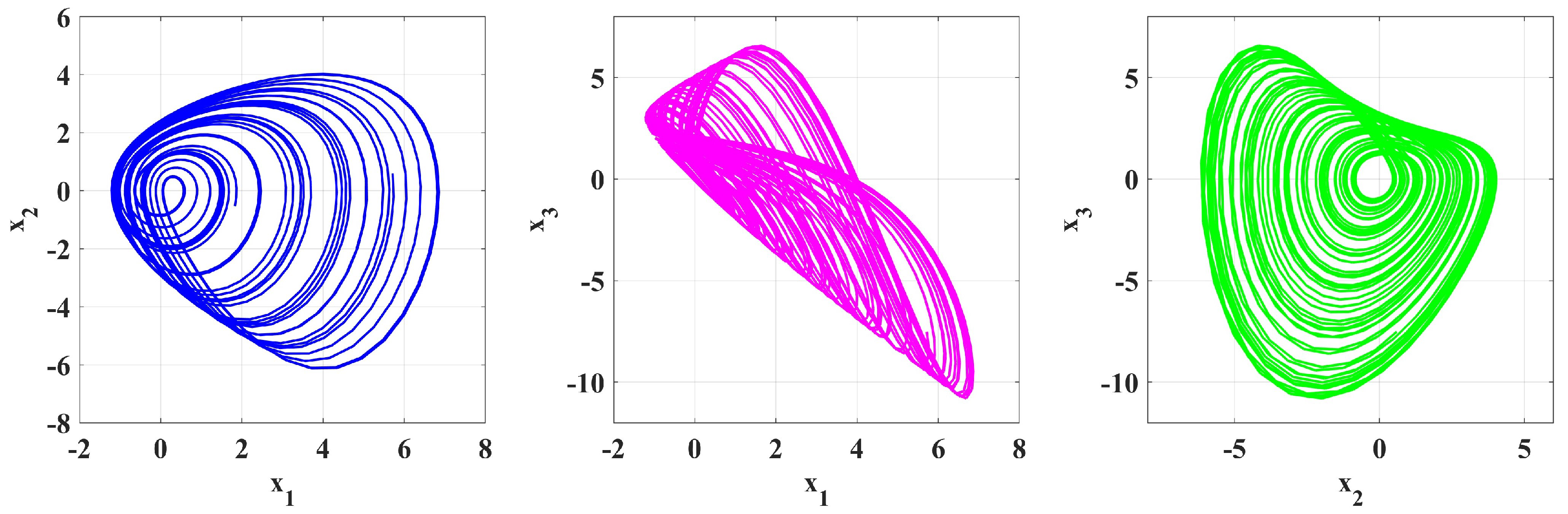
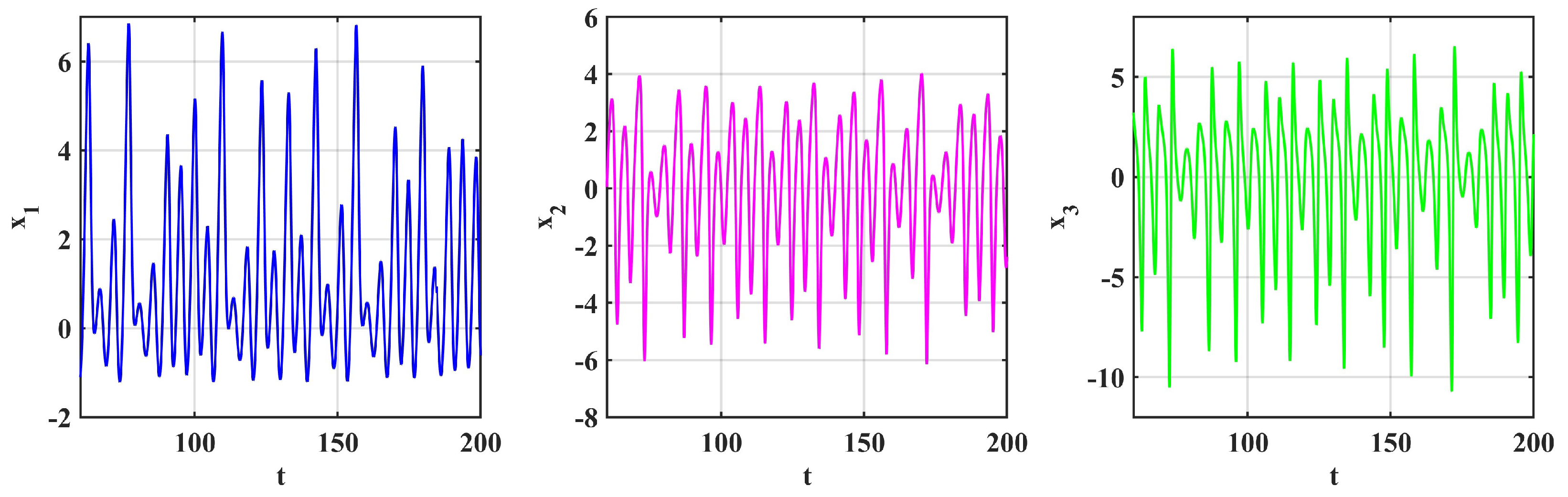
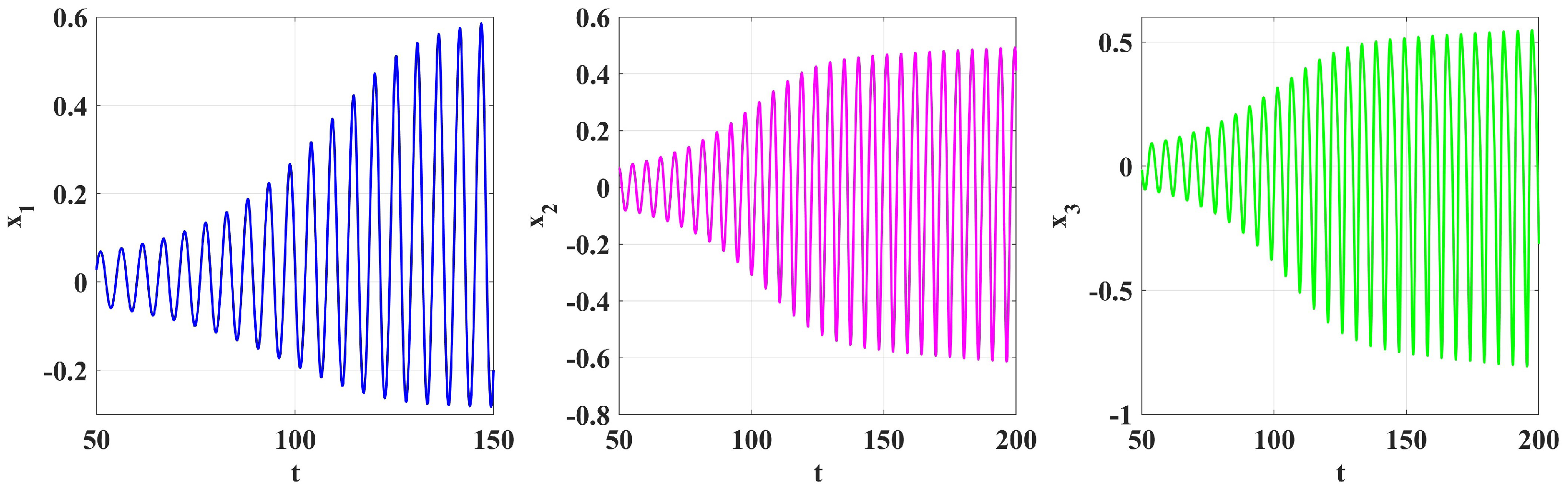
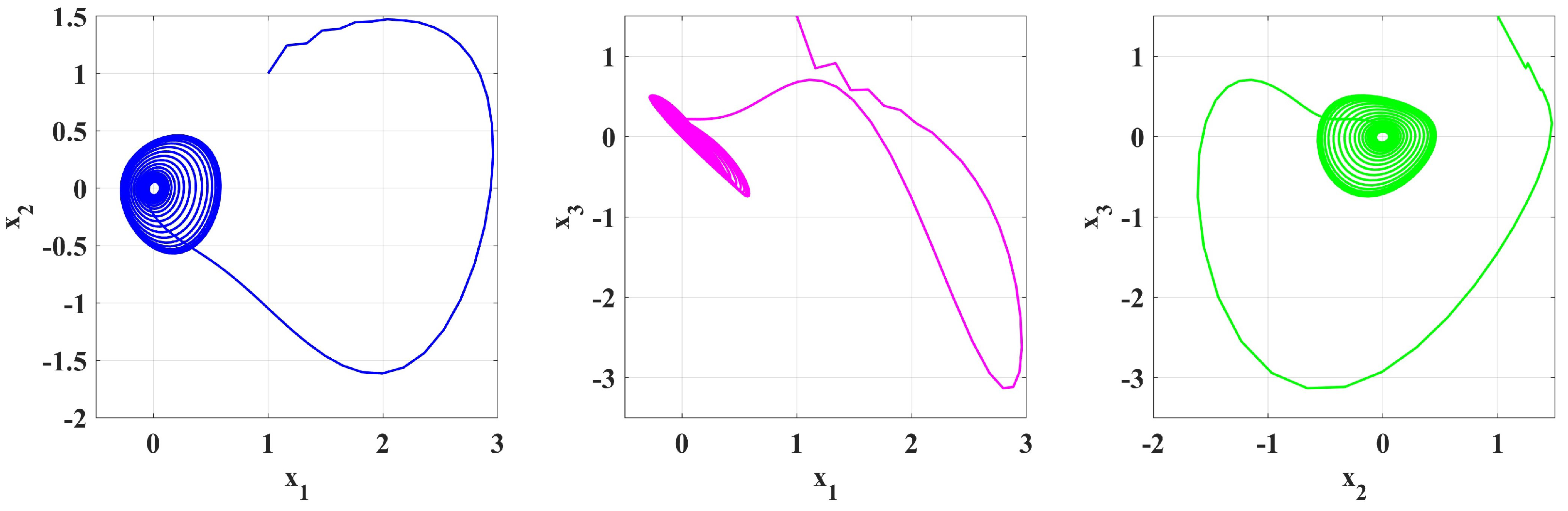
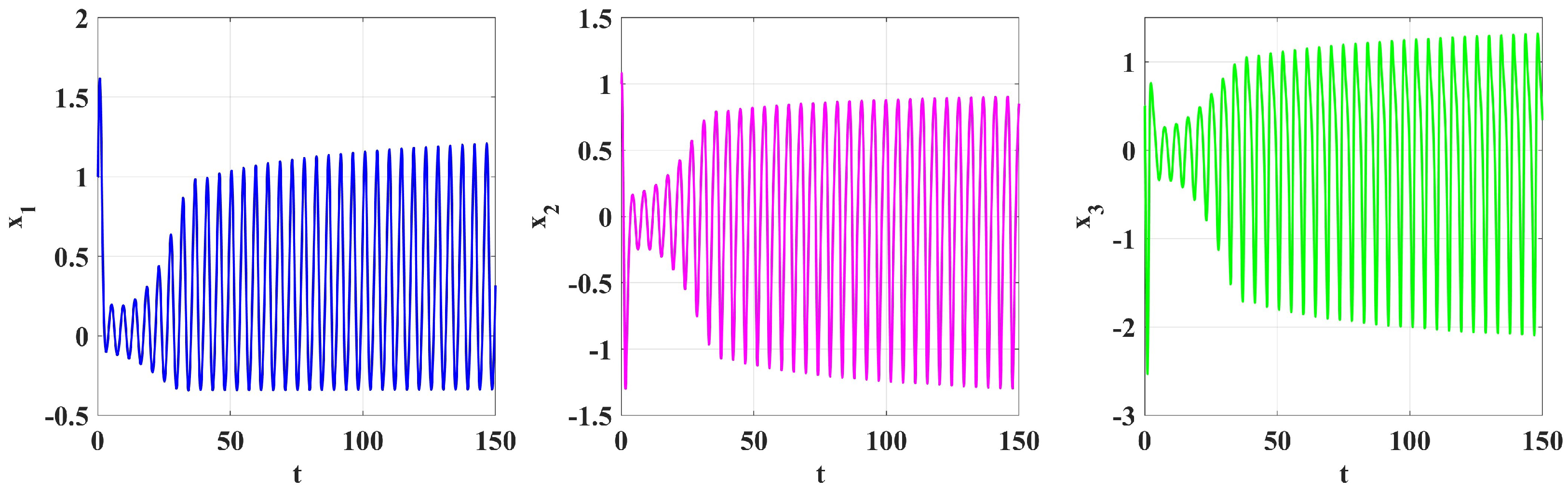
4. Numerical Simulation
5. Numerical Solutions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dalir, M.; Bashour, M. Applications of fractional calculus. Appl. Math. Sci. 2010, 4, 1021–1032. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Silva, M.F.; Barbosa, R.S.; Jesus, I.S.; Reis, C.M.; Marcos, M.G.; Galhano, A.F. Some applications of fractional calculus in engineering. Math. Probl. Eng. 2010, 2010, 639801. [Google Scholar] [CrossRef]
- Hasan, F.L.; Abdoon, M.A.; Saadeh, R.; Qazza, A.; Almutairi, D.K. Exploring analytical results for (2 + 1) dimensional breaking soliton equation and stochastic fractional Broer-Kaup system. AIMS Math. 2024, 9, 11622–11643. [Google Scholar] [CrossRef]
- Gumaa, F.E.L.; Abdoon, M.A.; Qazza, A.; Saadeh, R.; Arishi, M.A.; Degoot, A.M. Analyzing the impact of control strategies on Visceral Leishmaniasis: A mathematical modeling perspective. Eur. J. Pure Appl. Math. 2024, 17, 1213–1227. [Google Scholar] [CrossRef]
- Alsubaie, N.E.; Gumaa, F.E.L.; Boulehmi, K.; Al-Kuleab, N.; Abdoon, M.A. Improving influenza epidemiological models under Caputo fractional-order calculus. Symmetry 2024, 16, 929. [Google Scholar] [CrossRef]
- Liu, T.; Yin, X.; Liu, Q.; Hounye, A.H. Modeling SARS coronavirus-2 omicron variant dynamic via novel fractional derivatives with immunization and memory trace effects. Alex. Eng. J. 2024, 86, 174–193. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Rosół, M.; Mitkowski, W. Modeling of thermal traces using fractional order, a discrete, memory-efficient model. Energies 2022, 15, 2257. [Google Scholar] [CrossRef]
- Allagui, A.; Zhang, D.; Khakpour, I.; Elwakil, A.S.; Wang, C. Quantification of memory in fractional-order capacitors. J. Phys. D Appl. Phys. 2019, 53, 02LT03. [Google Scholar] [CrossRef]
- Rahman, Z.-A.S.; Jasim, B.H.; Al-Yasir, Y.I.A.; Hu, Y.-F.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A new fractional-order chaotic system with its analysis, synchronization, and circuit realization for secure communication applications. Mathematics 2021, 9, 2593. [Google Scholar] [CrossRef]
- Karaca, Y.; Baleanu, D. Advanced fractional mathematics, fractional calculus, algorithms and artificial intelligence with applications in complex chaotic systems. Chaos Theory Appl. 2023, 5, 257–266. [Google Scholar]
- Karaca, Y.; Baleanu, D.; Zhang, Y.-D.; Gervasi, O.; Moonis, M. Multi-Chaos, Fractal and Multi-Fractional Artificial Intelligence of Different Complex Systems; Academic Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Zhang, J.-X.; Zhang, X.; Boutat, D.; Liu, D.-Y. Fractional-Order Complex Systems: Advanced Control, Intelligent Estimation and Reinforcement Learning Image-Processing Algorithms. Fractal Fract. 2025, 9, 67. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Liu, J.; Ma, C.; Yan, H. Characteristic analysis of the fractional-order hyperchaotic complex system and its image encryption application. Signal Process. 2020, 169, 107373. [Google Scholar] [CrossRef]
- Dhakshinamoorthy, V.; Wu, G.-C.; Banerjee, S. Chaotic Dynamics of Fractional Discrete Time Systems; CRC Press: Boca Raton, FL, USA, 2024. Comput. Methods Programs Biomed. 2024, 254, 108306. [Google Scholar]
- Karaca, Y. Multi-chaos, fractal and multi-fractional AI in different complex systems. In Multi-Chaos, Fractal and Multi-Fractional Artificial Intelligence of Different Complex Systems; Elsevier: Amsterdam, The Netherlands, 2022; pp. 21–54. [Google Scholar]
- Naik, P.A.; Yavuz, M.; Qureshi, S.; Owolabi, K.M.; Soomro, A.; Ganie, A.H. Memory impacts in hepatitis C: A global analysis of a fractional-order model with an effective treatment. Comput. Methods Programs Biomed. 2024, 254, 108306. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Akgul, A.; Kacar, S. A new chaotic jerk system with two quadratic nonlinearities and its applications to electronic circuit implementation and image encryption. Int. J. Comput. Appl. Technol. 2018, 58, 89–101. [Google Scholar] [CrossRef]
- Khan, N.A.; Hameed, T.; Qureshi, M.A.; Akbar, S.; Alzahrani, A.K. Emulate the chaotic flows of fractional jerk system to scramble the sound and image memo with circuit execution. Phys. Scr. 2020, 95, 065217. [Google Scholar] [CrossRef]
- Wang, Q.; Sang, H.; Wang, P.; Yu, X.; Yang, Z. A novel 4D chaotic system coupling with dual-memristors and application in image encryption. Sci. Rep. 2024, 14, 29615. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: New York, NY, USA, 1974; p. 9780125255509. [Google Scholar]
- Solís-Pérez, J.E.; Gómez-Aguilar, J.F.; Atangana, A. Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag–Leffler laws. Chaos Solitons Fractals 2018, 114, 175–185. [Google Scholar] [CrossRef]
- Pu, Y.-F. Fractional-order Euler–Lagrange equation for fractional-order variational method: A necessary condition for fractional-order fixed boundary optimization problems in signal processing and image processing. IEEE Access 2016, 4, 10110–10135. [Google Scholar] [CrossRef]
- Ali, Z.; Rabiei, F.; Hosseini, K. Fractal-Fractional Third-Order Adams-Bashforth Method. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Bildik, N. Implementation to the Different Differential Equations of Homotopy Analysis, Differential Transformed and Adomian Decomposition Method. Int. J. Model. Optim. 2013, 3, 529–534. [Google Scholar] [CrossRef]
- Kshirsagar, K.; Nikam, V.; Gaikwad, S.; Tarate, S. Fuzzy Laplace-Adomian Decomposition method for solving Fuzzy Klein-Gordan equations. Authorea Inc. Aug. 2022. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, X.; Xu, A. Computations of Fractional Differentiation by Lagrange Interpolation Polynomial and Chebyshev Polynomial. Inf. Technol. J. 2012, 11, 557–559. [Google Scholar] [CrossRef]
- Buhader, A.A.; Abbas, M.; Imran, M.; Omame, A. Comparative analysis of a fractional co-infection model using nonstandard finite difference and two-step Lagrange polynomial methods. Partial Differ. Equ. Appl. Math. 2024, 10, 100702. [Google Scholar] [CrossRef]
- Ramalakshmi, K.; Sundaravadivoo, B. Necessary conditions for Ψ-Hilfer fractional optimal control problems and Ψ-Hilfer two-step Lagrange interpolation polynomial. Int. J. Dyn. Control 2024, 12, 42–55. [Google Scholar] [CrossRef]
- Alqahtani, A.M.; Chaudhary, A.; Dubey, R.S.; Sharma, S. Comparative analysis of the chaotic behavior of a five-dimensional fractional hyperchaotic system with constant and variable order. Fractal Fract. 2024, 8, 421. [Google Scholar] [CrossRef]
- Butt, A.I.K.; Ahmad, W.; Rafiq, M.; Baleanu, D. Numerical analysis of Atangana-Baleanu fractional model to understand the propagation of a novel corona virus pandemic. Alex. Eng. J. 2022, 61, 7007–7027. [Google Scholar] [CrossRef]
- Metsebo, J.; Abdou, B.; Ngatcha, D.T.; Ngongiah, I.K.; Kuate PD, K.; Pone JR, M. Analysis of a resistive-capacitive shunted Josephson junction with a topologically nontrivial barrier coupled to an RLC resonator. Chaos Fractals 2024, 1, 31–37. [Google Scholar]
- Bucio, A.; Tututi-Hernández, E.S.; Uriostegui-Legorreta, U. Analysis of the dynamics of a ϕ6 Duffing-type jerk system. Chaos Theory Appl. 2024, 6, 83–89. [Google Scholar] [CrossRef]
- Khan, A.; Li, C.; Zhang, X.; Cen, X. A two-memristor-based chaotic system with symmetric bifurcation and multistability. Chaos Fractals 2025, 2, 1–7. [Google Scholar] [CrossRef]
- Uddin, M.J.; Santra, P.K.; Rana SM, S.; Mahapatra, G. Chaotic dynamics of the fractional-order predator-prey model incorporating Gompertz growth on prey with Ivlev functional response. Chaos Theory Appl. 2024, 6, 192–204. [Google Scholar] [CrossRef]
- Berir, M. The impact of white noise on chaotic behavior in a financial fractional system with constant and variable order: A comparative study. Eur. J. Pure Appl. Math. 2024, 17, 3915–3931. [Google Scholar] [CrossRef]
- Saadeh, R.; Alshawabkeh, A.; Khalil, R.; Abdoon, M.A.; Taha, N.; Almutairi, D.K. The Mohanad transforms and their applications for solving systems of differential equations. Eur. J. Pure Appl. Math. 2024, 17, 385–409. [Google Scholar] [CrossRef]











| t | ||||||
|---|---|---|---|---|---|---|
| 0.1 | 1.0932 × | 1.1245 × | 1.0626 × | 1.0671 × | 3.9601 × | 2.2078 × |
| 0.2 | 1.2005 × | 1.2457 × | 1.0718 × | 1.0426 × | −1.9971 × | −4.1661 × |
| 0.3 | 1.3057 × | 1.3525 × | 1.0249 × | 9.5204 × | −7.2662 × | −9.3524 × |
| 0.4 | 1.4038 × | 1.4410 × | 9.2847 × | 8.1158 × | −1.1916 × | −1.3645 × |
| 0.5 | 1.4900 × | 1.5081 × | 7.8847 × | 6.3263 × | −1.5986 × | −1.7175 × |
| 0.6 | 1.5603 × | 1.5512 × | 6.1058 × | 4.2439 × | −1.9493 × | −2.0006 × |
| 0.7 | 1.6111 × | 1.5688 × | 4.0043 × | 1.9499 × | −2.2439 × | −2.2170 × |
| t | ||||||
|---|---|---|---|---|---|---|
| 1 | 1.5461 × | 1.0528 × | −4.6564 × | −4.0319 × | −2.6415 × | −1.4560 × |
| 2 | −9.6185 × | 3.4253 × | −2.2333 × | −8.5266 × | −3.7468 × | −5.7021 × |
| 3 | −1.6461 × | −2.5476 × | −5.3530 × | −5.0005 × | 2.8885 × | 4.7622 × |
| 4 | −5.1768 × | −2.3635 × | 2.1918 × | 3.1486 × | 1.8046 × | 6.3339 × |
| 5 | 1.7941 × | 3.5612 × | 1.6917 × | 5.8622 × | −2.4392 × | −3.6333 × |
| 6 | 1.5734 × | 6.3555 × | −1.8629 × | −2.2307 × | −3.3700 × | −1.1683 × |
| 7 | −2.6922 × | −4.1635 × | −2.6922 × | −1.0130 × | 1.5979 × | −2.0649 × |
| t | ||||||
|---|---|---|---|---|---|---|
| 1 | 1.6063 × | 1.4367 × | −3.8731 × | −4.5189 × | −2.7526 × | −2.3366 × |
| 2 | −3.7173 × | −8.3611 × | −2.4818 × | −2.0085 × | -5.7797 × | −4.3764 × |
| 3 | −2.0052 × | −1.5927 × | −8.0047 × | −6.0809 × | 3.4659 × | 2.7873 × |
| 4 | −8.9017 × | −6.7934 × | 2.8041 × | 2.3353 × | 2.7171 × | 2.1559 × |
| 5 | 2.4279 × | 2.4279 × | 2.8496 × | 2.8496 × | −2.9542 × | −2.9542 × |
| 6 | 2.8804 × | 2.4213 × | −2.3374 × | −2.0177 × | −5.8337 × | −4.9237 × |
| 7 | −1.4437 × | −1.2749 × | −4.9013 × | −4.2551 × | 1.8122 × | 1.5147 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allogmany, R.; Almuallem, N.A.; Alsemiry, R.D.; Abdoon, M.A. Exploring Chaos in Fractional Order Systems: A Study of Constant and Variable-Order Dynamics. Symmetry 2025, 17, 605. https://doi.org/10.3390/sym17040605
Allogmany R, Almuallem NA, Alsemiry RD, Abdoon MA. Exploring Chaos in Fractional Order Systems: A Study of Constant and Variable-Order Dynamics. Symmetry. 2025; 17(4):605. https://doi.org/10.3390/sym17040605
Chicago/Turabian StyleAllogmany, Reem, Nada A. Almuallem, Reima Daher Alsemiry, and Mohamed A. Abdoon. 2025. "Exploring Chaos in Fractional Order Systems: A Study of Constant and Variable-Order Dynamics" Symmetry 17, no. 4: 605. https://doi.org/10.3390/sym17040605
APA StyleAllogmany, R., Almuallem, N. A., Alsemiry, R. D., & Abdoon, M. A. (2025). Exploring Chaos in Fractional Order Systems: A Study of Constant and Variable-Order Dynamics. Symmetry, 17(4), 605. https://doi.org/10.3390/sym17040605








