Efficient Parallel Ray Tracing Algorithm for Electromagnetic Scattering in Inhomogeneous Plasma Using Graphic Processing Unit
Abstract
:1. Introduction
2. The Theoretical Approach
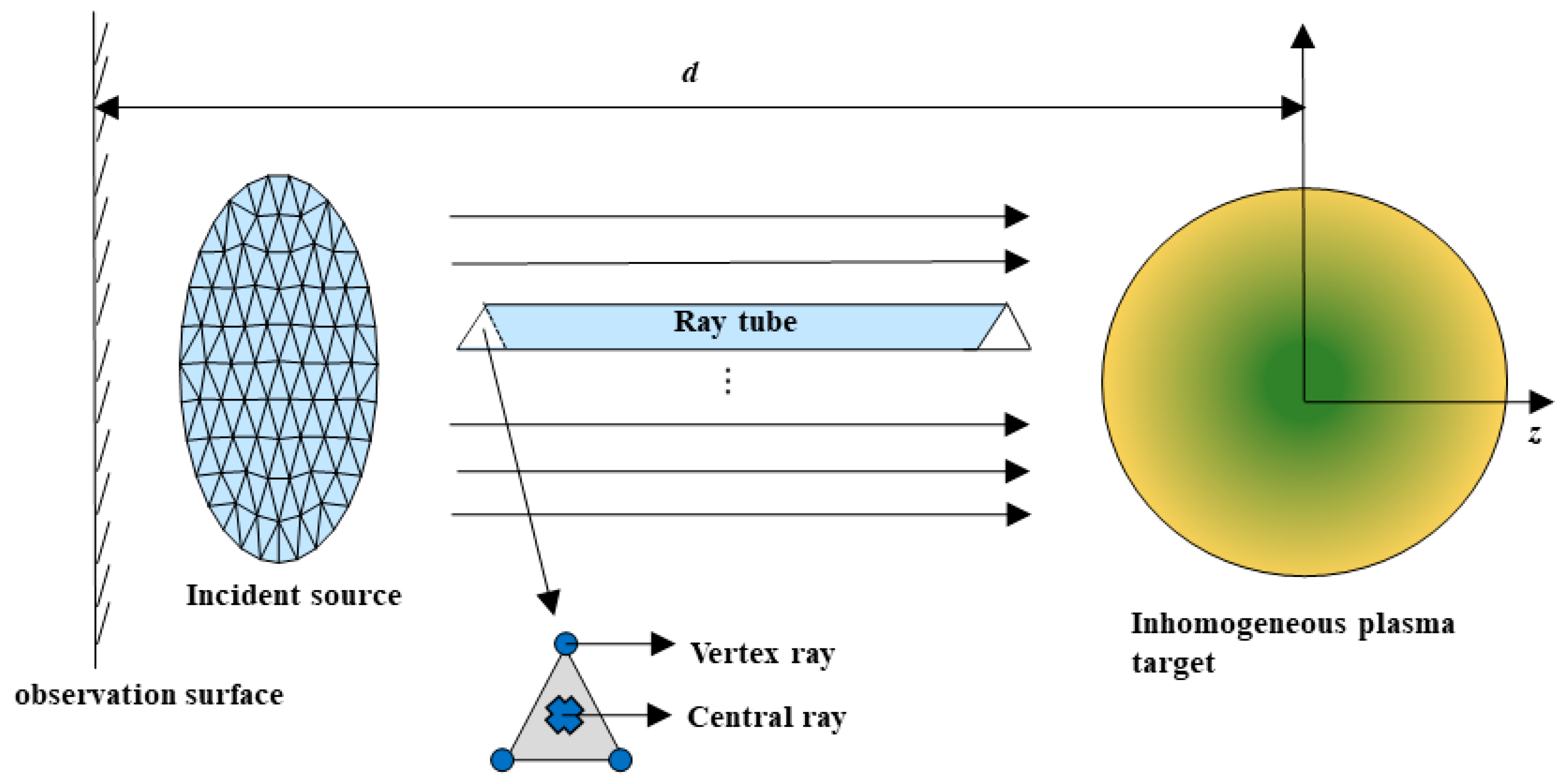
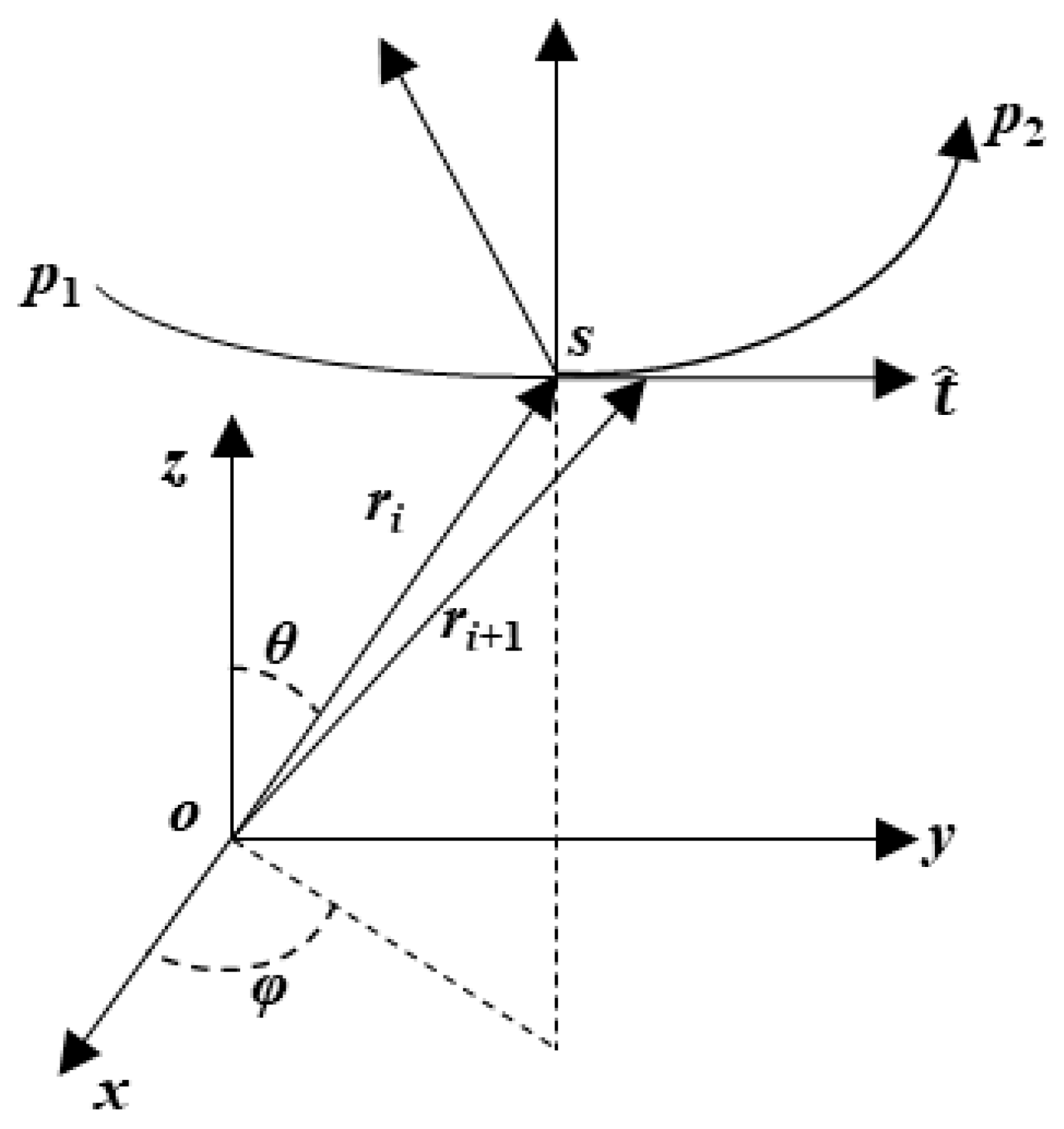
2.1. RT Theoretical for In-Homogeneous Plasma in Scattering Simulation
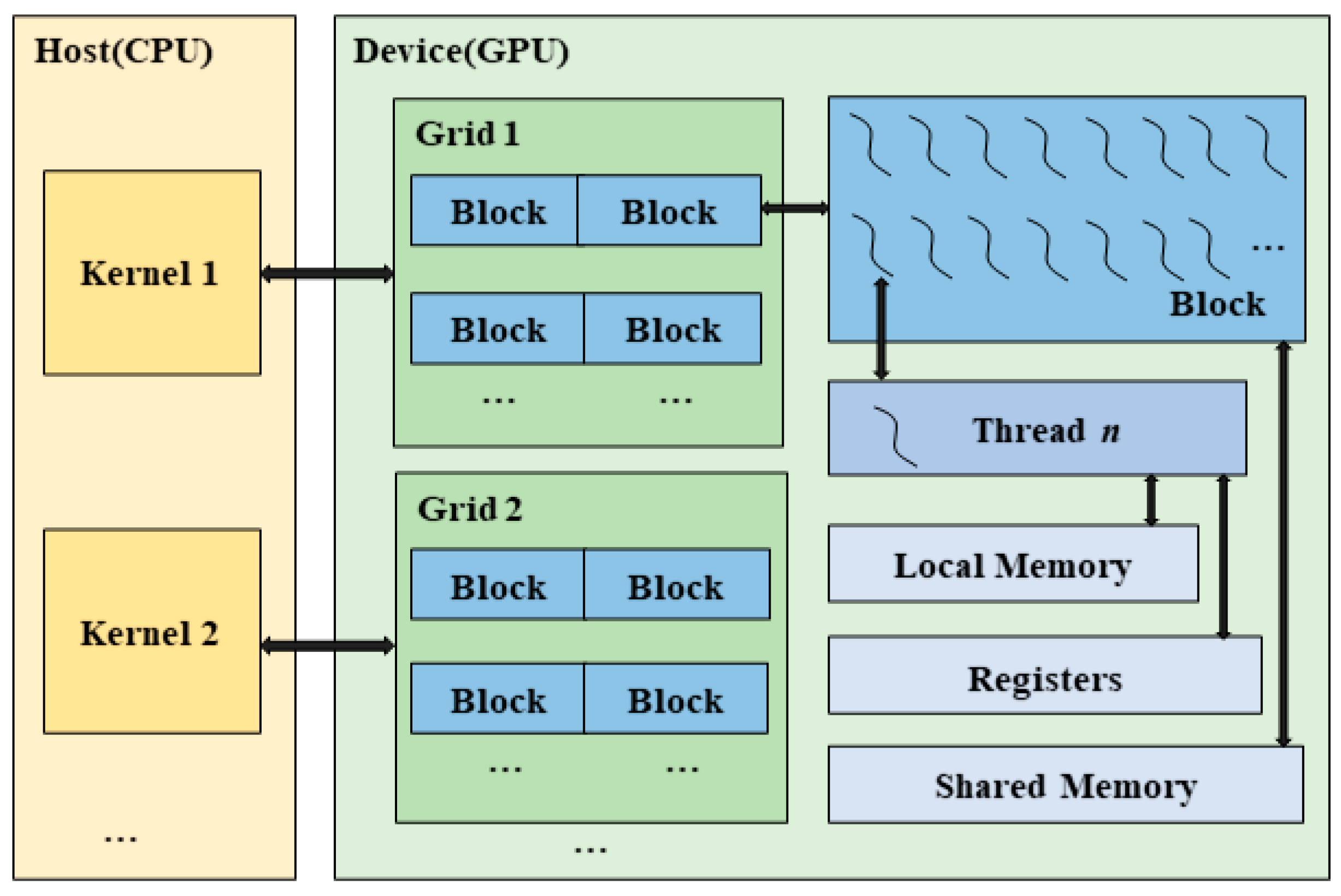
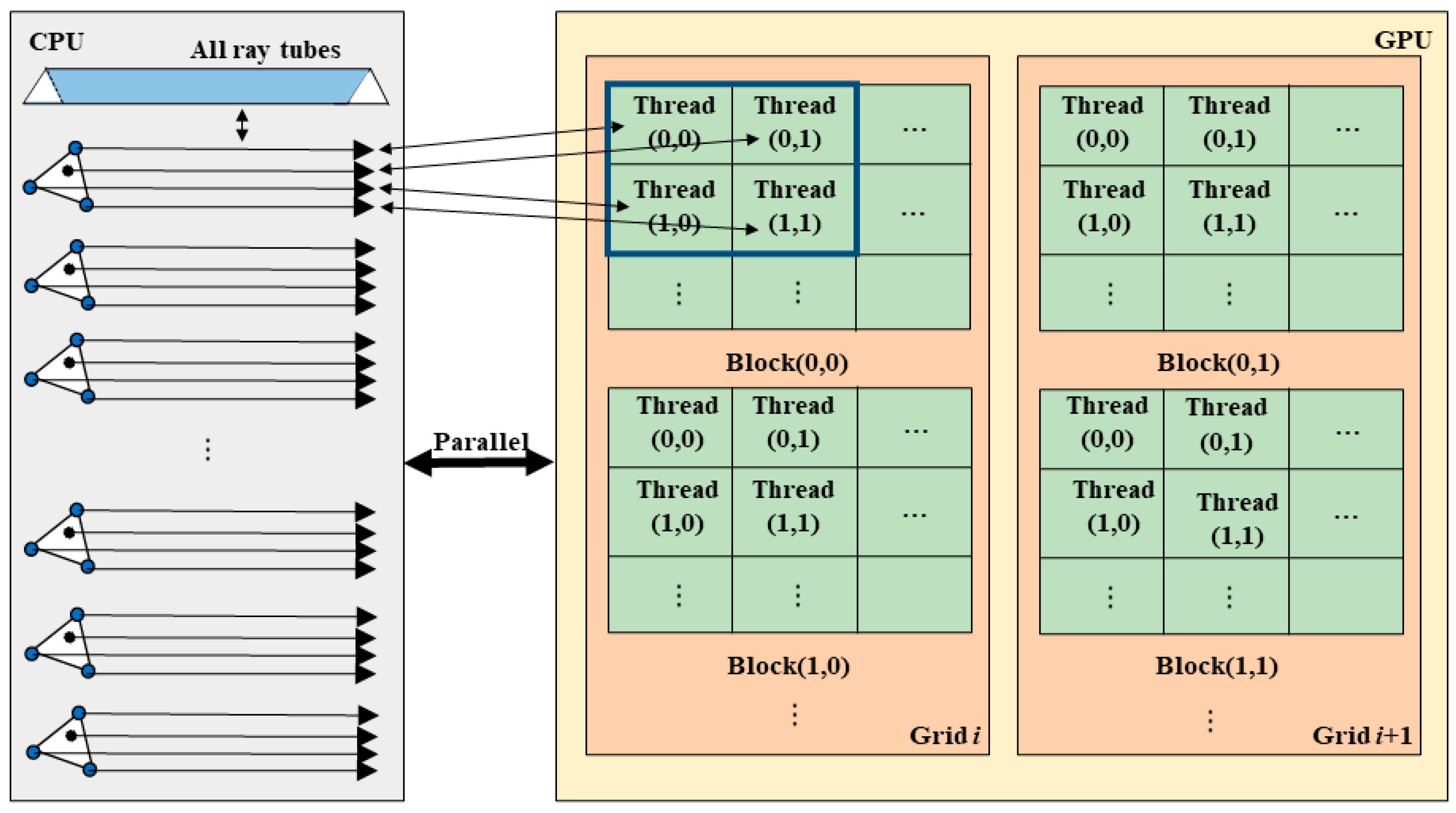
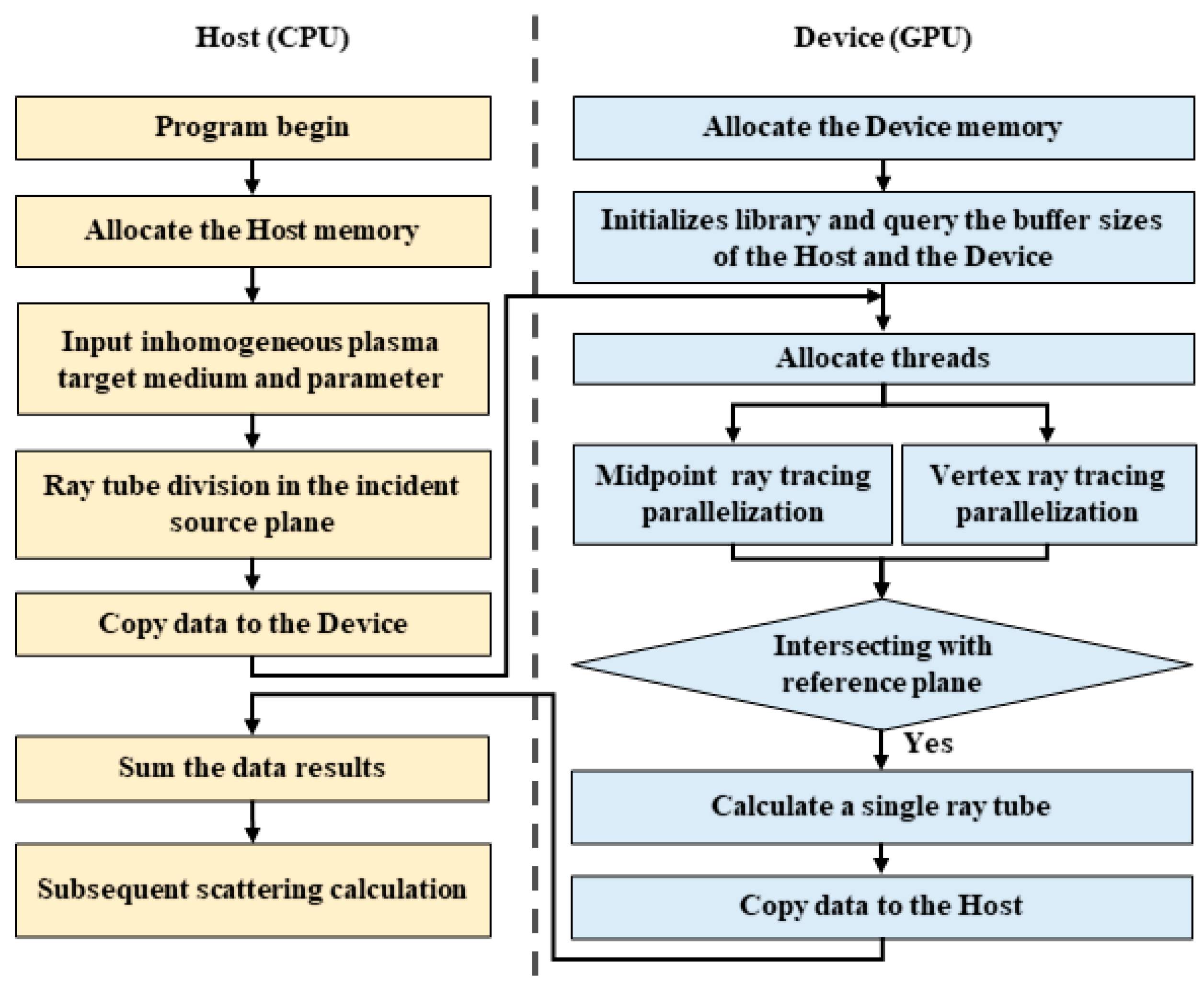
2.2. GPU Parallel Implementation of RT Method
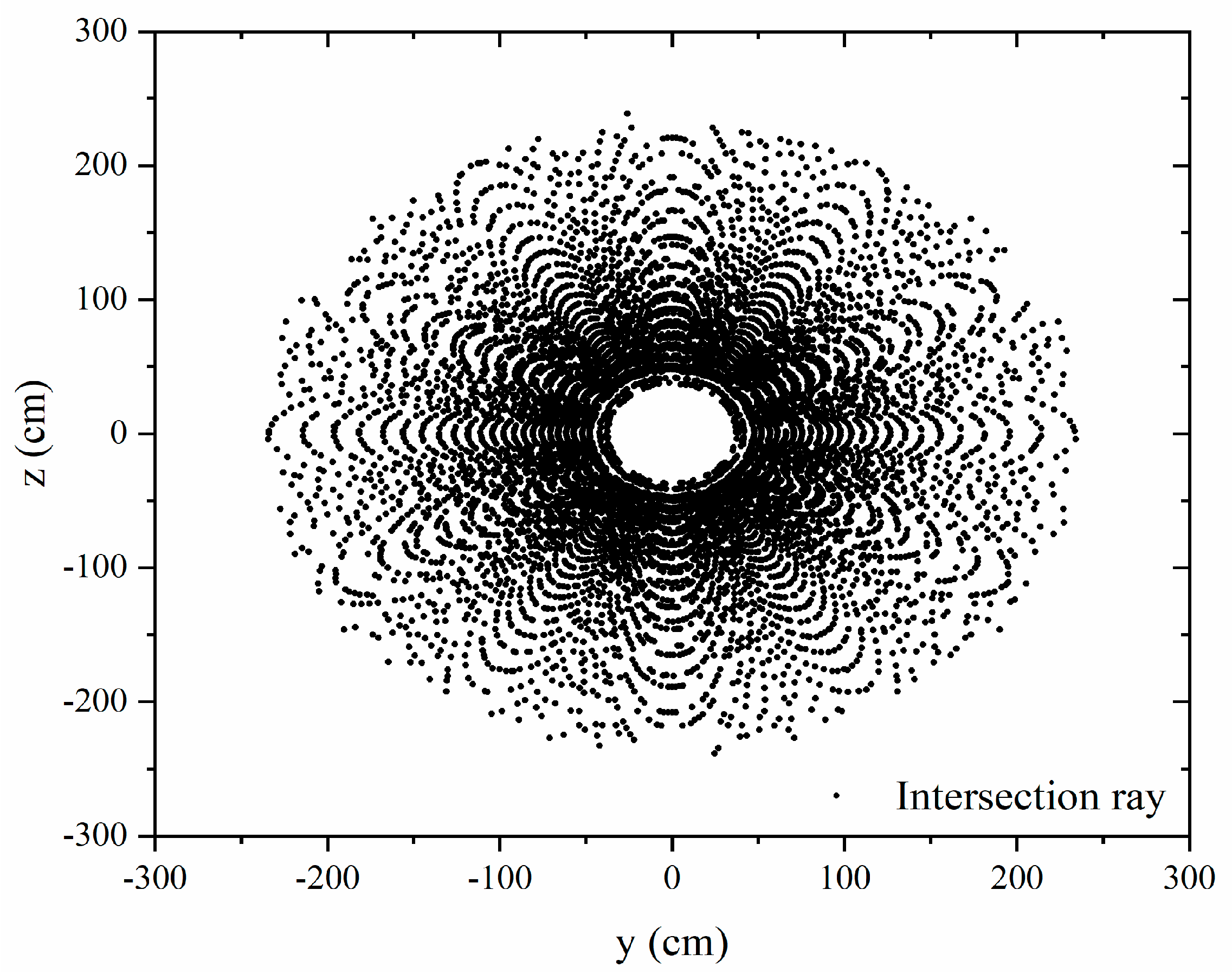
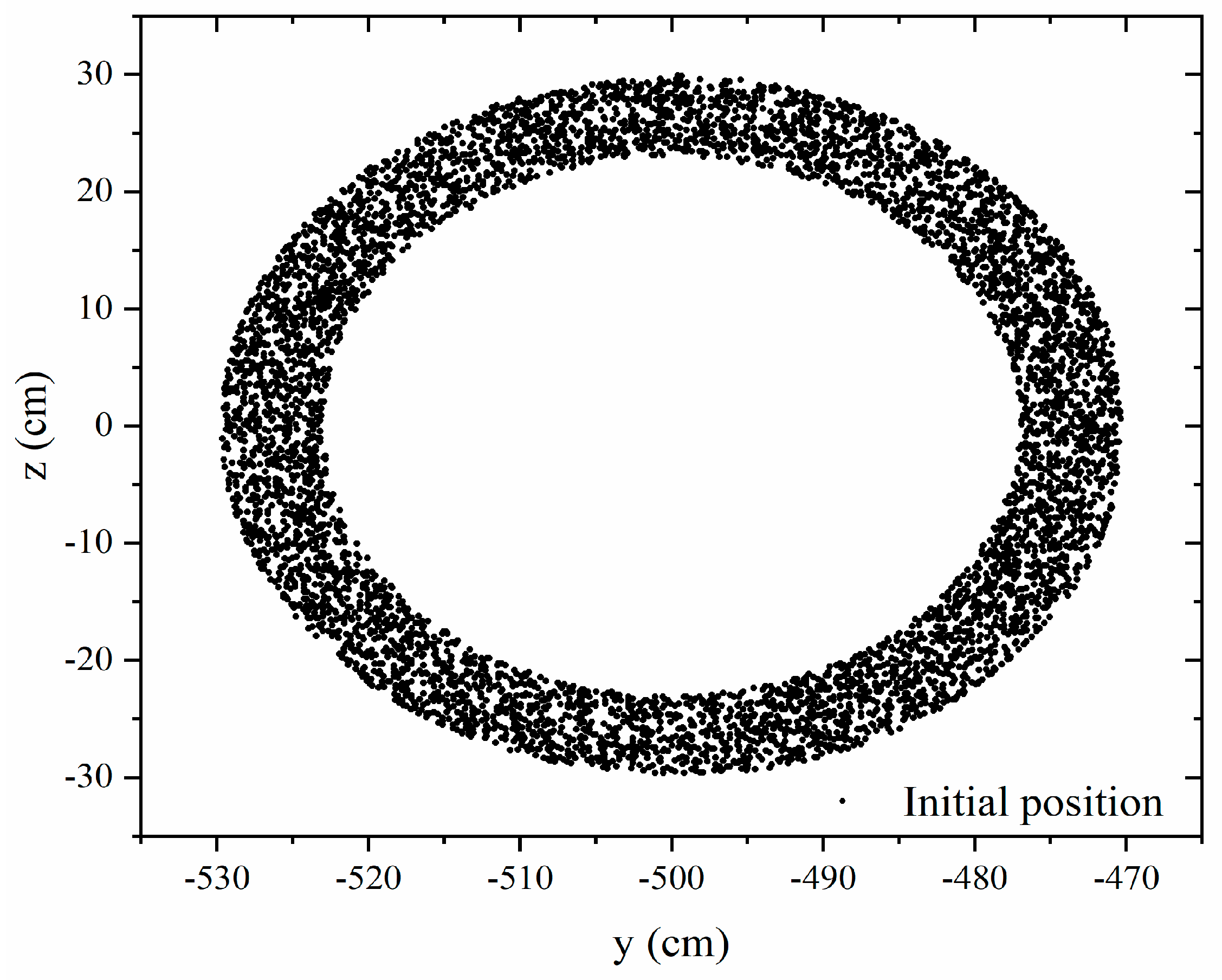
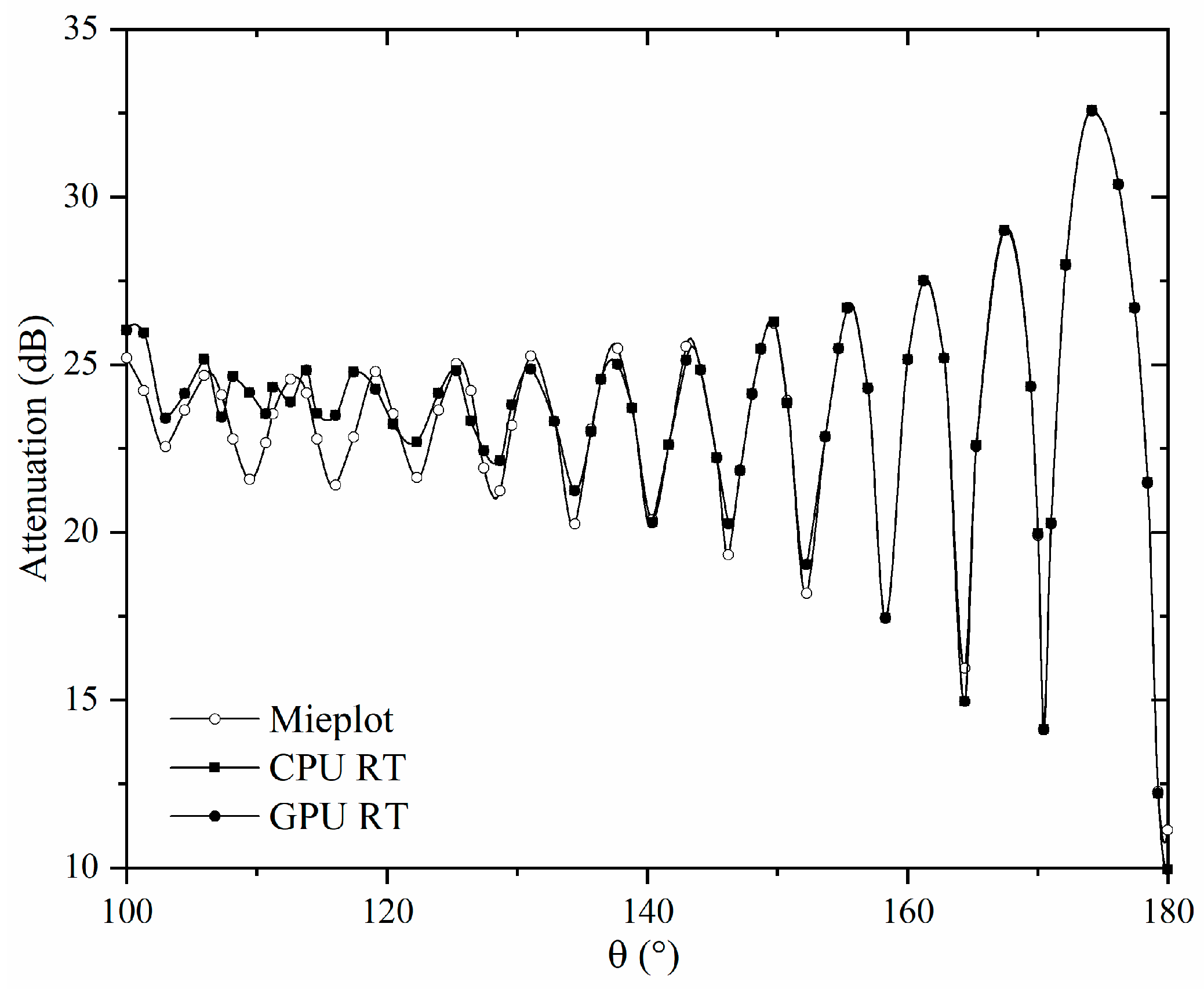
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RT | Ray Tracing |
| GPU | Graphic Processing unit |
| CUDA | Compute Unified Device Architecture |
| EM | Electromagnetic |
References
- Wang, Z.; Guo, L.; Li, J. Analysis of Echo Characteristics of Spatially Inhomogeneous and Time-Varying Plasma Sheath. IEEE Trans. Plasma Sci. 2021, 49, 1804–1811. [Google Scholar] [CrossRef]
- Cheng, G.; Liu, L. Direct Finite-Difference Analysis of the Electromagnetic-Wave Propagation in Inhomogeneous Plasma. IEEE Trans. Plasma Sci. 2010, 38, 3109–3115. [Google Scholar] [CrossRef]
- Khojeh, G.; Abdoli-Arani, A. Scattering and resonant frequency of a toroidal plasma covered by a dielectric layer. Chin. J. Phys. 2022, 77, 945–955. [Google Scholar] [CrossRef]
- Chen, K.; Xu, D.; Li, J.; Zhong, K.; Yao, J. Studies on the propagation properties of THz wave in inhomogeneous dusty plasma sheath considering scattering process. Results Phys. 2021, 24, 104109. [Google Scholar] [CrossRef]
- Yang, X. Modeling and Simulation of Wideband Radio Waves Traveling Through Plasma Coupling with Uniform Magnetic Fields. IEEE Trans. Plasma Sci. 2022, 50, 3824–3829. [Google Scholar] [CrossRef]
- Song, L.; Li, X.; Liu, Y. Effect of Time-Varying Plasma Sheath on Hypersonic Vehicle-Borne Radar Target Detection. IEEE Sens. J. 2021, 21, 16880–16893. [Google Scholar] [CrossRef]
- Ouyang, W.; Ding, C.; Liu, Q.; Lu, Q.; Wu, Z. Influence analysis of uncertainty of chemical reaction rate under different reentry heights on the plasma sheath and terahertz transmission characteristics. Results Phys. 2023, 53, 106983. [Google Scholar] [CrossRef]
- Cong, Z.; Chen, R.; He, Z. Numerical modeling of EM scattering from plasma sheath: A review. Eng. Anal. Bound. Elem. 2022, 135, 73–92. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, G.; Zheng, Z. Propagation of terahertz waves in a magnetized, collisional, and inhomogeneous plasma with the scattering matrix method. Optik 2019, 182, 618–624. [Google Scholar] [CrossRef]
- Ding, Y.; Bai, B.; Gao, H.; Niu, G.; Shen, F.; Liu, Y.; Li, X. An Analysis of Radar Detection on a Plasma Sheath Covered Reentry Target. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4255–4268. [Google Scholar] [CrossRef]
- Chung, S. FDTD simulations on radar cross sections of metal cone and plasma covered metal cone. Vacuum 2012, 86, 970–984. [Google Scholar] [CrossRef]
- Zhang, D.; Liao, W.; Sun, X.; Chen, W.; Yang, L. Study on the Electromagnetic Scattering Characteristics of Time-Varying Dusty Plasma Target in the BGK Collision Model-TM Case. IEEE Trans. Plasma Sci. 2025, 53, 116–121. [Google Scholar] [CrossRef]
- Singh, A.; Walia, K. Self-focusing of Gaussian laser beam in collisionless plasma and its effect on stimulated Brillouin scattering process. Opt. Commun. 2013, 290, 175–182. [Google Scholar] [CrossRef]
- Xiang, H.; Chen, J.; Ni, X.; Chen, Y.; Zeng, X.; Gu, T. Numerical Investigation on Interference and Absorption of Electromagnetic Waves in the Plasma-Covered Cavity Using FDTD Method. IEEE Trans. Plasma Sci. 2012, 40, 1010–1018. [Google Scholar] [CrossRef]
- Wei, B.; Li, L.; Yang, Q.; Ge, D. Analysis of the transmission characteristics of radio waves in inhomogeneous weakly ionized dusty plasma sheath based on high order SO-DGTD. Results Phys. 2017, 7, 2582–2587. [Google Scholar] [CrossRef]
- Chen, W.; Guo, L.; Li, J.; Liu, S. Research on the FDTD Method of Electromagnetic Wave Scattering Characteristics in Time-Varying and Spatially Nonuniform Plasma Sheath. IEEE Trans. Plasma Sci. 2016, 44, 3235–3242. [Google Scholar] [CrossRef]
- Zhang, M.; Liao, C.; Xiong, X.; Ye, Z.; Li, Y. Solution and design technique for beam waveguide antenna system by using a parallel hybrid-dimensional FDTD method. IEEE Antennas Wirel. Propag. Lett. 2016, 16, 364–368. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Gray, A.; Giannakis, I.; Patterson, A.; Wetter, L.; Hamrah, A. A CUDA-based GPU engine for gprMax: Open source FDTD electromagnetic simulation software. Comput. Phys. Commun. 2019, 237, 208–218. [Google Scholar] [CrossRef]
- Kim, K.H.; Park, Q.H. Overlapping computation and communication of three-dimensional FDTD on a GPU cluster. Comput. Phys. Commun. 2012, 183, 2364–2369. [Google Scholar] [CrossRef]
- Gunawardana, M.; Kordi, B. GPU and CPU-based parallel FDTD methods for frequency-dependent transmission line models. IEEE Lett. Electromag. 2022, 4, 66–70. [Google Scholar] [CrossRef]
- Liu, S.; Zou, B.; Zhang, L.; Ren, S. A multi-GPU accelerated parallel domain decomposition one-step leapfrog ADI-FDTD. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 816–820. [Google Scholar] [CrossRef]
- Stefanski, T.; Drysdale, T.D. Parallel ADI-BOR-FDTD algorithm. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 722–724. [Google Scholar] [CrossRef]
- Francés, J.; Otero, B.; Bleda, S.; Gallego, S.; Beléndez, A. Multi-GPU and multi-CPU accelerated FDTD scheme for vibroacoustic applications. Comput. Phys. Commun. 2015, 191, 43–51. [Google Scholar] [CrossRef]
- Zhou, Q.; Xu, W.; Feng, Z. A Coupled FEM-MPM GPU-based algorithm and applications in geomechanics. Comput. Geotech. 2022, 151, 104982. [Google Scholar] [CrossRef]
- Sellami, H.; Cazenille, L.; Fujii, T.; Hagiya, M.; Aubert-Kato, N.; Genot, A.J. Accelerating the Finite-Element Method for Reaction-Diffusion Simulations on GPUs with CUDA. Micromachines 2020, 11, 881. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Q.; Fu, S.; Wang, X.; Qiu, X.; Wu, H. Hybrid Full-Wave Analysis of Surface Acoustic Wave Devices for Accuracy and Fast Performance Prediction. Micromachines 2021, 12, 5. [Google Scholar] [CrossRef]
- Kee, C.Y.; Wang, C.F. Efficient GPU Implementation of the High-Frequency SBR-PO Method. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 941–944. [Google Scholar] [CrossRef]
- Gökkaya, E.; Saynak, U. An Approach for RCS Estimation Based on SBR Implemented on GPU. In Proceedings of the 2024 32nd Signal Processing and Communications Applications Conference (SIU), Mersin, Turkiye, 15–18 May 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Wu, X.; Su, L.; Wang, K.; Li, Y. GPU-accelerated Calculation of Acoustic Echo Characteristics of Underwater Targets. In Proceedings of the 2020 Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 14–16 April 2020; pp. 227–231. [Google Scholar] [CrossRef]
- Huo, J.; Xu, L.; Shi, X.; Yang, Z. An Accelerated Shooting and Bouncing Ray Method Based on GPU and Virtual Ray Tube for Fast RCS Prediction. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1839–1843. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, D. Research on Ray Tracing Algorithm and Acceleration Techniques using KD-tree. In Proceedings of the 2021 6th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 9–11 April 2021; pp. 107–110. [Google Scholar] [CrossRef]
- Yang, M.; Jia, J. Implementation and Optimization of Hardware-Universal Ray-tracing Underlying Algorithm Based on GPU Programming. In Proceedings of the 2023 6th International Conference on Artificial Intelligence and Big Data (ICAIBD), Chengdu, China, 26–29 May 2023; pp. 171–178. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Huang, J.; Wang, C.X. A Novel GPU Acceleration Algorithm Based on CUDA and MPI for Ray Tracing Wireless Channel Modeling. In Proceedings of the 2023 IEEE Wireless Communications and Networking Conference (WCNC), Glasgow, UK, 26–29 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Breglia, A.; Capozzoli, A.; Curcio, C.; Liseno, A. Ultrafast ray tracing for electromagnetics via kD-tree and BVH on GPU. In Proceedings of the 2015 31st International Review of Progress in Applied Computational Electromagnetics (ACES), Williamsburg, VA, USA, 22–26 March 2015; pp. 1–2. [Google Scholar]
- Meng, X.; Guo, L.; Fan, T. Parallelized TSM-RT Method for the Fast RCS Prediction of the 3-D Large-Scale Sea Surface by CUDA. IEEE J. Sel. Top. Appl. Earth. 2015, 8, 4795–4804. [Google Scholar] [CrossRef]

| (Pn, Tn) | CPU Serial | GPU Parallel (RTX 4060) | GPU Parallel (RTX 4090) |
|---|---|---|---|
| (1452, 2774) | 90.5 s | 8.8 s | 5.6 s |
| (2267, 4347) | 140.0 s | 12.9 | 7.9 s |
| (9062,17,813) | 577.5 s | 25.9 | 8.7 s |
| (36,268, 71,898) | 2358.9 s | 40.3 s | 10.0 s |
| (284,151, 565,796) | 15875.4 s | 271.1 s | 48.5 s |
| NVIDIA GeForce RTX Graphics Card | (1452, 2774) | (2267, 4347) | (9062, 17,813) | (36,268, 71,898) | (284,151, 565,796) |
|---|---|---|---|---|---|
| RTX 4060 | 10.3× | 10.8× | 22.3× | 58.5× | 52.6× |
| RTX 4090 | 16.2× | 17.7× | 66.4× | 235.9× | 327.3× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; He, X.; Wei, B. Efficient Parallel Ray Tracing Algorithm for Electromagnetic Scattering in Inhomogeneous Plasma Using Graphic Processing Unit. Symmetry 2025, 17, 627. https://doi.org/10.3390/sym17040627
Wang Y, He X, Wei B. Efficient Parallel Ray Tracing Algorithm for Electromagnetic Scattering in Inhomogeneous Plasma Using Graphic Processing Unit. Symmetry. 2025; 17(4):627. https://doi.org/10.3390/sym17040627
Chicago/Turabian StyleWang, Yijing, Xinbo He, and Bing Wei. 2025. "Efficient Parallel Ray Tracing Algorithm for Electromagnetic Scattering in Inhomogeneous Plasma Using Graphic Processing Unit" Symmetry 17, no. 4: 627. https://doi.org/10.3390/sym17040627
APA StyleWang, Y., He, X., & Wei, B. (2025). Efficient Parallel Ray Tracing Algorithm for Electromagnetic Scattering in Inhomogeneous Plasma Using Graphic Processing Unit. Symmetry, 17(4), 627. https://doi.org/10.3390/sym17040627






