Multi-Stage Stochastic Planning for Transmission Systems Considering Dynamic Frequency Stability
Abstract
:1. Introduction
1.1. Background and Challenge
1.2. State-of-the-Art Review
1.3. Research Gaps
1.4. Primary Focus and Contributions
2. Mathematical Formulation
2.1. Multi-Stage Stochastic Framework
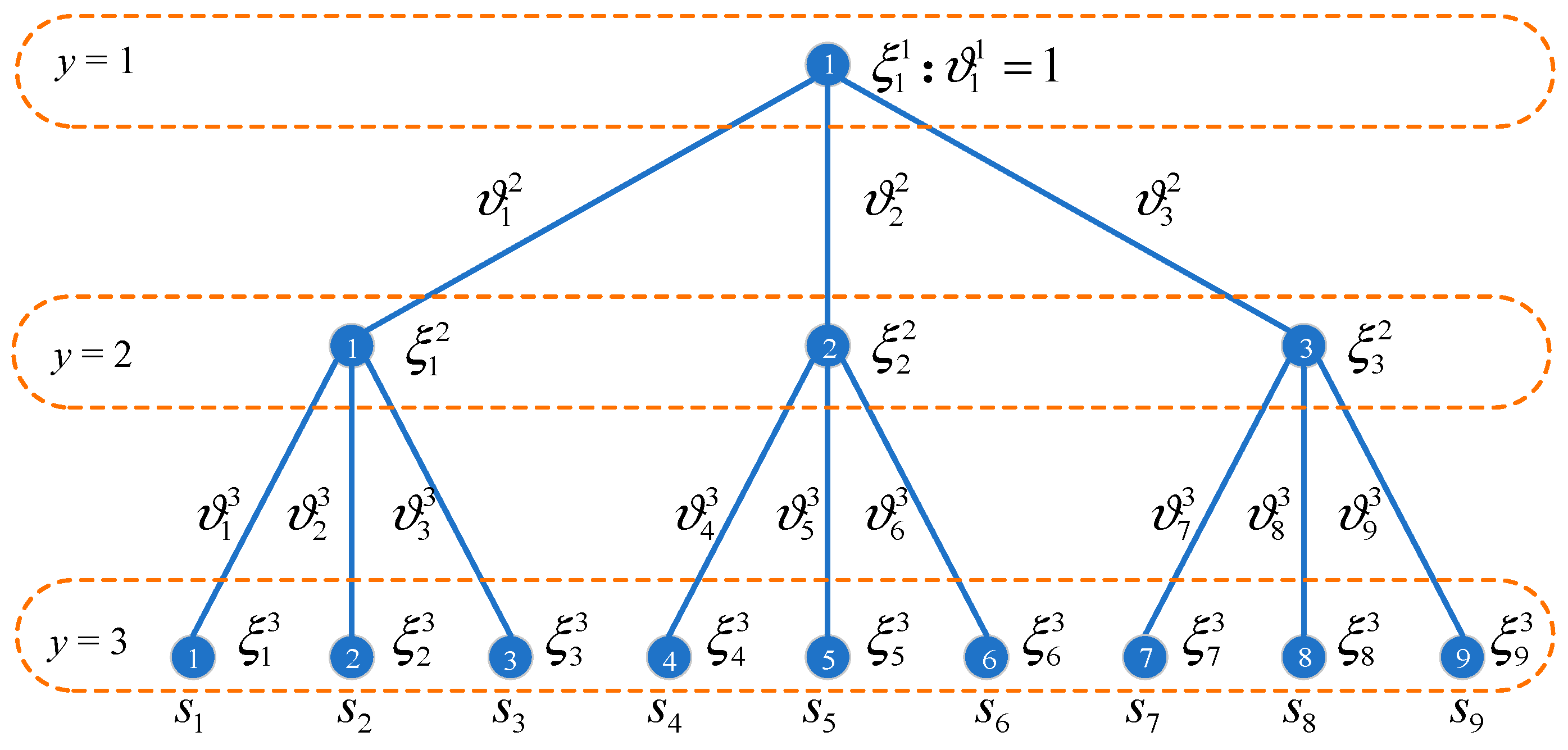
2.1.1. Scenario Tree for the Stage-by-Stage Uncertainty
2.1.2. Decision-Making Procedure
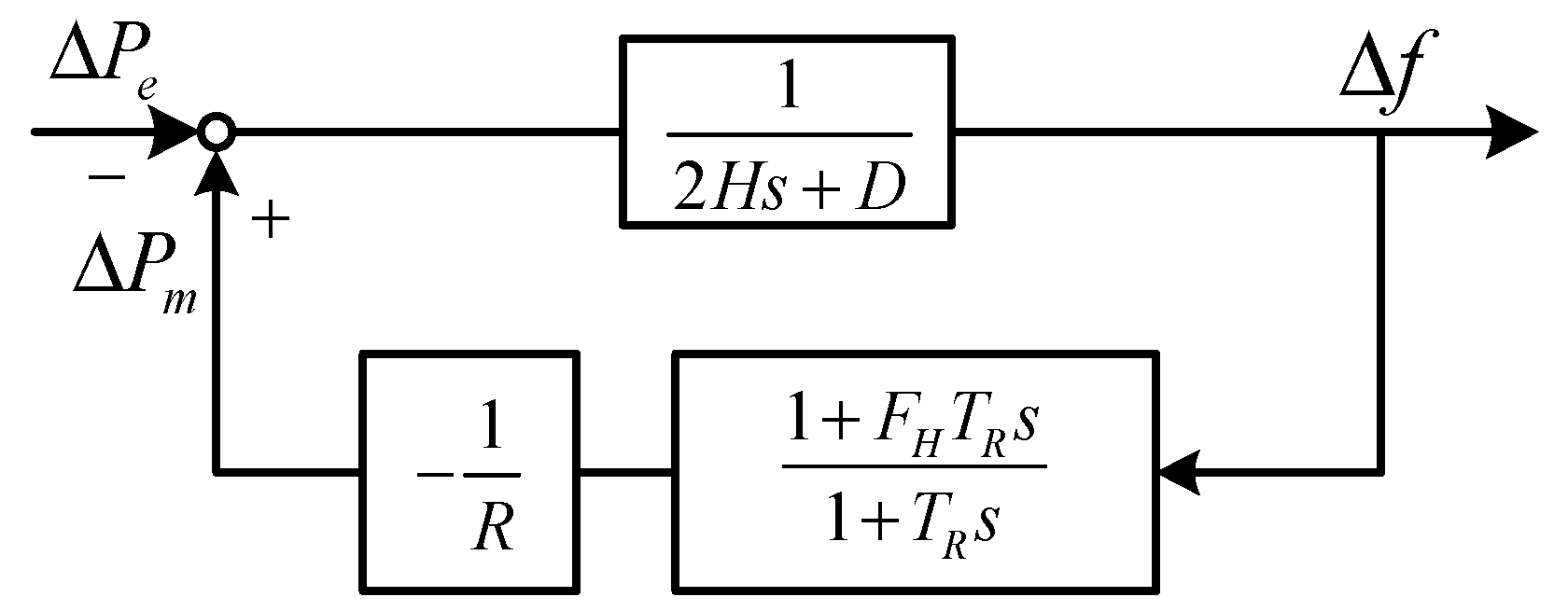
2.2. Dynamic Frequency Stability Constraints
2.3. Multi-Stage Stochastic Model Formulation
2.3.1. Objective Function
2.3.2. Limits on the Planning Decisions
2.3.3. Limits on the Power Balance
2.3.4. Limits on the Power Flow
2.3.5. Limits on the Power Outputs of RG and SG
2.3.6. Dynamic Frequency Stability
2.3.7. Nonanticipativity Constraints
3. Solution Method
3.1. Model Linearization
3.2. Model Decomposition
| Algorithm 1: Progressive hedging algorithm | |
| , Lagrange-multiplier vectors . . | |
| (36) | |
| in (35). in (37). | |
| (37) | |
| , and repeat iteration from step 2. | |
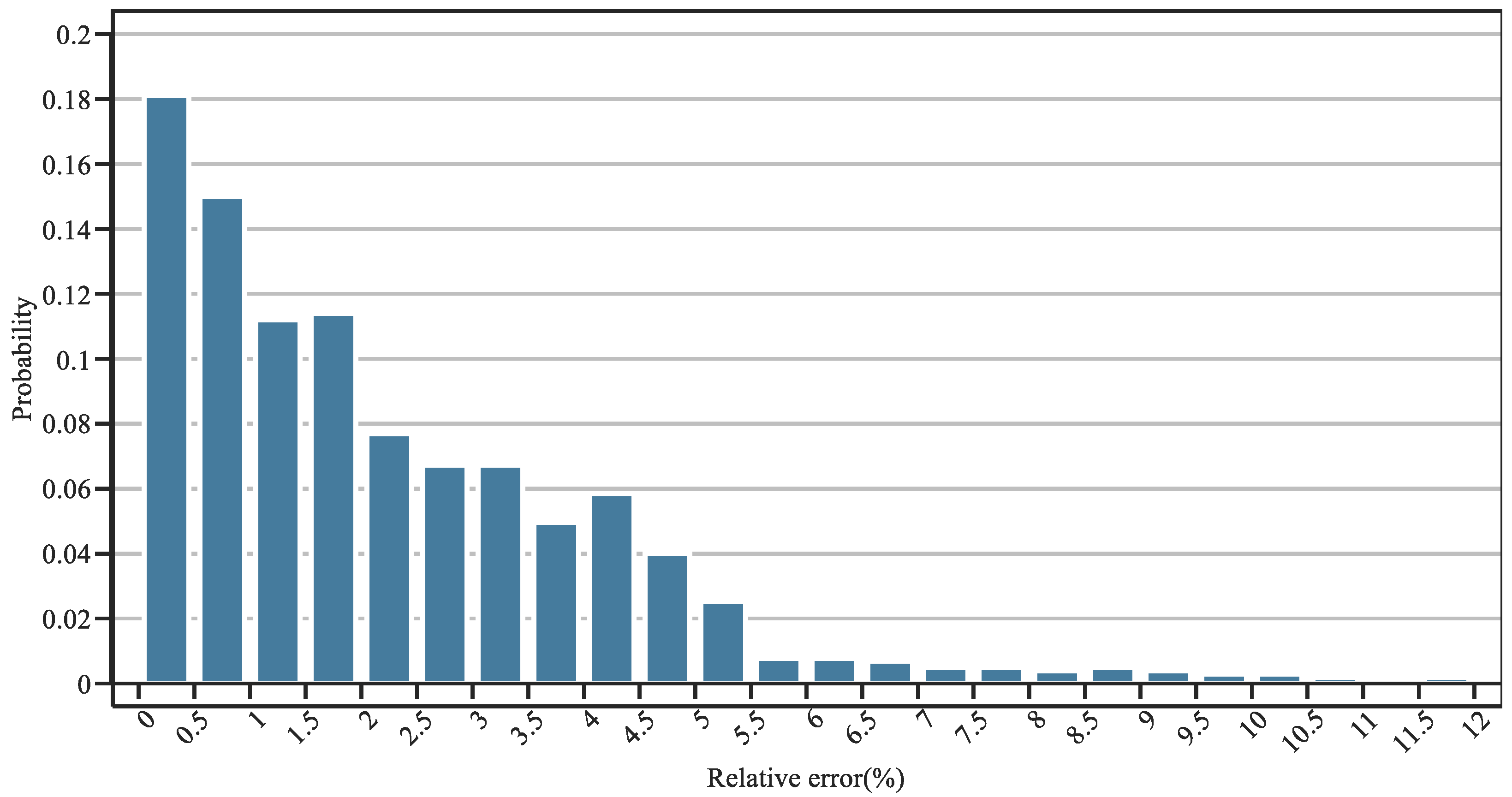
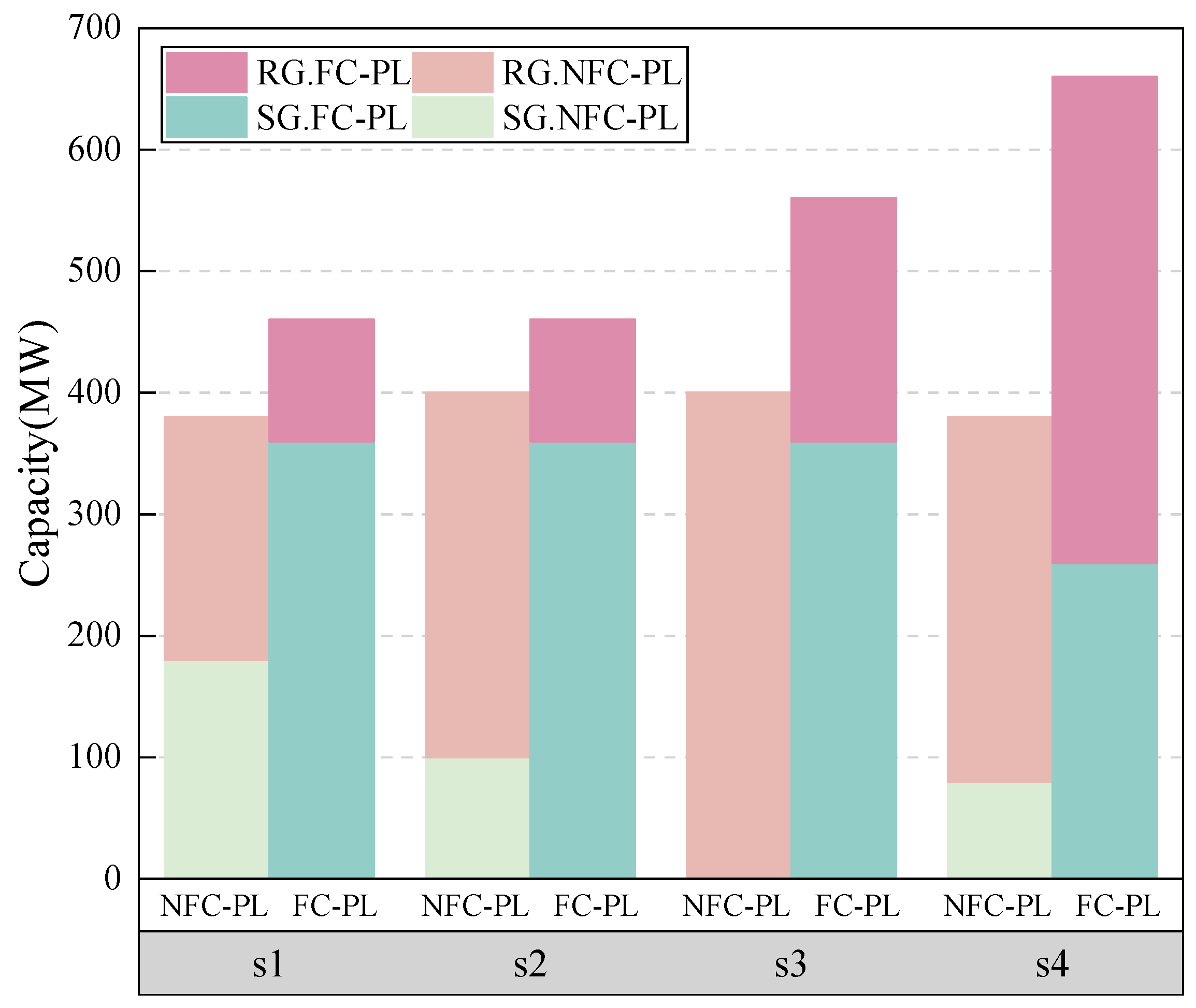
4. Case Studies
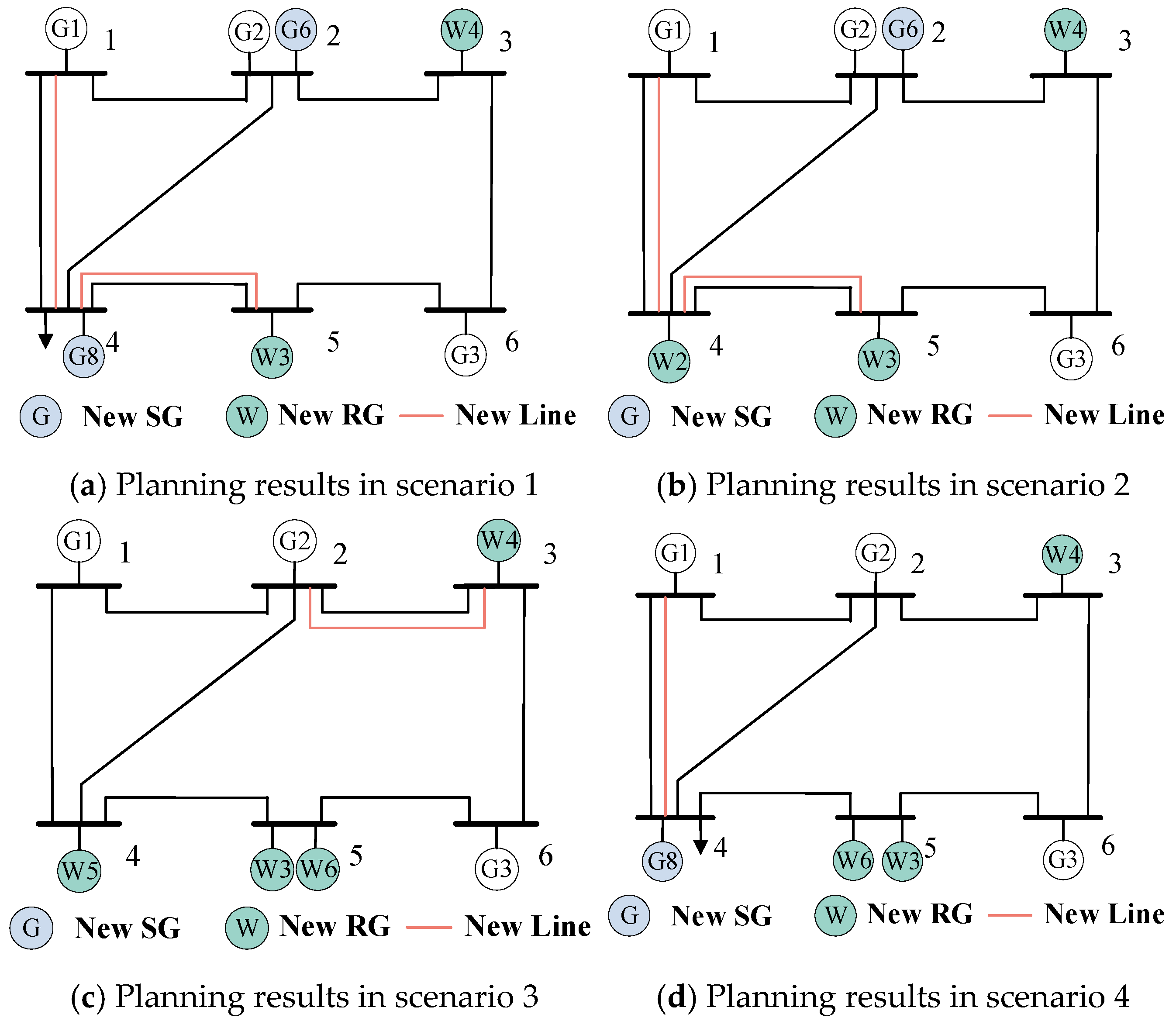
4.1. Simulations on Six-Bus Transmission System
4.1.1. Effectiveness of the Multi-Stage Planning Method
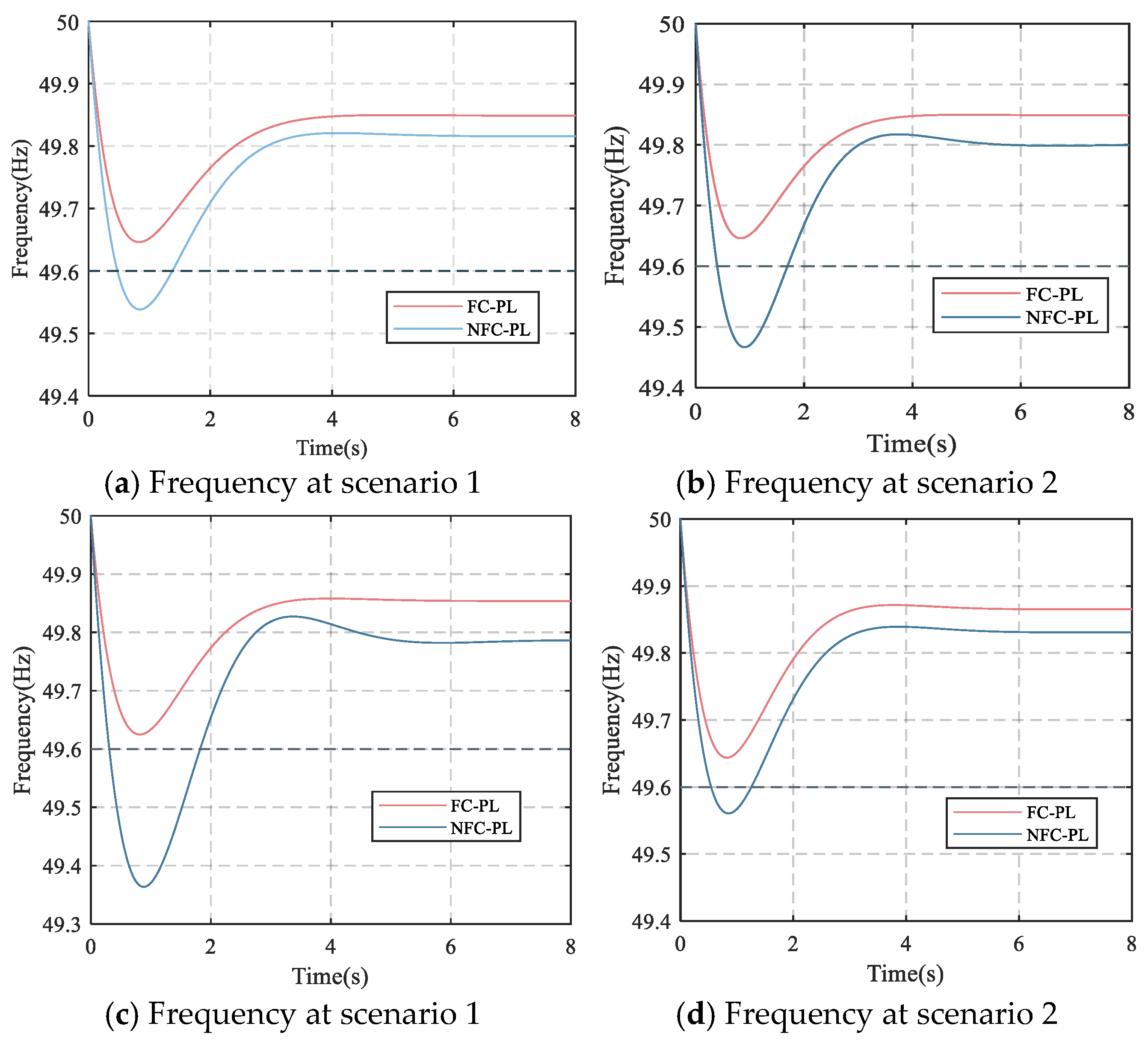
4.1.2. Effectiveness to Address the Frequency Stability
4.1.3. Effectiveness of the Decomposition Method
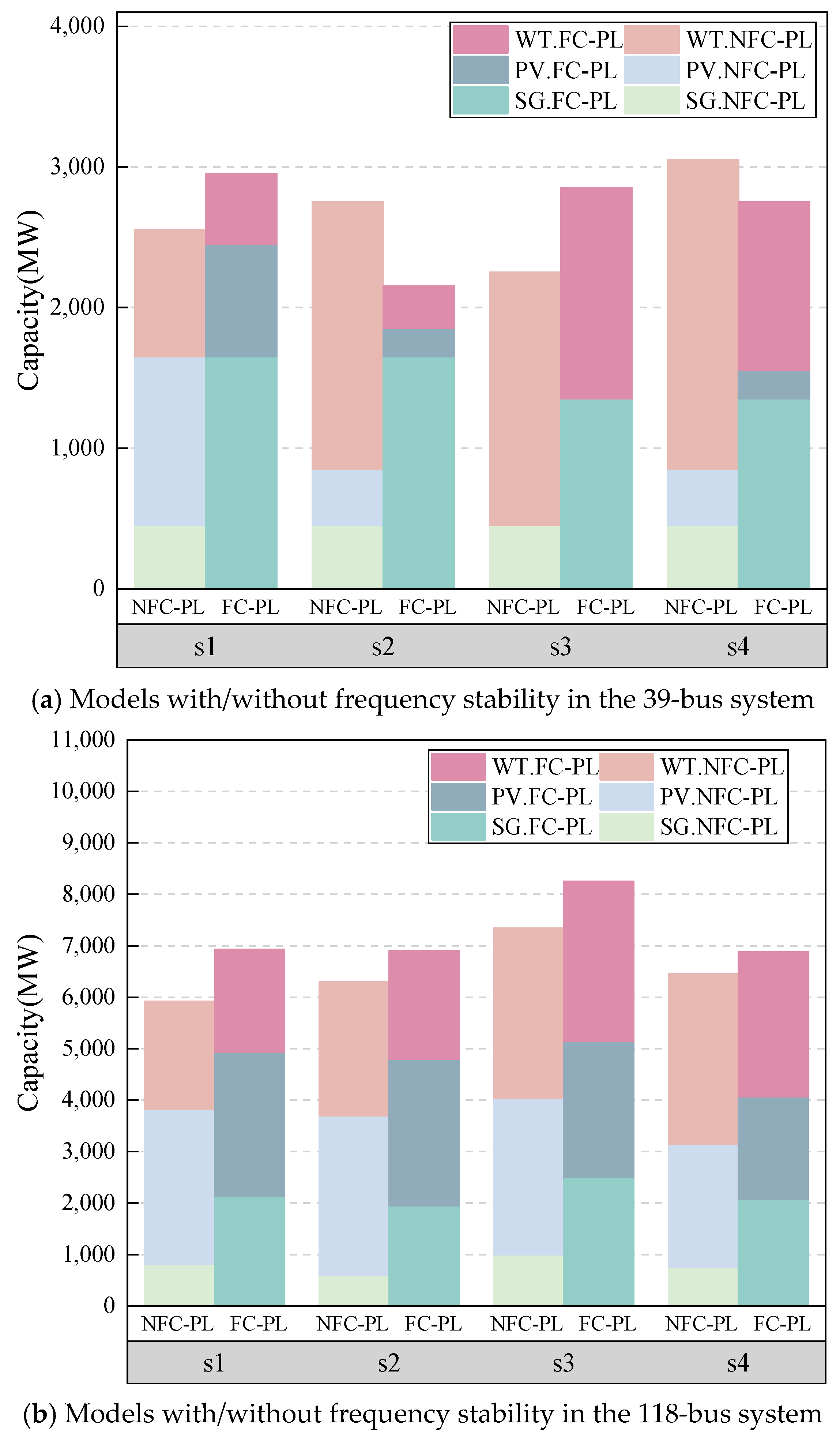
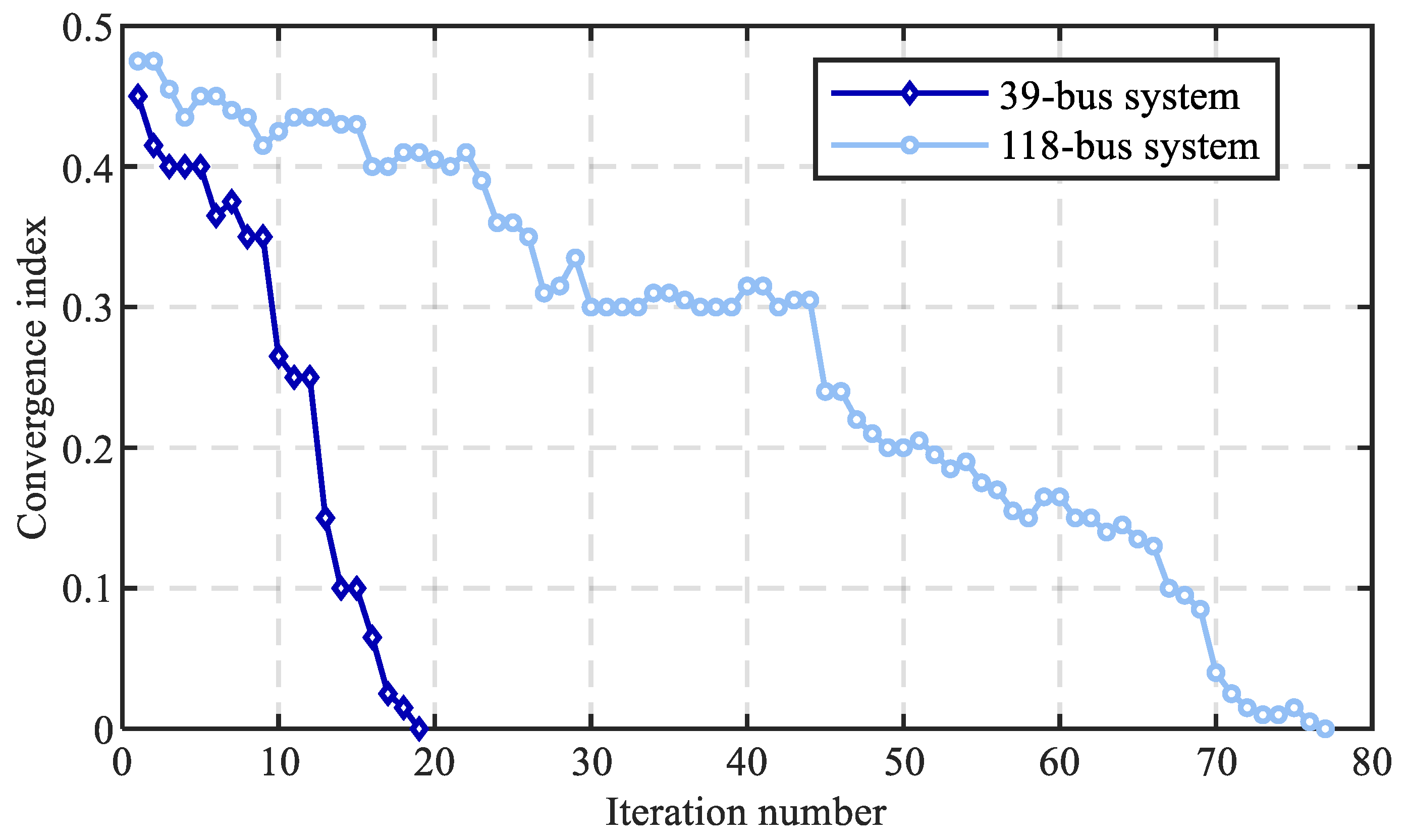
4.2. Simulations on 39-Bus and 118-Bus Transmission Systems
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Zhang, G.; Zhang, F.; Meng, K.; Dong, Z.Y. A distributed calculation method for robust day-ahead scheduling of integrated electricity-gas systems. Int. J. Electr. Power Energy Syst. 2022, 136, 107636. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, F.; Ding, L.; Meng, K.; Dong, Z.Y. Wind Farm Level Coordination for Optimal Inertial Control with a Second-Order Cone Predictive Model. IEEE Trans. Sustain. Energy 2021, 12, 2353–2366. [Google Scholar] [CrossRef]
- Golshani, A.; Sun, W.; Zhou, Q.; Zheng, Q.P.; Hou, Y. Incorporating Wind Energy in Power System Restoration Planning. IEEE Trans. Smart Grid 2019, 10, 16–28. [Google Scholar] [CrossRef]
- Hu, J.; Xu, X.; Ma, H.; Yan, Z. Distributionally Robust Co-optimization of Transmission Network Expansion Planning and Penetration Level of Renewable Generation. J. Mod. Power Syst. Clean Energy 2022, 10, 577–587. [Google Scholar] [CrossRef]
- Roldán, C.; Mínguez, R.; García-Bertrand, R.; Arroyo, J.M. Robust Transmission Network Expansion Planning Under Correlated Uncertainty. IEEE Trans. Power Syst. 2019, 34, 2071–2082. [Google Scholar] [CrossRef]
- Yin, S.; Wang, J. Generation and Transmission Expansion Planning Towards a 100% Renewable Future. IEEE Trans. Power Syst. 2022, 37, 3274–3285. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, T. Research on System Planning of Gas-Power Integrated System Based on Improved Two-Stage Robust Optimization and Non-Cooperative Game Method. IEEE Access 2021, 9, 79169–79181. [Google Scholar] [CrossRef]
- Alshamrani, A.M.; El-Meligy, M.A.; Sharaf, M.A.F.; Saif, W.A.M.; Awwad, E.M. Transmission Expansion Planning Considering a High Share of Wind Power to Maximize Available Transfer Capability. IEEE Access 2023, 11, 23136–23145. [Google Scholar] [CrossRef]
- Zhuo, Z.; Du, E.; Zhang, N.; Kang, C.; Xia, Q.; Wang, Z. Incorporating Massive Scenarios in Transmission Expansion Planning with High Renewable Energy Penetration. IEEE Trans. Power Syst. 2020, 35, 1061–1074. [Google Scholar] [CrossRef]
- Alnowibet, K.A.; Alrasheedi, A.F.; Alshamrani, A.M. Integrated stochastic transmission network and wind farm investment considering maximum allowable capacity. Electr. Power Syst. Res. 2023, 215, 108961. [Google Scholar] [CrossRef]
- Nguyen, N.; Almasabi, S.; Bera, A.; Mitra, J. Optimal Power Flow Incorporating Frequency Security Constraint. IEEE Trans. Ind. Appl. 2019, 55, 6508–6516. [Google Scholar] [CrossRef]
- Chu, Z.; Markovic, U.; Hug, G.; Teng, F. Towards Optimal System Scheduling with Synthetic Inertia Provision from Wind Turbines. IEEE Trans. Power Syst. 2020, 35, 4056–4066. [Google Scholar] [CrossRef]
- Wang, L.; Fan, H.; Liang, J.; Xu, L.; Li, T.; Luo, P.; Hu, B.; Xie, K. Multi-Area Frequency-Constrained Unit Commitment for Power Systems with High Penetration of Renewable Energy Sources and Induction Machine Load. J. Mod. Power Syst. Clean Energy 2024, 12, 754–766. [Google Scholar] [CrossRef]
- Carrión, M.; Dvorkin, Y.; Pandžić, H. Primary Frequency Response in Capacity Expansion with Energy Storage. IEEE Trans. Power Syst. 2018, 33, 1824–1835. [Google Scholar] [CrossRef]
- Cai, X.; Zhang, N.; Du, E.; An, Z.; Wei, N.; Kang, C. Low Inertia Power System Planning Considering Frequency Quality Under High Penetration of Renewable Energy. IEEE Trans. Power Syst. 2024, 39, 4537–4548. [Google Scholar] [CrossRef]
- Li, H.; Qiao, Y.; Lu, Z.; Zhang, B.; Teng, F. Frequency-Constrained Stochastic Planning Towards a High Renewable Target Considering Frequency Response Support from Wind Power. IEEE Trans. Power Syst. 2021, 36, 4632–4644. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, L.; Cheng, H.; Liu, D.; Zhang, J.; Li, G. Frequency-constrained Co-planning of Generation and Energy Storage with High-penetration Renewable Energy. J. Mod. Power Syst. Clean Energy 2021, 9, 760–775. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, F.; Zhang, X.; Wang, Z.; Meng, K.; Dong, Z.Y. Mobile Emergency Generator Planning in Resilient Distribution Systems: A Three-Stage Stochastic Model with Nonanticipativity Constraints. IEEE Trans. Smart Grid 2020, 11, 4847–4859. [Google Scholar] [CrossRef]
- Luo, F.; Bu, Q.; Ye, Z.; Yuan, Y.; Gao, L.; Lv, P. Dynamic Reconstruction Strategy of Distribution Network Based on Uncertainty Modeling and Impact Analysis of Wind and Photovoltaic Power. IEEE Access 2024, 12, 64069–64078. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, B.; Li, Q.; Zhou, G.; Wang, L.; Li, B.; Li, K. Fast Frequency Regulation Method for Power System with Two-Stage Photovoltaic Plants. IEEE Trans. Sustain. Energy 2022, 13, 1779–1789. [Google Scholar] [CrossRef]
- Shi, Q.; Li, F.; Cui, H. Analytical Method to Aggregate Multi-Machine SFR Model with Applications in Power System Dynamic Studies. IEEE Trans. Power Syst. 2018, 33, 6355–6367. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, Y.; Wang, J.; Liu, Z.; Chen, Z. Enhanced Frequency-Constrained Unit Commitment Considering Variable-Droop Frequency Control From Converter-Based Generator. IEEE Trans. Power Syst. 2023, 38, 1094–1110. [Google Scholar] [CrossRef]
- Orfanos, G.A.; Georgilakis, P.S.; Hatziargyriou, N.D. Transmission Expansion Planning of Systems with Increasing Wind Power Integration. IEEE Trans. Power Syst. 2013, 28, 1355–1362. [Google Scholar] [CrossRef]


| [4,5,6,7] | [8,9,10] | [15] | [16,17] | Proposed | |
|---|---|---|---|---|---|
| X-stage model | Two-stage stochastic | Two-stage robust | Two-stage stochastic | Two-stage stochastic | Three-stage stochastic |
| Progressive realization of uncertainties | × | × | × | × | √ |
| Frequency stability model | × | × | √ | √ | √ |
| Frequency mechanism | × | × | × | √ | √ |
| Model dimension | Low | Low | Low | High | Low |
| Scenario | Candidates | Planning Stage | ||
|---|---|---|---|---|
| Stage 1 | Stage 2 | Stage 3 | ||
| S1 | Line | - | 1–4, 4–5 | - |
| SG | - | G6 (100 MW) | G8 (80 MW) | |
| RG | W3 (100 MW), W4 (100 MW) | - | - | |
| S2 | Line | - | 1–4, 4–5 | - |
| SG | - | G6 (100 MW) | - | |
| RG | W3 (100 MW), W4 (100 MW) | - | W2 (100 MW) | |
| S3 | Line | - | - | 2–3 |
| SG | - | - | - | |
| RG | W3 (100 MW), W4 (100 MW) | W6 (100 MW) | W5 (100 MW) | |
| S4 | Line | - | - | 1–4 |
| SG | - | - | G8 (80 MW) | |
| RG | W3 (100 MW), W4 (100 MW) | W6 (100 MW) | - | |
| Candidates | Planning Stage | ||
|---|---|---|---|
| Stage 1 | Stage 2 | Stage 3 | |
| Line | 2–3 | 5–6 | 1–4 |
| SG | G6 (100 MW) | - | G8 (80 MW) |
| RG | W3 (100 MW) | - | W4 (100 MW) |
| Model | Objective Value (M$) | ||
|---|---|---|---|
| Capital Costs | Operational Costs | Total | |
| Multi-stage | 218.6 | 173 | 391.6 |
| Two-stage | 279.2 | 169.5 | 448.7 |
| Candidates | Uncertainty Model | Objective Function | Operational Constraints | Solution Algorithm | Frequency Constraints | |
|---|---|---|---|---|---|---|
| FC-PL | Line; SG; RG | Three-stage Stochastic | Equation (11) | Equations (14)–(22) | PHA | √ |
| NFC-PL | Line; SG; RG | Three-stage Stochastic | Equation (11) | Equations (14)–(22) | PHA | × |
| Scenario | Model | Frequency Stability Indices | ||
|---|---|---|---|---|
| fnadir (Hz) | RoCoF (Hz/s) | fss (Hz) | ||
| S1 | NFC-PL | 49.537 | 0.577 | 49.816 |
| FC-PL | 49.646 | 0.465 | 49.850 | |
| S2 | NFC-PL | 49.467 | 0.584 | 49.800 |
| FC-PL | 49.646 | 0.465 | 49.850 | |
| S3 | NFC-PL | 49.363 | 0.676 | 49.786 |
| FC-PL | 49.625 | 0.481 | 49.854 | |
| S4 | NFC-PL | 49.560 | 0.527 | 49.831 |
| FC-PL | 49.644 | 0.444 | 49.865 | |
| Solution Method | Objective Value (M$) | ||
|---|---|---|---|
| Capital Costs | Operational Costs | Total | |
| PHA | 220.1 | 175.2 | 398.5 |
| NDM | 218.6 | 173 | 391.6 |
| Test System | Objective Value (M$) | Improvement | |
|---|---|---|---|
| Multi-Stage | Two-Stage | ||
| 39-Bus | 1772.1 | 2118.8 | 16.3% |
| 118-Bus | 5127.3 | 6522.1 | 21.4% |
| Scenario | Model | Frequency Stability Indices | ||
|---|---|---|---|---|
| fnadir (Hz) | RoCoF (Hz/s) | fss (Hz) | ||
| S1 | NFC-PL | 49.513 | 0.519 | 49.795 |
| FC-PL | 49.619 | 0.431 | 49.819 | |
| S2 | NFC-PL | 49.519 | 0.552 | 49.796 |
| FC-PL | 49.605 | 0.469 | 49.807 | |
| S3 | NFC-PL | 49.537 | 0.559 | 49.767 |
| FC-PL | 49.625 | 0.461 | 49.829 | |
| S4 | NFC-PL | 49.494 | 0.512 | 49.786 |
| FC-PL | 49.624 | 0.437 | 49.825 | |
| Scenario | Model | Planning Stage | ||
|---|---|---|---|---|
| fnadir (Hz) | RoCoF (Hz/s) | fss (Hz) | ||
| S1 | NFC-PL | 49.537 | 0.527 | 49.753 |
| FC-PL | 49.611 | 0.437 | 49.835 | |
| S2 | NFC-PL | 49.503 | 0.561 | 49.742 |
| FC-PL | 49.621 | 0.445 | 49.817 | |
| S3 | NFC-PL | 49.495 | 0.572 | 49.724 |
| FC-PL | 49.607 | 0.457 | 49.869 | |
| S4 | NFC-PL | 49.554 | 0.523 | 49.699 |
| FC-PL | 49.632 | 0.414 | 49.805 | |
| Test system | Objective Value (M$) | ||
| NDM | PHA | Improvement | |
| 39-Bus | 1487.7 | 1535.3 | 3.2% |
| 118-Bus | 5214.6 | 5449.2 | 4.5% |
| Test system | Solution Time (min) | ||
| NDM | PHA | Improvement | |
| 39-Bus | 108.9 | 24.2 | 77.8% |
| 118-Bus | 1237.5 | 191.6 | 84.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, X.; Sun, H.; Zhao, G.; Qiao, G.; Lu, Z.; Xu, Y.; Li, W.; Zheng, T. Multi-Stage Stochastic Planning for Transmission Systems Considering Dynamic Frequency Stability. Symmetry 2025, 17, 632. https://doi.org/10.3390/sym17050632
Luan X, Sun H, Zhao G, Qiao G, Lu Z, Xu Y, Li W, Zheng T. Multi-Stage Stochastic Planning for Transmission Systems Considering Dynamic Frequency Stability. Symmetry. 2025; 17(5):632. https://doi.org/10.3390/sym17050632
Chicago/Turabian StyleLuan, Xiaoming, Huadong Sun, Guoliang Zhao, Guangyao Qiao, Zhengang Lu, Yunfei Xu, Weiguo Li, and Tao Zheng. 2025. "Multi-Stage Stochastic Planning for Transmission Systems Considering Dynamic Frequency Stability" Symmetry 17, no. 5: 632. https://doi.org/10.3390/sym17050632
APA StyleLuan, X., Sun, H., Zhao, G., Qiao, G., Lu, Z., Xu, Y., Li, W., & Zheng, T. (2025). Multi-Stage Stochastic Planning for Transmission Systems Considering Dynamic Frequency Stability. Symmetry, 17(5), 632. https://doi.org/10.3390/sym17050632





