Improvement of Microwave Heating Uniformity Using Symmetrical Stirring
Abstract
1. Introduction
2. Methodology
2.1. Multi-Physics Simulation
2.1.1. Geometry
2.1.2. Analysis of Electromagnetic Field
2.1.3. Analysis of Heat Transport
2.1.4. Analysis of Fluid Dynamics
2.1.5. Analysis of the ALE Method
2.1.6. Input Parameters
2.1.7. Multi-Physics Fields Coupling Calculation
2.2. Experimental Setup
3. Results and Discussion
3.1. Experimental Validation
3.2. Theoretical Calculation
3.2.1. Analysis of Electric Field
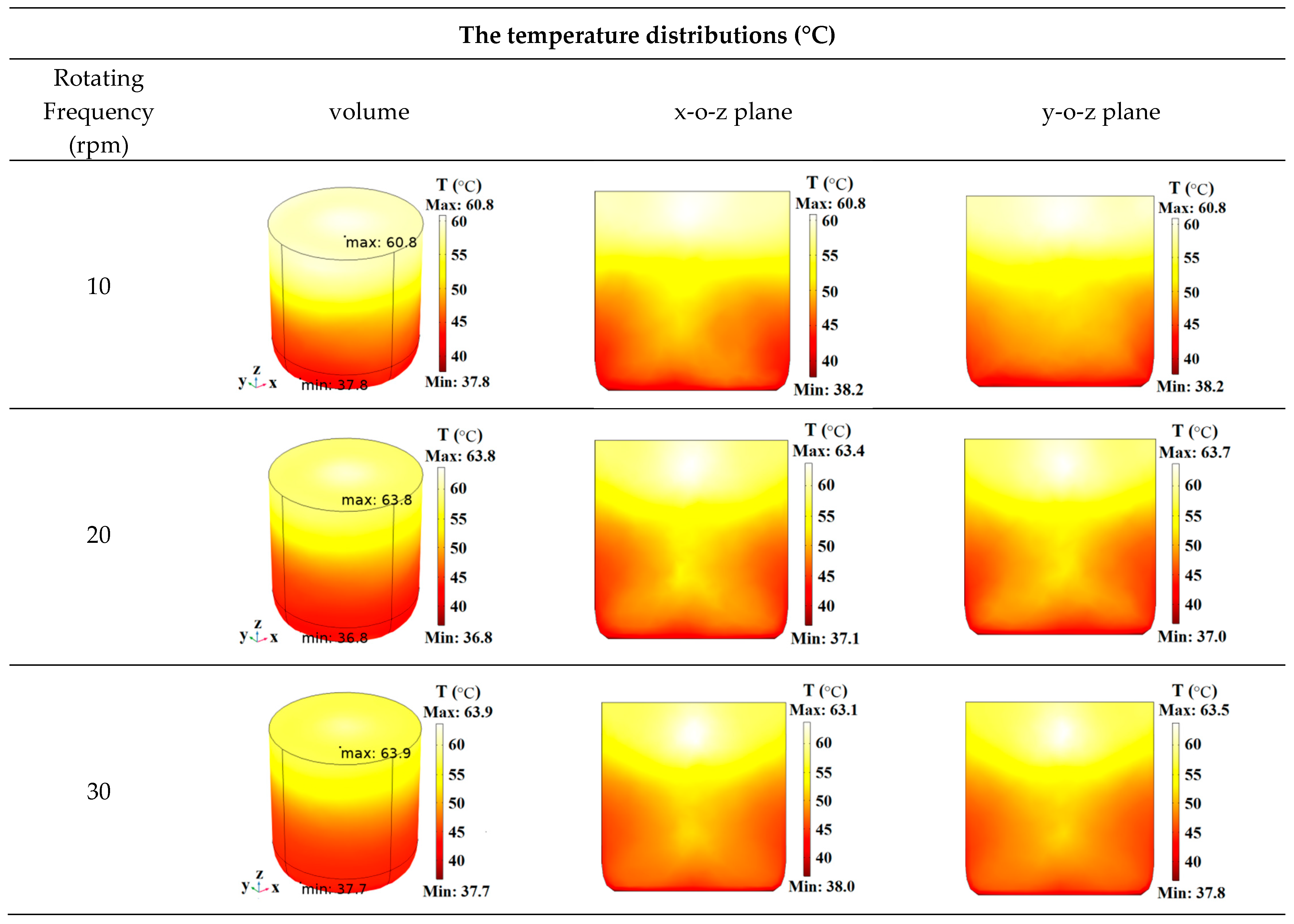
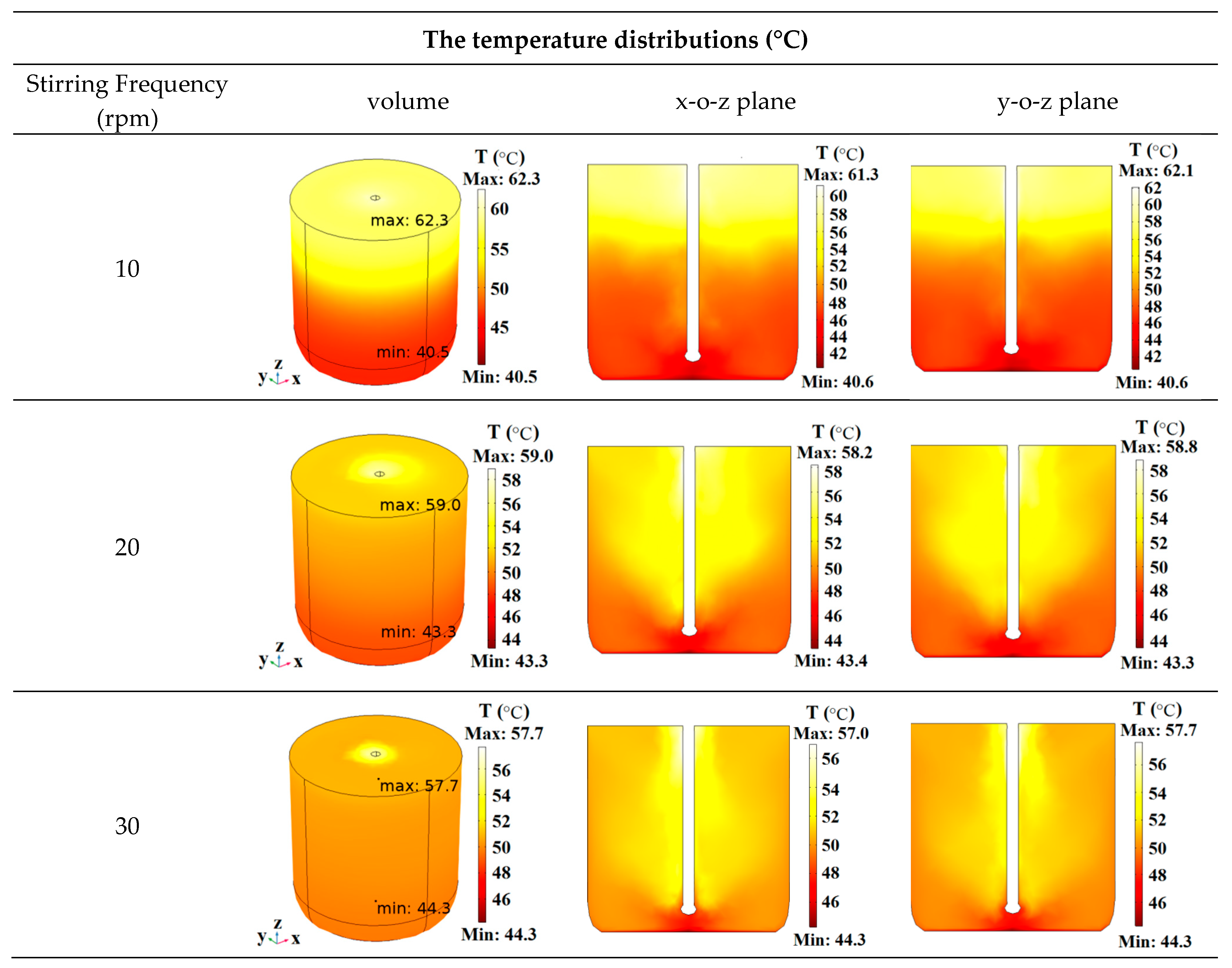
3.2.2. Analysis of the Temperature Field
3.2.3. COV of the Temperature
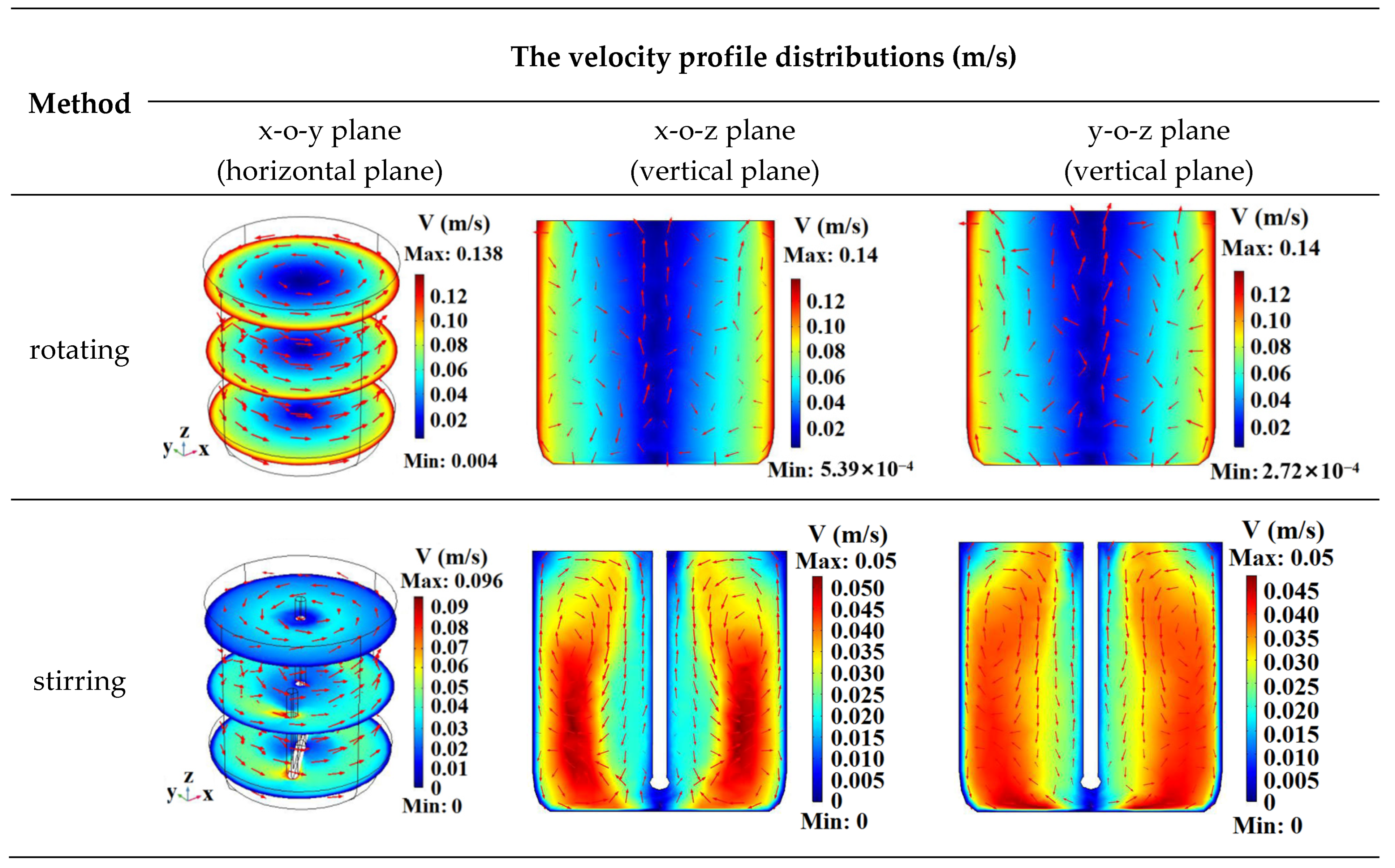
3.2.4. Analysis of the Velocity Field
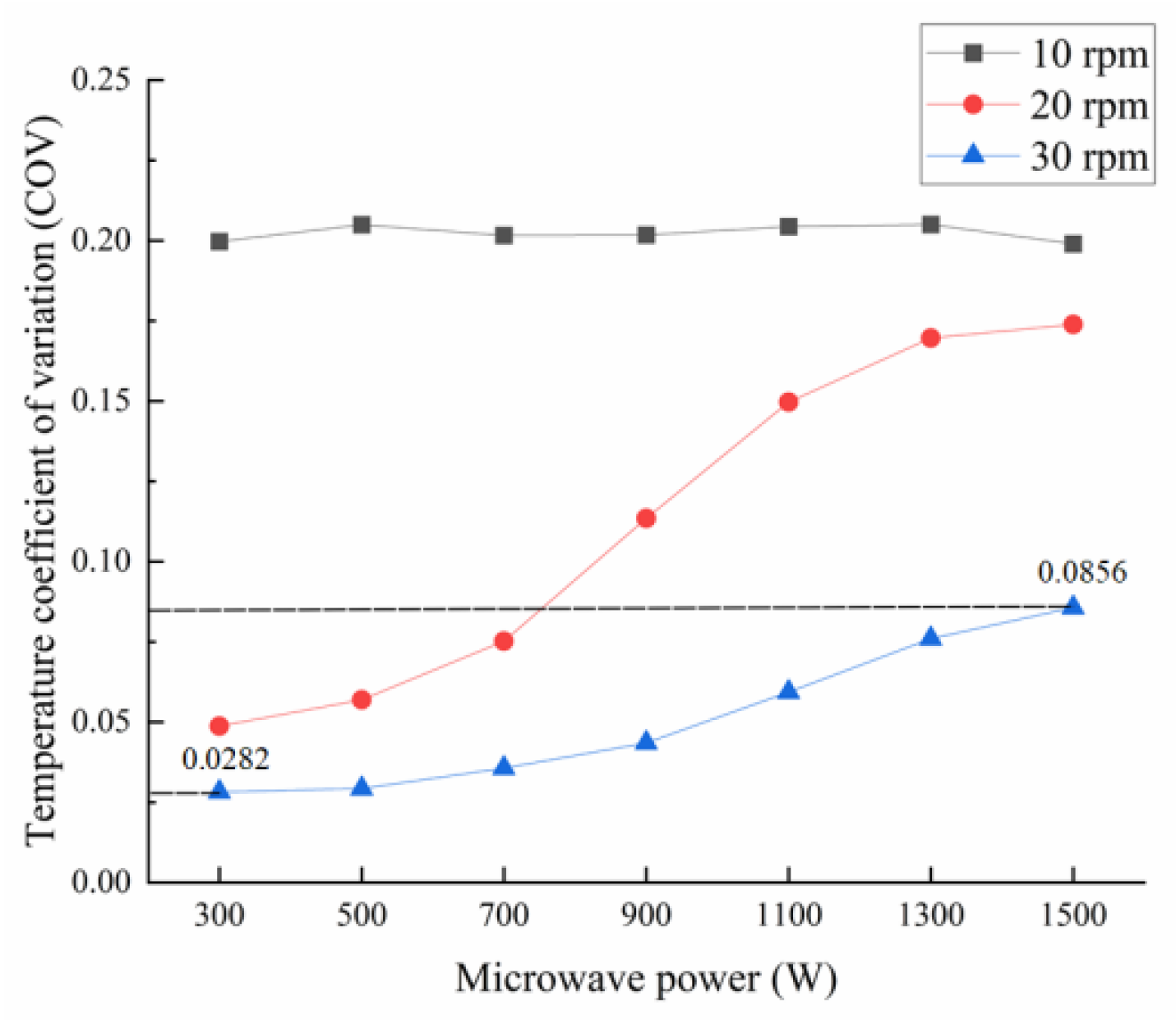
3.2.5. Analysis of the Effect of Microwave Power on Temperature COV with Stirring
4. Conclusions
- The coincidence between the experimental and calculated results demonstrated that the proposed FEM multi-physics calculation model is capable of predicting the temperature of a fluid subjected to microwave heating with stirring.
- The non-uniform temperature distribution of the water heated with the rotating turntable was primarily concentrated along the vertical plane, and the rotation had a very minimal effect on reducing the temperature difference. This characteristic of the temperature distribution was the result of the combined effect of the non-uniform electric field distribution and natural convection. In contrast, the temperature uniformity of the water heated with stirring improved because the forced convection enhanced the vertical flow of the fluid and effectively eliminated the vertical temperature difference. For the same rotational/stirring frequency, the COV of the water heated with a stirring paddle improved by 11.2–81.5% compared to that heated with rotation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Delouei, A.A.; Naeimi, H.; Sajjadi, H. An active approach to heat transfer enhancement in indirect heaters of city gate stations: An experimental modeling. Appl. Therm. Eng. 2024, 237, 121795–121806. [Google Scholar] [CrossRef]
- Hedeshi, M.; Jalali, A.; Arabkoohsar, A.; Amiri Delouei, A. Nanofluid as the working fluid of an ultrasonic-assisted double-pipe counter-flow heat exchanger. J. Therm. Anal. Calorim. 2023, 148, 8579–8591. [Google Scholar] [CrossRef]
- Hashemi, S.M.B.; Akbari, M.; Roohi, R.; Phimolsiripol, Y. Hurdle approaches using conventional thermal, microwave heating and ginger essential oil in vegetable juice mixture: Heat transfer modeling and microbial inactivation kinetics. LWT-Food Sci. Technol. 2024, 198, 115958–115967. [Google Scholar] [CrossRef]
- Jiao, X.; Diao, H.; Liu, T.; Yan, B.; Tang, X.; Fan, D. Single-mode microwave heating for food science research: Understanding specific microwave effects and reliability concerns. Food Phys. 2025, 2, 100048–100060. [Google Scholar] [CrossRef]
- Lee, Y.-C.; Hwang, C.-C.; Tsai, Y.-H.; Huang, Y.-T. Development and pasteurization of in-packaged ready-to-eat rice products prepared with novel microwave-assisted induction heating (MAIH) technology. Appl. Food Res. 2025, 5, 100697–100706. [Google Scholar] [CrossRef]
- Li, G.; Zhou, J. COMSOL-Based Simulation of Microwave Heating of Al2O3/SiC Composites with Parameter Variations. Symmetry 2024, 16, 1254. [Google Scholar] [CrossRef]
- Zhang, P.; Liang, C.; Chen, X.; Liu, D.; Ma, J. Insight into microwave heating patterns for sustainable decomposition of plastic wastes into hydrogen. Appl. Therm. Eng. 2025, 260, 124954–124966. [Google Scholar] [CrossRef]
- Zhang, S.; Qin, S.; Wan, W.; Li, J.; Liu, S.; Paik, K.-W.; He, P.; Zhang, S. Investigation on electromagnetic and heat transfer coupling of heating susceptor for selective microwave hybrid soldering: 3D multi-physics simulation and experiment. Appl. Therm. Eng. 2024, 255, 124047–124060. [Google Scholar] [CrossRef]
- Principato, L.; Spigno, G. Chapter 16—Microwave heating in food processing. In Food Packaging and Preservation; Jaiswal, A.K., Shankar, S., Eds.; Academic Press: Cambridge, MA, USA, 2024; pp. 299–329. [Google Scholar]
- Taguchi, Y.; Abea, A.; Llave, Y.; Sugihara, C.; Suzuki, F.; Hosoda, T.; Onizawa, K.; Sakai, N.; Fukuoka, M. Modeling of microwave thawing and reheating of multiphase foods: A case study for packed rice. J. Food Eng. 2025, 386, 112284–112294. [Google Scholar] [CrossRef]
- Yi, M.; Tang, X.; Liang, S.; He, R.; Huang, T.; Lin, Q.; Zhang, R. Effect of microwave alone and microwave-assisted modification on the physicochemical properties of starch and its application in food. Food Chem. 2024, 446, 138841–138853. [Google Scholar] [CrossRef]
- Chen, W.-H.; Liu, L.-X.; Khoo, K.S.; Sheen, H.-K.; Kwon, E.E.; Saravanakumar, A.; Chang, J.-S. Environmentally-friendly alkaline ionized water pretreatment and hydrolysis of macroalga via microwave-assisted heating to improve monosaccharide yield for bioethanol production. Process Saf. Environ. Prot. 2024, 189, 702–713. [Google Scholar] [CrossRef]
- Han, Y.; Meng, L.-Y.; Lin, R.; Kim, S.; Kim, T.; Wang, X.-Y. Evaluating the sustainability of microwave pre-cured high-volume slag concrete: Mechanical properties, environmental impact and cost-benefit analysis. J. Build. Eng. 2024, 96, 110663–110684. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, W.-H.; Ho, S.-H. Economic feasibility analysis and environmental impact assessment for the comparison of conventional and microwave torrefaction of spent coffee grounds. Biomass Bioenergy 2023, 168, 106652–106664. [Google Scholar] [CrossRef]
- Ahmad, F.; Zhang, Y.; Fu, W.; Zhao, W.; Xiong, Q.; Li, B. Microwave-assisted chemical looping gasification of sugarcane bagasse biomass using Fe3O4 as oxygen carrier for H2/CO-rich syngas production. Chem. Eng. J. 2024, 501, 157675–157687. [Google Scholar] [CrossRef]
- Fu, W.; Zhang, Y.; Cao, W.; Zhao, W.; Li, B. Microwave-assisted chemical looping gasification of plastics for H2-rich gas production. Chem. Eng. J. 2024, 499, 156225–156236. [Google Scholar] [CrossRef]
- Khodabandehloo, M.; Shabanian, J.; Harvey, J.-P.; Chaouki, J. Kinetic study of microwave heating-assisted chemical looping dry reforming of methane over magnetite. Int. J. Hydrogen Energy 2024, 96, 1079–1086. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Liu, Z.; Meng, X.; He, Y.; Zhang, Z. Study on the process of medical waste disinfection by microwave technology. Waste Manag. 2022, 150, 13–19. [Google Scholar] [CrossRef]
- Vadivambal, R.; Jayas, D.S. Non-uniform temperature distribution during microwave heating of food materials—A review. Food Bioprocess Technol. 2010, 3, 161–171. [Google Scholar] [CrossRef]
- Karlsson, M.; Carlsson, H.; Idebro, M. Microwave heating as a method to improve sanitation of sewage sludge in wastewater plants. IEEE Access 2019, 7, 142308–142316. [Google Scholar] [CrossRef]
- Horikoshi, S.; Serpone, N. Microwave flow chemistry as a methodology in organic syntheses, enzymatic reactions, and nanoparticle syntheses. Chem. Rec. 2019, 19, 118–139. [Google Scholar] [CrossRef]
- Alzubaidi, S.; Wallace, A.; Naidu, S. Single-arm prospective study comparing ablation zone volume between time zero and 24 h after microwave ablation of liver tumors. Abdom. Radiol. 2024, 49, 3136–3142. [Google Scholar] [CrossRef] [PubMed]
- Manickavasagan, A.; Jayas, D.S.; White, N.D.G. Non-uniformity of surface temperatures of grain after microwave treatment in an industrial microwave dryer. Drying Technol. 2006, 24, 1559–1567. [Google Scholar] [CrossRef]
- Baro, R.K.; Kotecha, P.; Anandalakshmi, R. Optimization of continuous-flow microwave processing with static mixers for enhanced heating uniformity. Food Bioprod. Process. 2025, 149, 401–414. [Google Scholar] [CrossRef]
- Wang, C.; Peng, Z.; Yang, F.; Zhu, H.; Yan, L. Uniformity improvement of microwave heating with switchable frequency selective surface. Case Stud. Therm. Eng. 2024, 61, 104919–104928. [Google Scholar] [CrossRef]
- Zhu, H.; He, J.; Hong, T.; Yang, Q.; Wu, Y.; Yang, Y.; Huang, K. A rotary radiation structure for microwave heating uniformity improvement. Appl. Therm. Eng. 2018, 141, 648–658. [Google Scholar] [CrossRef]
- Zhu, J.; Li, F.; Wang, H.; Yang, Z.; Chen, H.; Zhu, H. Numerical analysis of microwave-enhanced oil shale pyrolysis by rotation turntable based on the Arbitrary Lagrangian-Eulerian method. Fuel 2024, 371, 131925–131937. [Google Scholar] [CrossRef]
- Wang, L.; Kang, J.; Zhu, C.; Zhou, Z.; Wang, S.; Huang, Z. Modeling the RF heating uniformity contributed by a rotating turntable. J. Food Eng. 2023, 339, 111289–111302. [Google Scholar] [CrossRef]
- Yang, R.; Chen, J. Identification of turntable function in a solid-state microwave heating process with diverse frequency-shifting strategies applied. Innov. Food Sci. Emerg. Technol. 2024, 94, 103670–103682. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Feng, S.; Ma, W.; Zhang, Y.; Liu, C.; Liu, C.; Zheng, X. Analysis of heating uniformity considering microwave transmission in stacked bulk of granular materials on a turntable in microwave ovens. J. Food Eng. 2022, 319, 110903–110922. [Google Scholar] [CrossRef]
- Liu, M.; Zhou, D.; Peng, Y.; Tang, Z.; Huang, K.; Hong, T. High-efficiency continuous-flow microwave heating system based on metal-ring resonant structure. Innov. Food Sci. Emerg. Technol. 2023, 85, 103330–103343. [Google Scholar] [CrossRef]
- Yang, F.; Zhu, H.; Yang, Y.; Huang, K. High-Efficiency Continuous-Flow Microwave Heating System Based on Asymmetric Propagation Waveguide. IEEE Trans. Microw. Theory Tech. 2022, 70, 1920–1931. [Google Scholar] [CrossRef]
- Zhu, H.; Shu, W.; Xu, C.; Yang, Y.; Huang, K.; Ye, J. Novel electromagnetic-black-hole-based high-efficiency single-mode microwave liquid-phase food heating system. Innov. Food Sci. Emerg. Technol. 2022, 78, 103012–103021. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, X.; Ye, J. Arbitrary Lagrangian-Eulerian method for computation of rotating target during microwave heating—ScienceDirect. Int. J. Heat Mass Transf. 2019, 134, 271–285. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Models for CFD, 2nd ed.; DCW Industries, Inc.: La Canada, CA, USA, 1998. [Google Scholar]
- Taylor, J. An Introduction to Error Analysis; University Science Books: Mill Valley, CA, USA, 1982. [Google Scholar]
- Pitchai, K.; Chen, J.; Birla, S.; Gonzalez, R.; Jones, D.; Subbiah, J. A microwave heat transfer model for a rotating multi-component meal in a domestic oven: Development and validation. J. Food Eng. 2014, 128, 60–71. [Google Scholar] [CrossRef]
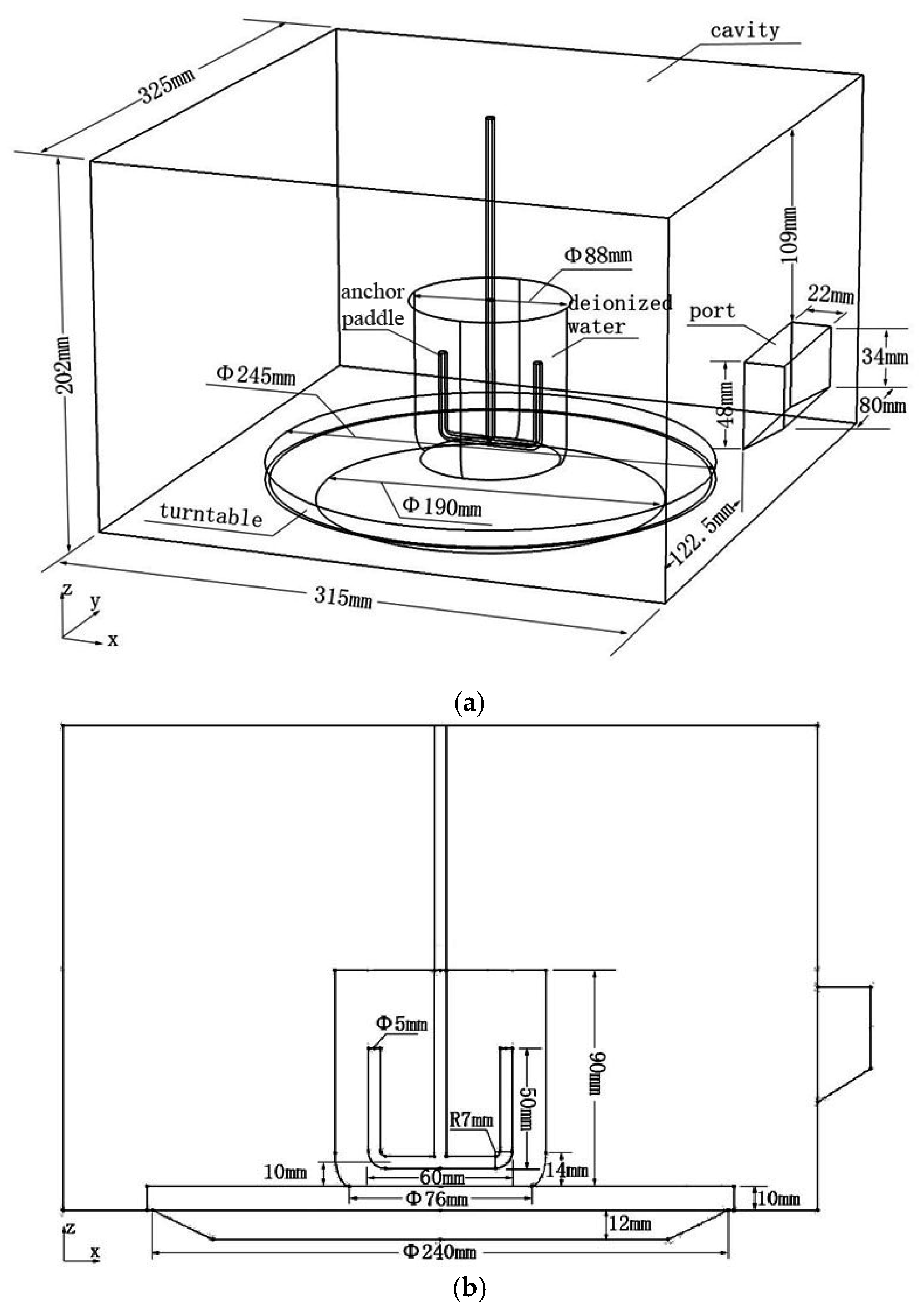
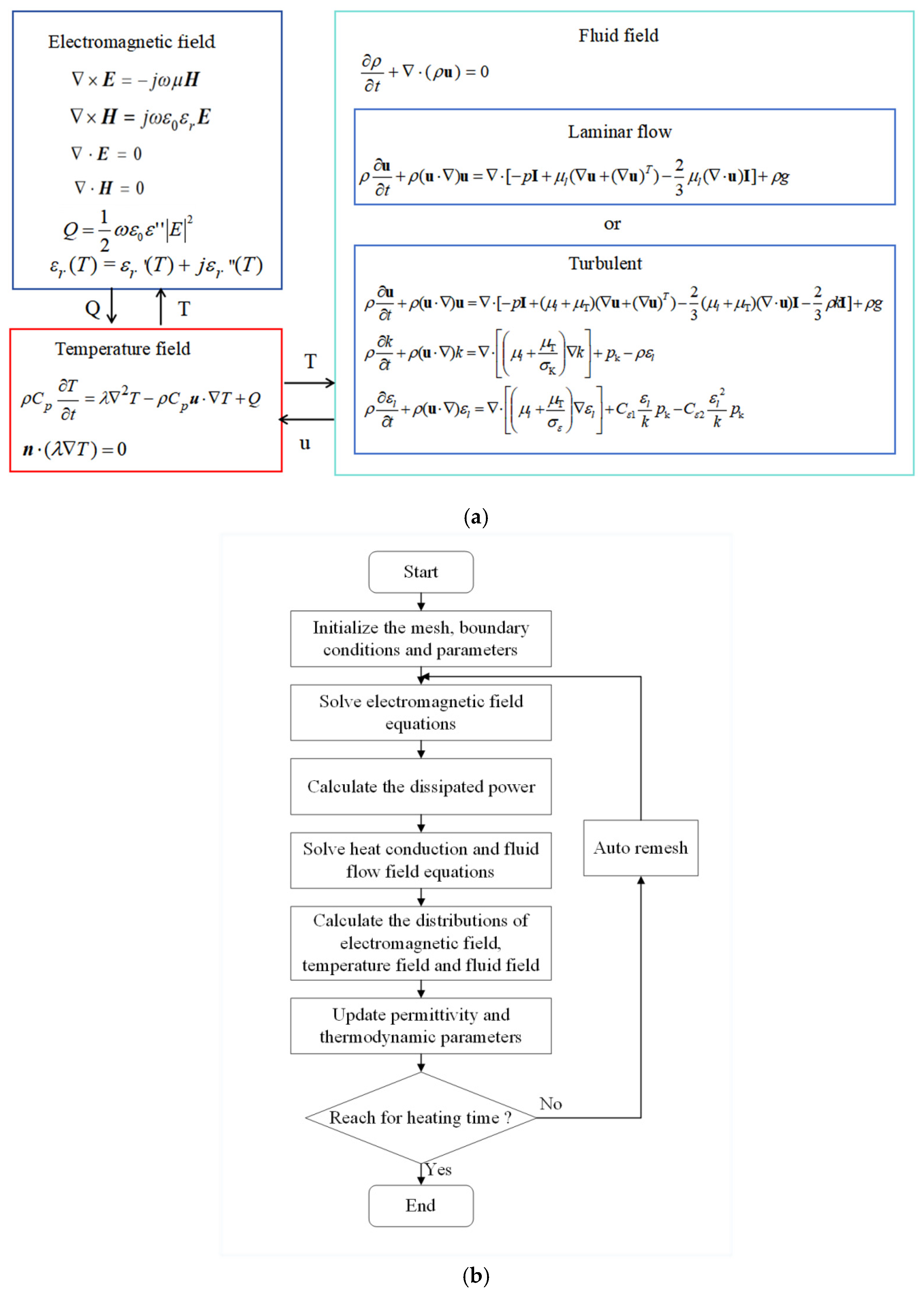
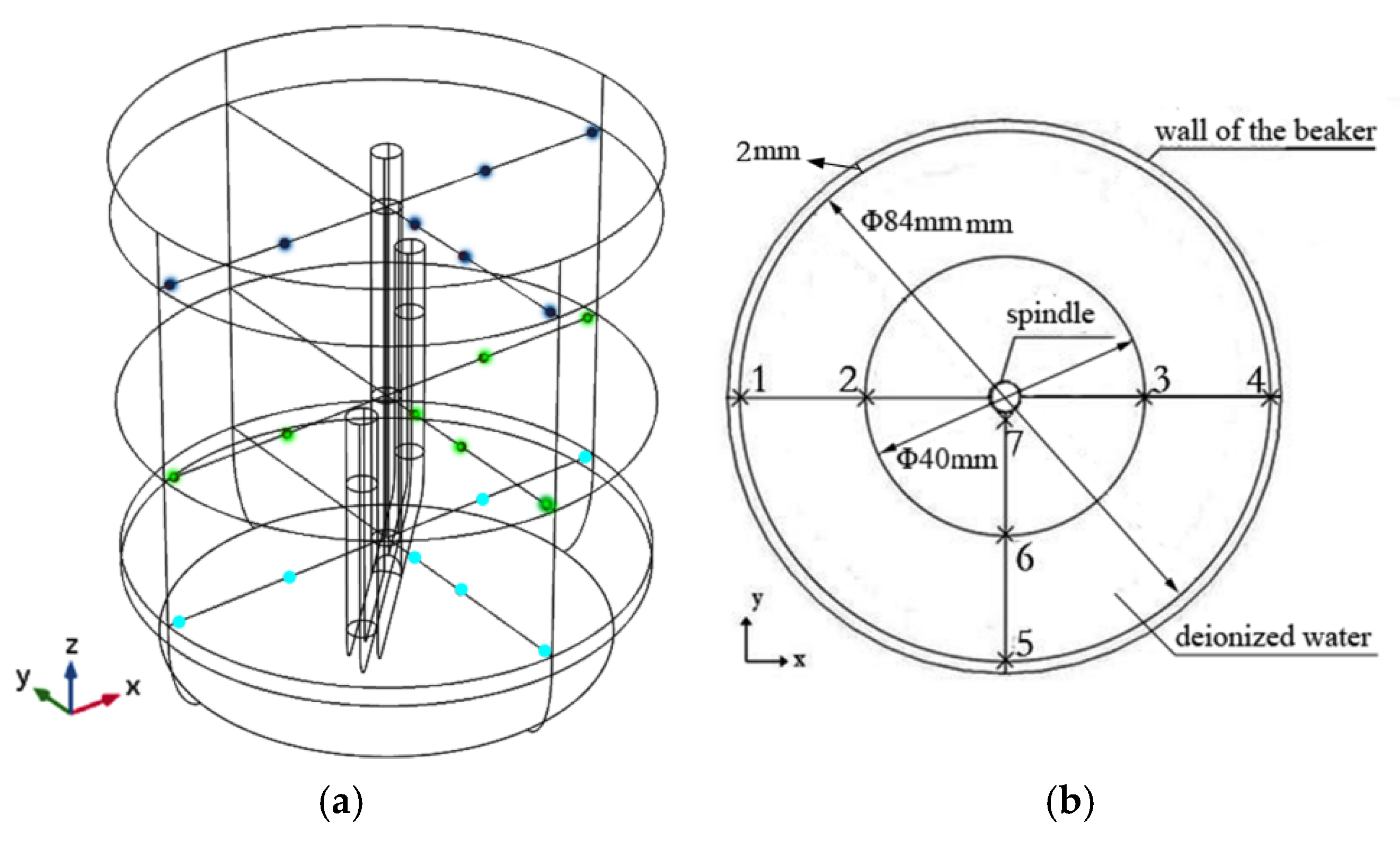
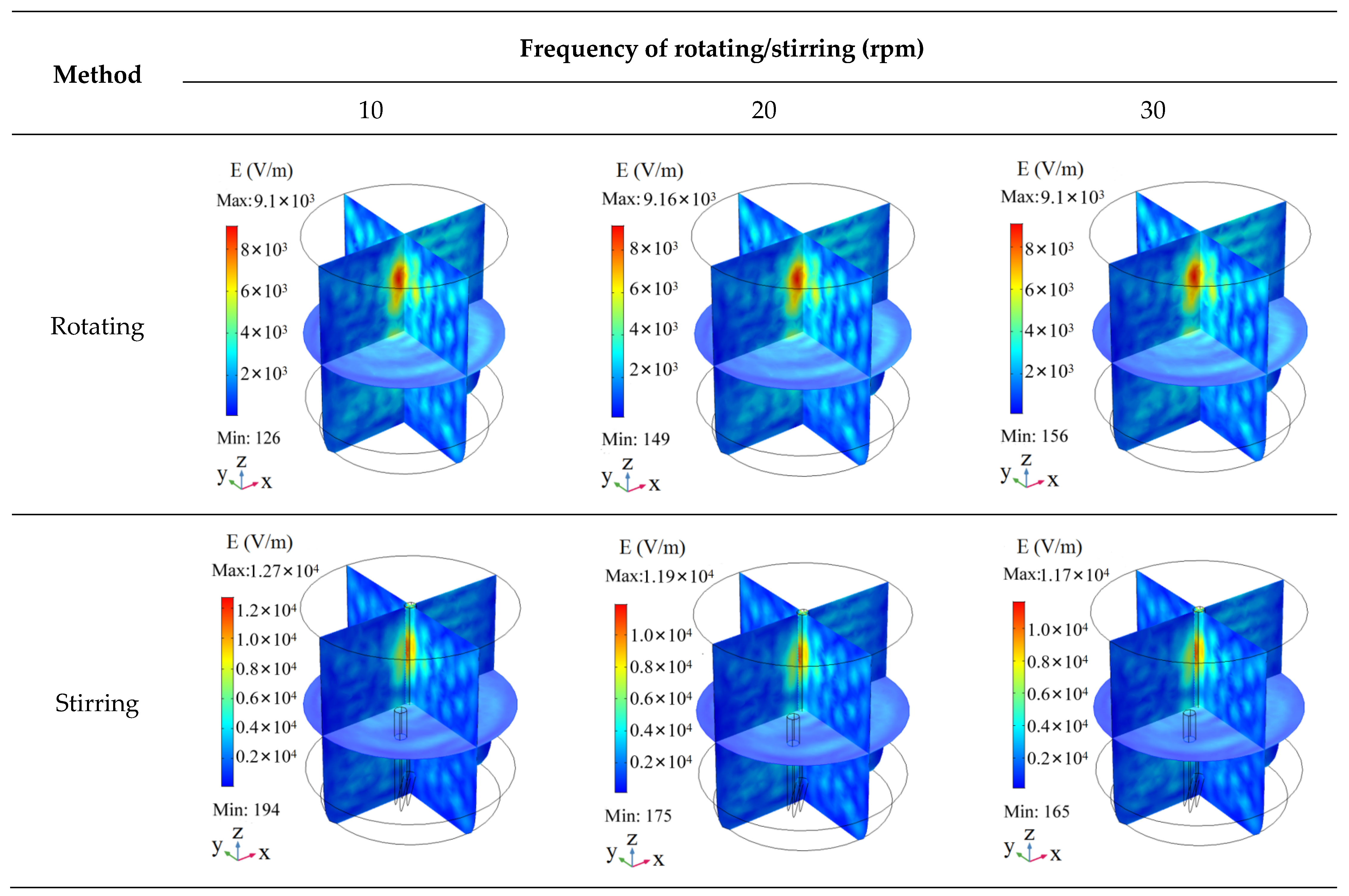
| Parameter | Value |
|---|---|
| 1 | |
| (S/m) | 5.5 × 10−6 |
| (kg/m3) | 838.47 + 1.4 × T − 3 × 10−3 × T2 + 3.72 × 10−7 × T3 |
| (W/m·K) | −0.87 + 0.09 × T − 1.58 × 10−5 × T2 + 7.98 × 10−9 × T3 |
| (J/kg·K) | 12,010.15 − 80.41 × T + 0.31 × T2 − 5.38 × 10−4 × T3 + 3.63 × 10−7 × T4 |
| (Pa·s) | 1.38 − 2 × 10−2 × T + 1.36 × 10−4 × T2 − 4.65 × 10−7 × T3 + 8.9 × 10−10 × T4 − 9.08 × 10−13 × T5 |
| Rotating Frequency | Measured Point | Low Plane | Middle Plane | High Plane | ΔT | ||||
|---|---|---|---|---|---|---|---|---|---|
| TA 1 | Ta 2 | TB 1 | Tb 2 | TC 1 | Tc 2 | ΔTAC 3 | ΔTac 4 | ||
| 10 rpm | 1 | 45.8 | 41.28 ± 0.097 | 49.9 | 46.54 ± 0.051 | 58.1 | 57.32 ± 0.086 | 12.3 | 16.04 ± 0.183 |
| 2 | 46.0 | 41.36 ± 0.103 | 49.9 | 47.52 ± 0.067 | 58.0 | 57.58 ± 0.037 | 12.0 | 16.22 ± 0.140 | |
| 3 | 46.0 | 40.54 ± 0.108 | 50.9 | 46.26 ± 0.051 | 58.2 | 57.54 ± 0.051 | 12.2 | 17.00 ± 0.159 | |
| 4 | 46.0 | 41.40 ± 0.071 | 49.8 | 46.54 ± 0.087 | 57.4 | 57.40 ± 0.071 | 11.4 | 16.00 ± 0.142 | |
| 5 | 45.9 | 41.64 ± 0.129 | 49.7 | 46.52 ± 0.086 | 58.1 | 57.18 ± 0.037 | 12.2 | 15.54 ± 0.166 | |
| 6 | 45.7 | 41.00 ± 0.100 | 49.7 | 46.28 ± 0.037 | 58.1 | 56.80 ± 0.045 | 12.4 | 15.80 ± 0.145 | |
| 7 | 45.8 | 41.04 ± 0.108 | 50.0 | 46.56 ± 0.081 | 58.5 | 56.78 ± 0.058 | 12.7 | 15.74 ± 0.166 | |
| 20 rpm | 1 | 44.6 | 42.14 ± 0.081 | 47.2 | 47.38 ± 0.058 | 57.2 | 55.90 ± 0.071 | 12.6 | 13.76 ± 0.152 |
| 2 | 48.0 | 42.18 ± 0.086 | 49.5 | 47.88 ± 0.058 | 58.0 | 56.40 ± 0.055 | 10.0 | 14.22 ± 0.141 | |
| 3 | 48.2 | 41.42 ± 0.058 | 49.5 | 46.68 ± 0.080 | 58.1 | 56.46 ± 0.051 | 9.9 | 15.04 ± 0.109 | |
| 4 | 44.5 | 41.90 ± 0.071 | 47.4 | 47.00 ± 0.071 | 57.1 | 56.32 ± 0.066 | 12.6 | 14.42 ± 0.137 | |
| 5 | 44.7 | 41.44 ± 0.108 | 47.6 | 46.86 ± 0.060 | 57.0 | 58.32 ± 0.066 | 12.3 | 16.88 ± 0.174 | |
| 6 | 48.2 | 41.46 ± 0.103 | 49.6 | 46.78 ± 0.037 | 58.1 | 57.12 ± 0.058 | 9.9 | 15.66 ± 0.161 | |
| 7 | 48.2 | 41.26 ± 0.068 | 51.3 | 47.06 ± 0.093 | 61.2 | 57.78 ± 0.058 | 13.0 | 16.52 ± 0.126 | |
| 30 rpm | 1 | 45.5 | 43.70 ± 0.141 | 48.0 | 47.18 ± 0.037 | 56.1 | 56.40 ± 0.071 | 10.6 | 12.70 ± 0.212 |
| 2 | 47.7 | 44.10 ± 0.071 | 49.6 | 48.58 ± 0.058 | 56.7 | 57.66 ± 0.051 | 9.0 | 13.56 ± 0.122 | |
| 3 | 47.8 | 42.76 ± 0.075 | 49.6 | 46.76 ± 0.075 | 56.8 | 56.64 ± 0.051 | 9.0 | 13.88 ± 0.126 | |
| 4 | 45.1 | 43.42 ± 0.066 | 48.1 | 46.20 ± 0.032 | 56.0 | 55.88 ± 0.058 | 10.9 | 12.46 ± 0.124 | |
| 5 | 45.3 | 42.56 ± 0.051 | 48.2 | 44.78 ± 0.058 | 55.9 | 56.22 ± 0.058 | 10.6 | 13.66 ± 0.109 | |
| 6 | 47.9 | 42.52 ± 0.066 | 49.9 | 47.48 ± 0.037 | 56.7 | 57.10 ± 0.063 | 8.8 | 14.58 ± 0.129 | |
| 7 | 48.6 | 42.54 ± 0.068 | 52.3 | 47.68 ± 0.058 | 60.1 | 57.88 ± 0.037 | 11.5 | 15.34 ± 0.105 | |
| Stirring Frequency | Measured Point | Low Plane | Middle Plane | High Plane | ΔT | ||||
|---|---|---|---|---|---|---|---|---|---|
| TA 1 | Ta 2 | TB 1 | Tb 2 | TC 1 | Tc 2 | ΔTAC 3 | ΔTac 4 | ||
| 10 rpm | 1 | 46.7 | 44.26 ± 0.051 | 49.0 | 46.60 ± 0.071 | 57.1 | 56.68 ± 0.058 | 10.4 | 12.42 ± 0.109 |
| 2 | 46.9 | 44.34 ± 0.087 | 49.4 | 46.64 ± 0.087 | 57.5 | 57.38 ± 0.066 | 10.6 | 13.04 ± 0.153 | |
| 3 | 47.1 | 44.12 ± 0.058 | 50.0 | 46.02 ± 0.086 | 57.5 | 56.64 ± 0.051 | 10.4 | 12.52 ± 0.109 | |
| 4 | 46.7 | 44.06 ± 0.087 | 48.8 | 46.04 ± 0.087 | 57.1 | 56.38 ± 0.066 | 10.4 | 12.32 ± 0.153 | |
| 5 | 46.7 | 43.80 ± 0.071 | 49.1 | 46.30 ± 0.071 | 57.1 | 57.34 ± 0.051 | 10.4 | 13.54 ± 0.122 | |
| 6 | 47.4 | 44.10 ± 0.095 | 49.5 | 46.32 ± 0.066 | 57.4 | 57.12 ± 0.037 | 10.0 | 13.02 ± 0.132 | |
| 7 | 45.0 | 44.08 ± 0.080 | 50.1 | 46.52 ± 0.037 | 58.9 | 56.96 ± 0.040 | 13.9 | 12.88 ± 0.120 | |
| 20 rpm | 1 | 48.7 | 46.52 ± 0.058 | 50.1 | 47.40 ± 0.071 | 51.4 | 51.54 ± 0.051 | 2.7 | 5.02 ± 0.109 |
| 2 | 48.6 | 46.54 ± 0.060 | 52.4 | 47.94 ± 0.051 | 52.0 | 51.56 ± 0.051 | 3.4 | 5.02 ± 0.111 | |
| 3 | 48.7 | 45.74 ± 0.051 | 52.6 | 46.70 ± 0.055 | 52.8 | 51.90 ± 0.032 | 4.1 | 6.16 ± 0.083 | |
| 4 | 48.7 | 46.00 ± 0.071 | 50.1 | 47.02 ± 0.058 | 51.3 | 52.20 ± 0.071 | 2.6 | 6.20 ± 0.142 | |
| 5 | 48.7 | 45.84 ± 0.051 | 50.0 | 46.80 ± 0.045 | 51.3 | 53.20 ± 0.071 | 2.6 | 7.36 ± 0.122 | |
| 6 | 48.7 | 45.82 ± 0.049 | 53.0 | 46.78 ± 0.058 | 52.3 | 53.40 ± 0.032 | 3.6 | 7.58 ± 0.081 | |
| 7 | 47.6 | 45.86 ± 0.051 | 53.3 | 47.00 ± 0.045 | 53.3 | 52.84 ± 0.051 | 5.7 | 6.98 ± 0.102 | |
| 30 rpm | 1 | 49.8 | 49.10 ± 0.071 | 50.3 | 49.40 ± 0.071 | 50.5 | 49.62 ± 0.058 | 0.7 | 0.52 ± 0.129 |
| 2 | 49.7 | 49.70 ± 0.055 | 51.4 | 50.20 ± 0.071 | 50.9 | 50.72 ± 0.066 | 1.2 | 1.02 ± 0.121 | |
| 3 | 49.8 | 48.08 ± 0.080 | 51.5 | 48.42 ± 0.058 | 51.0 | 49.00 ± 0.071 | 1.2 | 0.92 ± 0.151 | |
| 4 | 49.8 | 48.30 ± 0.032 | 50.3 | 48.86 ± 0.051 | 50.6 | 49.00 ± 0.045 | 0.8 | 0.70 ± 0.077 | |
| 5 | 49.8 | 48.12 ± 0.037 | 50.3 | 48.74 ± 0.051 | 50.6 | 48.98 ± 0.058 | 0.8 | 0.86 ± 0.095 | |
| 6 | 49.8 | 48.28 ± 0.080 | 51.6 | 48.80 ± 0.045 | 51.0 | 49.38 ± 0.037 | 1.2 | 1.10 ± 0.117 | |
| 7 | 48.9 | 48.34 ± 0.087 | 52.5 | 49.00 ± 0.071 | 51.7 | 49.98 ± 0.058 | 2.8 | 1.64 ± 0.145 | |
| Method | COV of Temperature | ||
|---|---|---|---|
| Frequency (rpm) | |||
| 10 | 20 | 30 | |
| Rotating | 22.3% | 22.3% | 19.5% |
| Stirring | 19.8% | 7.5% | 3.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, W.; Feng, X.; Gao, L.; Chen, K.; Chen, Y.; Shi, J.; Lao, H. Improvement of Microwave Heating Uniformity Using Symmetrical Stirring. Symmetry 2025, 17, 659. https://doi.org/10.3390/sym17050659
Tian W, Feng X, Gao L, Chen K, Chen Y, Shi J, Lao H. Improvement of Microwave Heating Uniformity Using Symmetrical Stirring. Symmetry. 2025; 17(5):659. https://doi.org/10.3390/sym17050659
Chicago/Turabian StyleTian, Wenyan, Xuxin Feng, Lin Gao, Kexin Chen, Yongjia Chen, Jiamin Shi, and Hailing Lao. 2025. "Improvement of Microwave Heating Uniformity Using Symmetrical Stirring" Symmetry 17, no. 5: 659. https://doi.org/10.3390/sym17050659
APA StyleTian, W., Feng, X., Gao, L., Chen, K., Chen, Y., Shi, J., & Lao, H. (2025). Improvement of Microwave Heating Uniformity Using Symmetrical Stirring. Symmetry, 17(5), 659. https://doi.org/10.3390/sym17050659





