Replication and Abstraction: Symmetry in Automated Formal Verification

Abstract

This article surveys fundamental and applied aspects of symmetry in system models, and of symmetry reduction methods used to counter state explosion in model checking, an automated formal verification technique. While covering the research field broadly, we particularly emphasize recent progress in applying the technique to realistic systems, including tools that promise to elevate the scope of symmetry reduction to large-scale program verification. The article targets researchers and engineers interested in formal verification of concurrent systems.

1. Introduction

Model checking is a verification technique that exhaustively examines a state-based representation of the system at hand [1,2]. Its main obstacle in practice is the state explosion problem: the exponential dependence of the size of the representation on the number of attributes characterizing a state. This problem is especially severe for concurrent systems, where state explosion is caused not only by the variable state space, but also by the existence of many components executing more or less independently. Such components are often replications of a generic behavioral description, for example identical worker threads in client-server architectures. Replication is the most serious contributor to state explosion in concurrent systems. On the other hand, replicated components usually induce a system model with a regular, symmetric structure, which can be reduced to a much smaller abstract model while preserving a significant class of properties.

Scope of this survey. In this article, we study the foundations of exploiting symmetry in model checking, as well as obstacles surrounding its applicability in practice. We start by formalizing the concept of symmetry in system models. We detail the principles behind symmetry reduction, and how they are implemented in explicit-state and symbolic model checkers. We discuss in detail the challenges that straightforward implementations face, such as the orbit problem of symbolic symmetry reduction and the existence of variables tracking process identities, and survey existing approaches that address these challenges. A treatment of how to detect symmetry from high-level system descriptions is, deliberately, postponed until the latter part of the article. We also touch upon slightly more exotic topics, such as reduction techniques for partially symmetric systems. Throughout this survey, we highlight tools that witness the practical significance of exploiting symmetry in designs, and illustrate the level of maturity some implementations have today. We conclude with an outlook on the role symmetry is likely to play in the future of formal verification, and an extensive literature list.

Symmetry is a tremendously broad subject in the sciences, the arts, and beyond. As a result, even in the comparatively narrow field of formal systems’ modeling — which is a prerequisite for applying automated verification techniques — there are several relevant notions of symmetry in designs. This survey focusses on the most significant flavor of symmetry in this field, namely symmetry that is due to the existence of many concurrent processes with the same, or a very similar, behavioral description. We mention other notions of symmetry, such as the independence of the program control flow of specific data values being manipulated, briefly in Section 2.3.

Another survey on symmetry? We are aware of three reasonably recent surveys of symmetry reduction techniques for model checking [3,4,5].

The focus of [3] is the work of P. Sistla and colleagues on symmetry reduction using annotated quotient structures. We do not survey such work here, since the techniques are specifically geared towards symmetry reduction in the presence of fairness constraints. While an important topic, it is somewhat orthogonal to more mainstream issues in symmetry reduction. Furthermore, there have been few developments in this area since the publication of [3], thus [3] remains an adequate review.

The contribution of [5] is a brief overview of the work of Donaldson and Miller on symmetry reduction techniques for explicit-state model checking. We do survey these techniques, since a number of papers continuing this line of work have subsequently appeared. Moreover, the methods are closely related to other, recently published techniques for symmetry reduction in explicit-state model checking that are not discussed in [5].

Of the existing surveys, closest in nature to ours is [4]. While [4] provides an encyclopedic (at the time of publication) discussion of papers on symmetry reduction, the present survey instead focusses on a) providing a tutorial-style introduction to symmetry reduction, presenting the theory from the ground up, with illustrative examples, and b) describing developments in the field that are not covered by [4]. Of these, the most notable are: recent techniques for efficiently computing orbit representatives in explicit-state model checking; new methods for exploiting symmetry via counter-abstraction; new methods for exploiting partial symmetry in systems; and the role of symmetry in SAT-based model checking.

Prerequisites. We assume the reader is familiar with elementary concepts of model checking. A Kripke structure is a transition system, where states are labeled with atomic propositions from some finite set AP, indicating which basic properties are true at each state. Formally, we write $M=(S,R,L)$, for a finite set of states S, a transition relation $R\subseteq S\times S$, and a labeling function $L:S\to 2^{\mathit{AP}}$. Sometimes it is useful to consider a set $S_0\subseteq S$ of initial states as part of the Kripke structure. Kripke structures are model-checked against classical temporal logics such as CTL*, and its sub-logics CTL and LTL [6]. For background on syntax and semantics of these logics, as well as on model checking algorithms, see for instance [7].

A group is a pair $(G,·)$ of a set G and an associative binary operation $·:G\times G\to G$ such that there exists an identity element $e\in G$. This is an element with the following property: for every $a\in G$, (i) $a·e=a$, and (ii) there exists an element $a^{-}\in G$ such that $a·a^{-}=e$. One can show that the identity element e is unique, as is the inverse element $a^{-}$, for $a\in G$. The element $a·b$ is called the product of a and b.

A permutation [acting] on a set Z is a bijective mapping $\pi :Z\to Z$. Permutations on a set form a group, with function composition as the operation. We denote the group of all permutations on a set Z by Sym Z. If Z is finite with cardinality n, then Sym Z has cardinality $n!$ (n factorial).

2. Immunity to Change: Symmetry in Kripke Structures

Symmetry is often explained as immunity to possible change [8]. This means that there are transformations that change the state of an object, but some aspects of the object remain invariant. If we are interested in those invariant aspects, then for us the object is immune to the change brought about by the transformations. The key to formalizing the concept of symmetry of a Kripke structure is therefore to specify what those transformations are. Our goal is to remove structure redundancy that is due to the existence of many replicated concurrent components, called processes. It is thus natural to consider transformations that permute the role of the processes in the system, and see what changes they cause to a system state. (Note that, while this type of symmetry transformation is the most intensely studied, there are others; see Section 2.3.)

2.1. Permutations Acting on States of a Kripke Structure

Let $M=(S,R,L)$ be a Kripke structure modeling a system of n concurrently executing processes communicating via shared variables. (Whether the execution model is asynchronous or synchronous or something else is not relevant for this survey.) A state $s\in S$ can be assumed to have the form $s=(g,l_1,\dots ,l_n)$, where the shared state g summarizes the values of all shared program variables, and the local state $l_i$ of process i summarizes the values of all local variables of process i. We model permutations of the processes by permutations on $\{1,\dots ,n\}$. A permutation $\pi$ can be extended to act on the state space S of the Kripke structure, as follows.

$$\pi (s)=\pi (g,l_1,\dots ,l_n)=(g^{\pi },l_{\pi (1)},\dots ,l_{\pi (n)})$$

(1)

That is, a permutation acts on a global state s by (i) acting on the shared state g in a way described below, and by (ii) acting on the processes’ local states by interchanging their indices. For example, let $s=(A,B,C)$ for a three-process system with no shared state and local states $A,B,C$; i.e., $l_1=A$, $l_2=B$, $l_3=C$. The left-shift permutation acts on s by left-shifting the local states in s, for example $l_{\pi (1)}=l_2=B$. We obtain:

(2)

For the shared variables summarized in g, things are a bit more complicated. Suppose there are k shared variables, for some $k\ge 0$, so that $g:=(g_1,\cdots ,g_k)$. In equation (1), the vector of values of shared variables in state $\pi (s)$ is $g^{\pi }$, which we denote $(g_1^{\pi },\cdots ,g_k^{\pi })$. We now explain how the $g_i^{\pi }$ are defined.

Some of the shared variables are unaffected by a permutation. Consider the binary semaphore variable in Figure 1 (left) that monitors access to a critical code section in a synchronization protocol. The semaphore is set to true whenever any process enters the critical code section. This action is not affected by permuting the process indices in a global state. We call variables like such a semaphore id-insensitive; a permutation acts on them like the identity: if the i-th shared variable is id-insensitive then $g_i^{\pi }:=g_i$.

Now consider the token variable $\mathit{tok}$ in Figure 1 (right). It ranges over process indices: its value is the identity of the process that is allowed to enter its critical section next; the initial value $\mathit{nd}$ is chosen nondeterministically from $\{1,\dots ,n\}$. We call such variables id-sensitive. How does a permutation act on an id-sensitive variable? That is, if the i-th shared variable is id-sensitive and $g_i$ is the value of this variable in state s, how do we define the value $g_i^{\pi }$ of the variable in state $\pi (s)$? Intuitively, the local state of process $g_i$ in state s must be the same as that of process $g_i^{\pi }$ in state $\pi (s)$. We thus have to solve the equation $s_{g_i}=s_{\pi (g_i^{\pi })}$ for $g_i^{\pi }$. The only solution that works in the general case, which manifests if the local states in s are pairwise distinct, is given by $\pi (g_i^{\pi })=g_i$. We thus define $g_i^{\pi }:={\pi }^{-}(g_i)$.

For example, consider the state $(3,N,T,C)$ of the three-process concurrent system derived from the skeleton in Figure 1. Processes 1, 2 and 3 are in local states $N,T,C$, respectively, and $\mathit{tok}$ has the value 3. The left-shift permutation $\pi$ from equation (2) changes the state to $(2,T,C,N)$ (as ${\pi }^{-}(3)=2$). As a result, the process possessing the token is in local state C, before and after applying the permutation.

We note that id-sensitive variables can also be local to processes. In this case, equation (1) does not define a suitable permutation action. We explain this (much more complicated) scenario in Section 4.3.

Excursion on group actions. The notation $\pi (s)$, for a permutation $\pi$ on $\{1,\dots ,n\}$ and a state s, is a widely accepted abuse. More carefully, the group G of permutations on $\{1,\dots ,n\}$ is extended to the set S of states of M using a group action. In general, given a group G and a set S, this is a mapping $\beta :G\times S\to S$ such that (i) for each $s\in S$, $\beta (\mathit{id},s)=s$, and (ii) for all $\pi$, $\sigma \in G$ and $s\in S$, $\beta (\pi ·\sigma ,s)=\beta (\pi ,\beta (\sigma ,s))$, where · is the group operation of G. Permutation $\pi \in G$ induces the mapping on S that is defined, for $s\in S$, by $s\mapsto \beta (\pi ,s)$. In particular, by (i), G’s identity id induces the identity function on S. It can be shown that the expression on the right-hand side of (1) defines a group action $\beta$ on S. The notation $\pi (s)$ should be viewed as a shorthand for $\beta (\pi ,s)$. Likewise, the extension $\pi :S\to S$ of $\pi$ to S really stands for the mapping obtained by “currying” $\beta$ into ${\beta }_{\pi }:S\to S$, defined by $s\mapsto {\beta }_{\pi }(s)=\beta (\pi ,s)$. Property 1 A group action on G and S enjoys the following properties. 1.  For every $\pi \in G$, the mapping $\pi :S\to S$ is a bijection. 2.  The set $\{\pi :S\to S|\pi \in G\}$ of functions forms a group under function composition. 3.  The relation on S defined by $$s\equiv tiffthereexists\pi \in Gsuchthat\pi (s)=t$$ is an equivalence relation. All of these properties will be crucial when we take advantage of symmetry in model-checking a Kripke structure. In particular, from Property 1.1, we conclude that $\pi (S)=S$. The quality of $\pi$ exposing symmetry of M is determined by how the other components of M react to being subjected to $\pi$.

2.2. Symmetry

Intuitively, a Kripke structure modeling a multi-component system exhibits symmetry if it is insensitive to interchanges of processes by certain permutations. Such permutations are called automorphisms:

Definition 2

An automorphism of a Kripke structure $M=(S,R,L)$ is a permutation $\pi$ on $\{1,\dots ,n\}$ such that

1. 

R is invariant under $\pi$: for any $(s,t)\in R$, $(\pi (s),\pi (t))\in R$, and

2. 

L is invariant under $\pi$: for any $s\in S$, $L(s)=L(\pi (s))$.

Symmetric transitions. Requirement 1 in Definition 2 states that applying an automorphism to any transition again results in a valid transition. A permutation acts on a transition by consistently interchanging components in the source and target states. Revisiting the example in Figure 1 (right), the skeleton allows any process to transit from local state C to local state N, accompanied by a modulo-increment of the token variable, so $(1,T,N,C)\to (2,T,N,N)$ is a valid transition. Applying the left-shift permutation given in equation (2), we obtain $(3,N,C,T)\to (1,N,N,T)$, which must also be a valid transition for the left-shift to be an automorphism of the induced Kripke structure. This is indeed the case in this example and for this particular permutation. On the other hand, the permutation that swaps 1 and 2 is not an automorphism of the Kripke structure: applying it to $(1,T,N,C)\to (2,T,N,N)$, we obtain $(2,N,T,C)\to (1,N,T,N)$. This pair is not a valid transition, since the skeleton requires that the token be passed on to the “next” process, 3, when process 2 leaves the critical section C.

Symmetric atomic propositions. Requirement 2 in Definition 2 states that the atomic propositions that appear as labels on the states must be insensitive to permutations of the processes. For example, if we want to restrict the state space search during model checking to the set of reachable states, we need an atomic proposition that refers to the initial states. Requirement 2 then entails that the set of initial states must be closed under permutation applications.

In practice, atomic propositions are usually given as indexed propositional formulas over the local states of the processes (or, more generally, over simple expressions involving the local variables). For example, the proposition $L_i$ would indicate that process i resides in local state L. Symmetry then simply means that the propositional formula is invariant under permutations in G; these permutations act on the propositions’ indices. Typical symmetric atomic propositions quantify over these indices, rather than mention any index explicitly. Examples of such propositions include

$$(\mathrm{a})\forall i:N_i(\mathrm{b})\exists i,j:i\ne j\wedge C_i\wedge C_j(\mathrm{c})\forall i:{\mathit{RUN}}_i\Rightarrow ⌝{\mathit{RUN}}_{(imodn)+1}$$

(3)

Atomic proposition (b), for instance, states that two (distinct) processes are in their critical section C. Intuitively, the symmetry of this formula is reflected by the indifference towards the identity of the two processes. Note that the use of quantifiers over $\{1,\dots ,n\}$ in these (propositional) formulas is to be understood as an appropriate conjunction or disjunction.

In these examples, the quantifier expressions such as $\forall i$ directly precede the indexed propositional expressions such as $C_i$, rendering the whole proposition symmetric. The direct precedence is critical. Consider the CTL liveness formula AG $\forall i:(T_i\Rightarrow \mathtt{AF}{C}_i)$, which expresses that whenever a process is in local state T, it will eventually proceed to local state C. In this formula, the indexed propositional expression $C_i$ is separated from the ∀ quantifier by the non-propositional operator AF. The unquantified expression $C_i$ itself is not invariant under permutations (since, e.g., different states are labeled with $C_1$ than with $C_2$). There is no way to extract symmetric atomic propositions from this formula.

A “cheap” solution to this problem is to consider instead the weaker communal progress formula $\mathtt{AG}\forall i:(T_i\Rightarrow \mathtt{AF}\exists j:C_j)$. It expresses that whenever a process is in local state T, there will eventually be some process that proceeds to local state C. Since the expression to the right of the implication is independent of i, we can equivalently rewrite this formula as $\mathtt{AG}(\exists i:T_i\Rightarrow \mathtt{AF}\exists j:C_j)$. We can now choose $\exists i:T_i$ and $\exists j:C_j$ as symmetric atomic propositions.

A stronger solution, which allows us to verify the original formula $\mathtt{AG}\forall i:(T_i\Rightarrow \mathtt{AF}{C}_i)$, is the following. Observe first that this formula is equivalent to $\forall i:\mathtt{AG}(T_i\Rightarrow \mathtt{AF}{C}_i)$ — the modality AG and the quantifier ∀ are both of a universal nature and commute. We now argue, using symmetry, that the new formula is in turn equivalent to $\mathtt{AG}(T_1\Rightarrow \mathtt{AF}{C}_1)$. To see that $\mathtt{AG}(T_1\Rightarrow \mathtt{AF}{C}_1)$ implies $\forall i:\mathtt{AG}(T_i\Rightarrow \mathtt{AF}{C}_i)$, let i be arbitrary, and let $\pi$ be a permutation such that $\pi (1)=i$. The existence of such a $\pi$ is guaranteed for example for transitive groups [9, def. 7.1]. Applying $\pi$ to the formula $\mathtt{AG}(T_1\Rightarrow \mathtt{AF}{C}_1)$ yields $\mathtt{AG}(T_i\Rightarrow \mathtt{AF}{C}_i)$. Provided that $\pi$ is an automorphism of the Kripke structure, the Kripke structure does not change due to the application of $\pi$, so the verification result stays the same.

We can now focus on the simpler formula $\mathtt{AG}(T_1\Rightarrow \mathtt{AF}{C}_1)$. This formula is still not invariant under permutations that change index 1, but under all others. That is, if G is the automorphism group of the Kripke structure, the simpler formula is symmetric with respect to the automorphism subgroup $\{\pi \in G:\pi (1)=1\}$. Informally, we have solved the problem of asymmetry in the formula $\mathtt{AG}\forall i:(T_i\Rightarrow \mathtt{AF}{C}_i)$ by factoring out process 1.

Symmetry. With Definition 2 in place, symmetry is simply defined as the existence of a (nontrivial) set G of automorphisms. We require the set G of permutations to be a group, so that we can extend them to act on S via a group action.

Definition 3

Let G be a group of permutations on $\{1,\dots ,n\}$. Kripke structure $M=(S,R,L)$ is symmetric with respect to G if every $\pi \in G$ is an automorphism of M.

Since the automorphisms of a Kripke structure form a group, too, denoted Aut M, we can rephrase this definition by requiring that G be a subgroup of Aut M.

We mention some important cases of symmetric systems. In applications where processes are completely interchangeable, all permutations are automorphisms, so we can choose $G:=Sym\{1,\dots ,n\}$. Such systems are referred to as fully symmetric. This case is not only frequent in practice, but is also easier to handle, and permits greater reduction, than other types of symmetry, as we shall see soon. When processes are arranged in a ring, such as in many instances of the dining philosopher’s problem, or in the example in Figure 1 (right), we may be able to rotate the ring without changing the structure. For G, we can choose the group of the n rotation permutations; we speak of rotational symmetry. Finally, symmetry groups occurring in practice are often direct products of smaller groups. Consider a solution of the Readers-Writers synchronization problem [10]. In this problem, the participating processes are partitioned into a set of r readers and a set of w writers. Within each set all processes are interchangeable; we can choose $G:=Sym\left\{1,\dots ,r\right\}\times Sym\{r+1,\dots ,r+w\}$. In general, the more permutations we can prove to be automorphisms, the more reduction can be obtained from the symmetry. Therefore, ideally we would like to take G to be the entire automorphism group of M. Sometimes, however, the exact group Aut M is unknown or expensive to determine; Definition 3 only requires G to be a subgroup of it.

We finally observe the following property, which can be concluded from the group properties of Aut M:

Property 4

If $\pi$ is an automorphism, then $(s,t)\in R$ exactly if $(\pi (s),\pi (t))\in R$.

The condition “$(s,t)\in R\mathrm{exactly}\mathrm{if}(\pi (s),\pi (t))\in R$” can be abbreviated as $R=\pi (R)$. Since also $S=\pi (S)$ and $L=\pi (L)$, in the sense of Definition 2, we can characterize an automorphism $\pi$ of M by the concise notation $M=\pi (M)$.

2.3. Discussion: Origin of Symmetry in Systems

We have attributed symmetry in a Kripke structure model of a system to the existence of many replicated and thus in some way interchangeable components. We note that there are other causes for symmetry. Data values that are indistinguishable to the temporal property under consideration introduce redundancy that can be formalized using symmetries. For example, consider a piece of hardware implementing the basic read and write functionality of a memory unit. We may want to verify that the value that is stored can later be retrieved — we don’t care what that value is. This phenomenon, called data symmetry, can be handled using the theory of data-independence, described in an early paper by Pierre Wolper [11]. Another source of symmetry, in models of software with dynamic memory management, two states may be regarded symmetric if their heaps are isomorphic. Techniques for canonizing heap representations have been developed [12,13] and used in practical model checkers [14,15]. Common to all these notions of symmetry is the fact that they can be formalized using bijections $\pi :S\to S$ on the state space S that leave the transition relation invariant. What differs is how these bijections act on state components (equation (1) is just one example, applying to processes as state components) and, accordingly, how these types of symmetry can be exploited during model checking. For the remainder of this survey, we focus on symmetry among replicated concurrent components, since this form occurs commonly in practice, and has been studied most extensively in the literature.

Before we discuss how we can make use of symmetry towards reducing state explosion, we note that it is of course necessary to have some means of establishing whether a system is symmetric. Automatic symmetry detection techniques are essential for symmetry reduction to be sound and viable. However, one can argue that such techniques are less important than techniques for exploiting information about symmetry during model checking. Knowing about symmetry is pointless if we cannot benefit from this knowledge, and in the absence of automatic symmetry detection techniques we can require symmetry to be specified manually; indeed, early implementations of symmetry worked under this proviso [16]. For this reason, we postpone the discussion of practical symmetry detection techniques to Section 7.

3. Symmetry Reduction as Existential Abstraction

In this section, we show that symmetry in a Kripke structure $M=(S,R,L)$ induces an abstract Kripke structure that is usually much smaller than M, and shares with M all temporal-logic properties over $AP$. In the subsequent sections, we will see how to take advantage of this reduced structure in practice, in order to reduce the impact of state explosion.

3.1. The Canonical Symmetry Quotient

The starting point is Property 1.3, which states that, given a group action of G on S, an equivalence relation on S is given by the orbit relation$\equiv \subseteq S\times S$, defined by

$$s\equiv t\mathrm{iff}\mathrm{there}\mathrm{exist}\pi \in G\mathrm{such}\mathrm{that}\pi (s)=t$$

(4)

In other words, the orbit relation relates two states if they are identical up to the particular arrangement of the processes in them. We have seen the state vectors $(3,N,T,C)$ and $(2,T,C,N)$ in Section 2.1 They are equivalent under the orbit relation provided the left-shift permutation is part of the symmetry group G. The equivalence class — orbit — of a state s is the set $\left[s\right]=\{\pi (s):\pi \in G\}$.

Like any equivalence relation on S, the orbit relation can be used to construct what is know as the canonical quotient structure $\overline{M}=(\overline{S},\overline{R},\overline{L})$ of M, algebraically denoted $M/\equiv$. This Kripke structure is defined as follows:

$$\begin{array}{ccc}\hfill \overline{S}& =& \left\{\right[s]:s\in S\}(\mathrm{set}\mathrm{of}\mathrm{equivalence}\mathrm{classes}\mathrm{of}\equiv )\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill \overline{R}& =& \{(\left[s\right],\left[t\right])\in \overline{S}\times \overline{S}:\exists s_0\in \left[s\right],t_0\in \left[t\right]:(s_0,t_0)\in R\}\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill \overline{L}([s])& =& L(s)\hfill \end{array}$$

(7)

Note that some restrictions on L are required to make sure $\overline{L}$ is well-defined. This is given by Definition 2.2, which states (in slightly different terms) that L agrees on all states in $\left[s\right]$. Figure 2 shows a small fully symmetric example Kripke structure for a 2-process mutual-exclusion scenario, and its quotient. The set of atomic propositions might include, for example, the labels $\forall i:N_i$, $\forall i:T_i$, and $\forall i:C_i$; a suitable labeling function L might then be defined as $L(N_1{N}_2)=\{\forall i:N_i\}$, $L(T_1{T}_2)=\{\forall i:T_i\}$, $L(C_1{C}_2)=\{\forall i:C_i\}$, and $L(s)=\varnothing$ for all other states s of M. This function assigns the same label to symmetric states; the derivation of $\overline{L}$ from L is immediate.

The formation of the symmetry quotient is an instance of existential abstraction [17], with the orbit relation as the underlying state equivalence. Existential abstraction always leads to a quotient Kripke structure that is able to simulate the original, via the canonical simulation relation associating states in S with their equivalence classes in $\overline{S}$. It turns out that in the special case of symmetry, M and $\overline{M}$ are even bisimilar [18]:

Theorem 5

([19]) Let M be a Kripke structure symmetric with respect to a group G. The quotient Kripke structure $\overline{M}$, derived from the orbit relation, is bisimilar to M.

The significance of the theorem lies in the fact that Kripke structures M and its symmetry quotient $\overline{M}$, being bisimilar, satisfy the same CTL* formulas [7]. Thus, a verification problem of the form $M,s\models f$ with CTL* formula f over symmetric atomic propositions (such as in equation (3)), can be replaced by the equivalent verification problem $\overline{M}$, $\left[s\right]\models f$. For example, both Kripke structures in Figure 2 satisfy the CTL* formula $\varphi =\mathtt{AG}(\exists i:T_i\Rightarrow \mathtt{AF}\exists j:C_j)$.

In addition to the preservation of temporal logic formulas, the other driving factor behind the popularity of symmetry as a reduction method is of course that the quotient is usually significantly smaller: an orbit can comprise up to $n!$ states of M. This is the case under full symmetry and for states whose n processes are in pairwise distinct local states; there are $n!$ distinct permutations of these local states. On the other hand, consider a fully symmetric state with no shared variables, i.e. of the form $(A,\dots ,A)$; its orbit has size 1. In the absence of shared variables, the total number of orbits irrespective of reachability, i.e. the size of the conceivable quotient state space, is given by the following property:

Property 6

For a fully symmetric Kripke structure M over n processes and l local states with no shared variables, the quotient with respect to the orbit relation has $\left(\begin{array}{c}n+l-1\\ n\end{array}\right)$ states.

The property follows from a combinatorial argument: under full symmetry, an orbit is a combination of l objects taken n at a time with repetition, whose number is given by the binomial coefficient in Property 6. This quantity can be estimated to be much smaller than $l^n$ (the number of states of M) if n and l are large. The reduction effect dwindles with decreasing size of the symmetry group. For example, under rotational symmetry, orbits have no more than n members, so we can expect savings of at most a linear factor. In the presence of shared variables, an upper bound on the number of quotient states, under full symmetry, is given by the formula of Property 6, multiplied by the product of the domain sizes of all shared variables. If the shared variables are all id-insensitive, this upper bound is precise.

3.2. The Quotient over Representative States

Recall the definition of $\overline{M}$’s transition relation:

$$\overline{R}=\{(\left[s\right],\left[t\right])\in \overline{S}\times \overline{S}:\exists s_0\in \left[s\right],t_0\in \left[t\right]:(s_0,t_0)\in R\}$$

(8)

Although states of the quotient model, such as $\left[s\right]$ and $\left[t\right]$, are formally defined as equivalence classes, it is unreasonable to encode them this way. Instead, we can define $\overline{S}$ to be a fixed set of representatives of each equivalence class. This has the practically useful and simplifying consequence that the abstract states are embedded in the concrete state space: $\overline{S}\subseteq S$; we can model states of $\overline{S}$ as we would model states of S. The definition of $\overline{R}$ changes in that the condition $s_0\in \left[s\right]$ in equation (8) becomes $s_0\equiv \overline{s}$:

$$\begin{array}{ccc}\hfill \overline{S}& =& \mathit{fixed}\mathit{set}\mathit{of}\mathit{representatives}\mathit{of}{\equiv }^{\prime }s\mathit{equivalence}\mathit{classes}\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \overline{R}& =& \{(\overline{s},\overline{t})\in \overline{S}\times \overline{S}:\exists s_0\equiv \overline{s},t_0\equiv \overline{t}:(s_0,t_0)\in R\}\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill \overline{L}(\overline{s})& =& L(\overline{s})\hfill \end{array}$$

(11)

The set $\overline{S}$ must contain at least one representative for each symmetry equivalence class. Ideally, $\overline{S}$ should in fact have a unique representative per class. In that case, the quotient Kripke structure as above is isomorphic to the canonical quotient defined in Section 3.1 over equivalence classes, and all conclusions drawn at the end of that section remain valid. Figure 3 repeats the 2-process mutual-exclusion scenario from Figure 2 and shows its representative quotient; compare this to the canonical quotient shown in the earlier figure. The unique representatives are chosen as the lexicographically least orbit members, under the alphabetical local state order $C<N<T$.

It is quite easy to see that the uniqueness condition is actually not necessary. In Section 5, we will see a case where it makes sense to permit several representatives per orbit, even if that means a loss of compression. For now, however, we consider $\overline{M}$ to be defined as in (9)-(11), over unique representative states.

Bibliographic notes on the foundations of symmetry in model checking. Early works on exploiting symmetry in finite-state verification were in the context of deciding reachability in Petri nets [20,21]. Initial results on symmetry reduction for model checking were obtained simultaneously by three research groups: Clarke, Filkorn and Jha [22], Emerson and Sistla [23], and Ip and Dill [24]. Extended versions of these papers were thereafter published in a special issue of the journal Formal Methods in System Design [9,19,25].

Of these foundational papers, the work of Clarke et al. presents a correspondence theorem showing that satisfaction of CTL* formulas is preserved under symmetry reduction. The papers also discuss the problem of detecting when states are equivalent, and investigate the combination of symmetry reduction with symbolic techniques. The papers of Emerson and Sistla present theoretical results for symmetry reduction in the general setting of μ-calculus model checking, and lay the foundations for an automata-theoretic method for exploiting symmetry which has since been used as a basis for exploiting symmetry under fairness assumptions. The work of Ip and Dill addresses the practical problem of identifying symmetry in an input program, presenting a language extended with a datatype for describing the presence of symmetry, and describing an extension of the Murφ verification system which uses this symmetry information to reduce state explosion.

4. Symmetry Reduction in Explicit-State Model Checking

In Section 3, we have shown that a model of a symmetric structure gives rise to a bisimilar and comparatively small quotient model over representative states. We now want to incorporate these ideas into an explicit-state model checking algorithm, i.e., one that stores and explores model states one by one. An asset that we wish to preserve of such algorithms is their ability to operate without pre-computing the set R of transitions. Instead, successors of states are determined on the fly, by converting model states into program states and then executing the program. In the context of symmetry reduction, this means that we want to avoid an a-priori construction of both the concrete transition relation R and the quotient relation $\overline{R}$.

4.1. Explicit-State Model Checking under Symmetry

The general principle underlying explicit-state model checkers exploiting symmetry is that any given model checking algorithm is modified by modifying its image computation. The standard image operation computes the set Image${}_R(U)=\{v\in S:\exists u\in U:(u,v)\in R\}$. The modified image operation proceeds in two stages:

stage 1:

given a representative state, compute its successors under the given program, i.e., its successors under the concrete transition relation R. This is possible since $\overline{S}\subseteq S$: representative states are just particular states of M, to which M’s image operation R, induced by the program, can be applied. This will, in general, result in non-representative states, not part of the quotient Kripke structure.

stage 2:

rectify the situation by mapping each obtained successor to its representative.

The result of this modified image operation is a set of successor states that belong to $\overline{S}$. Before we see the operation in action, let us discuss its correctness. Given a representative state $\overline{u}$, stage 1 applies to $\overline{u}$ the image operation Image${}_R$ under transition relation R. Stage 2 applies to the result the abstraction mapping $\alpha (V)=\{\overline{v}\in :\exists v\in V:v\equiv \overline{v}\}$, which maps states from a set $V\subseteq S$ to their respective representatives. The following lemma states that the image computed in the two-stage process is precisely the image that would have been computed under the quotient transition relation (equation (10)), namely ${\mathtt{Image}}_{\overline{R}}(\overline{U})=\{\overline{v}\in \overline{S}:\exists \overline{u}\in \overline{U},u\equiv \overline{u},v\equiv \overline{v}:(u,v)\in R\}$:

Lemma 7

For an arbitrary set $\overline{U}\subseteq \overline{S}$ of representatives, ${\mathtt{Image}}_{\overline{R}}\overline{U}=\alpha ({\mathtt{Image}}_R\overline{U})$.

A proof of this lemma can be found in [26].

This image operation is used in a model checking algorithm in the standard way: new states are compared against previously encountered states and, if new, added to some worklist. The set of stored states is, at all times, a subset of $\overline{S}$; non-representative states are only generated as an intermediate result of the modified image operation. As an example, Algorithm 1 shows the complete algorithm for explicit-state reachability analysis under symmetry, given a symmetric initial state set $S_0$ and a function error $:S\to \{true,false\}$ encoding an error condition (see also [9], p. 85). Containers Reached and Unexplored contain only elements from $\overline{S}$; the algorithm deviates from standard reachability analysis only in the applications of $\alpha$ in lines 1 and 5. We conclude that symmetry reduction is quite easy to implement if the representative mapping $\alpha$ is; this is the topic of Section 4.2.

Algorithm 1 Reachability Analysis under Symmetry

1: Reached $:=\{\alpha (s_0):s_0\in S_0\}$; Unexplored $:=$ Reached  2: while Unexplored $\ne \varnothing$ do  3:  remove an element $\overline{s}$ from Unexplored  4:  for all $t\in {\mathtt{Image}}_R(\overline{s})$ do  5:    $\overline{t}:=\alpha (t)$  6:    if $\overline{t}$ ∉ Reached then  7:     if error $(\overline{t})$ then  8:      return “error state $\overline{t}$ reached”  9:     end if 10:     add $\overline{t}$ to Reached and to Unexplored 11:    end if 12:  end for 13: end while 14: return “no error state reachable”

4.2. Mapping States to Representatives

The most important operation specific to symmetry reduction is to map a state to its representative. This operation is used in stage 2 of the image computation shown in the previous section. More generally, a representative mapping can be used to detect whether two states are equivalent: they are exactly if their representatives are the same (assuming the representatives are unique). Under arbitrary symmetries, state equivalence is known to be as hard as the graph isomorphism problem [16]. This problem, while considered tractable in practice, causes a lot of overhead for symmetry reduction that reduces its value considerably. To be effective, an explicit-state model checker must be capable of enumerating hundreds-of-thousands of states per second, thus calling out to a graph isomorphism checker for each visited state is likely to be expensive. Nevertheless, this strategy has been employed in practice with some success [27,28].

Fortunately, there are important and frequent special cases where representatives can be computed reasonably efficiently. It is useful to represent a state by the lexicographically smallest equivalent one. Fix a suitable total order on the set of local states. For states $s=(g,l_1,\cdots ,l_n)$ and $s^{\prime }=(g^{\prime },l_1^{\prime },\cdots ,l_n^{\prime })$, we say that s is lexicographically less than $s^{\prime }$, written $s{<}_{\mathrm{lex}}{s}^{\prime }$, if (i) $(l_1,\cdots ,l_n){<}_{\mathrm{lex}}(l_1^{\prime },\cdots ,l_n^{\prime })$, or (ii) $l_i=l_i^{\prime }$ for all $i\in \{1,\dots ,n\}$ and $g{<}_{\mathrm{lex}}{g}^{\prime }$ (recall that g and $g^{\prime }$ are vectors of values of shared variables).

For a small symmetry group, such as the rotation group, it is possible to simply try all permutations to determine the lexicographically least equivalent state. For the full symmetry group, and in the absence of shared variables, we can lexicographically sort a state vector $(l_1,\dots ,l_n)$. For example, $(A,C,A,B)$ and $(B,A,A,C)$ are equivalent local state vectors because the lexicographically least equivalent state for both is $(A,A,B,C)$. This can certainly be determined in $\mathcal{O}(nlogn)$ time. (Note that this method maps a state s to its representative $\overline{s}$ without explicitly computing the permutation $\pi$ such that $\pi (s)=\overline{s}$.)

Id-sensitive shared variables. Clearly, this sorting strategy also works in the presence of id-insensitive shared variables, on which permutations have no effect. However, extending sorting to handle id-sensitive shared variables requires caution. Suppose the vector g of shared variables contains id-sensitive variables $x_1,\cdots ,x_k$, in this order. For a state s, let $s(x_i)$ denote the value of variable $x_i$ ($1\le i\le k$). We seek a procedure that, given a state s, yields a state $s^{\prime }$ such that (i) the local states in $s^{\prime }$ appear in sorted order, (ii) the vector $(s^{\prime }(x_1),\cdots ,s^{\prime }(x_k))$ is as small as possible, and (iii) $s=\pi (s^{\prime })$ for some permutation $\pi$. Such a procedure can be used to detect state equivalence, since state $s^{\prime }$ is precisely the lexicographically least state equivalent to s. We compute $s^{\prime }$ as follows. Suppose the tuple of local states in s is $(l_1,\cdots ,l_n)$. We sort this tuple, yielding sorted local states $(l_1^{\prime },\cdots ,l_n^{\prime })$ in $s^{\prime }$. We then consider the $x_i$ in order. We set $s^{\prime }(x_i)=s^{\prime }(x_j)$ if there is some $j<i$ such that $l_{s(x_i)}=l_{s(x_j)}$. Otherwise, we set $s^{\prime }(x_i)=min\{j:l_j^{\prime }=l_{s(x_i)}\wedge \forall d<i:x_d\ne j\}$.

To illustrate this, suppose we have three id-sensitive variables, $x_1,x_2,x_3$. Consider states $s=((1,2,3),A,C,A,B)$ and $t=((3,4,2),B,A,A,C)$. Here, $s(x_1)=1$, $s(x_2)=2$, $s(x_3)=3$, and similarly for the id-sensitive variables of t. We compute the lexicographically least equivalent state $s^{\prime }$ for s by first sorting its local states component, yielding the tuple $(A,A,B,C)$. This gives us the partial state $s^{\prime }=((?,?,?),A,A,B,C)$. We then choose as a new value for $x_1$ the smallest process id j such that the local state for j in $s^{\prime }$ is the same as the local state for $s(x_1)$ in s. Since $s(x_1)=1$ and process 1 has local state A in s, we set $s^{\prime }(x_1)=1$. We now have $s^{\prime }=((1,?,?),A,A,B,C)$. By a similar argument, we choose $s^{\prime }(x_2)=4$, yielding $s^{\prime }=((1,4,?),A,A,C,B)$. When choosing a new value for $x_3$ in $s^{\prime }$, we do not pick 1: even though the local states for processes $s(x_3)$ and 1 in states s and $s^{\prime }$ respectively are both A, we have $s(x_1)\ne s(x_3)$, thus we require $s^{\prime }(x_1)\ne s^{\prime }(x_3)$. We therefore choose the second-smallest id of a process with local state A in $s^{\prime }$. This yields $s^{\prime }(x_3)=2$, and the final state $s^{\prime }=((1,4,2),A,A,B,C)$. Applying the same process to state t yields the lexicographically least state $t^{\prime }=s^{\prime }$; thus s and t are equivalent under full symmetry.

Composite groups. For a group G that decomposes as a disjoint product of subgroups H and K, a representative for state s can be computed by first computing the lexicographically least state $s^{\prime }$ equivalent to s under H, then computing the lexicographically least state $s^{″}$ equivalent to $s^{\prime }$ under K. Since, by basic group theory, $\left|G\right|=\left|H\right|\times \left|K\right|$, even if we must resort to trying all permutations of H and K, this will still be much more efficient than trying all permutations of G. Furthermore, it may be possible to handle H and K efficiently, e.g. if they are full symmetry groups or decompose into further products of subgroups. The idea of computing lexicographically least elements by decomposing a group as a product of subgroups was introduced in [16,29], and is studied extensively in [30,31].

4.3. Id-sensitive Local Variables

So far, we have considered a model of computation where the local states of distinct processes are id-insensitive. While we have permitted shared variables whose values are process ids, our model of computation cannot capture systems where processes have local variables whose values are themselves process ids. This scenario is required, for example, in distributed leader election algorithms where processes dynamically arrange themselves into a particular topological configuration [32]. We show that the action of a permutation on a state defined in equation (1) does not make sense in the presence of id-sensitive local variables, and define a suitable action. We then discuss the effect of id-sensitive local variables on the problem of detecting state equivalence under full symmetry.

Consider a system of three processes where the local state of a process is a pair $(\mathit{pc},\mathit{leader})$, with $\mathit{pc}$ being a program location taken from the set $\{A,B,C\}$ and $\mathit{leader}$ an id-sensitive local variable. An example global state is $s=((A,2),(B,2),(C,1))$. We can represent s using our existing model of computation by introducing fresh local state names to summarize $(\mathit{pc},\mathit{leader})$ pairs. Summarizing $(A,2)$, $(B,2)$ and $(C,1)$ by $A^{\prime }$, $B^{\prime }$ and $C^{\prime }$ respectively leads to the summarized global state $s^{\prime }=(A^{\prime },B^{\prime },C^{\prime })$. Suppose we now apply permutations to summarized states using the action described by equation (1). Applying the permutation $\pi$ that swaps 1 and 2 to $s^{\prime }$ yields $\pi (s^{\prime })=(B^{\prime },A^{\prime },C^{\prime })$. “De-summarizing” $\pi (s^{\prime })$ gives $\pi (s)=((B,2),(A,2),(C,1))$. This state does not fit our intuition as to the effect a permutation should have on a state. State s has the property: “the $\mathit{leader}$ variable of process 2 refers to itself”. Since $\pi$ exchanges 1 and 2, state $\pi (s)$ should have the property: “the $\mathit{leader}$ variable of process 1 refers to itself”, however, we have derived $\pi (s)$ such that the $\mathit{leader}$ variable of process 1 actually refers to process 2. State $\pi (s)$ is almost what we want: the states of processes 1 and 2 have indeed been exchanged. To reflect this change in the permuted state, we must additionally apply $\pi$ to modify the values of the $\mathit{leader}$ local variables, giving $\pi (s)=((B,1),(A,1),(C,2))$. This state has the desired property that “the $\mathit{leader}$ variable of process 1 refers to itself”.

Extended permutation action. We now formally define the action of a permutation on a state with id-sensitive local variables. For a system comprised of shared variables g, together with n processes where each process has k id-sensitive local variables, a state can be assumed to have the form:

$$(g,(l_1,r_{1,1},\cdots ,r_{1,k}),\cdots ,(l_n,r_{n,1},\cdots ,r_{n,k}))$$

Here $l_i$ and $r_{i,j}$ represent the id-insensitive local state and value of the j-th id-sensitive variable of process i, respectively ($1\le i\le n$, $1\le j\le k$). The action of a permutation on a state, defined in Section 2.1, naturally extends to act on states extended with id-sensitive local variables, as follows:

$$\begin{array}{ccc}\pi (s)& =& \pi (g,(l_1,r_{1,1},\cdots ,r_{1,k}),\dots ,(l_n,r_{n,1},\cdots ,r_{n,k}))\hfill \\ & =& (g^{\pi },(l_{\pi (1)},{\pi }^{-}(r_{\pi (1),1}),\cdots ,{\pi }^{-}(r_{\pi (1),k})),\dots ,(l_{\pi (n)},{\pi }^{-}(r_{\pi (n),1}),\cdots ,{\pi }^{-}(r_{\pi (n),k})))\hfill \end{array}$$

(12)

Extended state equivalence detection. Now that we have a sensible action for permutations in the presence of id-sensitive local variables, we return to our original goal: detecting state equivalence by mapping a state to its lexicographically least equivalent state. First, we must define what it means to compare states containing id-sensitive local variables lexicographically. We write

$$(g,(l_1,r_{1,1},\cdots ,r_{1,k}),\cdots ,(l_n,r_{n,1},\cdots ,r_{n,k})){<}_{\mathrm{lex}}(g^{\prime },(l_1^{\prime },r_{1,1}^{\prime },\cdots ,r_{1,k}^{\prime }),\cdots ,(l_n^{\prime },r_{n,1}^{\prime },\cdots ,r_{n,k}^{\prime }))$$

if one of the following holds:

• $(l_1,\cdots ,l_n){<}_{\mathrm{lex}}(l_1^{\prime },\cdots ,l_n^{\prime })$
• for some $1\le d\le k$, $l_i=l_i^{\prime }$ and $r_{i,j}=r_{i,j}^{\prime }$ for all $1\le i\le n$ and $1\le j<d$, and $(r_{1,d},\cdots ,r_{n,d}){<}_{\mathrm{lex}}(r_{1,d}^{\prime },\cdots ,r_{n,d}^{\prime })$
• $l_i=l_i^{\prime }$ and $r_{i,j}=r_{i,j}^{\prime }$ for all $1\le i\le n$, $1\le j\le k$, and $g{<}_{\mathrm{lex}}{g}^{\prime }$

For small symmetry groups, we can of course still compute the lexicographically least equivalent state by trying all permutations. However, in the case of full symmetry, we no longer have a polynomial time method for testing state equivalence. The sorting technique described in Section 4.2 no longer works, because exchanging the local states of any pair of processes i and j can result in changes to the local states of arbitrary processes holding references to i or j.

A pragmatic approach to computing representatives in the presence of id-sensitive local variables involves sorting states based only on the id-insensitive part of process local states [33]. While efficient, this strategy does not result in unique representatives. For example, consider a system with a single id-sensitive local variable per process. The states $s=((B,1),(A,1),(C,3),(A,3))$ and $t=((A,4),(B,2),(A,2),(C,4))$ are equivalent, viz. $s=\pi (t)$ with $\pi$ being the left-shift permutation. However, if we apply selection sort to s, comparing processes based on their id-insensitive local states only, we first apply the transposition $(12)$, then $(24)$, and finally transposition $(34)$, leading to state $s^{\prime }=((A,3),(A,4),(B,3),(C,4))$. Applying selection sort to t just involves applying transposition $(23)$, leading to state $t^{\prime }=((A,4),(A,3),(B,3),(C,4))$. This approach does not detect equivalence of s and t. The strategy is illustrated on the left hand side of Figure 4: sorting according to id-insensitive local state maps an equivalence class to a small number of representatives. As discussed in Section 3.2, this does not compromise the soundness of model checking. In practice, for systems with many id-insensitive local variables, the approach can provide a significant state-space reduction with a relatively low overhead for representative computation [33].

Nevertheless, for maximum compression, we would prefer a technique that detects state equivalence exactly, resulting in unique representatives. The above strategy can be extended to compute unique representatives by combining sorting with a canonization phase [33], as illustrated on the right of Figure 4. Having sorted a state according to the id-insensitive part of process local states, canonization is achieved by partitioning the set of process ids into cells such that ids in the same cell correspond to processes with identical control parts. All (non-trivial) permutations that preserve this partition are then considered, and the smallest image under these permutations selected as a representative. In the above example, given that we have computed state $s^{\prime }$ from s via sorting, we compute the partition $\mathbb{P}=\left\{\right\{1,2\},\{3\},\{4\left\}\right\}$. The only non-trivial permutation preserving $\mathbb{P}$ is the transposition $(12)$, and we find that $(12)s^{\prime }=((A,4),(A,3),(C,3),(B,4))$ which is larger than $s^{\prime }$, thus we deem $s^{\prime }$ to be the unique representative for s. Sorting state t yields $t^{\prime }$, which also gives rise to partition $\mathbb{P}$. Applying $(12)$ to $t^{\prime }$ gives $s^{\prime }$, which is smaller than $t^{\prime }$, thus we deem $s^{\prime }$ to be the unique representative for t. The extended procedure correctly regards s and t as being equivalent under full symmetry. The price for precision can be efficiency: in the worst case, where the control parts of all process local states are identical, $\mathbb{P}$ is $\left\{\right\{1,\cdots ,n\left\}\right\}$, which is preserved by all $n!$ permutations of $\{1,\cdots ,n\}$. However, for many states, $\mathbb{P}$ consists of many small cells, in which case just a few permutations must be considered to compute a unique representative. Furthermore, heuristics can be used to decide when the permutations preserving $\mathbb{P}$ are too numerous to consider exhaustively, accepting inexact state equivalence testing for such states. In practice, this strategy has been shown to provide maximum compression with acceptable runtime overhead on practical examples [33].

The above discussion, and the results of [33], are for the special case of full symmetry. Sorting can be seen as a “normalization” procedure, after which full canonization can optionally be applied. This approach is generalized in [34] to arbitrary symmetry groups for which a normalization procedure is available.

4.4. Explicit-State Model Checkers Exploiting Symmetry

Distinguished examples of explicit-state model checkers that either incorporate symmetry directly, or have been extended with symmetry reduction packages, include Murφ [35], Spin [36,37], Smc [38], and ProB [39].

Murφ offers one of the first serious implementations of symmetry reduction, but is limited to invariant properties under full symmetry. A set of identical processes can be modeled in Murφ using a special scalarset data type [25]; several orthogonal scalarsets can be specified in an input program, leading to full symmetry between processes of the same type. Focusing on full symmetry makes the problem of detecting state equivalence easier than for arbitrary symmetry. However, since Murφ allows id-sensitive local variables, precisely detecting state equivalence under full symmetry is still a challenge, as discussed in Section 4.3 For this reason, Murφ offers a heavyweight strategy (“canonicalization”) for computing unique representatives, and a less expensive strategy (“normalization”) which can result in multiple representatives per orbit. We discuss the use of scalarsets in Murφ in more detail in Section 7.2

Two serious efforts have been made to extend Spin with symmetry reduction capabilities:

• The SymmSpin tool [33,40] builds upon the theory of scalarsets developed for Murφ [25], extending Spin’s input language, ProMeLa, with scalarset datatypes through which the user can indicate the presence of full symmetry. The Spin model checking algorithm is modified to exploit symmetry using one of two strategies. The sorted strategy is the technique we described in Section 4.3, where states are normalized by sorting according to the id-insensitive part of process local states. This technique results in multiple representatives per orbit; the segmented strategy extends the sorted strategy to compute unique representatives, as also described in Section 4.3
• The TopSpin tool [41,42] is not based on the scalarset approach of [25]. Instead, symmetry is automatically detected by extracting a communication graph, the static channel diagram, from a ProMeLa program, and computing automorphisms of this graph, which induce automorphisms of the model associated with the program [43,44]. We describe this approach to symmetry detection in more detail in Section 7.3 TopSpin is not limited to full symmetry, and computes orbit representatives for a wider variety of symmetry groups by generalizing the reduction techniques employed by SymmSpin [30,31,34]. Recently, TopSpin has been extended to use vector instructions common in modern computer architectures to accelerate computation of representatives [45].

Symmetry reduction in the context of Spin is also the topic of [46,47]. However, neither paper provides a publicly available implementation.

Smc (Symmetry-based Model Checker) [38] is an explicit-state model checker purpose-built to exploit symmetry. Concurrent processes are specified via parameterized module declarations, such that symmetry between modules of the same type is guaranteed. Smc is distinguished from other explicit-state model checkers that exploit symmetry: rather than detecting state equivalence by canonizing explored states, Smc selects the first state encountered from any given orbit as the representative for the orbit. This is achieved via a hash function that guarantees mapping equivalent states to the same hash bucket, and a randomized algorithm that efficiently detects, with a high degree of accuracy, whether an equivalent state already resides in the hash bucket to which a new state is due to be stored. This randomized algorithm does not guarantee unique representatives: it is possible for multiple equivalent states to be unnecessarily stored. This does not compromise the soundness of model checking, and unique representatives are guaranteed for a special class of input programs, described in [38]. Smc is notable for incorporating support for various fairness constraints, based on the theory presented in [48].

ProB [39] is an explicit-state model checker for specifications written in the B modeling language. Symmetry occurs in B models as a result of deferred sets, the elements of which are interchangeable. ProB provides three methods for exploiting symmetry. The permutation flooding method [49] simply adds the entire equivalence class for a newly encountered state to the set of reached states. This does not provide a state-space reduction, since it does not reduce the number of states which must be stored. However, it does reduce the number of states for which a property must be explicitly checked, and has been shown to speed up model checking on a range of examples. ProB provides true symmetry reduction by using an extension of the Nauty graph isomorphism program [50] to canonize states during search [27,28], and approximate symmetry reduction based on symmetry markers [51,52]. Notably, the authors of ProB have invested effort in using the B method to automate correctness proofs for their symmetry reduction techniques [53].

5. Symmetry Reduction in Symbolic Model Checking

Symbolic model-checking algorithms operate on sets of states at a time, rather than individual states. Since the program text does not usually permit the computation of successors of many states in one fell swoop, we cannot rely on the program for image computations. Instead, we must first extract a transition relation of the model to be explored.

In the context of symmetry reduction, the question now is which transition relation we should build: R or $\overline{R}$? The obvious choice seems to build the transition set $\overline{R}$ of the reduced model, since we could then simply model-check using $\overline{R}$ and forget about symmetry. Section 5.1 explores this possibility for BDD-based symbolic symmetry reduction, and indicates a fundamental problem. The subsequent sections then focus on implementing symmetry reduction using a BDD representation of the concrete transition relation R. Section 5.5 discusses symmetry in SAT-based symbolic model checking.

5.1. The Orbit Problem of Symbolic Symmetry Reduction

Implementing $\overline{R}$ as equation (10) symbolically requires a propositional formula $f(s,\overline{s})$ that characterizes the orbit relation: it detects whether its arguments are symmetry-equivalent ($s_0\equiv \overline{s}$ in (10)). That is, f has the form $f(l_1,\dots ,l_n,{\overline{l}}_1,\dots ,{\overline{l}}_n)$ and evaluates to true exactly if the vector $(l_1,\dots ,l_n)$ of local states is a permutation (from the group G) of the vector $({\overline{l}}_1,\dots ,{\overline{l}}_n)$. (In order to illustrate the problem with implementing $\overline{R}$ we can safely ignore shared variables — their presence can only make this problem harder.) It turned out that for many symmetry groups, including the important full group, the binary decision diagram for this formula is of intractable size [9]. More precisely, for the standard setting of n processes with l local states each, the BDD for the orbit relation under full symmetry is of size at least $2^{min\{n,l\}}$. The practical complexity of the orbit relation can be much worse; even if, say, the number n of processes considered is small, its BDD tends to be intractably large.

As an intuition for this lower bound, consider the related problem of building a finite-state automaton that reads a word of the form $(l_1,\dots ,l_n,{\overline{l}}_1,\dots ,{\overline{l}}_n)$ and accepts it exactly if the first n letters are a permutation of the remaining n. One way is to let the automaton memorize, in its states, which of the $l^n$ possible vectors it read until the n-th letter, and then compare this information with the remaining n letters. Such memorization requires about $l^n$ different automaton states. Another way is to let the automaton count: While reading the first n letters, the counter for the letter just read is increased. While reading the remaining n letters, the corresponding counters are decreased; an attempt to decrease a zero-valued counter results in rejection. The set of possible values for all l counters must be encoded in about $n^l$ states. Either way, the automaton is of size exponential in one of the parameters.

Table 1. The BDD size of the orbit relation ≡ and the peak number of live BDD nodes, for full symmetry, a scenario without shared variables, various parameters n and l, and two variable orders: (a) concatenated, and (b) interleaved (these are explained in [26]). The peak number of live nodes depends on the BDD package, which in our case was Cudd [54]; ’—’ denotes a memory-out.

demonstrates this orbit problem of symbolic symmetry reduction empirically, in a convincing manner, even for small problem sizes.

These complexity bounds are independent of the way the BDD for the orbit relation is computed, since BDDs are uniquely determined, for a fixed variable ordering. On the other hand, what we really want to compute is $\overline{R}$; the orbit relation is needed only if we do this using equation (10). An alternative way is by first computing the concrete set R, and then mapping source and target in each transition to their respective representatives:

$$\overline{R}=\alpha (R)=\{(\alpha (s),\alpha (t))\in \overline{S}\times \overline{S}:(s,t)\in R\}$$

(13)

This, equivalent, definition does not need the orbit relation. Experiments have shown, however, that — unless R is trivially small — the BDD for $\overline{R}$ itself tends to be very large (although it is usually smaller than that for the orbit relation [55]). This led to an immediate abandoning of attempts to implement symmetry reduction via a symbolic representation of $\overline{R}$. In the remainder of this section, we present a selection of the many approaches that have been taken to circumvent the orbit problem.

5.2. Multiple Representatives

The motivation for detecting equivalent states is that we want to collapse them in order to reduce the size of the state space. Suppose we were to collapse only some of the equivalent states. This is quickly shown to be legal, since we do not lose information by keeping several equivalent states. Further, we still achieve some reduction. This scenario is depicted in Figure 5 (b). An orbit may now have multiple representatives (black disks), and a single state may be associated with more than one of them. This approach has, accordingly, become known as multiple representatives [9].

Why would we want to permit multiple representatives per orbit and thus potentially harm the compression effect of symmetry reduction? The answer is that the BDD representing a subrelation of the orbit relation ≡ may be smaller than that for the full relation, potentially avoiding the orbit problem of symbolic symmetry reduction. For instance, consider the set

$$\mathsf{\Pi }=\{(1i)\in Sym\{1,\dots ,n\}:i\in \{1,\dots ,n\left\}\right\}$$

(14)

of transpositions against 1 (note that $\mathsf{\Pi }$ is not a group). Now define $s{\equiv }_{\mathit{mult}}t$ exactly if there exists $\pi \in \mathsf{\Pi }$ such that $\pi (s)=t$. Under full symmetry, $s{\equiv }_{\mathit{mult}}t$ implies $s\equiv t$, so ${\equiv }_{\mathit{mult}}$ is a subrelation of ≡. The BDD for ${\equiv }_{\mathit{mult}}$ is much more compact than that for ≡. Intuitively, only n of the potentially $n!$ permutations must be tried in order to determine state equivalence.

The authors of [9] propose to use the relation ${\equiv }_{\mathit{mult}}$ in order to derive a multiple-representatives quotient, as follows. First determine a suitable set Rep of representative states. A choice that is compatible with the definition of $\mathsf{\Pi }$ used in (14) is

$$Rep=\{(g,l_1,\dots ,l_n):\forall i:2\le i\le n:l_1\le l_i\}$$

(15)

Re-using the N-T-C example from Figure 3 but for 3 processes, the state $(C,T,N)$ belongs to the set Rep, but is not a canonical representative, as $T>N$. Given Rep, we now define a representative relation $\xi$ as follows:

$$\xi (s,r):=s{\equiv }_{\mathit{mult}}r\wedge r\in Rep$$

(16)

Set $\xi$ relates states to representatives from Rep; some conditions need to be in place to make sure $\xi$ is left-total, so that every state is representable (see [9]). The multiple-representatives quotient is then defined as $M_{\mathit{mult}}=(Rep,R_{\mathit{mult}},L_{\mathit{mult}})$, where

$$R_{\mathit{mult}}(s,t):=\exists s^{\prime }\in S:\xi (s,s^{\prime })\wedge R(s^{\prime },t)$$

(17)

and $L_{\mathit{mult}}(s)=L(s)$. The authors suggest, somewhat implicitly, to build this quotient and then model-check over it, exploiting the earlier observation that the BDD for ${\equiv }_{\mathit{mult}}$ is much smaller than that for ≡.

An obvious disadvantage is that the symmetry reduction effect is negatively impacted by allowing multiple representatives per orbit. The relation ${\equiv }_{\mathit{mult}}$ chosen above makes the reduction effect approach a linear factor, down from the original exponential potential of symmetry. On the other hand, as the experiments in [9] have shown, this disadvantage is certainly compensated by the efficiency gain compared to orbit-relation based approaches. Last but not least, exploiting symmetry using multiple representatives provides benefits over ignoring symmetry altogether — the overhead introduced by the method is moderate enough. The multiple representatives approach is implemented in the symbolic model checker Symm (Section 5.6).

5.3. On-the-fly Representative Selection

The multiple representatives approach presented in the previous section ameliorates the orbit problem by building, instead of the full orbit relation, a subrelation that detects only some of the symmetric model states. From this subrelation, a mapping from states to (non-unique) representatives is derived and used to build a symmetry quotient.

A more algorithmic way of taming the orbit problem is to avoid computing such a quotient altogether, but instead removing symmetry on the fly. An approach by Barner and Grumberg proposes the following idea [56,57]. Suppose we are in round i of symbolic model checking, $\mathit{reached}\_\mathit{rep}$ is the set of representative states reached so far, and $S_i$ is the representative frontier (representative states discovered for the first time in the previous round); see Algorithm 2. We first symbolically form successors of these states with respect to the concrete transition relation R, to obtain $S_{i+1}$ (line 4; ignore line 3 for the moment). This set will of course not be restricted to representatives. We therefore apply a symmetrization function to $\mathit{reached}\_\mathit{rep}$ that adds, to $\mathit{reached}\_\mathit{rep}$, any state that is symmetric to any of the representative states in $\mathit{reached}\_\mathit{rep}$. Call the result $\mathit{full}\_\mathit{reach}$ (line 5). We now subtract from $S_{i+1}$ the set $\mathit{full}\_\mathit{reach}$ of previously seen states (line 6). As a result, the new $S_{i+1}$ is the new frontier set, containing only states occurring for the first time. Since we have not defined a priori a fixed set of representatives, we just stipulate that the states in $S_{i+1}$ represent their respective orbits. We do not care whether they are in any way canonical, or whether there may be redundancy due to several states in $S_{i+1}$ belonging to the same orbit.

Algorithm 2 Symbolic Symmetry Reduction by On-the-fly Representative Selection

1: $\mathit{reached}\_\mathit{rep}:=S_0$, $i=0$  2: while $S_i\ne \varnothing$ do  3:  choose $\mathit{under}\subseteq S_i$  4:  $S_{i+1}:={\mathtt{Image}}_R(\mathit{under})$  5:  $\mathit{full}\_\mathit{reach}:=\mathit{symmetrize}(\mathit{reached}\_\mathit{rep})$  6:  $S_{i+1}:=S_{i+1}\setminus \mathit{full}\_\mathit{reach}$  7:  if $S_{i+1}$ contains an error state then  8:    generate counterexample and stop  9:  end if 10:  $\mathit{reached}\_\mathit{rep}:=\mathit{reached}\_\mathit{rep}{S}_{i+1}$ 11:  $i:=i+1$ 12: end while 13: return “no error state reachable”

The advantage of this method is that it keeps only representative states (defined on the fly) during model checking, without one having to think about canonizing states or even a fixed set of representatives. Accordingly, no orbit relation or multiple representative equivalence relation is needed. There are also some drawbacks. One is that the symmetrization function applied to $\mathit{reached}\_\mathit{rep}$ can be expensive, and the result $\mathit{full}\_\mathit{reach}$ can be huge. The authors of [57] point out, however, that the result is a set of states, whereas the orbit relation is a set of pairs of states and thus inherently much more expensive to compute and store. Another potential problem is that the method still potentially relies on multiple representatives (whatever is in the final set $S_{i+1}$ is a representative). In the worst case, an orbit may be completely present in $S_{i+1}$. To alleviate this problem, the authors of [57] propose to underapproximate the current set $S_i$ before computing the image under R, and give heuristics for computing such underapproximations. In this case, the algorithm may only compute an underapproximation of the set of symbolically reachable states, which the authors suggest to counter by forcing the precision to increase over time.

The on-the-fly representative selection scheme has been implemented in IBM’s RuleBase model checker (Section 5.6).

5.4. Dynamic Symmetry Reduction

An alternative way of circumventing the orbit problem is by heeding the lessons we learned from implementing symmetry reduction in explicit-state algorithms (Section 4.1). Recall that, in order to preserve the on-the-fly nature of such algorithms, neither R nor $\overline{R}$ are built up front. Instead, successors of encountered states are formed by simulating the program for one step. The successor states are then mapped to the quotient state space $\overline{S}$ by applying an appropriate representative mapping.

The idea of forming successors with respect to R, followed by applying a representative map, is the basis of a technique called dynamic symmetry reduction, which offered a promising way of overcoming the antagony between symmetry and BDD-based symbolic data structures [26,58]. As in general symbolic model checking, we assume that we have a BDD representation of the transition relation R. At each symbolic exploration step, we form successors of the current set of states using a standard image operation with respect to R. The resulting (generally, non-representative) states are reduced to their quotient equivalents by applying a second image operation, namely, a symbolic version of the abstraction function $\alpha$ introduced in Section 4.1 For the special case of symbolic reachability analysis, this procedure is summarized in Figure 6 (a).

The broader idea employed by the algorithm in Figure 6 (a) is that abstract images, i.e. successors of a set of abstract states under the quotient transition relation, can be computed without using the quotient transition relation, using the following three steps: (i) the set of abstract states is mapped to the set of concrete states it represents using a concretization function $\gamma$; (ii) the concrete image is applied to those states; and (iii) the result is mapped back to the abstract domain using $\alpha$. Symmetry affords the simplification that $\gamma$ can be chosen to be the identity function, since abstract states — representatives — are embedded in the concrete state space; they represent themselves. Thus step (i) can be skipped. In Figure 6 (a), we apply EX${}_R$ (the concrete backward image operator) directly to the set Z of abstract states, obtaining a set of concrete successor states. Applying $\alpha$ produces the final abstract backward image result. The correctness of this procedure follows from Lemma 7.

What remains to be done is the non-trivial problem of implementing the abstraction mapping $\alpha$ symbolically. The general idea is to define a representative of an orbit as the orbit’s lexicographically least member, given some total order on the set of local states. Whether least orbit members can be found efficiently at all depends on the underlying symmetry group G. The authors of [26] make the assumption that there exists a “small” subset F of G with the following property:

$$\mathrm{A}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}z\mathrm{i}\mathrm{s}\mathrm{l}\mathrm{e}\mathrm{x}\mathrm{i}\mathrm{c}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{l}\mathrm{y}\mathrm{i}\mathrm{f}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{s}\mathrm{n}\mathrm{o}\pi \in F\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\pi (z){<}_{\mathrm{l}\mathrm{e}\mathrm{x}}z$$

(18)

Whether state z is least in its orbit can be detected efficiently using this property, by trying all permutations from F. If it is not, then there exists a permutation $\pi \in F$ that makes z smaller. Since ${<}_{\mathrm{lex}}$ is a strict order on the finite set of local states, this simple procedure is guaranteed to terminate, and eventually maps z to the lexicographically least member of its orbit.

The procedure can be applied to a set of states T, to obtain the set $\alpha (T)$ of representatives of states in T, as follows. For each permutation $\pi \in F$, we extract from T the subset ${\mathit{T}}_{\mathit{bad}}$ of elements t such that $\pi (t)$ is lexicographically less than t. If this set is non-empty, we apply $\pi$ to all elements in ${\mathit{T}}_{\mathit{bad}}$ and unite the result with the elements $T\setminus {\mathit{T}}_{\mathit{bad}}$. These steps are repeated until the set ${\mathit{T}}_{\mathit{bad}}$ is empty for every $\pi \in F$.

The authors of [26] call symmetry groups with a small set F of permutations with property (18) nice. Fortunately, this includes the full symmetry group, for which we can choose F to contain the $n-1$ transpositions of neighboring elements i and $i+1$, for $i<n$. It also includes the rotation group, for which we can choose F to be equal to G, which is small. While not every group is nice, note that the orbit relation is intractable essentially for every interesting symmetry group, including the full symmetry group. Figure 6 (b) shows the representative mapping $\alpha$ for the case of the full symmetry group, assuming the absence of shared variables for simplicity. Iterating through all nice permutations corresponds to the loop in line 2. The condition $l_p>l_{p+1}$ in line 3 implies that $(l_1,\dots ,l_n)$ is not lexicographically least. The $\mathit{swap}$ operation in line 6 can be accomplished by applying a standard BDD variable reordering routine that swaps the bits storing the local states of processes p and $p+1$. The cost of such a swap operation is exponential in the BDD variable distance of the bits to be swapped; this clearly favors choosing F to be the set of the $n-1$ neighbor transpositions [26].

We have now described how the (expensive) quotient image operation ${\mathtt{EX}}_R$ can be faithfully simulated using only the concrete transition relation R and an abstraction mapping $\alpha$. This result immediately gives rise to a general CTL model checking algorithm under symmetry: all we have to do is replace every image operation in the algorithm by the operation $T\mapsto \alpha ({\mathtt{EF}}_R(T))$. Universal CTL modalities can be handled by reducing them to existential ones. The authors of [26] further describe how the method needs to be refined in the presence of id-sensitive shared variables: in this case, the condition $l_p>l_{p+1}$ from line 3 in Figure 6 is too strong to identify states that are not lexicographically least.

In summary, the approach to symmetry reduction presented in this section is dynamic in the sense that, in order to canonize state sets, it applies a sorting procedure based on dynamic variable reordering. Compared to previous approaches to circumventing the orbit problem, dynamic symmetry reduction is exact, and it exploits symmetry maximally, in that orbit representatives are unique. These features have allowed dynamic symmetry reduction to outperform related techniques such as based on multiple representatives (Section 5.2), and, in some cases, on local state counters (Section 6). The technique has been implemented in the model checker Sviss (Section 5.6) and applied successfully to abstract communication protocols and concurrent software coarsely abstracted into Boolean programs. An idea based on dynamic symmetry reduction was also used in the Prism model checker, to symmetry-reduce probabilistic systems (Section 5.6).

5.5. Symmetry in SAT-based Model Checking

Yet another way of circumventing the orbit problem of BDD-based symmetry reduction is, naturally, to avoid BDDs. Model checking using SAT solvers is an alternative symbolic analysis method — it was in fact first advertised as “Symbolic Model Checking Without BDDs” [59]. The idea is that the set of reachable states of a Kripke structure can be represented symbolically as a propositional formula, provided the length of paths is bounded by some constant. Determining reachability of an error state up to the bound then amounts to a propositional satisfiability problem, for which surprisingly efficient solvers exist today. Spurred by the initial success of SAT-based bounded model checking for bug detection, several methods have been developed over the last few years towards unbounded model checking, using sophisticated termination detection methods. (Note that propositional formula representations of Boolean functions are not canonical, so termination detection is not as easy as it is with BDDs.)

A technique to apply symmetry reduction in SAT-based unbounded model checking was proposed by D. Tang, S. Malik, A. Gupta and N. Ip [60]. The technique builds on top of circuit cofactoring, a method of computing symbolic transition images by accelerated cube enumeration [61]. The idea of [60] is that, instead of computing concrete image states first and then converting the result to an equivalent set of representatives, one can use a representative predicate Rep to constrain the search to representative states. Specifically, in each symbolic unrolling step, the final state is constrained to satisfy Rep; it is then left to the SAT solver to find representative image states. While the same technique could be used in BDD-based symbolic symmetry reduction as well (Section 5), it is inefficient to do so, as the BDD for the set Rep tends to be large. In SAT-based model checking, in contrast, the cost of the SAT check is known not to be too sensitive to the size of the formula representation of Rep.

Not having to design an operation that converts non-representative to representative states simplifies the implementation of symmetry reduction. The cofactoring-based symmetry reduction method has been applied fairly successfully to some cache coherence and security protocols. In some examples, the speed-up reaches several orders of magnitude; the improvement is mostly due to a reduction in the number of cube enumerations required in the image computation step.

We point out that exploiting transition system symmetry in SAT-based model checking is very different from symmetry breaking that can be used to speed up propositional satisfiability checking or, more generally, constraint satisfaction checking [62]. In symmetry breaking, predicates are added during the search that prevent the solver from exploring variable assignments that are, in some syntactic sense, “symmetric” to previously explored assignments. This notion of formula symmetry is too weak to capture the (semantic) notion of transition relation symmetry that is used in model checking. Therefore, while symmetry breaking has its place in checking the satisfiability of SAT instances obtained during model checking, there is a need for specialized techniques such as [60] that exploit semantic symmetry found in transition systems.

5.6. Symbolic Model Checkers for Symmetric Systems

The class of symbolic model checkers with symmetry reduction support can be partitioned into two subsets. The first subset contains those that were published with the main, if not sole, intent of promoting newly developed symmetry reduction techniques. This subset includes the tools Symm, Sviss and Boom. The second subset contains more general tools, for which symmetry support was added in later development stages to improve performance on certain types of systems with replicated components. These tools often had achieved a fairly high degree of maturity by the time symmetry was added, and continue to be developed at present. This subset includes the tools RuleBase and Prism. In the following, we illustrate the symmetry-related aspects of Symm and Sviss, and sketch those of RuleBase and Prism. Boom is described at the end of Section 6.

(a) Symm is a BDD-based symbolic model checker with dedicated symmetry reduction support, described somewhat cursorily in [16]. Symm is intended for the verification of the full range of CTL properties for shared-variable multi-process systems. Symmetries of the system are specified by the user; Symm appears to support only full symmetry. The tool implements a suboptimal reduction algorithm based on multiple representatives (Section 5.2). The reduction was applied to the IEEE Futurebus protocol (see [16] for references). The savings achieved on this example are quite dramatic: roughly an order of magnitude on the time, and more than that on the memory use of the algorithm, measured in terms of the maximum BDD size encountered during the run of the algorithm.

(b) Sviss [63] is, like Symm, a BDD-based symbolic model checker for symmetric systems [58]. It supports full and rotational symmetry, as well as symmetries composed of fully or rotationally symmetric subsystems. Symmetries are specified by the user through declarations of process blocks: sets of symmetric processes. Process blocks can be declared to be a clique (enjoying full symmetry) or a ring (enjoying rotational symmetry). While primarily intended to boast dynamic symmetry reduction (Section 5.4), for comparison Sviss also permits multiple representative reduction (5.2) and orbit-relation based reduction (5.1).

The state space of the input system is described via a set of parameters (which can later be instantiated at the command line) and program variables of fixed-range enumerable types, such as Booleans and bounded integers, or arrays and vectors thereof. Unusual about Sviss is the fact that it does not have its own modeling language; instead the user relies on a (fairly rich) C++ library of routines for systems modeling. This library is restricted in that it only allows constructs that are implementable using BDDs with reasonable efficiency. It contains, for instance, logical and linear arithmetic operations, but no non-linear operations.

In addition to the full range of CTL properties, Sviss features past-time modalities, search operators, special-purpose invariant checks, and symmetry-specific operators, such as representative mappings of sets of states. Sviss has been used mainly for two types of systems: communication protocols, and Boolean device driver models. As is demonstrated in [58], the dynamic symmetry reduction method quite dramatically outperforms alternative symbolic methods known at the time.

(c) RuleBase is a powerful model checker developed at IBM Haifa [64]. It primarily targets hardware designs, which can be specified in conventional description languages such as Verilog and VHDL. For easy of use by verification engineers, the tool is equipped with an extension of CTL called Sugar as the specification language. RuleBase features an implementation of the on-the-fly representative selection method of Barner and Grumberg (Section 5.3). The symmetry group of the design under verification is supplied by the user, in the form of group generators. Notable is the capability of RuleBase to check safety and liveness properties under symmetry, a feature that not many symbolic model checkers enjoy. Experimental results comparing RuleBase with and without symmetry in fact show that RuleBase performs significantly better for checking liveness properties when symmetry is exploited. However, little improvement in performance has been shown for safety properties. This is attributed in large part to the symmetrization function $\sigma \_\mathit{step}$ that closes a set of representative states under permutation application. The “RuleBase – Parallel Edition” website [65] provides a lot of additional information on the tool. Symmetry is, however, mentioned only in the form of the publications [56,57], so the status of its use in RuleBase is unclear.

(d) The probabilistic model checker Prism [66] allows quantitative analysis of probabilistic models represented as Markov chains or Markov decision processes. The analysis uses a combination of multi-terminal BDDs (MTBDDs) and explicit data structures such as sparse matrices and arrays. Prism-Symm [67] extends Prism with symmetry reduction capabilities, based on dynamic symmetry reduction (Section 5.4) and has recently been integrated into the main tool [68]. Processes in Prism are specified by the user as modules; renaming allows a module description to be replicated multiple times. Prism can exploit full symmetry between a series of modules: the user specifies the number of modules appearing before and after this symmetric block. Currently, Prism does not check whether these modules truly are symmetric: it is up to the user to ensure full symmetry, otherwise unpredictable results may be obtained. Symmetry-reduced quantitative model checking with Prism is applied to four randomized algorithms in [68]. Exploiting symmetry leads to a state-space reduction of several orders of magnitude for larger model configurations. Mixed results are obtained with respect to the size of MTBDD required to represent the probabilistic transition matrix: in some cases, symmetry reduction leads to a reduction in the size of this MTBDD by a factor of more than two; in other cases the MTBDD blows up by a factor of up to ten. Symmetry reduction can be effective for probabilistic model checking despite this blow-up in MTBDD size, since Prism’s algorithms use a hybrid approach, based on a combination of symbolic and explicit data structures. For highly symmetric systems, the benefits afforded by the drastic reduction in reachable states often outweigh any associated increase in MTBDD size.

Prism has also been extended with symmetry reduction using counter abstraction via the Grip tool, which is described in Section 6.

6. Symmetry Reduction using Counter Abstraction

Counter abstraction is a form of symmetry reduction that is applicable both in explicit and symbolic model checking, which is why we devote a separate section to it. The starting point is the observation that, under full symmetry, two global states are identical up to permutations of the local states of the components exactly if, for every local state $L\in \{1,\dots ,\ell \{$, the same number of components reside in L:

$$\exists \pi :\pi (l_1,\dots ,l_n)=(m_1,\dots ,m_n)\mathrm{iff}(n_1^l,\dots ,n_{\ell }^l)=(n_1^m,\dots ,n_{\ell }^m)$$

(19)

where $n_L^l=\#\{i:l_i=L\}$ denotes the number of components in $(l_1,\dots ,l_n)$ that reside in local state L, similarly for $n_L^m$. That is, identity of sequences up to arbitrary permutations can be tested by comparing how often any given element occurs in the two sequences. The direction “⇒” holds independently of the set of permissible permutations, whereas the direction “⇐” requires that all permutations are available: there is no rotation permutation that maps the global state $(A,B,C)$ to the global state $(C,B,A)$. Note that detecting symmetry of two states via (19) decides the existence of a permutation between them without actually producing such a permutation.

At this point, it seems natural to ask the following question: if we are introducing counter vectors to test states for symmetry, why do we have to keep the local state vectors of the form $s=(l_1,\dots ,l_n)$ anyway? We can conclude from (19) that the counter vector $v=(n_1^l,\dots ,n_{\ell }^l)$ exactly characterizes the orbit of state s. Namely, every global state equivalent to s has the same counter representation v. Conversely, every global state with counter representation v is identical to s up to some (unknown, but not essential) permutation.

The idea of counter abstraction is precisely to rewrite a symmetric program $\mathbb{P}$, before building a Kripke structure, into one over counter vectors. We introduce a counter for each existing local state and translate a transition from local state A to local state B as a decrement of the counter for A and an increment of that for B. The resulting counter-abstracted program $\widehat{\mathbb{P}}$ gives rise to a Kripke structure $\widehat{M}$ whose reachable part is isomorphic to that of the traditional symmetry quotient $\overline{M}$. We can now model-check $\widehat{M}$ without further symmetry considerations, having implemented symmetry reduction on the program text.

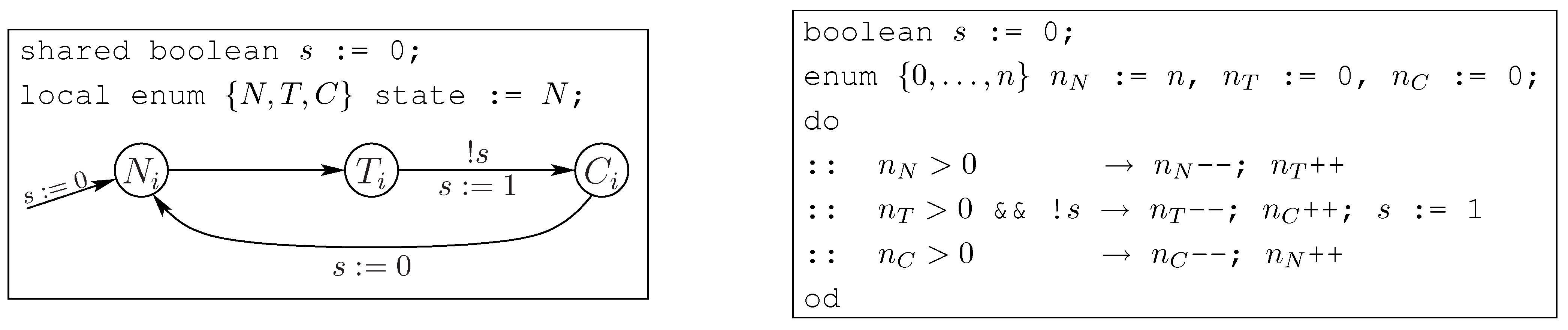
Let us look at an example. The behavior of a single process is given as the local state transition diagram in Figure 7 (left). The overall system is given by the asynchronous, parallel composition of n such processes; the processes can be in one of three local states N, T and C, of which N is initial. They communicate via shared variable s. The result of counter-abstracting this program is shown in the same figure on the right, in a guarded-command notation. The new program is single-threaded; thus there are no notions of shared and local variables. The atomic propositions used in properties to be checked also need to be translated to refer to the new program variables. For example, the classical Mutex property $\mathtt{AG}(\forall i,j\in \{1,\dots ,n\}:C_i\wedge C_j\Rightarrow i=j)$ becomes $\mathtt{AG}(n_C<2)$.

Let us discuss the complexity of model-checking the resulting program over counter variables. In the example in Figure 7, the Kripke structure corresponding to the program has shrunk from exponential size $\mathcal{O}(3^n)$ (for M) to low-degree polynomial size $\mathcal{O}(n^3)$ (for $\widehat{M}$). In general, counter abstraction can be viewed as a translation that turns a state space of potential size $l^n$ (n local states over $\{1,\dots ,l\}$) to one of potential size ${(n+1)}^l$ (l counters over $\{0,\dots ,n\}$). The abstraction therefore reduces a problem of size exponential in n to one of size polynomial in n. Let us summarize the pros and cons of the technique:

• Counter abstraction is an elegant way of implementing symmetry reduction specifically for fully symmetric systems. Such systems deserve special attention, as full symmetry is the most frequent and most profitable type of symmetry in practice.
• Counter abstraction is a means of circumventing the orbit problem in symbolic symmetry reduction (Section 5.1): no reduction mechanism of any kind needs to be applied to Kripke structure $\widehat{M}$, defined over the counter program; it can be analyzed using an off-the-shelf model checker. This observation was made first in [69], where the counter vectors were called generic representatives of symmetry equivalence classes. They are generic in the sense that they completely anonymize the processes.
• Counter abstraction requires a translation of the program text into one over counters, which can be challenging; particularly so if the program involves id-sensitive variables. The authors of [70] provide a solution that hinges, however, on restrictions on the ways such variables can be used in programs (i.e., restrictions that are stronger than necessary just to ensure symmetry of the Kripke structure resulting from the program). Program translation techniques for richer input languages than those considered in [69,70] have been proposed in [71].

Counter Abstraction and Local State Explosion

As we have seen for local state transition diagrams such as the one in Figure 7, counter abstraction reduces the Kripke structure complexity from exponential in n to polynomial in n and thus significantly remedies the state explosion dilemma. This view does not apply unchallenged, however, to realistic programs, where process behavior is given in the form of manipulations on local variables. The straightforward definition of a local state as a valuation of all local variables is incompatible in practice with the idea of counter abstraction: the number of local states generated in this way is simply too large. For example, a program with seven local Boolean variables and 10 lines of program text gives rise to already $2^7\ast 10>1000$ local states, all of which have to be converted into counters. In general, the state space of the counter program is of size $\Omega (n^{2^{|V_l|}})$, doubly-exponential in the number of local variables $V_l$. This phenomenon, which can seriously spoil the benefits of counter abstraction, has been dubbed local state explosion [72].

A solution to this problem was offered in [73]. The authors observe that counter abstraction, with a state space complexity of roughly $n^l$, suffers if the number of local states, l, is substantially larger than the number of processes, n. On the other hand, the number of occupied local states, with at least one process residing in them, is obviously bounded by n. Rephrasing this observation in terms of counters, it means that in a counter vector of high dimension l, most of the counters will be zero, in any given global state. This suggests an approach where, instead of storing the counter values for all local states in a global state, we store only the non-zero counters. Since the set of non-zero counters varies from state to state, a symbolic implementation of this idea is tricky but doable (see [73]).

We summarize that by carefully selecting which counters to keep in a global state representation, the worst-case size of the Kripke structure of the counter-abstracted program can be reduced from $\mathcal{O}(n^l)$ to $\mathcal{O}(n^{min\{n,l\}})$, thus completely eliminating the sensitivity to local state explosion. This method was successfully implemented in a tool called Boom [74] and used to analyze concurrent Boolean programs for a fixed but large number of threads. These programs, which capture the result of predicate-abstracting software written in general programming languages, tend to have many local states, especially in advanced iterations of the abstraction-refinement loop. Boom can certainly be seen as the first serious attempt at applying symmetry reduction techniques to general software.

Bibliographic notes on counter abstraction. Process counters have been used to simplify reasoning about multi-component systems at least since the mid 1980s, even in contexts that are not explicitly related to symmetry [75]. Incidentally, the term counter abstraction was actually coined by Pnueli, Xu, and Zuck, in the context of parameterized verification of liveness properties [76]. In that work, the counters are cut off at some value c, indicating that at least c components currently reside in the corresponding local state. In this section, we have used the term counter abstraction in the sense of an abstraction that is exact with respect to a given class of properties. The phrase “exact abstraction” may sound contradictory in general, but is widely accepted in the contexts of symmetry reduction and other bisimulation-preserving abstraction methods.

The idea of counter abstraction is readily extended to achieve symmetry reduction in probabilistic model checking [77]. The Grip tool (Generic Representatives in Prism) [78,79] translates symmetric Prism programs into a counter-abstract form for analysis by the probabilistic model checker Prism. Grip provides an alternative to Prism-Symm, the method of exploiting symmetry built into Prism (see Section 5.6). Like Prism-Symm, Grip has been shown to provide an orders-of-magnitude reduction in the number of reachable states associated with highly symmetric models, with a mixture of good and bad results for multi-terminal BDD sizes. Grip tends to outperform Prism-Symm when applied to programs consisting of a large number of modules with relatively few local states; Prism-Symm tends to fare better on a small number of more complex modules [71]. Grip is restricted to a subset of the Prismlanguage for which programs are symmetric by construction (c.f. Section 7.2). The advantage is that, unlike with Prism-Symm, soundness of symmetry reduction is guaranteed by the tool. A disadvantage is that the Grip input language does not include the full range of features available in Prism.

Counter abstraction has also been used to exploit virtual symmetry [80], a generalized notion of symmetry for partially symmetric systems discussed further in Section 8.

7. Deriving Symmetry from Input Programs

In Section 2.3, we briefly discussed the problem of detecting a suitable group of symmetries to exploit while model checking. There are two dimensions along which to consider this problem. One is the traditional “function problem” vs. “decision problem”: is our job to detect (quantify) symmetry, without any prior conjecture about the symmetry group, or to verify that some given group is a subgroup of Aut M. The other dimension is the level of abstraction at which the system is considered: a high-level program or a Kripke structure.

Generally, detection and verification of symmetry are expensive when performed at the full Kripke structure level. In addition, we usually want to avoid building the Kripke structure up-front. An approach that detects symmetry (or violations of it) on the Kripke structure on-the-fly is sketched in Section 8; however, most techniques detect or verify symmetry at the level of the input program. The justification for doing so is that an automorphism of the program text — intuitively, a permutation that leaves the program invariant — is also an element of Aut M for the induced Kripke structure M. This is an instance of the symmetry principle, stating that symmetry in the cause (= program) implies symmetry in the effect (= Kripke structure).

One problem with detecting or verifying symmetry at the program text level is that the Kripke structure may have more symmetries than the program promises. For instance, the program may have statements in it that are never executed; thus the transitions corresponding to such statements can be ignored in the symmetry condition. In practice, one has to strike a balance between the cost of detecting/verifying symmetry, and the reduction it promises. Choosing a less-than-optimal symmetry group is legal according to Definition 3 and may be more efficient than insisting on first finding the full group Aut M.

We further discuss the difficulty of the symmetry detection problem in general. We then describe conservative approaches to detecting symmetry based on input languages tailored towards symmetry, and based on the derivation of a graph from the input program text such that automorphisms of the graph induce automorphisms of the underlying model.

7.1. The Difficulty of Symmetry Detection in General

Suppose a Kripke structure M is derived from an input program describing the parallel composition of n processes, $P_1,\cdots ,P_n$ say, where each $P_i$ is an instance of a parameterized process template P. Informally, a permutation $\pi \in Sym\{1,\cdots ,n\}$ induces an automorphism of M if and only if, for $i,j\in \{1,\cdots ,n\}$ such that $\pi (i)=j$, the template P does not distinguish between i and j. For example, suppose $n=5$. The following program fragment singles out process 1, and distinguishes processes 2 and 3 from all other processes, but not from each other:

if $\mathit{tok}>3$ then

  $\mathit{tok}:=1$

end if

Since $\mathit{tok}$ is an id-sensitive variable, i.e., its value is a process id, the guard of the conditional will only evaluate to true when $\mathit{tok}$ refers to process 4 or 5. Furthermore, on executing this guard, $\mathit{tok}$ is set specifically to the id of process 1. This may affect the evaluation of other control-flow expressions involving $\mathit{tok}$. We might conclude that permutations mapping across the sets $\left\{1\right\}$, $\{2,3\}$, $\{4,5\}$, e.g. the left-shift permutation from equation (2) extended to act on the set $\{1,\cdots ,5\}$, cannot induce automorphisms of the underlying model. However, in practice, the above statements may not destroy symmetry: they may turn out to be unreachable.

In general, deciding whether a given process permutation induces an automorphism on the underlying model boils down to deciding whether “symmetry-breaking” statements, such as $\mathit{tok}:=1$ above, are reachable. Deciding reachability is equivalent to model checking a safety property for the unreduced Kripke structure underlying the program, which is precisely what we are trying to avoid. Thus, practical symmetry detection techniques must be conservative, facilitating detection of useful symmetry groups for sensibly-written input programs.

7.2. Input Languages Tailored for Symmetry

Symmetry detection can be simplified by designing an input language such that, for any description of a family of processes in this language, permutations of processes are guaranteed to induce automorphisms on the underlying model. This is the approach taken by the designers of the Murφ verification tool [35], the first explicit-state model checker to exploit symmetry.

A Murφ program consists of a set of transition rules, which are guarded commands over shared variables. Distinguished rules are also provided to specify initial values for variables; these rules determine the initial states associated with the state-space of a Murφ program. Starting with the initial states, the set of reachable states can be computed by iteratively applying transition rules to the set of reached states, adding newly generated states, until a fixpoint is reached.

Murφ has no explicit notion of processes. A family of n processes can be simulated via an array of size n, where elements of the array are records describing the state of a single process. To capture full symmetry between processes, Murφ includes a facility for introducing distinguished types to represent process ids. Such types are called scalarsets, and are introduced using the Scalarset keyword. For example, a program describing a system of ten clients and two servers, where clients (servers) can be in one of five (three) local states, and a shared token holding the identity of a particular client can be declared as follows:

The use of scalarsets is subject to a number of restrictions. Scalarset variables may not appear in arithmetic expressions, and may only be compared using the = and ≠ operators. Scalarsets of distinct types are not compatible, and scalarsets are not compatible with non-scalarsets. In the above example, it is permissible to index into array ClientState using the Client variable, but not into ServerState. Finally, the index variable associated with a for loop may only have scalarset type if the effect of the loop (executed atomically) is independent of the order of iterations. All but the last of these restrictions can be checked precisely and efficiently. The last restriction is not checked by the Murφ tool, presumably because it is difficult to check precisely; however, a conservative check could be implemented with relative ease using standard dependence tests [81].

The benefit of these restrictions is that a symmetry group for a program that uses scalarsets can be directly inferred. Suppose a program P declares scalarset type T: Scalarset (X), for some $X>0$. Then given any permutation $\pi \in Sym\{1,\cdots ,X\}$, $\pi$ induces an automorphism on the model associated with P; $\pi$ acts on a state by permuting the order of elements in arrays with index type T, and the values of variables of type T. More generally, if P contains d distinct scalarset types, $T_1,\cdots ,T_d$ (for some $d>0$), and $T_i$ has the form $T_i$: Scalarset ($X_i$), $(1\le i\le d)$, then permutations of the distinct scalarsets can be combined, potentially (save pathological examples) yielding a group of $X_1!\times \cdots \times X_d!$ induced permutations on the associated model. A detailed proof of this result is the main contribution of [25].

Limitations of scalarsets. There are three disadvantages of using scalarsets for symmetry detection:

• The user is forced to explicitly think about symmetry when modeling a system. Relieving this burden is one of the motivations for automatic symmetry detection methods, discussed in Section 7.3
• Scalarsets cannot be used to describe a single family of similar processes that are not all identical, but are partitioned into identical subsets. For example, we cannot use the rule shown in Figure 8 to concisely extend a description of the mutual exclusion problem to a description of the Readers-Writers synchronization problem. The rule uses the constant FirstWriter to partition processes into readers (processes 1–3) and writers (processes 4-5). The problem is that comparing scalarsets p and q with FirstWriter using the < and ≥ operators breaks the scalarset restrictions. We could rectify the situation by using two distinct scalarset types, one for reader processes and one for writer processes. This sensitivity to differences between components makes modeling rather inflexible, particularly when describing featured networks, such as in [82].
• Scalarsets are only designed to capture full symmetry between components of the same type. Scalarsets prohibit us from describing a system with a ring structure, using e.g. modular arithmetic to compute neighbor ids. Variants of the scalarset type to handle ring symmetry have been proposed [83], but not implemented in practice. Symmetries of systems with more general communication topologies can be captured using the graph isomorphism-based approaches described in Section 7.3

Related approaches. The scalarset approach has been adopted by the SymmSpin tool [33], which extends the Spin model checker with symmetry reduction capabilities, and by the timed model checker Uppaal [84].

Scalarsets are also used in the language of the symbolic model checker SMV [85], to indicate that values for a datatype are indistinguishable. However, the goal here is not to reduce state explosion, but rather to reduce case explosion: SMV uses temporal case splitting to break the verification of a property into many smaller verification problems, one for each possible value of a given variable. These verification problems may themselves be further decomposed via case splitting on the possible values of another variable, and so on. The resulting verification problems are, in practice, small enough to be handled via model checking; however, there may be an exponential blow-up in the number of cases to check. By declaring variables as scalarsets, SMV is able to reduce this case explosion, exploiting symmetry by solving only a representative set of verification problems, sufficient to verify the property under consideration [86,87].

The idea of tailoring an input language so that symmetry information can be automatically inferred is the basis for several purpose-built symmetry reduction tools, including Smc [38] (see Section 4.4), Sviss [58] (see Section 5.6) and Grip [78] (see Section 6). These approaches all share the limitation that they can only handle full symmetry between components of the same type.

7.3. Automatic Symmetry Detection via Graph Isomorphism

At the start of Section 7, we discussed the symmetry principle: symmetry in the cause implies symmetry in the effect. This principle can be exploited for purposes of automatic symmetry detection. In a concurrent system, symmetry between processes is usually reflected in symmetries of the communication structure associated with the system. It may be possible to extract a graphical representation of the communication structure for a system from the program text. The resulting graph is typically small, easily small enough for its automorphism group to be computed by an automatic tool such as Nauty [50]. Under suitable conditions, automorphisms of the communication structure graph induce automorphisms of the associated model, which can be exploited during model checking.

Automatic symmetry detection techniques based on graph isomorphism were first proposed in [19,23]. For a simple programming language, where processes are described using synchronization skeletons, and variables are shared between at most two processes, the communication relation, $\mathit{CR}$, associated with a program is an undirected graph whose nodes are process ids, such that there is an edge between two nodes if and only if the corresponding processes share a variable. A process is normal if it treats all of its neighbors in $\mathit{CR}$ identically; two processes are isomorphic if their local transitions are in one-to-one correspondence (see [19] for a rigorous definition of these concepts). For a program comprised of processes in normal form, such that processes i and j are isomorphic whenever $\pi (i)=j$ for some $\pi \in \mathit{Aut}(\mathit{CR})$, it can be shown that Aut$(\mathit{CR})$ induces a group of automorphisms on M, the model associated with the input program. This approach has been generalized to allow variables to be shared between multiple processes [16,29].

For models of computation where communication is via channels, e.g. for the ProMeLa language [37,88], symmetry can be derived by analyzing the static channel diagram, $\mathit{SCD}$, associated with an input program [89]. This is a directed, colored, bipartite graph. The nodes are the identities of processes and channels, and nodes are colored according to process and channel type. There is an edge from process i to channel c if the program text for process i includes a send statement of the form $c!\cdots$. Similarly, there is an edge from c to i if the program text for process i includes a receive statement of the form $c?\cdots$. The static channel diagram captures static information about links between processes. If channels are first class objects that can be sent in a message, the static links can be used to create additional, dynamic links between processes at runtime; these are not captured in the static channel diagram.

An example static channel diagram for a model of an email system is shown in Figure 9. The figure is adapted from [43], which also contains full details of the ProMeLa specification with which the static channel diagram is associated. The system consists of five client processes and a mailer process, represented by ovals. Each client has an associated incoming message channel, box. Clients send messages to the mailer via the network channel. A message includes a reference to the box channel for the message recipient, which the mailer uses to forward the message. Communication links from the mailer to client processes are thus established dynamically, and do not form part of the static channel diagram.

In [89] it is shown that, under restrictions similar to the normality and isomorphism requirements of [19,23], the group Aut$(\mathit{SCD})$ induces a group of automorphisms on the Kripke structure associated with a message passing program. The restriction is that the input program text must be invariant under all permutations $\alpha \in \mathit{Aut}(\mathit{SCD})$; the notion of invariance is defined formally in [89].

The automorphism group of the static channel diagram in Figure 9 consists of all permutations of client processes that simultaneously permute the associated box channels, for example, the permutation that simultaneously swaps client_1 with client_2 and box_1 with box_2.

Static channel diagram analysis is the basis of automatic symmetry detection techniques for ProMeLa [43,44] and is implemented in the TopSpin symmetry reduction tool [41]. The Saucy tool [90] is used to compute the group $\mathit{Aut}(\mathit{SCD})$. The original technique of [89] is enhanced by weakening the invariance requirement. Instead of giving up if it is determined that the program text is not invariant for some element of $\mathit{Aut}(\mathit{SCD})$, computational group theory is employed to compute the largest subgroup of $\mathit{Aut}(\mathit{SCD})$ under which the program text is invariant.

Comparison with approaches based on tailored input languages. Symmetry detection techniques based on graph isomorphism facilitate the automatic detection of symmetry, while the use of tailored input languages, as discussed in Section 7.2, can be seen as a means of specifying symmetry. Nevertheless, the graph isomorphism-based symmetry detection methods discussed above all place restrictions on the form of input programs. These restrictions are milder than those associated with the use of scalarsets; nevertheless, they mean that symmetry detection cannot be considered fully automatic: it is still up to the programmer to massage their problem into a form amenable to a particular tool.

Detecting symmetry via graph isomorphism has the advantage that it caters for arbitrary symmetry groups arising from the communication structures of concurrent systems. This advantage comes at a price. With tailored input languages that permit only full symmetry, symmetry reduction algorithms can be geared towards exploiting this kind of symmetry using strategies based on sorting, as discussed in Section 4.2 However, when symmetry is computed via graph isomorphism, the result is a set of group generators produced by a graph isomorphism tool such as Nauty or Saucy. These generators alone say nothing about the nature of the symmetry group. Without resorting to manual intervention, automatic techniques are required to analyze a group, given as generators, and determine its structure and a corresponding suitable symmetry reduction strategy. Techniques of this nature are the focus of [30,31], where computational group theory is applied to determine when a group has the structure of the fully symmetric group Sym$\{1,\cdots ,n\}$, for some n, or when a group decomposes as a product of subgroups, which can be handled via a composite symmetry reduction strategy (see Section 4.2).

8. Partial Symmetry Reduction

The techniques for symmetry reduction we have looked at so far in this survey rely on the ideal scenario of a transition relation that is invariant under any interchange of the components, as permitted by the symmetry group G. In other words, consistently renaming components in both source and target state of any transition yields again a valid transition in the Kripke structure. This condition can be formally violated by systems that nevertheless seem to be approximately symmetric. For example, consider an initially perfectly symmetric system whose design evolves into an asymmetric one through customizations on some components. Such customizations could for instance impose different component priorities that apply whenever there is contention for some resource. Since the behaviors of the components differ only in situations suspected to be rare, there is an obvious incentive to exploit the regular structure of these partially symmetric systems.

Techniques for exploiting partial symmetry come in two flavors. One is to impose constraints on how much the system model may deviate from a perfectly symmetric one, and to show which properties symmetry reduction, applied to these imperfectly symmetric systems, still preserves. The publications on near and virtual symmetry, sketched below, belong to this category. Another flavor is to leave it completely open how much symmetry exists, and design methods that can cope with arbitrarily poor symmetry, although the performance suffers the less symmetry there is. These methods comprise annotated quotient constructions, such as guarded quotients and lazy, adaptive symmetry reduction. We describe the main representatives of both flavors of techniques.

Near and virtual symmetry. One of the earliest attempts to apply symmetry reduction strategies to approximately symmetric systems is [69]. The authors present the notion of near symmetry, which is defined with respect to a Kripke structure $M=(S,R,L)$, as follows: a near-automorphism is a permutation $\pi$ such that L is invariant under $\pi$ and, for any transition $r:=(s,t)$, if $\pi (r)$ fails to be a transition of R, then s must be fully symmetric—that is, ${\pi }^{\prime }(s)=s$ for every permutation ${\pi }^{\prime }$ on $\{1,\dots ,n\}$. A system is then called near-symmetric if it has a (non-trivial) group $G_{\mathit{near}}$ of near-automorphisms. This definition obviously generalizes symmetry, where $\pi (r)\in R$ is required for all $\pi \in G$. It is also obvious that this definition captures some interesting asymmetric systems. For example, in resource allocation protocols, potential nondeterminism due to several components simultaneously requesting access to the same resource is often prevented using pre-assigned priorities. States with resource contention then allow some processes to move forward, but not others. If all other transitions are symmetric, the system may have near symmetry in the sense of [69]. The readers-writers problem is a paradigmatic model for such protocols.

But what does this generalized notion of symmetry buy us? It turns out that one of the main selling points of symmetry, namely that it allows a bisimilar quotient, is completely preserved by near symmetry. That is, the canonical quotient of M with respect to the near-automorphism equivalence relation,

$$s{\equiv }_{\mathit{near}}t\mathrm{iff}\mathrm{there}\mathrm{exists}\pi \in G_{\mathit{near}}\mathrm{such}\mathrm{that}\pi (s)=t,$$

is bisimulation-equivalent to M. This is interesting, as it points out that there is a gap between what is captured by the orbit relation, and its ability to induce a bisimilar quotient. This gap was investigated in depth in [91]. The authors characterize precisely how much the definition of state equivalence may be relaxed while maintaining the property that the canonical quotient is bisimilar to the given model. Concretely, a Kripke structure $M=(S,R,L)$ is called virtually symmetric with respect to a permutation group $G_{\mathit{virt}}$ if L is invariant under every permutation in $G_{\mathit{virt}}$ and, for every transition $(s,t)$ in the symmetrization of R, there exists a permutation $\pi \in G_{\mathit{virt}}$ such that $(s,\pi (t))\in R$. The symmetrization of R is the set ${\cup }_{\pi \in G_{\mathit{virt}}}\pi (R)$; note that this set equals R if M is symmetric with respect to $G_{\mathit{virt}}$.

Virtual symmetry was proven in [91] to be the most general condition that allows a bisimilar symmetry quotient. As such, it generalizes near symmetry, and also the related notion of rough symmetry introduced in [69]. A limitation of near, rough and virtual symmetry is that while bisimilarity makes these approaches suitable for full CTL* model checking, it also excludes many asymmetric systems, where bisimilarity simply does not permit much reduction. Another limitation, and one of great importance in practice, is that [69] and [91] leave it open how the imposed preconditions can be verified efficiently; the techniques presented seem to incur a cost proportional to the size of the unreduced Kripke structure. A strategy of identifying virtual symmetry in systems, by reducing it to the satisfiability of a Presburger Arithmetic formula, was proposed in [80], along with an implementation of full virtual symmetry reduction using generic representatives (Section 6).

Adaptive symmetry reduction, guarded quotient structures. The aforementioned limitations of virtual symmetry reduction and related methods were the driving force behind more flexible techniques based on annotated quotients. These techniques permit arbitrary asymmetric edges, but annotate the quotient Kripke structure that is being explored with additional information whenever an asymmetric transition is followed. The methods are more flexible than virtual symmetry, as no preconditions for their applicability exist, nor does the amount of symmetry in the model need to be precisely detected before model checking. Instead, these methods unite the symmetry detection, symmetry reduction, and verification steps. The advantages of this fell-swoop approach are that (i) unreachable parts of the system’s Kripke structure, which have no impact on the exploitable symmetry, can be ignored, and (ii) if the Kripke structure has symmetric substructures, those can be reduced to a subquotient.

Let us consider more closely the adaptive symmetry reduction approach to exploiting partial symmetry using annotations [92,93]. The idea is to annotate each reached state, space-efficiently, with information about whether and how symmetry is violated along the path to it. More precisely, the annotation is a partition of the set of all component indices: if the path to the state contains a transition that distinguishes two components (and thus violates symmetry), their indices are put into different partition cells. Only components in the same cell can be permuted during future explorations from the state—the algorithm adapts to the state’s history.

As an example, consider the variant of the Readers-Writers problem shown in Figure 10 (borrowed from [93]). There are two “reader” processes (indices 1, 2) and one “writer” (3). The edge from N to T is unrestricted and available to any process, as is the one from C back to N. There are two edges from T to C. The first (symmetric) is available to any process, provided no process is currently in its critical section C. The second (asymmetric) is available only to readers ($i<3$), and the writer must be in a non-critical local state. The intuition is that readers, who only read, may enter their critical sections simultaneously, as long as the writer is not residing in its own critical section.

With each process initially in local state N, the induced (asymmetric) 3-process Kripke structure has 22 reachable states. The adaptive symmetry reduction method, in contrast, constructs an annotated reachability tree of only 9 abstract states (Figure 11). The abstract state $\mathit{NTC}$, for example, represents the set of six concrete states obtained by permuting the local state tuple $(N,T,C)$ (red in Figure 10). None of these concrete states satisfies the condition $\forall j:s_j\ne C$. Thus, regarding local transitions from T to C, there is only the option of the second—asymmetric—edge, guarded by $i<3\wedge s_3\ne C$. Of the six concrete states, two satisfy this condition for an index i such that $s_i=T$, namely $(T,C,N)$ and $(C,T,N)$. In both cases, the edge leads to state $(C,C,N)$. The algorithm now must record the fact that this state is reached through an asymmetric edge: it needs to remember for the future that the initially assumed symmetry between process 3 and the other two has been violated and can not be exploited in further explorations. This is expressed succinctly in Figure 11 using the notation $\mathit{CC}|N$; this abstract state represents neither $(N,C,C)$ nor $(C,N,C)$. Also note that the annotated abstract state $\mathit{NC}|N$ is crossed out in Figure 11, as it is subsumed by the abstract state $\mathit{NNC}$: the latter was reached without symmetry violations and thus represents every concrete state represented by $\mathit{NC}|N$ (and more).

It is pointed out in [93] that the structure induced by Figure 10 is not virtually symmetric and hence not nearly or roughly symmetric. As a result, this Kripke structure is not bisimilar to its standard symmetry quotient, obtained by existential abstraction with respect to symmetry equivalence of states. Moreover, the reachable part of this quotient contains many states that are concretely unreachable, such as the state $(N,C,C)$. The standard quotient is thus unsuitable even for reachability analysis: it strictly overapproximates the set of reachable states.

The guarded annotated quotient construction presented by Sistla and Godefroid [3,94] can be seen as a generalization of the adaptive method discussed above (although the former preceded the latter). While adaptive symmetry reduction is specialized to reachability analysis, Sistla and Godefroid’s method is designed to preserve the full range of CTL* properties. Consequently, more information needs to be tracked during model checking. Initially, the given model M is symmetrized by adding transitions, resulting in the smallest symmetric super-structure $M^{\prime }$ of M. The edges of Kripke structure $M^{\prime }$ are then annotated with permutations, revealing which original edges the quotient edge maps back to. The result is known as guarded annotated quotient of M. In practice, the quotient is constructed on the fly, embedded in the model-checking process.

Both annotated quotient methods [94] and [93] have been applied to examples where global symmetry is destroyed by the introduction of process priorities. Compared to standard symmetry reduction, the efficiency depends on how “scattered” the symmetry group is — if it is nearly full, with very few processes having priorities distinct from those of others, standard symmetry (with a strict subgroup of the full symmetry group) may perform better, not suffering from the annotation overhead. Neither of the two methods have been implemented symbolically, which appears non-trivial due to this very overhead.

9. Summary

In this survey, we have attempted to give a very broad introduction to the use of symmetry in automated formal verification methods, particularly model checking. Symmetry reduction research has recently seen a renaissance, witnessed by the many pertinent publications just over the last few years. Although there have been survey articles on this topic before, they tend to fall out of date rather quickly. We have therefore emphasized new developments, as long as they appear promising, especially if there is work on these aspects by different sets of authors.

Even a survey of this size cannot possibly cover all aspects of the subject; we cursorily acknowledge the following:

• symmetry under fairness: A fairness constraint asserts that each component of a system be regularly (say, infinitely often) considered for execution and not perpetually ignored by the scheduler. Such a constraint is by nature asymmetric. This problem cannot easily be fixed by “factoring out” the process identity, as we did it in Section 2.2 with a liveness formula. Specialized techniques for combining symmetry and fairness have been proposed, based on extended algorithms and quotient structures [48,95,96].
• partial-order reduction: This method is, like symmetry, applicable in many situations that arise due to the existence of replicated components [97,98]. The idea is to avoid process interleavings that do not lead to relevant new states. In contrast to symmetry, it focuses on redundancy in transitions (not states), it is meaningfully applicable only in asynchronous concurrency (the concept of symmetry is in this sense more general; see Section 2.3), and it does not require the verification of global preconditions (such as the existence of symmetry in the design). These differences suggest that both symmetry and partial-order reduction can be applied to a (symmetric) system, sometimes with added benefits. This was investigated in detail in [99].
• parameterized model checking: Just like symmetry reduction, parameterized verification exploits replication in system designs. Suppose we are given an infinite family ${(M_n)}_{n=1}^{\infty }$ of Kripke structures representing concurrent systems, n indicating the number of components in instance $M_n$. The goal is to determine whether a given property holds for all instances $M_n$ of the family. One approach is to reduce this unbounded problem to the same problem over a finite subfamily ${(M_n)}_{n=1}^c$, for some small cutoff number c, or even over the single fixed-size system $M_c$. The idea is that c concurrent processes may suffice to exhibit all behavior that is relevant to the verification of the property. If the individual structures $M_n$ are symmetric (as is usually the case), symmetry reduction can be used to simplify the remaining verification problem for $M_c$. Intuitively, while parameterized verification reduces from (infinitely) many to few, symmetry reduces from large to small (see also [100,101]).

Over the last decade, CPU vendors have begun developing multi-core processors, in part due to the limits of single-core frequency scaling as a means of increasing processing power. However, to take advantage of the performance offered by multi-core processors, software developers have no choice but to write concurrent software, be it explicitly using threading libraries such as POSIX, or implicitly via parallel languages such as OpenMP and OpenCL. There is thus an urgent need for verification tools capable of analyzing multi-threaded software. If the data the threads operate on is abstracted away, we obtain a system of replicated identical components. Symmetry reduction may be the key technology for tackling state explosion in software verification in the multi-core era. Future challenges include automatic extraction of concurrent verification models from parallel source code, and automatic data abstraction of such models to expose the symmetry.