Recognition of Symmetric 3D Bodies
Abstract
: The paper deals with the recognition of symmetric three-dimensional (3D) bodies that can be rotated and translated. We provide a complete list of all existing combinations of rotation and reflection symmetries in 3D. We define 3D complex moments by means of spherical harmonics, and the influence of individual symmetry groups on complex moment values is studied. Each particular symmetry pre-defines certain moment values. These moments can no longer differentiate between two objects of the same symmetry, which decreases the recognition power of the feature set. They should not be included when constructing the invariants. Translation and rotation invariants up to the fourth order are presented and their performance is studied on both artificial and real data.1. Introduction
Automatic recognition of 2D and 3D objects from their digital images has become a well-established discipline in the last two decades. A lot of feature systems that enable to describe and recognize objects regardless of their particular position, orientation and size have been proposed and tested in the literature. Such features are called invariants. In most cases, invariants to translation, rotation and scaling (TRS) are sufficient, although invariants to more general object deformations also exist.
When testing most current general-purpose recognition systems, one immediately discovers that they perform poorly on symmetric objects. This fact has a straightforward mathematical explanation. Most features are “projections” of the image function onto a set of certain simple basis functions (for instance, Fourier coefficients are projections onto a harmonic basis, moments are projections onto polynomials, etc.). The basis functions usually exhibits some kind of symmetry. Depending on the kind of object symmetry, some features are always zero because the respective basis functions do not contribute to object description. This is a well-known fact even in 1D: the Fourier transform of an even function has all imaginary coefficients zero because we need only the cosine basis function for a complete expansion. The zero values themselves would not be a problem. However, when constructing invariants, we often create them as a product of selected features. If one factor in the product is zero, the whole invariant is zero and looses its recognition ability. This effect was thoroughly studied in 2D case in [1]. The authors demonstrated that recognition of symmetric objects and patterns requires designing of special invariants which do not contain any always-zero features.
Surprisingly, in the case of 3D objects this problem has not been addressed in the literature in a systematic way. At the same time, it is not a borderline problem because most natural and man-made objects have some kind of symmetry.
One can find two groups of papers relevant to this topic. The first one deals with the rotationally invariant pattern recognition of 3D bodies and describes creation of various sets of invariants but these papers ignore the symmetry issue. Sadjadi and Hall [2] derived three TRS invariants from moments of the second order. Guo [3] used different approach with the same result. Galvez and Canton [4] used the normalization approach to 3D recognition. Cyganski and Orr [5] proposed a tensor method for derivation of rotation invariants from geometric moments. The method of geometric primitives of Xu and Li [6,7] yields the same results. Kazhdan [8] studied registration of objects differing by 3D rotation, Kakarala and Mao [9] used bispectrum for derivation of TRS invariants. The work of Lo and Don [10] has the biggest impact on this area because they derived 3D TRS invariants from complex moments and the influence of rotation symmetry on the recognition can be in this representation advantageously studied. However, Lo and Don [10] presented only 12 invariants of the second and third order of limited discriminability, without any generalization to higher orders, and they ignored completely the issue of symmetric objects. Their approach was later used in [11], where the additional invariance to blurring was introduced, and most recently in [12], where several higher-order invariants were presented but still without studying the impact of symmetry.
The papers from the second group study the symmetry itself, but they do not consider the recognition task and the derivation of invariants. There have been many such papers and books from antiquity until now. The most relevant for us are those studying combinations of reflection and rotation symmetry, e.g., Weyl [13], Slavík et al. [14] (symmetry in mineralogy), Urch [15] (symmetry in chemistry), and the papers dealing with the relation between the object symmetry and its moments as Schmidt and Žďánská [16] (octahedral and icosahedral symmetry), Samoson et al. [17] (tetragonal, tetrahedral, octahedral, icosahedral and spherical rotation symmetry) and Mamone et al. [18] (tetrahedral, octahedral, icosahedral and spherical symmetry including both rotation and reflection).
The main goal of the paper is to introduce rotation invariants of arbitrary orders that are specifically designed for recognition of symmetric objects. To do so, we start the paper with a survey of all possible rotation and reflection symmetries in 3D including their combinations. Then we study complex moments, one of popular features in object recognition, and investigate the influence of particular symmetries on the moment values. Each particular symmetry pre-defines certain moment values (mostly sets certain moments equal to zero). These moments can no longer differentiate between two objects of the same symmetry. Even if this zero features are mixed with valued features, the success rate is usually lower than that provided by valued features only because the classifier works in a high-dimensional space. That’s why these zero features should be identified in advance and should not be included into the feature vector. We show how to design special rotation invariants which are suitable for recognition of symmetric 3D bodies. In contrast to Lo and Don [10] and other earlier papers, we present general formulae for constructing invariants which are not restricted to low order moments only. We demonstrate practical usage of such invariants by numerical experiments.
The paper is organized as follows. The term “symmetry” is recalled in Section 2, the survey of 2D case is in Section 3, the influence of the symmetry on 3D moments is analyzed in Section 4, the TRS invariants based on the complex moments are introduced in Section 5 and their behavior is shown in numerical experiments in Section 6. Section 7 concludes the paper.
2. Symmetry in 2D
In this paper we use the term symmetry in a common geometric sense. Let us have a transformation G of spatial coordinates x =(x1,...,xN) such that G : x → x′. Then the image f is called symmetric w.r.t. G if:
We deal with rotation and reflection symmetry only, the other kinds of symmetry, such as translational, scaling and skewing symmetry are irrelevant in the context of object recognition. They require infinite support and the scaling symmetry even requires infinite spatial resolution. It cannot be fulfilled in practice, so in reality we do not meet these two kinds of symmetry. Hence, G(x) can be expressed in a matrix form as:
In two dimensions, we recognize two basic symmetries—n-fold rotation symmetry and reflection symmetry. In the former case G is a rotation around the origin by angle α =2π/n (i.e., an object is mapped onto itself when rotated by 2πk/n, k =1, ···,n). The n is called the fold number of the rotation symmetry. In the latter case G is a reflection across a line passing through the origin. There is a well-known link between rotation and reflection symmetries [19]. If a function has n-fold rotation symmetry, then it has either n axes of the reflection symmetry or has no reflection symmetry at all. On the other hand, the existence of n symmetry axes always implies the n-fold rotation symmetry. The combined rotation and reflection symmetry is called dihedral symmetry. The functions having rotation symmetry without any reflection symmetry are called chiral. Hence, we have two sequences of symmetry groups—rotation groups:
3. Recognition of Symmetric 2D Objects
Various systems of features for description and recognition of planar objects have been proposed in literature (see for instance [20], Chapter 1, for a short survey and other references). Many of them perform poorly on symmetric objects. This is a contrast to human perception. For humans, symmetry serves as a useful additional information for recognition because our brain easily detects the type of symmetry. In automatic systems, features are often based on mathematical quantities which vanish or have the same value for all symmetric objects, which means they have no discrimination power. This is a significant drawback because in many applied tasks we want to classify man-made objects or natural shapes from their silhouettes. In most cases such shapes have some kind of symmetry. Different classes may or may not have the same symmetry that makes the task even more difficult. This is why we must pay attention to these situations and why it is necessary to design special invariants for each type of symmetry.
One of the most powerful and the most popular features for object recognition are invariants based on image moments [20]. Let us illustrate how moments are influenced by object symmetry and how to overcome this problem in 2D. Moments in general are projections of a function on the given polynomial basis. We may use various bases yielding different moment systems but in any case we face the symmetry problem because it is induced by the symmetry of the basis functions. Let us show how it works in the case of so-called complex moments, where the theory is the most transparent. For all other moment systems the principle stays the same.
The complex moment of a function f is defined as:
It follows from the definition that (the asterisk denotes complex conjugate). In polar coordinates (r, θ):
The reflection symmetry also constrains the moment values. Let us for simplicity illustrate this on the case when the symmetry axis is horizontal, i.e., f(x, y)= f(x, −y). Then which implies all complex moments must be real. For an arbitrary oriented axis we get another constraint on the moment phase. Such a pre-determination of the moment values regardless of the particular shape of f decreases the recognition power.
Table 1 summarizes the constraints for selected symmetry groups.
4. Recognition of Symmetric 3D Objects
In recognition of 3D objects we face similar problems as in 2D but the situation is much more complicated. Rotation in 3D has three degrees of freedom, is not commutative and there exist many more symmetry groups than in 2D. Hence, the generalization is not straightforward. We first study the existing symmetry groups and then we will investigate the impact of each particular symmetry on the moment values.
4.1. Rotation in 3D
Rotation in 3D can be expressed by various ways. Two common ways are by a rotation matrix and by Euler angles.
Definition 4.1 A 3D rotation matrix is:
The rotation matrix is the matrix of direction cosines, e.g., αzy is the angle between original position of z-axis and new position of y-axis.
Another way of rotation description in 3D are so called Euler angles α, β, and γ. The α is the angle of rotation around z-axis, the corresponding rotation matrix is:
The Euler angles can be recovered from the rotation matrix by:
4.2. Rotation and Reflection Symmetry in 3D
In 3D, the reflection symmetry is always with respect to a reflection plane and rotation symmetry is w.r.t. a symmetry axis. When categorizing the symmetry groups, we will always assume that the axis with the maximum fold number of the rotation symmetry coincides with the z-axis, and if there is a plane of the reflection symmetry containing the axis, it coincides with the xz-plane. If the reflection plane is perpendicular to the z axis, it coincides with the xy-plane. We can make this assumption without a loss of generality because we study such object properties which do not depend on the particular orientation. A survey of all 3D symmetry groups with the rotation and reflection symmetry is presented below.
Asymmetric extension of the 2D groups:
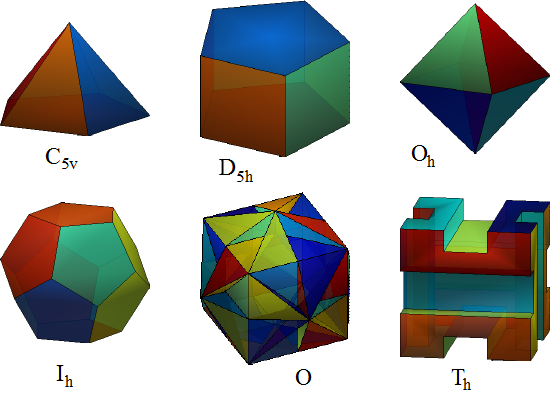
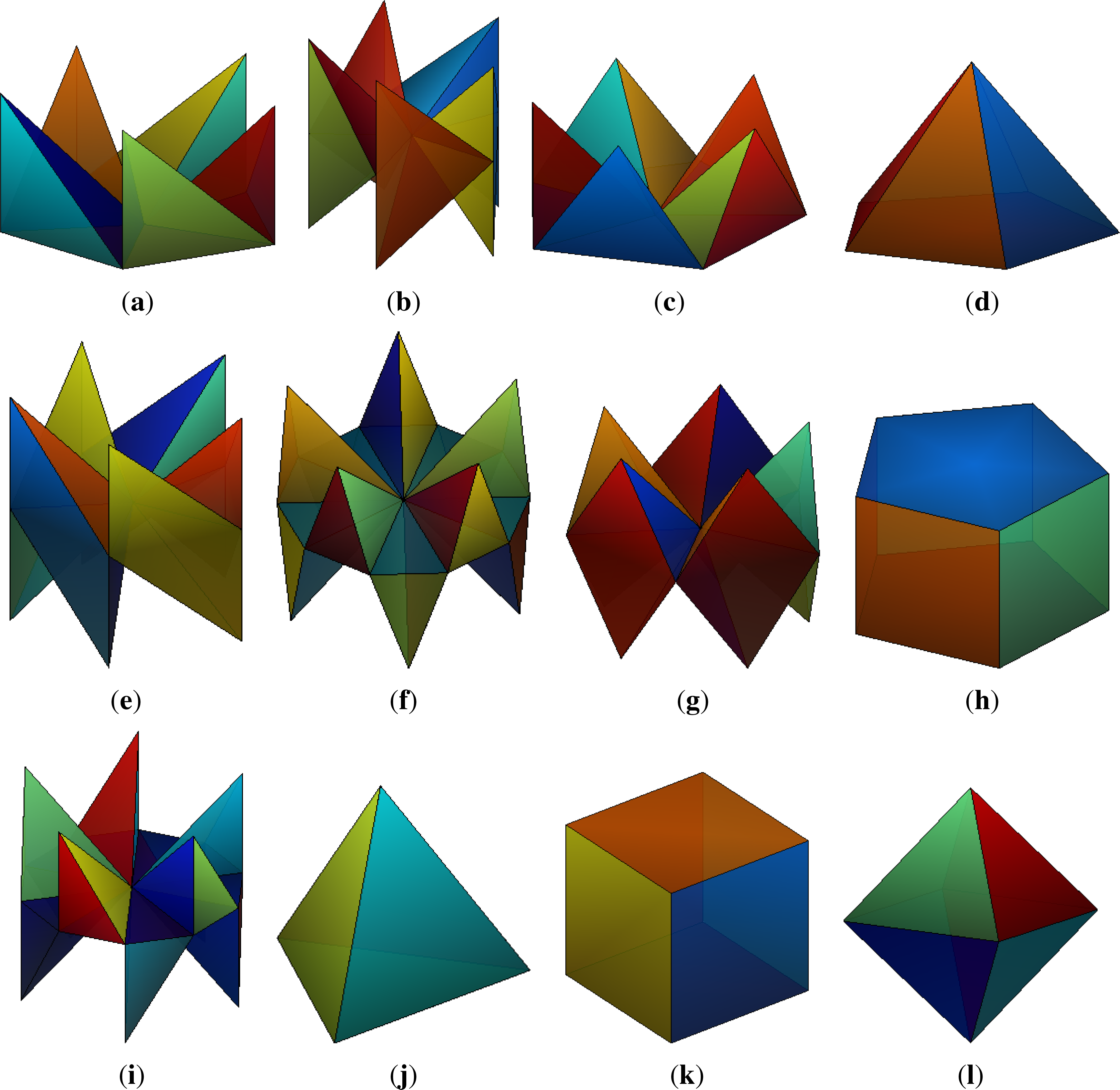
into 3D. We can imagine e.g., some chiral pyramid constructed on the 2D base with the symmetry group Cn. The group has still n elements. An example of a body with this symmetry is in Figure 1a.A single horizontal plane of the reflection symmetry. These symmetry groups are denoted as:
The symmetry group Cnh has 2n elements: n identical with Cn (the identity and n − 1 rotations) and other n, where the rotations are combined with the reflection. The objects resemble a “double pyramid”, where the bottom pyramid is a reflection of the top pyramid. An example of a body with this symmetry is in Figure 1b.The group can include n vertical planes of the reflection symmetry. Then we have:
The symmetry group Cnv has also 2n elements: n identical with Cn and n reflections. It is called pyramidal symmetry, because a pyramid built on a regular n-sided polygon has this type of the symmetry. Examples are in Figure 1c,d.We can generalize the 2D reflection as rotation by 180° in 3D. Then the symmetry is called dihedral (the term “dihedral” has this meaning in 3D) and we have a sequence:
The symmetry group Dn has 2n elements: n rotations by the z-axis (identical with Cn) and n rotations by π around axes perpendicular to z. We have again a double pyramid as in Cnh, but the bottom pyramid is a rotation by π of the top pyramid. An example from connected tetrahedrons is in Figure 1e.We can combine the dihedral symmetry with the reflection:
The symmetry group Dnh has 4n elements: 2n identical with Dn and other 2n combined with reflection across the horizontal plane. The reflections across one of n vertical planes can be expressed as combinations of the horizontal reflection and rotation. This symmetry is called prismatic, because a prism built on a regular n-sided polygon has this type of the symmetry. An examples are in Figure 1g,h.There is another group sequence:
without the horizontal reflection plane, but with symmetry to compound reflection across the horizontal plane and rotation by (2k +1)π/n for k =0, 1,...,n − 1. The number of elements of Dnd is 4n. It is called antiprismatic symmetry, because we would have to rotate the bottom half of the prism by π/n to obtain this type of symmetry. An example is in Figure 1f.The last group sequence:
contains the symmetry to the compound transformation from the previous case but without the corresponding simple rotations. S2n has 2n elements: n rotations by 4kπ/n and n compound transformations from the rotations by 2(2k +1)π/n and the reflections. The actual fold number of the rotation symmetry is n. An example is in Figure 1i.
Note that some of these groups are equivalent. For instance, C1h = C1v (a single reflection), D1 = C2 (a single rotation by π), D1h = C2v (a reflection in a plane and a rotation by π along a line in that plane), and D1d = C2h (a reflection in a plane and a rotation by π along a line perpendicular to that plane). The group S2 (sometimes called central symmetry) is a composition of a reflection in a plane and a rotation by π through a line perpendicular to that plane. Unlike D1d, in S2 both these transformations must be performed together.
All the above symmetry group sequences include at most one rotation axis with the fold number higher then two. However, there exist other symmetry groups such as regular polyhedra which do not fit into the above framework.
Full tetrahedral symmetry: the regular tetrahedron has four axes of three-fold symmetry, three axes of two-fold symmetry and six planes of the reflection symmetry. The symmetry group Td has 24 elements in total (the letter d means diagonal mirror planes). The regular tetrahedron is in Figure 1j.
Full octahedral symmetry: the cube and the octahedron have the same symmetry. It includes three axes of four-fold symmetry, four axes of three-fold symmetry, six axes of two-fold symmetry and nine planes of the reflection symmetry. The symmetry group Oh has 48 elements, Td is its subgroup. The cube and the octahedron are in Figure 1k,l.
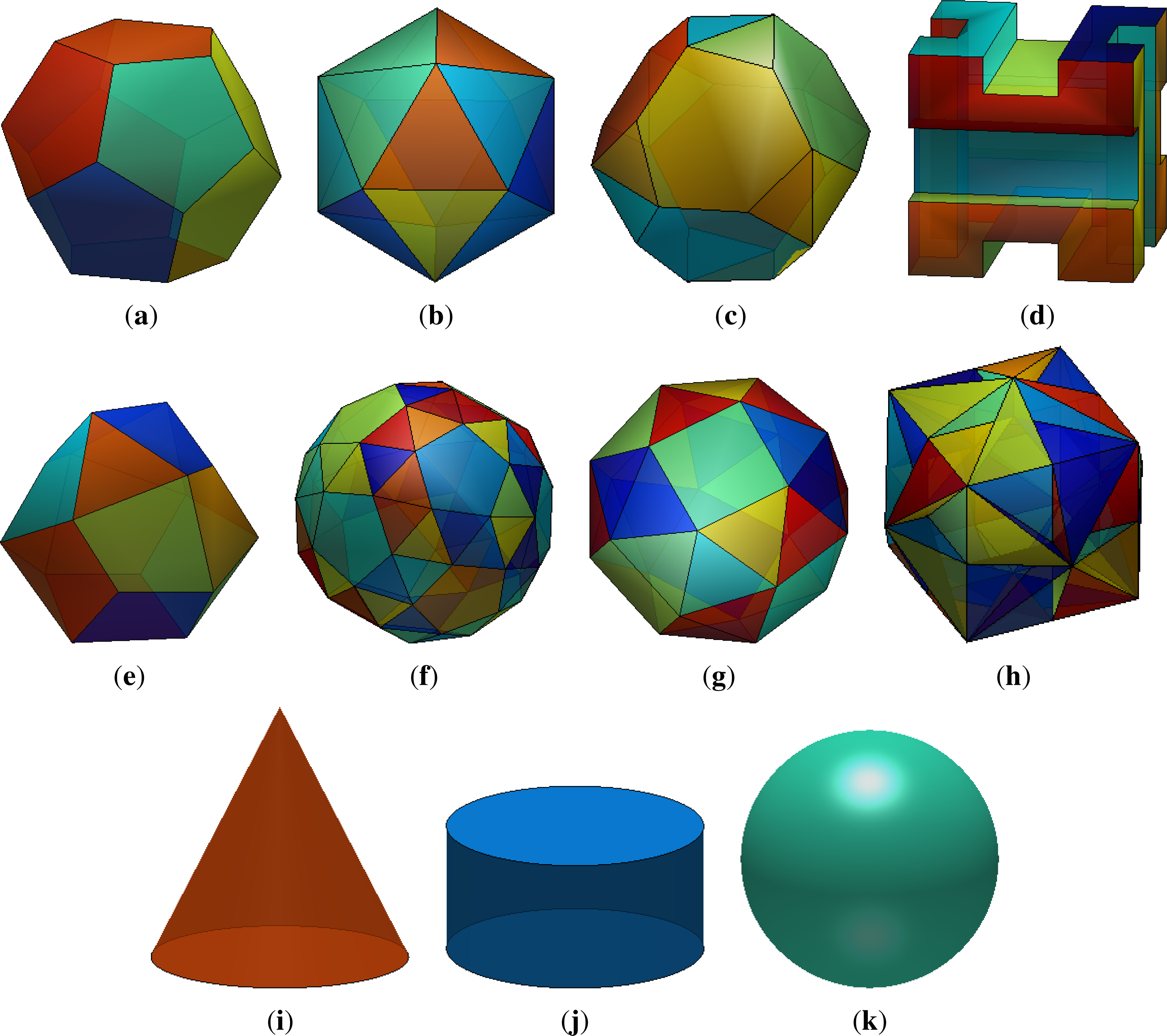
Full icosahedral symmetry: the dodecahedron and the icosahedron have also the same symmetry. It includes six axes of five-fold symmetry, 10 axes of three-fold symmetry, 15 axes of two-fold symmetry and 15 planes of the reflection symmetry. The symmetry group Ih has 120 elements. The dodecahedron and the icosahedron are in Figure 2a,b.
Pyritohedral symmetry Th: this group includes the same rotations as Td, but has only three planes of reflection symmetry, the rest are rotoreflections. This group has 24 elements (the letter h means horizontal mirror planes). Examples are in Figure 2c,d.
Chiral tetrahedral symmetry: the group T includes the same rotations as Td, but without the planes of the reflection symmetry. It has 12 elements. An example is in Figure 2e.
Chiral octahedral symmetry: the group O includes the same rotations as Oh, but without the planes of the reflection symmetry. It has 24 elements. Examples are in Figure 2g,h.
Chiral icosahedral symmetry: the group I includes the same rotations as Ih, but without the planes of the reflection symmetry. It has 60 elements. An example is in Figure 2f.
Finally, there exist three groups containing circular symmetry:
Conical symmetry group C∞v.
Cylindrical symmetry group D∞h.
Spherical symmetry group K.
Examples of these three groups are shown in Figure 2i,j,k. Summarizing, we have:
Seven infinite sequences of the symmetry groups, where each group has one main rotation axis and the other axes are at most twofold;
Seven separate symmetry groups with more than one rotation axes with the fold number higher than two;
Three infinite symmetry groups with some kind of circular symmetry.
The presented list of symmetry groups is complete. It has been proved that in 3D there are no other independent combinations of the rotation and reflection symmetries [13].
4.3. Complex Moments in 3D
The most natural way of the generalization of the complex moments into 3D leads through so-called spherical harmonics (e.g., [8] among others).
Definition 4.2 A spherical harmonic is:
The spherical harmonics form an orthonormal basis. If we have a function f(θ, ϕ) defined on the unit sphere, it can be expressed as a linear combination of the basis functions:
The complex moments can then be generalized into 3D such that the function ei(p−q)θ in their polar definition (3) is replaced by the corresponding spherical harmonic.
Definition 4.3 The 3D complex moment:
There is a relation between the spherical harmonic of negative and positive orders:
In the above definition, the complex moment is expressed in the spherical coordinates ρ, θ and ϕ:
Under a rotation, the spherical harmonics are transformed in a simple way:
Definition 4.4 If the rotation matrix R is decomposed into the Euler angles α, β, γ, then the Wigner D-function (also Wigner D-matrix) is defined as
Wigner d-functions with swapped lower indices can be obtained by the relation .
If we substitute (18) into Definition 4.3, we obtain the complex moment after the rotation by the matrix R
4.4. The Influence of Symmetry on 3D Complex Moments
The investigation of the influence of the symmetry on the 3D complex moments is complicated. A complete solution to this problem would require successive substitution of all elements of the corresponding symmetry group to the Equation (21), which is extremely laborious. We do not follow this approach in this paper. Instead, we show that many (possibly not all) constraints can be discovered by much simpler techniques.
If the object has an n-FRS and the rotation axis coincide with z-axis, then the Euler angles of a transformation from its symmetry group are α =0, β =0, and γ =2π/n. = 0 for m′ ≠ m and for m′ = m. Then (21) becomes
If there is an additional two-fold axis perpendicular to z (e.g., symmetry groups Dn and Dnh), then additional symmetry operation is the rotation by the Euler angles α =0, β = π, and γ =0. is non-zero only if m′= −m. Then and (21) becomes
If the object has the reflection symmetry across the xz-plane, then f(x, y, z) = f(x, −y, z), and in polar coordinates it holds f(ρ, θ, ϕ) = f(ρ, θ, −ϕ). For the spherical harmonics we have and for the complex moment . It implies for every ℓ and m.
The reflection symmetry across the yz-plane is similar. We have f(x, y, z) = f(−x, y, z) and in polar coordinates f(ρ, θ, ϕ) = f(ρ, θ, π − ϕ). For the spherical harmonics we have which yields . It implies for odd m and for even m, both for every ℓ. If the object has the reflection symmetry across the xy-plane, then f(x, y, z)= f(x, y, −z), f(ρ, θ, ϕ)= f(ρ, π − θ, ϕ), and for the spherical harmonics it holds for even l −|m| and for odd l −|m|. Consequently, for odd l −|m|.
If the object has the circular symmetry around the z-axis, then
If the object has spherical symmetry, then the complex moment does not also change during the arbitrary rotation around the y-axis, i.e., β is arbitrary. If is not dependent on β, then it equals one only if ℓ = m′= m =0 otherwise . It means only can by nonzero, for ℓ ≠ 0 or m ℓ ≠ 0.
We have derived the constraints (rules) for the seven infinite sequences of the symmetry groups Cn, Cnh, Cnv, Dn, Dnh, Dnd and S2n and for the three symmetry groups with a circular symmetry C∞v, D∞h and K. The constraints for the polyhedral symmetry groups Td, Oh, Ih, Th, T, O and I still remain to be found. To do so, we can use the rules for the longitudinal repetition m saying that m must be an integer multiple of the maximum fold number for the nonzero complex moment. The rule that l −|m| must be even applies to the group Oh only, where the reflection plane is perpendicular to the main four-fold rotation axis.
In principle we could use this approach also for the latitudinal repetition ℓ but it is too complicated in the case of the polyhedral groups. Instead, we use the group representation proposed by Mamone, Pileio and Levitt [18]. A group can be represented by matrices such that:
If we have some finite subgroup 𝔤 of the group and the sum of the characters of all elements of 𝔤 equals zero, then the sum of their representations equals zero, too:
If the group element G is a geometric transformation of coordinates in an n-dimensional space, it can transform function f as:
The representations of 3D orthogonal group O(3) are Wigner D-matrices. If the symmetry group is its subgroup, the constraints for the latitudinal repetition can be obtained as a sum of the characters of the individual symmetry operations. If the symmetry operation is rotation, the character is the trace of the corresponding Wigner D-matrix:
The full tetrahedral symmetry group Td contains:
identity,
eight rotations by 2π/3,
three rotations by π,
six reflections,
six rotoreflections by π/2,
The full octahedral symmetry group Oh contains:
identity,
six rotations by π/2,
eight rotations by 2π/3,
three rotations by π about a four-fold axis,
six rotations by π about a two-fold axis,
inversion,
six rotoinversions by π/2,
eight rotoinversions by 2π/3,
three reflections perpendicular to a four-fold axis,
six reflections perpendicular to a two-fold axis.
The full icosahedral symmetry group Ih contains:
identity,
12 rotations by 2π/5,
12 rotations by 4π/5,
20 rotations by 2π/3,
15 rotations by π,
inversion,
12 rotoinversions by 2π/5,
12 rotoinversions by 4π/5,
20 rotoinversions by 2π/3,
15 reflections,
The pyritohedral symmetry group Th contains:
identity,
eight rotations by 2π/3,
three rotations by π,
inversion,
eight rotoreflections by π/3,
three reflections.
The chiral symmetry groups include the same rotations as the full versions without all inversions. For the chiral tetrahedral group T we have:
The chiral octahedral symmetry group O:
The chiral icosahedral symmetry group I:
All these rules deal with the longitudinal repetition m and the latitudinal repetition ℓ separately. There are additional rules saying that the complex moments are zero for some additional particular combinations of the m and ℓ. We have created a few bodies with the specific symmetry and computed their complex moments, the results are in Tables 2 and 4.
If an object with the symmetry group Cnv for odd n is rotated such that it is symmetric to reflection across the yz-plane instead of the xz-plane, then there would be I in each second nonzero column, see Table 2 C5v. This rule applies also to the group Td.
The tables presented in this section show that for symmetric objects many moments are identically zero. This is a very important observation; if we want to recognize objects with certain symmetry, we should avoid invariants containing zero moments. This is the reason why the knowledge of the constraints found in this section is so important.
Figures 1 and 2 show some bodies used for the computation of the tables.
5. Invariants Based on Complex Moments in 3D
In this section, we show how to construct invariants to translation, rotation and scaling. Translation invariance is easily achieved by shifting the basis into the object centroid and scaling invariance can be obtained by normalization
In the following text we show how to achieve rotation invariance, which is far more difficult. The invariants are constructed as polynomials in moments, the coefficients of which are given by so called Clebsch–Gordan coefficients.
Definition 5.1 Clebsch–Gordan coefficient can be computed
The Clebsch–Gordan coefficients are used in group representation theory, see e.g., [21]. They arise from the explicit direct sum decomposition of the outer product of two irreducible representations of a group. Here, they are used for 3D analogy of 2D phase cancellation; they compensate changes of the spherical harmonics caused by their multiplication by the Wigner D-function when the object rotates.
The rotation invariants can be expressed by means of composite complex moment forms.
Definition 5.2 Composite complex moment form is
The form is the rotation invariant itself as well as , other invariants can be obtained as the tensor product of the composite complex moment forms and complex moments, where the sum of the upper indices equals zero. To obtain the rotation invariants, we can multiply a form and a complex moment
The number of the independent invariants ni is limited. We can estimate it as a difference between the number of moments nm and the number of degrees of freedom of the transformation np
Seemingly it would be possible to use only for the recognition and avoid the computation of the form products, but such description of an object would be strongly incomplete. For instance, there should be 77 invariants of the sixth order according to Equation (31), but we have just three invariants from single moments ( , and while is used for scaling normalization in both cases). Therefore we need the invariants obtained by phase cancellation by means of the tensor product of at least two composite complex moment forms. The moments describe only the distance distribution of the mass, not the directional distribution. The higher-order moments express the finer details of the object, but they are also more sensitive to noise, therefore we aim to use the lower-order moments preferably.
In the experiments, we use the following invariants: the second order:
The third and higher orders are expressed just by the composite complex moment forms. The third order: , , Φ6 = c3(3, 3)2c2, Φ7 = c3(3, 1)2c2, Φ8 = c3(1, 1)2c2, Φ9 = c3(3, 3)2c2(2, 2)2, , Φ11 = c3(3, 3)2c3(3, 1)2, Φ12 = c3(3, 3)2c3(1, 1)2, Φ13 = c3(3, 1)2c3(1, 1)2, the fourth order: Φ14 = c4, , , Φ17 = c4(4, 4)2c2, Φ18 = c4(4, 2)2c2, Φ19 = c4(2, 2)2c2, Φ20 = c4(4, 4)2c4, Φ21 = c4(4, 2)2c4, Φ22 = c4(2, 2)2c4, Φ23 = c4(4, 4)4c4, Φ24 = c4(4, 4)2c2(2, 2)2, Φ25 = c4(4, 2)2c2(2, 2)2, Φ26 = c4(2, 2)2c2(2, 2)2, Φ27 = c4(4, 4)2c3(3, 3)2, Φ28 = c4(4, 4)2c3(3, 1)2, Φ29 = c4(4, 4)2c3(1, 1)2, Φ30 = c4(4, 2)2c3(3, 1)2, Φ31 = c4(4, 2)2c3(1, 1)2, Φ32 = c4(2, 2)2c3(1, 1)2, , Φ34 = c4(4, 4)2c4(4, 2)2, Φ35 = c4(4, 4)2c4(2, 2)2, and Φ37 = c4(4, 2)2c4(2, 2)2. Their number is still higher then ni in Equation (31), therefore we have carried out another selection. We use only these 28 invariants Φ1–Φ17, Φ19–Φ23 and Φ32–Φ37.
The symmetry induces new dependencies in the invariants. A typical example is the circular symmetry. If we take a body with the conic symmetry C∞v, we can see in Table 4 C∞v that for m ≠ 0. If we substitute it into the formulas for Φ1–Φ37, they become much simpler. The invariants of the second order:
In the case of the cylindrical symmetry D∞h, can be nonzero, if m =0 and ℓ is even, it implies all invariants containing third-order moments (Φ4–Φ13 and Φ27–Φ32) equal zero. If the symmetry is spherical (K), then only Φ1 and Φ14 can be nonzero.
If we know the dependency, we can convert it into the zero. If for the bodies with the circular symmetry, it means:
If there is some other symmetry than circular, then the number of vanishing moments is not so high and searching for polynomial dependencies is computationally more demanding. We have identified the following dependencies for the two-fold rotation symmetry:
So, we have two types of the polynomial dependencies, the polynomial dependencies induced by some symmetry, e.g., for bodies with two-fold rotation symmetry only, and the general polynomial dependencies that equals zero for all bodies. The knowledge of the dependencies is important for recognition because dependent invariants only increase the dimensionality but do not contribute to the discrimination power of the system.
6. Numerical Experiments
To demonstrate the performance and numerical properties of the invariants, we present the results of three experiments. The first experiment uses ideal computer-generated bodies (both in surface and volumetric representations) and demonstrates the invariance property and the influence of the sampling. The second experiment works with real 3D objects scanned by a 3D scanner. It demonstrates namely the ability of the invariants to distinguish different objects. The last experiment was performed on objects from the Princeton Shape Benchmark dataset. Its main mission is to illustrate that is really important to use non-vanishing invariants.
The values of the moments decrease rapidly as their order increases if they are not normalized. To keep them in a reasonable interval, we apply so-called magnitude normalization with respect to the order
6.1. Artificial Bodies
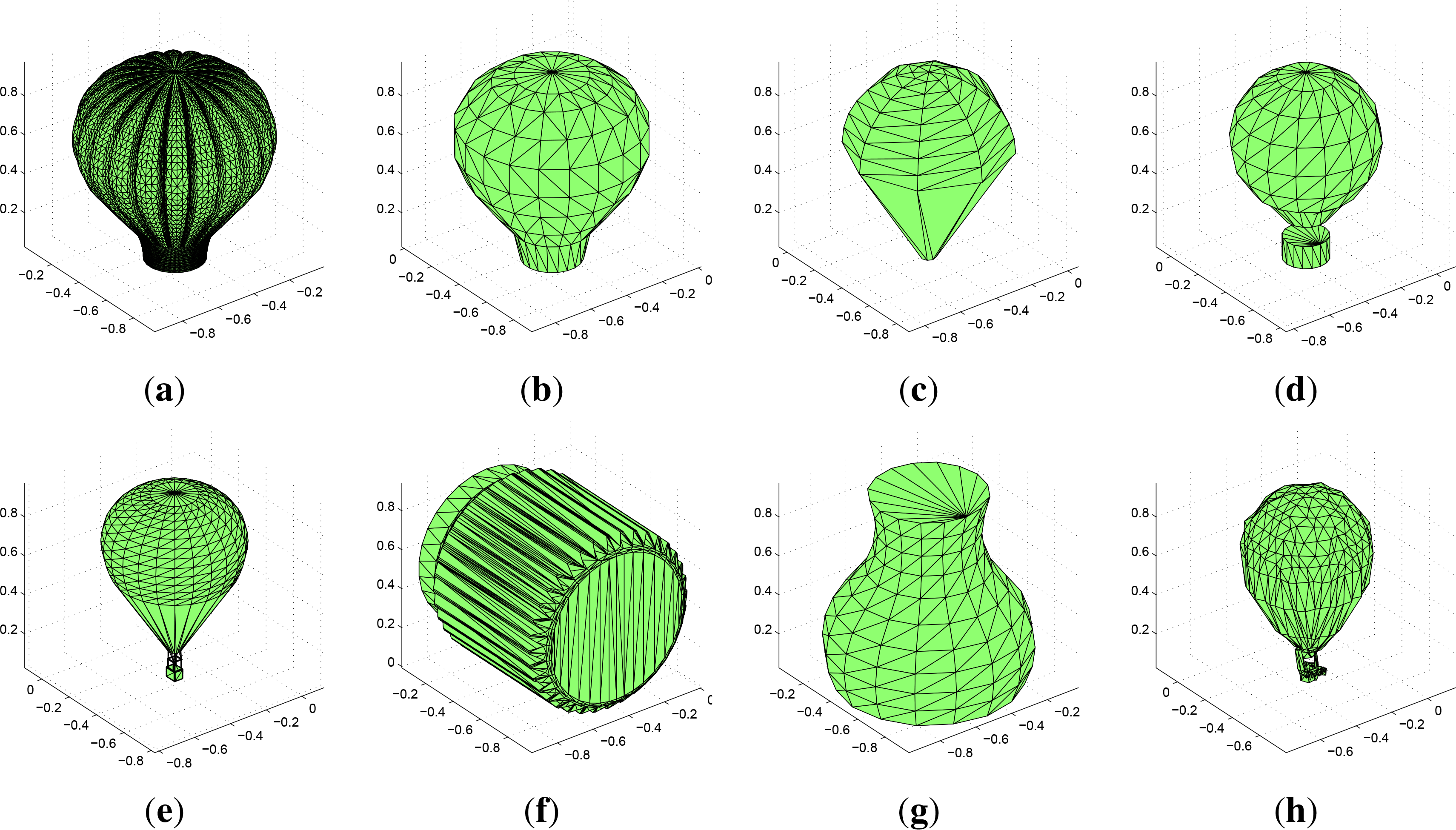
In this experiment, we used artificial objects of various kind and degree of symmetry. The object in Figure 3a is asymmetric and that in Figure 3b has the reflection symmetry only. The rectangular pyramid on Figure 3c has the symmetry group C2v, the pyramid and the prism in Figure 3d,e have 3-fold rotation symmetry. Unlike the regular tetrahedron, only one side of the triangular pyramid is regular triangle, the other three are isosceles triangles. We also used the bodies with the symmetry group Oh: cube and octahedron (Figure 1k,l) and the bodies with circular symmetry (Figure 2i,j,k). The circular symmetry was in the discrete space approximated by a 1000-fold rotation symmetry. We used 28 invariants Φ1–Φ17, Φ19–Φ23 and Φ32–Φ37 derived in the previous section in this experiment. These invariants are irreducible, i.e., there is neither linear nor product dependency among them. The bodies are defined by their triangulated surfaces. We used formulas from [23] to compute the volume moments of them.
For each object we generated 1000 random rotations and translations, then we calculated the values of the 28 irreducible invariants for each object and each rotation. The mean values of the invariants are in Table 5.
The only source of errors is numerical inaccuracy of the computer arithmetic (except the cone, the cylinder and the sphere, they were approximated by a high but finite number of triangles), therefore we can consider the values in Table 5 to be precise. We can see they correspond to the theoretical assumptions. The invariants Φ4–Φ13 and Φ32 of the cylinder, the cube and the octahedron are really zero, precisely as predicted by the theory. The values one of Φ1 and Φ14 of the sphere are not accidental; the invariants were normalized so the values of of the sphere would be 1, see Equation (32).
The maximum standard deviations inside one class (one body) are in the row “ideal” of Table 6, they illustrate the perfect invariance of the features. The standard deviation is calculated over the rotations, while the maximum is calculated over the invariants. The slightly bigger standard deviations 4 × 10−5 in the case of Oh are caused by the normalization to the degree, see Equation (33), without normalization the value is 2 × 10−14.
Then we repeated this experiment with the same bodies in volumetric representation, which is less accurate. Each body at each attitude was converted into the volumetric form in the cube 100 × 100 × 100 voxels, which is relatively coarse resolution allowing to study the impact of discretization. The moments were computed from the characteristic function that equals one in voxels inside the bodies and zero outside. The examples of the sampled data are in Figure 4, the standard deviations caused by the sampling are in the row “samp.” of Table 6.
6.2. Archeological Findings
This experiment is an example of behavior of the invariants on real objects. We chose five real objects—archeological findings from ancient Greece, as an example. The objects were scanned by a laser rangefinder from several sides and the measurements were combined together to obtain a 3D binary image of the object (see Figure 5). Since the rangefinder cannot penetrate inside the objects, the vases are considered full and closed on the top. As a result of the acquisition, we obtain a triangulated surface of the object. In this experiment we worked solely with binary shapes and ignored color and texture, they are shown for illustration only. We used 37 invariants Φ1–Φ37 in this experiment.
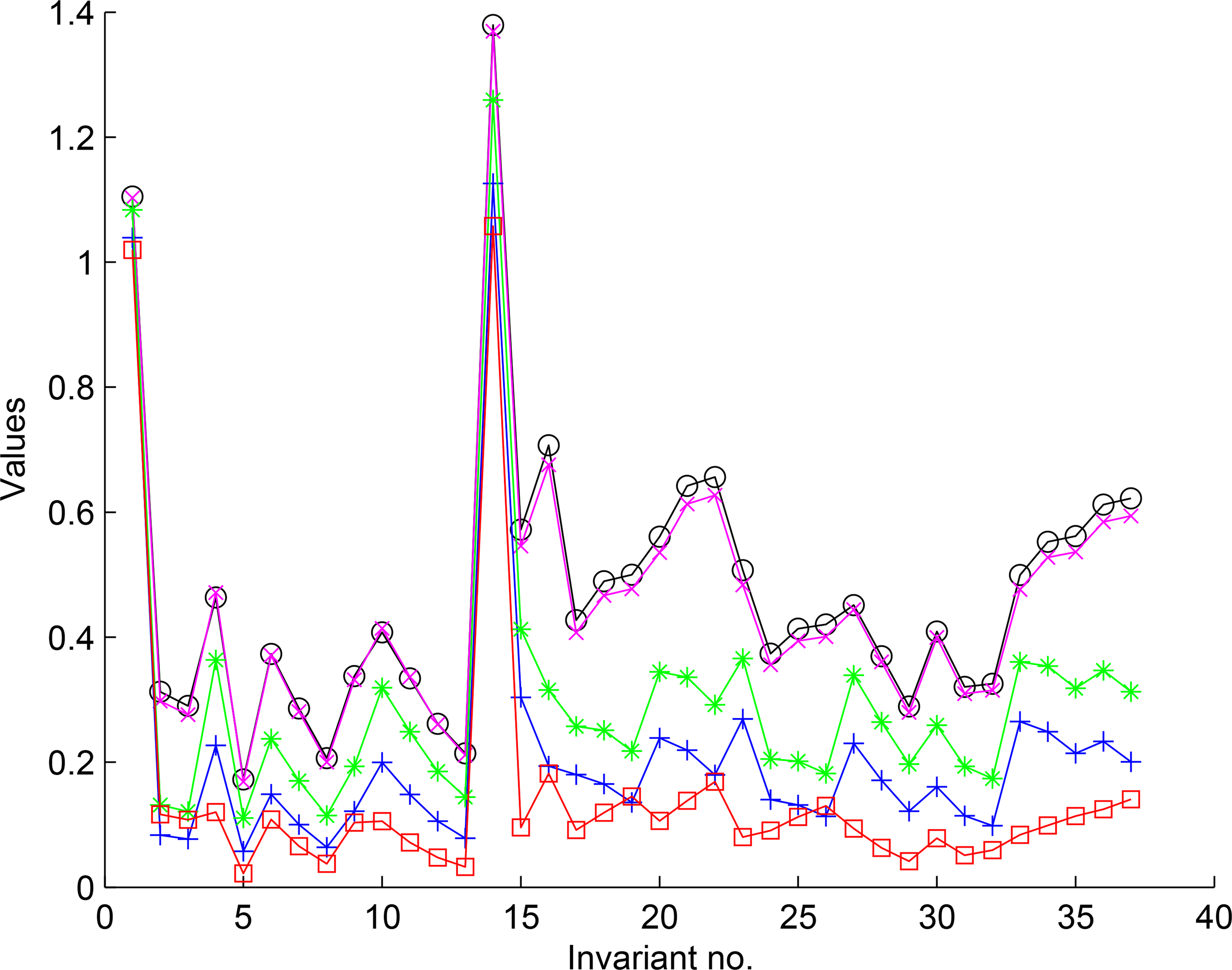
The absolute values of the invariants up to the 4th order of the objects can be seen in Figure 6. The objects in Figure 5a,b are two scans of the same vase which was rotated between the scannings. Their feature values differ from each other only slightly. Theoretically they should be the same but the scanner produces some errors. The objects in Figure 5c,d are two different objects of the same kind. We can see the differences between them are bigger than those between Figure 5a,b. The object in Figure 5e differs by a handle, but it still similar. The feature values are further more different. The graphs demonstrate not only the rotation invariance of the features but also their ability to distinguish similar but different objects. The objects in Figure 5a–d have approximate circular symmetry C∞v and the object in Figure 5e has reflection symmetry C1v.
An interesting question is what are the actual values of those invariants which should theoretically vanish due to the object symmetries. The invariants which should be zero due to the circular symmetry are in Table 7. We can see that the values of the objects Figure 5a–d are really very small, nevertheless it is true for Figure 5e, too. This is because the violation of the circular symmetry by the handle is small.
The values of the invariants zeroed by the two-fold rotation symmetry are in Table 8. This experiment shows that also in the case of real objects, where the symmetry is not exact due to measurement errors and object imperfection, the features which should theoretically vanish actually get very low values close to zero, providing no discrimination power. So, one has to analyze the object symmetry and discard the vanishing invariants from the feature vector. For instance, if we need to recognize the cube and the octahedron, the only non-zero invariants are Φ1, Φ14, Φ15 and Φ23. While Φ1, Φ14 and Φ15 have similar values for both the cube and the octahedron (see Table 5), only Φ23 is sufficiently discriminative, therefore the feature set should definitely include Φ23 in this case.
6.3. Princeton Shape Benchmark
In this experiment we demonstrate that the invariants which are for the given objects zero or close to zero are useless for object recognition. We used the objects from the Princeton Shape Benchmark (PSB) [24]. This dataset contains 1815 3D objects which are labeled from zero to 1814. Each object is represented by its triangulated surface.
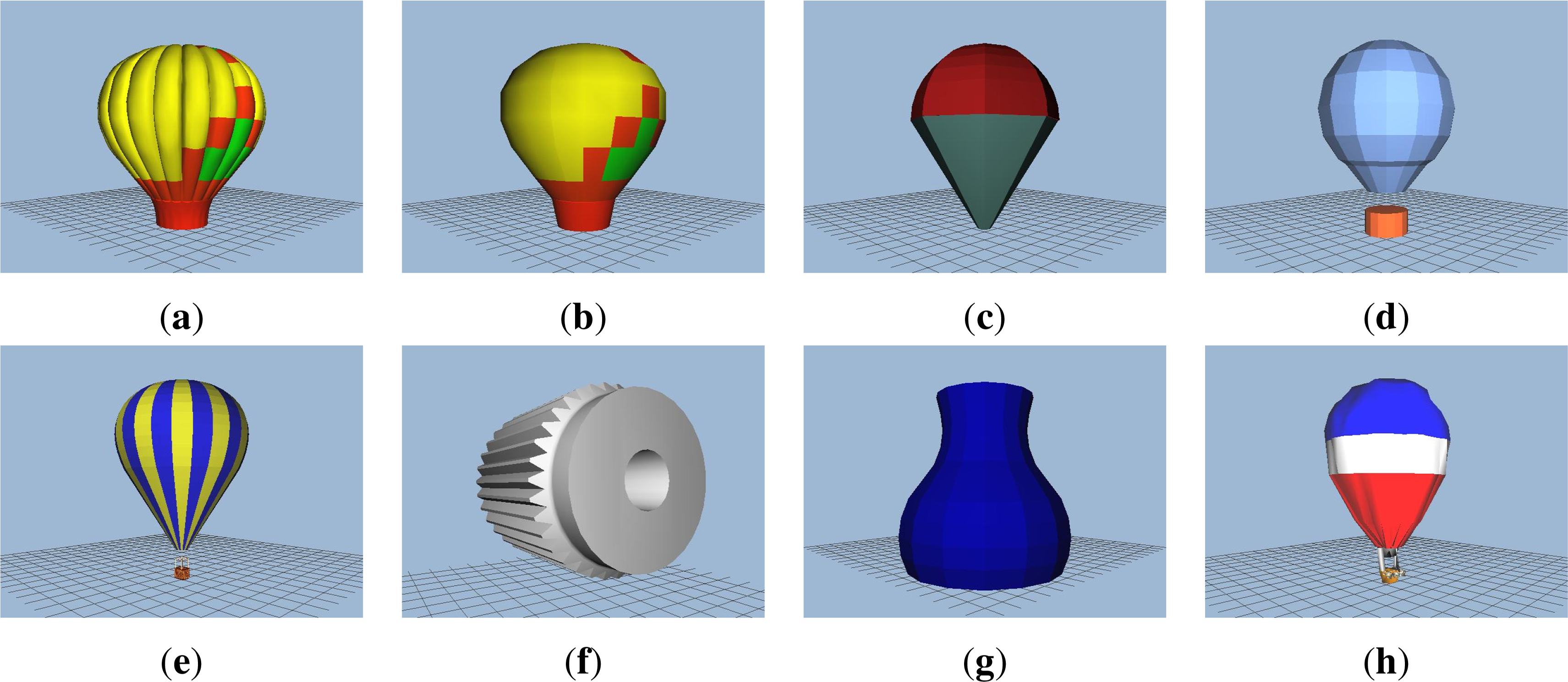
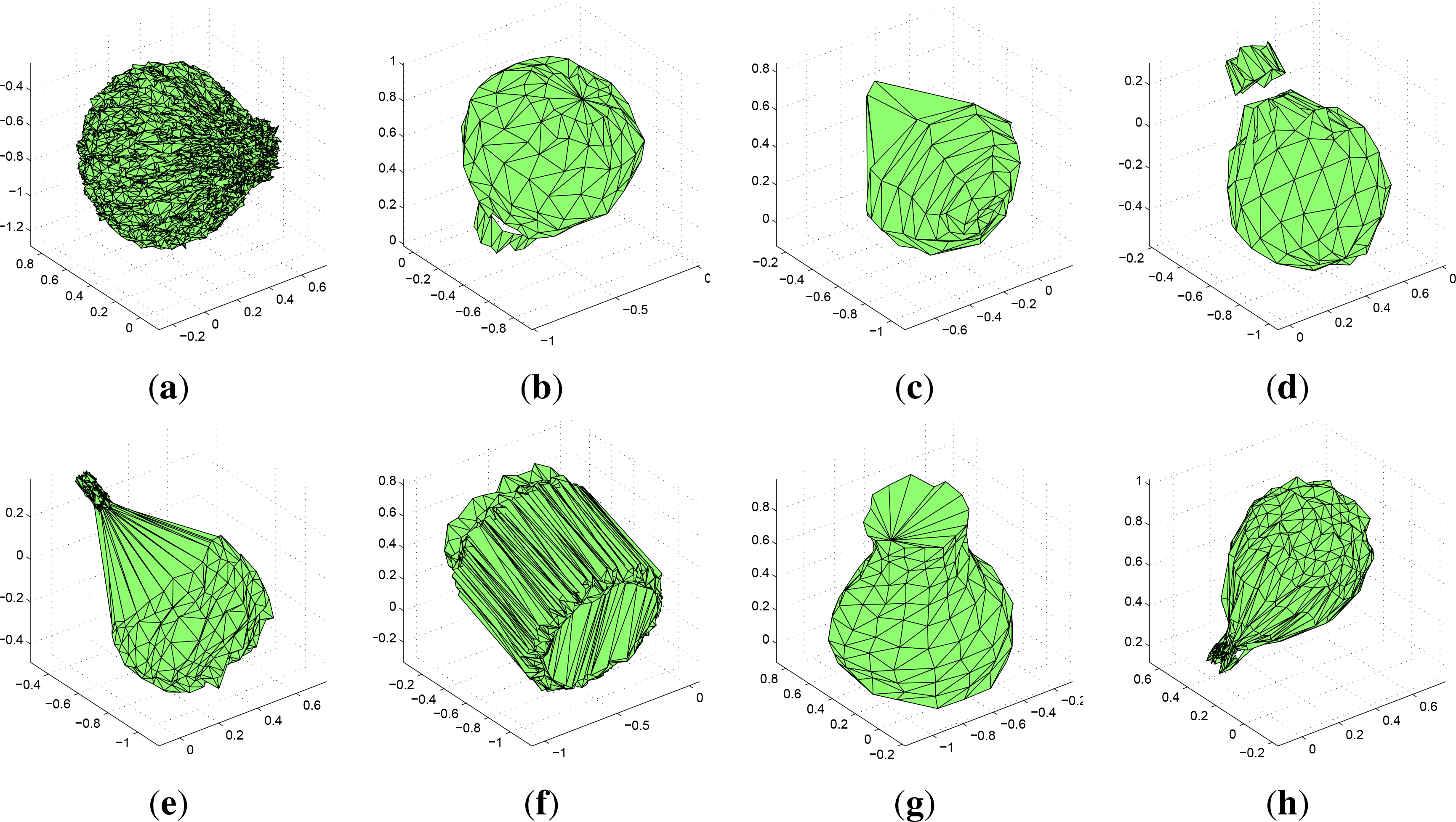
We intentionally chose eight objects that have a high degree of symmetry, see Figure 7. In the PSB, they are labeled as 1338, 1337, 760, 1343, 1344, 741, 527, and 1342, respectively. In a continuous representation they should have the C∞v symmetry. This is however not exactly true in the actual triangular representation. The symmetry group of the gear No. 741 is C36v, that of the hot air balloons No. 1338 and 1337 are C20v, the balloon No. 1343 and the vase No. 527 have C16v, and the ice cream No. 760 has only C8v. The symmetry group of the hot air balloon No. 1344 is C24v, but its gondola has only C4v. The balloon No. 1342 is not fully inflated, so it is not symmetric at all.
In our experiment we did not use the texture and worked with the shape only, hence our templates (class representatives) looked as depicted in Figure 8. To generate test objects, we added a noise to the coordinates of each vertex of the templates. The amount of the noise measured in terms of signal-to-noise ratio (SNR) was 25 dB, where SNR is here defined as
The test objects were classified by invariants using minimum-distance rule and majority vote: the minimum distance was found for each individual invariant and the final class assignment was made by majority vote.
First, we used the five invariants that are identically zero in the case of circular symmetry: , , , , and . Since the objects do not have exact circular symmetry, these invariants are able to recognize some test objects. The result was 12 errors out of 72 trials, i.e., the success rate 83%. When we added Φ14, which is non-zero, to the invariant vector, the number of errors decreased to six, i.e., the success rate increased to 92%. Now we removed all “zero” invariants and recognized solely by Φ14. The result was the same as before: six misclassifications but the algorithm run much faster. On the other hand, when we use the vector of “non-zero” invariants (Φ14, Φ10, Φ6) or (Φ14, Φ10, Φ4) we end up with three misclassifications only. This clearly illustrates that the “zero” invariants are useless even if they are not exactly zero and should not be included into the feature vector.
7. Conclusions
In this paper we proposed a general scheme for constructing 3D features, that are invariant to object rotation and translation. We presented 37 invariants in explicit form along with a general algorithm, how to construct invariants of arbitrary order. We paid particular attention to the influence of object symmetry on the feature values and showed how to design features if some of the objects in the dataset are symmetric. This issue has not been systematically studied in 3D so far, although most objects we meet in practical applications (man-made objects and natural shapes) exhibit certain symmetry.
The presented features are based on complex moments and spherical harmonics. Comparing to other approaches, moments allow to study the impact of symmetry in a transparent way and easier than the other features. At the same time, they are also computationally efficient because there exist fast algorithms for moment calculation both in 2D [25] and 3D [23]. We showed that object symmetry of various kind either makes certain invariants identically zero or introduces dependencies among the invariants. This must be taken into account when designing a 3D object recognition system. The constrained and zero invariants should not be included because they decrease the performance of the system.
It should be noted that this technique is not intended to be used as a detector of symmetry, even if it might provide a good estimate in some cases. The implication does not hold the other way around. Zero value of certain moments does not necessarily mean that the object is symmetric.
Acknowledgments
Thanks to the Grant No. P103/11/1552 of the Czech Science Foundation for financial support. Thanks to Clepsydra (KΛEΨYΔPA), The Digitization Center of Cultural Heritage in Xanthi, Greece ( http://clepsydra.ipet.gr) and especially to Christodoulos Chamzas for the models of the amphoras.
Author Contributions
Tomáš Suk generalized the idea about influence of symmetry on the object recognition to 3D, carried out the experiments and prepared first version of the text. Jan Flusser came with the original idea about influence of symmetry on the object recognition in 2D, proposed the experiments and performed final edit of the text.
Appendix A. Rotation Invariance
Theorem A.1 (1) The complex moment; (2) The composite complex moment form; (3) The tensor product of a composite complex moment form and a complex moment cs(ℓ, ℓ′)jcs′ ; and (4) The tensor product of two composite complex moment forms cs(ℓ, ℓ′)jcs′( ℓ″, ℓ′″)j are 3D rotation invariants.
Proof: The behavior of the complex moments in the rotation is given by
- (1)
If we take , it becomes . for all rotations R, therefore is rotation invariant.
- (2)
For briefness, the symbol (R) is omitted in , the Wigner D-function deals with the same rotation in this proof. The composite complex moment form after rotation is
The tensor product of two Wigner D-functions isIf we substitute it into Equation (A.2), we obtainThere are two relations of orthogonality of the Clebsch-Gordan coefficients. One of them can be writtenIf we substitute it into Equation (A.4), we obtainNow we introduce new index k′= m′+ m″, i.e., m″= k′ − m′ and obtainThe Wigner D-function is zero for k′< −j and k′>j, therefore we can shorten the sum and summarizeIt means the composite complex moment form behaves in rotation similarly as the moment itself. If j = k = 0, then again and is rotation invariant.- (3)
If we have a product of a form and a complex moment after rotation
Substitute the tensor product of the Wigner D-functions (Equation (A.3))The second relation of orthogonality of the Clebsch-Gordan coefficientsimplies the only relevant terms in the sum are that for k′ = k and m′ = −k and after substitution of the relation we obtainIt means cs(ℓ, ℓ′)jcs′ is rotation invariant.- (4)
Now we take two forms after the rotation
Substituting Equation (A.3) we obtainWe now substitute Equation (A.11) again with k′= k and k″= −kso cs(ℓ, ℓ′)jcs′ (ℓ″, ℓ′″)j is also rotation invariant.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Flusser, J.; Suk, T. Rotation Moment Invariants for Recognition of Symmetric Objects. IEEE Trans. Image Process 2006, 15, 3784–3790. [Google Scholar]
- Sadjadi, F.A.; Hall, E.L. Three dimensional moment invariants. IEEE Trans. Pattern Anal. Mach. Intell 1980, 2, 127–136. [Google Scholar]
- Guo, X. Three-Dimensional Moment Invariants under Rigid Transformation. In Proceedings of the Fifth International Conference on Computer Analysis of Images and Patterns CAIP’93; Chetverikov, D., Kropatsch, W., Eds.; Springer: Berlin/Heidelberg, Germany, 1993; Volume LNCS 719, pp. 518–522. [Google Scholar]
- Galvez, J.M.; Canton, M. Normalization and Shape Recognition of Three-dimensional objects by 3D Moments. Pattern Recognit 1993, 26, 667–681. [Google Scholar]
- Cyganski, D.; Orr, J.A. Object Recognition and Orientation Determination by Tensor Methods. In Advances in Computer Vision and Image Processing; Huang, T.S., Ed.; JAI Press: Greenwich, CT, USA, 1988; pp. 101–144. [Google Scholar]
- Xu, D.; Li, H. 3-D Affine Moment Invariants Generated by Geometric Primitives. In Proceedings of the 18th International Conference on Pattern Recognition ICPR’06, Hong Kong, China; 2006; pp. 544–547. [Google Scholar]
- Xu, D.; Li, H. Geometric Moment Invariants. Pattern Recognit 2008, 41, 240–249. [Google Scholar]
- Kazhdan, M. An Approximate and Efficient Method for Optimal Rotation Alignment of 3D Models. IEEE Trans. Pattern Anal. Mach. Intell 2007, 29, 1221–1229. [Google Scholar]
- Kakarala, R.; Mao, D. A theory of phase-sensitive rotation invariance with spherical harmonic and moment-based representations. In Proceedings of 2010 IEEE Conference on Computer Vision and Pattern Recognition CVPR’10, San Francisco, CA, USA, 13–18 June 2010; pp. 105–112.
- Lo, C.H.; Don, H.S. 3-D Moment Forms: Their Construction and Application to Object Identification and Positioning. IEEE Trans. Pattern Anal. Mach. Intell 1989, 11, 1053–1064. [Google Scholar]
- Flusser, J.; Boldyš, J.; Zitová, B. Moment Forms Invariant to Rotation and Blur in Arbitrary Number of Dimensions. IEEE Trans. Pattern Anal. Mach. Intell 2003, 25, 234–246. [Google Scholar]
- Suk, T.; Flusser, J. Tensor Method for Constructing 3D Moment Invariants. In Computer Analysis of Images and Patterns CAIP’11; Real, P., Diaz-Pernil, D., Molina-Abril, H., Berciano, A., Kropatsch, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume LNCS 6854–6855; pp. 212–219. [Google Scholar]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Slavík, F.; Novák, J.; Kokta, J. Mineralogy, 5th ed; Academia: Praha, Czech Republic, 1974. [Google Scholar]
- Urch, D.S. Orbitals and Symmetry; Penguin Books: Ringwood, Victoria, Australia, 1970. [Google Scholar]
- Schmidt, B.; Žďánská, P. Solution of the Time-dependent Schrödinger Equation for Highly Symmetric Potentials. Comput. Phys. Commun 2000, 127, 290–308. [Google Scholar]
- Samoson, A.; Sun, B.Q.; Pines, A. New angles in motional averaging. In Pulsed Magnetic Resonance: NMR, ESR, and Optics, A recognition of E. L. Hahn; Bagguley, D.M.S., Ed.; Oxford University Press: New York, NY, USA, 1992; pp. 80–94. [Google Scholar]
- Mamone, S.; Pileio, G.; Levitt, M.H. Orientational Sampling Schemes Based on Four Dimensional Polytopes. Symmetry 2010, 2, 1423–1449. [Google Scholar]
- Shen, D.; Ip, H.H.S.; Teoh, E.K. A Novel Theorem on Symmetries of 2D Images. Proceedings of the 15th International Conference on Pattern Recognition, Barcelona, Spain, 3–7 September 2000; 3, pp. 1014–1017.
- Flusser, J.; Suk, T.; Zitová, B. Moments and Moment Invariants in Pattern Recognition; Wiley: Chichester, UK, 2009. [Google Scholar]
- Elliot, J.P.; Dawber, P.G. Symmetry in Physics; MacMillan: London, UK, 1979. [Google Scholar]
- DIP. 3D Rotation Invariants from Complex Moments, 2011. Available online: http://zoi.utia.cas.cz/files/ccmf5irr.pdf (accessed on 27 August 2014).
- Sheynin, S.A.; Tuzikov, A.V. Explicit formulae for polyhedra moments. Pattern Recognit. Lett 2001, 22, 1103–1109. [Google Scholar]
- Shilane, P.; Min, P.; Kazhdan, M.; Funkhouser, T. The Princeton Shape Benchmark. Available online: http://shape.cs.princeton.edu/benchmark/ (accessed on 27 August 2014).
- Suk, T.; Höschl, C., IV; Flusser, J. Decomposition of Binary images—A Survey and Comparison. Pattern Recognit 2012, 45, 4279–4291. [Google Scholar]



| ℓ = p − q | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C5 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | C | 0 | 0 |
| D5 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | R | 0 | 0 |
| D6 | R | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | R |
| D∞ | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ℓ | ||||||||||||||||||||||||||
| 0 | R | R | ||||||||||||||||||||||||
| 1 | R | 0 | 0 | 0 | ||||||||||||||||||||||
| 2 | R | 0 | 0 | 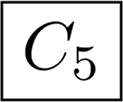 | R | 0 | 0 | 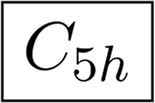 | ||||||||||||||||||
| 3 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 4 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | ||||||||||||||||
| 5 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | 0 | C | ||||||||||||||
| 6 | R | 0 | 0 | 0 | 0 | C | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||
| 7 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | 0 | 0 | 0 | C | 0 | 0 | ||||||||||
| 8 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||
| 9 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | ||||||
| 10 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | C | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | C | ||||
| 11 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 12 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | C | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | C | 0 | 0 |
| 0 | R | R | ||||||||||||||||||||||||
| 1 | R | 0 | 0 | 0 | ||||||||||||||||||||||
| 2 | R | 0 | 0 | 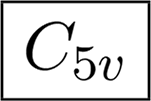 | R | 0 | 0 | 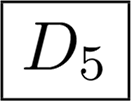 | ||||||||||||||||||
| 3 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 4 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | ||||||||||||||||
| 5 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | R | ||||||||||||||
| 6 | R | 0 | 0 | 0 | 0 | R | 0 | R | 0 | 0 | 0 | 0 | I | 0 | ||||||||||||
| 7 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | ||||||||||
| 8 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | ||||||||
| 9 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | ||||||
| 10 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | R | R | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 | R | ||||
| 11 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | I | 0 | ||
| 12 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | R | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 | R | 0 | 0 |
| 0 | R | R | ||||||||||||||||||||||||
| 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||||||
| 2 | R | 0 | 0 | 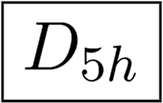 | R | 0 | 0 | 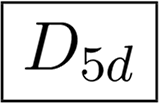 | ||||||||||||||||||
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 4 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | ||||||||||||||||
| 5 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||
| 6 | R | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | I | 0 | ||||||||||||
| 7 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| 8 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | ||||||||
| 9 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
| 10 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | R | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 | R | ||||
| 11 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 12 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | R | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 | R | 0 | 0 |
| m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ℓ | ||||||||||||||||||||||||||
| 0 | R | R | ||||||||||||||||||||||||
| 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||||||
| 2 | R | 0 | 0 | 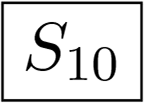 | 0 | 0 | 0 | 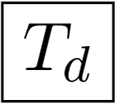 | ||||||||||||||||||
| 3 | 0 | 0 | 0 | 0 | R | 0 | 0 | R | ||||||||||||||||||
| 4 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | R | 0 | ||||||||||||||||
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||
| 6 | R | 0 | 0 | 0 | 0 | C | 0 | R | 0 | 0 | R | 0 | 0 | R | ||||||||||||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | R | 0 | 0 | R | 0 | ||||||||||
| 8 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | R | 0 | 0 | R | 0 | 0 | R | 0 | |||||||||
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | R | 0 | 0 | R | 0 | 0 | R | ||||||
| 10 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | C | R | 0 | 0 | R | 0 | 0 | R | 0 | 0 | R | 0 | ||||
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | R | 0 | 0 | R | 0 | 0 | R | 0 | 0 | ||
| 12 | R | 0 | 0 | 0 | 0 | C | 0 | 0 | 0 | 0 | C | 0 | 0 | R | 0 | 0 | R | 0 | 0 | R | 0 | 0 | R | 0 | 0 | R |
| 0 | R | R | ||||||||||||||||||||||||
| 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||||||
| 2 | 0 | 0 | 0 | 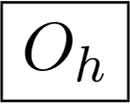 | 0 | 0 | 0 | 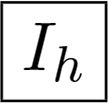 | ||||||||||||||||||
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 4 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||
| 6 | R | 0 | 0 | 0 | R | 0 | 0 | R | 0 | 0 | 0 | 0 | R | 0 | ||||||||||||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| 8 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
| 10 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | R | 0 | 0 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | R | ||||
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 12 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | R | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | R | 0 | 0 |
| 0 | R | R | ||||||||||||||||||||||||
| 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||||||
| 2 | 0 | 0 | 0 | 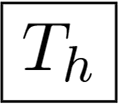 | 0 | 0 | 0 |  | ||||||||||||||||||
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | ||||||||||||||||||
| 4 | R | 0 | 0 | 0 | R | R | 0 | 0 | 0 | R | ||||||||||||||||
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||
| 6 | R | 0 | R | 0 | R | 0 | R | R | 0 | R | 0 | R | 0 | R | ||||||||||||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | I | 0 | ||||||||||
| 8 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | R | R | 0 | 0 | 0 | R | 0 | 0 | 0 | R | ||||||||
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | I | 0 | I | 0 | I | 0 | ||||||
| 10 | R | 0 | R | 0 | R | 0 | R | 0 | R | 0 | R | R | 0 | R | 0 | R | 0 | R | 0 | R | 0 | R | ||||
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | I | 0 | 0 | 0 | I | 0 | ||
| 12 | R | 0 | R | 0 | R | 0 | R | 0 | R | 0 | R | 0 | R | R | 0 | R | 0 | R | 0 | R | 0 | R | 0 | R | 0 | R |
| m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ℓ | ||||||||||||||||||||||||||
| 0 | R | R | ||||||||||||||||||||||||
| 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||||||
| 2 | 0 | 0 | 0 | 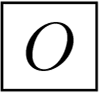 | 0 | 0 | 0 | 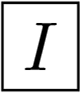 | ||||||||||||||||||
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 4 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||
| 6 | R | 0 | 0 | 0 | R | 0 | 0 | R | 0 | R | 0 | R | 0 | R | ||||||||||||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| 8 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||
| 9 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
| 10 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | R | 0 | 0 | R | 0 | R | 0 | R | 0 | R | 0 | R | 0 | R | ||||
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 12 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | R | 0 | 0 | 0 | R | R | 0 | R | 0 | R | 0 | R | 0 | R | 0 | R | 0 | R |
| 0 | R | R | ||||||||||||||||||||||||
| 1 | R | 0 | 0 | 0 | ||||||||||||||||||||||
| 2 | R | 0 | 0 | 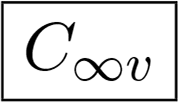 | R | 0 | 0 |  | ||||||||||||||||||
| 3 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 4 | R | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | ||||||||||||||||
| 5 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||
| 6 | R | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||
| 7 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| 8 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||
| 9 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
| 10 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 11 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 12 | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | R | R | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | ||||||||||||||||||||||||
| 2 | 0 | 0 | 0 | 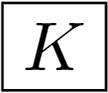 | ||||||||||||||||||||||
| 3 | 0 | 0 | 0 | 0 | ||||||||||||||||||||||
| 4 | 0 | 0 | 0 | 0 | 0 | |||||||||||||||||||||
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||||||
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||||||||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||||||
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||||
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||||
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||
| Inv. | C1 | C1v | C2v | C3v | D3h | Oh(c) | Oh(o) | C∞v | D∞h | K |
|---|---|---|---|---|---|---|---|---|---|---|
| Φ1 | 2.882 | 3.136 | 1.430 | 1.377 | 1.261 | 1.083 | 1.073 | 1.191 | 1.178 | 1.000 |
| Φ2 | 2.164 | 2.500 | 0.707 | 0.294 | 0.471 | 0 | 0 | 0 | 0.503 | 0 |
| Φ3 | −1.865 | −1.593 | 0.534 | −0.273 | −0.438 | 0 | 0 | 0 | 0.467 | 0 |
| Φ4 | −4.351 | −5.041 | −1.252 | −1.381 | −0.479 | 0 | 0 | −0.813 | 0 | 0 |
| Φ5 | −1.240 | −1.312 | −0.069 | −0.159 | 0 | 0 | 0 | 0 | 0 | 0 |
| Φ6 | 2.943 | 3.678 | 0.935 | 0.554 | −0.471 | 0 | 0 | 0.003 | 0 | 0 |
| Φ7 | −1.976 | −2.140 | 0.188 | −0.373 | 0 | 0 | 0 | 0 | 0 | 0 |
| Φ8 | 1.125 | −0.765 | 0.084 | 0.192 | 0 | 0 | 0 | 0 | 0 | 0 |
| Φ9 | −1.956 | 2.014 | 0.851 | −0.447 | 0.445 | 0 | 0 | 0 | 0 | 0 |
| Φ10 | 3.999 | 4.803 | 1.190 | 0.760 | 0.470 | 0 | 0 | 0.715 | 0 | 0 |
| Φ11 | −2.366 | −2.478 | −0.478 | −0.565 | 0 | 0 | 0 | −0.009 | 0 | 0 |
| Φ12 | 1.631 | 1.892 | 0.260 | 0.343 | 0 | 0 | 0 | 0 | 0 | 0 |
| Φ13 | −1.392 | 1.585 | −0.135 | −0.255 | 0 | 0 | 0 | 0 | 0 | 0 |
| Φ14 | 11.006 | 13.214 | 2.556 | 2.454 | 1.804 | 1.247 | 1.227 | 1.627 | 1.470 | 1.000 |
| Φ15 | 6.078 | 8.685 | 0.681 | 1.090 | 0.347 | 0.521 | 0.609 | 0.273 | 0.074 | 0 |
| Φ16 | 8.562 | 10.815 | 1.402 | 0.822 | 0.749 | 0 | 0 | 0.126 | 0.683 | 0 |
| Φ17 | −3.365 | −2.540 | 0.490 | −0.437 | −0.351 | 0 | 0 | −0.001 | 0.128 | 0 |
| Φ19 | −4.606 | −3.849 | 0.923 | −0.542 | −0.596 | 0 | 0 | 0 | 0.572 | 0 |
| Φ20 | −5.276 | −3.871 | 0.581 | −0.616 | −0.410 | 0 | 0 | −0.192 | 0.142 | 0 |
| Φ21 | 6.484 | 8.348 | 0.934 | 0.782 | −0.565 | 0 | 0 | 0.159 | 0.317 | 0 |
| Φ22 | −7.248 | −5.896 | 1.197 | −0.763 | −0.695 | 0 | 0 | −0.117 | 0.634 | 0 |
| Φ23 | −2.635 | 5.327 | 0.601 | −0.934 | −0.308 | −0.489 | 0.572 | 0.242 | 0.066 | 0 |
| Φ32 | −2.718 | 3.504 | 0.277 | −0.337 | 0 | 0 | 0 | 0 | 0 | 0 |
| Φ33 | 5.060 | 5.509 | 0.543 | 0.533 | 0.303 | 0 | 0 | 0.238 | 0.065 | 0 |
| Φ34 | −4.410 | 5.311 | 0.413 | −0.638 | 0.386 | 0 | 0 | −0.206 | 0.118 | 0 |
| Φ35 | 5.211 | 7.290 | −0.539 | 0.626 | 0.450 | 0 | 0 | 0.164 | 0.199 | 0 |
| Φ36 | 6.111 | 8.103 | 0.784 | 0.763 | 0.491 | 0 | 0 | 0.178 | 0.216 | 0 |
| Φ37 | −6.343 | 6.979 | 0.976 | −0.749 | 0.573 | 0 | 0 | −0.141 | 0.363 | 0 |
| Version | C1 | C1v | C2v | C3v | D3h | Oh(c) | Oh(o) | C∞v | D∞h | K |
|---|---|---|---|---|---|---|---|---|---|---|
| ideal | 1 × 10−13 | 2 × 10−13 | 3 × 10−14 | 3 × 10−14 | 2 × 10−8 | 4 × 10−5 | 4 × 10−5 | 2 × 10−10 | 2 × 10−8 | 7 × 10−11 |
| samp. | 0.3 | 0.3 | 0.3 | 0.009 | 0.02 | 0.03 | 0.04 | 0.1 | 0.02 | 0.0003 |
| Inv. | (a) | (b) | (c) | (d) | (e) |
|---|---|---|---|---|---|
| −0.113 | −0.097 | −0.035 | −0.073 | −0.057 | |
| −0.123 | −0.129 | −0.074 | −0.110 | −0.063 | |
| −0.085 | −0.084 | −0.048 | −0.073 | −0.039 | |
| −0.103 | −0.088 | −0.034 | −0.092 | 0.054 | |
| −0.101 | −0.085 | −0.030 | −0.073 | −0.044 |
| Inv. | (a) | (b) | (c) | (d) | (e) |
|---|---|---|---|---|---|
| −0.114 | −0.146 | −0.053 | −0.125 | −0.046 | |
| 0.056 | 0.074 | −0.038 | −0.069 | −0.016 | |
| −0.058 | 0.090 | −0.044 | 0.078 | −0.024 | |
| 0.080 | −0.116 | 0.059 | −0.069 | −0.031 | |
| −0.054 | −0.102 | −0.053 | −0.080 | −0.030 | |
| −0.063 | −0.063 | 0.040 | 0.064 | −0.035 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Suk, T.; Flusser, J. Recognition of Symmetric 3D Bodies. Symmetry 2014, 6, 722-757. https://doi.org/10.3390/sym6030722
Suk T, Flusser J. Recognition of Symmetric 3D Bodies. Symmetry. 2014; 6(3):722-757. https://doi.org/10.3390/sym6030722
Chicago/Turabian StyleSuk, Tomáš, and Jan Flusser. 2014. "Recognition of Symmetric 3D Bodies" Symmetry 6, no. 3: 722-757. https://doi.org/10.3390/sym6030722
APA StyleSuk, T., & Flusser, J. (2014). Recognition of Symmetric 3D Bodies. Symmetry, 6(3), 722-757. https://doi.org/10.3390/sym6030722