Abstract
Efficient utilization of human resources is an important force for the sustainable development of society and the economy. Against the backdrop of the development of economic globalization, the Chinese Government is presently implementing the strategy of “Strengthening the Nation with Talent” to assist the exploitation and management of human resources. Overseas talents have recently become an important resource. How to scientifically evaluate and classify overseas talents has become an important research topic, and it is necessary to seek a systematic decision aid. This paper introduces a novel methodology to evaluate and classify overseas talents in China under the intuitionistic relations environment. Firstly, we determine the weighted values of decision makers and criteria through defining geometry consistency. Secondly, we construct a non-linear Best-Worst-Method (BWM) model with intuitionistic preference relations. A highlight of this BWM model for intuitionistic relations is taking both positive and negative aspects into consideration, which is different from the original BWM. Finally, the proposed methodology is applied to an illustrative example of overseas talent evaluation, indicating the simultaneous efficiency and practicability of the method.
1. Introduction
International competition is becoming more and more severe, as a result of the development of economic globalization. Human resources have become part of the core of national competitiveness. This paper will focus on the evaluation of overseas talents in the Chinese situation. As the world’s largest developing country, China has unique advantages in attracting overseas talents. First of all, the Chinese culture provides an open and inclusive environment that is suitable for the development of overseas talents. China has always advocated cultural exchange between different nationalities, different countries and different areas. Moreover, China has always had a good tradition of respecting talents, recruiting remarkable people without stereotyping. After the reform and opening-up policy initiated in 1978, China has opened its door to welcome international friends from all over the world. Secondly, the rapid development of the Chinese economy and society has provided a broad space for overseas talents to start businesses. More and more overseas students and immigrants are being drawn to China and are becoming a new force in Chinese social development. Based on data from the Chinese Service Center for Scholarly Exchange, the ratio of overseas students who returned to work has reached 70%–80% percent. Thirdly, the Chinese Government attaches great importance to the role of overseas talents. At present, China is in an economic transition stage, and innovation has become the driving force. Overseas talents’ innovation behavior is an essential influencing factor in the nation’s innovative economic development [1]. Therefore, the Chinese Government strongly supports the introduction of overseas talents and expects them to contribute to technology industries. A series of talent introduction policies have been issued in succession, resulting in step by step improvement. In 2008, the central committee staff office of the Chinese Communist Party implemented a national plan named the Recruitment Program of Global Experts/Thousand-Talent Scheme. Moreover, some detailed plans followed this policy, for instance, the Young Overseas High-level Talents Introduction Plan, starting from 2011, whose purpose is to introduce the outstanding young talents of around 35 years of age; the Foreign High-level Experts Introduction Plan, starting from 2012, whose purpose is to introduce the overseas non-Chinese-origin experts who should work in China for three years continuously and nine months per year at least.
However, the gradual expansion of overseas talents in China creates new requirements for the management of overseas talent. In order to evaluate and classify foreign talents who have come to China, the Chinese government is required to build up a complete, systematic and scientific talents evaluation system. Therefore, this study aims to construct a targeted overseas talent evaluation index system based on the Chinese context and explores a combination of geometry consistency and the non-linear best-worst-method model. Furthermore, the study may enrich talent evaluation theory and provide a reference for overseas talents’ management by the Chinese Government and other developing countries.
According to the theory of talent evaluation, building a reasonable talent evaluation system is the foundation of human resource utilization. Academics have continuously explored human resource management. Lai [2] described the employee selection process as a multi-objective decision making problem. Iwamura and Lin [3] explained that the employee selection process required the accomplishment and aggregation of different factors. Labib, Williams and O’Connor [4] suggested an employee selection process that uses the Analytic Hierarchy Process (AHP) with four stages. As Chou, Sun and Yen [5] said, the pure AHP model for human resource evaluation and management has some shortcomings. On the one hand, the traditional evaluation method, such as the pure AHP method, mainly used explicit information to describe the evaluations. On the other hand, the criteria’s weights, which have great influence on the final results, are mostly obtained by the preference of decision makers [6]. To overcome these drawbacks, some scholars introduced fuzzy theory to the AHP methodology. Golec and Kahya [7] presented a hierarchical structure for selecting and evaluating the right employee based on five-scale measure tables. Zhong [8] analyzed the performance of high-level talents with the fuzzy evaluation method, which described the decisions by numbers from 1–9 and their reciprocals. Zhao et al. [9] studied the creative talents evaluation index system based on the nine-scale AHP method. Chou, Hsu and Yen [10] analyzed a country’s competitiveness in terms of their technological human resources with three kinds of criteria. In the last two years, some Chinese scholars did research on human resource and relevant policies [11,12,13,14,15]. Although these methods have further developed the traditional evaluation methods through the introduction of fuzzy theory, they are still not practical enough to deal with the case in our paper. As our study objective is overseas talents, they can be considered as the alternatives. The relevant government departments can organize some experts who are decision makers to evaluate alternatives using several criteria. That makes this problem turn into a multi-criteria decision making problem, which can be solved by Multi-Criteria Decision Making (MCDM) methods. Many scholars have studied this field [16,17,18,19]. We decided to utilize one kind of MCDM method to discuss the overseas talents’ evaluation and classification issues. Different useful tools have been produced for MCDM problems, such as the TOPSIS method [20], pairwise comparison [21] and elimination and choice translation reality [22]. Among them, pairwise comparison is a more practical tool for solving the overseas talents’ evaluation problem. Lazim and Norsyahida [23] studied pairwise comparison to deal with the MCDM problem. Suppose there is a set with n alternatives. We can compare them pairwise and obtain the following original decision matrix under a certain criterion:
where stands for the comparison result of over . Generally speaking, Decision Makers (DMs) can express their decision results based on Multiplicative Preference Relations (MPRs) [24] and Fuzzy Preference Relations (FPRs) [25]. However, DMs may sometimes not be sure about the intensities of preferences. This means that their results may be fluctuating in a certain range during the decision making process. In 1987, Satty and Vargas introduced Interval-Valued Multiplicative Preference Relations (IVMPRs) [26]. In 2004, Xu introduced Interval-Valued Fuzzy Preference Relations (IVFPRs) [27]. These two extensions allowed DMs to use interval valued numbers [28] to express their comparison results. However, IVFPRs and IVMPRs pay more attention to the preferred degree of alternative over , ignoring the non-preferred degree. In order to cope with this issue, the concept of Intuitionistic Multiplicative Preference Relations (IMPRs) [29] and Intuitionistic Fuzzy Preference Relations (IFPRs) [30] appear as extensions of the traditional multiplicative preference relations. An IMPR is given as , where is an Intuitionistic Multiplicative Number (IMN) given on the scale, where stands for the preferred degree and stands for the non-preferred degree of alternative over , including the hesitation information. An IFPR is given as , where is an interval multiplicative number in which the preferred degree is located. In order to evaluate overseas talents fully, we not only consider the preferred degree of one talent over another, but also discuss the non-preferred degree.
Many scholars have introduced various kinds of preference relations by studying decision matrix X [27,31,32,33,34]. Their applications are about different fields of multi-criteria decision making problems, such as management information systems, forecast theory and economic systems [29,35,36]. In general, we should make times of comparisons to finish the pairwise decision matrix X. Most studies about the original decision matrix have a similar assumption that is . Under this assumption, the number of pairwise comparisons decreased from to . If the number of alternatives is small, the pairwise comparison method is applicable. For example, Celik, Kandakoglu and Deha Er [37] proposed a multi-stage evaluation model under multiple criteria in order to manage the academic personnel selection and development in maritime education and training institutions. However, if the alternatives’ number is large, such as 20 candidates and 190-times of comparison, most published methods are not suitable. We need a method to decrease the comparison times, as well as ensuring reliability. Rezaei [38] proposed a decision making method: the Best-Worst-Method (BWM) Rezaei, Wang and Tavasszy [39] use BWM to propose an integrative approach that includes capabilities and willingness as two dimensions for evaluating and subsequently segmenting suppliers. Rezaei [40] applied a linear BWM to a car choosing problem. Compared to the other MCDM methods, BWM has not been applied and published widely. Rezaei et al. [41] apply the BWM to find the best suppliers from among the qualified suppliers. BWM’s biggest highlight is the pairwise comparison times dropping from to . As BWM noted, it is not hard for people to pick out the best one and the worst one among the alternatives under a certain criterion. Determining how much the best one is superior to the others and how much the others are superior to the worst are the difficult parts. BWM is an effective method to deal with comparison times’ problems. The BWM expressed the comparison results by numbers from and ignored the reciprocals of each pair to avoid the trouble caused by unequal distance between fractional comparisons. Rezaei [38] discussed a practical application of a college students’ cell phone selection problem. The result showed that without considering the reciprocals, the method was credible, as well. However, ignoring the reciprocals is not sufficient for some other situations, especially for the talent assessment problems, in which unequal distance between fractional comparisons does exist. This paper proposes a non-linear BWM model to cope with the overseas talents evaluation problem. As discussed above, this model will be built under the intuitionistic relations environment. This means that compared with the original BWM, decision makers not only assess how much the best one is superior to the others, but also assess how much the others are superior to the worst. So do the others to the worst. Then, constructing the non-linear BWM would simultaneously increase the efficiency and practicability of our method.
Besides, the consistency degree of decision matrix X is a very important property, which also attracts many scholars’ attention. In the process of pairwise comparison, generalized consistency means that if alternative is better than and is better than , then is better than . Furthermore, if the three preferred degrees of over , over and over satisfy the preference relations, then they satisfy consistency. Wang and Chen [42] discussed comparison consistency depending on the incomplete fuzzy linguistic preference relations. Liu et al. [43] introduced a goal programming model to deal with the incomplete interval multiplicative preference relation problems, which was based on the consistency property. Then, we also introduce a weight-determining system, based on geometry consistency defined in this paper. This methodology will help to calculate the weight vector of decision makers and criteria. For evaluating the overseas talent problem, we consider the weighting issues under the intuitionistic preference relations environment, which contains preferred degree and non-preferred degree. Decision makers are weighed according to their geometry consistent degree, the criteria’s weights obtained subsequently. Further, decision makers and criteria can obtain their weights by the consistency degree. We use an example from Jiang et al. [44], in which they focused on calculating the missing elements and did not give enough consideration to the consistency of decision matrices, to demonstrate the validity of our method.
The main contributions of this paper are two-fold. Firstly, we construct an evaluation system and introduce a geometry consistency degree to measure the criteria weights, with its validity demonstrated by a published example. Secondly, we construct a non-linear BWM model for intuitionistic preference relations and show its practicability by solving an overseas talent evaluation and classification problem. Both of the two points contribute to MCDM problems. The rest of the paper is organized as follows. Section 2 introduces definitions about the weight determination. In Section 3, we give the concrete procedures about BWM for intuitionistic relations. In Section 4, we examine a real example, which also belongs to an ongoing project led by the relevant department of Tianjin. The paper concludes in Section 5 with a summary of the advantages and drawbacks of our developments and suggesting some further research for the future.
2. Discussion on Criteria Weight
Saaty and Vargas gave the concept of interval-valued multiplicative relation in 1987, as follows:
Definition 1.
An Interval Valued Multiplicative Relation (IVMR) U on a non-empty finite set is defined as , where is named the interval valued fuzzy number and satisfies , , , and indicates that is between and times as important as [26].
Xia et al. proposed that we can write the interval valued fuzzy number in another way: . This introduced the definition of intuitionistic multiplicative preference relations.
Definition 2.
Let be a non-empty finite set with n elements. Then, the Intuitionistic Multiplicative Preference Relation (IMPR) is defined as , where is named an Intuitionistic Multiplicative Number (IMN) for all ; indicates the intensity to which is preferred to ; indicates the intensity to which is not preferred to ; both should satisfy the following conditions: , , , , [45].
In addition, let , i.e., . Here, represents the hesitation degree to which is preferred to , satisfying .
Obviously, Definition 2 developed the Definition 1 in the aspect of considering the hesitance, making the decision results closer to the practical problems.
Definition 3.
Let be a non-empty finite set with n elements. Its associated multiplicative reciprocal preference relation with and , [46]. The corresponding fuzzy reciprocal preference relation associated with X is given as follows:
where and , .
Depending on Definitions 2 and 3, we give the next definition:
Definition 4.
Let be the IMPR, where . Then, its Corresponding Interval Fuzzy Preference Relation (CIFPR) matrix is , where is given as follows:
where , , .
Definition 5.
Let be the IMPR, where , and its CIFPR be , where . Then, its fuzzy-based geometric index matrix is defined as:
i.e., .
In addition, we define:
where
Deriving from Definition 5, we obtain the following propositions about fuzzy-based geometric index.
- (1)
- .
- (2)
- It is obvious that, ; , if ; , if ; , if ; indicates which kind of preference relation of over is dominant, the preferred degree or the non-preferred degree.
- (3)
- Let and be two IMNs. If and , then .
Definition 6.
A CIFPR with respect to an IMPR is called geometry consistent, if it satisfies the next equation:
i.e.,
where , , are the multiplicative-based geometric indexes.
Definition 7.
For a fuzzy preference relation , where denotes the preference value for alternative over , , [47], its according geometry consistency matrix satisfies:
Jiang et al. [44] proposed the method that decomposed an intuitionistic multiplicative preference number into two matrices: a preferred matrix describing the positive information and a non-preferred matrix describing the negative information given by DM with respect to alternative over [44]. Then, we develop the next definition to calculate the missing elements of an incomplete IMP’s corresponding interval fuzzy preference relation matrix by calculating the missing elements of and , respectively.
Definition 8.
For an incomplete intuitionistic multiplicative preference relations , i.e., some elements are unknown, let be its corresponding fuzzy relation. We separate the matrix P into two parts, denoted by decomposing the matrix. One part is , where , if ; , if ; , if ; the other part is , where , if ; , if ; , if ,
From Equation (7), we rewrite it in the following way:
Based on Equation (9), we introduce the consistency degree of CIFPR :
for expert , , where , and , .
In addition, we can get the weight values for expert with respect to the consistency degree by:
where
Apply Equation (4) to get to calculate the the score value . Then, we can obtain the weight value of criteria :
where .
Example 1.
This example is chosen from Jiang et al. [44], which is calculated by the method proposed by Y. Jiang et al. in detail. In this example, there are five alternatives to choose from and a decision group with three decision makers , , whose weight vector is equal . Decision makers compare each pair of alternatives and give judgments, expressed as the incomplete IMPRs , shown as follows, where the missing elements have been marked differently.
Firstly, calculate the unknown elements of the decision results of the matrices , and . By Definition 4, obtain the corresponding fuzzy matrices. By Definition 8, decomposethe corresponding fuzzy matrices into two parts. By Definition 7, calculate the missing elements of : , , , , ; the missing elements of : , , ; the missing elements of : , , . Secondly, calculate the consistency degree of each DM’s decision matrix by applying Equation (9) and obtaining: , , . By Equation (11), we obtain the weight values for every expert: , , . Finally, apply Equation (12) to the weight vector of the criteria , and then, the ranking result is .
The final results calculated by Jiang et al. [44] is: , , , , , with a ranking . Obviously, there exists a difference about the ranking position about alternatives and , while their final scare values are really close to each other. Y. Jiang et al. focused on calculating missing values and ignored the consistency degree’s influence. Our paper uses a simple way to calculate the unknown elements and takes the decision matrices’ consistency degree into consideration, with simpler calculating processes and a reasonable conclusion.
3. A Non-Linear BWM for an Intuitionistic Relation
In order to cope with the overseas talent evaluating problem, we will introduce intuitionistic preference relations to express decision results. Additionally, a non-linear BWM model is constructed to rank alternatives
3.1. BWM for Intuitionistic Relations
Definition 9.
Let be a non-empty finite set with n alternatives and be a set with m criteria. Determine the best element and the worst element with respect to a certain criterion. Denote the comparison value over by , , in the form of an intuitionistic multiplicative number (IMN), composing a set and elements in it called best-grade comparisons. Denote the comparison value over by , , in the from of an IMN, composing a set , and elements in it are called the worst-grade comparisons. Moreover, the elements of and , , where is the preferred degree that over expressed by one integer between one and nine, and is the non-preferred degree that over , expressed by one number among , satisfying the conditions that, , and , which indicates that the hesitant degree is under consideration.
Definition 10.
For any three comparisons , and of a comparison set S, if it satisfies the following equation [36]:
i.e.,
we consider that the comparison set S based on X is consistent.
In order to discuss the consistence degree of the comparison result of Definition 9, introduce the following definition:
Definition 11.
For a set with n elements, each element has a weight value satisfying and for all i, where stands for the importance degree of in X. If the comparison value expressed by an IMN , satisfies and the non-preferred degree over satisfies , for all , then it means that this comparison is a standard comparison.
For a decision maker, it is easy to determine the best talent or the worst alternative under certain criteria. Additionally, choosing which is the better one between two alternatives is also not difficult. The trouble we usually fall into is the question to which degree one alternative is superior to another. In the next phase, we will study this question with a non-linear BWM model under intuitionistic preference relations. Let and be any two comparable alternatives of set X. First of all, just as the original BWM [38], the DM picks up the best one and the worst one under a criterion. According to Definition 9, the DM gives the preferred degree over expressed by , and the preferred degree over , expressed by . According to Definition 11, the standard condition: , , , . As DMs are all reasonable people, the equation is likely, , i.e., may not always exist. By Definition 10, this condition is also called consistent. Next, we will discuss the worst case about this condition: . By Definition 10, , considering the worst consistency condition exists when , ; then, we get two deviations ξ, η and obtain the following equations. The original equations are:
The equations that have the worst consistency degree are:
Rewrite Equations (20) and (21) in the following way:
where , .
By entering all of the possible values of and , we calculate and summarize in Table 1 and Table 2, where Table 1 is a little different from the one appearing in [38].

Table 1.
The maximum value of ξ about x.

Table 2.
The maximum value of ξ about y.
Here, we denote max ξ by the α consistency index (α-CI) and max η by the β consistency index (β-CI) . In addition, the consistent ratios value are , where the value of CI depends on the value of , and , where the value of CI depends on the value of .
3.2. Model Construction
In this section, we introduce the optimization model of BWM for intuitionistic preference relations. First of all, the decision maker should make sure the criteria set , with respect to an alternative set , which will be identified to give the pairwise comparisons. Additionally, just choose the best element and the worst element . Then, decision makers enter the comparison results about to others and the remaining ones to , satisfying the roles of Definition 9. Following that, comparison sets and are obtained. Since the deviation results derive from two aspects, the preferred degree and the non-preferred degree, we should consider the following problem:
where , , .
We can deal with the problem by solving the next systems:
min ξ s.t.:
where .
min η s.t.:
where . Next, we will give an example to show how this model works.
Example 2.

This a simple example, and we use it to show the above method with numbers. Here are three alternatives and four criteria. The expert compares every alternative under each criterion, depending on Definition 9. The comparison results are shown in Table 3, where , , , , , which are predefined by the special decision makers according to the relative department’s order.

Table 3.
The comparison results of every alternative under each criterion by the expert.
Apply the novel method by utilizing Equations (25) and (26) obtaining Equations (27) and (28):
min ξ, s.t.:
min η, s.t.:
We can calculate the weights of all three alternatives with Equations (27) and (28). In addition, we can get the weights under the other criteria in the same way, and we summarize them in Table 4, where (,,) are the weights of alternatives with the positive aspect and (,,) are the weights of talent with the negative aspect. The calculated weights are not the same as each other; however, the rankings are the same. It is easy to see that and . We can either rank the three alternatives based on the combination of the positive and negative aspect or only consider one aspect. The proposed non-linear model has a close connection with the original BWM, because of Definition 4. Transformation formula Equation (3) can change the number field of BWM into , in the form of a fuzzy number. Equation (3) changes the intuitionistic multiplicative number into an intuitionistic fuzzy number, in the form of . We can choose the average of , so the two models are transformed into the same number field. This transformation formula guarantees that our model will not violate the basic assumptions of the BWM.

Table 4.
The calculated comparison results of every alternative under each criterion by the expert.
3.3. Some Properties about the Non-Linear BWM for Intuitionistic Relations
1. Violation Degree (VD):
where and m is the number of all criteria.
describes the degree of some unreasonable conditions defined in the following:
In Example 2, for all cases , it shows that the calculated weights are good enough under this standard.
2. Deviation degree (DD):
We also calculate the total value of Euclidean distance between and , by where:
and m is the number of criteria.
The value of DD of Example 2 is .
During the group decision making process, we can obtain the violation degree and deviation degree of each decision maker. The higher the values of and , the better the decision results from the decision maker. Depending on the values, we may consider the decision maker weights further or omit some decision makers’ comparisons for their highest values of and .
4. The Illustrative Study
Tianjin, an economic center in the northern part of China, has constantly focused on the introduction of overseas talents. The relevant government agencies of the city have implemented some policies with regard to problems with respect to the introduction of overseas talents, such as how to evaluate and classify them based on the assessments and how to fairly offer them equitable treatment, which has become the main bottle neck. One important problem is improving assessment systems, including evaluation and classification. Here, we mainly discuss the evaluation part. Test samples are drawn out from the overseas talents who participated in the selection of the Tian Jin Haihe Friendship Award in 2015. To ensure the objectivity of the evaluation process, we omit specific information, such as the names of decision makers and overseas talents. We chose 20 overseas talents who came to the city for working or cooperating via the introduction by the government. With the purpose of making general statements for the 20 overseas talents, we list five criteria to evaluate them. The government assigned a group of three experts to evaluate the alternatives with each criterion.
We evaluated candidates from different aspects, considering some necessary qualities. In the early days, Harvard professor McClelland [48] proposed the concept of competency. He expounded on the relationship between individual and position from the quality and ability aspects. Spreitzer et al. [49] developed the prospector as an evaluation tool, which evaluated the managers’ potential to lead national and international enterprises. He researched managers from 21 countries and belonging to six major industries, who came to work in the United States, as multinational professional managers. The results of this research demonstrated the effectiveness of the prospector. Subsequently, more systematic talent evaluation problems were considered by researchers, including some Chinese scholars who did research mostly in the Chinese situation. Luo [50] considered that good internal ability and continuous creative ability were key points for the definition of talent. In addition, the creative achievements obtained by the talents should have a positive impact on the progress of society. Yan and Chen [51] conducted research based on case analysis and came to the conclusion that the marketer’s assessment was largely from three aspects, consisting of personality, knowledge and ability. Recently, Xu et al. [52] studied the talent evaluation index in regards to the high-level talents’ introduction in DongHu High-tech Zone. They constructed a high-level personnel evaluation index system containing four indexes, consisting of performance, ability, contribution and potential.
In this study, the criteria are sourced from Xu’s evaluation system [52], which was used to evaluate high-level talents in China. In addition, we collect advice from a sample of 15 experts, who are good at talent evaluation, in order to extract factors of overseas talents’ assessment. This group includes university professors, headhunting company managers, company executives and government review experts. We first explained the problem to these experts, and then, they were given some documents describing the criteria for evaluating overseas talents and a comprehensive list of the characteristics of overseas talents. Finally, after the interviews, we analyzed the information and created the index system of overseas talents’ evaluation, which contains basic quality, capacity, contribution, development potential and internationalization, as shown in Table 5.

Table 5.
Criteria to evaluate overseas talents and their descriptions.
It is important to notice that internationalization is a key-influencing factor for overseas talents [53]. On the one hand, global perspective refers to international experience and cognition of the world technology market [54]. Someone who has a global perspective may gain an insight into development opportunities, which may come from the differences between countries, such as the business opportunities that come from the technology and application differences between different countries, as well as differences in market demand and supply. On the other hand, overseas talents need to have good cross-cultural adaptability, which can help them to easily tackle the obstacles of cultural differences. Cross-cultural adaptability is a capability that appropriately deals with interactions among people from different countries and cultures [55]. Specifically, overseas talents with good cultural adaptability can identify similarities and differences between the new culture and their own culture and can actively coordinate the cultural conflicts, so that they can integrate into the new culture.
After constructing the criteria system, in order to evaluate and classify the chosen 20 overseas talents, we follow the subsequent decision making procedures, depending on the definitions and models from Section 2 and Section 3.
Step 1: From Definition 2, decision maker , , gives his/her decision matrix about criteria , (standing for basic quality, capacity, contribution, development potential and internationalization, respectively).
Calculate the consistency degree of each expert’s decision matrix, and then, by Equation (11), we obtain the weight values for every expert: , , ; by Equation (12) to the weight vector of the criteria .
Step 2: After the decision group enters data into the decision matrices, applying the same method with Example 2, we obtain the weighted ranking results, shown in Figure 1 and Figure 2.
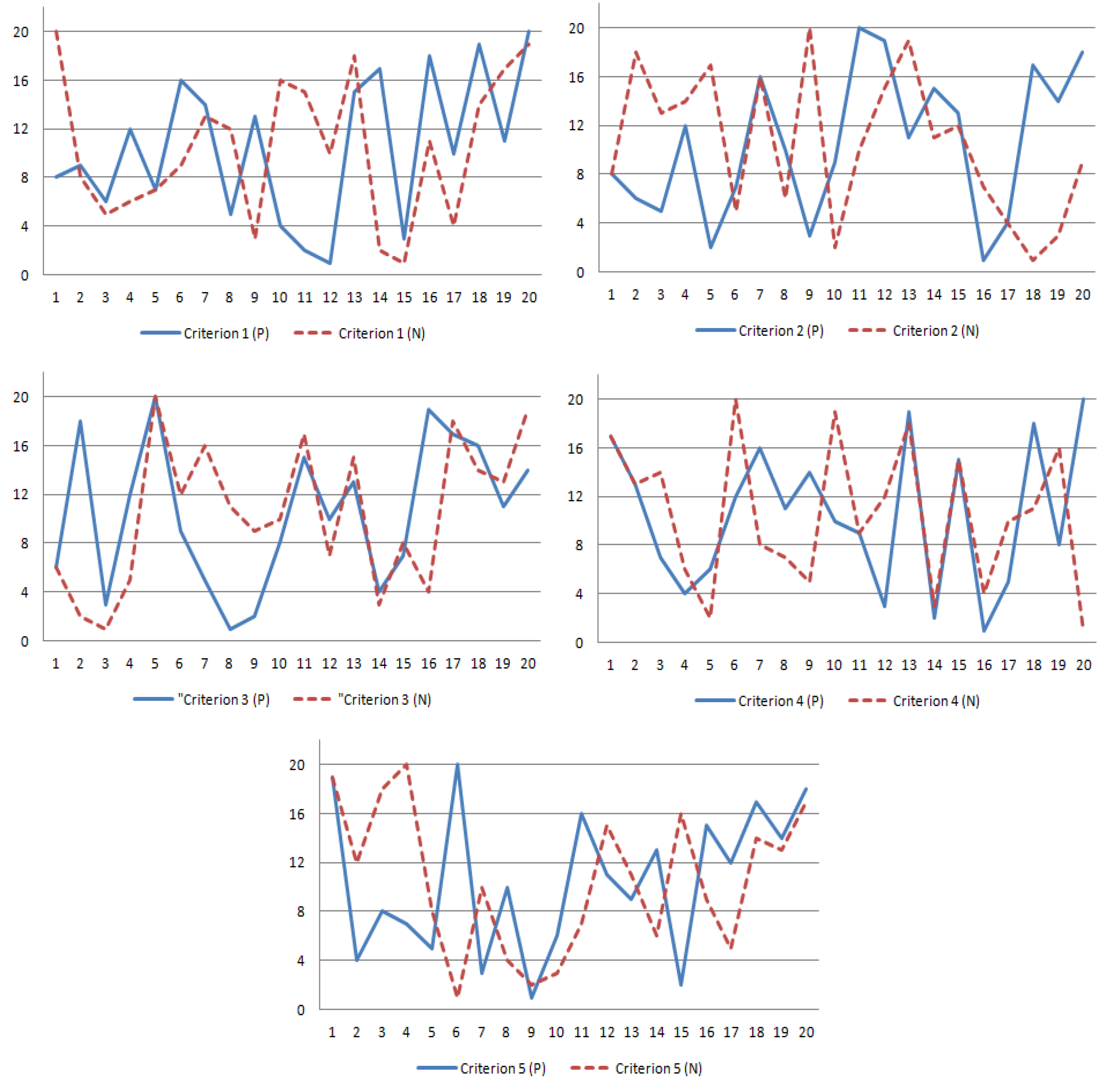
Figure 1.
Ranking results of all alternatives by the experts under each criterion.
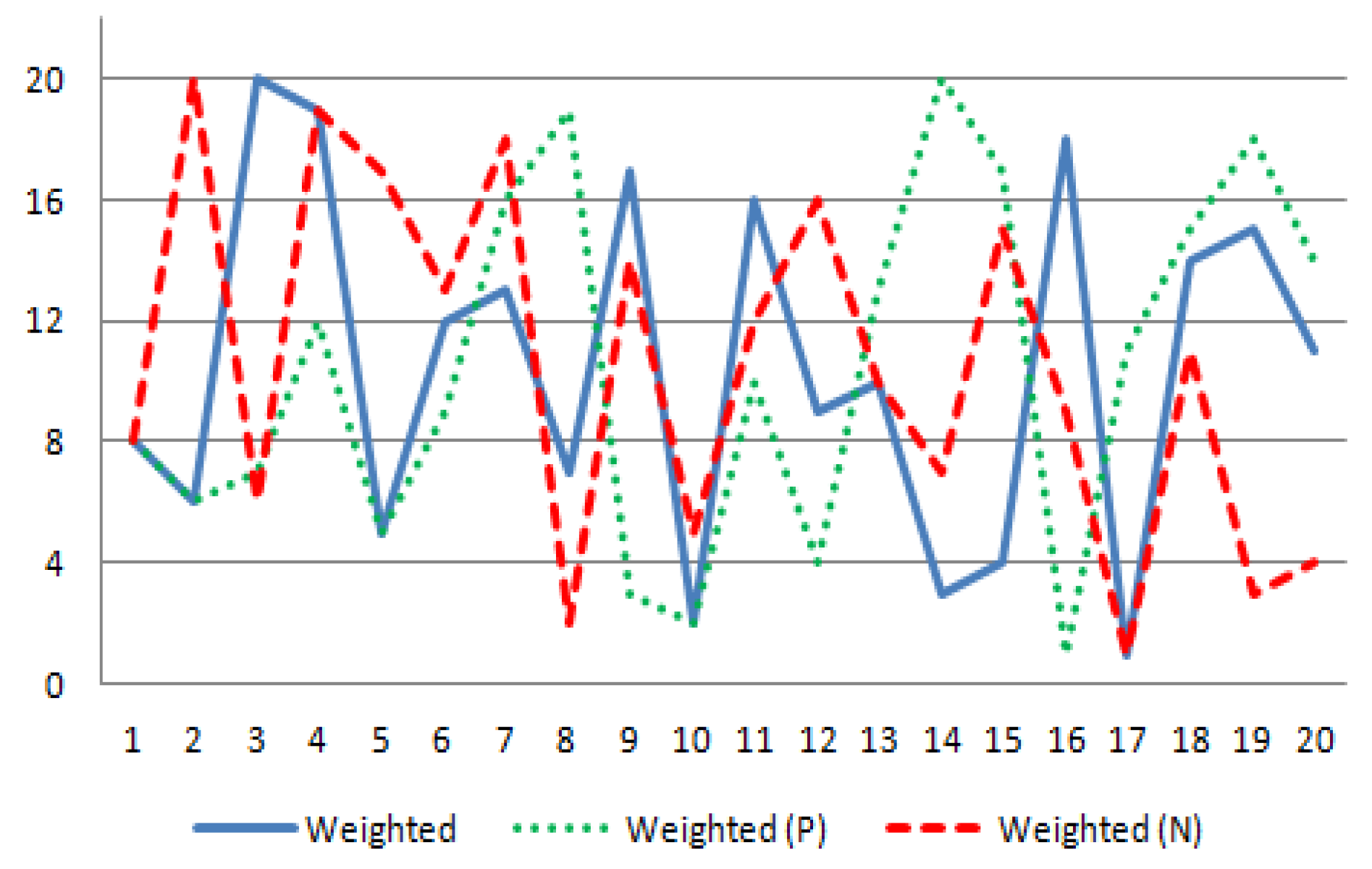
Figure 2.
Comparison results of the weighted result by the experts.
Figure 1 shows the rankings of all of the alternatives given by DMs in two aspects: the positive one (indicated by a blue solid line) and the negative one (shown by a red dashed line). The weighted results calculated by the experts are summarized in Figure 2, where the abscissa stands for the ranking number of its alternative located on the ordinate. Each alternative’s ranking number can be read from the figures. Overall, ranking results are different between the positive and negative aspects from all of the figures. This intuitive conclusion indicates that it is meaningful to introduce the intuitionistic preference relations. Figure 1 tells us that the best and worst alternatives with different criteria are different, illustrating that the criteria are recognizable for comparing the alternatives. This is useful for evaluating overseas talents from different aspects. More specifically, under Criterion 1 (basic quality), Alternative 8 is the best one in the positive aspect, and Alternative 20 is the worst one; Alternative 20 is the best one in the negative aspect, and Alternative 19 is the worst one. Taking the weights of the criteria and decision maker into consideration, we get the weights for all alternatives in the positive aspect, shown in the Figure 2 with a green dotted line; the weights for all alternatives in the negative aspect, shown in Figure 2 with a read dashed line; the 20 alternatives can be partitioned into three classes with respect to the average weight, shown in Figure 2 with a blue solid line: the first class contains alternatives ,,,,,; the second class contains alternative ,,,,,,; the third class contains alternative ,,,,,,. For each class, the government would offer them different treatments. As a key management method, the category divides objects into several categories or various types, in order to achieve the target of more intensive and more efficient management. Therefore, based on the category results, the relevant department can distinguish between different levels of foreign talents and offer various management and services in terms of green card applications, entry and exit control, child education, personal income tax relief, and so on.
Table 6 shows us the consistency degree of each criterion by every DM, such as element (0.4121,0.0409) from Table 6 that stands for positive consistency, which is 0.4121, and the negative one is 0.0409, with respect to decision maker , who has the smallest consistency value in two angles with criterion . The consistency degree is a very important reference standard, for low consistency may bring about the wrong decisions. Besides, the violation degree and deviation degree are also considerable. From Equation (29) and Equation (30), for each expert , , their violation degrees and deviation degrees can also be obtained as follows: , , ; , , . As reference standards, these calculations present the different deviations from different decision makers, which are convenient for analyzing the decision result more comprehensively.

Table 6.
The consistency degree of each criterion by the expert.
5. Conclusions and Further Research
This article studies the evaluation and classification of overseas talents in a Chinese context. We construct an evaluation-criteria system and propose a novel decision making methodology to rank the alternatives. These developments contribute to overseas talent management in China. Moreover, they provide valuable references for overseas talent management by the Chinese Government and in other developing countries. The advantages and limitations of the case discussed in this paper are now analyzed, in regard to the proposed methodology, human resources practices system and overseas talents’ evaluating method’s effectiveness, compared to the other methods for multi-criteria group decision making problems.
Advantages:
- (a)
- The proposed method contains two parts: one is about calculating the weights of criteria and decision makers; the other one is about ranking the alternatives based on the obtained weights. We introduce the fuzz-based geometric index matrix to calculate the consistency degree of decision makers, whose weights can be obtained. Additionally, the criteria’s weights are given subsequently. The importance of decision makers’ weights is obvious, which can also be shown in Example 1. Based on the original BWM, we develop it into the intuitionistic preference relation’s environment and construct a non-linear BWM. Then, the decision process can be more effective than the other pairwise-based decision making method.
- (b)
- This paper studies the overseas talents’ evaluation and classification problem of China. After summarizing the published related references and analyzing the Chinese context, we construct a criteria table for evaluation. Then, we apply the proposed method to rank 20 overseas talents and classify them. According to the specificity of human resource evaluation, we add the comparison of non-preferred degree by introducing the intuitionistic preference relation. This extension is more suitable for human’s decision making psychology, leading to the decision making process being closer to reality. Additionally, it also can decrease the subjective influence on the decision results. Research studies on the overseas talents of China are rare, and the published papers do not consider the situation as extensively as this paper dose. Therefore, this paper is meaningful for the human resources practices system.
- (c)
- We transform the talents evaluation problem into a Multi-Criteria Group Decision Making (MCGDM) problem, and solve it through a combination MCGDM methodology. For this proposed methodology, we develop the related methods to make them more effective. Example 1 can show the importance of considering geometry consistency degree, rather than paying more attention to calculating the missing elements in the reference of [44]. The illustrative study demonstrates the applicable of the proposed model. We also give two properties to measure whether the decisions are within the reasonable range. That ensures the effectiveness and reasonableness of our methodology.
Limitations:
- (a)
- The proposed method is based on intuitionistic preference relations. However, in some more complicated conditions, this tool may still be insufficient to describe decision makers’ hesitation degree. Decision making of alternatives with incomplete information is not a focus in this paper. As the decision problem in reality becomes gradually more complicated, it is unavoidable to deal with the complex problems that decision making results may be incomplete.
- (b)
- The method is suitable for the overseas talent evaluation and classification problem, whose number of criteria and alternatives is moderate. Compared with the general pairwise comparison methods, we improve the practicability by introducing BWM. However, faced with large numbers of alternatives, our method may have heavy workloads and high cost.
- (c)
- During the step of calculating criteria and decision makers’ weights, we consider the geometry consistency degree. The consistency of BWM with intuitionistic preference relations has not been considered in this paper. This consistency degree may bring uncertain influence on the ranking results.
To conclude this paper, we make suggestions for further research. Firstly, as the pairwise comparison has been developed to the interval intuitionistic preference relations, we hope our methodology can also be extended to this extent. Meanwhile, problems in regard to missing elements of the decision matrix could be explored. Secondly, we could consider how to measure the consistency degree of the BWM for intuitionistic preference relations. Additionally, we may give each decision maker a second weight, making the decision results more reasonable. Thirdly, the overseas talents’ evaluation and classification system is discussed in the Chinese context in this paper. The proposed methodology may be extended to other fields in further research, such as talent recruitment, investment decision making and supplier selection.
Acknowledgments
This research was supported by the National Natural Science Foundation of China (71272148) and the TianJinscience and technology planning project (15ZLZLZF00370).
Author Contributions
Qing Yang is responsible for the article’s theoretical demonstration, model construction. Xinshang You is responsible for the algorithms analysis and corresponding issues. Both Yang Q. and You X. take charge of English writing and structural adjustment. Zaisheng Zhang is in charge of the investigation, case analysis and foundation supporting. Tong Chen is responsible for the macro-direction.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qu, L. The Chinese Dream of the Overseas Returned Talents–crack the returnees entrepreneurial puzzle. New Economy. 2000, 11, 6–14. [Google Scholar]
- Lai, Y.J. IMOST: Interactive multiple objective system technique. J. Oper. Res. Soc. 1995, 46, 958–976. [Google Scholar] [CrossRef]
- Iwamura, K.; Lin, B. Chance constrained integer programming models for capital budgeting environments. J. Oper. Res. Soc. 1998, 46, 854–860. [Google Scholar] [CrossRef]
- Labib, A.W.; Williams, G.B.; O’Connor, R.F. An intelligent maintenance model (system): An application of the analytic hierarchy process and a fuzzy rule-based controller. J. Oper. Res. Soc. 1998, 49, 745–757. [Google Scholar] [CrossRef]
- Chou, Y.; Sun, C.; Yen, H. Evaluating the criteria for human resource for science and technology (HRST) based on an integrated fuzzy AHP and fuzzy DEMATEL approach. Appl. Soft Comput. 2012, 12, 64–71. [Google Scholar] [CrossRef]
- Ahmad, Z.; Azamathulla, H.M.; Ghani, A.A. ANFIS-based approach for estimation transverse mixing coefficient. IWA Water Sci. Technol. 2011, 63, 1004–1009. [Google Scholar] [CrossRef] [PubMed]
- Golec, A.; Kahya, E. A fuzzy model for competency-based employee evaluation and selection. Comput. Ind. Eng. 2007, 52, 143–161. [Google Scholar] [CrossRef]
- Zhong, L. Fuzzy comprehensive evaluation on performance of high-level talents. J. WUT Inf. Manag. Eng. 2011, 33, 505–508. (In Chinese) [Google Scholar]
- Zhao, W.; Lin, F.; Peng, J.; Bao, X.; Qu, B.; Bai, C. Building of evaluation theory model of innovative scientific & technical talents. Sci. Technol. Manag. Res. 2012, 24, 131–135. (In Chinese) [Google Scholar]
- Chou, Y.; Hsu, Y.; Yen, H. Human resources for science and technology: Analyzing competitiveness using the analytic hierarchy process. Technol. Soc. 2008, 30, 141–153. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X. Research on evaluation mechanism of innovation-driven science and technology talents during the 13th five-year plan in China. Technol. Econ. 2015, 8, 76–80. (In Chinese) [Google Scholar]
- Shen, N.; Meng, F.; Jiang, B.; Li, W. A research on the establishment of S&T talents evaluation system from the perspective of innovation driven strategy. Sci. Res. Manag. 2016, 4, 602–606. (In Chinese) [Google Scholar]
- Liu, X.; Duan, Y.; Zhu, Z. Study on scholars’ evaluation method based on co-author network. J. Intell. 2014, 33, 77–82. (In Chinese) [Google Scholar]
- Liu, Y.; Wu, L. The application of biodata in assessment of the leaders in public sectors. Chin. Public Adm. 2016, 6, 76–80. (In Chinese) [Google Scholar]
- Peng, Z.; He, D.; Peng, J.; Zhao, W. Research on quality oriented evaluation and discovery mechanism of scientific and technical talents. Sci. Technol. Manag. Res. 2015, 9, 53–61. (In Chinese) [Google Scholar]
- Vahdani, B.; Mousavi, S.M.; Tavakkoli-Moghaddam, R. A new design of the elimination and choice translating reality method for multi-criteria group decision making in an intuitionistic fuzzy environment. Appl. Math. Model. 2013, 37, 1781–1799. [Google Scholar] [CrossRef]
- Shen, F.; Xu, J.P.; Xu, Z.S. An automatic ranking approach for multi-criteria group decision making under intuitionistic fuzzy environment. Fuzzy Optim. Decis. Mak. 2015, 14, 311–334. [Google Scholar] [CrossRef]
- Qin, J.D.; Liu, X.W. Multi-attribure group decision making using combined ranking value under interval type-2 fuzzy environment. Inf. Sci. 2015, 297, 293–315. [Google Scholar] [CrossRef]
- Baležentis, Y.; Zeng, S. Group multi-criteria decision making based upon interval-valued fuzzy numbers: An extension of the MULTIMOORA method. Expert Syst. Appl. 2013, 40, 543–550. [Google Scholar]
- Huang, C.L.; Yoon, K.P. Multiple Attributes Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981. [Google Scholar]
- Bozoki, S.; Csato, L.; Temesi, J. An application of incomplete pairwise comparison matrices for ranking top tennis players. Eur. J. Oper. Res. 2016, 248, 211–218. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Karagiannidis, A. Application of the multi-criteria analysis method ELECTRE III for the optimization of decentralized energy systems. Omega 2008, 36, 766–776. [Google Scholar] [CrossRef]
- Lazim, A.; Norsyahida, Z. Integration of fuzzy AHP and interval type-2 fuzzy DEMATEL: An application to human resource management. Expert Syst. Appl. 2015, 42, 4397–4409. [Google Scholar]
- Saaty, T.L. A scaling method for priorities in hierarchical strutures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Orlovsky, S.A. Decision-making with a fuzzy preference relation. Fuzzy Sets Syst. 1978, 1, 155–167. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Uncertainty and rank order in the analytic hierarchy process. Eur. J. Oper. Res. 1987, 32, 107–117. [Google Scholar] [CrossRef]
- Xu, Z.S. Goal programming models for obtaining the priority vector of incomplete fuzzy preference relation. Int. J. Approx. Reason. 2004, 26, 261–270. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Systems 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Xia, M.M.; Chen, J. Preference relations based on intuitionistic multiplicative information. IEEE Trans. Fuzzy Syst. 2013, 22, 113–133. [Google Scholar]
- Szmidt, E.; Kacprzyk, J. Using intuitionistic fuzzy sets in group decision making. Control Cybern. 2002, 31, 1037–1053. [Google Scholar]
- Deschrijver, G.; Kerre, E.E. On the composition of intuitionistic fuzzy relations. Fuzzy Sets Syst. 2003, 136, 333–361. [Google Scholar] [CrossRef]
- Zhang, H.M. A consistency model for group decision making problems with interval multiplicative preference relations. Appl. Soft Comput. 2015, 26, 60–71. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Z.; Xu, J. Interval-valued intuitionistic multiplicative set. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2014, 22, 385–406. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Z.S.; Yu, X.H. Compatibility measures and consensus models for group decision making with intuitionistic multipllicative preference relations. Appl. Soft Comput. 2013, 13, 2075–2086. [Google Scholar] [CrossRef]
- Liao, H.C.; Xu, Z.S.; Xia, M.M. Multiplicative consistency of hesitant fuzzy preference relation and its application in group decision making. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 47–76. [Google Scholar] [CrossRef]
- Xu, Z.S. Priority weight intervals derived from intuitionistic multiplicative preference. IEEE Trans. Fuzzy Syst. 2013, 22, 624–654. [Google Scholar]
- Celik, M.; Kandakoglu, A.; Er, I.D. Structuring fuzzy integrated multi-stages evaluation model on academic personnel recruitment in MET institutions. Expert Syst. Appl. 2009, 36, 6918–6927. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Rezaei, J.; Wang, J.; Tavasszy, L. Linking supplier development to supplier segmentation using Best Worst Method. Expert Syst. Appl. 2015, 42, 9152–9164. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method: Some properties and a linear model. Omega 2016, 64, 126–130. [Google Scholar] [CrossRef]
- Rezaei, J.; Nispeling, T.; Sarkis, J.; Tavasszy, L. A supplier selection life cycle approach integrating traditional and environmental criteria using the best worst method. J. Clean. Prod. 2016, 135, 577–588. [Google Scholar]
- Wang, T.C.; Chen, Y.H. Incomplete fuzzy linguistic preference relations under uncertain environments. Inf. Fusion 2010, 11, 201–207. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, W.G.; Fu, J.H. A new method of obtaining the priority weights from an interval fuzzy preference relation. Inf. Sci. 2012, 185, 32–42. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Z.S.; Yu, X.H. Group decision making based on incomplete intuitionistic multiplicative preference relations. Inf. Sci. 2015, 295, 33–52. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S.; Liao, H.C. Preference relations based on intuitionistic multiplicative information. IEEE Trans. Fuzzy Syst. 2013, 21, 113–133. [Google Scholar]
- Alonso, S.; Herrera-Viedma, E.; Chiclana, F.; Herrera, F. A web based consensus support system for group decision making problems and incomplete preferences. Inf. Sci. 2008, 180, 4477–4495. [Google Scholar] [CrossRef]
- Lee, L.W. Group decision making with incomplete fuzzy preference relations based on the additive consistency and the order consistency. Expert Syst. Appl. 2012, 39, 11666–11676. [Google Scholar] [CrossRef]
- McClelland, D.C. Testing for competence rather than for intelligence. Am. Psychol. 1973, 28, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Spreitzer, G.; Mccall, M.; Mahoney, J. Early identification of international executive potential. J. Appl. Psychol. 1997, 82, 6–29. [Google Scholar] [CrossRef]
- Luo, H.T. Discussion on Talentism. Talent Dev. 2000, 7, 17–19. (In Chinese) [Google Scholar]
- Yan, T.; Chen, H. Study on the application of case analysis method. Sci. Manag. Res. 2004, 22, 116–120. (In Chinese) [Google Scholar]
- Xu, W.; Lan, L.; Zhang, H. Deconstructing the better-than-average effect. Sci. Technol. Process Policy 2014, 31, 125–128. (In Chinese) [Google Scholar]
- Wang, H. Contemporary Chinese Returnees; China Development Press: Beijing, China, 2007; pp. 12–32. [Google Scholar]
- Wright, R.W.; Ricks, D.A. Trends in international business research: Twenty-five years later. J. Int. Bus. Stud. 1994, 25, 687–701. [Google Scholar] [CrossRef]
- Tang, N.; Hong, Y. Preference relations based on intuitionistic multiplicative information. Cult. Intell. New Index Cross Cult. Adapt. 2005, 12, 11–14. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).